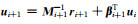矩形大定源是目前瞬变电磁法(TEM)中重要的野外工作装置(Fitterman and Stewart, 1986; Danielsen et al., 2003).但该观测方法资料反演依然是制约其应用的一个难题,因此目前在工程应用中, 主要基于视电阻率(Spies and Eggers, 1986; 白登海等, 2003; 张成范等, 2009)和一维反演的模型进行资料解释(Xue et al., 2004, 2012; 翁爱华等, 2008; Zhou and Xue, 2014; Li et al., 2016).在三维研究方面,大多数研究围绕三维正演模拟进行,SanFilipo和Hohmann(1985)首先采用积分方程法,后来Newman和Hohmann(1988)基于频率域电磁场模拟和时频转换技术,完成三维正演工作, 并且与SanFilipo和Hohmann(1985)的结果对比,验证算法的正确性; Wang和Hohmann(1993)采用时间域有限差分法并考虑模型空间磁导率的变化.在国内,孙怀凤等(2013)应用时间域有限差分法计算了矩形回线瞬变电磁响应,并将发射机关断效应考虑到模拟过程中; 李建慧等(2013)开展了利用G-S变换将矢量有限元得到的频率域三维响应变换为瞬变响应的研究.这些工作为瞬变电磁数据三维反演奠定了基础.
但直接用于大定源瞬变电磁数据反演的技术尚处于研究中,因此矩形大定源瞬变电磁三维反演解释研究同样远远落后于应用需要.虽然其他瞬变电磁反演的技术,从原理上也可以应用到本方法的资料反演中,如Wang等(1994)采用共轭梯度法完成井中瞬变电磁数据的三维时间域反演;Newman和Commer(2005)改进了Wang等(1994)和Zhdanov和Portniaguine(1997)的算法,在大型并行计算平台上实现了长偏移距瞬变电磁(LOTEM)数据的三维反演; 基于Haber等(2007)的工作,Oldenburg等(2013)利用线性方程组直接求解软件(MUMPS)在并行计算平台上解决大尺度多源时间域电磁数据三维反演问题.但直接将上述时间域反演方法应用于大定源TEM方法中存在困难,最主要的困难是三维大定源瞬变正演的实现及与反演技术的精巧结合.然而Mitsuhata等(2001)成功地从LOTEM数据中恢复出频率域数据,并应用频率域三维反演技术进行反演,获得良好效果(Sasaki et al., 2015).最近,Weng等(2017)完成了时间域到频率域的反演变换,并应用到大定源瞬变电磁数据到频率域响应转换.因此, 若能进一步完成大定源频率域电磁数据的三维反演技术,将可从频率域角度完成大定源瞬变电磁数据的三维解释.
为此,本文首先概述非线性共轭梯度反演算法的基本原理,然后采用交错网格有限差分技术计算三维模型频率域正演响应,且与Newman和Hohmann(1988)给出的结果对比,验证算法的正确性.最后分别给出的单个低阻异常体和不同埋深的双低阻异常体模型合成的数据进行的三维频率域反演,验证了算法的可行性和有效性.因此,基于本文算法,利用时频转换技术,可以对野外实测的矩形大定源瞬变电磁数据进行三维频率域反演,为瞬变电磁数据的三维解释奠定了基础.
2 三维频率域正演 2.1 基本原理为了克服地面矩形大定源电磁法在三维数值模拟过程中源描述的困难以及源奇异性对数值稳定性的影响,将其作用用背景场Ep代替.这样,三维正演数值模拟将针对异常二次电场Es进行.取正时谐,忽略位移电流,二次场Es满足(Commer, 2003)
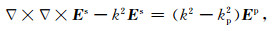
|
(1) |
式中kp2=-iωμp(σp+iωε),σ为电导率;μ和ε分别为背景模型的磁导率和介电常数,在模拟中近似等于真空中磁导率和介电常数.
式(1)采用交错网格有限差分技术离散(Yee, 1966; Alumbaugh et al., 1996),最后形成如下矩阵方程:

|
(2) |
其中K为大型系数矩阵,s为含有背景场和边界条件的右手项.由于剖分时,边界网格足够大,模拟区域中局部异常在最外边界处产生的二次电场的切向分量近似为零.该方程的求解采用最小残差方法(Mackie et al., 1994),利用散度校正提高计算精度和收敛速度.
大定源产生的背景场Ep的计算采用如下的思路:首先采用面积更小的方形虚框覆盖矩形大定源回线(翁爱华等,2010);然后,借助虚界面方法(Weng et al., 2016)计算方形虚源等效的各个圆回线在全空间中任意点的电场,叠加得到大定源回线产生的全空间背景场.
一旦计算出电场Es,有计算网格边界中点总场E=Es+Ep,进而可以通过

|
(3) |
求解网格单元表面中心处磁场(Kelbert et al., 2014),而具体计算点处的电磁场则由这些电场或者磁场通过空间插值得到(翁爱华等, 2012).
2.2 正确性验证三维大定源频率响应模拟精度验证采用如下的验证思路:将数值模拟的频率响应利用余弦变换(Patra and Mallick, 1979)进一步变换为时间响应,并将其与前人瞬变响应的精度比较反推频率响应的模拟精度.精度验证的模型来自Newman和Hohmann(1988),即均匀半空间嵌入一个三维低阻异常体模型,具体的异常体大小和观测装置如图 1所示.数值模拟时,以异常体中心在地面的投影为坐标原点,网格剖分数量为25×19×20个,最小网格大小为20 m×20 m×20 m.首先计算[-200, 200]区间内的测点的频率域响应,然后利用余弦变换获得感应电动势(感应电动势数据被1 m2的单匝接收线圈归一化).选取1 ms和30 ms两个时间道的计算结果与Newman和Hohmann(1988)的结果对比,结果如图 2所示.比较可见, 两种算法的结果具有较好的一致性,进而我们认为本文的频率响应是正确的.

|
图 1 含有低阻异常体的三维导电模型示意图 (Newman and Hohmann, 1988) (a)俯视面; (b)过原点xoz切向剖面. Fig. 1 Schematic diagram showing a model used to evaluate numerical accuracy of 3D modeling (adapted from Newman and Hohmann (1988)) (a) Plan view; (b) Vertical section through loop center in xoz plane. |

|
图 2 过异常体中心的瞬变电磁电压剖面.时间窗口为1 ms和30 ms 实线为Newman和Hohmann(1988)的结果. Fig. 2 Profiles of induced voltage at two time windows 1 ms and 30 ms through the abnormal body Solid lines are from Newman and Hohmann (1988). |
大定源瞬变电磁是近源电磁法,从观测时间上说属于晚期瞬变电磁测量;因此,将其瞬变响应变换到频率域,其频率响应低频成分明显,在一级近似条件下,场不随频率变化,可能不具有交流测深的功能.为了探讨这个问题,分别计算了图 1中异常体上方和外侧两个位置处有无异常体时的频率响应曲线,如图 3所示.从图可见,在准静态近似条件的频率范围内,响应实部确实与频率无关,但虚部与频率相关;并且在没有异常体时,两个测点的频率响应特征基本一样,其频率响应符合均匀半空间变化规律.当存在异常体时,两个测点频率响应的实部和对应的均匀半空间基本一样,但虚部在低频时完全偏离均匀半空间响应,高频基本没有变化.这个特征表明,图 1中模型异常体的存在只反映在相对低频的测深响应上;在高频时,探测深度没有达到异常体位置,故没有响应异常.因此,从频率响应可以得到如下结论,近区瞬变电磁法具有频率测深功能;只是这种响应特征主要通过虚部响应反映出来.传统意义上的近区不具有测深功能是从场强度,在近似条件下得到的,而测深感应被掩盖在比实部小很多的虚部响应中.在这个意义上,如果在频率域测量,则要求非常高的相位测量精度;而瞬变电磁通过测量感应电动势,以仪器的灵敏度换取测量精度.因此,虽然大定源瞬变电磁是近区测量,但从时间域变换到频率域,是可以获得地下深部信息的.

|
图 3 图 1剖面上两个不同位置处大定源装置垂直磁场频率响应曲线.计算点位置分别为(-100,0)(a)和(0,0)(b) 图中:Re-abnormal表示含有异常体三维模型的实部,Im-abnormal表示含有异常体三维模型的虚部,Re-halfspace表示均匀半空间模型的实部,Im-halfspace表示均匀半空间模型的虚部. Fig. 3 FD responses at two sites along the profile shown in Fig.1. Two sites are at (-100, 0) (a) and (0, 0) (b), respectively Re and Im represent real and imaginary part of Hz from a half space or a half space with a conductive body, respectively. |
地面矩形大定源三维频率反演采用非线性共轭梯度方法, 该方法通过计算非线性目标函数

|
(4) |
的梯度解决正则化反演问题(Avdeev, 2005; Egbert and Kelbert, 2012; Siripunvaraporn, 2012).式中m为模型参数,mref为参考模型矢量,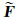
|
|
表 1 非线性共轭梯度反演基本流程 Table 1 Inversion flow of nonlinear conjugate gradient method |
根据Egbert和Kelbert (2012),目标函数的梯度g可以表示为
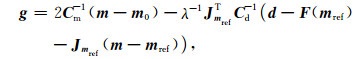
|
(5) |
式中
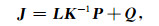
|
(6) |
及
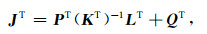
|
(7) |
这里
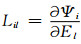

这样,从将梯度计算中J或者JT与向量乘积转换为系数矩阵K或者KT与相关矢量的乘积,即所谓的正演或者伴随正演(Egbert and Kelbert, 2012),从而只需要2次正演的计算量,并且不需要显式计算并存储灵敏度矩阵J.这是非线性共轭梯度方法成功应用于三维电磁数据的反演的最大特点.
4 反演结果 4.1 模型1图 4所示为100 Ωm的均匀半空间嵌入一个1 Ωm的低阻异常体模型.异常体大小为80 m×280 m×60 m,顶部埋深60 m.发射回线为300 m×600 m,位于异常体左侧,发射电流1 A.异常体中心在地面上的投影点为坐标原点.回线内布设14条测线,每条测点上14个测点,点距和线距均为40 m.在0.125~8192 Hz频率区间按照2的幂次方布置17个频点.模型剖分个数为18×19×20,最小网格的大小为40 m×40 m×10 m,x、y正负方向均有5个扩边网格,z正方向有5个扩边网格,扩边系数分别为2、2和1.5.

|
图 4 用于测试非线性共轭梯度算法的单个异常体模型 虚线矩形为数据采集范围. (a)俯视图,灰色为异常体,外面实线为大定源回线; (b)过x=0 m的纵断面. Fig. 4 Theoretical model to test NLCG inversion method. A conductive body of 1 Ωm is embedded in a 100 Ωm homogeneous half space (a) Top view; (b) Cross section through x=0 m. |
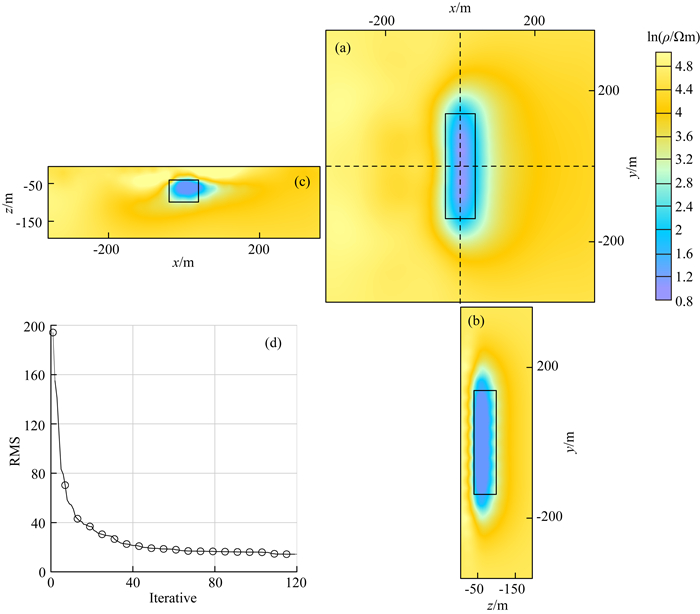
反演在PC上进行串行运算,Intel(R) Core(TM) i5-2320处理器,主频3.0 GHz,4 G内存.数据中加入5%的高斯随机噪声,均匀半空间模型作为反演的初始模型,迭代120次,用时4个小时.图 5给出了具体的反演结果.图 5a为深度75 m处的平面切片,该平面横切低阻异常体,具有较高的横向分辨率.过异常的x和y方向的断面图分别如图 5b和5c.从图可以看出,异常体的位置与理论模型一致,证明了矩形大定源非线性共轭梯度三维频率域反演的可行性和有效性.图 5d的迭代过程中均方根误差(RMS)的变化情况显示,随着迭代的进行,数据拟合误差逐渐减小,迭代稳定收敛,但在一定迭代次数后,误差减小变慢,收敛变慢.传统的大定源方法一般只处理中间一定区域的数据.在本例中,接收点位于矩形回线内外的任意位置,体现了本文的算法可以处理任意位置数据的优点.
|
图 5 反演三维电阻率切片和拟合差变化情况 (a) z=-75 m处电阻率平面分布图.图中矩形框表示异常体的平面位置.虚线分别为(b) x=0 m沿y方向电阻率断面图和(c) y=0 m沿x方向电阻率断面图; (d)为拟合差迭代变化曲线. Fig. 5 3D resistivity distribution at the end of inversion and RMS Rectangles indicate the locations of abnormal bodies. Dashed lines show location of vertical cross-section along x and y directions. (a) Plane view at z=-75 m. (b) Cross-section through x=0 m. (c) Cross-section through y=0 m. (d) RMS curve. |
图 6所示为100 Ωm的均匀半空间嵌入两个埋深不同、电阻率为5 Ωm的低阻异常体模型(Sasaki et al., 2015).异常体大小为400 m×800 m×500 m,埋深分别为200 m和400 m,工作布置与Sasaki等(2015)的一致,点距和线距都为400 m,构成9×5的测网.矩形大定源发射回线的边长为1000 m×1000 m,供电电流1 A.反演数据中加入5%的高斯随机噪声,从电阻率为100 Ωm的均匀半空间开始,经过110次迭代,得到的三维频率域反演的结果如图 7.从图可以看出,地面矩形大定源非线性共轭梯度三维频率域反演较准确地揭示出异常体的电性特征和空间位置.图 8的RMS曲线显示NLCG反演算法在前期收敛速度较快,但后期收敛速度变慢.显然,要想到达更高的拟合精度,需要较多的迭代次数,这也是非线性共轭梯度算法的弱点.值得指出的是,在本例中,对接收点位置没有要求,观测可以在矩形回线内外的任意位置上进行.在这点上,本文提出的正演和反演算法,可以实现矩形大定源全区观测数据的反演.

|
图 6 包含2个异常体的三维模型 (a)过异常体的沿x方向断面;(b)平面俯视图.图中圆圈表示接收机位置.内部的矩形实线表示发射源位置. Fig. 6 A 3D model with two abnormal bodies (a) Cross-section along x direction through the abnormal bodies; (b) Plane view. Open circles represent TEM receiver. Solid rectangle stands for transmitter. |

|
图 7 理论模型的三维反演结果 图中矩形框为导电异常体的位置. (a)为深度z=425 m的异常平面分布图,图中虚线为断面所在的位置.其中(b)为y=200 m的横剖面电阻率分布,(c)为沿y=-200的断面图. Fig. 7 3D model retrieved by the NLCG inversion (a) Inversed resistivity in the plan view at z=425 m and cross sections along y=200 m (b) and y=-200 m (c). Rectangles indicate positions of abnormal bodies. |

|
图 8 模型三维反演拟合差随迭代次数变化曲线 Fig. 8 RMS variations during the NLCG inversion |
本文通过数值模拟,研究了矩形大定源频率数据的非线性共轭梯度反演技术,并用理论模型验证了该算法的可行性和反演效果.通过数值分析,可以获得如下的结论:
(1) 采用交错网格有限差分针对二次电场满足的Helmholtz方程实现矩形大定源频率响应的三维数值模拟.模拟过程中,利用虚界面法结合大定源虚框等效原理获得背景场,克服了大定源数值模拟过程中源描述的困难以及源奇异性;与前人结果的一致性验证了本文正演算法准确性;
(2) 采用非线性共轭梯度反演方法,能由大定源频率电磁响应,获得地下电阻率的三维分布,从数值上验证了本文反演算法的可行性;
(3) 在数值计算过程中,参与反演计算的测点分布范围突破传统的回线中间1/3范围的要求,而是分布在整个回线内,甚至回线外.因此,本文提出的反演算法,具有更大的灵活性,并且可以提高大定源瞬变电磁的野外工作效率.
Alumbaugh D L, Newman G A, Prevost L, et al.
1996. Three-dimensional wideband electromagnetic modeling on massively parallel computers. Radio Science, 31(1): 1-23.
DOI:10.1029/95RS02815 |
|
Avdeev D B.
2005. Three-dimensional electromagnetic modelling and inversion from theory to application. Surveys in Geophysics, 26(6): 767-799.
DOI:10.1007/s10712-005-1836-x |
|
Bai D H, Meju M A, Lu J, et al.
2003. Numerical calculation of all-time apparent resistivity for the central loop transient electromagnetic method. Chinese Journal of Geophysics (in Chinese), 46(5): 697-704.
|
|
Commer M. 2003. Three-dimensional inversion of transient electromagnetic data:A comparative study[Ph. D. thesis]. Cologne:University of Cologne.
|
|
Danielsen J E, Auken E, Jørgensen F, et al.
2003. The application of the transient electromagnetic method in hydrogeophysical surveys. Journal of Applied Geophysics, 53(4): 181-198.
DOI:10.1016/j.jappgeo.2003.08.004 |
|
Egbert G D, Kelbert A.
2012. Computational recipes for electromagnetic inverse problems. Geophysical Journal International, 189(1): 251-267.
DOI:10.1111/gji.2012.189.issue-1 |
|
Fitterman D V, Stewart M T.
1986. Transient electromagnetic sounding for groundwater. Geophysics, 51(4): 995-1005.
DOI:10.1190/1.1442158 |
|
Haber E, Oldenberg D W, Shekhtman R.
2007. Inversion of time domain three-dimensional electromagnetic data. Geophysical Journal International, 171(2): 550-564.
DOI:10.1111/gji.2007.171.issue-2 |
|
Kelbert A, Meqbel N, Egbert G D, et al.
2014. ModEM:A modular system for inversion of electromagnetic geophysical data. Computers & Geosciences, 66: 40-53.
|
|
Li H, Xue G Q, Zhao P, et al.
2016. Inversion of arbitrary segmented loop source TEM data over a layered earth. Journal of Applied Geophysics, 128: 87-95.
DOI:10.1016/j.jappgeo.2016.03.017 |
|
Li J H, Zhu Z Q, Lu G Y, et al.
2013. Study on three-dimensional forward of transient electromagnetic method excited by loop source. Progress in Geophysics (in Chinese), 28(2): 754-765.
DOI:10.6038/pg20130224 |
|
Liu Y H, Yin C C.
2013. 3D inversion for frequency-domain HEM data. Chinese Journal of Geophysics (in Chinese), 56(12): 4278-4287.
DOI:10.6038/cjg20131230 |
|
Mackie R L, Smith J T, Madden T R.
1994. Three-dimensional electromagnetic modeling using finite difference equations:The magnetotelluric example. Radio Science, 29(4): 923-935.
DOI:10.1029/94RS00326 |
|
Mitsuhata Y, Uchida T, Murakami Y, et al.
2001. The Fourier transform of controlled-source time-domain electromagnetic data by smooth spectrum inversion. Geophysical Journal International, 144(1): 123-135.
DOI:10.1046/j.1365-246x.2001.00324.x |
|
Newman G A, Hohmann G W.
1988. Transient electromagnetic responses of high-contrast prisms in a layered earth. Geophysics, 53(5): 691-706.
DOI:10.1190/1.1442503 |
|
Newman G A, Commer M.
2005. New advances in three dimensional transient electromagnetic inversion. Geophysical Journal International, 160(1): 5-32.
|
|
Oldenburg D W, Haber E, Shekhtman R.
2013. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics, 78(1): E47-E57.
DOI:10.1190/geo2012-0131.1 |
|
Patra H P, Mallick K. 1979. Geosounding Principles. Vol.2. Amsterdam:Elsevier Science Ltd.
|
|
SanFilipo W A, Hohmann G W.
1985. Integral equation solution for the transient electromagnetic response of a three-dimensional body in a conductive half-sapce. Geophysics, 50(5): 798-809.
DOI:10.1190/1.1441954 |
|
Sasaki Y, Yi M J, Choi J, et al.
2015. Frequency and time domain three-dimensional inversion of electromagnetic data for a grounded-wire source. Journal of Applied Geophysics, 112: 106-114.
DOI:10.1016/j.jappgeo.2014.09.016 |
|
Siripunvaraporn W.
2012. Three-dimensional magnetotelluric inversion:An introductory guide for developers and users. Surveys in Geophysics, 33(1): 5-27.
DOI:10.1007/s10712-011-9122-6 |
|
Spies B R, Eggers D E.
1986. The use and misuse of apparent resistivity in electromagnetic methods. Geophysics, 51(7): 1462-1471.
DOI:10.1190/1.1442194 |
|
Sun H F, Li X, Li S C, et al.
2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time. Chinese Journal of Geophysics (in Chinese), 56(3): 1049-1064.
DOI:10.6038/cjg20130333 |
|
Wang T, Hohmann G W.
1993. A finite difference time domain solution for three dimensional electromagnetic modeling. Geophysics, 58(6): 797-809.
DOI:10.1190/1.1443465 |
|
Wang T, Oristaglio M, Tripp A, et al.
1994. Inversion of diffusive transient electromagnetic data by a conjugate-gradient method. Radio Science, 29(4): 1143-1156.
DOI:10.1029/94RS00617 |
|
Weng A H, Gao L L, Liu Y H.
2008. Inversion of TEM data from rectangular loop on a layered earth model. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 30(4): 314-316.
|
|
Weng A H, Liu Y H, Chen Y L, et al.
2010. Computation of transient electromagnetic field from a rectangular loop over stratified earth. Chinese Journal of Geophysics (in Chinese), 53(3): 646-650.
DOI:10.3969/j.issn.0001-5733.2010.03.019 |
|
Weng A H, Liu Y H, Jia D Y, et al.
2012. Three-dimensional controlled source electromagnetic inversion using non-linear conjugate gradients. Chinese Journal of Geophysics (in Chinese), 55(10): 3506-3515.
DOI:10.6038/j.issn.0001-5733.2012.10.034 |
|
Weng A H, Liu Y H, Yin C C, et al.
2016. Singularity-free Green's function for EM sources embedded in a stratified medium. Applied Geophysics, 13(1): 25-36.
DOI:10.1007/s11770-016-0549-x |
|
Weng A H, Li D J, Yang Y, et al.
2017. Transforming a time-domain electromagnetic signal to a frequency-domain electromagnetic response using regularization inversion. Geophysics, 82(5): E287-E295.
DOI:10.1190/geo2016-0505.1 |
|
Xue G Q, Li X, Song J P, et al.
2004. Theoretical analysis and numerical calculation of loop-source transient electromagnetic imaging. Chinese Journal of Geophysics, 47(2): 379-386.
DOI:10.1002/cjg2.v47.2 |
|
Xue G Q, Bai C Y, Yan S, et al.
2012. Deep sounding TEM investigation method based on a modified fixed central-loop system. Journal of Applied Geophysics, 76: 23-32.
DOI:10.1016/j.jappgeo.2011.10.007 |
|
Yee K S.
1966. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media. IEEE Transactions on Antennas and Propagation, 14(3): 302-307.
DOI:10.1109/TAP.1966.1138693 |
|
Zhang C F, Weng A H, Sun S D, et al.
2009. Computation of whole-time apparent resistivity of large rectangular loop. Journal of Jilin University (Earth Science Edition) (in Chinese), 39(4): 755-758.
|
|
Zhdanov M S, Portniaguine O.
1997. TIme-domain electromagnetic migration in the solution of inverse problems. Geophysical Journal International, 131(2): 293-309.
DOI:10.1111/gji.1997.131.issue-2 |
|
Zhou N N, Xue G Q.
2014. The ratio apparent resistivity definition of rectangular-loop TEM. Journal of Applied Geophysics, 103: 152-160.
DOI:10.1016/j.jappgeo.2014.01.015 |
|
白登海, MejuM A, 卢健, 等.
2003. 时间域瞬变电磁法中心方式全程视电阻率的数值计算. 地球物理学报, 46(5): 697–704.
|
|
李建慧, 朱自强, 鲁光银, 等.
2013. 回线源瞬变电磁法的三维正演研究. 地球物理学进展, 28(2): 754–765.
DOI:10.6038/pg20130224 |
|
刘云鹤, 殷长春.
2013. 三维频率域航空电磁反演研究. 地球物理学报, 56(12): 4278–4287.
DOI:10.6038/cjg20131230 |
|
孙怀凤, 李貅, 李术才, 等.
2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演. 地球物理学报, 56(3): 1049–1064.
DOI:10.6038/cjg20130333 |
|
翁爱华, 高玲玲, 刘云鹤.
2008. 矩形大定源瞬变测深数据模型约束反演. 物探化探计算技术, 30(4): 314–316.
|
|
翁爱华, 刘云, 陈玉玲, 等.
2010. 矩形大定源层状模型瞬变电磁响应计算. 地球物理学报, 53(3): 646–650.
DOI:10.3969/j.issn.0001-5733.2010.03.019 |
|
翁爱华, 刘云鹤, 贾定宇, 等.
2012. 地面可控源频率测深三维非线性共轭梯度反演. 地球物理学报, 55(10): 3506–3515.
DOI:10.6038/j.issn.0001-5733.2012.10.034 |
|
薛国强, 李貅, 宋建平, 等.
2004. 回线源瞬变电磁成像的理论分析及数值计算. 地球物理学报(2): 338–343.
|
|
张成范, 翁爱华, 孙世栋, 等.
2009. 计算矩形大定源回线瞬变电磁测深全区视电阻率. 吉林大学学报(地球科学版), 39(4): 755–758.
|
|
 2017, Vol. 60
2017, Vol. 60