在野外数据采集过程中,为了得到相对完整而规则的地震数据,在数据采集之前必须进行野外观测系统的设计,但由于采集设备、野外地形条件以及经济成本限制等原因,地震炮点和检波点通常会偏离原始设计位置,甚至有些炮点和检波点无法采集到有效的地震数据,从而导致地震数据沿空间方向常进行不规则欠采样,出现空间假频,影响到后续其它处理方法的效果,降低了地震勘探的分辨率(Trad, 2009;Herrmann, 2010;Ely et al., 2015;张华和陈小宏,2013).为了解决这种问题,最直接也是最有效的方法就是在野外重新进行数据采集,但从经济角度出发,显然不可能重新进行数据采集来完美的解决该问题.因此,必须在室内采取相应的不规则地震数据重建方法,使得缺失道数据得到有效地恢复.然而在目前已有的重建方法中,包括预测滤波方法(Spitz, 1991;Naghizadeh and Sacchi, 2007),降秩方法(Oropeza and Sacchi, 2011;Ma, 2013),数学变换方法(Zhang et al., 2013;白兰淑等,2014;唐欢欢和毛伟建, 2014;Yu et al., 2016)等,很少能够重建空间非均匀采样下的地震缺失道.但由于野外复杂地形条件的限制或者海上电缆的水平偏移,很多情况下野外地震数据常进行空间非均匀采样,如不加处理则会引起覆盖次数的变化(地下不均匀照明),在叠加成像时会形成扭曲的成像振幅(采集脚印),加重了空间假频现象的出现,影响后续成像处理.
为了解决空间非均匀采样下地震道不规则重建问题,地球物理领域常规处理方法为共面元叠加,从而将非均匀采样数据归位到均匀采样数据中来,满足后续其他处理方法的要求.然而共面元叠加处理方法忽略了每个面元内各道共中心点的真实位置,改变了部分地震道的振幅和相位,从而导致部分地震道位置出现严重偏差,降低了地震勘探资料的分辨率.另外一种方法就是基于波动方程的重建方法,然而该方法需要地下结构的先验信息,计算量非常巨大,对采样率要求也较高,从而也不能较好的解决该问题(Ronen, 1987;Fomel, 2003).尽管如此,许多学者采用基于数学变换的重建方法对该问题进行处理,Duijndam等(1999)提出基于傅里叶变换的二维非均匀数据重建方法,Hindriks和Duijndam(2000)将其扩展到三维,实现了三维非均匀采样重建技术.但是,Duijndam等人的傅里叶重建方法有其局限性,重建结果受最低速度和空间带宽的影响很大,随着采样间隔的逐渐增大,重建结果会逐渐变差.Xu等(2005)采用重新正交化的过程,提出了基于抗泄露傅里叶变换的重建方法,但该方法对具有严重假频的地震数据则重建效果不好.Zwartjes和Sacchi(2007)也提出了反假频的非均匀地震数据重建方法,该方法采用无假频的低频信息来重建有假频的高频信息,达到压制假频和恢复缺失道的目的,但当低频也具有假频时,则该方法则会失效.Jin(2010)提出基于阻尼最小范数傅里叶反演下的五维地震数据重建,该方法引入非均匀傅里叶变换方法,能够重建空间非均匀采样下的不规则缺失地震数据,但该方法抗假频能力不强.况且以上方法都是采用傅里叶变换作为稀疏基,尽管计算速度较快,但只适合处理近似线性同相轴或者平稳变化的地震信号,不能解决非线性同相轴或者非平稳地震数据的重建问题,尽管可以对其采用分窗口进行重建,但是窗口重叠部分重建效果仍然不佳.
曲波变换能够表征信号的局部细节特征,可以有效地重建非线性同相轴或者非平稳变化的地震数据,众多的研究结果也证明,基于曲波变换的数据重建方法效果显著(Naghizadeh and Sacchi, 2010;刘国昌等,2011;Zhang et al., 2015;王本锋等,2015).尽管如此,以往基于曲波变换的重建方法前提条件仍然是空间均匀采样,而对于空间非均匀采样信号,由于缺乏空间连续性,曲波变换则不能有效地探测出地震波前特征,从而导致以往曲波变换不能有效地重建空间非均匀采样下的地震缺失道,从而限制了该方法的进一步应用.为此,本文针对空间非均匀采样下地震数据重建问题,首先在常规二维曲波变换过程中引入非均匀傅里叶变换(Kunis, 2006),建立均匀曲波系数与空间非均匀采样下地震缺失道数据之间的规则化反演算子,然后使用线性Bregman方法进行反演计算得到均匀曲波系数,最后再进行二维均匀快速离散曲波反变换,从而形成基于二维非均匀曲波变换的高精度地震数据重建方法,以解决空间非均匀采样下的不规则缺失道重建问题.
2 理论基础地震数据的重建问题就是从不完整的数据中恢复出完整的地震数据,假设如下线性正演模型:

|
(1) |
这里y∈Rm代表采集的不完整地震数据;d∈Rn,且n≥m,表示待重建的完整数据;M∈Rn×m表示随机采样矩阵.假设数据x是d在曲波变换域C中的稀疏表示,则方程(1)可以写成

|
(2) |
这里上标H代表共轭转置矩阵.
方程(2)的稀疏解可以求解以下L1范数最优化问题得到

|
(3) |
在这个表达式中,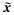
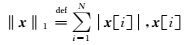
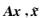
在方程(2)中,以往重建方法采用的算子CH为常规曲波反变换算子,事实上,该算子也可以为非均匀曲波反变换算子.为此,本文采用CUH和CNH来分别表示曲波反变换算子和非均匀曲波反变换算子.显然,如果采用曲波算子CUH进行非均匀采样数据重建,则会扭曲地震波场的真实位置.所以本文的主要工作就是构建非均匀曲波反变换算子CNH,并通过反演计算来重建非均匀采样下缺失道数据,并将其归位为均匀采样网格,从而实现基于非均匀曲波变换的高精度地震数据重建方法.
3 空间非均匀曲波变换Candès等(2006)提出第二代曲波(Curvelet)变换,免去了第一代曲波变换平滑分块、子带分解、正则化和脊波分析等一系列步骤,解决了大量数据冗余问题,从而使得曲波变换更容易理解,运算效率更好、实现更简单.第二代连续曲波变换的定义为

|
(4) |
式中y(x, t)表示地震数据,φj, l, k表示曲波函数,c(j, l, k)表示曲波系数,其中j表示尺度,l表示方向,k表示j尺度l方向上的矩阵系数.
实际上,Candès等(2006)提出的二维快速离散曲波变换有两种实现方式,一种是基于USFFT(unequally spaced FFT),另外一种基于wrapping算法(Wrapping-based transform),本文主要采用后一种算法.该离散算法主要进行了四个步骤,(1)对地震数据应用二维傅里叶变换,得到频率波数域系数;(2)在频率波数域形成角度楔形;(3)将每一个楔形围绕到原点进行重新装配;(4)对每一个装配好的楔形应用二维傅里叶反变换,得到离散曲波系数.在本文中,定义曲波正变换算子

|
(5) |
在这个方程中,F表示二维傅里叶变换,它实现了离散曲波变换第1步.T表示曲波拼接算子,即将频率波数域变换到曲波系数的过程,它实现了离散曲波变换第(2)—(4)步.
由于曲波正反变换算子满足CUCUH=I,因此可以定义曲波反变换算子:

|
(6) |
其中FH代表二维傅里叶反变换,将频率波数域转换到时间空间域中.TH表示曲波拼接反算子,即将曲波系数变换到频率波数域的过程.
在方程(5)中,由于二维傅里叶变换参与了快速离散曲波变换之中,因此常规的二维曲波变换不能处理非均匀采样数据,因为傅里叶变换是在均匀采样数据下进行处理的,如果将其处理非均匀采样数据,则会严重歪曲原始地震数据的真实位置,导致地震波场错乱或者严重破坏,得不到正确的频率波数域系数.然而,由于二维傅里叶反变换算子是克罗内克乘积,采用符号⊗表示.可以用FxH表示沿着空间轴的一维傅里叶反变换算子,FtH表示沿着时间轴的一维傅里叶反变换算子,因此方程(6)中的二维傅里叶反变换可定义为

|
(7) |
在这个分解变换中,时间方向是均匀理想采样,不需要重建.因此,可以用空间非均匀快速傅里叶变换NxH代替一维傅里叶反变换算子FxH.非均匀快速傅里叶变换实现的主要策略如下,首先将非均匀地震数据与某高斯短滤波器进行褶积,并对其结果进行均匀网格下密集采样,然后对密集采样后的数据进行快速傅里叶变换到频谱域,最后在频谱域进行反褶积校正,得到非均匀地震数据的频谱.因此新的非均匀曲波反变换算子可以定义为

|
(8) |
该算子可以将离散曲波系数与非均匀采样下不规则地震道建立相应的联系.再将该算子代入方程(3),此时A=MCNH,通过求解方程(3),从而可以得出均匀曲波系数.而对于该方程的求解,目前已经发展了诸多算法来求解该约束问题,本文选用线性Bregman方法来求解此L1范数最小化问题.
4 线性Bregman方法目前,由于线性Bregman方法在求解L1范数问题方面非常简单而高效,因此引起较大的关注,该方法主要将方程(3)最优化问题转为求解下述BP规则化问题(Yin, 2010; Lorenz et al., 2013, 2014):

|
(9) |
其中,λ是一个阈值权衡因子,在平衡L1范数和L2范数起到重要作用,可以在第一次迭代过程计算出,也可以取曲波系数总数的百分比所对应的值,σ表示数据中的噪声参数.算法1给出了线性Bregman方法求解非均匀曲波变换过程的伪代码.
算法1.求解非均匀曲波变换的线性Bregman方法
1:输入观测数据y,阈值λ
2: x0←, z0←0
3: for k=0, 1, …, K
4: zk+1=zk-tkAkHΠσ(Akxk-yk)
5: xk+1=Sλ(zk+1)
6: end for
投影函数Πσ(Akxk-yk)为

|
(10) |
该函数用来处理数据中的噪声,动态步长tk被定义为

|
(11) |
算法1中的软阈值函数为

|
(12) |
可以看出线性Bregman方法只有两行程序,且不需要太多的调节参数,因此实现非常简单.
在求解方程(3)得到均匀曲波系数后,重建后的地震波场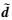

|
(13) |
在方程(13)中,CUH是常规二维曲波反变换算子.
5 数值模拟与应用实例 5.1 数值模拟为了衡量不同数据重建方法的效果,定义信噪比公式SNR=20log10‖d0‖2/‖d-d0‖2来进行对比,单位为dB,其中d0表示原始模型数据,d表示重建结果,信噪比越高,代表重建结果与模型数据越接近,处理效果越理想.
图 1a为采用50 Hz雷克子波合成的256道二维理论地震记录,该记录总共有4层地震反射波,每一层反射波能量有所差异,采样间隔为1 ms,道距为5 m,每道1024个采样点.为了显示同相轴局部特征,将图 1a局部放大,放大结果如图 2a所示.首先为了得到非均匀采样地震数据,对理论数据进行均匀傅里叶变换,然后再进行非均匀傅里叶反变换,得到新的空间非均匀采样下的256道地震数据,如图 1b所示,对应的信噪比为11.49dB,此时图 1b名义上的道距还是5 m,但每道地震数据道距极不均匀,其中最小道距接近0 m,最大道距接近10 m,其局部显示如图 2b所示.显然,将非均匀采样下地震数据在均匀采样网格上进行显示,则连续的地震波场将会被破坏,如果不进行处理,直接采用常规方法进行重建则会造成较大的误差,为此采用本文二维非均匀曲波变换进行重建.该处重建的含义为将非均匀采样数据归位为均匀采样地震数据,前后道数一样.重建后的道距仍然为5 m,重建结果如图 1c所示,重建后信噪比为45.17 dB,局部显示如图 2c所示,显然可以看出地震波场连续性显著提高,图 1d为其与理论地震数据的误差剖面图,图 2d为其局部放大,可以看出本文方法重建后的地震记录与原始记录非常接近,误差几乎忽略不计,重建后信噪比非常高,与原始地震记录相比较几乎没有视觉上的差异,表明基于非均匀曲波变换的重建方法精度高,重建前后保真度较好.

|
图 1 理论地震数据重建过程 (a)原始地震数据; (b)非均匀采样数据; (c)本文方法重建结果; (d)重建误差. Fig. 1 Reconstruction process of synthetic seismic data (a)Original seismic data; (b) Non-uniformly sampled data; (c) Reconstruction result by the proposed method; (d) Reconstruction error. |

|
图 2 图 1局部放大显示图 (a) 图 1a局部放大; (b) 图 1b局部放大; (c) 图 1c局部放大; (d) 图 1d局部放大. Fig. 2 Local zoomed-in images of Fig. 1 (a) Local zoomed-in image of Fig. 1a; (b) Local zoomed-in image of Fig. 1b; (c) Local zoomed-in image of Fig. 1c; (d) Local zoomed-in image of Fig. 1d. |
为了检验本文方法在非均匀采样下不规则缺失道重建效果,对非均匀采样数据(图 1b)进行50%随机欠采样,如图 3a所示,此时信噪比为2.74 dB.名义上的道距为10 m,但沿检波器方向的空间采样间隔极为不均匀,其道距范围在0~25 m之间,同相轴的连续性被破坏,需要对其进行重建.首先采用Duijndam等(1999)提出的基于非均匀傅里叶变换的方法进行重建,最低速度设置为1050 m·s-1,重建后的道距为5 m,重建结果如图 4a所示,重建后的信噪比为10.34 dB,图 4c为其局部放大,图 4e为重建结果与原始理论数据的误差剖面,可以看出尽管该方法能够在一定程度上重建出50%缺失道信息,但是重建效果相对较差,信噪比低.然后采用本文方法进行重建,重建结果如图 4b所示, 重建后的信噪比为17.92 dB,图 4d为其局部放大,图 4f为其与理论地震数据的误差剖面,可以看出重建后的地震波场连续性显著提高,误差较小.从局部放大图也可以看出本文方法效果更优,重建后同相轴更连续,能量损失较少.从中也可以说明傅里叶变换是全局变换,不能反映出地震波同相轴的局部特征,并且受频带范围和最小速度的影响,重建误差相对较大.而本文非均匀曲波变换方法则不受这些条件的影响,更能够有效的捕捉地震波前特征,从而重建效果更佳.

|
图 3 非均匀采样下欠采样地震数据 (a) 50%随机欠采样; (b) 50%规则欠采样. Fig. 3 Under-sampling seismic data for non-uniformly sampled grid (a) 50% random under-sampling; (b) 50% regular under-sampling. |

|
图 4 非均匀采样下随机缺失数据重建过程 (a)非均匀傅里叶变换重建结果; (b)本文方法重建结果; (c) 图 4a局部放大; (d) 图 4b局部放大; (e) 图 4a重建误差; (f) 图 4b重建误差. Fig. 4 Reconstruction process of non-uniformly sampled data with random missing traces (a) Reconstruction result by the non-uniform Fourier transform; (b) Reconstruction result bythe proposed method; (c) Local zoomed-in image of Fig. 4a; (d) Local zoomed-in image of Fig. 4b; (e) Reconstruction error of Fig. 4a; (f) Reconstruction error of Fig. 4b. |
为了进一步检验本文方法的反假频能力,对原始非均匀采样地震记录(图 1b)进行50%规则欠采样,规则欠采样结果如图 3b所示,对应的信噪比为2.73 dB,由于规则欠采样会在频率域产生与原始信号相同的假频能量,从而导致许多常规重建方法失效,所以需要采用非均匀抗假频的重建方法进行处理.同样首先采用基于非均匀傅里叶变换的方法进行重建,重建后道距为5 m,重建结果如图 5a所示,重建后信噪比为9.86 dB,图 5c为其局部放大,图 5e为其误差剖面图,可以看出缺失的地震道得到了一定程度上的恢复,但是重建后的误差相对较大,同相轴相对不连续,说明该方法抗假频能力差.然后采用本文方法进行抗假频重建,重建结果如图 5b所示, 重建后的信噪比为16.45 dB,图 5d为其局部放大,图 5f为其与理论地震数据的误差剖面,可以看出重建后的地震波场连续性显著提高,误差较小,从而也表明本文方法具有较强的反假频能力,能够进行非均匀采样下的不规则和规则缺失地震数据重建.

|
图 5 非均匀采样下规则缺失数据重建过程 (a)非均匀傅里叶变换重建结果; (b)本文方法重建结果; (c) 图 5a局部放大; (d) 图 5b局部放大; (e) 图 5a重建误差; (f) 图 5b重建误差. Fig. 5 Reconstruction process of non-uniformly sampled data with regular missing traces (a) Reconstruction result by the non-uniform Fourier transform; (b) Reconstruction result bythe proposed method; (c) Local zoomed-in image of Fig. 5a; (d) Local zoomed-in image of Fig. 5b; (e) Reconstruction error of Fig. 5a; (f) Reconstruction error of Fig. 5b. |
由于野外地震数据都含有噪声,需要进一步检验本文方法的抗噪声重建能力.为此,对图 1a加入高斯随机噪声,如图 6a所示,然后采用非均匀傅里叶变换得到新的256道非均匀含噪地震数据,并且对其随机采样得到128道非均匀采样含噪地震数据,如图 6b所示,再采用本文方法进行重建,其重建的结果如图 6c所示,图 6d为重建结果与原始含噪地震数据误差图,可以看出尽管非均匀地震数据含有不同程度的噪声,但从重建的结果来看,缺失的含噪地震波同相轴得到了恢复,整个波场较为连续,光滑,且重建前后的有效波能量损失较少,表明信号恢复效果较好,具有良好的抗噪能力,完全能够应用于实际资料的重建处理.

|
图 6 非均匀采样下含噪数据重建结果 (a)原始含噪数据; (b) 50%非均匀含噪数据; (c)本文方法重建结果; (d)重建误差. Fig. 6 Reconstruction results of the non-uniformly sampled noisy data (a) Original noisy seismic data; (b) 50% non-uniformly noisy data; (c) Reconstruction result by the proposed method; (d) Reconstruction error. |
图 7a为随机缺失30道的野外地震数据,该地震数据道距25 m,采样率4 ms,180道接收.图 7c为其二维频谱分析,可以看出在40 Hz左右出现假频,说明该地震记录道距过大,数据空间采样较为稀疏,严重影响到后续资料的处理.为此,利用本文非均匀曲波变换方法进行重建,不需要最低速度的假设条件,而且为了消除假频干扰,设置重建后输出道距约为15 m,共300道地震记录,重建结果如图 7b所示,图 7d为其二维频谱分析图,从中可以看出本文方法重建效果较好,重建后的地震波同相轴非常连续,并且由于重建后的道距变小,采样道数增多,因此消除了假频干扰,为后续的其它处理方法提供了较好的地震资料.为了详细显示其重建效果,图 8为重建前后局部放大图,局部放大位置为图 7a中的第71~109道,时间为0.78~1.46 s,由于重建前道距为25 m,重建后道距15 m,因此图 8a中的71~109道近似对应图 8b中的116~181道,从局部放大图中也可以看出,本文方法重建后地震波同相轴更连续光滑、采样率高,缺失的地震道也得到了有效的恢复.

|
图 7 野外缺失数据重建过程 (a)野外缺失地震数据(25 m道距); (b)本文方法重建结果(15 m道距); (c) 图 7a二维频谱; (d) 图 7b二维频谱. Fig. 7 Reconstruction process of field seismic data with missing traces (a) Field missing seismic data (sampling: 25 m); (b) Reconstruction result by the proposed method (sampling:15 m); (c) Amplitude spectrum of Fig. 7a; (d) Amplitude spectrum of Fig. 7b. |

|
图 8 图 7a~b局部放大图 (a) 图 7a局部放大; (b) 图 7b局部放大. Fig. 8 Local zoomed-in images of Fig. 7a~7b (a) Local zoomed-in image of Fig. 7a; (b) Local zoomed-in image of Fig. 7b. |
本文在常规曲波变换实现过程中引入非均匀快速傅里叶变换,建立均匀曲波系数与空间非均匀采样下地震缺失道之间的规则化反演算子,采用高效率的线性Bregman方法进行反演计算得到均匀曲波系数,从而形成了二维非均匀曲波变换方法,并且通过对该曲波系数进行常规二维曲波反变换处理,最终形成了基于二维非均匀曲波变换的地震数据重建方法.由于非均匀曲波变换方法具有常规曲波变换的优势特点,因此在重建过程中具有较高的保真度和信噪比.
理论和实际资料的处理也表明,该方法不仅可以对非均匀假频地震数据和非均匀含噪地震数据进行高精度重建,而且也可以将非均匀网格数据归位到任意指定的均匀采样网格,从而提高了信噪比和采样率.该方法可以看做是传统面元化处理方法的改进,能够有效地应用到叠前非均匀地震数据重建中去,为后续其它处理方法提供较好的规则化数据.因此,本文方法对于指导复杂地区数据采集、非均匀缺失道重建等方面具有重要的应用价值,对其它非均匀信号处理领域也具有重要的借鉴意义.
致谢本文使用到非均匀快速傅里叶变换程序包(https://www-user.tu-chemnitz.de/~potts/nfft/)、CurveLab程序包(curvelet.org)以及英属哥伦比亚大学SLIM小组相关软件(https://www.slim.eos.ubc.ca/),作者在此一并进行感谢.
Bai L S, Liu Y K, Lu H Y, et al.
2014. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing. Chinese J. Geophys., 57(9): 2937-2945.
DOI:10.6038/cjg20140919 |
|
Candès E, Demanet L, Donoho D, et al.
2006. Fast discrete curvelet transforms. SIAM Multiscale Modeling and Simulation, 5(3): 861-899.
DOI:10.1137/05064182X |
|
Duijndam A J W, Schonewille M A, Hindriks C O H.
1999. Reconstruction of band-limited signals, irregularly sampled along one spatial direction. Geophysics, 64(2): 524-538.
DOI:10.1190/1.1444559 |
|
Ely G, Aeron S, Hao N, et al.
2015. 5D seismic data completion and denoising using a novel class of tensor decompositions. Geophysics, 80(4): V83-V95.
DOI:10.1190/geo2014-0467.1 |
|
Fomel S.
2003. Seismic reflection data interpolation with differential offset and shot continuation. Geophysics, 68(2): 733-744.
DOI:10.1190/1.1567243 |
|
Herrmann F J.
2010. Randomized sampling and sparsity: Getting more information from fewer samples. Geophysics, 75(6): WB173-WB187.
DOI:10.1190/1.3506147 |
|
Hindriks K, Duijndam A J W.
2000. Reconstruction of 3-D seismic signals irregularly sampled along two spatial coordinates. Geophysics, 65(1): 253-263.
DOI:10.1190/1.1444716 |
|
Jin S.
2010. 5D seismic data regularization by a damped least-norm Fourier inversion. Geophysics, 75(6): WB103-WB111.
DOI:10.1190/1.3505002 |
|
Kunis S. 2006. Nonequispaced FFT: Generalisation and inversion [Ph. D. thesis]. Lübeck: University of Lübeck.
|
|
Liu G C, Chen X H, Guo Z F, et al.
2011. Missing seismic data rebuilding by interpolation based on curvelet transform. Oil Geophysical Prospecting, 46(2): 237-245.
|
|
Lorenz D A, Schöpfer F, Wenger S.
2013. The linearized Bregman method via split feasibility problems: analysis and generalizations. SIAM Journal on Imaging Sciences, 7(2): 1237-1262.
|
|
Lorenz D A, Wenger S, Schöpfer F, et al. 2014. A sparse Kaczmarz solver and a linearized Bregman method for online compressed sensing.//2014 IEEE International Conference on Image Processing (ICIP). Paris: IEEE, 1347-1351.
|
|
Ma J W.
2013. Three-dimensional irregular seismic data reconstruction via low-rank matrix completion. Geophysics, 78(5): V181-V192.
DOI:10.1190/geo2012-0465.1 |
|
Naghizadeh M, Sacchi M D.
2007. Multistep autoregressive reconstruction of seismic records. Geophysics, 72(6): V111-V118.
DOI:10.1190/1.2771685 |
|
Naghizadeh M, Sacchi M D.
2010. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data. Geophysics, 75(6): WB189-WB202.
DOI:10.1190/1.3509468 |
|
Oropeza V, Sacchi M D.
2011. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis. Geophysics, 76(3): V25-V32.
DOI:10.1190/1.3552706 |
|
Ronen J.
1987. Wave-equation trace interpolation. Geophysics, 52(7): 973-984.
DOI:10.1190/1.1442366 |
|
Spitz S.
1991. Seismic trace interpolation in the F-X domain. Geophysics, 56(6): 785-794.
DOI:10.1190/1.1443096 |
|
Tang H H, Mao W J.
2014. Amplitude preserved seismic data reconstruction by 3D high-order parabolic Radon transform. Chinese J. Geophys., 57(9): 2918-2927.
DOI:10.6038/cjg20140917 |
|
Trad D.
2009. Five-dimensional interpolation: Recovering from acquisition constraints. Geophysics, 74(6): V123-V132.
DOI:10.1190/1.3245216 |
|
Wang B F, Li J Y, Chen X H, et al.
2015. Curvelet-based 3D reconstruction of digital cores using the POCS method. Chinese J. Geophys., 58(6): 2069-2078.
DOI:10.6038/cjg20150621 |
|
Xu S, Zhang Y, Pham D, et al.
2005. Antileakage Fourier transform for seismic data regularization. Geophysics, 70(4): V87-V95.
DOI:10.1190/1.1993713 |
|
Yin W T.
2010. Analysis and generalizations of the linearized Bregman method. SIAM Journal on Imaging Sciences, 3(4): 856-877.
DOI:10.1137/090760350 |
|
Yu S W, Ma J W, Osher S.
2016. Monte Carlo data-driven tight frame for seismic data recovery. Geophysics, 81(4): V327-V340.
DOI:10.1190/geo2015-0343.1 |
|
Zhang H, Chen X H.
2013. Seismic data reconstruction based on jittered sampling and curvelet transform. Chinese J. Geophys., 56(5): 1637-1649.
DOI:10.6038/cjg20130521 |
|
Zhang H, Chen X H, Wu X M.
2013. Seismic data reconstruction based on CS and Fourier theory. Applied Geophysics, 10(2): 170-180.
DOI:10.1007/s11770-013-0375-3 |
|
Zhang H, Chen X H, Li H X.
2015. 3D seismic data reconstruction based on complex-valued curvelet transform in frequency domain. Journal of Applied Geophysics, 113: 64-73.
DOI:10.1016/j.jappgeo.2014.12.004 |
|
Zwartjes P M, Sacchi M D.
2007. Fourier reconstruction of nonuniformly sampled, aliased seismic data. Geophysics, 72(1): V21-V32.
DOI:10.1190/1.2399442 |
|
白兰淑, 刘伊克, 卢回忆, 等.
2014. 基于压缩感知的Curvelet域联合迭代地震数据重建. 地球物理学报, 57(9): 2937–2945.
DOI:10.6038/cjg20140919 |
|
刘国昌, 陈小宏, 郭志峰, 等.
2011. 基于curvelet变换的缺失地震数据插值方法. 石油地球物理勘探, 46(2): 237–245.
|
|
唐欢欢, 毛伟建.
2014. 3D高阶抛物Radon变换地震数据保幅重建. 地球物理学报, 57(9): 2918–2927.
DOI:10.6038/cjg20140917 |
|
王本锋, 李景叶, 陈小宏, 等.
2015. 基于Curvelet变换与POCS方法的三维数字岩心重建. 地球物理学报, 58(6): 2069–2078.
DOI:10.6038/cjg20150621 |
|
张华, 陈小宏.
2013. 基于jitter采样和曲波变换的三维地震数据重建. 地球物理学报, 56(5): 1637–1649.
DOI:10.6038/cjg20130521 |
|
 2017, Vol. 60
2017, Vol. 60

