地震数据正演,逆时偏移及全波形反演等方法均需要以高精度的地震波场数值模拟算法为基础.有限差分数值方法求解波动方程易于实现,内存需求少,因此在波场模拟和逆时偏移中得到广泛的应用(Hemon,1978;Mcmechan,1983;Villarreal et al., 1997;Matthew and Clive, 2006).但是,有限差分法中,空间网格和时间采样步长的选取受稳定性条件限制,而且差分计算的误差会导致地震波场中出现数值频散干扰.提高有限差分阶数(刘红伟等,2010)或采用通量校正传输(Tong and Ken, 1995)方法能够一定程度上压制频散,但需要引入额外的计算量;Zhang和Yao(2013)采用模拟退火法优化有限差分系数,无需增加额外计算量,即可降低频散影响.上述方法均能压制频散干扰,但无法从根本上消除频散,而且为保持差分算法的稳定性,通常无法选择较大的时间步长参数(Carcione et al., 2002;Moczo et al., 2007),因此对实际数据进行偏移成像时,往往需要预先对数据进行插值处理,增加了输入的数据量.
选择稳定和精确的波动方程求解方法是实现高精度地震波场正演模拟,提高逆时偏移成像质量的关键.Tal-Ezer等(1986, 1987)提出利用时间积分法实现声波方程波场模拟,能够获得比有限差分法波场模拟更高的计算精度和算法稳定性;Zhang和Zhang(2009)从单程波动方程的解析表达式出发,提出了一步波场延拓方法,该方法在双程波动方程中引入复波场,将其重构为类似单程波动方程的形式,进而得出波场延拓计算的解析递推公式,该方法可实现大时间步长的波场延拓,算法稳定性较强;Pestana和Stoffa(2010)提出快速展开法,仅保留了时间积分法(Tal-Ezer,1986;Tal-Ezer et al., 1987)递推公式的实数项,避免了复数波场运算,该类方法也被称为“两步法”(Robert and Zhang, 2008);Formel等(2013)进一步采用低秩法近似波动方程的递推公式,有效降低了波场模拟的计算量;Daniel和Reynam(2016)基于矩阵形式推导了一步波场延拓法(后文简称一步法),采用Chebyshev多项式近似e指数项,时间步长的选取无稳定性条件限制,在逼近Nyquist采样率的情况下仍可实现波场的稳定传播;Du等(2014)将上述波场模拟方法(Tal-Ezer et al., 1986, 1987;Zhang and Zhang, 2009;Pestana and Stoffa, 2010;Formel et al., 2013)归类命名为“递归时间积分延拓法”(RITE,Recursive integral time-extrapolation),指出该类方法均具有较高的稳定性,能够实现大时间步长条件下的波场模拟.近年来,“递归时间积分延拓法”的应用不再局限于各向同性介质,在复杂各向异性介质(Pestana et al., 2011;Pestana et al., 2012;Zhan et al., 2012;黄金强和李振春,2017)以及粘性介质(Sun et al., 2015)的正演、偏移、最小二乘偏移及全波形反演等方法中均取得了成功的应用(Sun et al., 2014;Santos and Pestana, 2015).
为降低逆时偏移方法的波场存储量,诸多学者展开了细致的研究.Feng等(2012)提出保存边界处单层波场的策略,通过变阶数有限差分实现波场逆推重建,但波场重建的精度有所降低;与之类似的有效边界存储方法(王保利等,2012)虽然能改善精度问题,实现波场的无损重建,但该方法也局限于在有限差分波场模拟方法中使用,并不适用于基于“递归时间积分延拓法”的逆时偏移计算.Symes(2007)提出的优化checkpoint方法,通过优选checkpoint降低波场存储量,但会引入较多的额外计算量,且实现过程较为复杂.Robert(2009)提出了随机边界条件,虽然不受波场模拟算法限制,而且无需存储临时波场,通过方程反推即可实现波场重建,但随机噪声的引入会影响偏移效果.综上所述,基于“递归时间积分延拓法”的逆时偏移方法的波场重建策略仍有待进一步研究探索.
本文从二维常密度声波方程出发,引入复波场,利用Chebyshev多项式和Jacobi-Anger展开式,推导了一步法波场模拟方程,相比于有限差分法,一步法更能适应大时间步长波场模拟,无数值频散干扰,算法稳定性强;随后本文将一步法地震波场模拟引入逆时偏移成像,并提出了一种适用于一步法逆时偏移方法的双缓冲区存储策略,在不增加计算量的前提下,二级缓冲区的引入大幅提升了内存重复利用率,有效降低了波场存储量.采用双缓冲区存储策略时,参数的选取对波场的内存占用量影响明显,因此本文进一步推导出令波场存储量占用最小的参数选取方案.模型试算结果表明,文中方法波场模拟精度高,逆时偏移成像质量好,波场存储成本低.
2 方法原理 2.1 矩阵表示的一步法波场延拓方法二维常密度声波方程可表示为
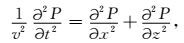
|
(1) |
式中,P=P(x, z, t)是压力场,v=v(x, z, t)是速度场.
在(1)式中引入复波场(Zhang and Zhang, 2009)
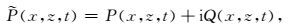
|
(2) |
式中,Q(x, z, t)是P(x, z, t)在时间方向上的希尔伯特变换,i是虚数单位.
定义伪差分算子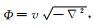
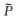
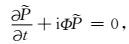
|
(3) |
(3) 式等价于双程波方程,可获得和常规声波波动方程相同的走时和振幅信息.
若速度v为常数,(3)式的解可表示为
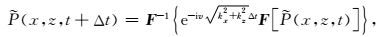
|
(4) |
式中,F和F-1分别为正、反傅里叶变换.
若速度v变化,(3)式的解可表示为(Zhang and Zhang, 2009)
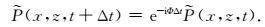
|
(5) |
为了简化复数运算,把(2)式代入(3)式,可得如下的耦合方程组:
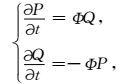
|
(6) |
令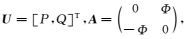
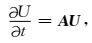
|
(7) |
方程(7)的解可表示为
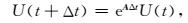
|
(8) |
为计算指数算子eAΔt,引入如下Jacobi-Anger展开式
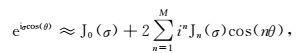
|
(9) |
式中,Jn为n阶一类贝塞尔函数.
若令
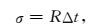
|
(10) |
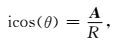
|
(11) |
则有
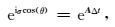
|
(12) |
式中,R为A的最大本征值.在二维情况下,可以选取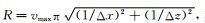
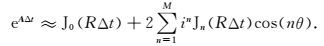
|
(13) |
由第一类Chebyshev多项式可知,若定义x=cos(θ),Tn(x)=cos(nθ),T0(x)=1,T1(x)=x=cos(θ),则有如下递推公式成立:
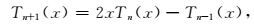
|
(14) |
若令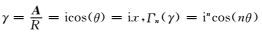
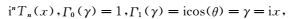
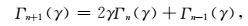
|
(15) |
则(13)式可进一步化简为
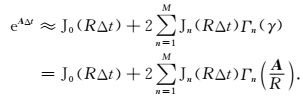
|
(16) |
为了确保(16)式收敛,需保证M>RΔt(Tal-Ezer,1986).将(16)式代入(8)式中并展开可得
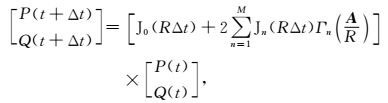
|
(17) |
(17)式即为一步法波场延拓递推公式.
对(17)式中Γn项进一步展开,可得
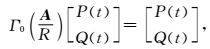
|
(18) |
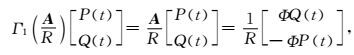
|
(19) |
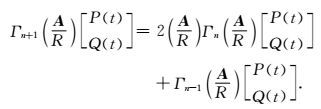
|
(20) |
由于矩阵A中的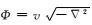
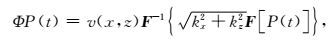
|
(21) |
式中,kx和kz为空间波数.为降低计算成本,本文采用GPU加速技术(刘国峰等,2009;李博等,2010;Liu et al., 2012;石颖等,2010;2013)实现上述算法,结合基于CUDA平台的CUFFT进行傅里叶变换计算,可大幅提升计算效率(郭雪豹等,2016).
一步法的算法稳定性要明显优于有限差分法,在时间采样率和空间网格间距的选取上具有更高的宽容度.理论上,时间采样间隔的选取仅受限于Nyquist采样定理(Daniel and Reynam, 2016),即
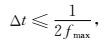
|
(22) |
式中,Δt为时间采样间隔,fmax为震源子波的最大频率.给定震源子波最大频率fmax后,关系式(Robert and Zhang, 2008;Du et al., 2014)
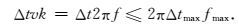
|
(23) |
在满足Nyquist定理的情况下,Δt的最大值为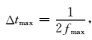
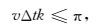
|
(24) |
假设Δx=Δz,有
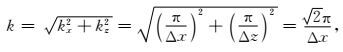
|
(25) |
由于地下介质为变速介质,为保证算法的全局稳定性,当v=vmax为地下介质最大速度时,将(25)式代入(24)式可得
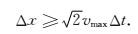
|
(26) |
综上可知,(26)式即为一步法的稳定性条件.
2.2 双缓冲区存储策略为节约存储空间,一些学者在利用有限差分数值方法进行逆时偏移计算时,提出存储正向传播的局部震源波场,再反向重建历史震源波场的方法(Feng,2012;王保利等,2012),但是此类方法不适用于本文研究的基于一步法波场延拓的逆时偏移方法.为此,本文提出了一种双缓冲区(一级缓冲区和二级缓冲区)存储策略.
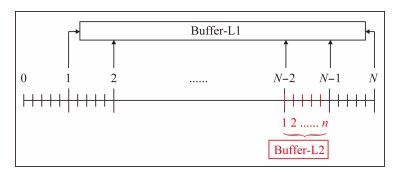
该方法首先定义一级缓冲区(Buffer-L1)和二级缓冲区(Buffer-L2),如图 1所示,再沿时间方向等间隔定义N个checkpoint,一级缓冲区用于存储所有checkpoint处的正传震源波场(含吸收边界),二级缓冲区用于存储某两个checkpoint间的正传震源波场(不含吸收边界).震源波场正传时,保存所有checkpoint处波场至一级缓冲区;当震源波场反传时,以预先载入一级缓冲区内的某checkpoint时刻波场为初始条件,将波场正传至下一个checkpoint时刻,期间保存两个checkpoint之间所有时刻的波场至二级缓冲区.以第N-2个checkpoint为例,当从第N-2个checkpoint向N-1个checkpoint正传震源波场时,保存第N-2个至N-1个checkpoint之间所有时刻的波场(不含吸收边界)至二级缓冲区,此时第N-2至N-1个checkpoint之间的波场覆盖更新了二级缓冲区内的原有波场(第N-1个checkpoint至第N个checkpoint之间的波场).检波点波场的反传与上述过程同时进行,并对二级缓冲区中的震源波场与反传的检波点波场进行零延迟互相关成像,以此类推,直至完成全部时刻的成像计算.
|
图 1 双缓冲区存储策略示意图 Fig. 1 Scheme for Duo-buffer storage strategy |
假设一级缓冲区需保存N个全波场(含吸收边界)数据,二级缓冲区需保存n个有效波场(不含吸收边界)数据,则N和n的选取直接影响缓冲区空间的占用,因此本文推导了使缓冲区存储占用最小的参数选取方案.为方便推导,存储量占用以数据网格点数为单位.
设二维模型的水平和垂直网格点数分别为Nx,Nz,吸收边界层数为B,则一个时刻的包含吸收边界的全波场数据的网格点数为S1=(Nx+2B)(Nz+2B),一个时刻的不包含吸收边界的有效波场数据的网格点数为S2=NxNz.为满足震源波场能够递推计算的初始条件,需在每个checkpoint处保存P(t)和Q(t)的全波场信息,则一级缓冲区所需保存的数据的网格点数为C1=2S1N;二级缓冲区用于临时保存两个一级缓冲区点之间的有效波场,用于互相关成像,仅需保存P(t)的有效波场信息,则二级缓冲区所需保存的数据的网格点数为C2=S2n.设时间方向的采样点数为T,理想情况下假设T可被N整除,则满足T=Nn.
据上可知,所需存储的所有数据的网格点数为
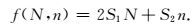
|
(27) |
为使总波场存储量占用最小,即选取N和n的值,满足f(N, n)最小.设g(N, n)=T-Nn作为限定条件,由拉格朗日乘子法可构建目标方程为
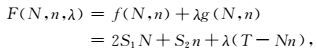
|
(28) |
(28)式对自变量求偏导可得方程组:
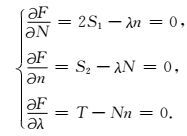
|
(29) |
求解(29)式可得

|
(30) |
在方法实现过程中,N和n需取整数,因此当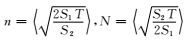
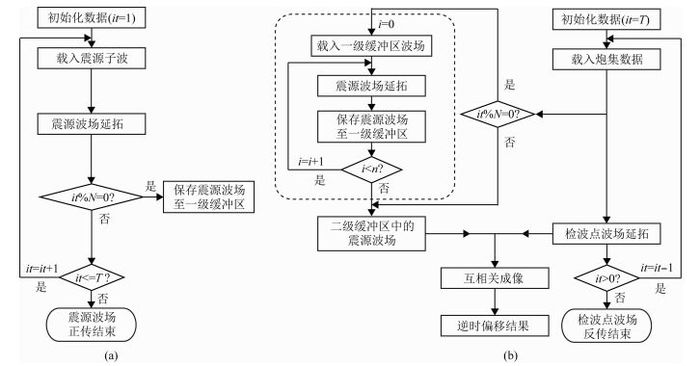
基于双缓冲区存储策略的逆时偏移算法如图 2所示.图中,it表示波场递推过程中时间方向的计数变量,i为读取二级缓冲区内的波场时的计数变量,N,n和T的含义同上文,虚线框标识部分即为根据图 1所示采用双缓冲区存储方法的波场重建过程.
|
图 2 基于双缓冲区存储方法的逆时偏移流程图 (a)震源波场正向传播流程;(b)震源波场重建及逆时偏移流程. Fig. 2 The flowchart of RTM based on Duo-buffer storage scheme (a) The flowchart of source wavefield forward propagation; (b) The flowchart of source wavefield reconstruction and RTM. |
采用有限差分法模拟地震波场时,空间网格间距和时间步长的大小是影响波场模拟精度的两个重要因素.为了对比分析,下文分别在不同空间网格间距的情况下,测试有限差分法和一步法模拟地震波场的精度.也进一步测试了在不同时间步长情况下,一步法波场模拟的精度.
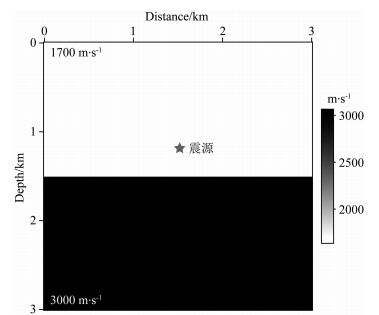
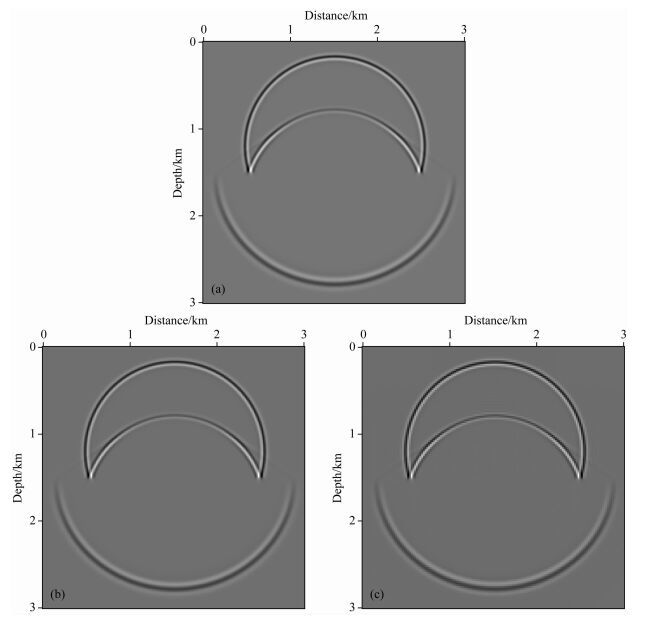
3.1.1 不同空间网格间距波场模拟本文设计如图 3所示的水平层状模型,测试不同网格间距对有限差分法和一步法波场模拟精度的影响.模型沿水平和垂直方向均为3 km,速度为1700 m·s-1的水层和速度为3000 m·s-1的岩层的分界面位于垂向1.5 km处.激发震源采用主频为20 Hz的雷克子波,位于水平方向1.5 km,垂直方向1.2 km处.选择空间网格间距分别10,15,20 m进行测试,因此三种情况下,模型沿水平方向和垂直方向的网格点数分别为301×301,201×201,151×151,时间采样步长恒定为1 ms,分别采用空间十阶有限差分法和一步法波场模拟,0.6 s时刻的波场快照如图 4和5所示.观察可知,随着空间网格间距的增加,有限差分法模拟的波场频散现象逐渐严重;一步法模拟的波场均较为稳定,误差干扰较小.
|
图 3 水平层状速度模型 Fig. 3 Velocity model of horizontal layered model |

|
图 4 有限差分法实现波场模拟的波场快照 (a)空间网格间距10 m;(b)空间网格间距15 m;(c)空间网格间距20 m. Fig. 4 The wavefield snapshot obtained by finite difference approaches (a) Space grid spacing is 10 m; (b) Space grid spacing is 15 m; (c) Space grid spacing is 20 m. |
|
图 5 一步法实现波场模拟的波场快照 (a)空间网格间距10 m;(b)空间网格间距15 m;(c)空间网格间距20 m. Fig. 5 The wavefield snapshot by one step method (a) Space grid spacing is 10 m; (b) Space grid spacing is 15 m; (c) Space grid spacing is 20 m. |
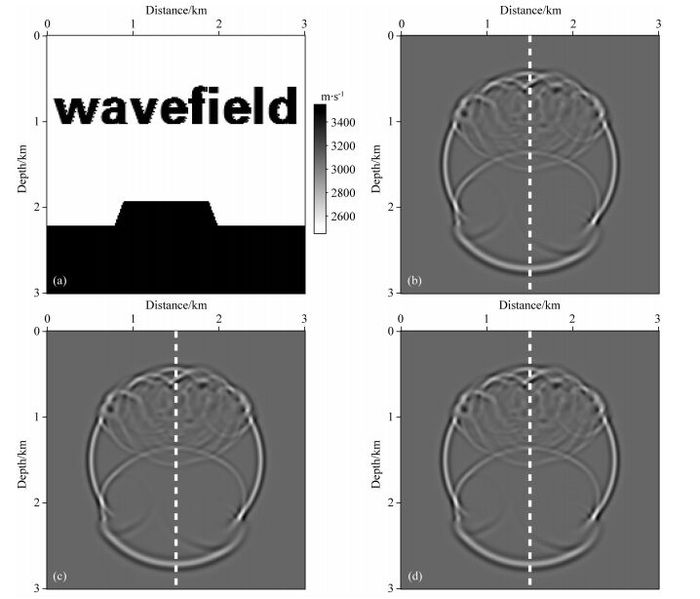
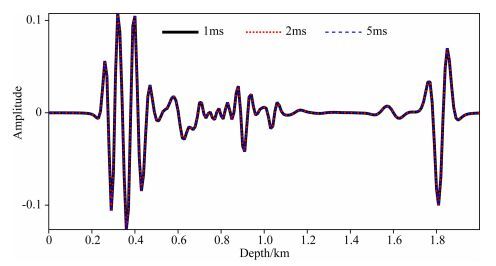
本文也设计如图 6a所示的复杂字母模型,用于测试时间步长对一步法波场模拟精度的影响.假定字母模型沿水平和垂直方向的网格点数均为201,空间网格间距为15 m,激发震源位于水平方向1.5 km,垂直方向1.5 km处,分别选择1 ms,2 ms和5 ms的时间步长进行一步法波场模拟测试,在0.4 s时刻的波场快照分别如图 6b,6c和6d所示,观察可知,随着时间步长的增加,采用一步法模拟的地震波场仍具有良好的稳定性.图 7显示了沿图 6b,6c和6d中虚线抽取的地震数据.对比分析进一步说明,对采用不同时间步长的三个模拟结果,基于一步法的地震波场模拟的精度高、稳定性好,抽取的单道数据吻合较好,地震波走时、振幅和相位都能保持一致.
|
图 6 不同时间步长的波场快照对比 (a)速度模型1;(b)时间步长为1 ms;(c)时间步长为2 ms;(d)时间步长为5 ms. Fig. 6 Comparison of wavefield snapshots with different time step (a) Velocity model 1; (b) Time step is 1 ms; (c) Time step is 2 ms; (d) Time step is 5 ms. |
|
图 7 单道数据对比(时间采样步长分别为1, 2, 5 ms) Fig. 7 Comparison of single trace(time step are 1 ms, 2 ms and 5 ms, respectively) |
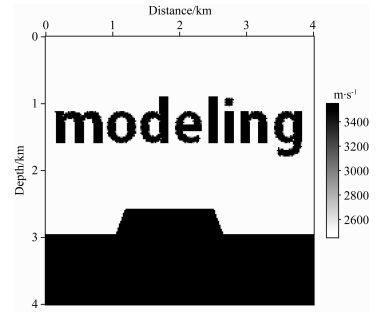
虽然一步法稳定性较好,但相比于有限差分法,其算法略加复杂,因此计算成本也有所增加.本文分别采用一步法和有限差分法进行地震记录正演模拟的耗时测试.正演模拟采用的速度模型为如图 8所示的复杂字母模型,水平和垂直方向的网格点数均为201,空间网格间距为20 m.震源位于地表水平方向1.5 km,震源子波选取主频15 Hz的雷克子波,记录时长为2 s.一步法中参数M=7,有限差分法采用时间二阶,空间十阶差分.一步法时间间隔选取5 ms,有限差分法选取时间间隔选取1 ms,即一步法正演的时间采样点数为500,有限差分法正演的时间采样点数为2000,正演所得共炮点道集数据如图 9所示,具体参数及耗时对比如表 1所示.
|
图 8 速度模型2 Fig. 8 Velocity model 2 |
|
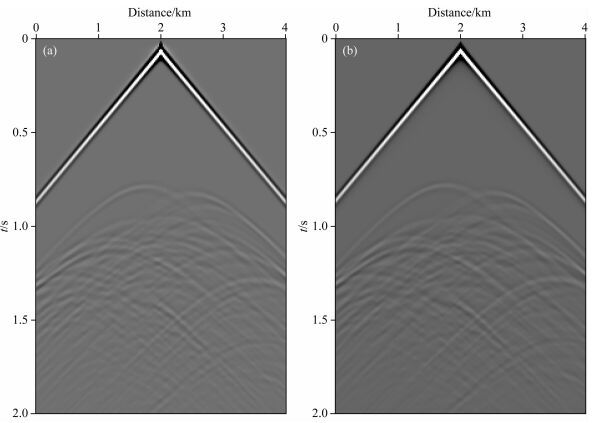
图 9 两种方法正演的共炮点道集对比 (a)一步法正演的单炮数据;(b)有限差分法法正演的单炮数据. Fig. 9 Comparison of common-shot gather modeled with two approaches (a) One step method; (b) Finite difference method. |
|
|
表 1 一步法和有限差分法正演计算耗时对比 Table 1 Modeling time-consuming comparison of between One step method and finite difference method |
由图 9可知,两种方法均能准确有效的进行地震数据正演模拟,由于一步法能采用更大的时间步长,因此所需模拟的时间点数相对更少,但由于其计算方法更加复杂,因此计算效率仍要低于有限差分法.
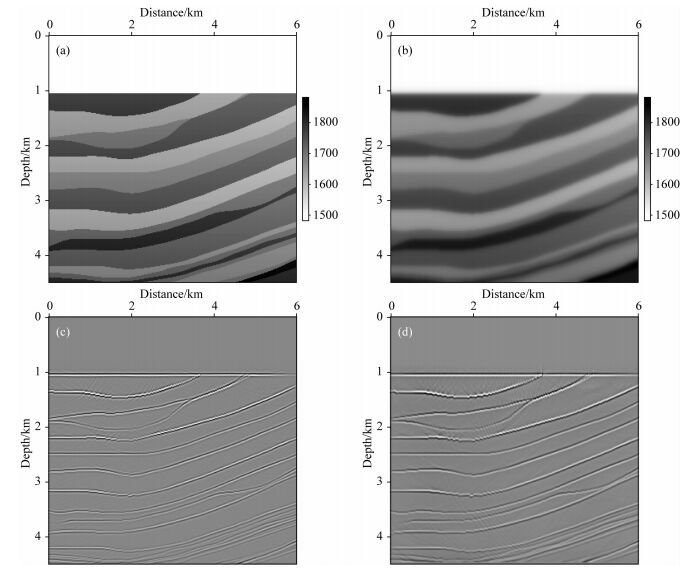
3.2 逆时偏移测试与存储量分析 3.2.1 逆时偏移测试本文采用Marmousi2的截断模型测试一步法逆时偏移成像,图 10a和10b分别为精确速度模型和平滑速度模型.模型沿水平方向和垂直方向的网格点数分别为400和300,空间网格间距为15 m,时间采样间隔为4 ms,采样点数为1500,设计主频15 Hz的雷克子波作为激发震源,20个震源的炮间距为300 m,沿水平方向0~6000 m范围内均匀分布,每炮199个检波器接收,均匀对称分布于震源两侧,检波器间距为15 m,最大偏移距为1485 m.分别采用一步法和有限差分法进行逆时偏移计算,两种情况均采用了e指数吸收边界条件和互相关成像条件.为了满足稳定性条件,利用有限差分法进行逆时偏移成像时,本文采用sinc函数插值方法对炮集数据进行时间方向插值,插值重建后的时间步长为1 ms,时间方向采样点数为6000.图 10c和10d分别为一步法逆时偏移和有限差分法逆时偏移成像结果.对比可知,一步法波场模拟不存在频散现象,波形传播稳定无畸变,聚焦性更强,逆时偏移成像的同相轴更清晰,剖面具有更高的信噪比.有限差分法受频散现象干扰,逆时偏移剖面分辨率相对较低,且具有较多成像噪声.
|
图 10 一步法和有限差分法逆时偏移测试 (a)准确速度模型;(b)平滑速度模型;(c)一步法逆时偏移剖面;(d)有限差分法逆时偏移剖面. Fig. 10 RTM test by one step and finite difference methods (a) Accurate velocity model; (b) Smoothed velocity model; (c) RTM profile obtained by one step method; (d) RTM profile by finite difference method. |
上述测试选取了100层网格的偏移孔径和50层网格的边界层,则计算全波场的网格点数为水平方向700,垂直方向400;其中有效波场网格点数为水平方向600,垂直方向300.根据2.2节内容可知,对应的S1为280000,S2为180000,T为1500,进而可计算出n和N分别为68和22,代入(17)式可得双缓冲区存储策略的波场存储量约为93.68 MB,与实测数据相符.在不增加额外计算量的情况下,以空间十阶差分为例,采用有效边界存储策略(王保利等,2012)计算逆时偏移所需波场存储约为205.08 MB,如表 2所示.
|
|
表 2 双缓冲区和有效边界方法的存储量对比 Table 2 Storage comparison between Dou-buffer and effective boundary method |
观察可知,相比于节约存储的有效边界存储方法,基于双缓冲区存储方法的逆时偏移成像所需的波场存储量更小,主要是由于一步法波场模拟可采用大时间步长,从而减小时间采样点数,进而减少了波场重建数量.另外,双缓冲区存储策略中二级缓冲区的重复利用以及缓冲区参数的最优化选取也进一步降低了波场的存储需求.
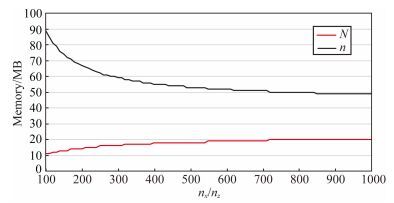
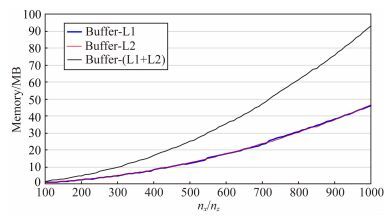
3.2.2 存储量分析为了定量表示本文方法在不同模型尺寸下的波场存储量占用情况,也测试了N和n随模型尺寸的变化情况,假设水平和垂直方向空间网格点相同,吸收边界层数为50,时间采样点数1000,根据(30)式可计算得到N和n随模型尺寸的变化曲线如图 11所示.由于本文方法可采用大时间步长进行波场模拟,时间采样点为1000时即可进行时长约4 s的波场模拟.因此由图 12可知,在二维空间情况下(假设横向和纵向网格点数相同,且均小于1000;每个网格点数据占用4bytes内存空间),本文方法能够将波场存储量控制在100 MB以下.较小的存储需求使本文方法对硬件要求较低,另根据前文所述可知,算法对一级缓冲区的访问为非连续访问,因此,应用GPU加速技术时,一级缓冲区可设置在主机内存端,能够进一步降低显存存储负担,提升本文方法的适用性.
|
图 11 N和n随模型尺寸的变化曲线 Fig. 11 The variation curves of N, n with different model sizes |
|
图 12 波场存储量随模型尺寸变化曲线 Fig. 12 The variation curves of wavefield storage with different model sizes |
(1) 本文基于一步法波场延拓方法开展波场模拟研究,并将其引入逆时偏移成像,提出了降低波场存储量的双缓冲区存储方法.该方法通过设置二级缓冲区以及选取最优参数,可在不增加逆时偏移计算量的情况下,大幅降低逆时偏移的波场存储量.相比于有限差分方法,一步法波场模拟稳定性强,受模型网格间距和时间步长影响小,无频散假象,波场模拟精度更高.但由于一步法波场延拓算法略加复杂,需要多次执行傅里叶变换,因此也带来了计算耗时的增加.
(2) 多个模型验证了文中方法是一种具有广阔发展前景的地震波场模拟方法,可成功应用于叠前逆时偏移成像,具有较大的工业应用潜力.此外,文中方法也可推广应用于最小二乘逆时偏移及全波形反演等方法中.
致谢感谢审稿专家和编辑部的大力支持.
Carcione J M, Herman G C, Kroode A P E T.
2002. Seismic modeling. Geophysics, 67(4): 1304-1325.
DOI:10.1190/1.1500393 |
|
Daniel E R, Reynam C P.
2016. One-step wave extrapolation matrix method for reverse time migration. Geophysics, 81(5): S359-S366.
DOI:10.1190/GEO2015-0555.1 |
|
D u, Fowler P J, Fletcher R P.
2014. Recursive integral time-extrapolation methods for waves: A comparative review. Geophysics, 79(1): T9-T26.
DOI:10.1190/GEO2013-0115.1 |
|
Feng B, Wang H Z.
2012. Reverse time migration with source wavefield reconstruction strategy. Journal of Geophysics & Engineering, 9(1): 69-74.
DOI:10.1088/1742-2132/9/1/008 |
|
Formel S, Ying L X, Song X L.
2013. Seismic wave extrapolation using low-rank symbol approximation. Geophysical Prospecting, 61(3): 526-536.
DOI:10.1111/j.1365-2478.2012.01064 |
|
Guo X B, Liu H, Shi Y.
2016. Time domain full waveform inversion based on frequency attenuation. Chinese J.Geophys., 59(10): 3777-3787.
DOI:10.6038/cig20161022 |
|
Hemon C.
1978. EQUATIONS D'ONDE ET MODELES*. Geophysical Prospecting, 26(4): 790-821.
DOI:10.1111/j.1365-2478.1978.tb01634.x |
|
Huang J Q, Li Z C.
2017. Modeling and reverse time migration of pure quasi-P-waves in complex TI media with a low-rank decomposition. Chinese J.Geophys., 60(2): 704-721.
DOI:10.6038/cjg20170223 |
|
Li B, Liu H W, Liu G F, et al.
2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J.Geophys., 53(12): 2938-2943.
DOI:10.3969/j.issn.0001-5733.2010.12.017 |
|
Liu G F, Liu H, Li B, et al.
2009. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation. Chinese J.Geophys., 52(12): 3101-3108.
DOI:10.3969/j.issn.0001-5733.2009.12.019 |
|
Liu G F, Meng X H, Liu H.
2012. Accelerating finite difference wavefield-continuation depth migration by GPU. Applied Geophysics, 9(1): 41-48.
DOI:10.1007/s11770-012-0312-x |
|
Liu H W, Liu H, Shi Y.
2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J.Geophys., 53(7): 1725-1733.
DOI:10.3969/j.issn.0001-5733.2010.07.024 |
|
Matthew H K, Clive M G.
2006. Explicit high-order reverse time pre-stack depth migration.76th Annual International Meeting. SEG Expanded Abstract, 25(1): 2353-2357.
DOI:10.1190/1.2370007 |
|
Mcmechan G A.
1983. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting, 31(3): 413-420.
DOI:10.1111/j.1365-2478.1983.tb01060.x |
|
Moczo P, Robertsson J O A, Eisner L.
2007. The finite-difference time domain method for modeling of seismic wave propagation. Advances in Geophysics, 48(8): 421-516.
DOI:10.1016/S0065-2687(06)48008-0 |
|
Pestana R C, Stoffa P L.
2010. Time evolution of the wave equation using rapid expansion method. Geophysics, 75(4): T121-T131.
DOI:10.1190/1.3449091 |
|
Pestana R C, Ursin B, Stoffa P L, et al.
2011. Separate P-And Sv-Wave Equations for Vti Media. Seg Technical Program Expanded Abstracts: 1227-1232.
|
|
Pestana R C, Ursin B, Stoffa P L, et al.
2012. Rapid expansion and pseudo spectral implementation for reverse time migration in VTI media. Journal of Geophysics and Engineering, 9(3): 291-301.
DOI:10.1088/1742-2132/9/3/291 |
|
Robert G C.
2009. Reverse time migration with random boundaries.79th Annual International Meeting. SEG Expanded Abstracts, 28: 2809-2813.
DOI:10.1190/1.3255432 |
|
Robert S, Zhang Y.
2008. Two-step explicit marching method for reverse time migration. SEG Technical Program Expanded Abstracts 2008: 2272-2276.
DOI:10.1190/1.3059337 |
|
Santos A W, Pestana R C.
2015. Time-domain multiscale full-waveform inversion using the rapid expansion method and efficient step-length estimation. Geophysics, 80(4): R203-R216.
DOI:10.1190/GEO2014-0338.1 |
|
Shi Y, Liu H, Zou Z.
2010. Surface-related multiples prediction based on wave equation and adaptive subtraction investigation. Chinese J.Geophys., 56(6): 2023-2032.
DOI:10.6038/cjg20130623 |
|
Shi Y, Wang W H, Li Y, et al.
2013. 3D surface-related multiple prediction approach investigation based on wave equation. Chinese J.Geophys., 56(6): 2023-2032.
DOI:10.6038/cjg20130623 |
|
Sun J, Fomel S, Hu J, et al.
2014. Least-squares reverse-time migration using one-step two-way wave extrapolation by non-stationary phase shift. Seg Technical Program Expanded Abstracts: 3967-3973.
DOI:10.1190/segam2014-1588.1 |
|
Sun J, Zhu T, Fomel S, et al.
2015. Viscoacoustic modeling and imaging using low-rank approximation. Geophysics, 80(5): A103-A108.
DOI:10.1190/GEO2015-0083.1 |
|
Symes W W.
2007. Reverse time migration with optimal checkpointing. Geophysics, 72(5): SM213-SM221.
DOI:10.1190/1.2742686 |
|
Tal-Ezer H.
1986. Spectral methods in time for hyperbolic equation. Siam Journal on Numerical Analysis, 23(1): 11-26.
DOI:10.1137/0723002 |
|
Tal-Ezer H, Kosloff D, Koren Z.
1987. An accurate scheme for seismic forward modelling. Geophysical Prospecting, 35(5): 479-490.
DOI:10.1111/j.1365-2478.1987.tb00830.x |
|
Tong F, Ken L.
1995. Elimination of numerical dispersion in finite-difference modeling and migration by flux-corrected transport. Geophysics, 60(6): 1830-1842.
DOI:10.1190/1.1443915 |
|
Villarreal A, Scales J A.
1997. Distributed three-dimensional finite-difference modeling of wave propagation in acoustic media. Computers in Physics, 11(4): 388-399.
DOI:10.1063/1.168610 |
|
Wang B L, Gao J H, Chen W C, et al.
2012. Efficient boundary storage strategies for seismic reverse time migration. Chinese J.Geophys., 55(7): 2412-2421.
DOI:10.6038/j.issn.0001-5733.2012.07.025 |
|
Zhan G, Pestana R C, Stoffa P L, et al.
2012. Decoupled equations for reverse time migration in tilted transversely isotropic media. Geophysics, 77(2): T37-T45.
DOI:10.1190/geo2011-0175.1 |
|
Zhang J H, Yao Z X.
2013. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics, 78(1): A13-A18.
DOI:10.1190/geo2012-0277.1 |
|
Zhang Y, Zhang G Q.
2009. One-step extrapolation method for reverse time migration. Geophysics, 74(4): A29-A33.
DOI:10.1190/1.3123476 |
|
郭雪豹, 刘洪, 石颖.
2016. 基于频域衰减的时域全波形反演. 地球物理学报, 59(10): 3777–3787.
DOI:10.6038/cjg20161022 |
|
黄金强, 李振春.
2017. 基于Low-rank分解的复杂TI介质纯qP波正演模拟与逆时偏移. 地球物理学报, 60(2): 704–721.
DOI:10.6038/cjg20170223 |
|
李博, 刘红伟, 刘国峰, 等.
2010. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报, 53(12): 2938–2943.
DOI:10.3969/j.issn.0001-5733.2010.12.017 |
|
刘国峰, 刘洪, 李博, 等.
2009. 山地地震资料叠前时间偏移方法及其GPU实现. 地球物理学报, 52(12): 3101–3108.
DOI:10.3969/j.issn.0001-5733.2009.12.019 |
|
刘红伟, 李博, 刘洪, 等.
2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报, 53(7): 1725–1733.
DOI:10.3969/j.issn.0001-5733.2010.07.024 |
|
石颖, 刘洪, 邹振.
2010. 基于波动方程表面多次波预测与自适应相减方法研究. 地球物理学报, 53(7): 1716–1724.
DOI:10.3969/j.issn.0001-5733.2010.07.023 |
|
石颖, 王维红, 李莹, 等.
2013. 基于波动方程三维表面多次波预测方法研究. 地球物理学报, 56(6): 2023–2032.
DOI:10.6038/cjg20130623 |
|
王保利, 高静怀, 陈文超, 等.
2012. 地震叠前逆时偏移的有效边界存储策略. 地球物理学报, 55(7): 2412–2421.
DOI:10.6038/j.issn.0001-5733.2012.07.025 |
|
 2017, Vol. 60
2017, Vol. 60


