地球介质各向异性是普遍存在的, 在油气勘探中有些复杂岩层或地质构造的各向异性可达50%以上,如页岩、盐丘侧翼和岩下构造等等,使用倾斜对称轴横向各向同性(TTI)介质或者正交各向异性(TOA)介质(Fowler et al., 2010; 吴国忱, 2010;Zhang, 2011),才能更好地描述地震波在其中的传播规律.如果不考虑各向异性因素的影响,在最终成像结果中走时和振幅会存在较大误差,反射同相轴不连续,分辨率低,成像效果差.目前各向异性逆时偏移成像方法一般分为两种:一种是基于P波和S波在频率-波数域偏振方向的差异求解各向异性介质Christoffel方程,进而得到时间-空间域分离算子用以分离P波,然后再利用分离出的P波进行逆时偏移成像(Dellinger and Etgen, 1990; Yan and Sava, 2009),但是这种方式采用的是各向异性弹性波方程,需要同时延拓求解纵、横波场,然后分离出纵波进行偏移成像,计算效率低,内存消耗大,参数需求多;另一种是求解各向异性拟声波方程得到伪纯P波,利用伪纯P波进行偏移成像.Alkhalifah(1998, 2000)从频散关系出发,提出了声学近似假设条件,人为设定沿着对称轴方向的横波速度为零,推导出VTI介质声学近似qP波频散关系式和四阶偏微分qP波方程,即拟声波方程.该方程简化了P波处理过程,为纵波勘探中各向异性逆时偏移成像提供了理论基础.在这个研究基础上,一些学者开展了很多关于各向异性介质qP波方程正演模拟和偏移成像方面的研究.为了提高计算效率,减少内存消耗,Du等(2005)、Zhou等(2006a)和Hestholm(2009)简化频散关系,利用不同的降阶方法推导出了不同形式的二阶耦合VTI介质qP波方程.梁锴和吴国忱(2005, 2007)在空间-频率域推导了VTI介质qP波方程.Duveneck等(2008)由胡克定律及质点方程出发,基于S波速为零的假设,推导了VTI介质二阶耦合qP波方程,解释了水平应力分量及垂直应力分量的物理意义.虽然利用声学近似方程更易在各向异性介质中实现qP波波场数值模拟及逆时偏移,但是由于其简单假定S波速为零,破坏了原刚度矩阵正定性,基于纵、横波耦合特性,会造成横波残留干扰以及数值计算不稳定等问题(Grechka et al., 2004; Fletcher et al., 2009; Fowler et al., 2010; Zhang et al., 2011;张岩和吴国忱,2013).为了解决这些问题,Liu等(2009)推导了qP波、qSV波的频散关系,然后利用L2范数约束,构建二阶纯qP波方程,解决了数值计算不稳定的问题.Fowler等(2010)给出了VTI介质二阶准P波方程的一般形式,并推导了S波速不为零时的VTI介质二阶耦合qP波和qSV波方程.Fletcher等(2009)、Zhan等(2011)、Zhang等(2009)、Zhou等(2006b)将VTI介质伪声波方程扩展到倾斜横向各向同性(TTI)介质,推导了TTI介质二阶耦合伪声波方程.程玖兵等(2013, 2014)推导了各向异性介质qP波伪纯模式波动方程,利用偏振矢量将纵、横波分离.Xu和Zhou(2014)、Xu等(2015)基于Alkhalifah提出的声学近似方程,构建梯度算子,推导了各向异性介质纯qP波方程.但是基于声学近似假设的方法是存在一定缺陷的,会产生假象干扰以及数值计算不稳定等问题.Grechka等(2004)证实了这种假象是由人为设定S波速为零时产生伪横波而引起的,简单地设定S波速为零并不能保证在声学近似的各向异性介质中沿着非对称轴方向的S波速度等于零,不仅会产是假象干扰,而且也会出现数值频散、数值计算不稳定等问题.Alkhalifah(2000)提出了将计算区域渐层范围内的各向异性参数设置为ε=δ,能够有效压制横波,但是这种方法改变了介质参数,对于地下散射点源产生的伪横波难以处理,不具一般性.本文在Tsvankin(1996)提出的VTI介质精确频散关系的基础上,利用Xu和Zhou(2014)提出的分解偏微分算子的方法,重新构建时间域VTI介质纯qP波方程,利用对称轴旋转,将其扩展到TTI介质,建立了TTI介质纯qP波方程.此推导过程无需设置S波速度为零,能够较精确地描述qP波在TTI介质中的传播规律,没有伪横波干扰,很好地解决由于方程多解性造成的数值误差问题,使数值计算更加准确、稳定、适用性更强、具有一般性.为了说明此方程的正确性,我们分别利用本文方程和Xu和Zhou(2014)提出的纯qP波方程在均匀TI介质进行qP波正演模拟,并将其结果进行了对比,验证了此方程的正确性.
但是应用此方程需要求解波数矢量,我们利用了一阶渐近近似(球形近似)来求解,由于各向异性参数的影响,这种近似方法在各向异性介质中会造成波场振幅不准确.沿着垂直于对称轴方向的波场振幅小,能量弱.为了解决这一问题,我们将椭圆分解的方法(椭圆近似)应用于此方程中构建时间域二阶纯qP波椭圆分解方程,并在均匀TI介质中进行了时间域qP波正演模拟.为了对比其振幅校正精确程度,基于Alkhalifah(2000)提出的频散关系,我们推导了qP波的解析解,并在均匀TI介质中进行了波数域qP波正演模拟;基于Xu等(2015)提出的纯qP波椭圆分解方程,我们也在均匀TI介质中进行了时间域qP波正演模拟.然后我们抽取由各方程模拟得到的各波场的单道波形进行了振幅对比,可以发现应用本文构建的纯qP波椭圆分解方程能较精确地对垂直于对称轴方向的振幅进行校正,校正后振幅不仅均衡,而且振幅值更加准确,并阐明应用本文构建的纯qP波椭圆分解方程能较精确对垂直于对称轴方向的进行振幅校正的原因,突出了本文构建的纯qP波椭圆分解方程的优势.为了验证本文构建的纯qP波方程的正确性和有效性,我们选取了均匀TI介质模型进行正演模拟并进行了振幅分析.为了验证本文构建的纯qP波椭圆方程的适用性,阐明其应用优势,我们选取了BP TTI模型进行了正演模拟,将其qP波正演结果和均匀TI介质模型振幅分析结果相结合,突出了本文构建的纯qP波椭圆分解方程的适应性及应用优势.为了验证了本文构建的纯qP波椭圆分解方程在逆时偏移中的可行性和适用性,本文选取逆冲模型和BPTTI模型进行了逆时偏移成像.
2 各向异性介质纯qP波方程Alkhalifah(2000)提出了声学近似频散关系,将沿着对称轴方向的横波速度设置为零,构建声学近似方程,忽略横波物理现象,描述qP波在各向异性介质中的传播特征.Alkhalifah提出的声学近似频散关系为:
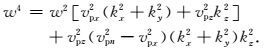
|
(1) |
Liu等(2009)通过开平方根求解得到纵、横波频散关系式,分别为:
qP波:
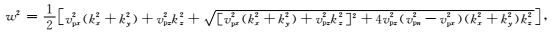
|
(2) |
qSV波:
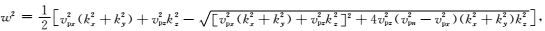
|
(3) |
其中w是频率,kx、ky和kz都代表波数,vpx=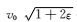
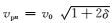
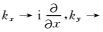
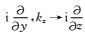
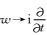
qP波:
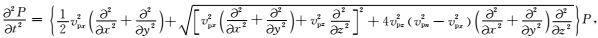
|
(4) |
qSV波:
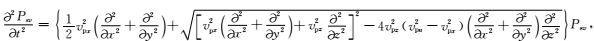
|
(5) |
其中P和Psv分别代表的是qP波波场和qSV波波场,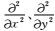
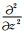
基于Alkhalifah的频散关系式和Liu等(2009)推导的纯qP波频散关系及偏微分方程,Xu和Zhou(2014)提出一种分解偏微分算子的办法,将方程(4)中的偏微分算子分解为一个差分算子(Laplace算子)和一个标量算子S,用于代表qP波的精确传播方向.其中标量算子S的精确求取在这种算法中是至关重要的,直接影响qP波的计算精度.代入vpx=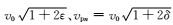
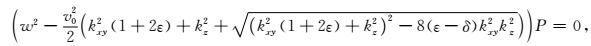
|
(6) |
其中w是频率,P为波场.引入空间波数矢量k=(kx, ky, kz),kxy为水平方向波数,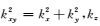
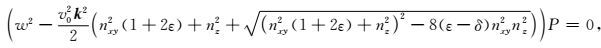
|
(7) |
其中,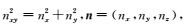
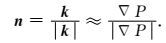
|
(8) |
于是,借助于Xu和Zhou(2014)分解偏微分算子的方法,直接基于Alkhalifah声学频散关系推导的标量算子S表达式为:
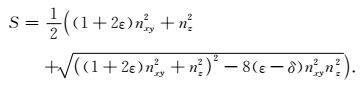
|
(9) |
但是这个标量算子S是直接由Alkhalifah的声学近似频散关系求解得到的,构建的二阶纯qP波方程,是由Alkhalifah的声学近似方程推导而来.由于Alkhalifah的声学近似频散关系直接设定横波速度为零,解耦得到的SV波是伪SV波(Liu et al., 2009).虽然Xu和Zhou(2014)提出了一种分解偏微分算子的方法,将近似频散关系因式分解直接解耦求得qP波的频散关系的二阶关系式,然后进行傅里叶变换,进而求取标量算子,解决了数值计算不稳定的问题,但其还是基于Alkhalifah近似频散关系的基础上提出的,破坏了原刚度矩阵的正定性,忽略了方程多解性,不符合纵、横波耦合特性,存在假象干扰,会导致较严重的数值误差.为了保证计算的准确、稳定,于是Xu和Zhou(2014)引入了衰减项d=1-nxy2-nz2,将方程(6)改写为:
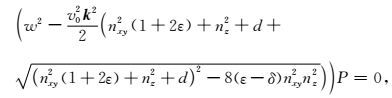
|
(10) |
从而推导了新的标量算子S的表达式为:
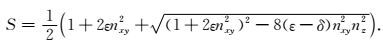
|
(11) |
Xu等(2014)利用方程(11)求得的标量算子构建了时间域二阶纯qP波方程,可以很好地压制干扰,减小数值误差,保证数值计算稳定,较精确地描述了qP波的传播特征,但是只有加入衰减项d,才能很好地压制干扰(见图 3).由于衰减项的引入,在构建纯qP波椭圆分解方程(Xu et al., 2015)进行振幅校正时,进而造成振幅不准确,振幅值偏小,下文详细说明(见图 8和9).因此为了避免引入衰减项,本文将Xu和Zhou(2014)采用的Alkhalifah(2000)提出的声学近似频散关系换为Tsvankin(1996)提出的精确频散关系,按照上述Xu和Zhou(2014)求取标量算子S的方法来求取本文所采用的标量算子S,然后构建时间域二阶纯qP波方程,无需引入衰减项,数值计算稳定,误差小,振幅更加准确.首先需求精确频散关系,Tsvankin(1996)采用的P波和SV波的相速度表达式为:

|
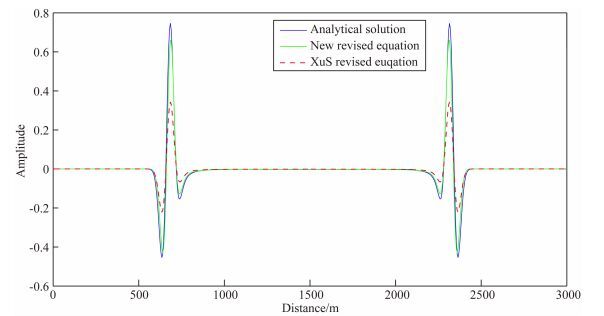
图 3 沿y轴中心方向qP波波场快照的二维切片 (a) qP波原始方程(方程(9)和(25));(b) Xu和Zhou(2014)的方程(方程(11)和(25));(c)本文方程(方程(23)和(25)). Fig. 3 2D seismic slices of snapshot of qP wavefield along the middle of y direction (a) Original qP wave equation(Equations (9) and (25)); (b) Xu′s equation (Equations (11) and (25)); (c) Equations proposed in this paper (Equations (23) and (25)). |
|
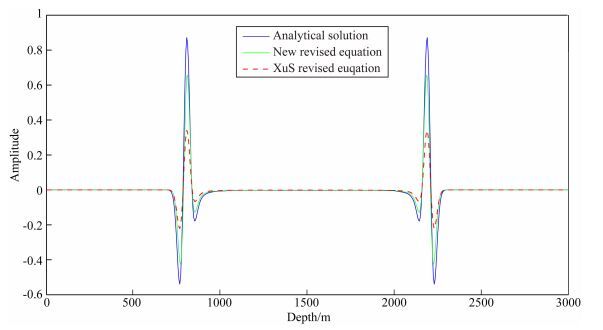
图 8 z=1.5 km处沿水平方向qP波场的单道波形图 蓝线:解析解方程;红虚线:Xu等(2015)的椭圆分解方程;绿线:本文椭圆分解方程. Fig. 8 Waveforms of qP wavefield at z=1.5 km in horizontal direction Blue solid line: analytical equation; Red dash line: Xu′s elliptical decomposed equation; Green solid line: elliptical decomposed equation proposed in this paper. |
|
图 9 x=1.5 km处沿垂直方向qP波场的单道波形图 蓝线:解析解方程;红虚线:Xu等(2015)的椭圆分解方程;绿线:本文椭圆分解方程. Fig. 9 Waveforms of qP wavefield at x=1.5 km in depth direction Blue solid line: analytical equation; Red dash line: Xu′s elliptical decomposed equation; Green solid line: elliptical decomposed equation proposed in this paper. |
P波:
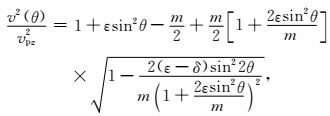
|
(12) |
SV波:
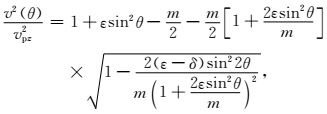
|
(13) |
其中θ表示沿着对称轴的相角,vpz表示纵波速度,vs0表示横波速度,ε和δ是各向异性参数(Thomsen, 1986).上式中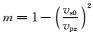
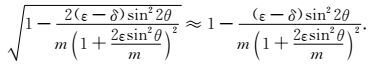
|
(14) |
将近似平方根算子的表达式(14)代入P波和SV波相速度表达式,得到P波和SV波相速度近似表达式为:
P波:
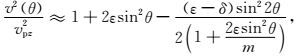
|
(15) |
SV波:
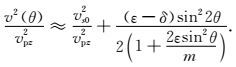
|
(16) |
根据相速度频率波数域关系式有:
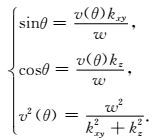
|
(17) |
将(17)代入方程(15)、(16)可得Tsvankin(1996)提出P波和SV波的精确频散关系为:
P波:
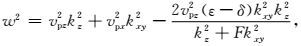
|
(18) |
SV波:
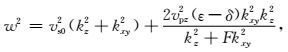
|
(19) |
其中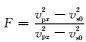
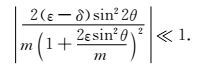
|
(20) |
结合方程(18),通过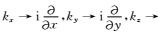
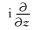
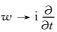
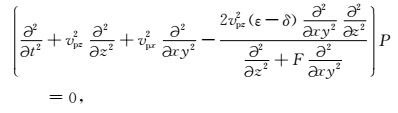
|
(21) |
其中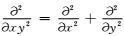
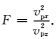
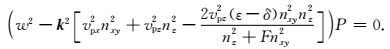
|
(22) |
在方程(22)中代入vpx、vpz、vpn、F各自的表达式,求得本文采用的标量算子S表达式为:
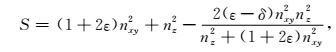
|
(23) |
其中nxy2=nx2+ny2,空间域k2=∇·∇,∇·表示散度,∇表示梯度,可将方程(23)代入方程(22)并简化,得到本文的时间域二阶纯qP波方程,其简化表达式为:
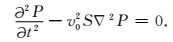
|
(24) |
方程(9)、(11)和(23)分别是标量算子S三种不同的求法,方程(24)是简化后的时间域二阶纯qP波方程,将三种不同的标量算子S分别代入方程(24)可以构建三种不同的纯qP波方程.其中利用方程(9)求得的标量算子构建的纯qP波方程来进行qP波数值模拟,其效果最差,数值误差最为严重.因为它是直接基于Alkhalifah声学近似频散关系利用Xu和Zhou(2014)提出的偏微分算子的分解方法而推导得到的,首先Alkhalifah声学近似频散关系是基于S波速为零提出的,简单地设定S波速为零并不能保证在声学近似的各向异性介质中沿着非对称轴方向的S波速度等于零(Grechka et al., 2004),会产生假象干扰,破坏了原刚度矩阵的正定性,忽略了多解性,因此会产生严重的数值误差.方程(11)是Xu和Zhou(2014)在方程(9)的基础上引入衰减项d推导得到的,用其求出的标量算子进行qP波数值模拟,假象干扰得到很好地压制,能较精确地描述qP波在介质中的传播规律.但是由于衰减项d的引入,对其在构建纯qP波椭圆分解方程(Xu et al., 2015)进行振幅校正时,会造成振幅不准确.方程(23)是基于Tsvankin精确频散关系利用Xu和Zhou(2014)提出的偏微分算子的分解方法推导得到的标量算子S的表达式,无需引入衰减项,能较精确地描述qP波在介质中的运动学特征,无假象干扰.但是在这些方程中标量算子S都是是利用波矢量来求取的,而波矢量是通过波场梯度一阶渐近近似得到的(见方程(8)),而在波场梯度趋近零的地方,标量算子S的计算是不准确的(Xu and Zhou, 2014).于是Xu和Zhou(2014)构建复合算子S∇P,并采取对其求散度的方式来改进了原始纯qP波方程(见方程(24)),一定程度地解决这问题,Xu和Zhou(2014)改进后的纯qP波方程简化表达式为:
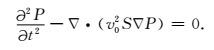
|
(25) |
然后分别将方程(9)(11)和(23)代入方程(25),即将标量算子S的三种不同求法代入方程(25),可以得到三种不同的纯qP波方程,其中将方程(11)代入方程(25)得到的纯qP波方程即是Xu和Zhou(2014)引入衰减项d而构建的纯qP波方程;将方程(9)代入方程(25)得到直接基于Alkhalifah声学近似频散关系推导的纯qP波方程,数值误差严重;将方程(23)代入方程(25)得到本文改进后的纯qP波方程,即本文采用的纯qP波方程,无需引入衰减项,改进后qP波波场求解方式能更加精确地描述qP波在介质中的运动学特征.
3 纯qP波椭圆分解方程虽然Xu和Zhou(2014)改进了各向异性介质中纯qP波的求解方法,构建复合算子S∇P,并对其求散度来求解qP波方程,以此来解决标量算子S计算不准确的问题,但是由于标量算子S中的一阶近似项,在垂直于对称轴方向上仍然会导致波场振幅弱(Xu et al., 2015).根据Xu和Zhou(2014)构建的二阶纯qP波方程,即方程(25),将其改写为:
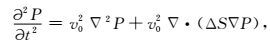
|
(26) |
其中标量算子S=1+ΔS.方程右边第一项为背景项,即各向同性项;第二项为校正项,用来校正由于背景项造成的频散误差,这种分解偏微分算子的方法可以看作是球形分解法.但是由于标量算子S计算存在渐近近似项,所以这种球形分解法的适用性差,仍然存在数值误差(Xu et al., 2015).
为了更好地解决这问题,减小标量算子S中近似项的影响,Xu等(2015)提出了一种椭圆分解方法,将方程(24)中的Laplace算子,即∇·∇,替换成一种椭圆差分算子,并对标量算子S进行修正得到椭圆差分算子Se,并使其仍能代表qP波相速度的精确方向,这种椭圆分解方法能对垂直于对称轴方向的波场振幅进行校正,使其更加均衡.Xu等(2015)构建的纯qP波椭圆分解方程的表达式为:
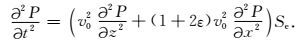
|
(27) |
对标量算子S进行修正得到椭圆差分算子Se,其推导过程为:
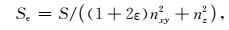
|
(28) |
修正后标量算子Se的表达式为:
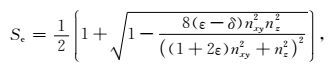
|
(29) |
其中v0为沿着对称轴方向的速度,其他参数物理意义和上文所述一样.但是这个椭圆差分算子Se是直接对基于Alkhalifah声学频散关系推导的标量算子S(即方程(9))进行修正而得到的,应用此算子进行qP波数值模拟,仍然会存在严重数值误差.于是引入衰减项d,将方程(11)按照方程(28)进行改写,即可以得到改进后的椭圆差分算子Se的表达式为:
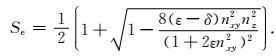
|
(30) |
借助于这种椭圆分解方法(Xu et al., 2015),本文对基于Tsvankin精确频散关系推导得到的标量算子S也进行修正,将方程(23)代入方程(28)进行改写,得到了本文采用的椭圆差分算子Se,其也仍能精确代表qP波相速度方向.本文采用椭圆差分算子Se的表达式为:
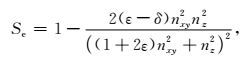
|
(31) |
然后将方程(30)代入方程(27)中构建出本文所用的纯qP波椭圆分解方程.
将方程(30)和(31)分别代入方程(27)能分别构建出改进后Xu等(2015)的纯qP波椭圆分解方程和本文采用的纯qP波椭圆分解方程,这两个方程的区别在于椭圆差分算子Se不同.因为本文的纯qP波椭圆差分算子Se仍然是基于Tsvankin精确频散关系推导得到的.由于方程(30)是通过引入衰减项而推导得到的,导致在对垂直于对称轴方向的振幅进行校正后振幅均衡但振幅值不准确,振幅值偏小,而方程(31)没有引入衰减项,采用椭圆分解法,更好地对垂直于对称轴方向的振幅进行校正,校正后的振幅均衡,并且振幅值也更加准确.为了验证这个观点,基于Alkhalifah的近似频散关系,推导出了qP波的解析解(Alkhalifah, 2000),其表达式为:
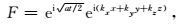
|
(32) |
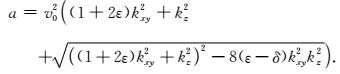
|
(33) |
然后分别利用这三个方程分别在均匀各向异性介质中进行了qP波数值模拟,其中qP波解析解方程在波数域实现qP波数值模拟,另外两个方程在时间域实现qP正演模拟,并抽取单道波形进行了振幅分析,阐明本文纯qP波椭圆分解方程能对垂直于对称轴方向的振幅进行很好地校正的原因,其校正后的振幅更加准确,下文通过模型试算作详细分析说明.
4 模型试算基于Tsvankin精确频散关系,本文构建了时间域二阶纯qP波方程和纯qP波椭圆分解方程,一方面很好地压制了假象干扰,数值计算更加准确、稳定.另一方面大大地减少了计算量和存储量,而且纯qP波椭圆分解方程采用了椭圆分解法,能更好地校正波场振幅,提高精度.然后分别采用本文构建的纯qP波方程、Xu和Zhou(2014)构建的纯qP波方程以及直接基于Alkhalifah近似频散关系利用偏微分算子分解法(Xu and Zhou, 2014)构建的纯qP波原始方程,实现了均匀各向异性介质中有限差分交错网格正演模拟,并将其结果进行对比分析,验证了本文构建的纯qP波方程的正确性.再利用本文构建的纯qP波椭圆分解方程,Xu等(2015)改进后的纯qP波椭圆方程以及qP波解析解方程进行均匀VTI介质正演模拟,沿垂直对称轴方向抽取单道进行振幅分析,说明了Xu等(2015)构建的qP波椭圆分解方程振幅均衡但不准确的原因,突出本文构建的纯qP波椭圆分解方程在振幅校正方面的优势,并将其应用于均匀TTI介质正演模拟.最后选取BP TTI模型分别利用Xu等(2015)构建的纯qP波椭圆分解方程和本文构建的纯qP波椭圆方程进行了正演模拟,对得到qP波波场快照进行分析,进一步说明了本文构建的纯qP波椭圆分解方程是正确的和有效的,且在振幅校正方面是具有一定优势的.
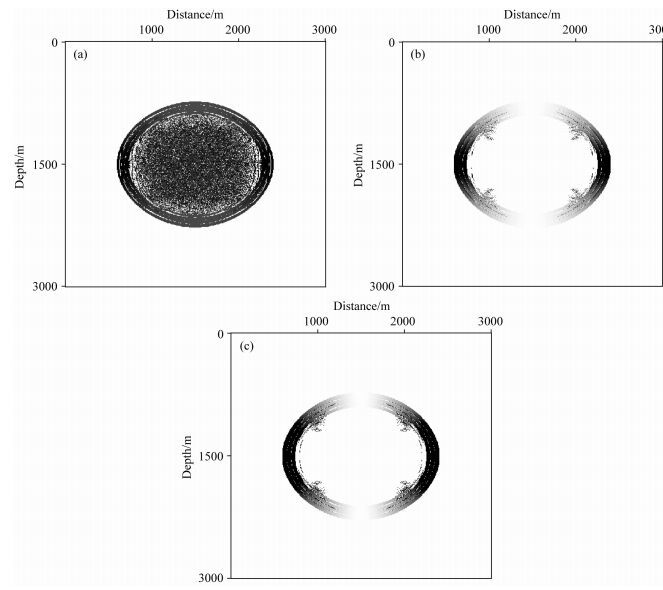
4.1 均匀各向异性介质模型正演模拟为了验证本文构建的纯qP波方程的正确性,本文分别用直接基于Alkhalifah近似频散关系利用偏微分算子分解法构建的纯qP波原始方程(方程(9)和(25))(Xu and Zhou, 2014)、Xu和Zhou(2014)提出的纯qP波方程(方程(11)和(25))以及本文构建的纯qP波方程(方程(23)和(25))在均匀各向异性介质中做了简单的数值模拟,并分别沿垂直于对称轴方向及对称轴方向抽取单道波形进行了对比分析.模型大小601×601×601,网格间距dx=dy=dz=5 m, 采样时间dt=1 ms.模型速度设为2000 m·s-1,各向异性参数ε=0.2、δ=0.1.震源采用雷克子波,主频为20 Hz,震源位置(1500, 1500, 1500).如图 1、图 2和图 3所示,分别是利用纯qP波原始方程、Xu和Zhou(2014)的方程以及本文构建的纯qP波方程在均匀VTI介质中进行了纯qP波正演模拟得到的标量算子S、混合算子S∇P和qP波波场快照.其中,图 1a、1b和1c分别是利用三种方程得到的t=0.1 s时沿y轴中心方向标量算子S的二维切片.由于这三种方程都是用梯度函数来近似求取波矢量,在梯度函数趋于零的位置,标量算子S的求取是不准确的,对复合算子S∇P求散度,能一定程度地解决这一问题(Xu and Zhou, 2014).因此文中也将方程(25)中复合算子S∇P输出并与标量算子S进行对比.如图 2所示,图 2a是利用由Alkhalifah近似频散关系直接推导的纯qP波方程(方程(9)和(25))进行纯qP波正演模拟得到的t=1.0 s时沿y轴中心方向复合算子S∇P的二维切片;图 2b是利用Xu和Zhou(2014)的纯qP波方程(方程(11)和(25))进行纯qP波正演模拟得到的在t=1.0 s时沿y轴中心方向复合算子S∇P的二维切片;图 2c是利用本文构建的纯qP波方程(方程(23)和(25))进行纯qP波正演模拟得到的在t=1.0 s时沿y轴中心方向复合算子S∇P的二维切片.不难发现,在梯度函数趋于零的位置,复合算子S∇P的求取较标量算子S准确. 图 3是应用这三种方程得到的t=1.0 s时沿y轴中心方向qP波波场快照二维切片.其中,图 3a利用由Alkhalifah近似频散关系直接推导的纯qP波方程进行纯qP波正演模拟得到的t=1.0 s时沿y轴中心方向qP波波场快照二维切片;图 3b是利用Xu和Zhou(2014)的方程行纯qP波正演模拟得到的t=1.0 s时沿y轴中心方向qP波波场快照二维切片;图 3b是利用本文构建的纯qP波方程进行纯qP波正演模拟得到的t=1.0 s时沿y轴中心方向qP波波场快照二维切片.
|
图 1 沿y轴中心方向标量算子S的二维切片 (a) qP波原始方程(方程(9)和(25));(b) Xu和Zhou(2014)的方程(方程(11)和(25));(c)本文方程(方程(23)和(25)). Fig. 1 2D seismic slices of scalar operator S along the middle of y direction (a) qP wave original equation (Equations (9) and (25)); (b) Xu′s equation (Equations (11) and (25)); (c) Equations proposed in this paper (Equations (23) and (25)). |

|
图 2 沿y轴中心方向复合算子S∇P的二维切片 (a) qP波原始方程(方程(9)和(25));(b) Xu等(2014)的方程(方程(11)和(25));(c)本文方程(方程(23)和(25)). Fig. 2 2D seismic slices of composition operator S∇P along the middle of y direction (a) Original qP wave equation (Equations (9) and (25)); (b) Xu′s equation (Equations (11) and (25)); (c) Equations proposed in this paper (Equations (23) and (25)). |
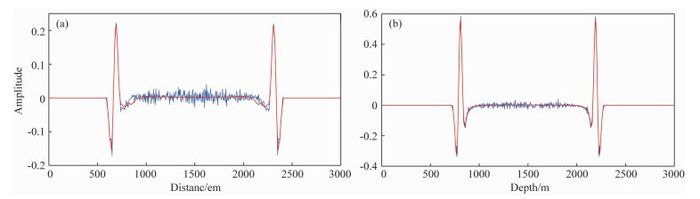
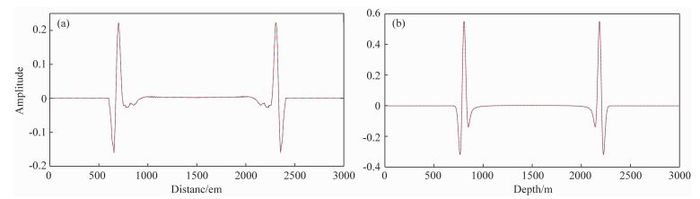
然后将图 1、图 2和图 3所示的正演模拟得到的结果相互对比分析,并分别沿x、z方向抽取了由这三种方程得到的qP波波场的单道(第301道)进行波形比较.如图 4和图 5所示,图 4表示的是将纯qP波原始方程(方程(9)和(25))与Xu和Zhou(2014)的纯qP波方程(方程(11)和(25))正演模拟得到的qP波波场分别沿x、z向抽取的第301道单道波形;图 5表示的是将Xu和Zhou(2014)的纯qP波方程(方程(11)和(25))和本文构建的纯qP波方程(方程(23)和(25))正演模拟得到的qP波波场分别沿x、z向抽取的第301道单道波形.可以发现,应用方程(9)和方程(25)进行各向异性介质中qP波正演模拟,即直接利用Alkhalifah近似频散关系构建的纯qP波原始方程进行各向异性介质中qP波正演模拟,其求解的标量算子S和复合算子S∇P都存在严重数值误差,这些数值误差就是由于直接假定横波速度为零而引起的,从而导致了正演模拟得到的qP波波场中存在一些假象干扰,不能准确描述qP波在介质中的传播规律.在方程(9)中加入衰减项d得到方程(11),利用方程(11)和方程(25),即Xu和Zhou(2014)的纯qP波方程,进行qP波正演模拟,其求解的标量算子S和复合算子S∇P数值误差小,能较精确地描述qP波在VTI介质中的传播特征.利用方程(23)和方程(25),即本文构建能较精确计算VTI介质中qP波的传播,而且不用加入衰减项,无假象干扰,数值误差小.而且通过图 4和图 5可以看出,沿x、z方向分别抽取的单道波形,其波场振幅值相差很大,因此利用这三种方程得到的波场沿垂直对称轴方向振幅都不准确,波场振幅都不均衡.
|
图 4 qP波场的单道波形对比1 (a) z=1.5 km处沿x方向抽取的单道波形;(b) x=1.5 km处沿z向抽取的单道波形.红虚线:Xu和Zhou(2014)方程(方程(11)和(25))蓝线:qP波原始方程(方程(9)和(25)). Fig. 4 First comparison of single trace of qP wavefield (a) Waveforms of single trace of qP wavefield at z=1.5 km in x direction; (b) Waveforms of single trace of qP wavefield at x=1.5 km in z direction. Red dash line: Xu′s equation(Equations (11) and (25)); blue solid line: original qP wave equation (Equations (9) and (25)). |
|
图 5 qP波场单道波形对比2 (a) z=1.5 km处沿x方向抽取的单道波形;(b) x=1.5 km处沿z向抽取的单道波形.红虚线:Xu和Zhou(2014)方程(方程(11)和(25))蓝线:本文方程(方程(23)和(25)). Fig. 5 Second comparison of single trace of qP wavefield (a) Waveforms of single trace of qP wavefield at z=1.5 km in x direction; (b) Waveforms of single trace of qP wavefield at x=1.5 km in z direction. Red dash line: Xu′s equation (Equations (11) and (25)); blue solid line: equations proposed in this paper(Equations (23) and (25)). |
然后将Xu和Zhou(2014)的方程和本文方程应用于TTI介质中,需要分别对这两个方程进行了坐标轴旋转,可设TI介质对称轴和XOZ平面内的观测系统Z轴夹角为θ,此角度称为极角;与XOY平面内X轴夹角设为φ,称为方位角.因此可引入旋转矩阵R将方程(25)由VTI介质转换为TTI介质中,旋转矩阵R为(Zhan et al., 2012):
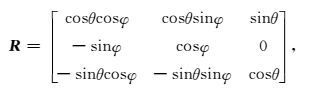
|
(34) |
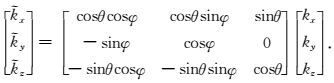
|
(35) |
由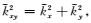
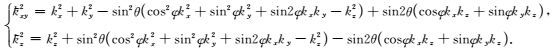
|
(36) |
根据本文提到的相方向单位矢量的求取方式(见式(5)),可以将式(36)代入式(5)得到TTI介质相方向单位矢量求取表达式为:
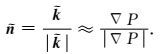
|
(37) |
将式(36)和(37)代入方程(11)和(23)中可以得到TTI介质中Xu和Zhou(2014)求取标量算子S方程式和TTI介质中本文提出的标量算子S方程式为:Xu和Zhou(2014)标量算子:
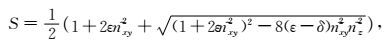
|
(38) |
本文标量算子:
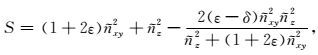
|
(39) |
其中:
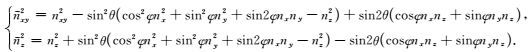
|
(40) |
然后将方程(36)、(38)、(39)和(40)分别代入方程(25)(即纯qP波简化方程)分别可以得到Xu和Zhou(2014)的TTI介质纯qP波方程和本文的TTI介质纯qP波方程,分别利用这两个方程进行了TTI介质中的纯qP波正演模拟,选取倾角θ为45°,方位角φ为0°,其他各向异性参数与VTI介质中的各向异性参数一样.图 6表示的是均匀TTI介质中利用Xu和Zhou(2014)的纯qP波方程和本文方程所得到的纯qP波正演模拟结果,较精确地描述TTI介质中的qP波传播规律.其中,图 6a、6b和6c分别是在t=1.0 s时利用Xu和Zhou(2014)的纯qP波方程得到沿y轴中心方向标量算子S、混合算子S∇P及qP波波场快照的二维切片;图 6d、6e和6f则分别是在t=1.0 s时利用本文方程得到沿y轴中心方向标量算子S、混合算子S∇P及qP波波场快照的二维切片.对比分析可以说明,本文构建的纯qP波方程(方程(39)、(40)和(25))能够较精确地描述TTI介质中qP波的传播特征,同Xu和Zhou(2014)的方程效果相当,验证了本文方法的正确性.虽然这两中方程都能较为精确地描述qP波在各向异性介质中的传播规律,但是利用其得到的波场沿垂直对称轴方向振幅都不准确,波场振幅都不均衡.

|
图 6 TTI介质中纯qP波正演模拟(方程(36)、(38)、(39)、(40)和(25)) (a) t=0.1 s时沿y轴中心方向标量算子S的二维切片(方程(36)、(38)、(40)和(25));(b) t=0.1 s时沿y轴中心方向复合算子S∇P的二维切片(方程(36)、(38)、(40)和(25));(c) t=0.1 s时沿y轴中心方向qP波波场快照的二维切片(方程(36)、(38)、(40)和(25));(d) t=0.1 s时沿y轴中心方向标量算子S的二维切片(方程(36)、(39)、(40)和(25));(e) t=0.1 s时沿y轴中心方向复合算子S∇P的二维切片((方程(36)、(39)、(40)和(25));(f) t=0.1 s时沿y轴中心方向qP波波场快照的二维切片((方程(36)、(39)、(40)和(25)). Fig. 6 Pure qP wave forward modeling in TTI medium (Equations (36), (38), (39), (40) and (25)) (a) 2D seismic slice of scalar operator S along the middle of y direction at time t=0.1 s(Equations (36), (38), (40) and(25)); (b) 2D seismic slice of scalar operator S∇P along the middle of y direction at time t=0.1 s(Equations (36), (38), (40) and (25)); (c) 2D snapshot of qP wavefield along the middle of y direction at time t=0.1 s (Equations (36), (38), (40) and (25)); (d) 2D seismic slice of scalar operator S along the middle of y direction at time t=0.1 s (Equations (36), (39), (40) and (25)); (e) 2D seismic slice of scalar operator S∇P along the middle of y direction at time t=0.1 s (Equations (36), (39), (40) and (25)); (f) 2D snapshot of qP wavefield along the middle of y direction at time t=0.1 s (Equations (36), (39), (40) and (25)). |
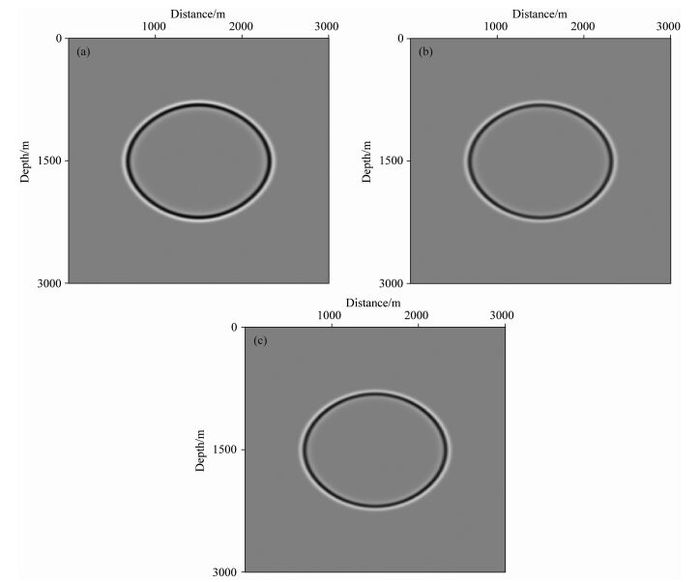
从图 3、图 4、图 5和图 6可以发现,不管是在VTI介质中还是在TTI介质中,qP波场振幅不均衡,沿着垂直于对称轴方向的振幅不准确.于是我们分别利用Xu等(2015)的纯qP波椭圆分解方程、本文的纯qP波椭圆分解方程和解析解方程进行了VTI介质中的qP波正演模拟.模型大小601×601×601,网格间距dx=dy=dz=5 m, 采样时间dt=1 ms.模型速度设为2000 m·s-1,各向异性参数ε=0.2、δ=0.1.震源采用雷克子波,主频为20 Hz,震源位置(1500, 1500, 1500).其中,图 7a是t=0.1 s时利用qP波解析方程得到的VTI介质中沿y轴中心方向的qP波波场快照二维切片;图 7b是t=0.1 s时利用Xu等(2015)的纯qP波椭圆分解方程得到的VTI介质中沿y轴中心方向的qP波波场快照二维切片;图 7c是t=0.1 s时利用本文构建的纯qP波椭圆分解方程得到的VTI介质中沿y中心方向的qP波波场快照二维切片.然后我们分别沿垂直于对称轴方向和对称轴方向抽取了这三个波场的单道波形进行振幅分析,图 8是沿垂直于对称轴方向抽取的单道波形图,图 9是沿对称轴方向抽取的单道波形图.通过振幅对比可以发现,本文构建的纯qP波椭圆分解方程和Xu等(2015)提出的纯qP波椭圆分解方程都能很好地对振幅进行校正,使其更加均衡,但是利用本文构建的纯qP波椭圆分解方程得到的qP波波场振幅值更加接近解析解.因为本文方程在求取标量算子S时不用引进衰减项d来压制假象干扰,减小数值误差,由于衰减项的引入,从而导致振幅校正不准确.
|
图 7 VTI介质中不同纯qP波椭圆分解方程正演模拟(方程(27)、(30)、(31)、(32)和(33)) (a) t=0.1 s时沿y轴中心方向的qP波波场快照二维切片(方程(32)和(33));(b) t=0.1 s时qP波场沿y轴中心方向的qP波波场快照二维切片(方程(27)和(30));(c) t=0.1 s时沿y轴中心方向的qP波波场快照二维切片(方程(27)和(31)). Fig. 7 Forward modeling of different pure qP wave elliptical decomposed equations in VTI medium (Equations (27), (30), (31), (32) and (33)) (a) 2D snapshot of qP wavefield along the middle of y direction at time t=0.1 s(Equations (32) and (33)); (b) 2D snapshot of qP wavefield along the middle of y direction at time t=0.1 s(Equations (27) and (30)); (c) 2D snapshot of qP wavefield along the middle of y direction at time t=0.1 s (Equation (27) and (31)). |
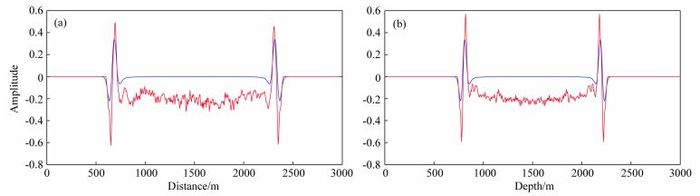
为了验证这一想法的正确性和有效性,先利用本文基于Alkhalifah近似频散关系推导的未加衰减项的纯qP波椭圆分解方程(27)和(29)进行qP波正演模拟.如图 10所示,图 10a即是利用未加衰减项的纯qP波椭圆分解方程在VTI介质中进行qP波正演模拟得到的t=0.1 s时波场快照二维切片,图 10b即是利用改进的Xu等(2015)的纯qP波椭圆分解方程得到的t=0.1 s时波场快照二维切片.其他参数与上文一样.然后分别沿垂直于对称轴和平行于对称轴方向抽取单道(第301道)波形,进行振幅分析,如图 11所示,可以发现,利用的未加衰减项的纯qP波椭圆分解方程得到的qP波波场,虽然存在严重的数值误差,但是其振幅较利用改进的Xu等(2015)的纯qP波椭圆分解方程得到的波场振幅大,而且振幅均衡.因此可以知道,加入衰减项后,会导致了波场振幅校正不准确,振幅均衡但振幅值偏小.

|
图 10 VTI介质中不同纯qP波椭圆分解方程正演模拟(方程(27)、(29)和(30)) (a)未加衰减项(方程(27)和(29));(b)加衰减项(方程(27)和(30)). Fig. 10 Forward modeling of qP waves using different pure elliptical decomposed equations in VTI medium (Equations (27), (29) and (30)) (a) Equations without attenuating terms added (Equations (27) and (29)); (b) Equations with attenuating terms added (Equations (27) and (30)). |
|
图 11 VTI介质中qP波场单道波形分析 (a, b)说明同图 4、5;红线:未加衰减项(方程(27)和(29));蓝线:加衰减项(方程(27)和(30)). Fig. 11 Waveform analysis of single trace of qP wavefield in VTI medium Red line: equations without attenuating terms (Equations (27) and (29)); Blue line: equations with attenuating terms (Equations (27) and (30)). |
因此,相比于Xu等(2015)提出的纯qP波椭圆分解方程,利用本文构建纯qP波椭圆分解方程得到的qP波波场振幅更加准确,能更为准确地描述各向异性介质中地震波的运动学特征.然后将其推广到TTI介质中,根据前文提到坐标轴旋转方法而得到波数旋转表达式(见方程(38)、(39)和(40)),可以将其代入椭圆差分算子(见方程(30)和(31))中得到Xu等(2015)TTI介质中椭圆差分算子和本文提出的TTI介质中椭圆差分算子,公式为:Xu等(2015)椭圆差分算子:
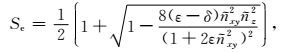
|
(41) |
本文椭圆差分算子:
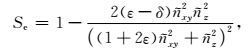
|
(42) |
其中:
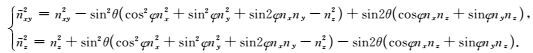
|
将方程(41)、(42)和(40)分别代入方程(27)(即纯qP波椭圆分解方程)分别可以得到Xu等(2015)提出的TTI介质纯qP波椭圆分解方程和本文提出的TTI介质纯qP波椭圆分解方程,然后将式(36)(旋转波数表达式)分别代入这两个方程及解析解方程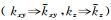

|
图 12 TTI介质中不同纯qP波椭圆分解方程正演模拟(方程(41)、(42)、(40)、(27)、(35)、(36)、(32)和(33)) (a) t=0.1 s时沿y轴中心方向的qP波波场快照二维切片(方程(36)、(32)和(33));(b) t=0.1 s时沿y轴中心方向的qP波波场快照二维切片(方程(36)、(27)、(41)和(40));(c) t=0.1 s时沿y轴中心方向的qP波波场快照二维切片(方程(36)、(27)、(42)和(40)). Fig. 12 Forward modeling of different pure qP wave elliptical decomposed equations in TTI medium (Equations (41), (42), (40), (27), (36), (32)和(33)) (a) 2D snapshot of qP wavefield along the middle of y direction at time t=0.1 s(Equations (36), (32) and (33)); (b) 2D snapshot of qP wavefield along the middle of y direction at time t=0.1 s (Equations (36), (27), (41) and (40)); (c) 2D snapshot of qP wavefield along the middle of y direction at time t=0.1 s (Equations (36), (27), (42) and (40)). |
通过均匀TI介质中正演模拟结果,可以知道,本文构建的纯qP波方程和纯qP波椭圆分解方程都能较精确描述qP波在TI介质中的传播特征,其中本文基于Tsvankin精确频散关系构建的纯qP波方程,无需引入衰减项,也能保证数值计算稳定、准确,其计算精度与Xu和Zhou(2014)提出的纯qP波方程相当,但是Xu和Zhou(2014)引入了衰减项,用来压制干扰以提高计算精度.但是利用本文构建的纯qP波方程进行数值运算时,会导致垂直对称轴方向的振幅不均衡,因此本文利用椭圆分解法(Xu et al., 2015)构建了纯qP波椭圆分解方程,其在振幅校正方面较Xu等(2015)构建的纯qP波椭圆分解方程更有优势,由于没有引进衰减项,其校正后的振幅值也更为准确.
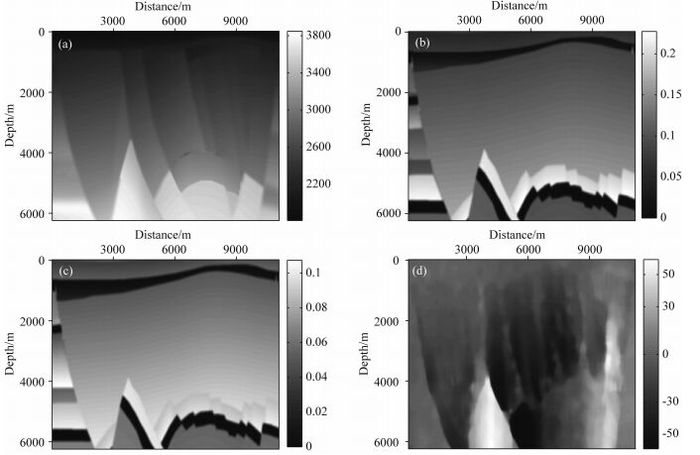
4.2 BP模型正演模拟为了突出本文构建的纯qP波椭圆分解方程的优势和适应性,以二维情况为例进行说明,本文选取了BP TTI模型(部分)进行正演模拟.如图 13所示,我们截取BP模型的一部分,模型大小为1771×1001,网格间距为dx=6.25 m,dz=6.25 m.图 13a、13b、13c和13d分别为模型的P波速度场、ε模型、δ模型以及θ模型.震源采用主频为30 Hz的雷克子波,时间采样间隔dt=0.7 ms,采用MPML吸边界条件(Dmitriev and Lisitsa, 2012),其宽度npad=48.先将震源设在(5500, 3000)处,我们分别应用的Xu等(2015)构建的纯qP波椭圆分解方程和本文的纯qP波椭圆分解方程对BP模型进行正演试算.如图 14所示,图 14a和14b分别表示的是应用Xu等(2015)提出的纯qP波椭圆分解方程和本文构建的纯qP波椭圆分解方程所得到的t=1.4 s时的qP波波场快照.对比图 14a和14b,明显发现两者波场能量值不一样,波场振幅值差异.可以发现图 14b中红箭头所指区域波场振幅值要高于图 14a中红箭头所指区域波场振幅值,根据前文对均匀TI介质模型的试算,可以知道利用本文推导的纯qP波椭圆分解方程由于没有引进衰减项对qP波振幅值校正更为准确,其校正后振幅值也要高于利用Xu等(2015)构建的纯qP波椭圆分解方程对qP波振幅值进行校正后的振幅值,进一步说明了本文构建了纯qP波椭圆分解方程对于复杂模型中波场振幅值校正也是有效的,而且较Xu等(2015)构建的纯qP波椭圆分解方程更有优势,由于没有引进衰减项,其校正后的振幅值也更为准确.
|
图 13 BP部分模型:P波速度场(a)、ε模型(b)、δ模型(c)、θ模型(d) Fig. 13 Part of BP model: P wave velocity(a), ε model(b), δ model(c), θ model(d) |
|
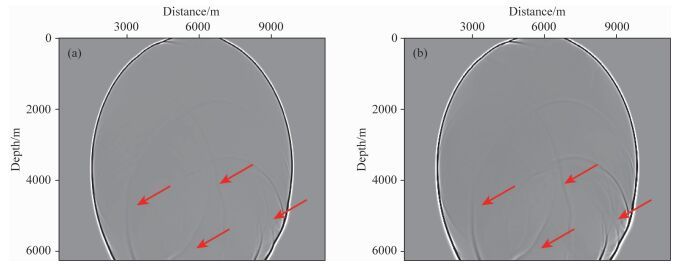
图 14 BP模型正演模拟波场快照对比(方程(27)、(40)、(41)和(42)) (a) Xu等(2015)的纯qP波椭圆分解方程;(b)本文的纯qP波椭圆分解方程. Fig. 14 Comparison of snapshots of qP wavefield in BP model(Equations (27), (40), (41) and (42)) (a) Xu′s elliptical decomposed equation; (b) Elliptical decomposed equation proposed in this paper. |
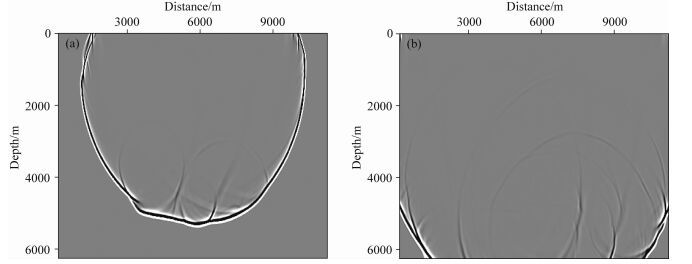
在TI介质正演模拟中,角度剧烈变化易导致数值计算不稳定,为了验证本文构建的纯qP波椭圆分解方程在角度剧烈变化处仍能保证数值计算的稳定,我们将震源点设在(5500, 0)处,利用本文构建的纯qP波椭圆分解方程对BP模型进行了正演试算.如图 15所示,图 15a和15b分别是利用本文构建的纯qP波椭圆分解方程对BP模型进行正演试算而得到的t=2.1 s和t=2.8时的波场快照,从qP波场传播情况可以看出,角度剧烈变化处数值计算仍是稳定、准确的,而且数值误差小.这表明了利用本文构建的纯qP波椭圆分解方程对于复杂TTI模型也是适用的,数值计算稳定性强,假象干扰少,进而验证了本文构建纯qP波椭圆分解方程的方法是可行而且有效的,突出了其应用优势.
|
图 15 BP模型正演模拟波场快照(方程(27)、(40)和(42)) 震源位置(5500, 0):(a) t=2.1 s时qP波波场快照;(b) t=2.8 s时qP波波场快照. Fig. 15 Snapshots of qP wavefield in BP model (Equations (27), (40) and (42)) Source at (5500, 0) : (a) Snapshot of qP wavefield at t=2.1 s; (b) Snapshot of qP wavefield at t=2.8 s. |
根据上文的模型正演试算,可知本文构建的纯qP波椭圆分解方程能较为精确地描述qP波在TI介质中的传播特征,而且在振幅校正方面具有一定的优势.为了验证本文构建的纯qP波椭圆分解方程在逆时偏移中的可行性,在二维情况下,本文分别选取选取了逆冲模型(见图 16)和BPTTI部分模型(见图 13)进行逆时偏移成像,其中逆冲模型给定了θ模型,也可以看作是简单TTI模型.通过利用本文构建的纯qP波椭圆分解方程对这两种模型进行逆时偏移成像,可以验证本文构建的纯qP波椭圆分解方程在TI介质逆时偏移成像中的可行性和适用性.
|
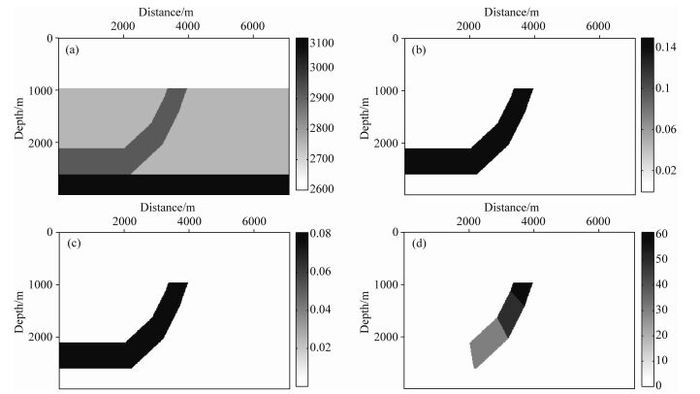
图 16 逆冲模型:P波速度场(a)、ε模型(b)、δ模型(c)、θ模型(d) Fig. 16 Thrust model: P wave velocity(a), ε model (b), δ model (c), θ model(d) |
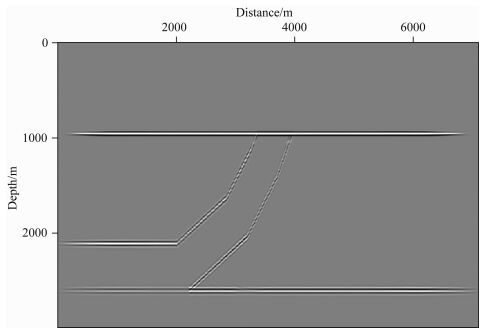
如图 16所示,分别是逆冲模型的P波速度场,ε模型、δ模型和θ模型.同样是采用30 Hz的雷克子波,共布设142炮,炮间隔为50 m,每炮检波器个数为650,均匀分布于震源两侧,检波器间隔为10 m,时间采样长度为2.75 s,时间采样间隔为0.5 ms,边界条件采用MPML吸收边界条件(Dmitriev and Lisitsa, 2012),其宽度为npad=32(网格点),成像条件采用震源归一化互相关.图 17是应用本文椭圆分解方程得到的逆冲模型逆时偏移成像结果.从图 17中可以看出,逆冲模型断层构造成像清晰,在高陡倾角断层面处也有很好的成像效果,同相轴连续性较好.
|
图 17 逆冲模型逆时偏移结果 Fig. 17 Reverse time migration results of thrust model |
应用本文纯qP波椭圆分解方程(方程(27)、(40)和(42))对逆冲模型(TTI)进行了逆时偏移成像,通过其成像结果分析可知本文构建的纯qP椭圆分解方程在TI介质逆时偏移成像中是可行的,验证了本文的纯qP波椭圆分解方程构建方法的可行性.
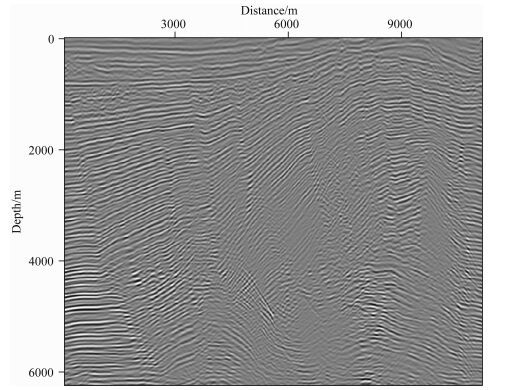
5.2 BP模型逆时偏移为了说明本文构建的纯qP波椭圆分解方程对复杂TI模型的适用性,我们选取了部分BP TTI模型来进行逆时偏移.如上文图 13所示,即是我们要进行逆时偏移成像的BP TTI模型,我们已经采用这个模型进行了正演试算,这里就不对其参数做详细地说明.震源采用30 Hz的雷克子波,共布设220炮,炮间隔为50 m,每炮检波器个数为650,均匀分布于震源两侧,检波器间隔为6.25 m,时间采样长度为4.76 s,时间采样间隔为0.7 ms,边界条件采用MPML吸收边界条件,其宽度为npad=48(网格点),成像条件采用震源归一化互相关.图 18是应用本文构建的纯qP波椭圆分解方程得到的BP模型逆时偏移成像结果.从图 18中可以看出,BP模型深层构造同相轴连续性较好,断块构造较为清晰,表明了本文构建的纯qP波椭圆分解方程构建方法可以应用于复杂TTI模型逆时偏移成像中,验证此方程的适用性.
|
图 18 BP模型逆时偏移结果(部分) Fig. 18 Reverse time migration results of part of BP model |
Xu和Zhou(2014)利用声波近似频散关系,将四阶拟声波方程中的偏微分算子分解成一个Laplace算子和一个标量算子S,构建了二阶纯qP波方程.本文利用Tsvankin(1996)提出的精确频散关系,利用近似展开的方法,同样地将偏微分算子分解,推导出各向异性介质中二阶纯qP波方程.
(1) 这个推导过程无需设置横波速度为0,所以求取的标量算子S更加准确,不用引入衰减项d,就能很好地压制假象干扰,减小数值误差,但是Xu和Zhou(2014)的纯qP波方程人为设置了横波速度为0,只有引入衰减项d,才能很好地压制假象干扰.
(2) 标量算子S的求取需要求解波矢量,波矢量用波场梯度近似,导致了波场振幅的不准确、不均衡,基于Xu等(2015)提出的椭圆分解法,将其应用于本文构建的二阶纯qP波方程中推导出了纯qP波椭圆分解方程,很好地对波场振幅进行了校正,并与Xu等(2015)构建的纯qP波椭圆分解方程对比分析.可以知道,由于本文纯qP波椭圆分解方程中没引入衰减项,校正后的波场振幅值均衡而且更加准确.
(3) 本文将交错网格有限差分算法(参考由Alkan等(2013)提出的DG网格差分算法)和MPML吸收边界条件(Dmitriev and Lisitsa, 2012)应用于均匀TI介质、复杂BP TI模型的正演模拟中,通过qP波波场快照对比和振幅分析,验证了本文方程的正确性、有效性和适用性,并突出了本文构建的qP波椭圆分解方程在振幅校正方面的优势.
(4) 本文将构建的各向异性纯qP波椭圆分解方程应用于叠前逆时偏移技术中,采用归一化互相关成像条件,对TI模型(逆冲模型和BP模型)实现了逆时偏移成像,能够对高陡构造很好地成像,同相轴连续性较好,符合模型真实的构造特征,验证了本文方程在逆时偏移成像中的可行性和对复杂TI介质的适用性.
虽然本文构建的各向异性纯qP波方程能够较准确地描述qP波在各向异性介质中的运动学特征,但是地震波在透射与反射过程中会出现能量损失,而且还存在波场逆时传播高频不稳定、深部能量弱等问题,如何实现各向异性介质中纯qP波保幅成像,还需要进一步的研究.
Alkan E, Demir V, Elsherbeni A Z, et al. 2013. Double-Grid Finite-Difference Frequency-Domain (DG-FDFD) Method for Scattering from Chiral Objects.: Morgan & Claypool Publishers.
|
|
Alkhalifah T.
1998. Acoustic approximations for processing in transversely isotropic media. Geophysics, 63(2): 623-631.
DOI:10.1190/1.1444361 |
|
Alkhalifah T.
2000. An acoustic wave equation for anisotropic media. Geophysics, 65(4): 1239-1250.
DOI:10.1190/1.1444815 |
|
Cheng J B, Chen M G, Wang T F, et al.
2014. Description of qP-wave propagation in anisotropic media, Part Ⅱ: Separation of pure-mode scalar waves. Chinese Journal of Geophysics, 57(10): 3389-3401.
DOI:10.6038/cjg20141025 |
|
Cheng J B, Kang W, Wang T F.
2013. Description of qP-wave propagation in anisotropic media, Part Ⅰ: Pseudo-pure-mode wave equations. Chinese Journal of Geophysics, 56(10): 3474-3486.
DOI:10.6038/cjg20131022 |
|
Dellinger J, Etgen J.
1990. Wave-field separation in two-dimension anisotropic media. Geophysics, 55(7): 914-919.
DOI:10.1190/1.1442906 |
|
Dmitriev M N, Lisitsa V V.
2012. Application of M-PML absorbing boundary conditions to the numerical simulation of wave propagation in anisotropic media. Part Ⅱ: Stability. Numer. Analys. Appl., 5(1): 36-44.
DOI:10.1134/S1995423912010041 |
|
Du X, Bancroft J C, Lines L R. 2005. Reverse-time migration for tilted TI media.//2005 SEG Annual Meeting. Houston, Texas: SEG, 1930-1933.
|
|
Duveneck E, Milcik P, Bakker P M, et al. 2008. Acoustic VTI wave equations and their application for anisotropic reverse-time migration.//2008 SEG Annual Meeting. Las Vegas, Nevada: SEG, 2186-2190.
|
|
Fletcher R P, Du X, Fowler P J.
2009. Reverse time migration in tilted transversely isotropic (TTI) media. Geophysics, 74(6): WCA179-WCA187.
DOI:10.1190/1.3269902 |
|
Fowler P J, Du X, Fletcher R P.
2010. Coupled equations for reverse time migration in transversely isotropic media. Geophysics, 75(1): S11-S22.
DOI:10.1190/1.3294572 |
|
Ge Z, Pestana R C, Stoffa P L. 2011. An acoustic wave equation for pure P wave in 2D TTI media.//81st Annual International Meeting. SEG, 168-173.
|
|
Grechka V, Zhang L B, Rector J W.
2004. Shear waves in acoustic anisotropic media. Geophysics, 69(2): 576-582.
DOI:10.1190/1.1707077 |
|
Hestholm S.
2009. Acoustic VTI modeling using high-order finite differences. Geophysics, 74(5): T67-T73.
DOI:10.1190/1.3157242 |
|
Liu F Q, Morton S A, Jiang S S, et al. 2009. Decoupled wave equations for P and SV waves in an acoustic VTI media.//2009 SEG Annual Meeting. Houston, Texas: SEG, 2844-2848.
|
|
Thomsen L.
1986. Weak elastic anisotropy. Geophysics, 51(10): 1954-1966.
DOI:10.1190/1.1442051 |
|
Tsvankin I.
1996. P-wave signatures and notation for transversely isotropic media: an overview. Geophysics, 61(2): 467-483.
DOI:10.1190/1.1443974 |
|
Wu G C, Liang K.
2005. Quasi P-wave forward modeling in frequency-space domain in VTI media. Oil Geophysical Prospecting, 40(5): 535-545.
|
|
Wu G C, Liang K.
2007. High precision finite difference operators for qP wave equation in VTI media. Progress in Geophysics, 22(3): 896-904.
|
|
Wu G C, Liang K, Yin X Y.
2010. The analysis of phase velocity and polarization feature for elastic wave in TTI media. Chinese Journal of Geophysics, 53(8): 1914-1923.
|
|
Xu S, Zhou H B.
2014. Accurate simulations of pure quasi-P-waves in complex anisotropic media. Geophysics, 79(6): T341-T348.
DOI:10.1190/geo2014-0242.1 |
|
Xu S, Tang B, Mu J, et al. 2015. Quasi-P wave propagation with an elliptic differential operator.//2015 SEG Annual Meeting. New Orleans, Louisiana: SEG, 4380-4384.
|
|
Yan J, Sava P.
2009. Elastic wave-mode separation for VTI media. Geophysics, 74(5): WB19-WB32.
DOI:10.1190/1.3184014 |
|
Zhan G, Pestana R C, Stoffa P L.
2012. Decoupled equations for reverse time migration in tilted transversely isotropic media. Geophysics, 77(2): T37-T45.
DOI:10.1190/geo2011-0175.1 |
|
Zhang H Z, Zhang G Q, Zhang Y. 2009. Removing S-wave noise in TTI reverse time migration.//79th Annual International Meeting, SEG Expanded Abstracts. SEG, 2849-2853.
|
|
Zhang Y, Wu G C.
2013. Methods of removing pseudo SV-wave artifacts in TTI media qP-wave reverse-time migration. Chinese Journal of Geophysics, 56(6): 2065-2076.
DOI:10.6038/cjg20130627 |
|
Zhang Y, Zhang Houzhu, Zhang Guanquan.
2011. A stable TTI reverse time migration and its implementation. Geophysics, 76(3): WA3-WA11.
DOI:10.1190/1.3554411 |
|
Zhou H B, Zhang G, Bloor R. 2006a. An anisotropic acoustic wave equation for VTI media.//68th Annual International Conference and Exhibition. SPE, EAGE.
|
|
Zhou H B, Zhang G Q, Bloor R. 2006b. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media.//2006 SEG Annual Meeting. New Orleans, Louisiana: SEG, 194-198.
|
|
程玖兵, 康玮, 王腾飞.
2013. 各向异性介质qP波传播描述I:伪纯模式波动方程. 地球物理学报, 56(10): 3474–3486.
DOI:10.6038/cjg20131022 |
|
程玖兵, 陈茂根, 王腾飞, 等.
2014. 各向异性介质qP波传播描述Ⅱ:分离纯模式标量波. 地球物理学报, 57(10): 3389–3401.
DOI:10.6038/cjg20141025 |
|
吴国忱, 梁锴.
2005. VTI介质频率-空间域准P波正演模拟. 石油地球物理勘探, 40(5): 535–545.
|
|
吴国忱, 梁锴.
2007. VTI介质qP波方程高精度有限差分算子. 地球物理学进展, 22(3): 896–904.
|
|
吴国忱, 梁锴, 印兴耀.
2010. TTI介质弹性波相速度与偏振特征分析. 地球物理学报, 53(8): 1914–1923.
|
|
张岩, 吴国忱.
2013. TTI介质qP波逆时偏移中伪横波噪声压制方法. 地球物理学报, 56(6): 2065–2076.
DOI:10.6038/cjg20130627 |
|
 2017, Vol. 60
2017, Vol. 60

