储层参数,如矿物含量、孔隙度、油气饱和度等,是储层储能参数和产能参数计算的重要输入,是地震油藏描述和地震油藏监测的目标属性.地震振幅信息包含了丰富的弹性和储层信息,如何利用地震资料实现储层参数反演是当前地震储层研究的热点.现阶段,应用程度较高的储层参数预测方法是首先利用地震反演从地震振幅信息获取弹性信息,进一步在弹性信息基础上反演储层参数.经过几十年的发展,基于褶积模型的地震反演理论与应用已相对成熟(Maureau and van Wijhe,1979;Angeleri and Carpi, 1982;Sen and Stoffa, 1991;Pendrel et al., 2000;Ma,2001;Sen and Roy, 2003;Hampson and Russell, 2005).国内外学者针对从弹性参数到储层参数的反演取得了一系列研究成果.Doyen(1988)将考虑空间约束的地质统计学方法应用于从地震资料预测孔隙度的研究工作中;Blangy(1992)提出利用岩石物理模型构建弹性参数与储层参数之间的物理关系,并实现储层参数的反演;Marion和Jizba(1997)将基于岩石物理模型的储层参数反演方法用于实际的项目研究并取得了较好的预测结果;Mukerji等(2001)将岩石物理理论、统计识别技术与地质统计学方法相结合反演储层参数;Bosch等(2002)比较了三种常用分类方法(聚类分析、高斯分类和判别分析)在储层分类中的应用效果;Fu(2002, 2004)和吴媚等(2008)提出应用非线性岩性物性褶积模型建立波阻抗与储层参数(粘土含量、孔隙度)关系,利用神经网络方法实现确定性反演、统计反演和非线性理解的结合,并将该方法应用于实际区块取得较好效果;Bachrach(2006)利用统计岩石物理模型实现孔隙度与饱和度的同时估计;Spikes等(2007)提出一种井数据与地震约束下的概率反演方法来实现储层参数预测;Grana和Rossa(2010)在贝叶斯理论框架下,假设储层参数服从混合高斯分布,利用统计岩石物理模型,进行储层参数后验概率分布估计和储层参数反演;巴晶等(2013)基于Biot-Rayleigh方程得到了非饱和岩石的多尺度岩石物理建模,预测了不同尺度下地震响应特征与储层参数之间的定量关系,提出了一种基于弹性阻抗的储层参数反演方法;印兴耀等(2014)利用弹性阻抗反演稳定性,提出一种基于弹性阻抗的储层物性参数预测方法,避免由于密度反演不准确而使得物性参数反演存在较大的误差的问题;桂金咏等(2015)将基于统计岩石物理的贝叶斯储层参数反演推广到双相介质.
应用较为广泛的储层参数反演方法可以分为多元统计方法(Doyen,1998;Mukerji et al., 2001;Bosch et al., 2002)、岩石物理建模方法(Blangy,1992;Marion and Jizba, 1997;Spikes et al., 2007;Grana and Rossa, 2010;巴晶等,2013;印兴耀等, 2014;桂金咏等,2015)及混合方法(Fu, 2002, 2004)等.与基于弹性参数与储层参数间统计关系的统计方法相比,岩石物理建模方法具有物理意义明确、模型精度高等优点(Bosch et al., 2010).对于基于岩石物理模型的储层参数反演,岩石物理模型的合理性和适用性起着至关重要的作用(Bosch et al., 2010).由于岩石内部矿物成分排列方式、孔隙形状及孔隙流体分布特征的差异较大,学者提出了大量的岩石物理模型来描述岩石储层参数与弹性参数之间的关系.如接触理论(Mindlin, 1949;Digby, 1981;Walton, 1987)和接触-胶结理论(Dvorkin and Nur, 1996)常被用于高孔未固结或弱交接沉积岩的岩石物理建模中.Avseth等(2005)将接触-胶结理论应用于纯净砂岩中,并能够高精度地预测岩石的弹性特征.包体模型因其考虑了孔隙的形状能够更好地描述固结岩石的岩石物理特征(Kuster and Toksöz, 1974;Sheng, 1990;Berryman, 1992).包体模型在泥页岩、碳酸盐岩和固结砂岩中都有成功的应用(Hornby et al., 1994;Agersborg et al., 2008;Dræge et al., 2006).此外,经验模型也是较为常用的岩石物理模型(Krief et al., 1990;Nur et al., 1998).除了接触-胶结模型、包体模型及经验模型外,随着数值岩心技术的发展,三维数值岩石物理模型越来越地应用于页岩气等非常规油气藏的弹性特征描述中(Zhang et al., 2016).其中,经验模型和接触-胶结模型因其数学形式相对简单、储层参数与弹性参数之间为线性关系或可以进行线性化等优点,在基于岩石物理模型的储层参数反演中应用广泛(Spikes et al., 2007;Bosch,2010;Grana,2012;巴晶等, 2013桂金咏等,2015).自洽模型与微分等效介质模型等包体模型的应用,由于数学形式复杂、储层参数与弹性参数之间没有解析表达式、孔隙影响涉及迭代运算等问题,在储层参数反演中应用有限(Johansen et al., 2013;印兴耀等, 2014).为了将包体模型应用于储层参数反演并兼顾计算效率,Keys和Xu(2002)提出了Xu-White模型(Xu and White, 1995)的近似形式.Grana(2016)针对包体模型的泰勒展开式进行高阶截止,实现包体模型的线性化.
作为解决非线性优化问题最有效的方法之一,信赖域方法被广泛应用于各个领域(Conn et al., 2000;Busygin,2006;Zhang et al., 2010).该方法特别适用于解决组合优化、最小二乘问题、约束特征值等问题.相比线性搜寻算法,信赖域方法有可靠和稳健的结果,可以用于病态问题,并有很强的收敛性(Yuan,1999).不同于在每次迭代中进行搜索的线性搜索方法,信赖域方法通过求解信赖域子问题,进行试探步长的计算.由于信赖区域约束,非凸模型可以用在信赖域子问题,因此信赖域算法对于非凸和病态问题都具有较强的适用性(Yuan,2015).冯国峰(2006)通过把信赖域技术和同伦方法引入到二维波动方程反问题的数值求解过程中,极大减少了多尺度反演算法的计算量.田玥和陈晓非(2006)将拟牛顿法与信赖域法相结合的反演方法用于地震震中和一维速度结构的联合反演,结果表明该方法不仅具有较高的计算效率和较高的反演精度, 同时也具有更强的总体收敛性,且对初始值不敏感.曾奇等(2011)应用信赖域方法于一维大地电磁反问题中,该方法表现出较强的抗噪能力.尽管最小二乘方法对于高斯噪声有着较强的压制作用,但是当数据中存在离群异常值或反演本身多解性较强时,会存在求解稳定性性问题.
本文将信赖域方法应用于基于包体模型的储层参数反演中,并利用纵向约束实现对离群噪声的压制.通过模型参数,针对该方法的计算效率、抗噪能力及不同弹性参数输入组合进行测试,表明了该方法的可行性和有效性.最后,将该方法应用于中孔-中渗砂岩储层的储层参数反演中,得到储层参数的空间分布.
2 方法原理 2.1 岩石物理建模岩石物理模型是描述岩石弹性参数与储层参数之间定量关系的有效工具.以砂泥岩地层为例,岩石物理模型能够将弹性参数(纵波阻抗Pimp、纵横波速度比VP/VS、密度ρ)描述为粘土含量C、孔隙度φ、含水饱和度SW的函数.在中低孔隙度渗透率砂岩储层中,基于包体模型的Xu-White模型是较为常用描述储层参数与弹性参数的工具(Xu and White, 1995).这里以Xu-White模型为例,说明岩石物理建模的基本流程和基于包体模型的岩石物理关系特征.
岩石基质的弹性模量等效,即按照岩石固体矿物成分的体积比例,将岩石固体等效为一种均匀介质,常用的方法包括Wyllie时间平均方程(Wyllie et al., 1956)和Voigt-Ruess-Hill平均方法(Avseth et al., 2005).记Ks、Kc、Kw、Kh分别为石英、粘土、地层水和烃类的体积模量,μs、μc、μw、μh分别为石英、粘土、地层水和烃类的剪切模量,ρs、ρc、ρw、ρh分别为石英、粘土、地层水和烃类的密度,C、φ、SW分别为粘土含量、孔隙度和含水饱和度.利用Voigt-Ruess-Hill平均方法建立的岩石基质弹性模量和密度分为Km、μm和ρm:

|
(1) |
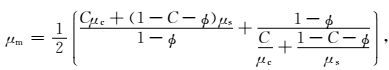
|
(2) |
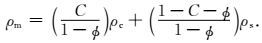
|
(3) |
在获得岩石基质等效模型的基础上,需要考虑岩石孔隙结构对于岩石弹性特征的影响,主要体现在对于干岩石弹性模量的建模上.在Xu-White模型中,利用微分等效介质模型或者自洽模型(Kuster andToksöz, 1974;Berryman, 1992)将干孔隙作为包体加载到岩石基质等效模型中,获得包含矿物和孔隙影响的干岩石模型.Kd、μd和ρd分别为依据微分等效介质模型(Berryman,1992)计算的干岩石体积模量、剪切模量和密度:
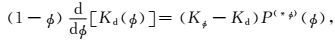
|
(4) |
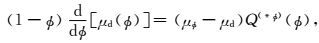
|
(5) |
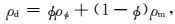
|
(6) |
其中,
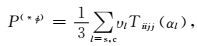
|
(7) |
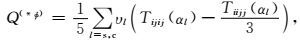
|
(8) |
式中,Kφ、μφ、ρφ分别为包体(填隙物)的体积模量、剪切模量和密度.在耦合方程(4) 和(5) 中,Kd和μd的初始值为Km和μm,P(*φ)和Q(*φ)为和孔隙结构相关的几何因子,υs和υc分别为石英孔隙和粘土孔隙的体积分数,αs和αc分别为石英孔隙和粘土孔隙的纵横比,Tiijj(αl)和Tijij(αl)为孔隙纵横比的函数(Keys and Xu, 2002).从式(4) 和(5) 中可以看出,包体的体积是逐渐加入背景中的,因此等效后的体积模量和剪切模量不存在解析形式.由于包含了反映孔隙几何结构的参数,基于包体的方法能够在考虑孔隙度整体影响的同时考虑将孔隙度结构,能够更好描述成岩阶段(中低孔隙度)的情况.由于包体模型长波长一次散射假设的要求,在干岩石建模一步中包体(填隙物)的速度和密度均置为0,保证等效结果与地震频带的一致性.
对于岩石孔隙中的地层流体,常用的方法是利用Batzle-Wang等实验室方法(Batzle and Wang, 1992),建立孔隙流体在不同温度压力环境下的弹性模型,并按照饱和度信息利用Wood方程(Wood,1955)计算等效孔隙流体的体积模量Kf和密度ρf:
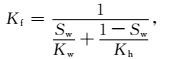
|
(9) |
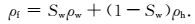
|
(10) |
利用Gassmann方程,在岩石基质模型、干岩石模型和流体模型基础上,实现孔隙流体的替换,建立包含实际流体特征的岩石物理模型(Gassmann,1951).包含流体岩石的体积模量Ksat、剪切模量μsat和密度ρsat为
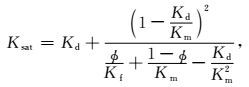
|
(11) |
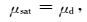
|
(12) |
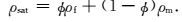
|
(13) |
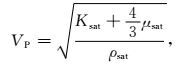
从公式(12) 中可以看出,流体替换前后岩石的等效剪切模型不发生变化,横波速度对流体的敏感性来自于孔隙流体造成的密度响应.由于Gassmann方程可以理解为Biot方程(Biot,1956)的低频极限,因此岩石物理建模结果符合地震资料的频带特征.包含流体岩石的纵波速度VP和横波速度VS:
|
(14) |
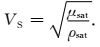
|
(15) |
基于最小二乘方法,储层参数反演中的目标函数可以表示为
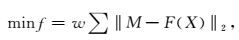
|
(16) |
其中w为权重系数,M为观测变量,F(X)为模型函数,X为求解变量.在储层参数反演中,X=[C, φ, Sw],包括矿物体积含量(粘土含量C)、孔隙度(φ)、含水饱和度(Sw)等,在井上可以通过测井地层评价来获得.M=[Pimp, VP/VS, ρ],包括纵波阻抗(Pimp)、纵横波速度比(VP/VS)、密度(ρ)等,根据不同的叠前反演方法,可以获得不同的参数组合.F为2.1中建立的岩石物理模型.当利用基于包体模型的Xu-White模型构建储层参数X([C, φ, Sw)]与弹性参数M([Pimp, VP/VS, ρ])之间的关系时,岩石物理函数F不仅是没有解析形式的、而且涉及迭代计算问题,储层参数与弹性参数之间是非线性关系.
在非线性反演理论中该问题可以通过基于全局优化算法(如蒙特卡洛、神经网络、遗传算法等)或者局部优化算法求解.但是全部优化算法需要海量的迭代次数才能保证收敛,计算效率低.局部优化算法根据校正步长确定方式的不同可分为线搜索算法和信赖域算法.线搜索算法先计算出参数的校正方向,再优化一个校正步长.根据所用校正方向不同有梯度法、共轭梯度法、拟牛顿法、牛顿法等,不同的校正梯度收敛速度不同,但对于多模问题,都存在着可能陷入局部极值的问题,即搜索不到有效的步长使目标函数收敛到全局最小.
信赖域方法虽然也基于目标函数的局部导数,但研究表明相比线搜索方法,能更好解决局部极值问题.其基本思想是先给定一个信赖域半径,以当前模型位置为中心,以该信赖域半径为距离划定一个扰动区域.然后通过求解这个区域内的“信赖域子问题”优化出最优的校正量.根据反演目标函数的收敛情况决定是否接收扰动、或进一步保持或扩大或缩小信赖域半径继续迭代.
第k次迭代步信赖域子问题形式为

|
(17) |
其中gk为目标函数的梯度,Hk为Hess矩阵,Δk为信赖域半径,d为优化得到的校正量.
求解式(11) 得到校正量dk后,求解
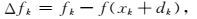
|
(18) |
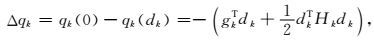
|
(19) |
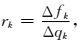
|
(20) |
其中Δfk为目标函数的实际下降量,Δqk为信赖域子问题优化校正量时预测的下降量,通过两者的比值rk修正下一次迭代的信赖域半径.rk接近1时表明迭代收敛很好可增大信赖域半径,rk小于零则表示不收敛,需要缩小信赖与半径.
信赖域方法的算法如下:
(1) 选取初始参数:参数初始值x0,初始信赖域半径Δ0,半径伸缩比例0<τ1<1<τ2,判断阈值0≤p0<p1<p2<1,收敛精度0≤ε≪1;令k=0;
(2) 计算梯度gk,若‖gk‖≤ε停止迭代;
(3) 构建信赖域子问题,并求解得到dk;
(4) 利用式(20) 计算rk;
(5) 判断并确定修正信赖域半径;
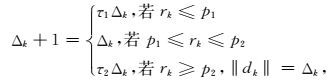
|
(21) |
(6) 若rk≥p0,保留原参数xk+1=xk;否则更新参数xk+1=xk+dk;令k=k+1,返回步骤(2).
2.3 约束最小二乘法根据反演理论,最小二乘反演对于数据中的高斯型噪声有很好的压制作用.然而当数据中存在非高斯型噪声,如有多解性或离群(outlier)异常值存在,最小二乘求解存在稳定性问题.对于这个问题,我们对其解进行空间的平坦约束.
然而考虑到反演的多解性以及其没有对各点进行相关约束,考虑对纵向空间点样本连续进行约束,我们加入纵向约束,则上式可以变为
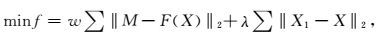
|
(22) |
其中X1为X纵向空间的前一样点,λ为控制因子.当存在多解或者离群噪音的情况下,上式施加最平坦最小约束(空间一阶导数最小),并用因子λ调节数据拟合和模型约束在总体目标函数中的权重.本文所用方法认为模型变量在纵向空间上具有相当连续性和平坦度.当存在数据误差导致无约束反演结果的连续性或平坦度被破坏时,通过增大平坦约束因子λ而适当降低数据拟合度使反演结果符合空间的平坦假设.
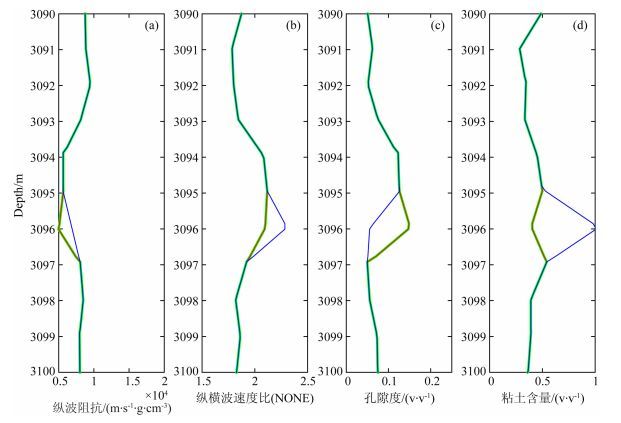
分别使用式(16) 和式(22) 对某理论模型数据进行反演,从图 1中可以看到,大部分情况两种最小二乘法反演得到的结果与原始观测数据基本重合,然而在3096段,式(16) 没有拾取到最佳反演结果,而式(22) 与观测数据则完全一致,说明了式(22) 在一定程度上优于式(16).
|
图 1 最小二乘方法对比 绿色为观测曲线,蓝色为正常最小二乘曲线,红色为改进最小二乘曲线.(a)纵波阻抗;(b)纵横波速度比;(c)孔隙度;(d)粘土含量. Fig. 1 Comparison between two different least square methods The green curves from observations, the blue curves from the common least square method and the red curves from the improved least square method. (a) P-wave impedance; (b) VP/VS; (c) Porosity; (d) Volume of clay. |
通过对上述模型数据的分析,我们可以看到改进的最小二乘法可以有效的避免一些反演多解性的问题,而又保持了反演的有效性.
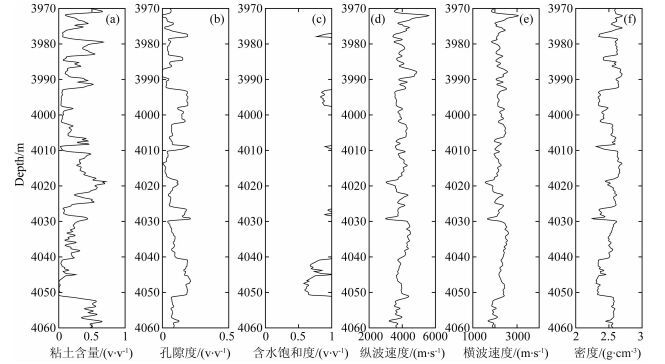
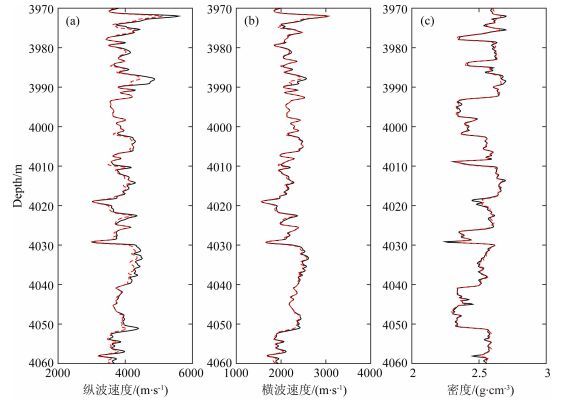
3 模型测试为了验证基于约束最小二乘与信赖域的储层参数反演方法的可行性,选取某井测量3970~4065 m层段作为测试的目标段.图 2为目标段测井地层评价获得的储层参数曲线(粘土含量、孔隙度、含水饱和度)和弹性曲线(纵波速度、速度、密度).以储层参数曲线为输入,根据公式(1) 到(15) 给出的Xu-White模型岩石物理关系式,正演弹性曲线.如图 3所示,黑色曲线为井上实测的纵波速度、横波速度和密度曲线;红色虚线为岩石物理正演的纵波速度、横波速度和密度曲线.正演曲线和测试曲线的相关度依次为纵波速度97.2%,横波速度96.1%,密度97.4%,验证了岩石物理的合理性和准确性.
|
图 2 目标段储层参数曲线与弹性曲线 (a)粘土含量;(b)孔隙度;(c)含水饱和度;(d)纵波速度;(e)横波速度;(f)密度. Fig. 2 The reservoir property and elastic logs in target zone (a) Volume of clay; (b) Porosity; (c) Water saturation; (d) P-velocity; (e) S-velocity; (f) Density. |
|
图 3 目标段实测弹性曲线与岩石物理正演弹性曲线对比 黑色为实测曲线,红色为岩石物理正演曲线.(a)纵波速度;(b)横波速度;(c)密度. Fig. 3 The comparison between real elastic logs and rock physics forwarding logs The black line is real and the red line is from rock physics forwarding. (a) P-velocity; (b) S-velocity; (c) Density. |
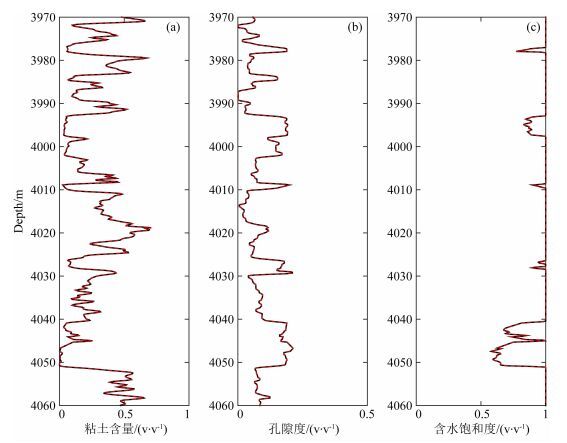
为了验证反演方法的有效性,以不含任何噪声的岩石物理正演弹性曲线(纵波阻抗、纵横波速度比和密度)为输入,反演储层参数(粘土含量、孔隙度和饱和度).从图 4可以看出,红色虚线所代表的反演储层参数与黑色曲线所代表的实测储层参数高度重合.储层参数反演得到的粘土含量、孔隙度和饱和度与实际值之间的相关性分别达到99.9%、99.9%和99.9%,证实了反演方法的有效性.
|
图 4 目标段储层参数曲线与岩石物理反演储层参数曲线对比(正演弹性曲线为输入) 黑色为实测曲线,红色为岩石物理反演曲线.(a)粘土含量; (b)孔隙度; (c)饱和度. Fig. 4 The comparison between real reservoir property logs and rock physics inversion ones (forwarding elastic logs as input) The black line is real and the red line is from rock physics inversion. (a) P-velocity; (b) S-velocity; (c) Density. |
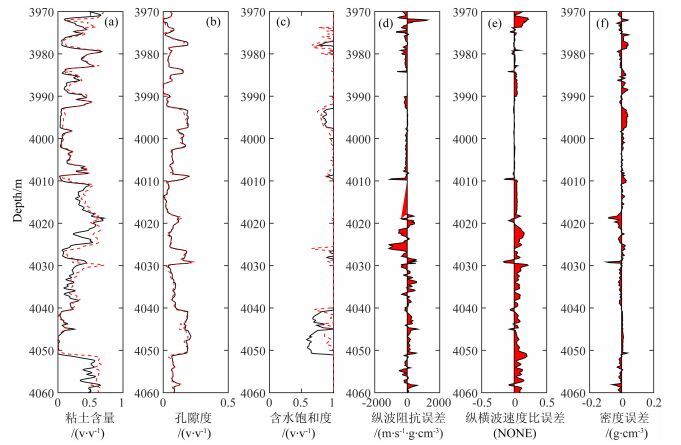
图 5给出了以实测弹性曲线(纵波阻抗、纵横波速度比和密度)为输入情况下,反演得到的储层参数曲线以及实测弹性曲线与岩石正演曲线之间的误差.与图 4中的反演结果相比,反演结果同实际的储层参数存在一定的差异,反演得到的粘土含量、孔隙度和饱和度与实际值之间的相关性分别为90.2%、97.6%和34.6%:(1) 反演的孔隙度曲线与实际曲线之间一致性最强,3977~3978 m和3993~3998 m两处预测孔隙度偏低,主要受到实测密度与正演密度相比偏高、导致储层预测结果偏致密造成的.4440~4450 m处预测孔隙度偏高,其原因是受到含气性预测偏低干扰.当含气性预测偏低时,反演得到的孔隙度只能偏高,才能保证反演结果与纵波阻抗值一致.(2) 反演得到的粘土含量曲线同实际的粘土含量曲线趋势基本一致,预测偏高的层段(4015~4030 m、4055~4060 m),主要是因为实测的纵横波速度比高于岩石物理正演结果,导致高纵横波速度比的粘土成分高于实际情况.(3) 测试层段共有上下两套含气砂岩,其中顶部含气砂岩在含水饱和度反演结果上表征较为清晰,底部含气砂岩预测失真,预测结果含气性偏低.对比两套砂岩的纵横波速度比曲线,第一套含气砂岩段实测纵横波速度比曲线与岩石物理正演曲线基本一致,第二套含气砂岩段实测纵横波速度比曲线明显高于岩石物理正演曲线,导致无法有效预测出该含气层.
|
图 5 目标段储层参数曲线与岩石物理反演储层参数曲线对比(实测弹性曲线为输入)及图 3中实测弹性曲线与岩石物理正演曲线之间的误差 黑色为实测曲线,红色为岩石物理反演曲线.(a)粘土含量; (b)孔隙度; (c)饱和度; (d)纵波阻抗误差; (e)纵横波速度比误差; (f)密度误差. Fig. 5 The comparison between real reservoir property logs and rock physics inversion ones(real elastic logs as input) and the difference between real elastic longs and rock physics forwarding ones in Fig. 3 The black line is real and the red line is from rock physics inversion. (a) P-velocity; (b) S-velocity; (c) Density; (d) Delta of P-impedance; (e) Delta of VP/VS; (f) Delta of density. |
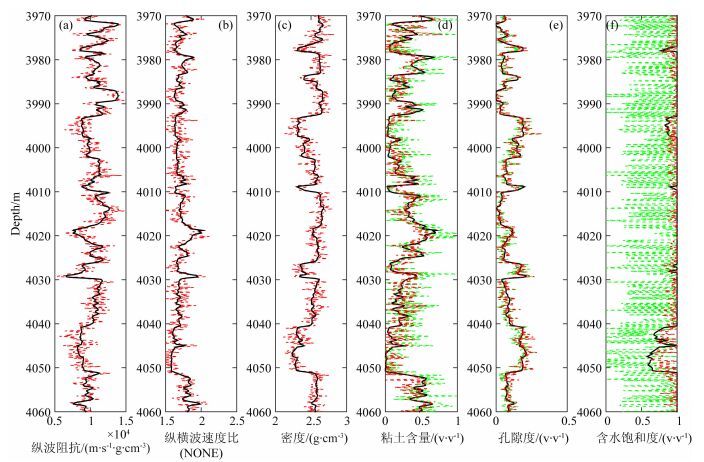
为了进一步明确噪声对于储层参数反演的影响,将高斯随机噪声加入到岩石物理正演的弹性曲线中作为储层参数反演的输入.如图 6所示,(a)、(b)和(c)分别为纵波阻抗、纵横波速度比和密度曲线,其中黑色实线是岩石物理正演的弹性曲线,红色虚线为正演曲线加入高斯随机噪声后的弹性曲线(信噪比为4).图中(d)、(e)和(f)为储层参数反演得到的粘土含量、孔隙度和含水饱和度曲线,其中黑色是实际的储层参数曲线,绿色为未加入垂向约束的反演结果,红色为加入垂向约束的反演结果.对于未使用垂向约束的储层参数反演,反演得到的粘土含量、孔隙度和含水饱和度同实际值之间的相关系数分别为74.9%、84.1%和28.5%,加入垂向约束的相关系数分别为77.8%、86.0%和48.0%.从图中曲线和相关系数可见,加入垂向约束后,提升了反演的稳定性和抗噪能力,改善了反演质量.
|
图 6 储层参数反演噪声敏感性分析 (a)纵波阻抗;(b)纵横波速度比;(c)密度;(d)粘土含量;(e)孔隙度;(f)含水饱和度. Fig. 6 The analysis of influence of noise on reservoir inversion results (a) P-impedance; (b) VP/VS; (c) Density; (d) Volume of clay; (e) Porosity; (f) Water Saturation. |
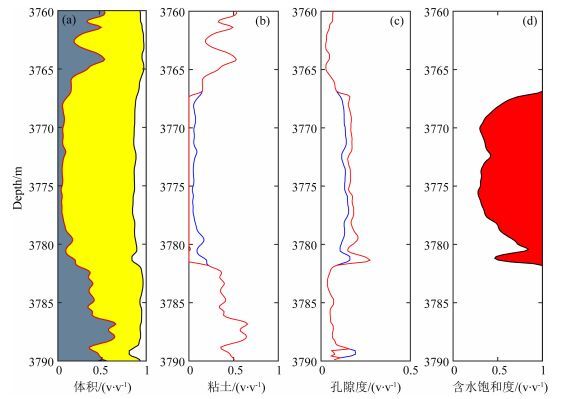
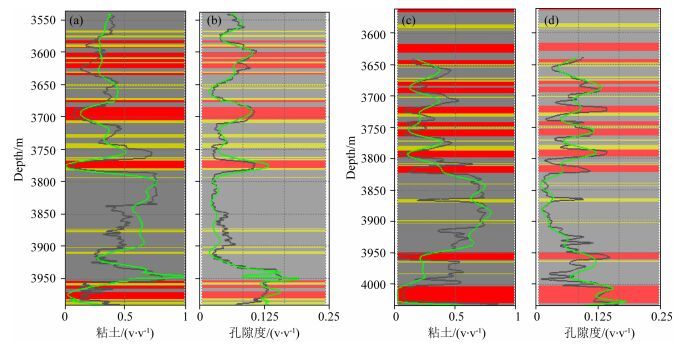
在储层参数反演中,反演的目标参数个数,受到输入弹性信息的限制.常规的叠前反演只能提供三个独立弹性参数(如纵波阻抗、纵横波速度比和密度),导致储层参数反演的目标不能高于三个.当地震道集的信噪比较低且入射角偏小时,叠前道集携带的密度信息较为有限,难于获得可靠的密度结果(Buland and More, 2003;Russell et al., 2011).当仅有纵波阻抗和纵横波速度比为输入时,储层参数反演只能计算两个参数,无法同时得到粘土含量、孔隙度和饱和度信息.图 7给出了假设含水饱和度为100%前提下,利用纵波阻抗和纵横波速度比反演粘土粘土含量和孔隙度的结果.从图 7可见,对于含水地层,反演得到的孔隙度和粘土含量与实际值相一致;对于含气层,反演得到的粘土含量偏低、孔隙度偏高.当储层含气时,储层的纵横波速度比和纵波阻抗都会降低.在两参数反演中,由于在含气层假定含水饱和度为100%,反演结果通过降低粘土含量和提高孔隙度,得到同含气层一样的低纵横波速度比和低纵波阻抗的弹性响应.尽管在含气层段储层参数反演的定量性降低,但是对于粘土含量较低、孔隙度较高的优质储层,仍然能够有效地进行定性识别.
|
图 7 两参数储层参数反演(局部放大) 蓝色为模型曲线,红色为反演曲线.(a)矿物体积; (b)粘土含量; (c)孔隙度; (d)含水饱和度. Fig. 7 Two parameter invert by forward elastic curves (Zoom in) The blue curves from modeling, the red curves from inversion. (a) Volume of mineral; (b) Volume of clay; (c) Porosity; (d) Water saturation. |
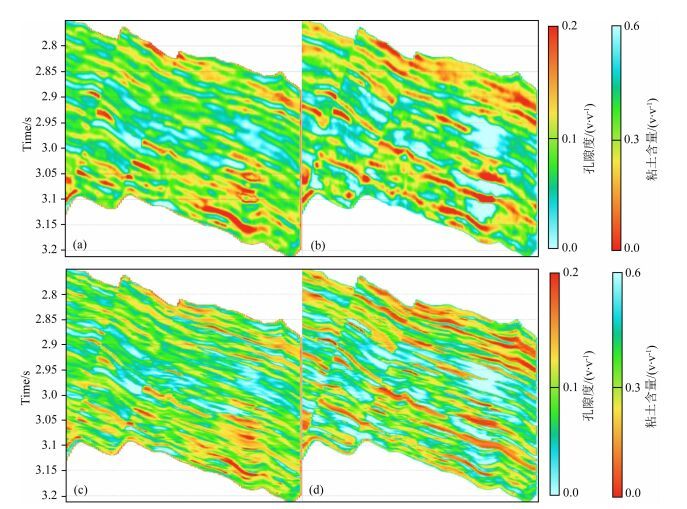
由于地震数据有限带宽的固有特点,导致常规叠前反演得到的弹性信息与井上弹性信息相比,缺乏明显的高频成分.因此,需要考虑地震反演弹性参数有限频带特征,对于储层参数反演的影响.利用地质统计学模拟得到储层参数,利用岩石物理正演将储层参数转化为纵波阻抗、纵横波速度比和密度等弹性参数,进行地震道集正演.然后,基于叠前同时反演方法,由合成道集反演出纵波阻抗和速度比,并进一步利用储层参数反演实现弹性参数到储层参数(粘土含量、孔隙度)的转换.图 8给出了反演结果同正演模型之间的对比.同实际模型相比,反演结果在垂向上将多套储层特征合并成一套,垂向分辨率明显降低.这是由于地震有限带宽的性质造成的.同时,反演结果对于储层横向变化的刻画也失去了模型原有的锐利边界.此外,反演结果的数值同模型数值之间也存在一定差异.图 9为在两参数储层参数反演数据体上随机抽取的两口伪井结果.反演得到的粘土含量和孔隙度(绿色)和高频切除的实际参数(黑色)之间仍然具有较好的相关性.
|
图 8 两参数储层参数反演(叠前反演纵波阻抗、纵横波速度比为输入) (a)反演的孔隙度; (b)反演的粘土含量; (c)模型孔隙度; (d)模型粘土含量. Fig. 8 Two parameter inverted by forward elastic curves (P-wave impedance and VP/VS inverted by pre-stack seismic) (a) Inverted porosity; (b) Inverted Volume of clay; (c) Input model porosity; (d) Input model volume of clay. |
|
图 9 伪井反演储层参数与模型参数对比 黑色为高频切除的模型曲线,绿色为反演曲线.(a)和(b)为第一口伪井的粘土含量和孔隙度; (c)和(d)为第二口伪井的粘土含量和孔隙度. Fig. 9 Reservoir parameter comparison between the pseudo well and model The black curves for high-cutting modeling ones, the green curves for inversion results. (a)—(b) Volume of clay and porosity from the first pseudo well; (c)—(d) Volume of clay and porosity from the second pseudo well. |
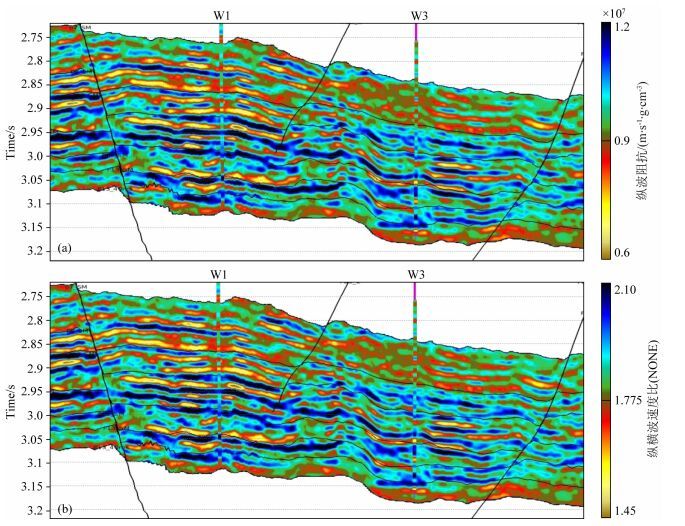
将本方法应用于某中低孔渗含气砂岩岩性油气藏研究区,该研究区目的层砂岩整体上呈现“泥包砂”特征,垂向上发育多套砂岩,横向上砂体连续性很差,为典型岩性油气藏.同时,砂岩内部非均质性较强,孔隙度差别较大,低孔隙度伴随的低渗透率特征,导致井间产能差异显著.需要通过粘土含量的预测,来有效识别砂体分布,并进一步结合孔隙度信息进行高效井优选.图 10为由叠前同时反演方法得到的纵波阻抗和纵横波速度比结果.在井点处,反演结果和井上的实测结果一致性较强,保证了储层参数反演输入数据的质量.
|
图 10 叠前反演结果与井数据对比 (a)纵波阻抗; (b)纵横波速度比. Fig. 10 Comparison between well curves and pre-stack seismic inverted results (a) P-wave impedance; (b) VP/VS. |
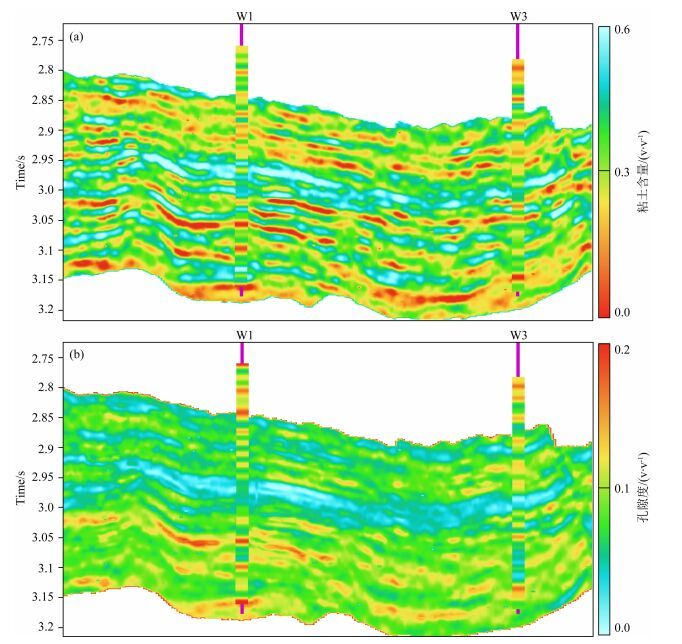
图 11为储层参数反演的结果.从图中的粘土含量反演结果中,能够清晰呈现砂泥岩的空间分布细节,可以用于砂体展布分析、边界刻画等地质研究工作.结合图中孔隙度反演结果,能够在砂体识别的基础上,评价砂体的储集能力,为井位优选工作提供依据.
|
图 11 储层参数反演粘土含量和孔隙度 (a)粘土含量; (b)孔隙度. Fig. 11 Inverted volume of clay and porosity (a) Volume of clay; (b) Porosity. |
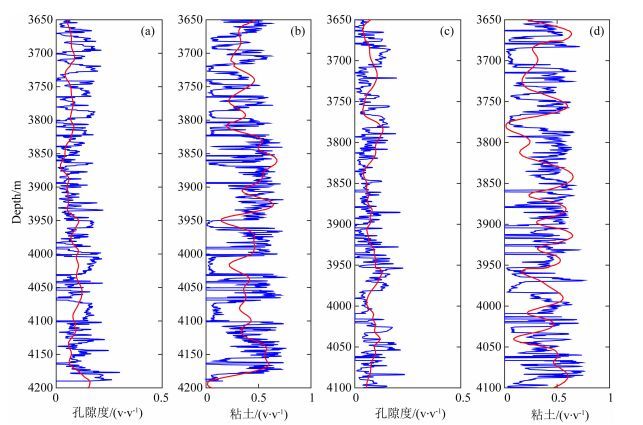
对于本应用中这样典型的岩性油气藏,储层参数可以进一步用于地质建模和油藏模拟工作,因此需要对反演结果的定量性进行分析.图 12为井点处储层参数反演结果与井上储层参数之间的对比.从图中可以看出,尽管由于地震有限频带造成红色的反演结果与蓝色的井上储层参数在分辨率上存在一定的差异,但是反演结果能够反应储层参数的变化趋势,用于砂泥岩变化和孔隙度的发育特征分析.
|
图 12 反演结果与实测对比 蓝色为实测曲线,红色为反演曲线.(a)和(b)为W1井的孔隙度和粘土含量; (c)和(d)为W3井的粘土含量和孔隙度. Fig. 12 Comparison between the inverted and the measured The blue curves from measured, the red curves from inversion. (a) and (b) for porosity and volume of clay of W1. (c) and (d) are porosity and volume of clay from W3. |
本文提出了基于约束最小二乘与信赖域的储层参数反演方法.通过理论数据分析,证明了该方法的有效性,信赖域方法的使用保证了反演的计算效率,垂向约束的引入能够有效提高反演方法的抗噪能力,在实际工区中取得了较好的效果.
(1) 本文利用信赖域方法收敛速度快、全局寻优的优点,实现诸如包体模型等非线性岩石物理模型的储层参数反演工作.通过理论模型正反演分析,验证了反演方法的有效性.
(2) 理论模型分析表明,不同的储层参数对于弹性数据噪声的敏感性存在差异,孔隙度和粘土含量的抗噪能力,明显高于含水饱和度.本文通过引入垂向约束,一定程度上提升了反演方法的抗噪能力,特别是改善了对噪声较为敏感的含水饱和度参数.在实际工作中,直接利用储层参数反演预测含水饱和度,需要特别关注弹性参数的噪声水平,并开展细致的可行性分析工作.
(3) 当地震道集信噪比较低、入射角较小时,仅利用叠前反演提供纵波阻抗和纵横波速度比信息,两参数的储层参数反演(假设含水饱和度100%,反演粘土含量和孔隙度)仍能够用于优质储层的识别和定性分析.对于中低孔隙度-渗透率储层,在非含气段,反演得到的粘土含量和孔隙度与实测曲线较为一致;在高含气段,粘土含量预测结果略低、孔隙度预测略高,对于优质储层存在放大效应.将两参数反演应用于某岩性油气藏的储层描述工作中,得到了可靠的粘土含量和孔隙度结果.
致谢本文作者感谢评审专家的指导意见.
Agersborg R, Johansen T A, Jakobsen M, et al.
2008. Effects of fluids and dual-pore systems on pressure-dependent velocities and attenuations in carbonates. Geophysics, 73(5): N35-N47.
DOI:10.1190/1.2969774 |
|
Angeleri G P, Carpi R.
1982. Porosity prediction from seismic data. Geophysical Prospecting, 30(5): 580-607.
DOI:10.1111/gpr.1982.30.issue-5 |
|
Avseth P, Mukerji T, Mavko G. 2005.
Quantitative Seismic Interpretation:Applying Rock Physics Tools to Reduce Interpretation Risk. New York: Cambridge University Press.
|
|
Ba J, Yan X F, Chen Z Y, et al.
2013. Rock physics model and gas saturation inversion for heterogeneous gas reservoirs. Chinese J. Geophys. , 56(5): 1696-1706.
DOI:10.6038/cjg20130527 |
|
Bachrach R.
2006. Joint estimation of porosity and saturation using stochastic rock-physics modeling. Geophysics, 71(5): O53-O63.
DOI:10.1190/1.2235991 |
|
Batzle M L, Wang Z J.
1992. Seismic properties of pore fluids. Geophysics, 57(11): 1396-1408.
DOI:10.1190/1.1443207 |
|
Berryman J G.
1992. Single-scattering approximations for coefficients in Biot's equations of poroelasticity. The Journal of the Acoustical Society of America, 91(2): 551-571.
DOI:10.1121/1.402518 |
|
Biot M A.
1956. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. Low-frequency range. The Journal of the Acoustical Society of America, 28(2): 168-178.
|
|
Blangy J P. 1992. Integrated seismic lithologic interpretation:The petrophysical basis. Stanford:Stanford University.
|
|
Bosch M, Mukerji T, Gonzalez E F.
Seismic inversion for reservoir properties combining statistical rock physics and geostatistics:a review. Geophysics, 75(5): 75A165-75A176.
DOI:10.1190/1.3478209 |
|
Bosch M, Zamora M, Utama W.
2002. Lithology discrimination from physical rock properties. Geophysics, 67(67): 573-581.
|
|
Buland A, Omre H. Bayesian linearized AVO inversion. Geophysics, 2003, 68(1):185-198.
|
|
Busygin S.
2006. A new trust region technique for the maximum weight clique problem. Discrete Applied Mathematics, 154(15): 2080-2096.
DOI:10.1016/j.dam.2005.04.010 |
|
Conn A R, Gould N I M, Toint P L. 2000. Trust-Region Methods, MPS-SIAM Series on Optimization. Philadelphia:Society for Industrial and Applied Mathematics.
|
|
Digby P J.
1981. The effective elastic moduli of porous granular rocks. Journal of Applied Mechanics, 48(4): 803-808.
DOI:10.1115/1.3157738 |
|
Doyen P M.
1988. Porosity from seismic data:A geostatistical approach. Geophysics, 53(10): 1263-1275.
DOI:10.1190/1.1442404 |
|
Dræge A, Johansen T A, Brevik I, et al.
2006. A strategy for modelling the diagenetic evolution of seismic properties in sandstones. Petroleum Geoscience, 12(4): 309-323.
DOI:10.1144/1354-079305-691 |
|
Dvorkin J, Nur A.
1996. Elasticity of high-porosity sandstones:Theory for two North Sea data sets. Geophysics, 61(5): 1363-1370.
DOI:10.1190/1.1444059 |
|
Fu L Y. 2002. Joint lithologic inversion.//Wong P, Aminzadeh F, Nikravesh M eds. Soft Computing for Reservoir Characterization and Modeling. Berlin Heidelberg:Springer, 511-530.
|
|
Fu L Y.
2004. Joint inversion of seismic data for acoustic impedance. Geophysics, 69(4): 994-1004.
DOI:10.1190/1.1778242 |
|
Gassmann F. 1951. Vber die Elastizität poröser Medien.//Vierteljahresschrift der Naturforschenden Gesellschaft in Zurich 96. 1-23.
|
|
Grana D, Rossa E D.
2010. Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion. Geophysics, 75(3).
|
|
Grana D, Mukerji T, Dvorkin J, et al. Stochastic inversion of facies from seismic data based on sequential simulations and probability perturbation method.//Seg Technical Program Expanded. 1949:1769-1773.
|
|
Grana D.
2016. Bayesian linearized rock-physics inversion. Geophysics, 81(6).
|
|
Gui J Y, Gao J H, Yong X S, et al.
2015. Inversion of reservoir parameters based on dual-phase media theory. Chinese J. Geophys. , 58(9): 3424-3438.
DOI:10.6038/cjg20150934 |
|
Hampson D P, Russell B H. 2005. Simultaneous inversion of pre-stack seismic data.//75th Annual International Meeting, SEG Technical Program Expanded Abstracts. Houston, Texas:SEG, 1633-1637.
|
|
Hornby B E, Schwartz L M, Hudson J A.
1994. Anisotropic effective-medium modeling of the elastic properties of shales. Geophysics, 59(10): 1570-1583.
DOI:10.1190/1.1443546 |
|
Johansen T A, Jensen E H, Mavko G, et al.
2013. Inverse rock physics modeling for reservoir quality prediction. Geophysics, 78(2): M1-M18.
DOI:10.1190/geo2012-0215.1 |
|
Keys R G, Xu S Y.
2002. An approximation for the Xu-White velocity model. Geophysics, 67(5): 1406-1414.
DOI:10.1190/1.1512786 |
|
Krief M, Garat J, Stellingwerff J, et al.
1990. A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic). The Log Analyst, 31(6): 355-369.
|
|
Kuster G T, Toksöz M N.
1974. Velocity and attenuation of seismic waves in two-phase media:Part Ⅰ. Theoretical formulations. Geophysics, 39(5): 587-606.
|
|
Ma X Q.
2001. A constrained global inversion method using an overparameterized scheme:Application to poststack seismic data. Geophysics, 66(2): 613-626.
DOI:10.1190/1.1444952 |
|
Marion D, Jizba D. 5. Acoustic Properties of Carbonate Rocks:Use in Quantitative Interpretation of Sonic and Seismic Measurements.//Carbonate Seismology. 1997:75-94.
|
|
Maureau G T F R, van Wijhe D H.
1979. The prediction of porosity in the Permian (Zechstein 2) carbonate of eastern Netherlands using seismic data. Geophysics, 44(9): 1502-1517.
DOI:10.1190/1.1441021 |
|
Mindlin R D.
1949. Compliance of elastic bodies in contact. Journal of Applied Mechanics, 16: 259-268.
|
|
Mukerji T, Avseth P, Mavko G, et al.
2001. Statistical rock physics:Combining rock physics, information theory, and geostatistics to reduce uncertainty in seismic reservoir characterization. The Leading Edge, 20(3): 313-319.
DOI:10.1190/1.1438938 |
|
Nur A, Mavko G, Dvorkin J, et al.
1998. Critical porosity:A key to relating physical properties to porosity in rocks. The Leading Edge, 17(3): 357-362.
DOI:10.1190/1.1437977 |
|
Pendrel J, Debeye H, Pedersen-Tatalovic R, et al.
2000. Estimation and interpretation of P and S impedance volumes from simultaneous inversion of P-wave offset seismic data. Seg Expanded Abstracts, 30(505): 146.
|
|
Russell B H, Gray D, Hampson D P.
2011. Linearized AVO and poroelasticity. Geophysics, 76(3): C19-C29.
DOI:10.1190/1.3555082 |
|
Sen M K, Stoffa P L.
1991. Nonlinear one-dimensional seismic waveform inversion using simulated annealing. Geophysics, 56(10): 1624-1638.
DOI:10.1190/1.1442973 |
|
Sen M K, Roy I G.
2003. Computation of differential seismograms and iteration adaptive regularization in prestack seismic waveform inversion. Geophysics, 68(6): 2026-2039.
DOI:10.1190/1.1635056 |
|
Sheng P.
1990. Effective-medium theory of sedimentary rocks. Physical Review B, 41(7): 4507-4512.
DOI:10.1103/PhysRevB.41.4507 |
|
Spikes K, Mukerji T, Dvorkin J, et al.
2007. Probabilistic seismic inversion based on rock-physics models. Geophysics, 72(5).
|
|
Tian Y, Chen X F.
2006. Simultaneous inversion of hypocenters and velocity using the quasi-Newton method and trust region method. Chinese J. Geophys. , 49(3): 845-854.
DOI:10.3321/j.issn:0001-5733.2006.03.029 |
|
Walton K.
1987. The effective elastic moduli of a random packing of spheres. Journal of the Mechanics and Physics of Solids, 35(2): 213-226.
DOI:10.1016/0022-5096(87)90036-6 |
|
Wood A B. 1955. A Textbook of Sound. 3rd ed. New York:The MacMillan Co., 360.
|
|
Wu M, Fu L Y, Li W X.
2008. A high-resolution nonlinear inversion method of reservoir parameters and its application to oil/gas exploration. Chinese J. Geophys. , 51(2): 546-557.
DOI:10.3321/j.issn:0001-5733.2008.02.027 |
|
Wyllie M R J, Gregory A R, Gardner L W.
1956. Elastic wave velocities in heterogeneous and porous media. Geophysics, 21(1): 41-70.
DOI:10.1190/1.1438217 |
|
Xu S Y, White R E.
1995. A new velocity model for clay-sand mixtures. Geophysical Prospecting, 43(1): 91-118.
DOI:10.1111/gpr.1995.43.issue-1 |
|
Yin X Y, Cui W, Zong Z Y, et al.
2014. Petrophysical property inversion of reservoirs based on elastic impedance. Chinese J. Geophys. , 57(12): 4132-4140.
DOI:10.6038/cjg20141224 |
|
Yuan Y X. 1999. A review of trust region algorithms for optimization.//Proceedings of the 4th International Congress on Industrial & Applied Mathematics (ICIAM 99). Edinburgh:ICIAM, 271-282.
|
|
Yuan Y X.
2015. Recent advances in trust region algorithms. Mathematical Programming, 151(1): 249-281.
DOI:10.1007/s10107-015-0893-2 |
|
Zeng Q, Shi X M, Wu Y S, et al.
2011. A study of one-dimensional magnetotelluric sounding inversion using the trust region algorithm. Progress in Geophysics , 26(3): 885-893.
DOI:10.3969/j.issn.1004-2903.2011.03.013 |
|
Zhang H C, Conn A R, Scheinberg K.
2010. A derivative-free algorithm for least-squares minimization. SIAM Journal on Optimization, 20(6): 3555-3576.
DOI:10.1137/09075531X |
|
Zhang W H, Fu L Y, Zhang Y, et al.
2016. Computation of elastic properties of 3D digital cores from the Longmaxi shale. Applied Geophysics, 13(2): 364-374.
DOI:10.1007/s11770-016-0542-4 |
|
巴晶, 晏信飞, 陈志勇, 等.
2013. 非均质天然气藏的岩石物理模型及含气饱和度反演. 地球物理学报, 56(5): 1696–1706.
DOI:10.6038/cjg20130527 |
|
桂金咏, 高建虎, 雍学善, 等.
2015. 基于双相介质理论的储层参数反演方法. 地球物理学报, 58(9): 3424–3438.
DOI:10.6038/cjg20150934 |
|
冯国峰. 波动方程反问题的多尺度-信赖域反演方法. 哈尔滨: 哈尔滨工业大学, 2006.
http://cdmd.cnki.com.cn/Article/CDMD-10213-2006136067.htm |
|
田玥, 陈晓非.
2006. 利用拟牛顿法和信赖域法联合反演震中分布与一维速度结构. 地球物理学报, 49(3): 845–854.
DOI:10.3321/j.issn:0001-5733.2006.03.029 |
|
吴媚, 符力耘, 李维新.
2008. 高分辨率非线性储层物性参数反演方法和应用. 地球物理学报, 51(2): 546–557.
DOI:10.3321/j.issn:0001-5733.2008.02.027 |
|
印兴耀, 崔维, 宗兆云, 等.
2014. 基于弹性阻抗的储层物性参数预测方法. 地球物理学报, 57(12): 4132–4140.
DOI:10.6038/cjg20141224 |
|
曾奇, 师学明, 武永胜, 等.
2011. 一维大地电磁信赖域反演法研究. 地球物理学进展, 26(3): 885–893.
DOI:10.3969/j.issn.1004-2903.2011.03.013 |
|
 2017, Vol. 60
2017, Vol. 60


