地球物理学报  2016, Vol. 59 Issue (5): 1608-1615   PDF    
引用本文
林旭, 罗志才. 2016. 位移和加速度融合的自适应多速率Kalman滤波方法. 地球物理学报, 59(5): 1608-1615, doi: 10.6038/cjg20160506   
Lin X, Luo Z C. 2016. A new adaptive multi-rate Kalman filter for the data fusion of displacement and acceleration. Chinese J. Geophys. 59(5):1608-1615,doi:10.6038/cjg20160506.   
位移和加速度融合的自适应多速率Kalman滤波方法
林旭1,2, 罗志才2,3,4    
1. 成都理工大学地球科学学院, 成都 610059;
2. 武汉大学测绘学院, 武汉 430079;
3. 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079;
4. 测绘遥感信息工程国家重点实验室, 武汉 430079
收稿日期 2015-05-14, 2015-12-15 收修定稿
基金项目: 国家重点基础研究发展计划(973计划)(2013CB733302),国家自然科学基金项目(41174062,41131067),中央高校基本科研业务费专项资金项目(2012214020206),地球空间环境与大地测量教育部重点实验室开放基金(12-02-09)联合资助.
作者简介: 林旭,男,1986年生,讲师.主要从事航空重力测量数据处理与应用研究.E-mail: xulin@whu.edu.cn
通讯作者: 罗志才,男,1966年生,教授.主要从事物理大地测量研究.E-mail: zhcluo@sgg.whu.edu.cn
摘要: 多速率Kalman滤波方法可用于低采样率的位移和高采样率的加速度数据融合,而未知的噪声协方差信息则显著制约着多速率Kalman滤波精度.本文通过将多速率Kalman滤波转换为传统的单速率Kalman滤波,建立了Kalman滤波增益的自协方差矢量与未知的加速度谱密度和观测噪声参数间的线性函数模型,并采用最小二乘估计方法对未知的噪声协方差参数进行估计,进而有效地提高了多速率Kalman滤波精度. 数值仿真和震动台实验结果验证了本文方法的正确性和有效性.
关键词: 多速率采样     位移     加速度     自适应Kalman滤波     自协方差最小二乘法     RTS平滑    
A new adaptive multi-rate Kalman filter for the data fusion of displacement and acceleration
LIN Xu1,2, LUO Zhi-Cai2,3,4    
1. College of Earth Sciences, Chengdu University of Technology, Chengdu 610059, China;
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
4. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan 430079, China
Abstract: The multi-rate Kalman filter can be used for the data fusion of displacement and acceleration, which were sampled at different frequencies. However, the noise covariance matrices, especially the process noise covariance matrix, are usually unavailable in the practical applications. With inappropriate noise covariance matrices, the state estimates of multi-rate Kalman filter is suboptimal. In this paper, a new adaptive multi-rate Kalman filter, which is based on the autocovariance least-squares method, is proposed. For a given set of displacement and acceleration data sampled at different frequencies, the data fusion problem is formulated as the single-rate Kalman filter rather than the multi-rate Kalman filter. And the correlations between the innovations were used to establish a relationship to the unknown parameters about the noise covariance matrices. Therefore, the unknown parameters can be estimated by solving the least-squares problem. The validity of the proposed method is demonstrated by a numerical example and an earthquake engineering test from the Large High-Performance Outdoor Shake Table.
Key words: Multi-rate sampling     Displacement     Acceleration     Adaptive Kalman filter     Autocovariance least squares     RTS smoother    
1 引言

地震数据通常是以加速度的形式给出，而速度和位移则是通过加速度的一次积分和二次积分获得.然而这看似简单的数值积分过程，却由于低频的仪器和环境噪声等原因，使得由加速度积分得到的速度和位移存在漂移现象(Boore，2001).Iwan等(1985)、Wang等(2011)和Li等(2011，2012)采用分段拟合的方法去除基线漂移，但其中关键的时间特征点的选择仍然是制约此方法应用的难点问题.

位移作为地震数据处理中的重要观测量，可通过GPS数据处理直接得到.日本Kyoto大学的Hirahara等(1994)提出利用GPS进行地表位移监测和地震分析.此后，Ge等(2000)、Larson(2009)、方荣新等(2013)和Chang等(2014)对GPS在地震学领域的应用展开了研究.由于GPS采样率与加速度计相比仍然较低，GPS监测的地表形变对低频信号更为敏感，相关的研究结果也表明，现有的高频GPS网络可用于监测由中大型地震引起的地表位移(Larson et al.，2003)，这将是对现有的地震监测网络的极大补充.

将GPS位移和加速度计获取的加速度信息进行融合处理，可充分发挥GPS位移和加速度计的固有特性.Smyth和Wu(2007)提出基于常速度模型的多速率Kalman滤波，将位移作为观测量，加速度作为控制量，实现不同采样率下的位移和加速度数据融合，联合GPS位移及加速度信息后得到的位移精度明显优于仅利用单一传感器所获得的位移精度.Bock等(2011)和Melgar等(2013)将此方法用于GPS和强震仪的数据融合，并应用于地震形变监测，取得了较好的状态估计精度.考虑到设备成本，Tu等(2013)采用MESE加速度计替代强震仪，并进行了模拟实验.Li等(2013)采用此方法进行GPS和加速度信息的紧组合，有效地提高了位移的估计精度.无论是采用GPS和强震仪或者加速度计进行数据融合，其本质上是将低采样率的位移数据和高采样率的加速度数据进行融合，而采用多速率Kalman滤波方法进行数据融合时，则需要解决噪声协方差信息未知的问题，先验噪声协方差信息的偏差必然会对多速率Kalman滤波的精度产生影响.

虽然Bock等(2011)也曾对多速率Kalman滤波中噪声协方差参数的选取进行过相关讨论，但其并未给出有效的参数选取方法，上述文献均采用经验方法来确定多速率Kalman滤波模型的噪声协方差参数.Niu和Xu(2014)虽然提出了一种基于方差分量估计的自适应多速率Kalman滤波算法，但其仅能在观测噪声协方差已知的前提下，对未知的状态噪声协方差进行估计，并非完整意义上的自适应算法.自适应Kalman滤波是一种噪声协方差估计的有效方法，国内外众多学者也围绕其展开了丰富的研究，然而相关的研究仅涉及单速率Kalman滤波，并未给出多速率Kalman滤波的噪声协方差估计方法.针对这一问题，本文提出了自适应多速率Kalman滤波方法，通过将多速率Kalman滤波转换为传统的单速率Kalman滤波，建立Kalman滤波增益的自协方差矢量与未知的加速度谱密度和位移噪声方差间的线性函数模型，并采用最小二乘估计方法进行相应的噪声估计.

2 多速率Kalman滤波

Smyth和Wu(2007)将位移作为观测量，加速度作为控制量，采用基于常速度模型的多速率Kalman滤波方法进行低采样率的位移数据和高采样率的加速度数据融合，其状态方程如下：

式中，x(t)=[x(t)ẋ(t)].a(t)表示加速度观测值，α(t)表示状态噪声，α～N(0，Qc)，其中Qc满足如下结构：

q为状态噪声的谱密度.将GPS位移作为观测值，可建立如下的Kalman滤波观测方程：

C=[1 0]，β(t)表示观测噪声，β～N(0，Rc).

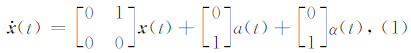
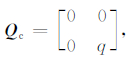
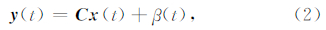
用τa表示加速度观测值的采样周期，τd表示位移观测值的采样周期，τd=Mτa，M表示加速度观测值与位移观测值间的采样频率比.则式(1)和(2)的离散形式可表示为

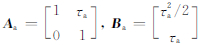式中，aka表示加速度观测值，ykd表示位移观测值，且其状态噪声协方差Qa和观测噪声协方差Rd分别满足如下关系：

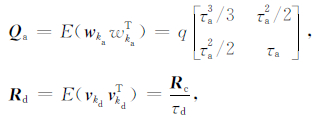
其中，状态噪声协方差矩阵Qa是关于谱密度q和采样周期τa的矩阵.

当M=1时，可采用标准Kalman滤波进行状态估计，即一步状态预测、一步状态更新；当M＞1时，此时的Kalman滤波过程则是先进行M步步长为τa状态预测和一步状态更新.假设滤波初值x0=[0 0]T，初始状态的方差阵P0+=I，并用上标“-”表示状态预测值，上标“+”表示状态估值.

一步步长为τa的预测状态：

其对应的预测状态协方差矩阵为

由式(4)可知，进行M步步长为τa的状态预测后的预测状态为

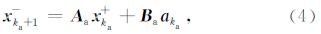
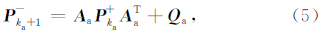
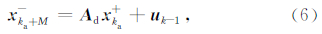
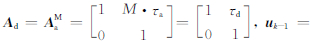
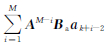式中，.其对应的预测状态协方差阵为

其中，

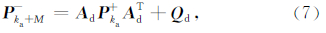
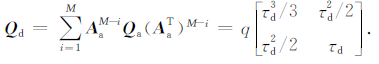
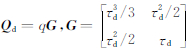同时为了便于描述，令，协方差矩阵Qa是关于谱密度q和采样周期τd的矩阵.

通过对比式(4)、(5)和式(6)、(7)可知，进行M步步长为τa状态预测等效于进行了一步步长为τd的状态预测，其对应的状态转移矩阵为Ad，系统控制输入项为uk-1，对应的状态噪声协方差矩阵为Qd.通过式(4)、(5)到式(6)、(7)的转换，将多速率Kalman滤波方法转换为传统的单速率Kalman滤波方法.

进行M步步长为τa的状态预测后，进行一次状态更新，此时的Kalman滤波新息为

则此时的滤波增益矩阵为

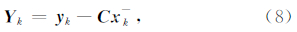
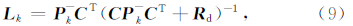状态估值为

状态估值的协方差矩阵为

3 自适应算法

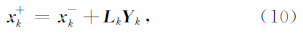
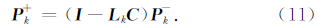
最优Kalman滤波方法是建立在函数模型和随机模型均精确已知的基础上，而由于传感器自身噪声特性和测量环境等多方面因素的影响，随机模型一般难以先验获得.而有偏的先验随机模型必然会对状态估计的精度产生影响，甚至会导致滤波发散.Odelson等(2006)，Rajamani和Rawlings(2009)提出的自协方差最小二乘噪声协方差估计方法是一种自适应Kalman滤波算法，其直接建立新息的相关函数R(N)s与未知的噪声协方差之间的线性函数模型，并采用最小二乘方法进行参数估计，噪声协方差估计精度较传统的自适应算法有着明显提高：

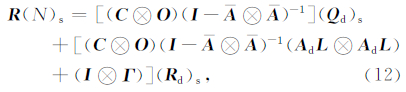
式中，“”表示克罗内克积算子，下标“s”表示矩阵按列序排列，L代表稳态时的Kalman滤波增益，矩阵O、ΓĀ、的具体定义详见Odelson(2006).自协方差最小二乘法在进行噪声协方差估计时是对噪声协方差矩阵中的各元素分别进行估计，并未顾及各元素的相关性.然而，从式(7)中可以看出，通过公式转换后的单速率Kalman滤波模型的噪声协方差矩阵Qd满足特定结构，即Qd=qG，矩阵G为已知矩阵，其仅与位移的采样周期τd相关，因此，对状态噪声协方差矩阵Qd的估计可将其转换为谱密度q的求解.

顾及(Qd)s=Gsq，将其代入式(12)，整理可得

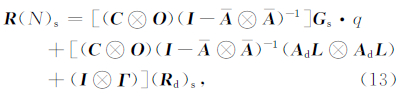
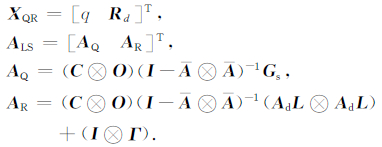
因为状态噪声协方差矩阵Qd是关于谱密度q和采样周期τd的矩阵，而GPS位移的采样周期是已知的，因此求解出未知的谱密度q则确定了未知的Qd.通过构造基于新息的状态空间模型，将{Yk}新息的相关函数R(N)表示为谱密度q和观测协方差矩阵Rd的函数，由此可同时对q、Rd进行估计，进而确定Kalman滤波模型的噪声协方差矩阵.式(13)可采用最小二乘估计的方法进行求解：

其中

本文提出的自适应算法的本质是将多速率Kalman滤波的噪声估计问题转换为传统的单速率Kalman滤波的噪声估计问题，并顾及未知的状态噪声协方差矩阵所具有的特定结构，将状态噪声协方差估计转换为谱密度的确定，最后采用最小二乘法进行未知参数估计.

为了提高状态估计精度，可对Kalman滤波结果进行平滑处理.RTS平滑是一种固定区间最优平滑算法，其利用固定时间区间中的所有观测值yk来估计区间内每一时刻的状态xk，具有较高的计算效率，其具体的公式推导过程可参考Simon(2006).

4 仿真与实验

采用以下两个算例对本文提出的自适应多速率位移和加速度融合的Kalman滤波(AMKF)方法进行验证.

算例1：带线性漂移的正弦扫频信号

假设位移是带线性漂移的正弦扫频信号，其时间序列分别满足如下等式：

式中a=π/9，b=2π/5，c=0.1.则其速度和加速度的时间序列为

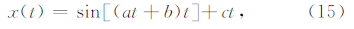
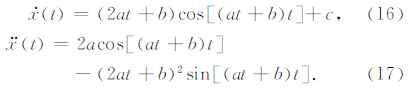
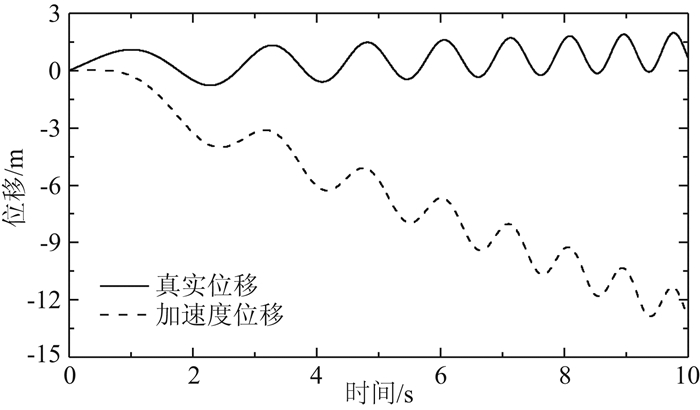
正弦扫频信号的位移时间序列和仅由加速度信息恢复的位移时间序列见图 1.位移中的线性漂移通过微分后，无法被加速度传感器识别，即将加速度信息进行二次积分后无法恢复原始信号的线性漂移.为了对本文提出的自适应多速率Kalman滤波算法进行验证，假设加速度的采样率为1000 Hz，位移的采样率为100 Hz，采样频率比为10，分别向位移和加速度真值中添加白噪声，添加噪声后的位移和加速度的信噪比SNR=5.并采用以下3种方法对观测值进行处理.

图 1 位移的时间序列 Fig. 1 Time series of displacement

方法1：仅由位移观测值通过自适应Kalman滤波(AKF)对位移和速度进行估计，并对估计结果进行RTS平滑；

方法2：采用多速率Kalman滤波算法(MKF)进行位移和加速度的融合，其噪声参数q=1、R=0.1，并对估计结果进行RTS平滑；

方法3：采用AMKF进行位移和加速度的自适应融合，并对估计结果进行RTS平滑.

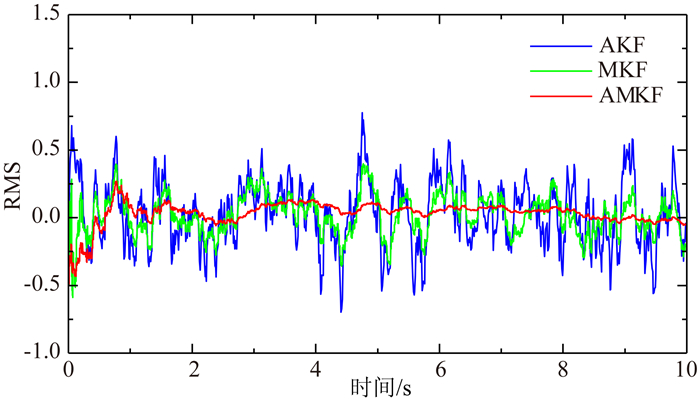
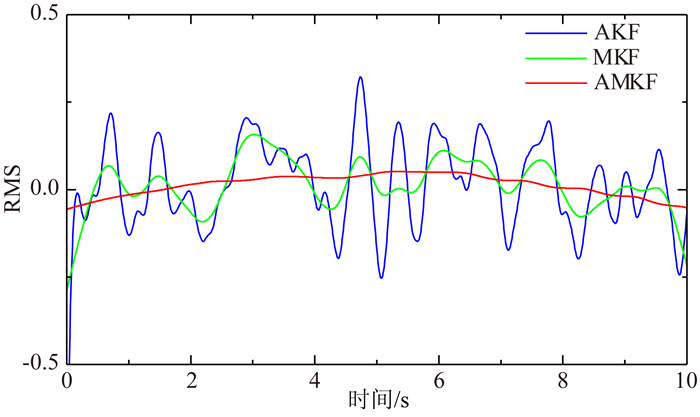
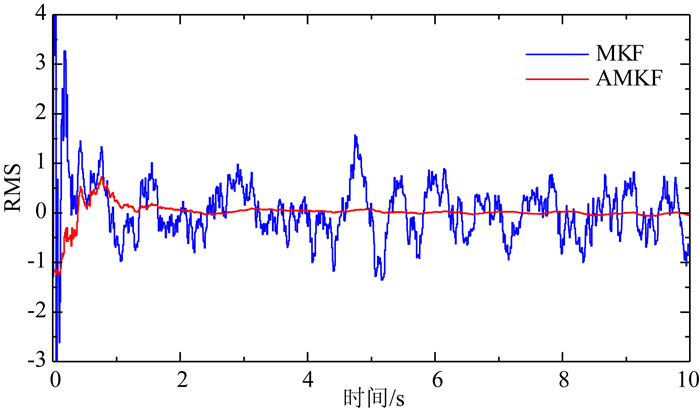
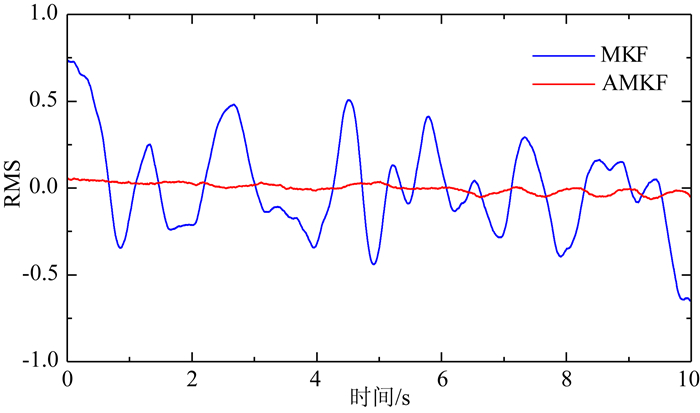
图 2和图 3分别给出了采用AKF、MKF和AMKF估计的位移及其平滑结果；图 4和图 5分别给出了采用MKF和AMKF估计的速度及其平滑结果.以上3种方法的滤波和平滑的统计结果见表 1.

图 2 位移的滤波结果 Fig. 2 RMS of displacements by forward filter

图 3 位移的平滑结果 Fig. 3 RMS of displacements by RTS smoother

图 4 速度的滤波结果 Fig. 4 RMS of velocities by forward filter

图 5 速度的平滑结果 Fig. 5 RMS of velocities by RTS smoother

表 1 3种方法的均方根误差 Table 1 RMS of displacements and velocities by AKF, MKF and AMKF

从以上结果可以看出：

(1)仅由位移观测值通过AKF方法得到的位移和速度的估计精度最差，由位移计算速度时会使得速度项的高频误差放大，因此其速度项误差特别大；

(2)采用MKF方法进行位移和加速度融合，其状态估计精度较AKF方法有着明显提高，其中位移的估计精度较AKF方法提高了40%，由于有了加速度信息的加入，其速度估计精度较AKF方法提高了83%；

(3)先验噪声协方差参数对多速率Kalman滤波方法的影响不容忽视，采用AMKF方法其能有效地对未知的噪声协方差参数进行估计，因此由其估计得到的状态精度最高.其中位移和速度的估计精度较AKF方法分别提高了73%和98%，较MKF方法分别提高了56%和89%；

(4)采用RTS平滑方法能有效地提高Kalman滤波的估计精度，并能克服Kalman滤波初值所带来的误差影响，平滑后AMKF的位移和速度估计精度分别提高了49%和53%.

算例2：震动台实验

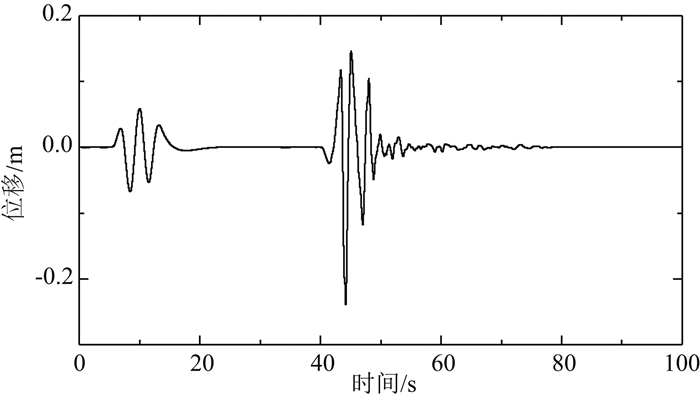
本算例所用数据来自于美国加利福利亚大学大型高性能室外震动台进行的一次地震模拟实验，此次实验模拟了1994年发生在美国的Northridge地震.整个系统的核心部件是MTS，用于输出频率为1024 Hz的地震位移，其波形见图 6，有2个采样率为50 Hz的高频GPS接收机分别布设在震动台内外，用于记录整个过程中的位移变化，并在震动平台上布设有2个采样率为240 Hz的加速度计(PA1和PA2)用于记录整个过程中震动平台的加速度信息.为了采用多速率Kalman滤波进行50 Hz的高频GPS和240 Hz的加速度计的数据融合，将240 Hz的加速度计输出重采样为250 Hz.

图 6 模拟的位移波形图 Fig. 6 Displacement waveform

采用常速度模型对震动台的运动过程进行建模，仅使用GPS位移观测值通过AKF方法进行位移和速度估计；同时仅使用两个加速度计的观测数据通过一次积分得到速度，通过两次积分得到位移，两种方法得到的位移和速度的均方根误差见表 2.从表中可以看出，仅使用高频GPS估计得到的位移精度较高，而由加速度计PA1和PA2积分得到的位移精度相对较差，较GPS位移精度低了近一个量级；由加速度计PA1积分得到的速度精度最高，由加速度计PA2积分得到速度精度略差，而由GPS位移通过滤波估计得到的速度精度最差.

表 2 仅由GPS或加速度计恢复的位移和速度的均方根误差 Table 2 RMS of GPS-only and acceleration-only solutions

MKF方法的滤波精度取决于加速度谱密度和观测噪声协方差Rd，其中，加速度谱密度q的计算则显得尤其复杂.Bock等(2011)指出，即使是选取极其不合适的加速度谱密度q进行多速率Kalman滤波，在通过RTS平滑后，其位移估计精度均能得到大幅度提高，即RTS方法能有效克服加速度谱密度q对位移估计所带来的误差影响.作为一种状态估计方法，MKF的状态向量不仅包括位移项，还包括速度项，然而，Bock(2011)并未对加速度谱密度q对速度估计的影响进行讨论.

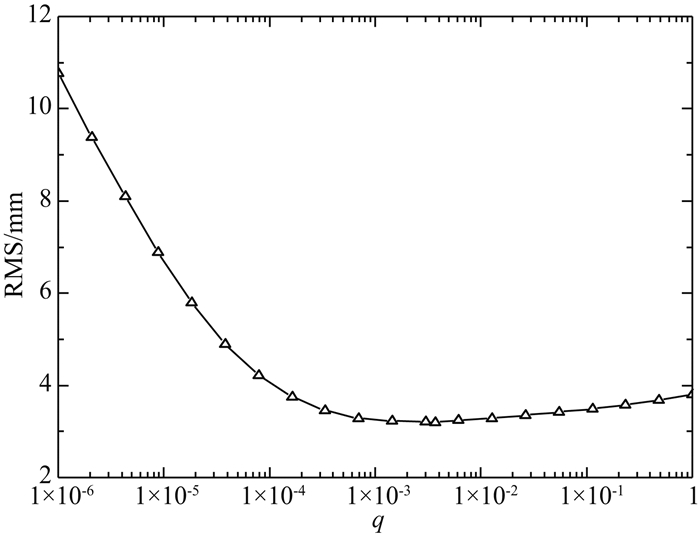
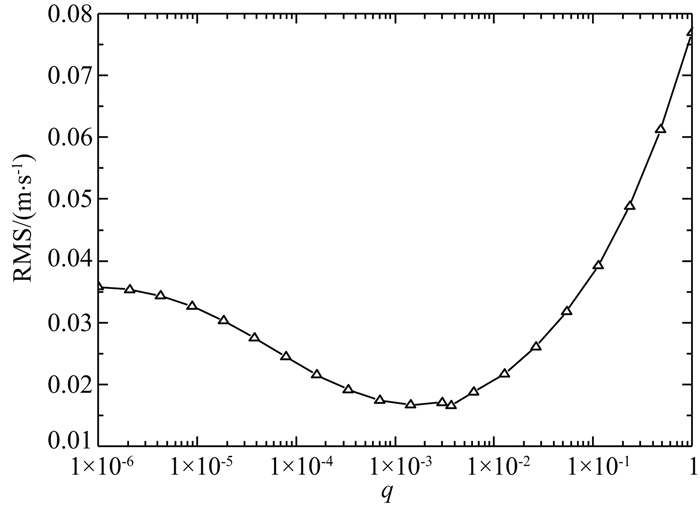
为了深入分析加速度谱密度参数q对MKF方法的影响，首先采用AMKF方法对未知的噪声协方差参数q和Rd进行估计，表 3给出了采用AMKF方法估计出的q和Rd，并以GPS/PA1为例，分别选取不同的q值(Rd为AMKF方法得到的估值)进行MKF滤波，其位移项和速度项的RMS见图 7和8.从图 7和8中可以看出，q的选取对MKF的估计精度有着明显影响，当q=3.70×10-3时，位移项和速度项的估计精度最高，这表明本文提出的AMKF方法能有效地估计出未知的噪声协方差参数；当q选取偏小，且远离最优估值时，位移项的估计精度迅速下降，当q选取偏大，且远离最优估值时，速度项的估计精度迅速下降.同时也看出，速度的估计精度对MKF噪声参数的选取更为敏感，其原因在于，虽加入了加速度观测信息后，MKF的状态(位移和速度)估计精度均得到提高，但位移项的估计精度主要依赖于原始的GPS位移观测值，而速度项则受GPS位移和加速度观测信息的联合影响，噪声协方差参数则起着调制GPS位移和加速度信息权重的作用，因此速度项的解算精度对噪声参数更为敏感.

表 3 噪声协方差参数的估值 Table 3 The estimates of noise covariance parameters by AMKF

图 7 位移项的RMS Fig. 7 The RMS of position with different values of q by MKF

图 8 速度项的RMS Fig. 8 The RMS of velocity with different values of q by MKF

表 4分别给出了AMKF滤波及q=1×10-6和q=1时(Rd为AMKF方法得到的估值)MKF滤波的统计结果.结合表 4和表 2可以看出，当选取q=1×10-6时，GPS/PA1和GPS/PA2的位移估计精度分别为0.0108 m和0.0151 m，远远低于仅使用GPS时的位移估计精度0.0034 m；当选取q=1时，其速度估计精度分别为7.69×10-2 m·s-1和7.80×10-2 m·s-1，也比仅由单一传感器(GPS或是加速度计)估计得到的速度精度4.94×10-2 m·s-1、2.78×10-2 m·s-1和4.33×10-2 m·s-1差.AMKF方法的位移估计精度分别为0.0032 m和0.0033 m，较q=1×10-6时的位移估计精度提高了70%和78%，较q=1时的提高了16%和13%；同时AMKF方法的速度估计精度分别为1.65×10-2m·s-1和2.13×10-2 m·s-1，较q=1×10-6时的位移估计精度提高了75%和60%，较q=1时的提高了79%和73%.采用RTS平滑后，MKF和AMKF方法的估计精度均有着不同程度的提高，当q=1时，位移项的估计精度与AMKF的位移估计精度基本相当，但速度项的估计精度较差，不仅远低于AMKF的速度估计精度，还低于仅由加速度信息积分恢复的速度精度，这表明RTS平滑算法只能在一定程度上克服未知噪声协方差信息带来的误差影响，要想提高GPS位移和加速度的融合精度，关键还在确定未知的噪声协方差信息.

表 4 由MKF和AMKF估计得到的位移和速度的RMS Table 4 RMS of displacement and velocity by multi-rate Kalman filter and adaptive multi-rate Kalman filter

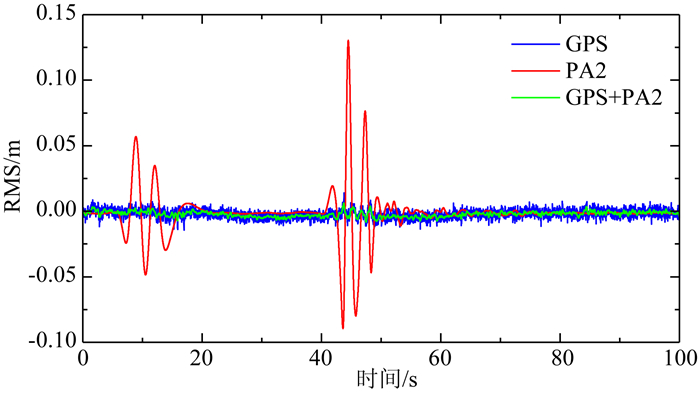
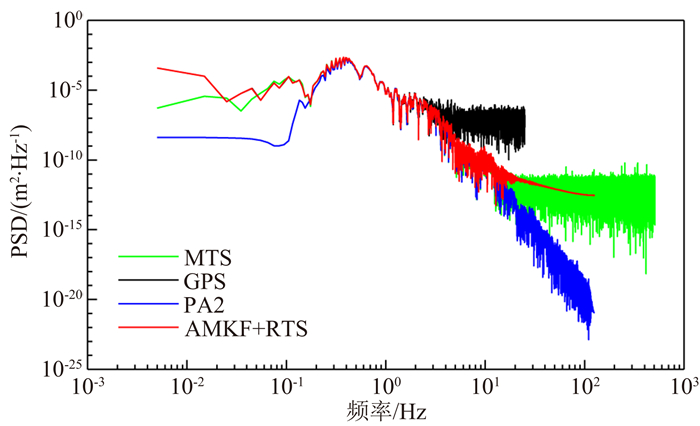
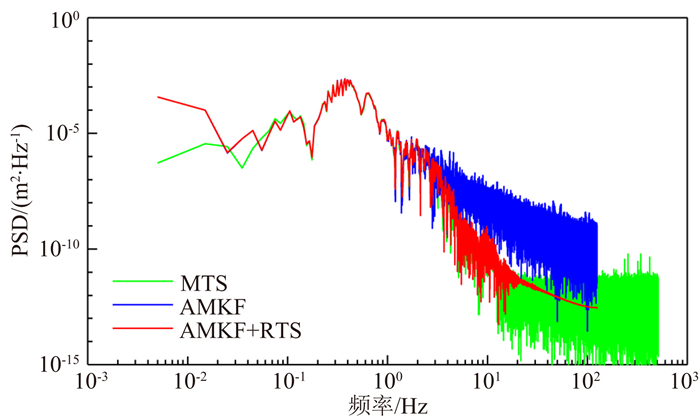
同时，以加速度计PA2为例，图 9给出了GPS位移、由加速度计PA2积分得到的位移以及采用AMKF并平滑后的位移的误差时间序列，图 10给出了MTS位移、GPS位移、由加速度计PA2通过积分得到的位移以及采用AMKF并平滑后的位移的功率谱密度.从图 9和10中可以看出，GPS对低频位移信号较为敏感，虽然由加速度计PA2积分得到的位移误差相对较大，但其对高频信息更为敏感，采用AMKF方法进行不同速率的GPS和加速度计的数据融合，能充分发挥GPS对低频信号更为敏感以及加速度计对高频信号更为敏感的优势，而采用AMKF并经RTS平滑处理后的位移不仅在低频部分与GPS信息吻合较好，而且在高频部分与加速度计恢复的位移也保持较好的一致性.图 11给出了MTS位移、采用AMKF得到的位移及其平滑后的位移的功率谱密度.从图中可以看出，采用AMKF得到的位移和平滑后的位移均能较好恢复低频段的信号，而通过RTS平滑后能有效地抑制高频噪声.

图 9 位移误差 Fig. 9 RMS of displacements

图 10 位移的功率谱密度 Fig. 10 Power spectral densities of displacement

图 11 Kalman滤波和平滑的功率谱密度 Fig. 11 Power spectral densities comparisons between AMKF and smoothed AMKF displacement

从以上结果可以看出：

(1)加速度谱密度参数对MKF方法的影响不容忽视，当加速度谱密度参数选取不恰当时，其位移和速度的估计精度将严重退化.特别是速度项的估计精度对加速度谱密度参数的选取更加敏感，此时的MKF方法不仅无法通过数据融合发挥GPS和加速度计的各自优势，且严重影响了数据融合精度；

(2)不管噪声参数如何选取，RTS平滑方法均能在一定程度上提高MKF方法的估计结果，但当加速度谱密度参数选取不恰当时，即使通过RTS平滑，其估计结果仍然很偏差，这表明MKF方法的估计精度主要依赖于先验噪声参数；

(3)AMKF方法能有效克服未知的加速度谱密度参数对MKF方法带来的误差影响，并充分发挥GPS传感器对低频信号敏感、加速度计对高频信号更加敏感的特点，AMKF方法估计得到的位移不仅在低频部分与GPS信息吻合较好，而且在高频部分与加速度计恢复的位移也保持较好的一致性. 5 结论

未知噪声参数的选择必然会对多速率Kalman滤波的估计精度产生影响，虽然RTS平滑算法能在一定程度上改善由于先验噪声参数选取所带来的误差影响，但多速率Kalman滤波方法的状态估计精度更为主要的还是依赖于先验噪声参数，当先验的噪声偏差较大时，会使得多速率Kalman滤波的状态估计精度严重退化.

顾及未知噪声参数对多速率Kalman滤波方法带来的误差影响，本文提出了一种自适应的多速率Kalman滤波方法，通过将多速率Kalman滤波转换为传统的单速率Kalman滤波，并建立Kalman滤波增益的自协方差矢量与未知的加速度谱密度参数和观测噪声参数间的线性函数模型，采用最小二乘估计方法进行加速度谱密度参数和观测噪声的估计.数值仿真和震动台实验结果表明，本文提出的自适应多速率Kalman滤波算法能克服先验噪声偏差对状态估计产生的影响，提高状态估计精度.

致谢    感谢Cecil H. and Ida M. Green Institute of Geophysics and Planetary Physics的Diego Melgar提供的震动台实验数据.

参考文献
[1] Bock Y, Melgar D, Crowell B W. 2011. Real-time strong-motion broadband displacements from collocated GPS and accelerometers. Bulletin of the Seismological Society of America, 101(6): 2904-2925.
[2] Boore D M. 2001. Effect of baseline corrections on displacements and response spectra for several recordings of the 1999 Chi-Chi, Taiwan, earthquake.Bulletin of the Seismological Society of America,91(5): 1199-1211.
[3] Chang Y C, Fu C C, Zhi J Z, et al. 2014. Preseismic deformation associated with the 2014 MS7.3 Yutian earthquake derived from GPS data. Geodesy and Geodynamics, 5(2): 48-53.
[4] Fang R X, Shi C, Song W W, et al. 2013. Real-time GNSS seismometer and its accuracy. Chinese Journal of Geophysics (in Chinese), 56(2): 450-458, doi: 10.6038/cjg20130209.
[5] Ge L L, Han S W, Rizos C, et al. 2000. GPS seismometers with up to 20 Hz sampling rate. Earth, Planets and Space, 52(10): 881-884.
[6] Hirahara K, Nakano T, Hoso Y, et al. 1994. An experiment for GPS strain seismometer.// Proceedings of the Japanese Symposium on GPS. Tokyo, Japan, 67-75.
[7] Iwan W D, Moser M A, Peng C Y. 1985. Some observations on strong-motion earthquake measurement using a digital accelerograph. Bulletin of the Seismological Society of America, 75(5): 1225-1246.
[8] Larson K M. 2009. GPS seismology. Journal of Geodesy, 83(3-4): 227-233.
[9] Larson K M, Bodin P, Gomberg J. 2003. Using 1-Hz GPS data to measure deformations caused by the Denali fault earthquake. Science, 300(5624): 1421-1424.
[10] Li H, Yao Y S, Zheng S M, et al. 2011. Baseline correction for digital strong-motion records by using the pre-event portion. Geodesy and Geodynamics, 2(1): 43-46.
[11] Li H, Wu J C, Yao Y S, et al. 2012. Baseline correction for near-fault ground motion recordings of the 2008 Wenchuan MS8.0 earthquake. Geodesy and Geodynamics, 3(2): 60-70.
[12] Li X X, Ge M R, Zhang Y, et al. 2013. High-rate coseismic displacements from tightly integrated processing of raw GPS and accelerometer data. Geophysical Journal International, 195(1): 612-624.
[13] Melgar D, Bock Y, Sanchez D, et al. 2013. On robust and reliable automated baseline corrections for strong motion seismology. Journal of Geophysical Research-Solid Earth, 118(3): 1177-1187.
[14] Niu J M, Xu C J. 2014. Real-time assessment of the broadband coseismic deformation of the 2011 tohoku-oki earthquake using an adaptive kalman filter. Seismological Research Letters, 85(4): 836-843.
[15] Odelson B J, Rajamani M R, Rawlings J B. 2006. A new autocovariance least-squares method for estimating noise covariances. Automatica, 42(2): 303-308.
[16] Rajamani M R, Rawlings J B. 2009. Estimation of the disturbance structure from data using semidefinite programming and optimal weighting. Automatica, 45(1): 142-148.
[17] Simon D. 2006. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches. New York: Wiley.
[18] Smyth A, Wu M L. 2007. Multi-rate Kalman filtering for the data fusion of displacement and acceleration response measurements in dynamic system monitoring. Mechanical Systems and Signal Processing, 21(2): 706-723.
[19] Tu R, Wang R, Ge M, et al. 2013. Cost-effective monitoring of ground motion related to earthquakes, landslides, or volcanic activity by joint use of a single-frequency GPS and a MEMS accelerometer. Geophysical Research Letters, 40(15): 3825-3829.
[20] Wang R, Schurr B, Milkereit C, et al. 2011. An improved automaticscheme for empirical baseline correction of digital strong-motion records. Bulletin of the Seismological Society of America, 101(5): 2029-2044.
[21] 方荣新, 施闯, 宋伟伟等. 2013. 实时GNSS地震仪系统实现及精度分析. 地球物理学报, 56(2): 450-458, doi: 10.6038/cjg20130209.