2. 中国科学院页岩气与地质工程重点实验室, 中国科学院地质与地球物理研究所, 北京 100029;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
瞬变电磁法是一种时间域人工源电磁法,广泛应用于金属矿、石油、煤炭等化石能源探测中(薛国强等, 2007; Xue et al., 2012a, 2012b).目前浅部资源开发殆尽,探测深部资源成为趋势.传统的瞬变电磁法的探测深度和探测精度难以满足深部资源探测的要求,发展大深度探测的瞬变电磁法探测新技术和新装备迫在眉睫(滕吉文, 2010; 薛国强等, 2013).英国爱丁堡大学的Wright等(2001)提出了多道瞬变电磁法(Multi-channel Transient Electromagnetic method, MTEM)新技术.与传统瞬变电磁法相比,该方法具有采用大功率接地源发射、阵列式接收、伪随机二进制序列(Pseudo-random binary sequence, PRBS)作为激励等特点(Hobbs et al., 2006; Ziolkowski et al., 2007a, 2007b; 薛国强等, 2015; Li et al., 2016),已成功应用于油藏监控和油气资源探测领域(Ziolkowski et al., 2010),而且探测深度和探测精度可望达到对深部矿产资源进行探测的要求.
然而,由于与传统瞬变电磁法存在的众多不同,多道瞬变电磁法的数据处理及解释与传统瞬变电磁法存在明显区别.一方面,传统瞬变电磁法在激励源的关断期间接收纯二次场信号,而多道瞬变电磁法采用伪随机二进制序列作为激励源,采集的是源发射期间的全波形响应.为此,传统的基于纯二次场衰减曲线反演方法不能直接应用于多道瞬变电磁法数据,需要研究适用于PRBS信号激励源数据的处理及解释方法.另一方面,多道瞬变电磁法采用接收阵列进行数据采集,数据量大且对于测线上的每个观测点均可获得多个偏移距下的多次覆盖数据(Ziolkowski et al., 2007b).由于探测深度与偏移距、电阻率、时间等多个因素相关,为充分利用不同偏移距数据对地下不同深度目标体的覆盖,需要发展适用于多道瞬变电磁法多次覆盖数据的反演方法.
基于以上分析,本文对多道瞬变电磁法共中心点道集数据一维反演进行了研究.首先,通过反卷积处理从PRBS激励源响应中提取直接包含地下介质信息的大地脉冲响应.针对现有的对大地脉冲响应积分获得上升沿阶跃响应存在的技术难点,本文提出采用反向积分算法从大地脉冲响应中进一步恢复出下降沿阶跃响应.最后,对于所提取的共中心点道集数据,采用多偏移距OCCAM联合反演,得到地下地质的地电信息.反演结果表明共中心点道集数据的反演在不同目标体深度以及有噪声干扰的情况下,均可获得较好的反演结果.
2 多道瞬变电磁法原理MTEM方法的关键技术在于采用电偶极源发射源信号,采用电偶极阵列在源的轴向采集响应数据(Wright et al., 2002; Ziolkowski et al., 2007b; Zhdanov, 2010).MTEM数据采集系统的平面简图如图 1所示.

|
图 1 MTEM数据采集装置示意图 Fig. 1 Schematic diagram of source-receiver configuration of MTEM acquisition |
假设大地为线性时不变系统,接收电极对采集的响应信号可表示为源激励信号与大地脉冲响应的卷积的形式:
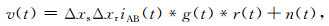
|
(1) |
其中Δxs是源电极距,Δxr是接收电极距,iAB(t)是源电流强度,*表示卷积,g(t)是大地脉冲响应,r(t)为接收仪器有关的系统响应,n(t)为不相关的噪声信号.与常规瞬变电磁法在源信号关断期间采集纯二次场信号不同,在多道瞬变电磁法中,采集系统记录的为源信号发射和关断期间的全波形信号.通过在源附近采用与接收系统相同的记录设备采集源电流信号,并根据式(1),采用反卷积方法提取与地下介质电性结构相关的大地脉冲响应.
3 纯二次场响应提取由于多道瞬变电磁法采集的为全波形信号,传统基于纯二次场响应的反演方法不能直接应用于多道瞬变电磁法数据的反演.为此,本文首先采用反卷积的方法从PRBS全波形数据中提取大地脉冲响应,并提出采用反向积分算法从大地脉冲响应恢复得到下降沿阶跃响应.
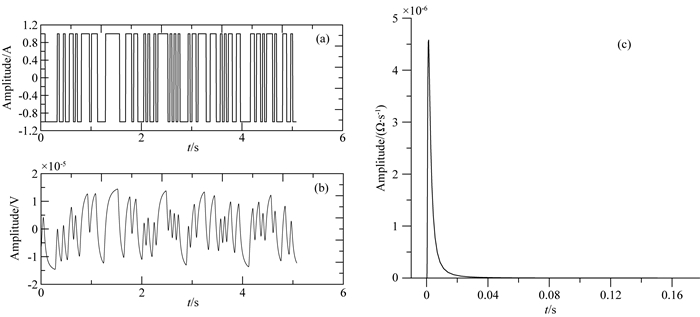
3.1 大地脉冲响应由于采用反卷积方法从接收响应中提取大地脉冲响应,多道瞬变电磁法可采用PRBS信号作为发射源信号.PRBS信号能够压制随机噪声,增加有用信号的频带宽度,获得更好信噪比的响应.当采用PRBS信号作为激励源时,得到的全波形响应与常规瞬变电磁法所得的衰减曲线不同.图 2b为正演模拟得到的PRBS响应信号,对应的源波形信号如图 2a所示,正演模型为电阻率为100 Ωm的均匀半空间,偏移距为1000 m.由图可知,不同于常规瞬变电磁纯二次场响应,伪随机码激励源响应包含源的一次场响应和感应产生的二次场响应.因此,须采用反卷积方法提取大地脉冲响应,以获得地下介质信息.
|
图 2 理想情况下反卷积提取大地脉冲响应 (a) 7阶PRBS信号;(b) 7阶PRBS信号激励源响应;(c)对(a)和(b)反卷积得到的大地脉冲响应. Fig. 2 Extracting earth impulse responses by deconvolution (a) PRBS sequence of 7 order; (b) Response exited by 7_order PRBS sequence; (c) Impulse responses from deconvolution of (a) and (b). |
PRBS信号具有二值自相关特性(Mutagi, 1996; 陈海龙和李宏,2005),考虑长度为N的PRBS信号,其自相关函数Rss为
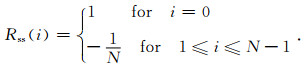
|
(2) |
基于此二值自相关特性,在最小二乘意义上采用式(1)进行反卷积计算提取大地脉冲g(t)响应问题可转换为求解如下维纳-何甫方程(Pipkin, 1991; Noor, 1993):
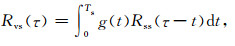
|
(3) |
其中Rvs为源电流与接收响应的互相关函数,Ts为大地脉冲响应的最晚时间道.通过源电流和接收电压的互相关计算,接收响应中的不相关噪声得到了压制.式(3)可以写成矩阵形式:
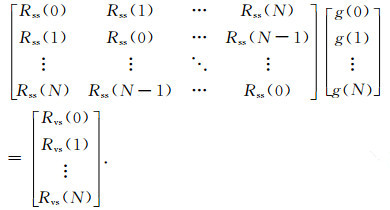
|
(4) |
矩阵方程(4)左端的系数矩阵为对称矩阵,且沿主对角线的平行线排列的元素全部相等.因此,这个N+1阶方阵实际上由N+1个元素确定,这种方阵被称为托布列兹(Toepliz)阵(Golub and Van Loan, 2012).相应的方程组被称为托布列兹方程组,它的解可以采用莱文森递归算法进行快速求解,得到大地脉冲响应(邹谋炎, 2001).图 2a为采用反馈移位寄存器所得到的7阶PRBS信号,图 2b为正演所得到的电阻率为100 Ωm,偏移距为1000 m时的伪随机码响应,图 2c为采用上述算法从图 2a和图 2b中恢复得到的大地脉冲响应.当采用不含噪声数据时,所恢复的大地脉冲响应与真实大地脉冲响应之间的相对误差小于1%.
3.2 下降沿阶跃响应在实际中,由于大地脉冲响应早期幅值变化较大且存在空气波的干扰,对其进行反演拟合难以收敛到稳定的解.因此需要进一步处理以实现多道瞬变电磁数据的反演.根据频时转换的余弦变换公式,
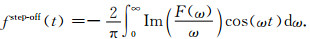
|
(6) |
在任意时刻,上阶跃响应与下阶跃响应之和为直流响应值F(0),图 3给出了电阻率为20 Ωm的均匀半空间下,上升沿阶跃响应与下降沿阶跃响应之间的关系.由图可知,在早期上升沿阶跃响应与下降沿阶跃响应具有相等的幅值,均为直流响应F(0)的一半.在晚期,上升沿阶跃响应逐渐趋近于直流响应值,而下降沿阶跃响应逐渐衰减至零.
|
图 3 上阶跃响应与下阶跃响应之间的关系 Fig. 3 Relationship between step-up and step-down responses |
由于阶跃函数与脉冲函数的相互关系以及大地为线性时不变系统的假设,理论上,对大地脉冲响应进行直接积分可以得到上升沿阶跃响应.然而,多道瞬变电磁法实测数据所恢复的大地脉冲响应早期受到空气波的干扰,直接对大地脉冲响应进行积分难以获得稳定的积分值.本文通过研究上升沿阶跃响应与下降沿阶跃响应的对偶关系,给出了由大地脉冲响应恢复下降沿阶跃响应的反向积分算法.图 3给出了采用Ziolkowski等(2007b)和Connell (2011)所推导的均匀半空间下上升沿阶跃响应和下降沿阶跃响应的解析解公式,计算的20 Ωm均匀半空间下偏移距为1000 m时的上升沿阶跃响应和下降沿阶跃响应.另外,计算了图 3所示每个时间道上升沿阶跃响应与下降沿阶跃响应之和.从图中可以看出,上升沿阶跃响应和下降沿阶跃响应的早期值均为F(0)/2.在晚期,上阶跃响应趋向于直流响应值F(0),而下降沿阶跃响应逐渐衰减至零.根据上升沿阶跃响应与下降沿阶跃响应如图 3所示的对偶关系,从大地脉冲响应幅值很小的晚期进行反向积分,可以得到下降沿阶跃响应.下面给出基于梯形积分公式的反向积分公式:
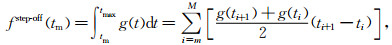
|
(7) |
其中tmax为积分起点,即最晚时间道,M为对应的时间道序号.采用该算法计算下降沿阶跃响应无需直流响应值,同时能避开早期空气波的干扰.为了验证该算法,对电阻率分别为20 Ωm和100 Ωm的均匀半空间,偏移距为1000 m时的大地脉冲响应进行积分,并将积分结果与直接采用解析解计算的下降沿阶跃响应进行对比.如图 4所示,反向积分获得的衰减曲线与解析解之间的相对误差很小,几乎可忽略不计.
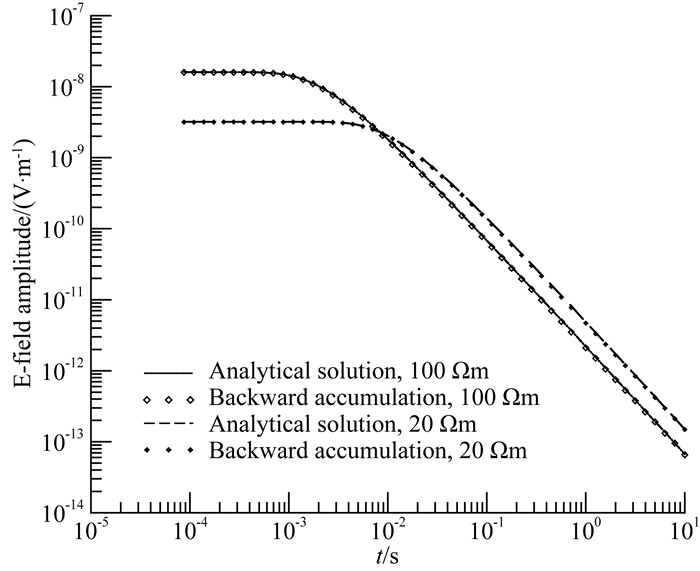
|
图 4 反向积分获得的阶跃响应与解析解的对比 Fig. 4 Comparison of analytical solution and step-off response from backward integration |
由于多道瞬变电磁法采用接收阵列采集响应数据,对于每个记录点均可获得不同偏移距的多次覆盖数据.如图 5a所示,当在发射点A处向大地注入源信号,在接收点A采集响应信号时,记录点A为发射点与接收点的中心位置(Ziolkowski et al., 2007b).记录点位置与偏移距分别采用公式(8)和公式(9)进行计算.
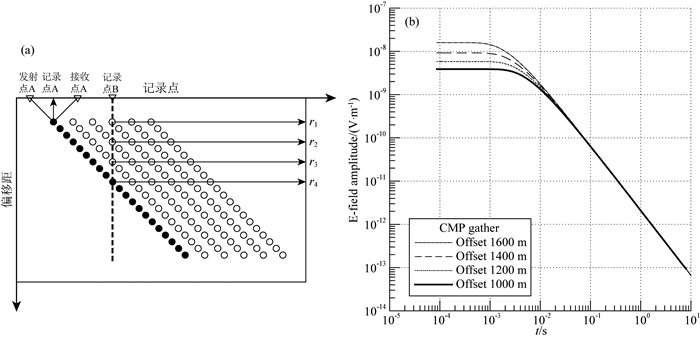
|
图 5 (a)阵列式数据采集系统及(b)共中心点道集示意图 Fig. 5 Schematic diagrams of data collection array (a) and resulting common middle-point gather (b) |
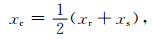
|
(8) |
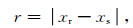
|
(9) |
其中xs和xr分别为发射点和接收点的坐标,xc为观测点坐标,r为偏移距.由于采用接收阵列采集数据,在某一发射点处发射时,可以得到不同记录点、不同偏移距的数据.对于图 5a所示数据采集系统,在发射点A所采集到的数据为图中实心圆点所示.当完成发射点A处的数据采集后,整个发射-接收阵列将沿测线向前平移以完成此条测线的数据采集.因此,对于任一记录点,如记录点B,将获得不同偏移距下的响应数据.将该记录点各个偏移距下的数据整理为一个数据体,称之为共中心点道集.共中心点道集内的响应数据的个数取决于观测系统的布设方式,对于图 5a中的数据采集系统,在记录点B可以获得r1,r2,r3,r4四个偏移距下的数据,如图中虚线所示.图 5b给出了100 Ωm均匀半空间下,1000mm, 1200mm, 1400mm, 1600 m四个偏移距下的下降沿阶跃响应所组成的共中心点道集示意图.
5 联合反演算法由于对共中心点道集进行反演,在每个记录点均有多个偏移距下的数据,需要进行联合反演以充分利用各个偏移距对不同深度的覆盖.反演的基本算法采用OCCAM算法,通过在目标函数中引入模型粗糙度的正则化项,最终得到满足目标拟合残差的最光滑模型.OCCAM算法的目标函数U为
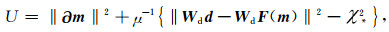
|
(10) |
其中m=(m1, m2, …, mN)为模型向量,d=(d1, d2, …, dM)为数据向量,F为正演算子,χ*为目标拟合残差,∂为粗糙度矩阵,用于计算模型的粗糙度,Wd=diag (σ1-1, σ2-1, …, σM-1)为数据误差加权矩阵.μ为拉格朗日乘子,用于平衡模型粗糙度和拟合残差对目标函数的影响.
OCCAM方法是一种将非线性问题线性化的反演算法.根据泰勒定理,采用局部线性化的思想,有
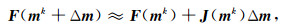
|
(11) |
其中,mk+Δm=mk+1,J(mk)为雅可比矩阵,
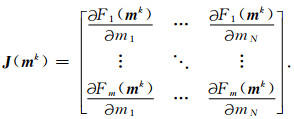
|
(12) |
通过如式(11)所示近似,正则化最小二乘问题(10)可以通过(13)式进行迭代求解,
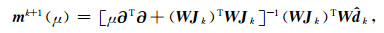
|
(13) |
其中
对于多道瞬变电磁法共中心点道集数据,本文采用多个偏移距下的响应进行联合反演,共同产生一个地电模型.假设共中心点道集内,不同偏移距响应数量为k,则在反演过程中,数据向量、正演算子、雅可比矩阵均应进行拓展,
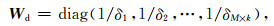
|
(14) |
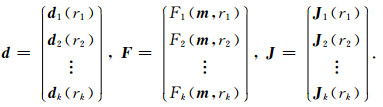
|
(15) |
其中数据向量d和正演函数F的维度为M×k,加权矩阵W的维度为(M×k)×(M×k),雅克比矩阵J的维度为(M×k)×N.
在多道瞬变电磁法的观测方式中,探测深度与偏移距呈正相关(Ziolkowski et al., 2007b; Li et al., 2015),同时与电阻率相关.另外,由于多道瞬变电磁法最终得到的是多个时间道的电磁响应,随着电磁场的扩散,时间与深度之间本身存在对应关系.因此,为了充分利用共中心点道集内不同偏移距对不同深度范围的覆盖,提高多道瞬变电磁法在各个深度范围的分辨率,我们根据共中心点道集内偏移距不同,对反演中的灵敏度矩阵进行加权处理.
构造一个灵敏度加权矩阵Wm,对不同偏移距范围的灵敏度函数进行加权.在多道瞬变电磁法中,对不同深度范围内的目标体存在一个最佳探测偏移距.对于深度为d处的目标体,其最佳探测偏移距r约为2d < r < 4d(Ziolkowski et al., 2007a).以此为基础,我们对灵敏度矩阵的加权算法为:对于偏移距为r的响应,当模型参数mi所对应的深度di < r/4时,其对应灵敏度函数的权值设置为100%;当r/4 < di < r/2,对应权值设置为75%;当di>r/2,对应权值为50%.最后,共中心点道集内偏移距最大的响应所对应的灵敏度函数不加权.最终,得到的灵敏度矩阵为:
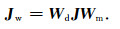
|
(16) |
将得到的灵敏度矩阵代入迭代方程(13),通过一维线性搜索算法选择μ.在拟合残差达到目标拟合残差后,引入模型粗糙度计算,最终得到满足目标拟合残差的最光滑模型.
6 模拟数据反演算例根据以上算法,采用Fortran语言编制了反演程序.反演的基本模型为一维层状模型,采用如前所述算法提取下降沿阶跃响应.瞬变电磁响应的时间道数为51道,采用对数等间距的时间序列.在OCCAM反演中,由于反演模型层数较多,采用厚度相等的层状模型进行反演是一种常见策略(Key, 2009; Sudha et al., 2014).另外,在多道瞬变电磁法中,模型分辨率不仅与深度有关,且与数据点的偏移距也存在较大的关系.为此,在本文的研究中,采用厚度相等的层状模型进行反演,反演模型的层数为40层,每层的厚度为50 m,反演参数为电阻率.反演所采用的数据为整理的共中心点道集,同时对下降沿阶跃响应单支曲线进行反演以作为对比.反演过程中的拟合残差是反演结果模型的响应与观测数据(此处为真实模型的响应)之间的相对误差,计算公式为:
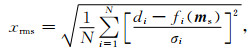
|
(17) |
其中di为真实模型的响应,fi(ms)为反演结果模型的响应数据,N为数据点的个数,σi为每个数据点的标准偏差.在本文的数值试验及多道瞬变电磁法实测数据采集中,均没有对每个数据点的误差进行估算.因此,本文参考了Ziolkowski等(2007b)的处理方式,将每个时间道的标准偏差σi设置为其幅值的1%.
6.1 低阻薄层模型为了对比单支衰减曲线与共中心点道集联合反演的反演效果,首先采用低阻薄层模型进行反演计算.反演的初始模型为电阻率为1 Ωm的均匀半空间,H型薄层模型的低阻层位于500~600 m深度,电阻率为5 Ωm,背景电阻率为100 Ωm,目标拟合残差为1.反演的目标为恢复深度为500 m处的低阻层的存在,为此采用偏移距为目标体深度2倍左右的数据,分别采用了800 m、1000 m、1200 m偏移距下的单支曲线,同时采用这三个偏移距的数据组成的共中心点道集进行了反演.图 6a表示共中心点道集数据,图 6b为共中心点道集内偏移距1000 m响应的拟合情况.反演结果如图 6c所示,对于H型模型,偏移距为800 m, 1000 m和1200 m的单支曲线的反演结果均可以反映低阻目标层的存在,但是与共中心点道集的反演结果对比,单支曲线的反演结果的目标层的电阻率吻合更好.另外,由于联合反演算法中减弱了偏移距较小的响应对反演深部目标体的影响,单支曲线对目标层以下的背景层的电阻率反演效果较差,而共中心点道集的反演效果较好.
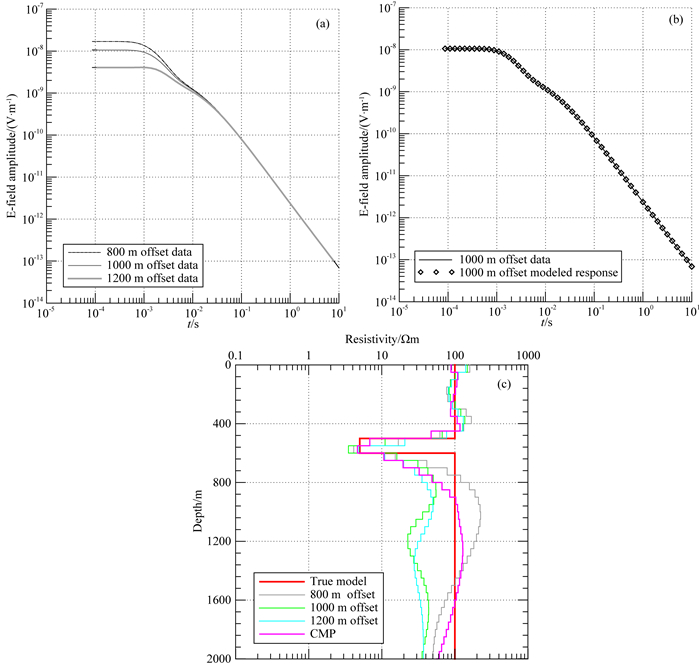
|
图 6 低阻薄层模型反演结果 (a)共中心点道集数据;(b)共中心点道集内1000 m偏移距数据拟合情况;(c)反演结果. Fig. 6 Inversion results of model H with low-resistivity thin layer (a) Common middle point gather data; (b) Fitted offset data at 1000 m; (c) Inversion results. |
为了更进一步对比共中心点道集联合反演与单支曲线的反演对由浅及深整个深度范围内的目标层的反演效果.设计如下五层模型.五层模型的电阻率
分别为100 Ωm,70 Ωm,30 Ωm,60 Ωm和20 Ωm,各层的深度范围分别为0~200 m, 200~500 m, 500~700 m,700~1000 m,1000~底层.模型的电阻率满足ρ1>ρ2>ρ3 < ρ4>ρ5,在这个模型中Q型模型(ρ1>ρ2>ρ3),K型模型(ρ3 < ρ4>ρ5),H型模型ρ2>ρ3 < ρ4等三层模型均得到了体现.该五层模型包含了三种典型的三层模型,能在一定程度上反映反演方法对各种模型和各个深度范围的反演效果.与前述反演中目标层深度为500 m情形不同,此处反演的目标为识别深度为200 m,500 m,700 m,1000 m收发距的电性分界面.为了提高反演对700 m和1000 m深度的电性层的分辨能力,采用了1600 m偏移距处的数据.反演共采用了800 m、1000 m、1600 m偏移距下的单支曲线,同时采用这三个偏移距组成的共中心点道集进行了反演,反演的目标拟合残差为1.
图 7给出了反演结果,从图中可以看出,800 m偏移距单支曲线的反演结果较好反映出了浅部地层,但是深部电阻率偏离真实模型.1000 m和1600 m偏移距下的反演结果无法反映出浅部高阻层,对第三层和第四层的电阻率的反映效果好,对于较深部区域的低阻基底,1600 m偏移距下的反演结果要好于800 m和1000 m偏移距下的反演结果.由此可见,单支曲线的反演结果无法单独反演出所有五层模型,然而共中心点道集的联合反演结果基本给出了各层的电阻率和深度信息,在不同目标体深度情况下,均可获得较好的探测效果.因此,采用多道瞬变电磁法观测方式获得单个测点的共中心点道集进行联合反演解释,可以获得较好的探测效果.
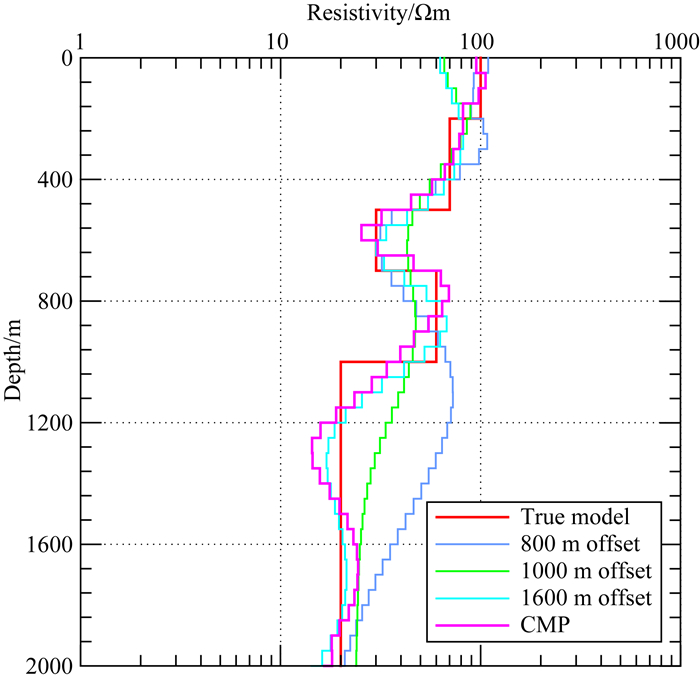
|
图 7 典型五层模型反演结果 Fig. 7 Inversion result for typical 5-layer model |
为了研究反演算法的稳定性,在模拟数据中添加噪声后再进行反演.首先,在模拟数据中添加均值为零、标准偏差为3%的高斯噪声.采用上述反卷积算法和反向积分算法获得下降沿阶跃响应.采用Munkholm和Auken (1996)提出的噪声模型,对得到的下降沿阶跃响应采用对数等间距积分采样,并对采样得到的数据按时间道进行多次叠加.因此,生成噪声数据随时间衰减,符合瞬变电磁响应曲线的衰减特性.由于在模拟数据中添加了噪声,当拟合残差过小时,迭代过程开始拟合所添加的噪声.为此,将反演的目标拟合残差设为2,其他反演参数与图 7中的反演参数一致.
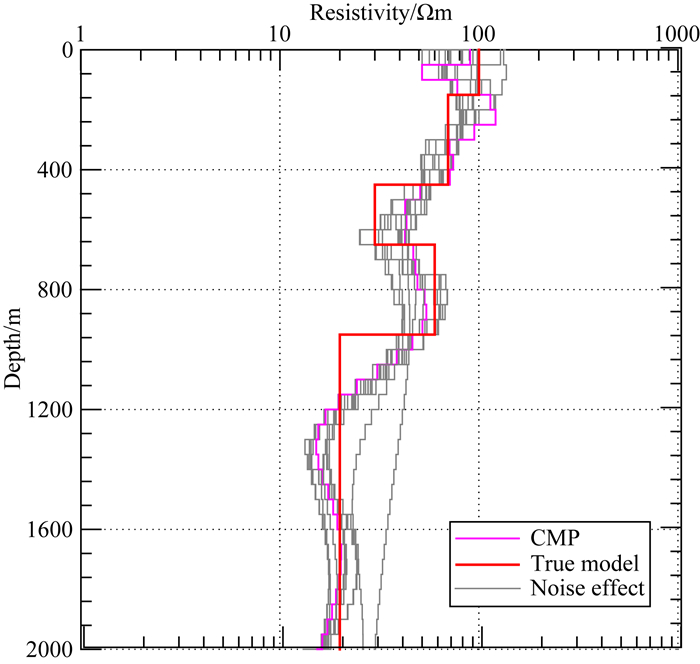
|
图 8 对数据添加噪声后典型模型反演结果 Fig. 8 Inversion result of data added with noisy on typical 5-layer model |
图 8给出了对添加噪声后的共中心点道集数据的反演结果.图中红色曲线表示拟合残差为2时的反演结果,灰色曲线簇表示当拟合残差低于2时得到的模型.当拟合噪声的反演结果拟合残差小于2时,有两支偏离深部地层的电阻率,其余的反演结果均能较好地反映深部的电阻率.这反映了采用不同偏移距组合的共中心点道集数据进行反演具备一定的抗干扰能力.从图中可以看到,共中心点道集反演结果浅部地层受到噪声的影响较大,对深部地层的电阻率的反演效果较好.这是由于所采用的三个偏移距范围内,在拟合残差小于2的模型空间中的模型较多且浅层电阻率差异较大.因此,当目标拟合残差为2时(红色曲线所示),所得到的浅部反演结果较差.当目标拟合残差小于2时(灰色曲线所示),浅部的反演结果得到改善.因此对于多道瞬变电磁法观测方式而言.为提高整个深度范围内对目标体的分辨能力,需要获得多个偏移距下信噪比较高的数据.
7 结论为了加速多道瞬变电磁法装备的研发进程,本文对多道瞬变电磁法数据进行了一维反演研究.首先,针对多道瞬变电磁法所采集的伪随机码激励源全波形数据,采用反卷积方法提取大地脉冲响应.由于上升沿阶跃响应早期幅值难以获取以及大地脉冲响应早期的空气波的存在,对脉冲响应的直接积分难以获得准确幅值的上升沿阶跃响应.为此,通过分析上升沿阶跃响应与下降沿阶跃响应的对偶关系,提出采用反向积分算法恢复下降沿阶跃响应.通过计算表明,反向积分恢复的下降沿阶跃响应能够很好地与解析解对应,该方法为一种简单有效的提取下降沿阶跃响应的积分算法.
其次,针对多道瞬变电磁法阵列式采集方式所得到的多次覆盖数据,本文的联合反演方法能够更充分地利用不同偏移距对不同深度的覆盖.单支曲线反演结果和共中心点道集联合反演结果的对比表明,所采用的联合反演策略在不同目标体深度情况下,均可获得更好的结果.最后,对多道瞬变电磁法数据进行加噪后进行反演,反演结果能够恢复出模型特征.本文的研究表明,在不同目标体深度及有噪声干扰的情况下,共中心点道集数据联合反演计算能获得较好的结果.
| Chen H L, Li H. 2005. Generation and analysis of PN sequence based on MATLAB. Computer Simulation (in Chinese), 22(5): 98-100. | |
| Connell D. 2011. A comparison of marine time-domain and frequency-domain controlled source electromagnetic methods [Master's thesis]. San Diego: University of California. http://escholarship.org/uc/item/1fq462vq | |
| Golub G H, Van Loan C F. 2012. Matrix Computations. Vol.3. Baltimore: JHU Press. | |
| Hobbs B, Ziolkowski A, Wright D. 2006. Multi-Transient Electromagnetics (MTEM)-controlled source equipment for subsurface resistivity investigation.//18th EM Induction Workshop. El Vendrell, Spain. | |
| Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers. Geophysics, 74(2): F9-F20. DOI:10.1190/1.3058434 | |
| Li H, Xue G Q, Zhou N N, et al. 2015. Appraisal of an array tem method in detecting a mined-out area beneath a conductive layer. Pure and Applied Geophysics, 172(10): 2917-2929. DOI:10.1007/s00024-015-1075-0 | |
| Li H, Xue G Q, Zhao P, et al. 2016. The Hilbert-Huang transform-based Denoising Method for the TEM response of a PRBS source signal. Pure and Applied Geophysics, 173(8): 2777-2789. DOI:10.1007/s00024-016-1308-x | |
| Munkholm M S, Auken E. 1996. Electromagnetic noise contamination on transient electromagnetic soundings in culturally disturbed environments. Journal of Environmental and Engineering Geophysics, 1(2): 119-127. DOI:10.4133/JEEG1.2.119 | |
| Mutagi R N. 1996. Pseudo noise sequences for engineers. Electronics & Communication Engineering Journal, 8(2): 79-87. | |
| Noor M A. 1993. Wiener-Hopf equations and variational inequalities. Journal of Optimization Theory and Applications, 79(1): 197-206. DOI:10.1007/BF00941894 | |
| Pipkin A C. 1991. Wiener-Hopf equations.//A Course on Integral Equations. New York: Springer, 160-172. http://clm.utexas.edu/fietelab/QuantNeuro/WH_equations_Seung.pdf | |
| Sudha, Tezkan B, Siemon B. 2014. Appraisal of a new 1D weighted joint inversion of ground based and helicopter-borne electromagnetic data. Geophysical Prospecting, 62(3): 597-614. DOI:10.1111/gpr.2014.62.issue-3 | |
| Teng J W. 2010. Strengthening exploration of metallic minerals in the second depth space of the crust, accelerating development and industralization of new geophysical technology and instrumental equipment. Progress in Geophys. (in Chinese), 25(3): 729-748. DOI:10.3969/j.issn.1004-2903.2010.03.001 | |
| Wright D, Ziolkowski A, Hobbs B. 2002. Hydrocarbon detection and monitoring with a multicomponent transient electromagnetic (MTEM) survey. The Leading Edge, 21(9): 852-864. DOI:10.1190/1.1508954 | |
| Wright D A, Ziolkowski A, Hobbs B A. 2001. Hydrocarbon detection with a multi-channel transient electromagnetic survey.//SEG Technical Program Expanded Abstracts. SEG, 1435-1438. http://library.seg.org/doi/abs/10.1190/1.1816373 | |
| Xue G Q, Li X, Di Q Y. 2007. The progress of TEM in theory and application. Progress in Geophys. (in Chinese), 22(4): 1195-1200. | |
| Xue G Q, Bai C Y, Yan S, et al. 2012a. Deep sounding TEM investigation method based on a modified fixed central-loop system. Journal of Applied Geophysics, 76: 23-32. DOI:10.1016/j.jappgeo.2011.10.007 | |
| Xue G Q, Qin K Z, Li X, et al. 2012b. Discovery of a large-scale porphyry molybdenum deposit in Tibet through a modified TEM exploration method. Journal of Environmental & Engineering Geophysics, 17: 19-25. | |
| Xue G Q, Chen W Y, Zhou N N, et al. 2013. Short-offset TEM technique with a grounded wire source for deep sounding. Chinese J. Geophys. (in Chinese), 56(1): 255-261. DOI:10.6038/cjg20130126 | |
| Xue G Q, Yan S, Di Q Y, et al. 2015. Technical analysis of multitransient electromagnetic method. Journal of Earth Sciences and Environment (in Chinese), 37(1): 94-100. | |
| Zhdanov M S. 2010. Electromagnetic geophysics: Notes from the past and the road ahead. Geophysics, 75(5): 75A49-75A66. DOI:10.1190/1.3483901 | |
| Ziolkowski A, Carson R, Wright D. 2007a. New technology to acquire, process, and interpret transient EM data.//EGM 2007 International Workshop. Italy. http://www.geoconvention.com/archives/2007/068S0130.pdf | |
| Ziolkowski A, Hobbs B A, Wright D. 2007b. Multitransient electromagnetic demonstration survey in France. Geophysics, 72(4): F197-F209. DOI:10.1190/1.2735802 | |
| Ziolkowski A, Parr R, Wright D, et al. 2010. Multi-transient electromagnetic repeatability experiment over the North Sea Harding field. Geophysical Prospecting, 58(6): 1159-1176. | |
| Zou M Y. Deconvolution and Signal Recovery (in Chinese).Beijing: National Defence Industry Press, 2001: 143-144. | |
| 陈海龙, 李宏. 2005. 基于MATLAB的伪随机序列的产生和分析. 计算机仿真, 22(5): 98–100. | |
| 滕吉文. 2010. 强化第二深度空间金属矿产资源探查, 加速发展地球物理勘探新技术与仪器设备的研制及产业化. 地球物理学进展, 25(3): 729–748. DOI:10.3969/j.issn.1004-2903.2010.03.001 | |
| 薛国强, 李貅, 底青云. 2007. 瞬变电磁法理论与应用研究进展. 地球物理学进展, 22(4): 1195–1200. | |
| 薛国强, 陈卫营, 周楠楠, 等. 2013. 接地源瞬变电磁短偏移深部探测技术. 地球物理学报, 56(1): 255–261. DOI:10.6038/cjg20130126 | |
| 薛国强, 闫述, 底青云, 等. 2015. 多道瞬变电磁法(MTEM)技术分析. 地球科学与环境学报, 37(1): 94–100. | |
| 邹谋炎. 反卷积和信号复原.北京: 国防工业出版社, 2001: 143-144. | |
 2016, Vol. 59
2016, Vol. 59

