地球物理学报  2014, Vol. 57 Issue (7): 2269-2277   PDF    
引用本文
李志娜, 李振春, 王鹏. 2014. 基于改进线性Radon变换的井孔地震上下行波场分离方法. 地球物理学报, 57(7): 2269-2277, doi: 10.6038/cjg20140721   
LI Zhi-Na, LI Zhen-Chun, WANG Peng. 2014. Wavefield separation by a modified linear Radon transform in borehole seismic. Chinese J. Geophys. (in Chinese), 57(7): 2269-2277, doi: 10.6038/cjg20140721   
基于改进线性Radon变换的井孔地震上下行波场分离方法
李志娜1, 李振春1, 王鹏2    
1. 中国石油大学(华东)地球科学与技术学院, 青岛 266580;
2. 中国石油大学(华东)石油工程学院, 青岛 266580
投稿时间:2013-8-26    最后修改时间: 2014-5-15 .
基金项目：国家重点基础研究发展计划（973计划）（2011CB202402）、国家自然科学基金（40974073）、中央高校基本科研业务费专项资金（14CX06017A）、山东省自然科学基金（ZR2013DL012）联合资助.
作者简介：李志娜，女，1986年生，在读博士，主要从事地震资料处理方面的研究.E-mail：lizhina00@hotmail.com
摘要：反射波场分离是井孔地震资料处理中极其重要的一个环节，波场分离的质量直接影响成像结果的精度.不管是VSP还是井间地震资料，其反射波时距曲线都近似直线型，根据这一特征，本文提出一种改进的线性Radon变换方法来进行井孔资料的反射波上下行波场分离.该方法基于频率域线性Radon变换，通过引入一个新的变量λ来消除变换算子对频率的依赖性，避免了求取每一频率分量对应的不同变换算子，显著降低了计算成本;文中在求解该方法对应的最小二乘问题时，引入了发展较为成熟的高分辨率Radon变换技术来进一步提高波场分离的精度.采用本文方法进行井孔地震资料的上下行波场分离可以在保证分离精度的前提下有效地提高计算效率.根据上下行波在λ-f域内分布的特殊性，设计简单的滤波算子就可实现上下行波场的分离.最后通过合成数据试算以及实际资料处理（VSP数据和井间地震数据）验证了该方法的可行性和有效性.
关键词： 波场分离     线性Radon变换     高分辨率     VSP     井间地震    
Wavefield separation by a modified linear Radon transform in borehole seismic
LI Zhi-Na1, LI Zhen-Chun1, WANG Peng2    
1. School of Geosciences, China University of Petroleum, Qingdao 266580, China;
2. School of Petroleum Engineering, China University of Petroleum, Qingdao 266580, China
Abstract: In borehole seismic, wavefield separation is an important issue which has great influence on data imaging. For both VSP and cross-well seismic data, the reflection time-distance curves are approximately straight lines. According to this characteristic, a modified linear Radon transform is presented in this paper for upgoing and downgoing wavefield separation in borehole seismic. On the basis of the frequency-domain linear Radon transform, this method is implemented by introducing a new variable λ so as to make the transform operator independent of the frequency, which avoids the calculation of different transform operators for each frequency component, large computational cost is decreased. Besides, in order to further improve the accuracy of wavefield separation, we introduce the sophisticated high-resolution Radon transform to deal with the least squares problem corresponding to this method in this paper. With the application of this method, significant improvement in accuracy and computational efficiency can be obtained in upgoing and downgoing wavefield separation for borehole seismic data. What's more, according to the particularity of the distribution of upgoing and downgoing wavefield in λ-f domain, wavefield separation can be easily performed by simple filter operators. Examples from synthetic data and real borehole seismic data (both VSP data and cross-well seismic data) proved that this method is feasible and valid.
Key words: Wavefield separation     Linear Radon transform     High-resolution     VSP     Cross-well seismic    

1 引言

在地面地震勘探中，经常会面临由于地表风化层衰减造成采集的反射波质量差，期望信号中混杂了相干波或随机噪声等困扰.随着地震勘探对高分辨率采集处理需求的不断提高，为了解决地面地震勘探存在的这些弊端，诸多专家对井孔地震勘探开展了大量的研究(Moon et al., 1986).近年来，井孔地震勘探受到了国内外地球物理界的普遍关注，其中SEG、EAGE等著名国际学术交流会议中都对该技术专门设立了专题.井孔地震勘探即将接收系统、地震能量激发系统分别或同时沉放到现有井中进行地震数据采集，从而得到井下或者井地联合地震数据的一种技术(董世泰和杜春，2002).该技术中以VSP和井间地震这两种主要技术最为引人关注，国内外对这两项技术的研究也取得了突破性的进展，VSP技术已被广泛用于商业生产中，而井间地震在国外也逐渐商业化.采用井孔地震技术，避开了低速带对高频信号的吸收，在一定程度上解决了地面勘探存在的一些问题.

井孔地震资料，不管是VSP还是井间地震，都具有高分辨率、波场复杂，能同时接收到上下行波场，且上下行波场线性特征明显的特点(宋海燕，2009).但是，其上行波和下行波是干涉在一起的，在对该种采集资料进行处理解释之前需要对其进行波场分离(宋海燕，2009; 曹辉等，2004).由于反射波波场分离的精度直接影响地下构造成像的精度，这也将间接制约后续解释的合理性.因此，深入开展井孔地震数据上下行波场分离技术研究是非常有必要的.而上下行波场的线性特征为采用线性Radon变换进行井孔地震资料的上下行波场分离提供了充分的理论依据.

国外，Carswell等(1984)、Moon等(1986)最先将线性Radon变换应用于VSP资料的波场分离中，Mars等(1999)对线性Radon变换在井间地震波场分离中的应用进行了详细讨论，Boelle等(1998)采用线性Radon分解对井孔地震资料实现了波场分离.国内，李元钦等(1990)、王维红等(2006)、Song等(2010)、曾有良等(2007)都对线性Radon变换在井孔资料波场分离中的应用做过大量的研究.研究中发现，最初发展的线性Radon变换在变换域波场能量聚焦效果差，严重影响井孔资料波场分离的精度.为了获取高质量的波场分离效果，基于线性Radon变换的改进技术不断地应运而生.

在地震勘探资料处理中，计算精度和计算效率是地球物理工作者不得不考虑的两个重要因素，为了提高Radon变换的精度和降低计算成本，国内外专家做了大量的探究.其中，为了提高计算精度，Sacchi和Ulrych(1995)提出了频率域的高分辨率Radon变换算法，继而Cary(1998)、Herrmann等(2000)、Nowak和Imhof(2004)等人进一步发展了该技术，通过高分辨率技术可以使得变换域内波场能量更为收敛，保证了波场分离的精度；而在提高计算效率方面，除了对Radon变换快速求解算法的研究(Sacchi et al., 1999; Wang et al., 2009)以外，Abbad等(2011)在一个新的域内提出了基于抛物Radon变换(PRT)的快速改进PRT方法，该方法实现快速有效，通过引入新的变量消除变换算子对频率的依赖性，极大地提高了计算效率.Li等(2013)在Abbad基础上对线性Radon变换进行了改进，并将其用于井孔资料的波场分离中.

高精度的处理结果往往要以高计算成本作为代价.本文中，综合考虑计算精度和计算效率，作者提出了一种新的波场分离方法.首先，借鉴Abbad的思想，通过引入新的变量λ对线性Radon变换进行改进，消除变换算子对频率的依赖性，避免了对每个频率分量都进行变换算子求取的过程，极大地提高了计算效率；同时，为了提高波场分离的精度，结合高分辨率技术，在求解该方法对应的最小二乘问题时，采用了在模型空间加入柯西分布的高分辨率Radon技术(Sacchi and Ulrych， 1995)，并通过共轭梯度法迭代实现最小二乘问题的求解.然后，根据λ-f域内上下行波场分布的特殊性选取合适的滤波算子来进行上下行波场的分离.最后，通过合成数据以及实际井孔资料上下行波场分离处理对本文方法的可行性和有效性进行了验证. 2 改进线性Radon变换原理及实现

由于线性Radon变换可以将具有一定斜率的直线在Radon域映射为一个点，因此，根据井孔地震资料中上、下行波同相轴具有明显的线性特征以及其传播速度方向是相反的这一特点，通常可采用线性Radon变换来进行井孔地震资料反射波的分离.在采用线性Radon变换进行反射波上下行波场分离的过程中，野外采集的离散井孔地震数据，D(xn，t)，可以表示为沿不同斜率的一系列射线路径的叠加求和(Abbad et al., 2011; Li et al., 2013; 张保卫，2007)

(1)式即为线性Radon变换的反变换表达式，其中，xn为偏移距，t为双程走时，p为视慢度(斜率)，τ为截距时间，M(p，τ)为线性Radon变换域结果.Nx为井孔地震数据的道数，Np为p选取的采样点数.Radon变换可以在时间域实现也可以在频率域实现.考虑到频率域运算的高效性，本文中将以频率 域的线性Radon变换为基础进行进一步 的研究讨论.将(1)式转换到频率域得其反变换频域表达式如下：

用矩阵形式可表示为

其对应的正变换表达式为

其中，L nj(f)=e－2πifpjxn，n=1，…，Nx；j=1，…，Np.由此可见，算子 L(f)是一个与频率有关的矩阵，对于频率域的每一个频率分量，算子 L 都对应有不同的矩阵形式，因而在采用常规的线性Radon变换进行波场分离过程中需要对每个频率分量都进行算子 L 、 L H、 L －1、(L H)－1的求取.为了消除变换算子对频率的依赖性，Abbad等(2011)对抛物Radon变换(PRT)进行了改进，通过在PRT中引入变量λ=qf(q表示曲率)来使得抛物Radon变换算子与频率无关，避免了对每个频率分量都进行变换算子及其逆求取的过程，极大地提高了计算效率.考虑到井孔地震记录中上下行波同相轴都表现为具有不同斜率(p为常数)的射线，借鉴Abbad的思想，本文中我们对线性Radon变换进行改进，通过在线性Radon变换中引入一个新的变量λ=pf来消除线性Radon变换算子 L 对频率的依赖性，其单位为m－1.则由λ=pf可知，上下行波场在λ-f域内将表现为过原点且以p为斜率的射线，这正是后文中进行上下行波场分离的理论依据.于是，式(3)对应的λ-f域线性Radon反变换可以表示为

其中，L nj(λ)=e－2πiλjxn，n=1，…，Nx；j=1，…，Nλ=Np.

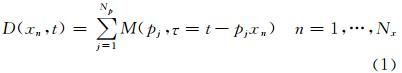
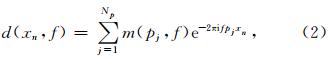
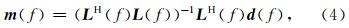
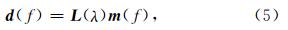
根据(5)式采用最小平方方法，使下面的目标函数最小即可求得 m .

对 m 求导并令其导数为零，即可求得其正变换表达式如下：

式(7)和式(5)对应的即为改进的λ-f域线性Radon变换的正反变换对.该方法中由于算子 L(λ)与频率无关，在给定离散采样值λ的前提下，对于所有的频率分量，矩阵 L 、 L H及其逆运算仅需计算一次即可.而常规的线性Radon变换算法中则需对每个频率分量都计算其对应的矩阵 L 、 L H及其逆，因此，该方法相比常规的线性Radon变换可以有效地提高计算效率.

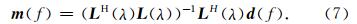
在常规线性Radon变换中，求解最小二乘问题时阻尼因子选取不当将会造成解不稳定、变换域内能量分散等问题，这将严重影响井孔资料上下行波场分离的精度.为了提高Radon变换的稳定性和精度，高分辨率Radon变换算法得到了广泛的应用.本文将高分辨率算法应用于改进的线性Radon变换中，通过在模型空间采用柯西准则(Sacchi and Ulrych， 1995)进行稀疏约束以此提高λ-f域线性Radon变换的稳定性和精度.在最小二乘意义下，该问题可转化为使得如下目标函数最小

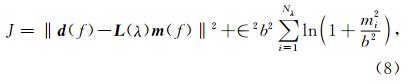
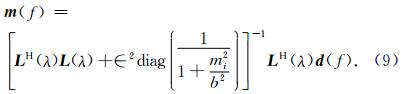
其中，Nλ为模型空间λ点数，∈，b为约束模型空间稀疏性的两个常数.(8)式中对 m 求导并令其导数为零，可得

文中我们采用共轭梯度法(CG)并通过多次迭代来对该最小二乘问题进行求解.

为了能有效压制假频，在λ-f域实现线性Radon变换也需要对参数进行合理的选择.Turner(1990)提出在线性Radon变换中为了防止假频产生Δp应满足

其中，f=1/T，xmax，xmin分别为最大炮检距和最小炮检距，Δp为p采样间隔.结合λ定义，推导可得λ的采样间隔应满足

又根据采样定理，fmax≤ 1/2ΔT 以及ΔT= ∂t(p，x)/∂x Δx=pΔx(Guitton，2001; Abma et al., 1999)，取pmax为p 最大值，则

其中，Δx为炮检距间隔.(12)式即为线性Radon变换域中，为了防止产生空间假频Δx应满足的关系式，Turner(1990)也曾给出这一结论，则同样根据λ定义，可推导出λ-f域另外一个重要参数λmax应满足的关系式

(13)式适用于λ>0时，而当λ<0时，通过推导我们可以得出如下类似的结论：

于是，由式(13)和式(14)可得

式(11)、(15)即是为了防止产生假频对应的λ参数选取范围.由此可见，λ值的扫描范围仅依赖于最大偏移距、最小偏移距以及空间采样率，而与频率无关. 3 上下行波场分离

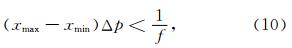
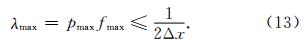
采用上述改进的λ-f域高分辨率线性Radon变换进行井孔地震数据波场分离的理论依据可描述为：由于井孔地震数据中的上行波和下行波同相轴近似线性且具有相反符号的斜率，在λ-f域内它们将表现为具有相反符号斜率且过原点的射线，这非常有利于λ-f域内上下行波场分离时滤波算子的选取，通过选取合适的滤波算子即可实现上下行波场的分离.在此，我们通过引入如下简单的滤波矩阵 F +和F －来进行井孔资料上下行波场的分离.

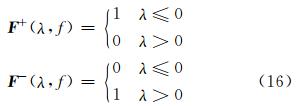
其中，F + 是上行波滤波算子，F － 是下行波滤波算子.于是，上行波场和下行波场可以分别表示如下：

m +表示模型空间的上行波场，m －表示模型空间的下行波场，而 m 为模型空间改进的λ-f域高分辨率线性Radon变换结果.

在对上下行波进行滤波以后，我们将模型空间的上行波场 m +和下行波场 m －，分别变换回数据空间，即可得到井孔地震数据上下行波场分离的结果.该方法利用上下行波场在λ-f域内分布的特殊性，通过选取简单的滤波算子就可以实现反射波的分离，同时也避免了波场分离时Radon域内的截断效应，在一定程度上提高了波场分离的精度. 4 数值试算

本文中，我们将以井孔地震中最为常见的VSP和井间地震为例，采用改进的λ-f域高分辨率线性Radon变换来进行上下行波场的分离，并通过模型试算和实际资料处理来验证本文方法在井孔地震数据上下行波分离中的可行性和有效性.需要指出，根据波场传播的速度方向不同，该方法同样适用于其他的波场分离，如多分量井孔地震中纵横波的分离等，本文中将不对其进行详细讨论. 4.1 模型试算

首先，采用一简单的合成数据来模拟井孔资料中近似线性的上下行波场.该模型包含6个同相轴(其中包含3个上行波同相轴和3个下行波同相轴)，共41道接收，偏移距为25 m，采样点数为2801，采样率为0.001 s，合成数据如图 1a所示.该数据在λ-f域内的映射如图 1b所示，为了防止假频产生，我们根据式(11)和式(15)来进行Δλ和λmax的选取，在此，由xmax=1000 m，xmin=0 m，Δx=25 m，计算得Δλ<0.001，｜λmax｜≤0.02，于是，图 1b中选取｜λmax｜=0.018，Δλ=0.00036，Nλ=101，由图可见线性同相轴清晰地映射到λ-f域内过原点的射线上，没有假频的产生.为了说明该方法与传统方法的差异，我们对合成数据进行频率域高分辨率线性Radon变换(图 1c)，并对两种方法进行直观对比，如图 1b，1c所示，在λ-f域内，记录中线性的上下行波同相轴表现为经过原点的具有不同斜率的射线，其中，分布于右半部分的具有正斜率的射线对应为下行波而分布于左半部分具有负斜率的则对应为上行波；但在τ-p域内，上下行波则表现为分布在不同区域的能量聚焦的点，其中，分布在p<0区域内的为上行波，而分布在p>0区域内的为下行波.由此可见，本文方法与传统的方法在Radon域内所呈现的特征是截然不同的.此外，在τ-p域内，由于截断效应的影响，聚焦点附近存在拖尾现象，这对于上下行波场的分离是极为不利的，但是在λ-f域内，能量集中在λ=0两侧的射线上，在一定程度上避免了常规方法存在的拖尾现象.因而，本文方法相比常规的频率域高分辨率Radon算法不仅提高了计算效率，同时对Radon域内波场分离精度的提高也有一定的改善.根据λ-f域内上下行波场的可分离性，可以采用滤波算子 F +和F －来进一步实现上下行波的分离.

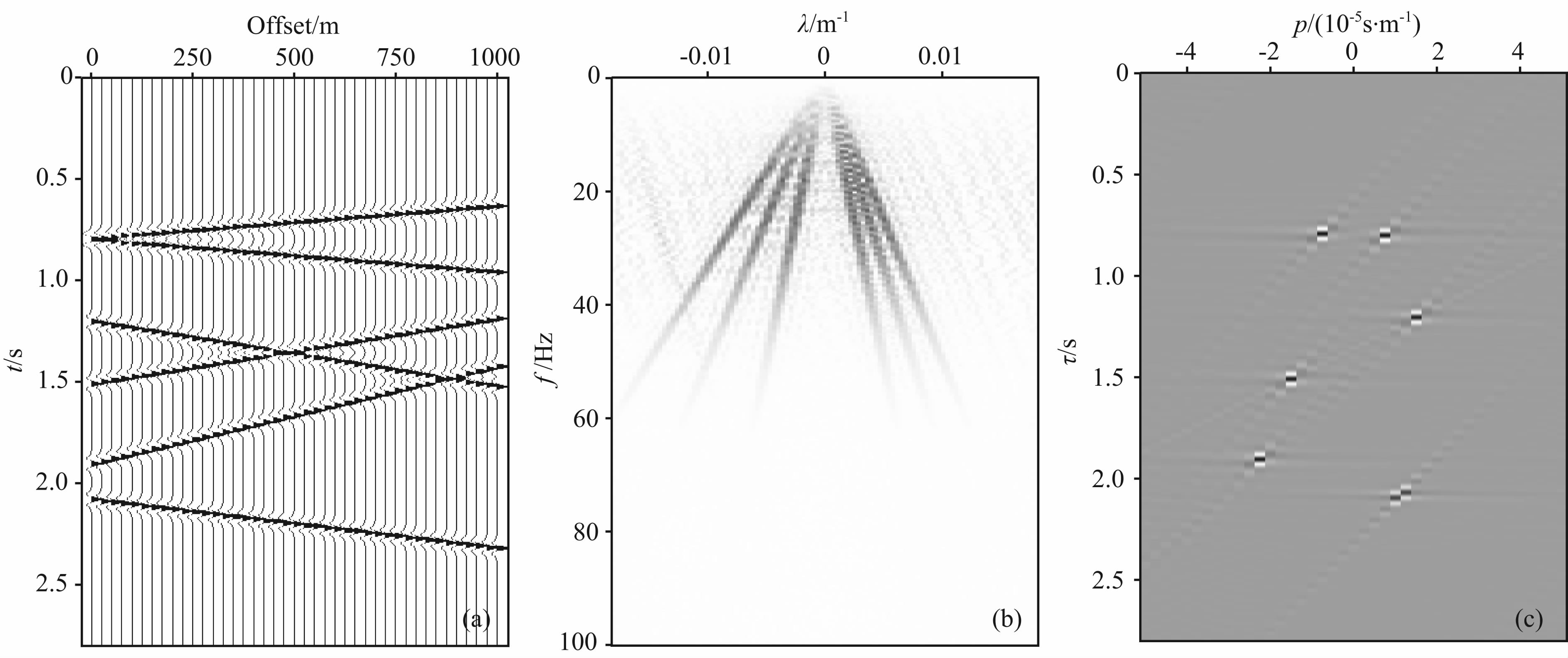图 1 合成数据Radon变换结果对比 (a)合成数据；(b)λ-f域高分辨率线性Radon变换结果；(c)τ-p域高分辨率线性Radon变换结果. 图(b)中线性同相轴在λ-f域内表现为经过原点的射线，而在图(c)中τ-p域内则表现为聚焦的点. Fig. 1 Synthetic data and its modified linear Radon transform result (a)Synthetic data;(b)λ-f domain high-resolution linear Radon transform result;(c)τ-p domain high-resolution linear Radon transfrom result. The events in λ-f domain act along radial lines passing through the origin in figure(b)，while they show focus points in τ-p domain in figure(c).

为了进一步验证本文方法的优势，我们就其波场分离的精度以及计算效率与目前应用较为广泛的f-k滤波以及常规的线性Radon变换进行对比.图 2所示即为分别采用f-k滤波、高分辨率线性Radon变换和本文方法分别进行波场分离后的结果对比图.其中，图 2a—2c依次为采用f-k滤波、常规线性Radon变换和λ-f域线性Radon变换进行波场分离后的上行波场.而图 2d—2f分别为对应的下行波场.通过对比可以发现，在f-k滤波结果中存在明显的剩余能量，上下行波未得到有效的分离，这是由于f-k滤波法在波数域存在Rieber混合现象造成了上下行波场能量不能得到有效的分离；常规线性高分辨率Radon变换波场分离结果则得到了一定的改善，但是上下行波场之间的影响还清晰可见，这与传统Radon变换方法存在的截断效应影响是有直接关系的；而采用本文方法得到的波场分离结果则要明显优于前两种方法，该方法避免了f-k滤波法的Rieber混合现象也避免了常规线性Radon变换的截断效应，既能有效地消除上下行波场之间的影响，又没有假频的引入，同时振幅得到了很好的保持、波形也更为一致.表 1中对三种方法进行上下行波场分离所需要的计算时间进行了对比，由表中数据结合上下行波场分离的效果可知，f-k滤波法计算效率最高，但是精度却相对较低，而采用传统的高分辨率线性Radon变换和本文方法波场分离效果相比f-k滤波法都有一定的改善，但是传统方法在计算效率方面却远远不如本文方法，且传统方法中由于拖尾现象的存在，使得Radon域内进行波场分离时会受到一定的影响，从而造成近偏移距和远偏移距数据在波场分离后存在较多的剩余能量，而本文方法则避免了拖尾现象的影响，波场分离效果在一定程度上得到了改善.因此，模型试算结果证明了采用本文方法进行井孔地震资料波场分离可以在显著降低计算成本的前提下又能得到精度较高的上下行波场分离结果.

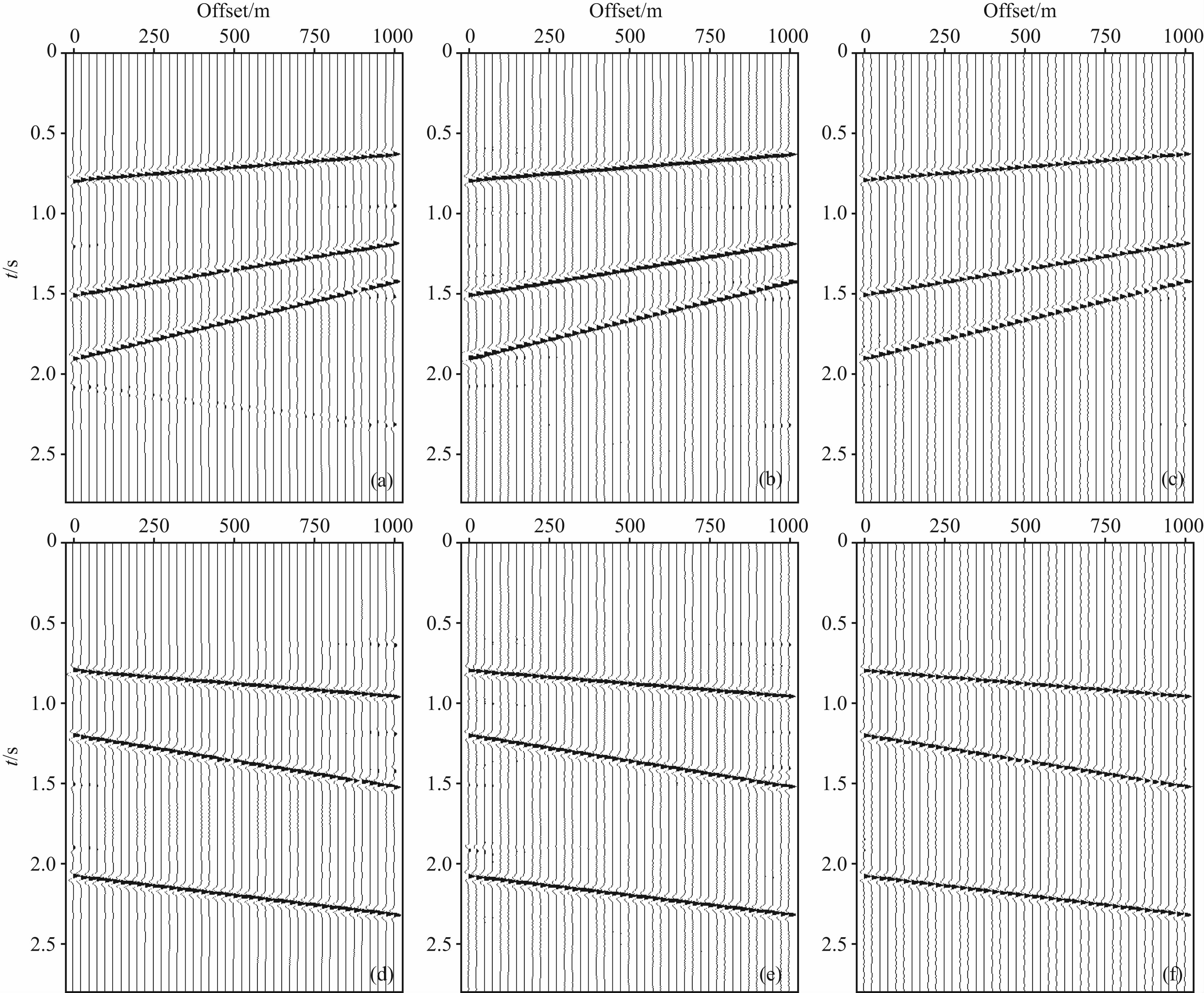图 2 不同方法上下行波场分离结果对比 (a)经f-k滤波得到的上行波场；(b)高分辨率线性Radon变换得到的上行波场；(c)本文方法得到的上行波场； (d)经f-k滤波得到的下行波场；(e)高分辨率线性Radon变换得到的下行波场；(f)本文方法得到的下行波场. Fig. 2 Comparation of wavefield separation results with different methods Upgoing wavefield obtained by(a)f-k filtering，(b)high-resolution linear Radon transform，(c)method in this paper， and downgoing wavefield obtained by(d)f-k filtering，(e)high-resolution linear Radon transform，(f)method in this paper.

表 1 不同方法上下行波场分离耗时对比 Table 1 Comparison of time consuming on wavefield separation by different methods

改进的线性Radon变换具有计算高效，波场分离实现简单的特点.但是，需要注意的是，同传统Radon变换一样，该方法也是基于上下行波场的视速度方向不同来进行波场分离.理论上来讲，对于具有典型视速度差异的同相轴在λ-f域内都可以实现分离，但是，根据λ-f域内波场分布特征可知，该方法对于视速度差异很小的同相轴间的分离会由于在λ-f域内射线能量分布紧密而受到一定的影响.而在处理实际数据时，地下介质较为复杂，一般情况下，井孔地震数据的反射波时距曲线不再为直线，但是仍然近似直线型，可以采用积分的思想，将反射波同相轴局部分段视为直线，根据本文方法实现的原理，对于局部具有一定斜率的同相轴该方法仍是适用的，因此，该方法对于复杂介质情况下同相轴不再为直线的波场分离仍是适用的，其能量的分布特征还是一致的，上行波分布在λ<0的区域内，而下行波则相反. 4.2 实际资料处理

下面将本文所述方法应用于实际井孔地震数据的波场分离中来进一步验证该方法的有效性和实用性.图 3所示为对VSP实际采集数据进行上下行波场分离的试算结果.其中，图 3a为实际的VSP单炮 记录，采样率0.5 ms，记录时间为3 s，道间距为50 m，由图可见上下行波场线性特征明显.采用本文方法进行λ-f域高分辨率Radon变换所得结果如图 3b所示，图中可以看出，在λ-f域内右半部分分布有较强的下行波能量，而在左侧上行波能量则相对较弱，选取滤波算子在λ-f域进行上下行波场的分离，并将分离后的数据反变换回数据空间得到分离后的上行波场和下行波场分别如图 3c、3d所示，从图中可以看出上下行波场得到了很好的分离.图 4所示为井间地震实际资料上下行波场分离的结果.由于井间地震数据中直达波能量较强，会严重影响上下行反射波场的分离，因而在进行反射波波场分离前需要先对其 进行切除，图 4a所示为切除直达波后的实际 井间地震炮记录，其采样率0.5 ms，记录时间为0.5 s，道间距为3 m，偏移距范围为369 m至-231 m，图中可以看到复杂的上下行波场，在炮记录中它们表现为近似的直线，因此，可以采用本文λ-f域高分辨率线性Radon变换算法来进行上下行波场的分离.图 4b为λ-f域高分辨率线性Radon变换结果，可明显看到左右两侧分别分布有能量较强的上下行波场.图 4c、4d分别为采用本文方法得到的上行波和下行波，可以看出上下行波场分离效果理想，波形振幅都得到了很好的保持.由图 3c—3d和4c—4d可见，采用本文的λ-f域线性Radon变换对井孔地震资料进行反射波波场分离处理可以得到较好的上下行波场分离结果.这一结论也再次验证了本文方法在井孔地震数据反射波波场分离中的可行性、有效性和实用性.

图 3 VSP实际资料波场分离结果 (a)实际VSP炮记录；(b)λ-f域线性Radon变换结果；(c)分离后的上行波；(d)分离后的下行波. Fig. 3 Wavefield separation results of VSP real data (a)Real VSP shot gather;(b)λ-f domain linear Radon transform result; (c)Separated upgoing wavefield;(d)Separated downgoing wavefield.

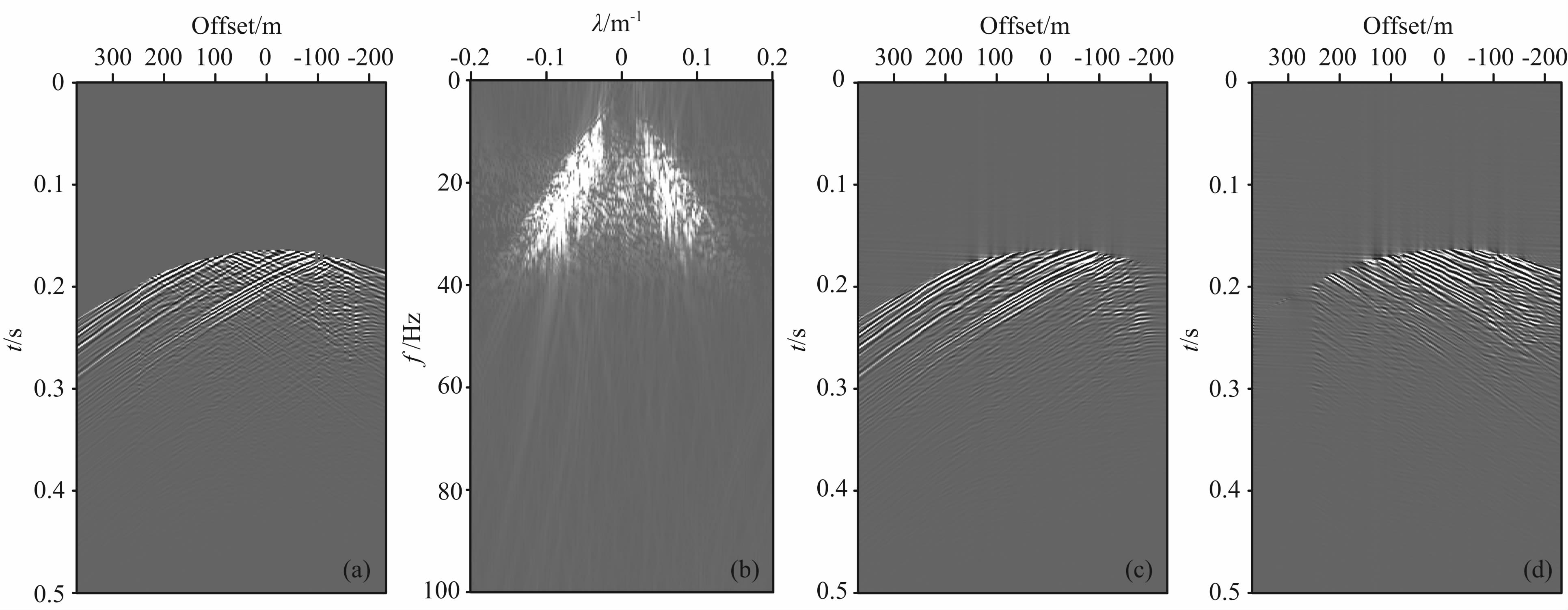图 4 井间地震实际资料波场分离结果 (a)经直达波切除后的实际井间地震炮记录；(b)λ-f域线性Radon变换结果； (c)分离后的上行波；(d)分离后的下行波. Fig. 4 Wavefield separation results of cross-well real data (a)Real cross-well shot gather after direct wave removing;(b)λ-f domain linear Radon transform result; (c)Separated upgoing wavefield;(d)Separated downgoing wavefield.
5 结论

本文在前人研究基础上提出了一种改进的高分辨率线性Radon变换算法，对该方法的原理及实现进行了详细的介绍，并将该方法应用于井孔地震数据的反射波场分离中.该方法通过引入新变量λ来消除变换算子对频率的依赖性，从而避免了对每个频率分量都计算对应变换算子及其逆的过程，有效地提高了计算效率；此外，采用高分辨率算法，保证了该方法对应最小二乘问题求解的精度和稳定性.变量λ的引入还使得井孔数据中近似线性的上下行 波在λ-f域内表现为具有不同斜率且过原点的射线，根据这一特征可以方便地选取滤波算子来进行上下行波的分离，在一定程度上避免了常规线性Radon变换中的截断效应，提高了波场分离的精度.最后，采用本文方法对合成数据和实际井孔地震资料进行上下行波场分离处理，得到了较好的波场分离效果，这为井孔地震数据反射波成像奠定了良好的基础.

致谢 作者感谢两位匿名审稿专家的宝贵意见，感谢SU和Madagascar软件提供的绘图支持.

参考文献
[1] Abbad B, Ursin B, Porsani M J. 2011. A fast, modified parabolic Radon transform. Geophysics, 76(1): V11-V24, doi: 10.1190/1.  3532079.
[2] Abma R, Sun J, Bernitsas N. 1999. Antialiasing methods in Kirchhoff migration. Geophysics, 64(6): 1783-1792, doi: 10.1190/1.  1444684.
[3] Boelle J, Canadas G, Hugonnet P. 1998. Wavefield separation in borehole seismic by linear Radon decomposition. 68th Ann. Internat Mtg., Soc. Expi. Geophys..   Expanded Abstracts, 272-275.
[4] Cao H, Tang J L, Guo Q S, et al. 2004. The wavefield separation and application of seismic crosshole method. Geophysical Prospecting for Petroleum (in Chinese), 43(6): 518-522, doi: 10.3969/j.issn.1000-1441.2004.06.002.
[5] Carswell A, Tang R, Dillistone C, et al. 1984. A new method of wave field separation in VSP data processing. 54th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 40-42.
[6] Cary P W. 1998. The simplest discrete Radon transform. 68th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 17(1): 1999-2002.
[7] Dong S T, Du C. 2002. The actuality and development of downhole seismic exploration equipment. Equipment for Geophysical Prospecting (in Chinese), 12(4): 227-234, doi: 10.3969/j.issn.1671-0657.2002.04.001.
[8] Guitton A. 2001. Solutions to data and operator aliasing with the parabolic Radon transform.   Stanford Exploration Project, 108: 1-14.
[9] Herrmann P, Mojesky T, Mageson M, et al. 2000. De-aliased, high-resolution Radon transforms. 70th Ann. Internat Mtg., Soc. Expi. Geophys..   Expanded Abstracts, 1953-1956.
[10] Li Y Q, Miu Y G, Wu L. 1990. Application of the Radon transform to VSP wave field separation. Oil Geophysical Prospecting (in Chinese), 25(6): 653-661.
[11] Li Z N, Li Z C, W P, et al. 2013. Wavefield separation by a modified linear Radon transform in borehole seismic. 83th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 642-646.
[12] Mars J, Rector J W, Lazaratos S K. 1999. Filter formulation and wavefield separation of cross-well seismic data. Geophysical Prospecting, 47(5): 611-636, doi: 10.1046/j.1365-2478.1999.00147.  x.
[13] Moon W, Carswell A, Tang R, et al. 1986. Radon transform wave field separation for vertical seismic profiling data. Geophysics, 51(4): 940-947, doi: 10.1190/1.  1442151.
[14] Nowak E J, Imhof M G. 2004. Diffractor localization via weighted Radon transforms. 74th Ann. Internat Mtg., Soc. Expi. Geophys..   Expanded Abstracts, 2108-2111.
[15] Sacchi M D, Porsani M. 1999. Fast high resolution parabolic Radon transform. 69th Ann. Internat Mtg., Soc. Expi. Geophys..   Expanded Abstracts, 1477-1480.
[16] Sacchi M D, Ulrych T J. 1995. High-resolution velocity gathers and offset space reconstruction. Geophysics, 60(4): 1169-1177, doi: 10.1190/1.  1443845.
[17] Song H Y. 2009. 3C borehole seismic data wavefield separation and application (in Chinese). Qingdao: China University of Petroleum (Huadong).
[18] Song J G, Feng Y P, Zuo J J, et al. 2010. Application of high-resolution Radon transform in cross well seismic.   2010 3rd International CISP, 6: 2966-2970.
[19] Turner G. 1990. Aliasing in the tau-p transform and the removal of spatially aliased coherent noise. Geophysics, 55(11): 1496-1503, doi: 10.1190/1.  1442797.
[20] Wang J F, Ng M, Perz M. 2009. Fast high-resolution Radon transforms by greedy least-squares method. 79th Ann. Internat Mtg., Soc. Expi. Geophys..   Expanded Abstracts, 3128-3132.
[21] Wang W H, Shou H, Liu H, et al. 2006. High resolution τ-p transform using in linear events wavefield separation. Progress in Geophysics (in Chinese), 21(1): 74-78, doi: 10.3969/j.issn.1004-2903.2006.01.012.
[22] Zeng Y L, Yue Y X, Shan Q T, et al. 2007. VSP wavefield separation based on high-resolution Radon transformation. Geophysical Prospecting for Petroleum (in Chinese), 46(2): 115-119,173, doi: 10.3969/j.issn.1000-1441.2007.02.003.
[23] Zhang B W. 2007. Radon transform and its application in seismic data processing (in Chinese). Xi'an: Chang'an University.
[24] 曹辉, 唐金良, 郭全仕等. 2004. 井间地震反射波场分离及应用研究. 石油物探, 43(6): 518-522, doi: 10.3969/j.issn.1000-1441.2004.06.  002.
[25] 董世泰, 杜春. 2002. 井中地震勘探仪器的现状与发展. 物探装备, 12(4): 227-234, doi: 10.3969/j.issn.1671-0657.2002.04.  001.
[26] 李元钦, 牟永光, 吴律. 1990. Radon变换在VSP波场分离中的应用.   石油地球物理勘探, 25(6): 653-661.
[27] 宋海燕. 2009. 三分量井孔地震资料波场分离与应用［硕士论文］.   青岛: 中国石油大学(华东).
[28] 王维红, 首皓, 刘洪等. 2006. 线性同相轴波场分离的高分辨率τ-p变换法. 地球物理学进展, 21(1): 74-78, doi: 10.3969/j.issn.1004-2903.2006.01.  012.
[29] 曾有良, 乐友喜, 单启铜等. 2007. 基于高分辨率的Radon变换的VSP波场分离方法. 石油物探, 46(2): 115-119,173, doi: 10.3969/j.issn.1000-1441.2007.02.  003.
[30] 张保卫. 2007. Radon变换及其在地震数据处理中的应用［硕士论文］.   西安: 长安大学.