地球物理学报  2014, Vol. 57 Issue (4): 1133-1140   PDF    
引用本文
刘向君, 朱洪林, 梁利喜. 2014. 基于微CT技术的砂岩数字岩石物理实验. 地球物理学报, 57(4): 1133-1140, doi: 10.6038/cjg20140411   
LIU Xiang-Jun, ZHU Hong-Lin, LIANG Li-Xi. 2014. Digital rock physics of sandstone based on micro-CT technology. Chinese J. Geophys. (in Chinese), 57(4): 1133-1140, doi: 10.6038/cjg20140411   
基于微CT技术的砂岩数字岩石物理实验
刘向君, 朱洪林, 梁利喜    
油气藏地质及开发工程国家重点实验室, 西南石油大学, 成都 610500
投稿时间:2013-4-26    最后修改时间: 2013-10-8 .
基金项目：国家自然科学基金石化联合基金重点项目（U1262209）资助.
第一作者简介：刘向君，女，1969年生，西南石油大学现任教授、博导，主要从事岩石物理与油气井井壁稳定方面的研究.E-mail：liuxiangjunswpi@163.com
摘要：数字岩石物理技术可弥补传统岩石物理实验的诸多不足，为岩石物理学研究提供一个新平台.本文以常规砂岩为研究对象，利用微CT扫描结合先进的图像处理技术建立了具有真实孔隙结构特征的三维数字岩芯模型；应用Avizo软件内含的多种形态学算法进行数字岩芯孔隙结构量化及表征研究，统计获取了孔隙度、孔隙体积分布及孔径分布特征，建立了等价孔隙网络模型；将Avizo与多场耦合有限元软件Comsol完美对接，实现了孔隙尺度的渗流模拟并计算获得绝对渗透率，对于考虑固相充填孔隙的情况，模拟计算了岩石有效弹性参数，并与近似Gassmann方程良好验证.本文所提出的将Avizo与Comsol结合使用的方法丰富了现有的数字岩石物理研究手段，为其大规模发展提供了一条新途径.
关键词： 数字岩石物理     砂岩     孔隙结构     微CT扫描     岩石物理参数    
Digital rock physics of sandstone based on micro-CT technology
LIU Xiang-Jun, ZHU Hong-Lin, LIANG Li-Xi    
State Key Laboratory of Oil & Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China
Abstract: Digital rock physics technology makes up for the disadvantages of traditional petrophysical experiments, and has opened up a new platform for petrophysics research. Taking sandstone as study object, this paper introduces a systematic process of digital rock physics: based on micro-CT scanning and advanced image processing technology we build a three-dimensional digital core model with real pore structure characteristics; with the application of Avizo software which contains a variety of morphological algorithm, the research of quantification and characterization of the pore structure is conducted, the porosity, pore volume distribution and pore size distribution characteristics are obtained by statistical methods, and the equivalent pore network model is built; the Avizo and Comsol multiphysics softwares are interactively combined in this paper, which realize the pore-scale flow simulation as well as the absolute permeability calculation; for the case of the solid phase pore-filling, the effective elastic parameter of the rock is simulated, the result has a good validation with the approximate Gassmann equation. Our study enriches the existing research approaches of digital rock physics, simultaneously opens up a new pathway for its wide-scale development.
Key words: Digital rock physics     Sandstone     Pore structure     Micro-CT scanning     Petrophysical parameters    
1 引言

岩石是一种天然的多孔介质，其内部除了固体基质还分布有大量不规则的孔隙以及孔隙空间流体，这些组分的物理性质以及微观孔隙结构特征直接影响着宏观岩石物理属性，如强度、弹性模量、渗透率、电阻率、声波速度等.模拟孔隙尺度的物理现象、理解微观作用机理是准确获取岩石物理性质的关键，探明岩石微观组构与宏观物性之间的内在联系，对于解决石油、地质等地球物理领域中的实际工程问题具有十分重要的意义，而这一切仅靠传统岩石物理研究手段是实现不了的.近年来，国内外已有学者(Φren and Bakke， 2002；Arns et al., 2004a，2004b；Hu，2007；Okabe and Blunt， 2005；Zhao et al., 2007)通过多种方法建立了能够刻画孔隙空间分布的三维数字岩芯，在此基础上开展数值模拟，从而计算岩石物性参数.这种方法被称为数字岩石物理，由于研究是基于数字化平台的虚拟实验，因而具有可重复性，可同时模拟多重物理响应并探讨相互关系，且微观影响因素可控，还能模拟传统岩石物理实验难以测量的物理量，并节省大量人力物力资源.数字岩石物理的这些优势，使其逐渐成为地球物理学的研究热点.

尽管如此，现有的主要研究成果还集中在国外，主要来自于挪威的Numerical Rock团队(2002,2011)、澳大利亚国立大学的Arns(2004)、 Knackstedt等人(2002)、英国帝国理工学院的Okabe 等人(2005)、 Hu等人(2007)，美国斯坦福大学的Keehm(2003)、Sain(2010)，德国卡尔斯鲁厄大学的Saenger等人(2004，2008)以及美国的数字岩石物理公司Ingrain(2010).而国内目前还处于方兴未艾的阶段，中国石油大学的Zhao等人(2007)、Liu等人(2009a，2009b)、陶果等人(2005)、岳文正等人(2004)，以及西南石油大学的Su等人(2010)开展了相应研究，取得了一定的成果.由于渗流机理在提高采收率中的重要地位，前面的研究大多集中于渗流特性模拟，且均采用格子玻兹曼方法或基于帝国理工的两相流代码；对岩石声、电、弹性性质的研究还比较零散，且其中的数值模拟大都基于Garboczi教授的开源代码；在数字岩芯建模方法的选择上，由于微CT成本太高，多数学者基于二维薄片信息采用数学方法进行三维重构，而这会导致微观孔隙结构过于理想化或随机化，无法反映真实；在研究对象的选择上，几乎都以澳大利亚国立大学提供的枫丹白露砂岩或Bera砂岩数字岩芯为载体(两者可视为均质纯砂岩，结构简单)，而对复杂岩石研究缺乏.但总的来说，前面的研究无论是侧重于数字岩芯的三维重构或孔隙网络模型构建，还是后期的岩石物理数值模拟分析，都为推动数字岩石物理这一新技术的发展做出了不可磨灭的贡献，只是研究手段还可以再丰富些、研究内容还应该更为全面、系统化.综合上述分析，本文以常规砂岩样品为例，通过微CT扫描结合先进的三维可视化软件Avizo建立了具有真实孔隙结构特征的三维数字岩芯模型，在此基础上，利用Avizo强大的几何模型前处理、后处理功能，将Avizo与多场耦合有限元软件Comsol完美对接，实现了多种岩石物理参数的数值模拟，从而在避免繁琐的算法研究和程序开发的同时，为数字岩石物理的大规模发展提供了一条新的途径，也为该领域的研究人员提供了一套可借鉴的研究思路.

2 三维数字岩芯建模
2.1 微CT成像

微CT扫描作为一种无损检测物体内部结构的技术，是当前建立三维数字岩芯最直接和最准确的方法，其原理是根据岩石中不同密度的成分对X射线吸收系数不同以达到区分孔隙和骨架的目的.本研究中岩芯三维图像的采集均在美国Xradia公司生产的MicroXCT-400(图 1a)上完成，其最高采样分辨率可达1 μm.实验样品为直径约8 mm的圆柱体砂岩(图 1b)，一个样品可获取983张980×1005像素的二维CT切片图，空间分辨率为2.1 μm/体素，将这些二维切片图依次叠加组合便得到岩样的三维灰度图像.图 1c为其中一张切片的灰度图，灰色、白色的岩石骨架(高密度)和黑色的孔隙(低密度)在图像中清晰可辨.

图 1 微CT技术流程 (a)微CT仪器；(b)岩样；(c)CT切片；(d)滤波后切片；(e)二值化结果.Fig. 1 The process of micro-CT technology (a)MicroXCT-400;(b)Rock sample;(c)One of CT slices;(d)The slice after filtering;(e)The result of binarization.
2.2 图像处理

微CT扫描获得的岩芯灰度图像中存在各种类型的系统噪声，降低图像质量的同时也不利于后续的定量分析，因此图像处理第一步是通过滤波算法增强信噪比.针对三维图像，比较常用的滤波算法有低通线性滤波、高斯平滑滤波及中值滤波，通过综合对比三种算法的滤波效果，本研究中选用中值滤波器.岩芯灰度图像经中值滤波器进行滤波处理之后，孔隙和岩石骨架之间的过渡变得自然，边界也变得 平滑，同时也尽可能地保留了图像重要特征信息(图 1d).但为了更好地区分及量化孔隙和骨架，还需采用图像分割方法对灰度图像进行合理的二值划分.图像二值化的关键在于分割阈值的选取，鉴于本文用于微CT扫描的岩芯已知实测孔隙度，所以可采用基于岩芯孔隙度寻求到的最佳分割阈值来对图像进行分割.以实测孔隙度为约束寻求分割阈值k*的公式如下：

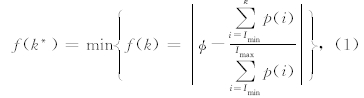
式中，岩芯孔隙度为φ，灰度阈值为k，图像的最大、最小灰度值分别为Imax、Imin，灰度值为i的体素数为p(i)，灰度低于阈值的体素表征孔隙，其余代表骨架.以最终搜寻到的k*作为分割阈值，得到分割后的二值图像(图 1e)，其中黑色为孔隙，白色为骨架.在此基础上，还可根据实际需要，采用数学形态学算法对其作进一步精细处理，即通过开运算移除孤立体素，通过闭运算填充细小孔洞，连接邻近体素.

2.3 3D体表面重建

理论上数字岩芯尺寸越大，就越能准确表征岩 石的微观孔隙结构和宏观特性，然而数字岩芯尺寸越大，对计算机存储和运算能力要求就越高，因此折衷方案是选取代表元体积(REV)，姜黎明等(2012)通过多次试验表明当数字岩芯大小为200×200×200体素时，其物理性质(比如孔隙度、弹性模量等)几乎不再受尺寸的影响.在本文研究中，出于计算存 储和计算速度的考虑，选取代表元体积为200×200×200体素.

采用Marching Cube 算法从图像处理结果的REV三维数据体中提取表面的三角面片集，再用光照模型对三角面片进行渲染，进而形成岩芯的三维 体表面图像，至此三维数字岩芯建模工作完成(图 2).

图 2 数字岩芯模型 (a)孔隙和骨架；(b)骨架(孔隙透明)；(c)孔隙(骨架透明).Fig. 2 Digital core model (a)Pore and frame;(b)Frame(with pore transparent);(c)Pore(with frame transparent).
3 数字岩石物理实验

在数字岩芯的基础上，通过各种形态学算法及数值模拟手段，可以统计、计算多种岩石物理参数，这即是所谓的数字岩石物理实验.

3.1 孔隙结构量化及表征

基于上述步骤所建数字岩芯的孔隙模型中(图 2c)，大部分孔隙与孔隙之间接触紧密，很难区分单 个孔隙的边界，这不利于后期定量统计孔隙体积分布及孔径分布.为此，需要识别出每个孔隙的边界，并对其进行标记.本文在研究中采用快速分水岭算法进行孔隙边缘检测，其基本原理是把图像看作地学上的拓扑地貌，图像上每一像素点的灰度值表示该点海拔高度，每一个局部极小值及其影响区域称为集水盆地，集水盆地的边界则形成分水岭.通过该算法每个孔隙都能清楚地识别，类似于都贴上了独有的标签(图 3a)，可以很方便地对号提取以进行定量分析.一旦每个孔隙体积确定，可以统计出孔隙体积的分布直方图(图 3c)，还可以根据下面公式计算孔隙度：

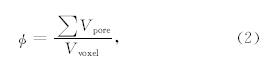
式中，孔隙度φ为小数，Vpore 为单个孔隙体积，单位pix3，Vvoxel为总体素的体积，单位pix3，pix是指一个像素，在本文研究中为2.1 μm.
图 3 孔隙结构量化及表征 (a)孔隙标记图；(b)孔隙网络模型；(c)孔隙体积分布；(d)孔隙直径分布.Fig. 3 Quantification and characterization of pore structure (a)Label image of pore;(b)Pore network model;(c)The distribution of pore volume;(d)The distribution of pore diameter.

由表 1可见，计算所得孔隙度略低于实测孔隙 度，分析误差来源，主要是图像处理平滑造成，剔除 掉的一部分小孔对计算孔隙度应有所贡献.

表 1 孔隙度计算结果 Table 1 The computation result of porosity

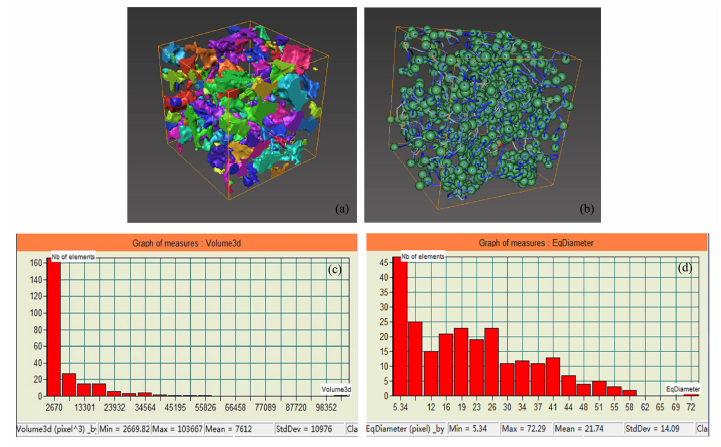
为了更加简明直观地展示孔隙空间的拓扑结构，本文在数字岩芯的基础上，采用形态学细化算法获取孔隙空间中轴线，并将中轴线节点定义为孔隙，节点之间的连接线定义为喉道，由此建立了能够简化表征孔隙空间拓扑结构的等价孔隙网络模型(图 3b)，图中球体表征孔隙，管束表征喉道.球体体积与相应位置的孔隙体积近似相等，每个孔隙的等效孔径则可通过公式(3)确定，最终统计得到孔径分布直方图(图 3d).

式中，等效孔隙直径Deq单位为pix.

3.2 绝对渗透率数值模拟

岩石的绝对渗透率衡量的是饱和单相流体通过其孔隙空间的能力，这就要求岩石内部必须存在相互连通的有效孔隙，才能提供相应渗流路径.因此，在绝对渗透率的数值模拟中，为保证数模能顺利进行并较快收敛，首先需对数字岩芯的孔隙空间进行连通性测试，移除孤立“死孔”，然后再对孔隙空间进行四面体网格剖分及优化，最后通过有限元求解器实现数值模拟.本文采用Comsol软件的不可压缩Navier-Stokes方程模块来完成孔隙空间的微流动模拟，流体基本属性按常态下水的参数赋值，模型中相对立的两面分别作为速度入口及压力出口边界，其余流动边界及孔壁视为无滑移壁面(流速为0).据此分别模拟了X、Y、Z三个方向的渗流特性，模拟得到三个方向的速度场分布及流线图如图 4.

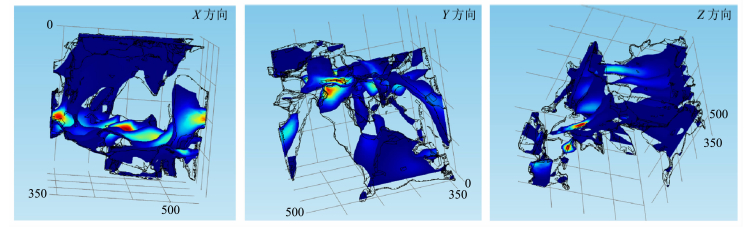图 4 速度场分布(颜色越亮，流速越大)Fig. 4 The distribution of velocity field in the X，Y，Z directions(the brighter the colors，the higher the velocity)

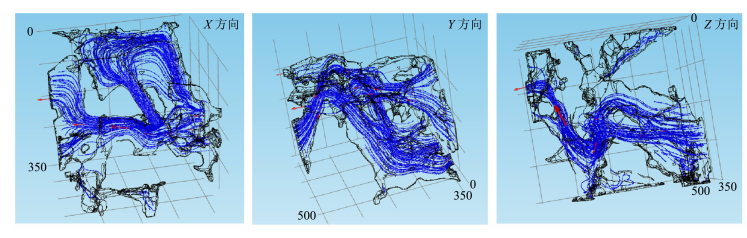图 5 流线图Fig. 5 The streamline in the X，Y，Z directions
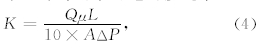
在数值模拟结果中，由出口或入口边界上对流动速度进行积分，可以得到通过岩样的体积流量，再代入达西定律公式(4)中即可求得绝对渗透率：

式中，流量Q单位cm3·s-1，岩芯截面积A单位cm2，岩芯长度L单位cm，流体黏度μ单位为mPa·s，压差ΔP单位MPa，计算所得渗透率K单位为μm2.三个方向的渗透率模拟结果见表 2.分别计算三者的算术平均值、几何平均值、调和平均值并与实验室气测、液测结果进行对比，发现计算结果均低于气测值，且看不出有明显的联系，这是由于气体滑脱效应的存在，同一岩石的气测渗透率为液测结果的3~5倍不等，而通过与液测结果的对比可看出：三个方向渗透率的几何平均与实验结果较为接近.
表 2 渗透率结果对比 Table 2 The comparison of permeability result
3.3 弹性参数数值模拟

岩石的弹性参数(体积模量、剪切模量等)在地球物理勘探与测井领域发挥着重要作用.从结构上看，岩石是由骨架和孔隙流体组成的复合介质，岩石的弹性实则是各组分弹性性质综合而成的有效弹性.因此，多孔岩石的弹性参数不仅取决于固体骨架的弹性性质，岩石中孔隙的大小、几何形状以及孔隙流体性质都会对岩石总体弹性参数产生一定的影响，定量研究这之间的关系也一直是地球物理领域关注的热点，对于油气勘探开发中储层的预测具有重要指导意义.时至今日，国际上比较有代表性的经典理论及经验公式包括：微分有效介质理论、Voigt-Reuss-Hill模型、Hashin-Shtrikman边界方程、自洽理论、Gassmann方程、Wyllie公式、Raymer方程、百灵方程等.其中，流体替换Gassmann方程是研究孔隙饱和流体对岩石声波速度影响最常用的理论，国内外已有学者(Saenger，2008；姜黎明等，2012)基于三维数字岩芯分别通过有限元/旋转-交错网格有限差分技术模拟了流体替换对岩石弹性性质的影响，并与Gassmann方程计算结果进行了对比验证，结果吻合度较高，证实了数值模拟复杂孔隙岩石有效弹性参数的可靠性.然而该方程的基本假设之一 是孔隙空间饱和无摩擦流体，对于孔隙充填物为黏滞性稠油、沥青的情况不再适用.为此，Ciz和Shapiro(2007)提出了针对高黏度物质或固相充填孔隙的近似Gassmann公式：

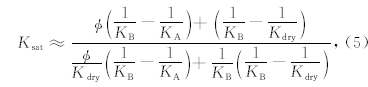
式中，Ksat、KB、KA、Kdry分别指有效体积模量、基质矿物体积模量、孔隙充填相体积模量、干岩石体积模量，单位均为GPa，孔隙度φ为小数.公式(5)是一个近似固相替换方程，其准确度依赖于岩石的孔隙结构，为评价其有效性，采用传统物理实验方法无法实现，因此，本文采用Comsol软件的结构力学模块开展数值模拟研究.基于三维数字岩芯模型用有限元求解孔隙尺度的线弹性方程，其理论基础是最小势能原理，对于给定的数字岩芯，施加一个宏观的体积应变，在周期性边界条件的控制下，利用共轭梯度法通过把体系的弹性势能最小化来求取由这个外加应变引起的平均应力，进而求得岩石的有效弹性参数.

数值模拟中，矿物基质体积模量KB根据Hill(1963)的研究取为36 GPa，体积应变赋为0.001，基于简化后的网格(图 6)，模拟了六种不同孔隙充填相(KA分别取0.1 GPa、5.1 GPa、10.1 GPa、15.1 GPa、20.1 GPa、25.1 GPa)的岩石有效体积模量.其中，公式(5)中干岩石体积模量Kdry不同于气体饱和岩石的体积模量，它对应于孔隙相体积模量为0的情况，而气体具有不可忽略的体积模量，因此通过实验获得理想的Kdry比较困难，一般通过经验公式求得.而本文采用数值模拟计算Kdry时，为保障数模运算能够完成且又不影响结果，取孔隙充填相KA为0.0001 GPa，计算得到Kdry约为21 GPa.图 7为KA取25.1 GPa时模拟结果应力分布图，由图可见局部高应力区出现在孔隙充填相的边缘附近.

图 6 简化网格Fig. 6 The simplified grid

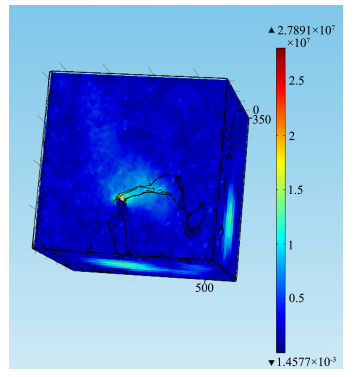图 7 应力分布图(KA=25.1 GPa)Fig. 7 The stress distribution(KA=25.1 GPa)

将数值模拟所得到的岩石有效体积模量与公式(5)计算出的结果进行对比(图 8)，发现两者基本吻合，再次证明：无论是孔隙中饱和流体还是固相充填，基于岩石的微观结构用有限元的方法模拟复合岩石的弹性性质都是可行且可靠的.

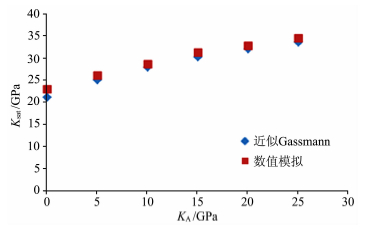图 8 有效体积模量结果对比Fig. 8 The results contrast of effective bulk modulus
4 结论与展望

(1)利用微CT扫描结合先进的三维可视化软件Avizo建立的数字岩芯可以精细地捕捉岩石真实孔隙结构特征，基于数字岩芯模型开展数字岩石物理实验，可以准确地获取孔隙度并统计得到孔隙体积分布、孔径分布特征，以及能够简化表征孔隙空间拓扑结构的孔隙网络模型；

(2)将Avizo与多场耦合有限元软件Comsol对接，可以形象直观地模拟流体在真实孔隙空间的渗流过程，并计算获得绝对渗透率；

(3)运用Comsol软件模拟计算了固相充填孔隙情况下岩石的有效弹性参数，数模结果与固相替换近似Gassmann方程能够很好的相互验证.

随着计算机技术的发展，数字岩石物理必将成 为一项重要的技术手段参与到油气田的开发建设.

本文的研究提供了数字岩石物理一套新的方法体系，同时也为进一步研究低渗致密砂岩的相渗、岩电、声波传播及其相互联系奠定了基础.

参考文献
[1] Arns C H, Bauget F, Ghous A, et al. 2004a. Digital Core Laboratory: petrophysical analysis from 3D imaging of reservoir core fragments. Petrophysics, 46(4): 260-277.
[2] Arns C H, Knackstedt M A, Pinczewski W V, et al. 2004b. Virtual permeametry on microtomographic images. Journal of Petroleum Science and Engineering, 45(1-2): 41-46.
[3] Ciz R, Shapiro S A. 2007. Generalization of Gassmann equations for porous media saturated with a solid material. Geophysics, 72(6): A75-A79.
[4] Derzhi N, Dvorkin J, Diaz E, et al. 2010. Comparison of traditional and digital rock physics techniques to determine the elastic core parameters in cretaceous formations, Abu Dhabi. SPE138586.
[5] Rezaei-Gomari S, Berg F, Mock A, et al. 2011. Electrical and petrophysical properties of siliciclastic reservoir rocks from pore-scale modeling. SCA International Symposium, Texas, 18-21.
[6] Hill R. 1963. Elastic properties of reinforced solids: some theoretical principles. Journal of the Mechanics and Physics of Solids, 11(5): 357-372.
[7] Hu D, Touati M, Blunt M J. 2007. Pore network modeling: analysis of pore size distribution of Arabian core samples. SPE105156.
[8] Hu D. 2007. Micro-CT imaging and pore network extraction . London: Imperial College.
[9] Jiang L M, Sun J M, Liu X F, et al. 2012. Numerical study of the effect of natural gas saturation on the reservoir rocks' elastic parameters. Well Logging Technology (in Chinese), 36(3): 239-243.
[10] Keehm Y. 2003. Computational rock physics: transport properties in porous media and applications . Stanford: Stanford University.
[11] Knackstedt M A, Arns C H, Pinczewski W V, et al. 2002. Computation of linear elastic properties from microtomographic images: methodology and match to theory and experiment. Geophysics, 67(5): 1396-1405.
[12] Liu X F, Sun J M, Wang H T. 2009a. Numerical simulation of rock electrical properties based on digital cores. Applied Geophysics, 6(1): 1-7.
[13] Liu X F, Sun J M, Wang H T. 2009b. Reconstruction of 3-D digital cores using a hybrid method. Applied Geophysics, 6(2): 105-112.
[14] Okabe H, Blunt M J. 2005. Pore space reconstruction using multiple-point statistics. Journal of Petroleum Science and Engineering, 46(1-2): 121-137.
[15] Φren P E, Bakke S. 2002. Process based reconstruction of sandstones and prediction of transport properties. Transport in Porous Media, 46(2-3): 311-343.
[16] Saenger E H, Bohlen T. 2004. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid. Geophysics, 69(2): 583-591.
[17] Saenger E H. 2008. Numerical methods to determine effective elastic properties. International Journal of Engineering Science, 46(6): 598-605.
[18] Sain R. 2010. Numerical simulation of pore-scale heterogeneity and its effects on elastic, electrical and transport properties . Stanford: Stanford University.
[19] Su N, Duan Y G, Chen W, et al. 2010. Three-dimensional reconstruction of micro pore structure. International Conference on Computational and Information Sciences (ICCIS). 120-123.
[20] Tao G, Yue W Z, Xie R H, et al. 2005. A new method for theoretical modeling and numerical experiments on petrophysical studies. Progress in Geophysics (in Chinese),20(1): 4-11.
[21] Wang K W, Sun J M, Geng S C, et al. 2006. Percolation network study of shale effects on rock electrical properties under different salinity. Chinese J. Geophys. (in Chinese), 49(6): 1867-1872.
[22] Yue W Z, Tao G, Zhu K Q. 2004. Simulation of electrical properties of rock saturated with multi-phase fluids using lattice gas automation. Chinese J. Geophys. (in Chinese), 47(5): 905-910.
[23] Zhao X C, Yao J, Yi Y J. 2007. A new stochastic method of reconstructing porous media. Transport in Porous Media, 69(1): 1-11.
[24] 姜黎明, 孙建孟, 刘学锋等. 2012. 天然气饱和度对岩石弹性参数影响的数值研究. 测井技术, 36(3): 239-243 .
[25] 陶果, 岳文正, 谢然红等. 2005. 岩石物理的理论模拟和数值实验新方法. 地球物理学进展, 20(1): 4-11 .
[26] 王克文, 孙建孟, 耿生臣等. 2006. 不同矿化度下泥质对岩石电性影响的逾渗网络研究. 地球物理学报, 49(6): 1867-1872 .
[27] 岳文正, 陶果, 朱克勤. 2004. 饱和多相流体岩石电性的格子气模拟. 地球物理学报, 47(5): 905-910.
基于微CT技术的砂岩数字岩石物理实验
刘向君, 朱洪林, 梁利喜