2. 中海油研究总院, 北京 100027;
3. 中国石油大学(北京)地球物理与信息工程学院, 北京 102249
2. CNOOC Research Institute, Beijing 100027, China;
3. College of Geophysics and information Engineering, China University of Petroleum (Beijing), Beijing 102249, China
现阶段,随着石油地质理论与地震处理解释技术的进步、地震与钻探设备的发展,向深层寻找油气已经成为现阶段石油工业保持稳产或提高产量主要研究方向之一[1-4].
近十年来,储层流体识别技术发展迅速,从最初上世纪80年代的基于地震振幅异常的“定性”识别技术发展到现阶段的基于流体因子的“定量”识别技术[5-7],并且随着叠前地震反演的发展,流体因子的构建方式也从最初的基于弹性参数相对变化量的运算模式发展到现在的基于岩石物理意义明确的弹性参数运算模式[8-12].国内外学者基于弹性参数提出了不同的流体因子类型,Goodway等人提出了利用介质拉梅模量参数识别流体的LMR技术[13];Quakenbush等人提出了基于纵横波阻抗的泊松阻抗概念[14];Russell等人基于多孔弹性介质理论提出了Russell流体因子[15];宁忠华和贺振华等人则利用高次幂组合方式构建了高灵敏度流体因子[16].随着研究的深入,国内外一些学者为了降低流体因子计算过程中的不确定性以及累计误差,实现流体因子的可靠估算,围绕叠前地震反演与流体识别的有效结合进行了相应的研究,比如,Chi等[17]研究了基于AVO反演的拉梅模量直接提取方法;王保丽等[18]基于Gray近似推导了包含拉梅模量参数的弹性阻抗方程,实现了基于弹性阻抗反演的拉梅参数直接提取;印兴耀等[19]则推导了包含Gassmann流体项的弹性阻抗公式,研究了Gassmann流体项的直接提取方法,取得了很好的流体识别效果.
但是,受埋藏深度影响,深层储层经过较为强烈的压实与后期成岩作用改造,其原生孔隙基本消失,且多表现为致密特征,深层储层表现出的岩石物理特性与浅层存在差异;加之深层地震资料存在大角度信息缺失、信噪比低和高频信号弱等问题,限制了常规叠前地震反演的应用效果,特别是无法获得可靠的密度项信息,从而影响了后续流体因子的间接计算精度.目前,国内外专门针对深层进行流体识别研究的成果较少,但是Dillon等人[20]以及Zhou和Hilterman[21]结合实际工区资料分析了不同流体因子的储层流体识别效果,认为Russell流体因子对固结碎屑岩储层的适用性最高,而考虑到深层储层一般属固结致密岩层,因此Russell流体因子可以满足对深层孔隙流体的敏感指示.另外,李爱山等人利用岩石物理经验公式改写了弹性阻抗方程,通过两个角度弹性阻抗实现了纵横波阻抗的提取[22],其方法虽然对岩石物理经验关系依赖较大,但为我们研究深层叠前反演提供了研究思路.本文为了实现敏感流体因子的小角度直接反演,建立了凸显Russell流体因子的反射特征近似公式,并进一步推导了新的两项弹性阻抗方程,基于贝叶斯弹性阻抗反演结果实现了Russell流体因子的直接估算,为深层储层流体识别提供了敏感且可靠的流体因子数据支撑.
2 基本公式 2.1 基于新AVO近似的两项弹性阻抗方程Russell等人基于Biot-Gassmann理论研究了多孔介质弹性模量参数与孔隙流体的关系,借助于改写的纵横波速度表达式提出了Russell流体因子F[15],其表达式为

|
(1) |
其中,ρ表示多孔饱和流体介质密度;f=β 2M,其可以表征孔隙流体效应,β是Biot系数(物理意义是抽空条件下每个单位体积变化中孔隙体积的变化),M是模量参数(其物理意义是在不改变孔隙体积的前提下,把流体压入地层孔隙所需要的压力);IP表示纵波阻抗;IS表示横波阻抗;c=(VP/VS)2 dry,表示干岩石的纵横波速度比的平方.
为了实现基于小角度地震资料的Russell流体因子直接估算,在仅有小角度入射的假设前提下,对Fatti提出的AVO近似公式进行了重新推导,得到了包含Russell流体因子相对变化量和纵波阻抗相对变化量的新AVO近似公式为(具体推导过程见附录A)

|
(2) |
其中,F和IP分别表示反射界面两侧介质的Russell流体因子与纵波阻抗的平均值;ΔF和ΔIP分别表示反射界面两侧介质的Russell流体因子与纵波阻抗之差;θ是平均入射角;γsat2和γdry2分别表示饱和流体岩石和干燥岩石的纵横波速度平方比的平均值.
公式(2)为Russell流体因子的直接反演提供了理论基础.考虑到深层地震资料信噪比普遍较低,而基于入射角度部分叠加资料的弹性阻抗(Elastic impedance,简称EI)反演在一定程度上可以降低随机噪音对反演结果的影响,因此,为了利用弹性阻抗反演在抗噪性和稳定性上的优势,在此根据Connolly提出的弹性阻抗方程的构建方式[23],基于公式(2)推导了包含Russell流体因子以及纵波阻抗的两项弹性阻抗方程(具体推导过程见附录B),具体表示形式为

|
(3) |
其中,F和IP分别表示多孔介质的Russell流体因子和纵波阻抗;

由于公式(3)计算的弹性阻抗数值受入射角度的影响较大.借鉴Whitcombe提出的弹性阻抗标准化方法,进一步对公式(3)进行标准化处理[24],最终得到

|
(4) |
其中,F0和IP0分别表示多孔介质的Russell流体因子和纵波阻抗参数的平均值.
公式(4)消除了入射角度对数值量纲的影响,不仅方便了不同角度弹性阻抗数据之间的异常分析,而且提高了弹性参数提取的稳定性.
除了弹性参数数目的差异,公式(4)与其他形式弹性阻抗的最大区别即方程中包含了γdry2参数.针对γdry2的计算方法,国内外学者进行了大量的研究,Russell和印兴耀等人分别提出了基于实验室测量与Gassmann方程的计算方法[15, 19],具体到实际应用,需根据工区条件灵活选择估算方法,只有得到了适用于研究工区的γdry2才能保证方程的近似精度与Russell流体因子提取的可靠性.
2.2 近似精度分析为了验证新弹性阻抗方程的合理性,在此基于模型数据分析由公式(4)得到反射系数的近似精度.设计了两套双层砂岩模型,具体的弹性参数取值如表 1所示,其中,模型一中的上下层砂岩孔隙流体相同,上下层均为含水砂岩,但是上覆砂岩的孔隙度为25%,下覆砂岩的孔隙度为15%;模型二中的上下层砂岩的孔隙流体不同,上覆砂岩为含气砂岩(含水饱和度为20%,含气饱和度为80%),下覆砂岩为含水砂岩,但是砂岩的孔隙度相同,均为25%.假设最大入射角度为30度,分别利用精确Zoeppritz方程,Connolly提出的常规EI方程,新推导的AVO近似公式(公式(2))以及新推导的EI方程(公式(4))计算这两套砂岩模型分界面处的反射系数,并定量比较了新推导的EI方程和Connolly EI方程与精确Zoeppritz方程之间的误差,具体比较结果如图 1和图 2所示.
|
|
表 1 两种砂岩模型参数 Table 1 Parameters of the two sand model |

|
图 1 模型一反射系数计算结果与误差比较图 (a)反射系数计算结果比较;(b)新两项EI和常规Connolly EI与Zoeppritz方程的误差比较. Fig. 1 The comparison between the reflection coefficients and the corresponding errors of model 1 (a) Comparison between the reflection coefficients; (b) Comparison between the errors of different reflection coefficients. |

|
图 2 模型二反射系数计算结果与误差比较图 (a)反射系数计算结果比较;(b)新两项EI和常规Connolly EI与Zoeppritz方程的误差比较. Fig. 2 The comparison between the reflection coefficients and the corresponding errors of model 2 (a) Comparison between the reflection coefficients; (b) Comparison between the errors of different reflection coefficients. |
从图 1a可以看到,当界面两侧孔隙流体相同,孔隙不同的时候,公式(2)与公式(4)计算的反射系数均与精确Zoeppritz结果有较好的匹配;从图 1b可以看到,入射角度小于10°时,公式(4)与Connolly EI计算的反射系数与精确Zoeppritz结果几乎一致,但是随着入射角度的增加,两者逐渐偏离精确解,但是基于公式(4)的近似精度要高于Connolly EI,且从21°开始,公式(4)与精确解的偏差有逐渐减小的趋势,公式(4)的最大误差仅为-1×10-3.从图 2a可以看到,当界面两侧孔隙度相同,孔隙流体不同的时候,公式(2)与公式(4)计算的反射系数仍然可以较好吻合Zoeppritz精确解,但是公式(2)的近似精度要高于公式(4);从图 2b可以看到,入射角度小于5°时,公式(4)与Connolly EI计算的反射系数与Zoeppritz精确解匹配良好,随着入射角度的增加,基于公式(4)的计算结果逐渐偏离Zoeppritz精确解,在30°时达到最大误差,误差数值为3×10-3.分析其原因,我们知道弹性阻抗推导过程中的对数化假设前提的是界面两侧弹性参数差异较小,当界面两侧砂岩孔隙中分别饱和气和水的时候,界面两侧孔隙流体之间的差异对Russell流体项的影响要大于孔隙度差异产生的影响,从而使新弹性阻抗在较大入射角度时产生一定的误差.但是,考虑到模型设计中选用的含气饱和度高达80%,而实际埋藏压实严重的深层储层的含气饱和度远没有这么高,且如果孔隙流体含油的时候,界面两侧的流体差异的影响会进一步减弱,从而可以保证公式(4)的合理性.因此总体来说,在仅有小角度入射的深层情况下,基于公式(4)计算的反射系数完全可以满足近似精度,利用公式(4)进行叠前EI反演并提取Russell流体因子是可行的.
3 参数估算 3.1 弹性阻抗反演在估算Russell流体因子之前,需要首先进行弹性阻抗反演.本文在贝叶斯反演理论框架下,通过求解最大后验概率密度函数来构建弹性阻抗的反演目标函数.
基于贝叶斯理论得到的反射系数r的后验概率密度函数可表示为

|
(5) |
其中,向量d表示叠前角度部分叠加数据向量;向量R表示待反演角度反射系数向量;I表示地质信息,即测井先验信息;P(R|d,I)表示后验概率密度函数;P(d|R,I)表示似然函数,用于表示正演记录与实际观察数据之差,即噪音的分布;P(R|I)是先验概率密度函数,表示待反演参数的分布;P(d|I)表示边缘分布,其数值一般取常数.
由于地震数据中的噪音信息一般服从正态分布假设,且是相互独立的,在此假设似然分布符合Gauss分布;为了保护地下的弱反射信息,假设先验分布符合Cauchy分布,根据公式(5)构建包含待反演反射系数r的后验概率密度函数,即

|
(6) |
其中,N是地震采样点数;σn表示角度部分叠加数据的噪音方差;σm表示模型反射系数的方差;G表示正演子波矩阵;R表示待反演的反射系数矩阵;d表示角度部分叠加数据矩阵.
对公式(6)取对数,并省略常数项,通过求解最大后验概率可以得到如下反演目标函数

|
(7) |
其中:

|
考虑到得到的反演结果是相应入射角度θ的反射系数,为了约束反射系数结果与弹性阻抗数值之间的吻合程度,将不同角度弹性阻抗与相应角度反射系数之间的关系作为趋势约束引入目标函数(7)中[25],得到最终的反演目标函数,即

|
(8) |
其中,λ是约束系数;P是积分算子矩阵;η是相应角度的弹性阻抗模型数据矩阵.
公式(8)左侧的GTG是用来约束实际地震数据与模型褶积记录之间的吻合程度,εQ是用来约束反射系数的稀疏程度,λPTP则用来约束反演结果的趋势.采用迭代重加权最小二乘算法(Iterative Reweighted Least Squares,IRLS)对反演目标函数(8)进行目标寻优,具体过程为:
(1)给定待反演参数初值,若无足够信息,可将参数初值向量赋为一个缺省零向量;
(2)计算给定初值的解R=(GTG+εQ+ λPTP)-1(GTd+PT η);
(3)利用得到的结果计算加权矩阵Q并进一步优化目标解,即反复迭代求解R=(GTG+εQk-1 + λPTP)-1(GTd+PT η).其中,Qk-1=Q(rk-1),上标k表示迭代次数;
(4)迭代计算,当满足容忍条件时跳出计算过程.
通过如上搜索算法最终得到反问题的解,即相应角度θ的反射系数r,将其代入方程(9),可进一步得到最终的弹性阻抗数据EI(θ,t).

|
(9) |
其中:t是时间采样点;t0是起始时间.
3.2 参数提取基于弹性阻抗与弹性参数的关系可以直接提取Russell流体因子和纵波阻抗参数.根据公式(4)可以知道弹性参数与弹性阻抗之间是非线性关系,增加了参数估算的难度,在此对公式(4)进行对数处理,将其变为线性表达式.然后利用方程(10)计算入射角度为θ的权重系数a(θ)和b(θ),其中弹性阻抗数据EI(t,θ)采用井旁道的弹性阻抗反演结果,F(t)与IP(t)则采用伪测井数据,在此为了保持井震数据的统一,将伪测井数据进行了Backus平均处理.公式为

|
(10) |
针对两个不同的入射角度(θ1和θ2)分别进行计算,得到对应的四个系数(即a(θ1)、b(θ1);a(θ2)、b(θ2)).将四个系数代入公式(11)并求解lnF(t)和lnIP(t),对结果进行指数化处理即可得到任意采样点处的Russell流体因子与纵波阻抗参数.公式为

|
(11) |
公式(11)可以进一步表示为AX=B,其中X是待求取的弹性参数矩阵,A是系数矩阵,而系数矩阵A的条件数可以表征方程求解的稳定性,即条件数越小表明求解稳定性越高.针对深层储层的实际情况,在此基于小入射角假设的假设前提,分别计算公式(11),以及常规Connolly EI和基于Fatti近似的EI的系数矩阵条件数,通过比较三种条件数的大小来分析参数估算方法的稳定性.
这三种方法的最小角度均设为5°,最大角度设为10°到25°,由于本文提出的方法仅需要两个角度,而针对另外两种需要三个角度的方法,则将中角度取为小角度和大角度的平均值.分别计算三种方法系数矩阵的条件数,结果如图 3所示.从图中可以看到,随着最大入射角度的增加,三种方法的条件数均降低,即合理的选取大角度数据可以提高参数求解的稳定性和精度;并且从图中可以看到,新的两项EI的条件数要明显低于另外两种方法,即本文方法更加适用小角度情况下的参数估算.另外,考虑到三项方法估算的是纵横波速度、密度或者纵横波阻抗、密度,还需要间接计算才能得到最终的Russell流体因子,而两项方法可以直接估算得到Russell流体因子,因此,利用两项EI的直接估算的结果要优于三项EI的间接估算结果.

|
图 3 系数矩阵的对数条件数随最大入射角度的变化趋势线 Fig. 3 The logarithm condition number of the coefficient matrix variation with the maximum incident angle |
为了验证Russell流体因子直接估算方法的可行性与优越性,在此选取部分Marmousi2模型的正演模拟记录,采用本文方法直接估算Russell流体因子,并与其他方法估算的Russell流体因子进行比较.选用的模型如图 4所示,在模型的1.7~1.8s,道号500~700存在一个含气层,而2.4~2.6s,道号500~1000之间存在一个含油层,从图中可以看到气层和油层在Russell流体因子中都有较为明显的低值异常显示,且含气层数值要低于含油层,而纵波阻抗对两种含烃储层没有明显的异常显示,说明Russell流体因子可以敏感指示模型的流体类型.图 5是不加噪音的情况下,采用本文方法利用5°和15°叠前部分叠加资料直接估算的Russell流体因子和纵波阻抗结果,从图中可以看到估算结果与模型参数吻合很好,说明了本方法对参数的估算是可行的.为了验证直接估算方法优势,加入20%的白噪音,分别采用三种方法估算Russell流体因子,这三种方法分别是:

|
图 4 Marmousi2模型测试数据 (a)Russell流体因子的模型数据;(b)纵波阻抗的模型数据. Fig. 4 Marmousi2 test model (a) Russell fluid factor model; (b) P-wave impedance model. |

|
图 5 不加噪音的反演结果 (a)Russell流体因子直接估算结果;(b)纵波阻抗直接估算结果. Fig. 5 The inversion result with no noise (a) The direct estimated Russell fluid factor; (b) The direct estimated P-wave impedance. |
1)利用5°和15°数据直接估算Russell流体因子;
2)基于Fatti近似的弹性阻抗估算纵横波阻抗,再间接计算Russell流体因子,利用的角度数据体是5°,10°和15°数据;
3)基于常规弹性阻抗反演先估算纵横波速度以及密度参数,再间接计算相应的Russell流体因子参数,利用的角度数据体也是5°,10°和15°数据.
三种方法的估算结果如图 6所示,虽然在气层与油层位置均有异常显示,但是从细节上可以发现三种结果均受到噪音影响产生了一定程度的误差,相比较而言,直接估算结果的抗造能力最强,基于Fatti近似弹性阻抗的间接估算结果次之,而基于常规弹性阻抗的间接计算结果则受噪音影响最大.其主要原因是间接估算方法会引入累计误差,受大角度缺失的影响,常规弹性阻抗反演本身就无法稳定的得到密度与横波速度信息,并且受噪音影响会在间接计算Russell流体因子的过程中产生最大的累计误差,而基于Fatti近似弹性阻抗的间接计算方法虽然较常规方法稳定,但是受噪音影响仍然会引入一定的累计误差.

|
图 6 加入20%噪音之后的Russell流体因子结果 (a)基于两项弹性阻抗的直接估算结果;(b)基于Fatti近似弹性阻抗的间接计算结果;(c)基于常规弹性阻抗的间接计算结果. Fig. 6 The estimated Russell fluid factor with 20% noise (a) The direct estimated result with two-term El inversion; (b) The indirect estimated result with Fatti-approximation-based El inversion; (c) The indirect estimated result with Connolly El inversion. |
为了更加直观地比较直接估算方法与基于Fatti近似弹性阻抗的间接估算方法的抗噪性,从图 6a和图 6b中抽取第600道和第800道数据进行比较,结果如图 7所示.从图中可以看到,直接估算结果与模型数据的吻合程度较高,而间接估算方法则产生相对较大的误差,虽然两种方法的计算结果均对气层都有较为明显的指示,但这主要是测试数据简单理想化的原因,针对深层更为复杂的储层,笔者认为由于间接估算所造成的累计误差对流体识别的负面影响会更为明显.

|
图 7 加入20%噪音之后单道Russell流体因子比较图 (a)第600道的Russell流体因子比较图;(b)第800道的Russell流体因子比较图. Fig. 7 The single trace comparison between Russell fluid factors with 20% noise (a) Comparison between Russell fluid factors of number 600 trace; (b) Comparison between Russell fluid factors of number 800 trace. |
模型测试验证了本方法的可行性与在流体识别中的有效性,并且在提取Russell流体因子方面具有较好的抗噪性.
5 实际应用及效果分析将方法应用于某实际工区数据,工区目的砂体埋藏较深,为典型的构造-岩性复合圈闭.首先利用测井资料估算研究工区的γdry与γsat参数,然后根据弹性参数之间的关系进一步计算所需的伪测井曲线,包括EI曲线以及Russell流体因子F等流体因子曲线.基于岩石物理统计,知道Russell流体因子对该工区含流体类型有较好的区分,且通过比较流体指示系数,进一步分析了Russell流体因子与其他常规流体因子(纵波阻抗IP,泊松阻抗IP -cIS,纵横波速度比VP/VS,拉伸模量λ和拉梅流体因子λρ)的流体区分敏感程度.表 2即计算的相应流体因子流体指示系数,根据Dillon等人的定义,流体指示系数越小说明对两种流体的区分越敏感,从图 8所示的流体指示系数直方比较图可以看到,Russell流体因子对孔隙流体类型的区分能力最强,说明Russell流体因子可以为本工区的储层流体识别提供直观有效的判别依据.
|
|
表 2 常用流体因子敏感度统计表 Table 2 The sensitivity statistical result of common fluid factors |

|
图 8 流体指示系数比较图 1.IP;2.IP-cIS;3.VP/VS;4.F;5.λ;6.λρ. Fig. 8 Comparison between the fluid indication coefficients |
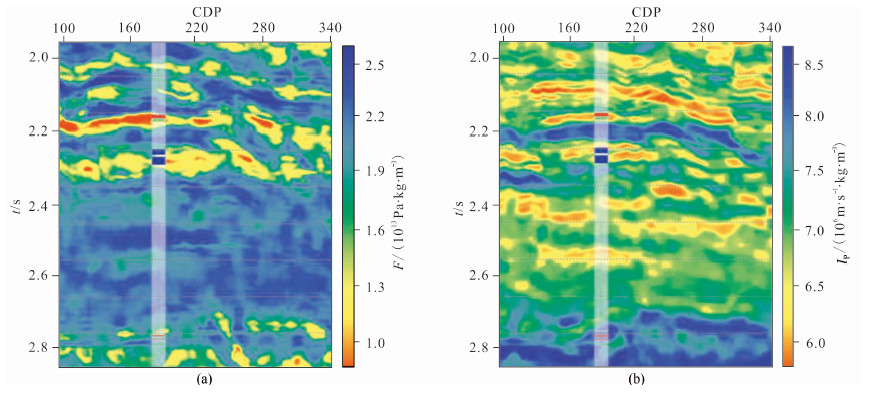
针对深层进行了必要的叠前资料预处理之后,选用某测线进行实际应用分析,图 9即为研究测线的两个角度部分叠加数据,其中心角度分别是8°和18°.图 9中的柱状曲线为测井解释结果,红色表示含气层,绿色表示含油层,蓝色表示含水层.从图中可以看到,受分辨率限制,2.12~2.16s之间的含气层和含油层在地震数据上无法有效的区分.利用本文方法对图 9两个数据分别进行EI反演,并直接估算Russell流体因子与纵波阻抗,结果如图 10所示.图中所投柱状曲线为测井解释结果,从图 10(a)可以看到Russell流体因子可以较好的区分目的储层,2.12~2.16s之间的油气层和2.22~2.27s之间的水层均有低值异常显示,且油气层数值要明显低于水层,从而较好的实现了储层含流体类型的有效区分,而估算的纵波阻抗则无法分辨储层流体类型,这与岩石物理统计的结果也是一致的.

|
图 9 两个角度的部分叠加数据剖面 (a)小角度叠加数据;(b)中角度叠加数据. Fig. 9 The partial angle stack seismic data (a) Near-offset stack seismic section; (b) Mid-offset stack seismic section. |
|
图 10 基于两角度EI反演的直接估算结果剖面 (a)Russell流体因子数据;(b)纵波阻抗数据. Fig. 10 The direct estimated results with two-term El inversion (a) Russell fluid factor section; (b) P-wave impedance section. |
为了验证实际应用中小角度直接估算方法的优越性,在此针对相同测线,采用两种间接计算的方法估算Russell流体因子,分别是:
1)利用三个角度叠加数据进行常规EI反演,首先估算纵横波速度和密度,然后再间接计算Russell流体因子;
2)利用三个角度叠加数据进行基于Fatti近似的EI反演,首先估算纵横波阻抗和密度参数,然后间接计算Russell流体因子.
两种方法利用的三个角度数据分别是5°、12°和18°,且估算结果如图 11所示.图 11a为利用间接方法1)估算的结果,从图中可以看到,在2.12~2.16s的油气层和2.22~2.27s的水层区域均有低值异常显示,但是两者数值区间几乎一致,无法有效的区分流体类型,并且砂体横向展布连续性欠佳,分析其主要原因即在小角度情况下利用三个角度提取的纵横波速度与密度参数不稳定,且间接计算进一步引入了累计误差.图 11b是利用间接方法2)估算的结果,可以看到2.12~2.16s的油气层有明显的低值异常显示,而对2.22~2.27s水层的表征不明显,分析认为与方法1)相似,仅在小角度范围内利用三个角度EI进行纵横波阻抗提取的稳定性欠佳,且根据模型测试的结论知道间接计算造成的累计误差进一步影响了Russell流体因子参数质量,但是相比较方法1),基于Fatti近似EI在估算参数方面具有更高的稳定性,因此相比较图 11a,其横向连续性有所提高.

|
图 11 基于三角度EI反演方法间接计算的Russell流体因子剖面 (a)基于常规EI反演的间接计算结果;(b)基于Fatti近似EI的间接计算结果. Fig. 11 The indirect estimated Russell fluid factor sections with three-term EI inversion (a) The Russell fluid factor with Connolly EI inversion; (b) The Russell fluid factor with Fatt-approximation-EI inversion. |
通过以上分析知道,在小角度范围内利用本文提出的方法可以有效的估算Russell流体因子,相比较其他常规的计算方法,直接提取的结果具有更高的可靠性,进而在深层储层流体识别方面具有较好的实际应用价值.
6 结论针对深层地震资料的缺失大角度信息、低信噪比等特点,本文研究了两项弹性阻抗反演与Russell流体因子的直接估算方法,在深层储层流体识别中取得了较好的应用效果.通过研究得到如下结论:
(1)Russell流体因子能够较好的满足深层孔隙流体的敏感指示需求,且本文推导的包含Russell流体因子的两项AVO近似公式与两项弹性阻抗方程可以较好的满足小角度入射的近似精度要求.
(2)利用弹性阻抗反演估算Russell流体因子能够较好的减小随机噪音的影响,且基于贝叶斯反演框架下的Cauchy先验正则约束进一步提高了反演的可靠性.
(3)模型试算与实际应用表明,在小角度入射情况下,基于两角度弹性阻抗的参数估算稳定性更高,且直接估算避免了误差累计,提高了Russell流体因子的估算精度.
(4)本方法是针对深层储层无法有效获取大角度入射信息情况下提出的利用Russell流体因子进行储层流体识别的方法,在实际应用中需首先基于岩石物理流体敏感统计分析确保Russell流体因子确实具有流体指示敏感性,然后利用本方法才可能取得理想的流体识别效果.另外,针对叠前资料远道拉伸严重且资料品质较差的地区,也同样可以采用本文方法折中的发掘储层的孔隙流体信息,以实现储层的可靠流体识别.
附录AFatti等人于1994年对Aki-Richards近似公式的表示形式进行了重新推导,给出包含波阻抗相对变化量的近似公式[12],即

|
(A1) |
其中,


在小角度入射情况下,考虑到密度项的权重系数较小,且密度项本身的变化也很小,因此两项近似即可满足小角度的近似精度,此时的反射系数近似公式可以表示为

|
(A2) |
将公式(A2)两边同乘以IP2,可以将(A2)式变形为

|
(A3) |
Russell流体因子的表达式为

|
(A4) |
其中,γdry表示干岩石的纵横波速度之比.
对公式(A4)两边取微分,则有

|
(A5) |
即

|
(A6) |
将(A6)代入(A3)可以得到

|
(A7) |
即

|
(A8) |
又因为:

|
(A9) |
考虑到反射界面两侧阻抗变化较小的情况下,利用阻抗的对数形式可以满足反射系数的近似精度,即

|
(B1) |
其中,EI表示弹性阻抗;ΔEI表示界面两侧弹性阻抗之差;EI表示界面两侧弹性阻抗之和.
将公式(A9)代入公式(B1),可以得到

|
(B2) |
如公式(B1)所示的,利用对数微分表示参数的相对变化量,可以将(B2)进一步变形为

|
(B3) |
经过进一步化简,可以得到

|
(B4) |
经过积分运算与指数化处理,可以得到

|
(B5) |
其中,
由于公式(B5)的量纲随入射角度变化剧烈,不利于不同角度弹性阻抗之间的数值比较,且会影响最终参数提取的稳定性.在此,借鉴Whitcombe的弹性阻抗标准化思想[24],通过引入常数F0和IP0,将公式(B5)改写为

|
(B6) |
其中,F0和IP0分别表示Russell流体因子和纵波阻抗的平均值.
公式(B6)即最终得到的包含Russell流体因子的标准化两项弹性阻抗方程.
| [1] | 朱光友, 张水昌. 中国深层油气成藏条件与勘探潜力. 石油学报 , 2009, 30(6): 793–802. Zhu G Y, Zhang S C. Hydrocarbon accumulation conditions and exploration potential of deep reservoirs in China. Acta Petrolei Sinica (in Chinese) , 2009, 30(6): 793-802. |
| [2] | 杨文采, 于常青. 深层油气地球物理勘探基础研究. 地球物理学进展 , 2007, 22(4): 1238–1242. Yang W, Yu C Q. On basic research problems in applied geophysics for deep oil and gas fields. Progress in Geophysics (in Chinese) , 2007, 22(4): 1238-1242. |
| [3] | 程冰洁, 徐天吉, 李曙光. 频变AVO含气性识别技术研究与应用. 地球物理学报 , 2012, 55(2): 608–613. Cheng B J, Xu T J, Li S G. Research and application of frequency dependent AVO analysis for gas recognition. Chinese J. Geophys. (in Chinese) , 2012, 55(2): 608-613. |
| [4] | Russell B H, Gray D, Hampson D P. Linearized AVO and poroelasticity. Geophysics , 2011, 76(3): C19-C29. DOI:10.1190/1.3555082 |
| [5] | 郑静静, 印兴耀, 张广智. 流体因子关系分析以及新流体因子的构建. 地球物理学进展 , 2011, 26(2): 579–587. Zheng J J, Yin X Y, Zhang G Z. Fluid factor analysis and the construction of the new fluid factor. Progress in Geophysics (in Chinese) , 2011, 26(2): 579-587. |
| [6] | 吴小洁, 顾汉明. 双相介质的AVO资料中蕴含的流体信息的定量分析. 地球物理学进展 , 2009, 24(3): 1013–1018. Wu X J, Gu H M. Quantitative analysis of fluid information contained in seismic AVO data in porous media. Progress in Geophysics (in Chinese) , 2009, 24(3): 1013-1018. |
| [7] | 彭真明, 李亚林, 巫盛洪, 等. 碳酸盐岩储层多角度弹性阻抗流体识别方法. 地球物理学报 , 2008, 51(3): 881–885. Peng Z M, Li Y L, Wu S H, et al. Discriminating gas and water using multi-angle extended elastic impedance inversion in carbonate reservoirs. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 881-885. |
| [8] | Yin X Y, Yuan S H, Zhang F C. Rock elastic parameters calculation from elastic impedance. CPS/SEG Technical Program Expanded Abstracts, 2004: 538-542. http://www.oalib.com/references/18988238 |
| [9] | 杨培杰, 印兴耀. 非线性二次规划贝叶斯叠前反演. 地球物理学报 , 2008, 51(6): 1876–1882. Yang P J, Yin X Y. Non-linear quadratic programming Bayesian prestack inversion. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1876-1882. |
| [10] | 宗兆云, 印兴耀, 吴国忱. 基于叠前地震纵横波模量直接反演的流体检测方法. 地球物理学报 , 2012, 55(1): 284–292. Zong Z Y, Yin X Y, Wu G C. Fluid identification method based on compressional and shear modulus direct inversion. Chinese J. Geophys. (in Chinese) , 2012, 55(1): 284-292. |
| [11] | Smith G C, Gidlow P M. Weighted stacking for rock property estimation and detection of gas. Geophysical Prospecting , 1987, 35(9): 993-1014. DOI:10.1111/gpr.1987.35.issue-9 |
| [12] | Fatti J L, Smith G C, Vail P J, et al. Detection of gas in sandstone reservoirs using AVO analysis: A 3-D seismic case history using the geostack technique. Geophysics , 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [13] | Goodway B, Chen T, Downton J. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters:"λρ", "μρ", & "λ/μ fluid stack", from P and S inversions. 67th Annual International Meeting, SEG, Expanded Abstracts, 1997: 183-186. |
| [14] | Quakenbush M, Shang B, Tuttle C. Poisson impedance. The Leading Edge , 2006, 25(2): 128-138. DOI:10.1190/1.2172301 |
| [15] | Russell B H, Hedlin K, Hilterman F J, et al. Fluid-property discrimination with AVO: A Biot-Gassmann perspective. Geophysics , 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [16] | 宁忠华, 贺振华, 黄德济. 基于地震资料的高灵敏度流体识别因子. 石油物探 , 2006, 45(3): 239–242. Ning Z H, He Z H, Huang D J. High sensitive fluid identification based on seismic data. Geophysical Prospecting for Petroleum (in Chinese) , 2006, 45(3): 239-242. |
| [17] | Chi X G, Han D H. Fluid property discrimination by AVO inversion. 76th Annual International Meeting, SEG, Expanded Abstracts, 2006: 2052-2056. http://www.oalib.com/references/18988251 |
| [18] | 王保丽, 印兴耀, 张繁昌. 基于Gray近似的弹性波阻抗方程及反演. 石油地球物理勘探 , 2007, 42(4): 435–439. Wang B L, Yin X Y, Zhang F C. Gray approximation-based elastic wave impedance equation and inversion. Oil Geophysical Prospecting (in Chinese) , 2007, 42(4): 435-439. |
| [19] | 印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别. 石油地球物理勘探 , 2010, 45(3): 373–380. Yin X Y, Zhang S X, Zhang F C, et al. Utilizing Russell Approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification. Oil Geophysical Prospecting (in Chinese) , 2010, 45(3): 373-380. |
| [20] | Dillon L, Schwedersky G, Vásquez G, et al. A multiscale DHI elastic attributes evaluation. The Leading Edge , 2003, 22(10): 1024-1029. DOI:10.1190/1.1623644 |
| [21] | Zhou Z Y, Hilterman F J. A comparison between methods that discriminate fluid content in unconsolidated sandstone reservoirs. Geophysics , 2010, 75(1): B47-B58. DOI:10.1190/1.3253153 |
| [22] | 李爱山, 印兴耀, 陆娜, 等. 两个角度弹性阻抗反演在中深层含气储层预测中的应用. 石油地球物理勘探 , 2009, 44(1): 87–92. Li A S, Yin X Y, Lu N, et al. Application of elastic impedance inversion with two angle stack gathers to predict gas-bearing reservoir of mid-deep layer. Oil Geophysical Prospecting (in Chinese) , 2009, 44(1): 87-92. |
| [23] | Connolly P. Elastic impedance. The Leading Edge , 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [24] | Whitcombe D N. Elastic impedance normalization. Geophysics , 2002, 67(1): 60-62. DOI:10.1190/1.1451331 |
| [25] | 宗兆云, 印兴耀, 张繁昌. 基于弹性阻抗贝叶斯反演的拉梅参数提取方法研究. 石油地球物理勘探 , 2011, 46(4): 598–604, 609. Zong Z Y, Yin X Y, Zhang F C. Elastic impedance Bayesian inversion for lame parameters extracting. Oil Geophysical Prospecting (in Chinese) , 2011, 46(4): 598-604, 609. |
 2013, Vol. 56
2013, Vol. 56



