许多天然裂缝性储层岩石,如碳酸盐岩、致密砂岩等,通常包含两种类型的空隙:刚性孔隙和柔性裂缝[1-2],这两类空隙通常被流体所充填,而裂缝的定向排列将诱导地震各向异性,因而同时考虑了介质的双相性和各向异性的双相各向异性介质模型将更接近于实际流体饱和裂缝性储层介质.
双相介质理论充分考虑了介质物性结构、流体性质以及固体骨架与孔隙流体的相互作用对弹性波传播的影响.研究发现,在波传播过程中含流体孔隙介质中存在两种重要的波诱导流体流动形式-Biot流动和喷射流动,它们作为一个耦合过程共同对波的传播产生影响.1993年,Dvorkin和Nur[3]基于孔隙各向同性一维问题,将这两种流体流动机制有机地统一起来,提出了Biot-Squirt(BISQ)模型,并通过与实验观测数据对比,发现该模型较仅考虑宏观流动(Biot流动)的Biot模型[4-5]更准确地预测了波的衰减和频散.Parra[6]、Yang和Zhang [7]将其推广到高维横向各向同性和一般各向异性情况.之后,国内外一些学者对BISQ模型进行了更为深入的研究,使BISQ模型的基本理论和应用范围得到进一步完善和拓展[8-13].然而,BISQ模型在实际应用中将面临一个重要的问题,即该模型建立的过程中引入了一个描述喷射流动机制的微尺度参数---特征喷流长度,而该参数本身物理意义并不十分明确,也不易实验测得,它的引入大大降低了BISQ模型准确预测实际岩石中波衰减和频散的能力[14].鉴于此,Diallo和Appel[15]对孔隙流体压力公式进行重新推导,提出了一种不依赖于特征喷流长度参数的改进BISQ模型;随后,Diallo等[16]进行了自然条件和有孔隙围压条件下两套岩石物理学实验,并将改进BISQ模型和原BISQ模型预测的理论值与实验数据进行对比,发现改进BISQ模型预测的波相速度与实测数据吻合更好,表明该模型具有更大的实际应用潜力.
裂缝诱导的各向异性一直是地震各向异性研究中的热点问题,国内外学者对此开展了大量的研究工作[17-24].目前,常用的裂缝各向异性介质模型主要包括Hudson模型[22]、Thomsen模型[23]和Schoenberg模型[24].对于含定向裂缝的饱和孔隙介质,Hudson模型仅适用于裂缝孤立的情况,未考虑背景孔隙的效应,而Thomsen模型尽管考虑了裂缝与孔隙液压连通的情况,但对裂缝形状仍有一定限制,且这两种模型的适用性均限定在小裂缝密度范围内. Schoenberg模型,也即线性滑动模型,则忽略裂缝的形状和微结构,将裂缝看成是满足线性滑动边界条件的无限薄且非常松软的地层或平面[25],具有一般性.进一步地,Gurevich[26]利用线性滑动模型和各向异性Gassmann方程,直接由各向同性背景孔隙岩石的弹性参数和干裂缝岩石的裂缝柔度参数,推导出裂缝性孔隙介质的等效弹性模量,该方法充分考虑了裂缝与孔隙的连通性且无需限定裂缝形状,更具普适性.
将双相介质理论与裂缝各向异性理论相结合,建立更为符合实际裂缝性储层的理论介质模型对于裂缝性油气藏地震响应的分析具有重要意义. Parra[8]结合BISQ模型和Thomsen模型研究了含垂直裂缝的孔隙介质中渗透率各向异性对地震波衰减和频散的影响.结合BISQ模型和Hudson模型,轩义华等[27]研究了双相HTI介质的地震波场二维正演;张显文等[28]研究了三维双相正交裂隙各向异性介质中地震波衰减和频散的方位特性.杜启振等[25, 29]、孔丽云等[30]结合Biot模型和线性滑动模型建立了裂缝诱导HTI双孔隙介质模型,并进行了波场数值模拟和裂缝参数分析.
由于双相介质理论的相对不完善性和裂缝模型的局限性,以上研究中所建立的模型的适用范围将受到一定限制.本文的研究旨在从双相各向异性理论角度出发,针对裂缝性储层岩石,建立一种适用性更广的裂缝性孔隙介质模型,并针对其进行波场数值模拟与分析.为此,本文结合基于改进BISQ机制[15]的双相介质理论与Gurevich裂缝各向异性理论[26],建立基于改进BISQ机制的双相HTI介质模型,并推导出其二维三分量波传播方程,该方程各物理参量均具有明确物理意义和物理可实现性;然后采用高精度的伪谱法求解该方程,实现了该类介质的波场数值模拟,并且根据模拟结果具体分析了近似理想相界和黏滞相界高频、低频情况下波的传播特征,与此同时研究了波在介质界面处的反射与透射现象;最后,对波在基于改进BISQ机制的双相HTI介质中的传播特征进行了总结.
2 基于改进BISQ机制的双相HTI介质模型及波传播方程 2.1 模型建立的假设前提(1) 干燥的裂缝性孔隙岩石由一组垂直平行排列的裂缝嵌入到满足统计各向同性性质的孔隙背景岩石中构成(见图 1).孔隙之间以及孔隙与裂缝之间相互连通,裂缝和孔隙的最大尺寸远小于弹性波波长.

|
图 1 基于改进BISQ机制的双相HTI介质模型示意图 裂缝走向为y方向,介质对称轴沿x方向. Fig. 1 Schematic of two-phase HTI medium model based on reformulated BISQ mechanism Fracture strike direction is y-direction, symmetry axis of the medium is along the x-direction. |
(2) 孔隙和裂缝由一种各向同性、具有黏滞性和可压缩性的流体所饱和.
(3) 孔隙流体可在波传播方向上和横向上发生流动,受波的挤压作用,流体能够从软孔隙(孔喉或粒间细小裂隙)或裂缝中喷出,泵入刚性孔隙中,流体渗流遵守广义达西定律.忽略热弹性效应,孔隙流体与岩石基质也不发生化学作用.
(4) 固体和流体之间相互作用、相互影响的力学耦合效应具有各向异性.
2.2 三维孔隙流体压力表达式含流体孔隙介质中波诱导流体流动的过程即是孔隙流体压力的平衡过程,孔隙流体压力表达式的确定对于波传播方程的建立以及波传播特性的研究至关重要.基于Parra[6]、Yang和Zhang [7]的方法,将基于改进BISQ机制的一维波动孔隙流体压力表达式推广为三维HTI介质中三维波动孔隙流体压力:
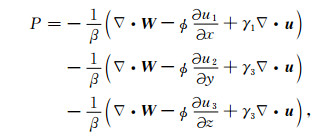
|
(1) |
(1) 式的具体推导见附录A.式中第一项代表与x方向波动有关的Biot流动和喷射流动对总孔隙流体压力的贡献,后两项则分别代表与y、z方向波动有关的两种流体流动对总孔隙流体压力的贡献.其中W=φ(U-u)表示相对固-流位移矢量,U=(U1,U2,U3)T和u=(u1,u2,u3)T分别表示流相和固相位移矢量,而ui和Ui(i=1,2,3)则分别表示固相和流相质点在笛卡尔坐标系三个正交方向x、y和z上的位移分量;φ是孔隙度;β表示双相介质压缩率系数,其表示为β=φ/Kf+1/Q,其中Kf为流体的体积模量,1/Q的表达式见附录A;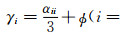
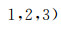

|
其中,Ks为固体颗粒体积模量,c110、c120、c130为干燥情况下固体骨架的弹性刚度张量c0的元素,对于HTI介质有:
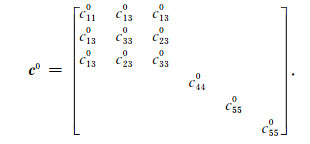
|
采用Diallo和Appel[15]的表示方法,令

|
F表示Biot流动系数.在双相各向同性情况下,(1)式可改写为
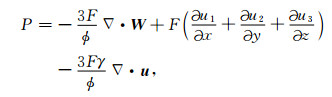
|
(2) |
(2) 式与Diallo和Appel[15]给出的基于改进BISQ机制的双相各向同性介质的孔隙流体压力公式相一致.
将W和γi(i=1,3)的表达式代入(1)式,并整理得:
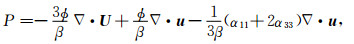
|
(3) |
(3) 式即为以固相和流相位移分量为基本未知量的基于改进BISQ机制的三维双相HTI介质中孔隙流体压力表达式.
2.3 双相HTI介质等效刚度参数结合线性滑动理论和Gassmann各向异性流体替换方程,流体饱和裂缝性孔隙介质的等效刚度参数可以写为各向同性背景孔隙岩石弹性模量、裂缝弱度和流体模量的显式表达式[26]:
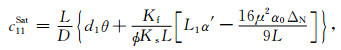
|
(4a) |

|
(4b) |
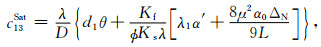
|
(4c) |
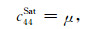
|
(4d) |
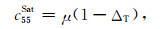
|
(4e) |
其中,
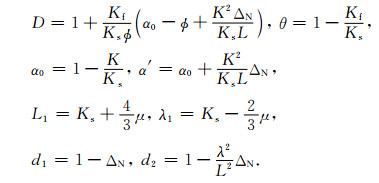
|
λ、μ、K=λ+2μ/3和L=λ+2μ分别为各向同性背景孔隙岩石的拉梅常数、体积模量和P波模量,其中λ、μ可由干燥情况下各向同性背景孔隙岩石的纵波速度vp、横波速度vs计算得到;流体体积模量Kf可由流体密度ρf和流体声速v0来确定,即Kf=ρfv02;ΔN和ΔT分别为裂缝法向和切向弱度参数,可利用地震波速度测量值间接计算得到.
当裂缝性孔隙介质由一种流体饱和时,(4)式即给出了双相HTI介质的等效刚度参数的显式表达,若取流体体积模量Kf=0,则可得到干燥情况下固体骨架弹性刚度张量c0的相应元素.
2.4 波传播方程Biot模型、BISQ模型和改进BISQ模型,三者实质性的差别在于孔隙流体压力的不同,而本构关系、几何方程和运动方程可写为相同的表达形式.因此,根据Yang和Zhang [7] 提出的包含BISQ机制和固流耦合各向异性效应的孔隙弹性波动理论,给出基于改进BISQ机制双相HTI介质的本构关系、几何方程、运动方程以及二维三分量波传播方程.
本构关系:
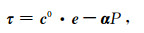
|
(5) |
其中,τ为总应力张量,e为固体骨架应变张量,孔隙流体压力P由(3)式给出.
几何方程:

|
(6) |
其中,下标i,j=(1,2,3)分别表示x,y,z方向分量,文中后续公式中i,j意义同此.
运动方程:
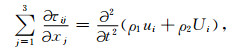
|
(7a) |
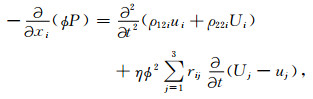
|
(7b) |
其中τij为总应力张量分量;ρ1=(1-φ)ρs,ρ2=φρf,ρs为固相的密度;ρ22i=ρ2 -ρ12i,ρ12i=-ρai,ρai为xi方向的固-流耦合附加质量密度;η为流体黏滞系数;rij为流体阻抗系数张量r的元素,r=k-1,k为渗透率张量;对于HTI介质k=diag(k11,k33,k33);其他变量的物理意义同前文.
利用式(3)、(5)、(6)、(7)即可导出以固相和流相位移ui和Ui为基本未知量的基于改进BISQ机制的双相HTI介质波传播方程.在二维x-z平面内这组方程是由以下7个方程构成的偏微分方程组:
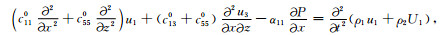
|
(8a) |

|
(8b) |
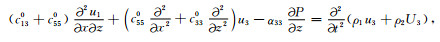
|
(8c) |
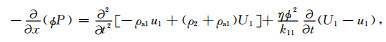
|
(8d) |
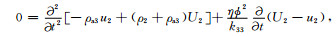
|
(8e) |
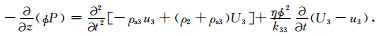
|
(8f) |

|
(8g) |
伪谱法的基本原理是空间微分利用傅里叶变换求解,时间微分采用差分格式近似[31].因而其对空间微分的计算能够达到谱精度,在空间方向没有网格频散误差的产生,快速傅里叶变换的应用更使其成为一种计算精度和效率都较高的波动方程数值解法而被广泛应用于地震波场数值模拟研究中.一些学者利用伪谱法分别对黏弹各向异性介质、双相各向异性介质、随机孔隙介质等复杂介质的波场进行了数值模拟[31-35].
伪谱法的高精度、无空间网格频散的特点决定了其与有限差分、有限元法相比更适于孔隙介质的波场模拟,原因在于孔隙介质是一种耗散介质,传播于其中的弹性波会因能量耗散而产生速度频散,伪谱法的应用则可最大程度地避免任何频段内这种与介质性质相关的物理频散与网格数值频散的混淆.
3.1 伪谱法波场模拟的递推公式以等空间步长h沿x和z方向对计算区域进行网格剖分,取x=ih,z=jh,其中i、j为整数,表示空间网格点.模拟计算的时间步长为Δt,则计算时间t=nΔt,其中n为整数,表示离散时间采样点,也即伪谱法计算的第n个递推步.用傅里叶变换计算(8)式中的空间导数,用二阶中心差分计算时间导数,则可得基于改进BISQ机制的双相HTI介质波传播方程的伪谱法求解递推公式,具体形式见附录B.
3.2 稳定性条件和吸收边界条件结合横向各向同性介质中弹性波方程伪谱解法的稳定性条件[36],给出基于改进BISQ机制双相HTI介质中波传播位移方程的伪谱解法稳定性条件的近似表达式为
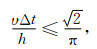
|
(9) |
式中,
为消除人工边界反射,采用简便实用的Cerjan衰减边界[37],即沿人工边界向外扩充N个网格点,进入扩充区域内的波场通过乘以下面的因子
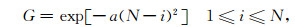
|
(10) |
逐渐衰减为零,其中a为衰减系数,可通过试验确定最佳值.
4 数值模拟与分析为了考察本文提出的基于改进BISQ机制的双相HTI介质模型在描述含流体裂缝性孔隙介质中弹性波传播性质的有效性,选取不同的模型进行波场数值模拟研究.
4.1 模型1:近似理想相界单层模型为了详细分析基于改进BISQ机制的双相HTI介质中可能存在的各种弹性波的传播特性,第一个模型设计为流体黏滞性非常小的近似理想相界单层模型.模型大小为2550 m×2550 m,介质物性参数分别为:干燥情况下各向同性背景孔隙介质的纵、横波速度vp=3800 m/s、vs=2160 m/s,孔隙度φ=0.2,固相密度ρs=2650 kg/m3,固相体积模量Ks=38 GPa,裂缝法向弱度ΔN=0.2、裂缝切向弱度ΔT=0.32,x和z方向渗透率k11=4×10-10 m2和k33=1.5×10-9 m2,流体黏滞系数η=1×10-10 Pa·s,流体密度ρf=1000 kg/m3,流体声速c0=1500 m/s,x和z方向的固流耦合密度ρa1=420 kg/m3和ρa3=450 kg/m3.其他计算参数选择为:空间采样间隔Δx=Δz=10 m,时间步长为Δt=5× 10-4 s.震源子波采用Ricker子波,震源位置(1270 m,1270 m),主频为30 Hz,三分量模拟中震源分别为z、y方向集中力源.图 2a、图 2b分别给出了近似理想相界情况下基于改进BISQ机制的双相HTI介质中固相和流相位移三分量在t=0.3 s时刻的波场快照.为了便于分析波传播过程中引起的固相和流相质点振动特性,图 2c给出了分别由固相x分量和z分量、流相x分量和z分量合成的固相和流相质点位移矢量图.

|
图 2 模型1的固相(a)、流相(b)位移三分量t=0.3 s时波场快照和质点位移矢量图 (a1,b1)固相和流相位移x分量;(a2,b2)固相和流相位移y分量;(a3,b3)固相和流相位移z分量;(c1,c2)固相和流相质点位移矢量图. Fig. 2 Wavefield snapshots of three-component displacement and vectograms of particle displacement in solid phase and fluid phaseat t=0.3 s of model 1 (a1, b1)x-component in solid phase and fluid phase; (a2, b2)y-component in solid phase and fluid phase; (a3, b3)z-component in solid phase and fluid phase; (c1, c2) vectograms of particle displacement in solid phase and in fluid phase. |
从图 2中各分量的波场快照可以看出,波场中各波前面都非常清晰,没有网格数值频散的产生,表明了伪谱法在孔隙介质波场数值模拟中的有效性和精确性.
分析模型1的波场数值模拟结果:(1)从图 2a(a1、a3)和图 2b(b1、b3)可以看出,波场快照中包含3种不同的波,它们由外向内依次为:快准P波、准SV波和慢准P波,固相和流相波场快照中慢准P波能量较强,清晰可见,这与无耗散方程所描述的慢P波传播特征相同;(2)对比固相(图 2a)与流相(图 2b)的波场及位移矢量图(图 2c)可见,快准P波引起固相和流相质点同相位振动且固相质点振动略强于流相质点,而慢准P波则引起固相和流相质点反相位振动且流相质点振动明显强于固相质点,这些现象与Biot模型中质点振动特性相同[38];(3)固相和流相x、z分量中的快准P波、准SV波和慢准P波以及y分量中的SH波,这4种波的波前面均呈椭圆形,准SV波的波前面出现波面尖角现象;对比波场三分量,在改进BISQ机制所描述的两种流体流动耦合作用下,双相HTI介质中仍存在横波分裂;这些与李红星等[13]进行的基于BISQ机制双相横向各向同性介质的波场数值模拟所揭示的波传播现象相一致,均体现了双相各向异性介质中各向异性所引起的波场特征.
慢准P波的存在、固相和流相质点的振动特性以及各种波的波前面传播特征共同表明:基于改进BISQ机制的双相HTI介质具有双相性和裂缝各向异性,模型中背景孔隙介质主导了介质的双相性,而裂缝系统则诱导了介质的各向异性.
4.2 模型2:不同频率黏滞相界单层模型为了考察黏滞相界模型中不同频率情况下波的传播特征,取流体黏滞系数η=0.001 Pa·s,其他介质参数与模型1中的参数一致.震源子波采用Ricker子波,震源位置(1270 m,1270 m),加载方式同模型1.低频情况下的波场数值模拟选择参数:震源主频为地震波频率范围内f=30 Hz,空间采样间隔Δx=Δz=10 m,时间步长为Δt=5×10-4 s;高频情况下的波场数值模拟选择参数:震源主频为声波测井频率范围内f=15 kHz,空间采样间隔Δx=Δz=0.02 m,时间步长为Δt=1×10-6 s.图 3给出了低频和高频情况下黏滞相界模型中固相位移三分量在t=0.3 s时刻的波场快照.

|
图 3 模型2的固相位移三分量t=0.3 s时波场快照 (a)低频波场;(b)高频波场;(a1,b1):x分量;(a2,b2):y分量;(a3,b3):z分量. Fig. 3 Wavefield snapshots of three-component displacement in solid phaseat t=0.3 s of model 2 (a) Wavefield in low frequency; (b) Wavefield in high frequency; (a1, b1):x-component; (a2, b2):y-component; (a3, b3):z-component. |
对比图 3a和图 3b可以看出,在黏滞相界模型中,低频情况下波场快照上观测不到慢准P波,而在高频情况下则可较为明显地观测到慢准P波;另外,高频情况下快准P波、准SV波的传播速度比低频情况下略快,这与Diallo和Appel[15]的理论分析结果相一致,这表明基于改进BISQ机制的双相HTI介质的弹性性质频率相关.以上波传播现象的物理解释为:低频情况下,在波半个周期内,波诱导的流体压力很容易达到平衡,软孔隙或裂隙中的流体被缓慢挤出,流体喷射流动容易变得松弛,且此时Biot流动主要受黏滞剪切力控制,因而在两种流动机制作用下,孔隙流体与骨架之间产生较强的黏滞摩擦作用,致使慢纵波传播速度慢且衰减大,表现为弥散性,这也解释了实际地震勘探频段很难观测到慢P波的原因;而高频情况下,在波半个周期内,流体压力没有时间达到完全平衡,从而产生流体压力梯度,孔隙流体从软孔隙或裂隙中喷出,产生较强的喷射流动效应,此时惯性力对Biot流动的影响也相对增强,因而高频情况下孔隙流体与骨架的黏滞相互作用很弱,慢纵波速度变大且衰减变小,呈传播性,同时流体压力不完全平衡也使得孔隙介质的刚性相对增加,快准P波和准SV波的波速略有增大.比较图 3(a2)与图 3(b2)可见,y分量中SH波的波前面形态在高频和低频情况下基本是一致的,表明SH波不受喷射流动作用的影响,这一点也可从方程(8b)和(8e)中看出.其物理原因在于,y分量SH波的质点振动始终垂直于x-z平面,因而不受二维x-z平面内喷射流动的影响.
4.3 模型3:不同频率双层介质模型为了分析基于改进BISQ机制双相HTI介质中波在介质分界面处的反射和透射特征,设计了一个大小为2550 m×2550 m双层介质模型,界面深度为1480 m.模型上层介质参数为:
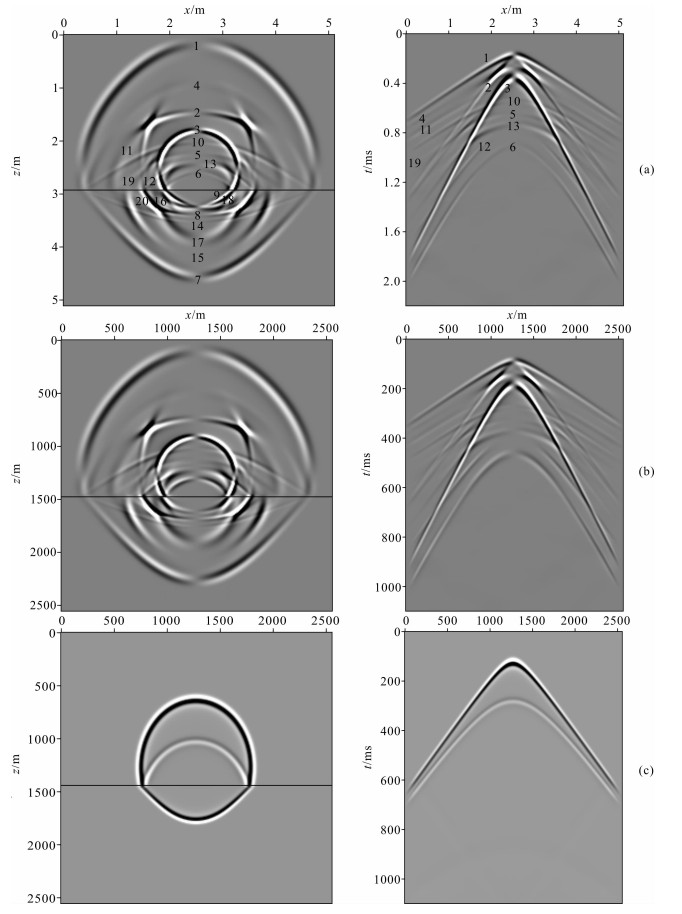
干燥情况下各向同性背景孔隙介质的纵、横波速度分别为vp=2700 m/s、vs=1600 m/s,其他模型参数同模型1;下层介质参数为:干燥情况下各向同性背景孔隙介质的纵、横波速度分别为vp=4800 m/s、vs=2600 m/s,固相密度ρs=2950 kg/m3,η=0.001 Pa·s,其他模型参数同模型1.低频和高频情况下波场数值模拟计算的震源参数和加载方式,空间采样间隔和时间步长同模型2.选取流相x分量低频和高频情况下快准P波、准SV波和慢准P波的波场快照(t=0.3 s)和合成地震记录来分析3种波在介质分界面处的反射和透射特征,见图 4(a、b);选取流相y分量分析SH波的反射、透射特征,见图 4c.
|
图 4 模型3的流相位移波场快照(左图)和合成地震记录(右图) (a)高频x分量;(b)低频x分量;(c)y分量. 1直达快准P波,2直达准SV波,3直达慢准P波,4反射快准P波,5反射准SV波,6反射慢准P波,7透射快准P波,8透射准SV波,9透射慢准P波,10快准P波产生的反射转换准SV波,11准SV波产生的折射转换快准P波,12准SV波产生的反射转换慢准P波,13慢准P波产生的反射转换准SV波,14快准P波产生的透射转换准SV,15准SV波产生的透射转换快准P波,16准SV波产生的透射转换慢准P波,17慢准P波产生的透射转换快准P波,18慢准P波产生的透射转换准SV波,19连接准SV波折射转换快准P波11和反射准SV波5的首波,20连接准SV波透射转换快准P波15和透射准SV波8的首波. Fig. 4 Wavefield snapshots (left) and seismic synthetic records (right) of displacement in fluid phase of model 3 (a)x-component in high frequency; (b)x-component in low frequency; (c)y-component. 1 Direct fast quasi-Pwave (qP1 wave), 2 Direct quasi-SV wave (qSV wave), 3 Direct slow quasi-P wave (qP2 wave), 4 Reflected qP1 wave, 5 Reflecte dqSV wave, 6 Reflected qP2 wave, 7 Transmitted qP1 wave, 8 Transmitted qSV wave, 9 Transmitted qP2 wave, 10 Reflected converted quasi-SV wave by fast quasi-P wave (qP1-qSV), 11 Refracted qSV-qP1 12 Reflected qSV-qP2, 13 Reflected qP2-qSV, 14 Transmitted qP1-qSV, 15 Transmitted qSV-qP1, 16 Transmitted qSV-qP2, 17 Transmitted qP2-qP1, 18 Transmitted qP2-qSV, 19 The head wave linking 11 to 5, 20 The head wave linking 15 to 8. |
分析图 4(a、b)可知:快准P波、准SV波和慢准P波在双层介质分界面处均发生了反射和透射现象,并出现了转换波;在高频时(图 4a),波场快照中可同时观测到多种波,这些波大致可以分为以下5类:(1)直达波类:直达快准P波、直达准SV波和直达慢准P波;(2)反射波类:反射快准P波、反射准SV波、反射慢准P波;(3)透射波类:透射快准P波、透射准SV波、透射慢准P波;(4)转换波类:由快准P波在界面反射之后形成的反射转换准SV波,由准SV波在界面折射之后形成的折射转换快准P波,由准SV波在界面反射之后形成的反射转换慢准P波,由慢准P波在界面反射之后形成的反射转换准SV波,由快准P波在界面透射之后形成的透射转换准SV波,由准SV波在界面透射之后形成的透射转换快准P波和慢准P波,由慢准P波在界面透射之后形成的透射转换快准P波和准SV波;(5)首波类:连接由准SV波形成的折射转换快准P波11和反射准SV波5的波前面19,连接由准SV波形成的透射转换快准P波15和透射准SV波8的波前面20;而在低频时(图 4b),由于下层介质为黏滞相界,因而与高频波场相比缺少了透射慢准P波9和由准SV波产生的透射转换慢准P波16.分析图 4c可知:SH波在界面处也发生反射和透射现象,但只有同类波的产生而没有转换波.
由以上可见,双层基于改进BISQ机制的双相HTI介质模型中的波场信息非常丰富,每种波的入射都将在分界面处产生多种波.深入研究裂缝性孔隙介质模型中地震波在分界面处的反射、透射现象,分析各种波的传播特征,能够加深对裂缝性储层介质地震响应的认识,进而有助于利用多波地震资料对裂缝性油气藏进行更为深入的研究,具有重要的理论和实际意义.
5 结论将改进BISQ模型与Gurevich裂缝各向异性理论相结合,建立了一种更具有普适性的裂缝性孔隙介质模型,即基于改进BISQ机制的双相HTI介质模型,推导了介质的二维三分量波传播方程,采用伪谱法实现该类介质的波场数值模拟,通过对模拟结果进行分析,得出以下结论:
(1) 伪谱法模拟精度高,压制网格空间频散效果好,且易于实现,是一种进行孔隙介质中波场数值模拟的高精度算法.
(2) 在理想相界情况下,固相和流相三分量波场中均可观测到快准P波、慢准P波、准SV波和SH波4种波,4种波的波前面形态特征和快、慢准P波的质点振动特性表明,基于改进BISQ机制的双相HTI介质模型兼具裂缝各向异性特征和孔隙弹性特征.
(3) 在黏滞相界情况下,低频时慢准P波迅速衰减,呈弥散性,在波场快照中无法观测到,这是实际地震勘探频段内很难观测到慢P波的重要原因,因为实际的含流体孔隙介质通常具有较强的黏滞性;高频时,由于固流黏滞摩擦作用减弱,慢准P波呈传播性;受喷射流动效应的影响,快准P波和准SV波的传播比低频时略快;SH波的传播不受喷射流动效应的影响,低、高频传播特征基本一致.
(4) 快准P波、准SV波和慢准P波在双层介质的分界面处均发生反射、透射和波型转换现象,从而使得波场信息非常丰富;高频情况下,慢准P波能量较强,且其在界面反射和透射后会产生转换快准P波和准SV波,因而在声波测井频段内对于高孔渗裂缝性孔隙介质中波传播特征的分析,可能需要考虑慢纵波通过界面时在波场转换中的作用;二维情况下,y分量只能观测到SH波及其反射和透射波.
本文针对裂缝性储层建立了基于改进BISQ机制的双相HTI介质模型,波场数值模拟结果证实了其合理性和有效性,为从双相各向异性理论角度研究裂缝性储层的地震响应奠定了理论基础.
附录ADvorkin和Nur[3]通过二维轴对称流体质量守恒方程将Biot流动和喷射流动统一起来处理,方程形式为:
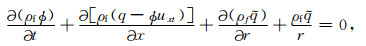
|
(A1) |
其中:q为x方向的体积渗滤速度,与x方向的流体位移有关,q=φUxt;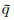

将发生在波传播方向和其垂向的流体流动作为柱坐标系(x,z,r)下三维流体流动模型沿轴向x方向和径向r方向的分量[15],则径向的流体位移νr可以由Ur来代替,因而可以定义流相位移矢量为U=(Ux,Uz,Ur),固相位移矢量为u=(ux,uz,ur).在该定义下,则x方向的体积渗滤速度为q=φUxt,而r方向的体积渗滤速度可表示为
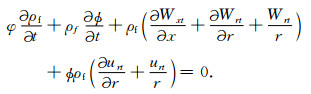
|
(A2) |
孔隙度的变化量与骨架的形变量以及流体压力的变化量有关,在一般各向异性情况下,可表示为[7]

|
(A3) |
其中:dφ、dP分别为孔隙度变化量和流体压力变化量;α为有效应力之孔隙弹性系数张量,可表示为 

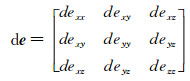


|
(A4) |
Dvorkin和Nur[3]给出了描述流体压缩性的线性关系式:
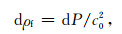
|
其中c0为流体中声波速度,则有

|
(A5) |
将(A4)、(A5)式代入(A2)式,并整理得:
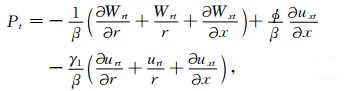
|
(A6) |
假设流相和固相位移的时间相关性由eiωt表示[15],则(A6)式中变量对时间的偏微分等价于与iω的乘积,因而有

|
(A7) |
在笛卡尔直角坐标系下,有
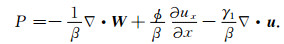
|
(A8) |
在三维波动情况下,采用Parra的方法[6]得到三维HTI介质中三维波动孔隙流体压力表达式为
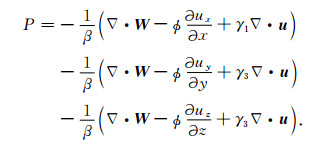
|
(A9) |
基于改进BISQ机制的双相HTI介质波传播方程的伪谱法求解递推公式可以表示为
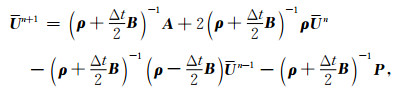
|
(B1) |
其中,

|
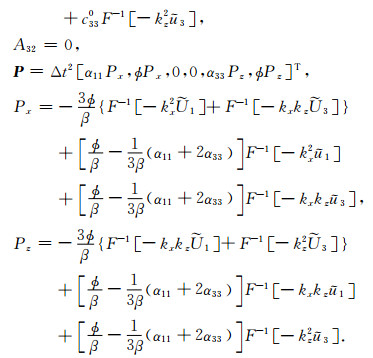
|
F-1[·]表示x-z空间二重傅里叶逆变换,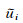

| [1] | Nelson R A. Geological Analysis of Naturally Fractured Reservoirs. London: Gulf Professional Publishing Company, 2001. |
| [2] | Gurevich B, Brajanovski R, Galvin R J, et al. P-wave dispersion and attenuation in fractured and porous reservoirs-Poroelasticity approach. Geophysical Prospecting , 2009, 57(2): 225-237. DOI:10.1111/gpr.2008.57.issue-2 |
| [3] | Dvorkin J, Nur A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms. Geophysics , 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [4] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, Ⅰ: low frequency range. J. Acoust. Soc. Am. , 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [5] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, Ⅱ: high frequency range. J. Acoust. Soc. Am. , 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [6] | Parra J O. The transversely isotropic poroelastic wave equation including the Biot and the squirt mechanisms, Theory and application. Geophysics , 1997, 62(1): 309-318. DOI:10.1190/1.1444132 |
| [7] | Yang D H, Zhang Z J. Poroelastic wave equation including the Biot/squirt mechanism and the solid/fluid coupling anisotropy. Wave Motion , 2002, 35(3): 223-245. DOI:10.1016/S0165-2125(01)00106-8 |
| [8] | Parra J O. Poroelastic model to relate seismic wave attenuation and dispersion to permeability anisotropy. Geophysics , 2000, 65(1): 202-210. DOI:10.1190/1.1444711 |
| [9] | 杨宽德, 杨顶辉, 王书强. 基于Biot-Squirt方程的波场模拟. 地球物理学报 , 2002, 45(6): 853–861. Yang K D, Yang D H, Wang S Q. Wavefield simulation based on the Biot/Squirt equation. Chinese J. Geophys (in Chinese) , 2002, 45(6): 853-861. |
| [10] | 杨宽德, 宋国杰, 李静爽. Biot流动和喷射流动耦合作用下波传播的FCT紧致差分模拟. 地球物理学报 , 2011, 54(5): 1348–1357. Yang K D, Song G J, Li J S. FCT compact difference simulation of wave propagation based on the Biot and the squirt-flow coupling interaction. Chinese J. Geophys (in Chinese) , 2011, 54(5): 1348-1357. |
| [11] | 聂建新, 杨顶辉, 杨慧珠. 基于非饱和多孔隙介质BISQ模型的储层参数反演. 地球物理学报 , 2004, 47(6): 1101–1105. Nie J X, Yang D H, Yang H Z. Inversion of reservoir parameters based on the BISQ model in partially saturated porous media. Chinese J. Geophys (in Chinese) , 2004, 47(6): 1101-1105. |
| [12] | 聂建新, 杨顶辉, 巴晶. 含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究. 地球物理学报 , 2010, 53(2): 385–392. Nie J X, Yang D H, Ba J. Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay. Chinese J. Geophys (in Chinese) , 2010, 53(2): 385-392. |
| [13] | 李红星, 刘财, 陶春辉. 基于横向各向同性BISQ模型的弹性波高阶交错网格有限差分数值模拟. 石油地球物理勘探 , 2007, 42(6): 686–693. Li H X, Liu C, Tao C H. Elastic wave high-order staggering grid finite-difference numerical simulation based on transversely isotropic BISQ model. Oil Geophysical Prospecting (in Chinese) , 2007, 42(6): 686-693. |
| [14] | Gurevich B, Lopatnikov S L. Velocity and attenuation of elastic waves in finely layered porous rocks. Geophys. J. Int. , 1995, 121(3): 933-947. DOI:10.1111/gji.1995.121.issue-3 |
| [15] | Diallo M S, Appel E. Acoustic wave propagation in saturated porous media: reformulation of the Biot/Squirt flow theory. J. Appl. Geophys. , 2000, 44(4): 313-325. DOI:10.1016/S0926-9851(00)00009-4 |
| [16] | Diallo M S, Prasad M, Appel E. Comparison between experimental results and theoretical predictions of P-wave velocity and attenuation at ultrasonic frequency. Wave Motion , 2003, 37(1): 1-16. DOI:10.1016/S0165-2125(02)00018-5 |
| [17] | Crampin S. A review of wave motion in anisotrpic and cracked elastic-media. Wave Motion , 1981, 3(4): 343-391. DOI:10.1016/0165-2125(81)90026-3 |
| [18] | Crampin S. Anisotropy in exploration seismics. First Break , 1984, 2(3): 19-21. |
| [19] | 张中杰, 滕吉文, 贺振华. EDA介质中地震波速度、衰减与品质因子方位异性研究. 中国科学(E辑) , 1999, 29(6): 569–574. Zhang Z J, Teng J W, He Z H. Azimuthal anisotropy of seismic velocity, attenuation and Q value in viscous EDA media. Science in China (Series E) (in Chinese) , 1999, 29(6): 569-574. |
| [20] | 张中杰. 多分量地震资料的各向异性处理与解释方法. 哈尔滨: 黑龙江教育出版社, 2002 . Zhang Z J. Multi-Component Seismic Data Processing and Interpretation for Anisotropy (in Chinese). Harbin: Heilongjiang Education Press, 2002 . |
| [21] | Zhang Z J, Wang G J, Harris J M. Multi-component wavefield simulation in viscous extensively dilatancy anisoropic media. Physics of the Earth and Planetary Interiors , 1999, 114(1-2): 25-38. DOI:10.1016/S0031-9201(99)00043-6 |
| [22] | Hudson J A. Wave speeds and attenuation of elastic waves in material containing cracks. Geophys. J. R. Astr. Soc. , 1981, 64(1): 133-150. DOI:10.1111/j.1365-246X.1981.tb02662.x |
| [23] | Thomsen L. Elastic anisotropy due to aligned cracks in porous rock. Geophys. Prosp. , 1995, 43(6): 805-829. DOI:10.1111/gpr.1995.43.issue-6 |
| [24] | Schoenberg M, Sayers C M. Seismic anisotropy of fractured rock. Geophysics , 1995, 60(1): 204-211. DOI:10.1190/1.1443748 |
| [25] | 杜启振, 孔丽云, 韩世春. 裂缝诱导各向异性双孔隙介质波场传播特征. 地球物理学报 , 2009, 52(4): 1049–1058. Du Q Z, Kong L Y, Han S C. Wavefield propagation characteristics in the fracture-induced anisotropic double-porosity medium. Chinese J. Geophys (in Chinese) , 2009, 52(4): 1049-1058. |
| [26] | Gurevich B. Elastic properties of saturated porous rocks with aligned fractures. J. Appl. Geophys. , 2003, 54(3-4): 203-218. DOI:10.1016/j.jappgeo.2002.11.002 |
| [27] | 轩义华, 何樵登, 孟庆生, 等. 基于BISQ机制的双相EDA介质的波场分析. 石油地球物理勘探 , 2006, 41(5): 550–556. Xuan Y H, He Q D, Meng Q S, et al. Wavefield analysis of biphase EDA medium based on BISQ mechanism. Oil Geophysical Prospecting (in Chinese) , 2006, 41(5): 550-556. |
| [28] | 张显文, 王德利, 王者江, 等. 基于BISQ机制三维双相正交裂隙各向异性介质衰减及频散方位特性研究. 地球物理学报 , 2010, 53(10): 2452–2459. Zhang X W, Wang D L, Wang Z J, et al. The study on azimuth characteristics of attenuation and dispersion in 3D two-phase orthotropic crack medium based on BISQ mechanism. Chinese J. Geophys (in Chinese) , 2010, 53(10): 2452-2459. |
| [29] | Du Q Z, Wang X M, Ba J, et al. An equivalent medium model for wave simulation in fractured porous rocks. Geophysical Prospecting , 2012, 60(5): 940-956. DOI:10.1111/gpr.2012.60.issue-5 |
| [30] | 孔丽云, 王一博, 杨慧珠. 裂缝诱导HTI双孔隙介质中的裂缝参数分析. 地球物理学报 , 2012, 55(1): 189–196. Kong L Y, Wang Y B, Yang H Z. Fracture parameters analyses in fracture-induced HTI double-porosity medium. Chinese J. Geophys (in Chinese) , 2012, 55(1): 189-196. |
| [31] | 郭智奇, 刘财, 杨宝俊, 等. 粘弹各向异性介质中地震波场模拟与特征. 地球物理学进展 , 2007, 22(3): 804–810. Guo Z Q, Liu C, Yang B J, et al. Seismic wave fields modeling and feature in viscoelastic anisotropic media. Progress in Geophysics (in Chinese) , 2007, 22(3): 804-810. |
| [32] | 刘财, 郭智奇, 杨宝俊, 等. 黏弹各向异性介质中波的反射与透射问题分析. 地球物理学报 , 2007, 50(4): 1216–1224. Liu C, Guo Z Q, Yang B J, et al. Analysis of reflection and transmission problems of waves in viscoelastic anisotropic media. Chinese J. Geophys (in Chinese) , 2007, 50(4): 1216-1224. |
| [33] | 刘洋, 李承楚. 双相各向异性介质中弹性波传播伪谱法数值模拟研究. 地震学报 , 2000, 22(2): 132–138. Liu Y, Liu C C. The study on elastic wave propagation numerical modeling with the pseudo-spectral method in two-phase anisotropic media. Acta Seismologica Sinica (in Chinese) , 2000, 22(2): 132-138. |
| [34] | 李红星, 陶春辉. 双相各向异性随机介质伪谱法地震波场特征分析. 物理学报 , 2009, 58(4): 2836–2842. Liu H X, Tao C H. Features analysis of seismic wave field in two-phase anisotropic random medium with the pseudo-spectral method. Acta Physica Sinica (in Chinese) , 2009, 58(4): 2836-2842. |
| [35] | Liu J, Ba J, Ma J W, et al. An analysis of seismic attenuation in random porous media. Science China Ser G-Physic Mechanics Astronomy , 2010, 53(4): 628-637. DOI:10.1007/s11433-010-0109-y |
| [36] | 张文生, 何樵登. 二维横向各向同性介质的伪谱法正演模拟. 石油地球物理勘探 , 1998, 33(3): 310–319. Zhang W S, He Q D. Pseudo-spectral forward modeling in 2-D transversally isotropic medium. Oil Geophysical Prospecting (in Chinese) , 1998, 33(3): 310-319. |
| [37] | Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equation. Geophysics , 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [38] | Zhu X, McMechan G A. Numerical simulation of seismic responses of poroelastic reservoirs using Biot theory. Geophysics , 1991, 56(3): 328-339. DOI:10.1190/1.1443047 |
| [39] | Biot M A. General theory of three-dimensional consolidation. J. Appl. Phys. , 1941, 12(2): 155-164. DOI:10.1063/1.1712886 |
 2013, Vol. 56
2013, Vol. 56


