全波形反演(Full Waveform Inversion,简写为FWI)一词最早由Pan等人(1986)提出,但该方法的思想在20世纪80年代初就已提出,核心框架是建立在Tarantola的数据拟合基础之上,而传统FWI寻优过程中的梯度一般通过伴随方法来确定[1-4].在近10年期间,FWI得到了迅猛发展,并应用到全球局部和区域地壳和上地幔结构研究[5]、油气勘探中为偏移成像提供更精确的背景速度[6]、储层定量研究[7-8]以及岩性流体识别和裂隙特征研究[9]等领域,为地球动力学研究和油气勘探提供了具有更高分辨率的地下图像.
FWI是通过评价模拟数据与观测数据之间的“匹配”程度来确定地下参数变化的,尽管它在理论上具有更高的成像精度,但到目前为止FWI使用还不是很广.在地震学领域FWI还没有替代传统的走时层析和有限频层析技术,在勘探地震学领域FWI也没有替代传统的地震数据处理和解释流程.除了诸多实际问题(如信噪比问题、低频缺乏问题、震源子波问题、地震波在复杂介质中传播的描述问题,等等)外,强烈的非线性问题是目前FWI在理论方法上遇到的最大难题.
FWI强烈的非线性问题源自于地震波传播的复杂性,该复杂性也决定了从地震观测数据反演地下介质的物性参数是一个复杂的过程.目前常规的地震勘探是将这个复杂问题进行分解来解决的.通常通过NMO速度分析、偏移速度分析、走时层析成像等方法解决宏观速度模型(即速度变化的低波数成分),利用地震成像(叠加、偏移等)解决介质结构(即速度变化的高波数成分),然后在相对保幅处理的基础上,通过AVO反演、波阻抗反演以及地震波属性分析等途径反演介质的物性参数.这种传统的地震成像与反演方式的一个优点是可以进行人工干预,当然这需要花费更多的人力和时间.
面对地震反演的强烈非线性难题,FWI也不应该是一个“黑匣子”,理应通过分步骤、分尺度逐步实现,这就是FWI的反演策略问题.
FWI反演策略的实质是如何分步骤、分尺度解决一个复杂的反演问题,核心是在每一步反演中如何利用不同地震数据子集构造一个非线性程度更低的目标函数,提高每步反演的收敛性,同时还要逐步提高FWI反演的分辨率.
造成FWI强烈非线性的因素很多,单一反演策略往往显得捉襟见肘.除了诸如资料信噪比、观测孔径、地震子波等一些实际问题外,引起FWI强烈非线性问题的根本原因在于地震数据和地下参数之间关系的复杂性,体现在技术上就是目标函数的强烈非线性问题.FWI中的诸多技术问题都与所选择的目标函数有关.目标函数的非线性越强,对初始模型的要求越高,也要求使用更加精细的反演策略.因此,目标函数在FWI中起到至关重要的作用,它体现了地震数据随介质物性参数的变化关系(称为灵敏度核函数),这是地震学中的核心问题之一.不同目标函数下地震信息扰动与地下物性参数扰动之间的关系,这又是地震反演中的核心问题.对这个问题认识的程度,直接决定了目标函数选择是否恰当、反演方法的选择是否合理、初始模型精度是否满足要求、以及应该选择什么样的反演策略.因此,详细研究地震数据不同信息随介质物性参数变化之间的关系(这种关系体现在目标函数的性态上),是更好地实现分步骤、分尺度全波形反演的基础.尽管全面了解目标函数随地下任一点参数的变化关系并不现实,但可以从某个角度观察目标函数的性态,具体可以从目标函数随地下参数不同尺度变化性态的角度进行研究.
在这个问题上,Claerbout[10]发现地面反射地震数据不能提供地下超短波长介质信息,Snieder等[11]讨论了分解速度变化的长短波长分量的可能性,刘玉柱和董良国[12]通过数值试验讨论了反射地震波形的反演能力,Hicks和Pratt[13]在对地震数据随物性参数变化关系进行分析的基础上,建议反演时“先短后长”,而Wang和Rao[9]以及许多学者都建议先用走时反演速度变化的长波长分量,再用波形反演短波长分量.
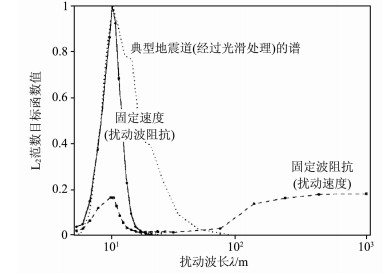
在这方面,Jannane等[14]做出了突出性贡献.他们以反射地震数据的L2范数作为目标函数,通过地震波传播正演模拟,得到了目标函数随速度和波阻抗摄动尺度之间的变化关系(见图 1).结果发现,地震反射波走时对长波长敏感,而振幅对短波长(一个波长附近)敏感,难以利用地震数据来反演中等摄动尺度(一般几个波长)的速度信息(也可见Sears等[15]).随后该文献被大量引用,对各种反演方法和策略的提出起到了至关重要的作用.为此2010年的SEG年会上还专门就该文章举办一个专题讨论会,许多学者围绕该问题进行了评述[16].
|
图 1 Jannane等(1989)[14]得到的目标函数随速度和波阻抗摄动尺度之间的变化关系曲线 Fig. 1 Dependence of the misfit functions on the perturbation scale of velocity and impedance[14] |
但由于当时计算能力不足等原因,Jannane等(1989)[14]当时的研究还存在以下缺陷:
(1) 只讨论了L2范数下的目标函数(而目前FWI用到多种形式的目标函数);
(2) 物性参数只讨论了纵波速度、密度和波阻抗,而目前FWI要反演的参数还有介质的吸收系数以及各向异性参数等;
(3) 只讨论了物性参数在纵向上的不同空间波数的变化,而目前FWI要求反演三维空间的物性参数变化;
(4) 只是对整个地震记录计算单一的目标函数值,没有研究地震记录中特定数据子集的目标函数变化,影响了FWI中反演策略的详细制定.而选用不同数据子集进行分步骤、多尺度反演是解决地震反演强烈非线性问题的有效途径.通过特定数据子集目标函数性态的分析,可以为地震反演的不同阶段选择合理的数据子集和具体的反演策略提供理论指导.这些数据子集包括:特定震相(如初至波、面波、反射波、折射波等)、特定信息(如走时、振幅、相位、频率成分等)、特定“孔径”(如偏移距段、时间段等),等等;
(5) Jannane等当时的试验最大偏移距只有1760 m(而目前的一些陆上或海上地震观测的最大炮检距已经超过10 km),由于不同偏移距地震数据对参数变化的反应是有差别的,因此用如此小的最大偏移距地震数据得到的结论难免存在一定的片面性.
上述缺陷致使Jannane等得出的结论对实际FWI的指导可能具有一定的局限性,影响了有针对性的FWI反演策略的制定,对构造更好的目标函数也是不利的.因此,无论是从对地震波传播的深入认识方面,还是从提升FWI理论思路、优化反演策略、构造更有效目标函数以及选择更合理的参数化方式等方面,都有必要针对这个问题展开深入细致的研究.另外,这个问题的研究对其它的地震波反演理论和方法研究(如走时反演、AVO反演等)以及实际应用也有重要的指导意义.
本文从变密度声波方程出发,以高精度地震波传播数值模拟为手段,系统研究地震数据不同信息(如不同偏移距的地震数据、地震道的包络等)随介质不同物性参数(速度、密度、波阻抗、体积模量)的不同空间摄动尺度之间的关系,并分析这些变化关系在不同目标函数下的具体变化性态,以弥补Jannane等试验的不足,以便为全波形反演中目标函数的选择、数据协方差矩阵的构造、反演策略的制定提供理论指导.
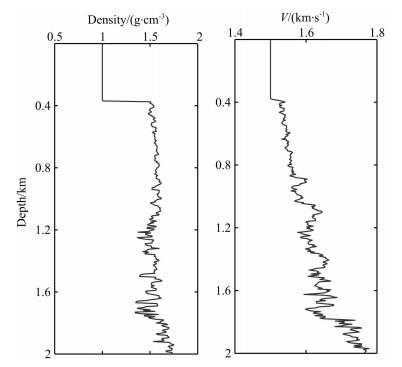
2 试验方案 2.1 参考模型选择海上一口井的测井数据作为参考模型,模型深度2075 m,密度ρ0(z)和速度V0(z)随深度的变化曲线见图 2.
|
图 2 参考模型的密度和速度随深度变化曲线 Fig. 2 Density and velocity curve with depth of the reference model |
为了分析物性参数不同摄动尺度在不同目标函数上的表现,对不同物性参数作不同尺度λ的正弦摄动.例如,密度沿深度的摄动方式为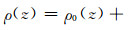
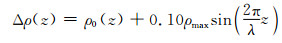
|
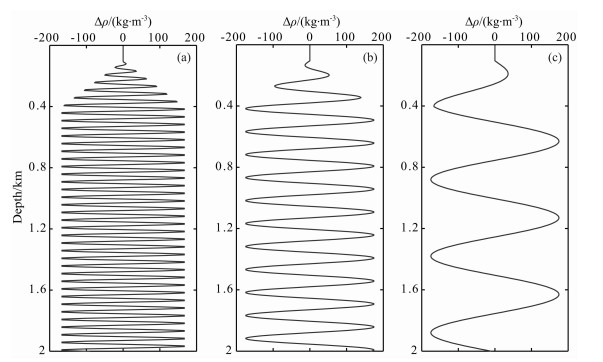
图 3 三个尺度的密度摄动Δρ(z)曲线 (a)λ=50 m;(b)λ=150 m;(c)λ=500 m. Fig. 3 Typical density perturbations in three scales |
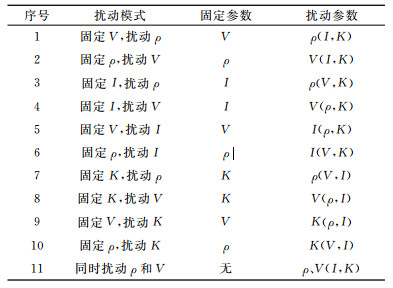
为了分析不同参数摄动在目标函数上的不同表现,按表 1中的11种参数摄动方式进行不同摄动尺度的模型试验.这里不仅考虑了速度V和密度ρ的扰动,还考虑到了波阻抗I和体积模量K的扰动;不仅考虑了单参数扰动,还考虑了双参数的同时扰动.
|
|
表 1 模型参数摄动方式 Table 1 Perturbation schemes of model parameters |
对不同参数摄动后的模型,这里不再过多展示.需要说明的是,在固定一个物性参数(如速度)而摄动另一个物性参数(如密度)时,另外两个物性参数(如波阻抗和体积模量)也会随之摄动.
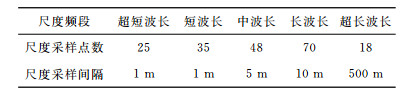
对于扰动尺度,定义不同尺度的范围为:超短波长0 m≤λ≤25 m、短波长25 m≤λ≤60 m、中波长60 m≤λ≤300 m、长波长300 m≤λ≤1000 m和超长波长λ≥1000 m[14].为了比较完整地再现整个摄动尺度范围内目标函数随尺度变化的性态,在小尺度采样较密,在大尺度采样较稀,共选取了196个尺度样点,具体尺度采样情况见表 2.
|
|
表 2 摄动尺度采样分布情况 Table 2 Sampling distribution of the parameter perturbation scale |
在地震全波形反演中,可以根据反演的需要选择不同的衡量观测数据和模拟数据之间匹配程度的目标函数.这里,只分析三种目标函数:
(1) 不同观测孔径地震数据的基于L1模和L2模的目标函数;
(2) 基于地震道包络构造的L1模和L2模的目标函数,具体包络可以通过Hilbert变换计算得到;
(3) 基于地震数据的Laplace变换构造的L1模和L2模的目标函数.
2.4 地震数据模拟方法采用高阶差分方法进行地震波正演模拟[17],最大偏移距为9600 m,道间距10 m,每炮961道,采样间隔1 ms,模拟记录时间7 s,地震子波主频为30 Hz(特别指定除外).
3 目标函数性态分析与全波形反演策略利用上述试验方案,分析基于全部地震数据及其子集(如不同偏移距地震数据、地震道包络、地震道Laplace变换后信号)的两种范数(L1和L2)的目标函数随不同物性参数不同摄动尺度的变化特征.
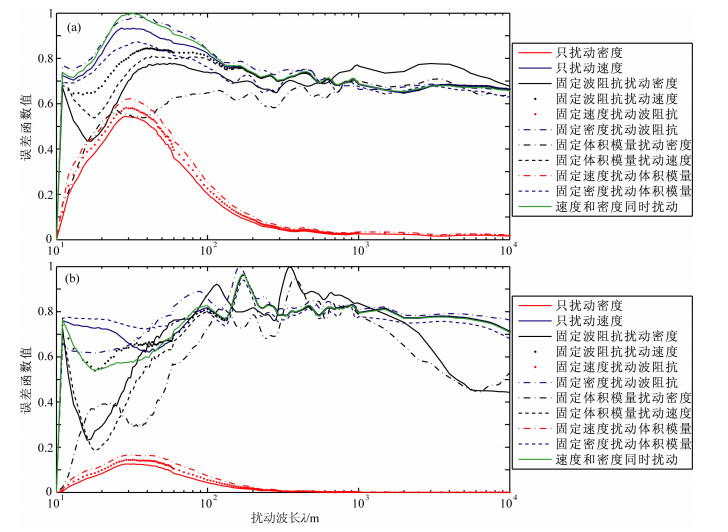
3.1 所有偏移距数据构造的目标函数随不同参数摄动尺度的变化关系图 4是利用所有偏移距(0~9600 m)地震数据计算的L1和L2范数目标函数随不同物性参数的不同摄动尺度的敏感曲线.两种目标函数变化趋势宏观上基本一致(图 4a和图 4b),因此,后面主要分析L2范数.差别在于L1范数适合于误差呈现Laplace分布的数据,反演更稳定,但灵敏度低;而L2范数适合于误差呈现Gauss分布的数据,反演时对较大的异常值更敏感[18].
|
图 4 所有偏移距地震数据计算的目标函数随不同物性参数不同摄动尺度的敏感曲线 (a)L1范数;(b)L2范数. Fig. 4 Dependence of the misfit functions on the perturbation scale of different media parameters according to seismic data in offset between 0 to 9600 m (a) L1 norm; (b) L2 norm. |
图 4中的11条扰动曲线大致可以分为两大类:第一大类是只扰动密度而保持速度不变(红线1、5和9),其余的只要速度扰动的全部归为第二大类.
速度不变只扰动密度的第一大类的目标函数随不同物性参数不同摄动尺度的变化相对比较简单.这一类只在较小摄动尺度(摄动波长小于200 m)时才呈现出较好的二次型形态,说明目标函数对密度的较小尺度摄动具有很强的敏感度.在密度摄动波长较大(波长大于200 m)时目标函数基本接近于零.根本原因在于密度的摄动不改变地震波的走时,但小尺度的密度摄动会引起反射波振幅的变化,进而影响目标函数值.因为反射波振幅的变化与密度的摄动具有相对较好的线性关系,从而使目标函数随密度小尺度摄动呈现为较好的二次型;但中长尺度的密度摄动不但不能改变地震波走时,对反射波的振幅也基本没有影响.因此,利用反射波无法反演较大尺度的密度摄动成分,这就是反演中模型的“零空间”问题.
而对第二大类目标函数曲线,除了L1范数目标函数随速度的小尺度摄动性态稍好外,在中长尺度速度摄动的L1范数目标函数以及在速度的所有摄动尺度上的L2范数目标函数的性态均较差(尤其是L2范数),目标函数值相对较大,但随速度摄动尺度而剧烈变化(尤其是中长尺度).因此,反演速度的各种摄动尺度成分时,如果一次性同时利用小偏移距和大偏移距的地震数据(0~9600 m)信息进行全波形反演并不是很有利.而Jannane等(1989)[14]的试验结果却是,L2范数目标函数随速度的小尺度摄动曲线表现为较好的二次型,进而他们得出了可以较好地反演速度的小尺度摄动成分的结论.从本文后面的分析结果可以看出,他们得出这样的结论的原因在于只是用了小偏移距(小于1760 m)的地震数据.
值得说明的是,对含有速度摄动的第二大类,在中波长范围虽然目标函数曲线变化比较复杂,但目标函数值还是比较高的,说明目标函数对速度的中波长摄动成分还是有一定的敏感度的,只是非线性程度比较高而已.这与Jannane等(1989)认为反射地震数据无法分辨速度摄动的中波长成分的结论是不同的.本文认为Jannane的结论是由于只用了小偏移距(小于1760 m)的反射地震数据的缘故.
图 4是0~9600 m偏移距的所有地震数据的变化在目标函数上的综合反映.实际上,不同物性参数的不同尺度摄动,在不同孔径接收的反射波上的反映是不同的.分析不同参数变化后不同偏移距地震数据的不同变化,对制定合理的反演策略非常必要.
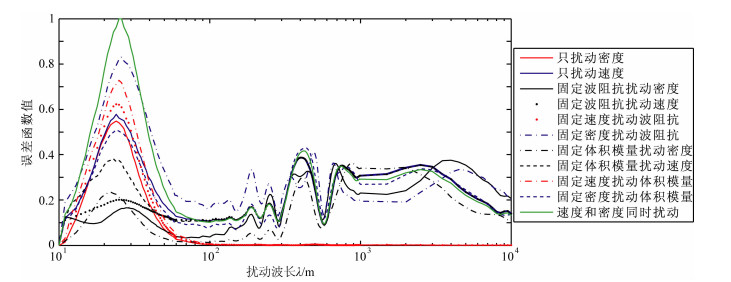
3.2 不同偏移距数据构造的目标函数随不同参数摄动尺度的变化关系图 5是利用小于600 m偏移距的地震数据计算的L2范数目标函数随不同物性参数的不同摄动尺度的敏感曲线.可以看出,图 5与图 4b差异非常明显,说明物性参数的不同尺度摄动在不同偏移距的反射地震数据上反映有很大差别,因此,在全波形反演中考虑偏移距的因素是非常必要的.图 5中的11条扰动曲线大致可以分为4类:
|
图 5 小于600 m偏移距地震数据的目标函数随不同物性参数不同摄动尺度的敏感曲线 Fig. 5 Dependence of the misfit functions (L2 norm) on the perturbation scale of different media parameters according to seismic data in offset between 0 to 600 m |
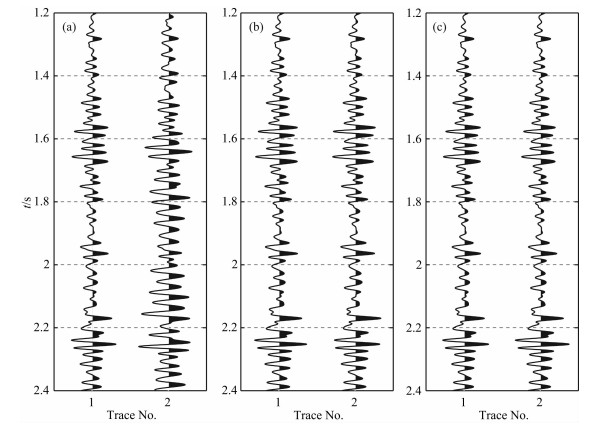
第一类:扰动密度而保持速度不变(红实线1).只要速度不变,扰动波阻抗或扰动体积模量的情况与此类似(红线5和9).这三条曲线不完全重合,是由于扰动不同参数致使密度的扰动量不同所致.这一类曲线,在密度的较小尺度摄动(摄动波长小于60 m)时呈现出很好的二次型,说明目标函数对密度的较小尺度摄动具有很强的敏感度.在中长波长(波长大于60 m)的密度摄动范围目标函数基本为零,说明中长波长的密度摄动对反射波基本没有影响.因此,利用偏移距小于600 m的反射地震数据无法反演中长尺度的密度摄动成分.原因在于密度的摄动不改变地震波的走时,但小尺度的密度摄动会引起反射波振幅的变化(图 6a),进而影响目标函数.而中长尺度的密度摄动前后的波形基本没有变化,不但不能改变地震波走时,对反射波的振幅也没有影响(图 6b,图 6c).
|
图 6 偏移距500 m时密度摄动前(左)、后(右)的地震波形 (a)小尺度(λ=30 m);(b)中尺度(λ=100 m);(c)大尺度(λ=1000 m). Fig. 6 Comparisons of the seismic trace of 500 m offset generated from the reference model and the perturbed models when the density is disturbed (a) Short-wavelength perturbations (λ=30 m); (b) Middle-wavelength perturbations (λ=100 m); (c) Long-wavelength perturbations (λ=1000 m). |
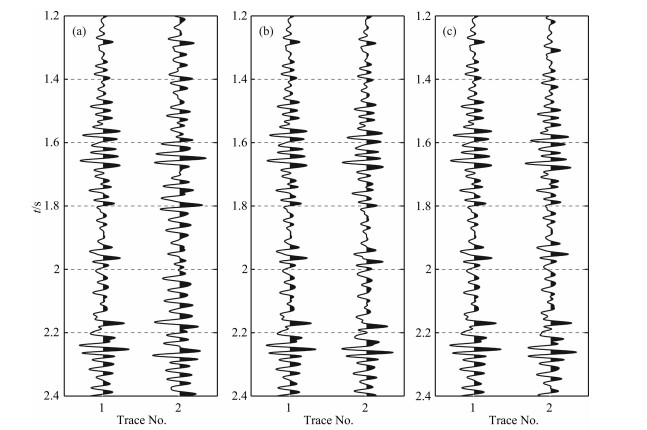
第二类:扰动速度而密度保持不变(蓝实线2).只要密度不变,扰动波阻抗或扰动体积模量的情况与此类似(见蓝线6和10),只是由于扰动不同参数致使速度的扰动量不同而造成三条曲线有所差别,但变化趋势基本一致.在速度的较小尺度摄动(摄动波长小于60 m)时目标函数的变化与第一类相似,呈现出较好的二次型形态,目标函数对速度的小尺度摄动具有很强的敏感度,根源在于小尺度的速度摄动主要引起反射波振幅的变化(图 7a).因此,在初始速度模型含有真实地下模型的中长尺度变化成分时,利用小偏移距反射地震数据通过FWI可以较好地反演出速度摄动的高波数成分,这一点比全偏移距地震数据有很大的改善(见图 4b),这也进一步印证了前面所说的进行分偏移距FWI的必要性.与第一类差别比较大的是,在速度摄动的中长波长范围,即使是小偏移距地震反射数据的目标函数变化也比较复杂.具体表现为:在60~200 m的中波长段,摄动前后反射波的振幅变化不大(图 7b),目标函数值随速度摄动尺度的变化并不大,说明利用小偏移距反射数据反演这些速度摄动的中波长成分比较困难(这与Jannane等人的结论基本一致,因为都是只利用了小偏移距的地震数据),但在该波数段目标函数并不为零,说明在速度的摄动前后反射波还是不同的,主要是反射波走时的微小变化所引起.在速度较大尺度摄动范围(λ≥200 m),目标函数值相对较大,且随速度摄动尺度的变化而快速变化,根本原因在于中长尺度的速度摄动引起了反射波走时的变化(图 7c),从而引起的“周波跳跃”造成了目标函数的剧烈变化,给利用小偏移距反射数据反演速度摄动的中长波长成分带来了难度.因此,地震波形反演要求初始宏观速度模型中含有速度的中长波长成分,以避免产生“周波跳跃”现象,即要求初始模型和真实模型产生的地震反射波的走时差要小于半个周期[19-20].
|
图 7 偏移距500 m时速度摄动前(左)、后(右)的地震波形 (a)小尺度(λ=30 m);(b)中尺度(λ=100 m);(c)大尺度(λ=1000 m). Fig. 7 Comparisons of the seismic trace of 500 m offset generated from thereference model and the perturbed models when the velocity is disturbed (a) Short-wavelength perturbations (λ=30 m); (b) Middle-wavelength perturbations (λ=100 m); (c) Long-wavelength perturbations (λ=1000 m). |
第三类:速度和密度同时同步扰动(绿线11).这时曲线形态与第二类基本一致,主要区别在于:小尺度的速度和密度同步摄动实际上就是波阻抗的小尺度的摄动,主要引起反射波振幅的变化(由于是速度和密度的同步摄动,致使反射波振幅变化比单一小尺度的速度和密度摄动引起的反射波振幅变化更加剧烈,目标函数随速度和密度同步小尺度摄动呈现出更好的二次型.可见,利用小偏移距反射波的波形可以较好地反演小尺度的波阻抗摄动成分,但要同时反演速度和密度的小尺度摄动可能比较困难,因为小偏移距反射波振幅的变化是小尺度速度摄动和小尺度密度摄动二者共同作用的结果,两者的作用是耦合在一起的).从第一类曲线的分析可知,由于密度的中长尺度摄动对反射波基本没有影响,因此,在速度和密度同时同步扰动的中长尺度摄动区域,目标函数的变化主要是速度的中长尺度摄动引起的.这时目标函数的变化趋势当然与第二类曲线基本一致,“周波跳跃”现象不可避免.这时,利用小偏移距反射数据无法反演密度摄动的中长波长成分,而且反演速度摄动的中长波长成分也比较困难.
第四类:保持波阻抗不变,扰动速度(或密度)(黑线3和4).由于I=ρV,这时为保持波阻抗不变,密度(或速度)必然以相反的方向进行摄动.这一类的目标函数变化趋势在中长波长频段与只摄动速度时基本一致,说明这时主要是速度的中长尺度摄动在起作用,而密度的中长尺度摄动对近偏移距地震反射波基本没有影响.由第二类曲线的分析可知,这时要反演速度或密度的中长尺度摄动成分还是有难度的.在短波长段尽管表现为二次型,但与只摄动速度相比目标函数值明显偏低,这主要是由于速度和密度沿相反的方向摄动所致.
而保持体积模量不变而扰动速度(或密度)(黑线7和8)也可划归这一类,与保持波阻抗不变而扰动速度(或密度)的目标函数曲线主要差别是:在速度或密度的较小尺度摄动(摄动波长小于60 m)时目标函数具有更好的二次型形态,主要原因是参数小尺度摄动后反射波振幅发生了变化.
当然,为简单方便起见,如果只利用近偏移距的反射波形进行反演,我们也可以将后三类归为一大类,即共分为两大类:第一大类是只扰动密度而保持速度不变(红线1、5和9),其余的只要速度扰动的全部归为第二大类.速度不变的第一大类的目标函数相对简单,而第二大类由于速度的摄动而致使目标函数变得比较复杂.
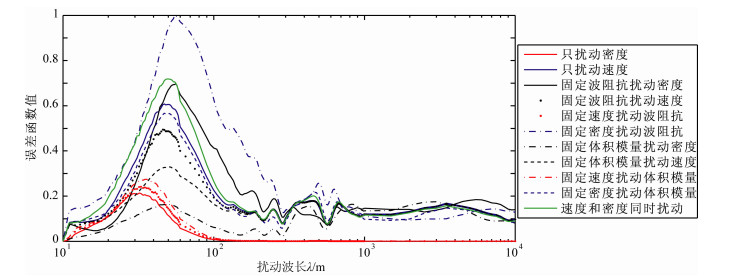
图 8、图 9和图 10分别是利用偏移距600~1200 m、1200~1800 m和1800~2400 m地震反射数据计算的L2范数目标函数随不同物性参数的不同摄动尺度的变化曲线.
|
图 8 偏移距600~1200 m地震数据的目标函数随不同物性参数不同摄动尺度的敏感曲线 Fig. 8 Dependence of the misfit functions (L2 norm) on the perturbation scale of different media parameters according to seismic data in offset between 600 m to 1200 m |
|
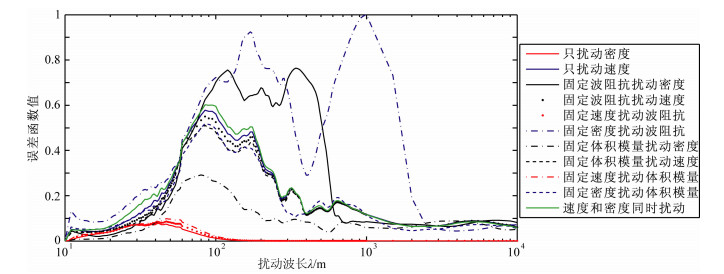
图 9 偏移距1200~1800 m地震数据的目标函数随不同物性参数不同摄动尺度的敏感曲线 Fig. 9 Dependence of the misfit functions (L2 norm) on the perturbation scale of different media parameters according to seismic data in offset between 1200 m to 1800 m |
|
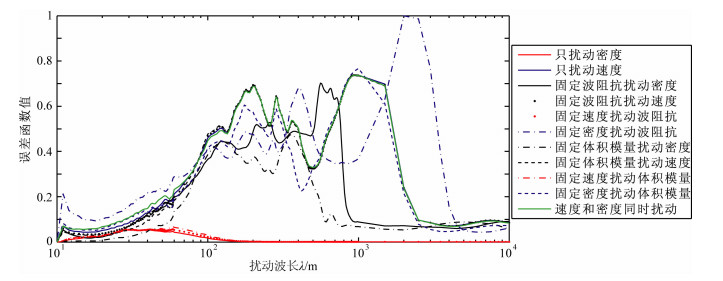
图 10 偏移距1800~2400 m地震数据的目标函数随不同物性参数不同摄动尺度的敏感曲线 Fig. 10 Dependence of the misfit functions (L2 norm) on the perturbation scale of different media parameters according to seismic data in offset between 1800 m to 2400 m |
可以看出,利用不同偏移距段地震反射数据计算的目标函数曲线的总体形态没有本质的变化,仍然可以分为前面所述的两大类.第一大类均是只对密度的较小尺度摄动具有很强的敏感度,而在中长波长的密度摄动范围目标函数值基本为零,说明中长波长的密度摄动对大偏移距的反射波也没有影响(值得说明的是,AVO反演中利用大偏移距反射波更利于反演密度参数,那是因为AVO反演的是界面两侧的密度差,即密度摄动的高频成分,而密度摄动的高频成分在不同偏移距反射波上都有很好的反映,见图 4-5、图 8-10).对第一大类目标函数曲线随不同偏移距的主要变化是:随偏移距的增大,目标函数的峰值对应的密度摄动波长有稍许提高.说明随偏移距增大,利用反射波能反演的密度摄动的波数成分有稍许展宽;也就是说,大偏移距反射波对密度的反演能力有稍许提高.从另外的第二大类的8条目标函数曲线可以发现,随偏移距的增大,反射波形对速度摄动的短波长成分的反演能力逐渐降低(这也是造成图 4的全偏移距地震数据的目标函数在速度小尺度摄动时性态不好的原因,也是Jannane得出的目标函数在速度的小尺度摄动时表现为二次型这个结论有失偏颇的根源,显然是因为他们没有注意到速度的小尺度摄动在不同偏移距的反射地震数据上有不同的反映这个事实),但对速度摄动的中长波长成分的反演能力有明显提高.当然,偏移距增大的同时“周波跳跃”的现象也更加明显,非线性问题更加突出.
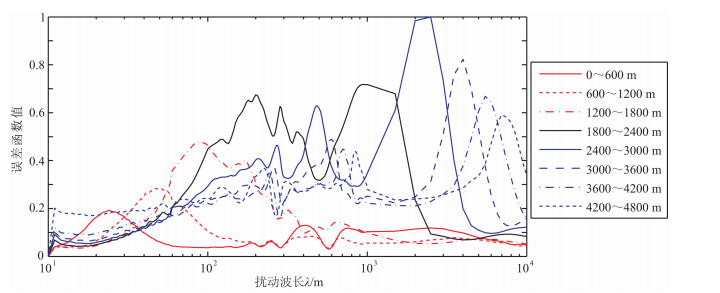
上述结论也可以从0~4800 m不同偏移距段的目标函数随速度不同摄动尺度的关系可以看出(图 11).小偏移距反射波数据有利于反演速度摄动的短波长信息,而随偏移距的增大,反射波对速度摄动的超短以及短波长摄动成分(0~60 m)的反演能力逐渐降低,但对速度摄动的中波长(60~300 m)以及长波长(300~1000 m)摄动成分的反演能力有所增强(具体表现为:随偏移距的增大,二次型峰值向中长波长移动).而大偏移距反射波数据中蕴含着丰富的中长波长信息,有利于反演背景速度(尽管非线性程度较高),这一点与Jannane的结论不同.
|
图 11 偏移距0~4800 m地震数据的目标函数随速度摄动尺度的敏感曲线 Fig. 11 Dependence of the misfit functions (L2 norm) on the velocity perturbation scale according to seismic data in offset between 0 to 4800 m |
因此,在地震全波形反演中,可以采用分偏移距的反演策略,即用大偏移距数据反演速度变化的长波长成分,然后利用小偏移距地震数据反演速度变化的短波长成分.
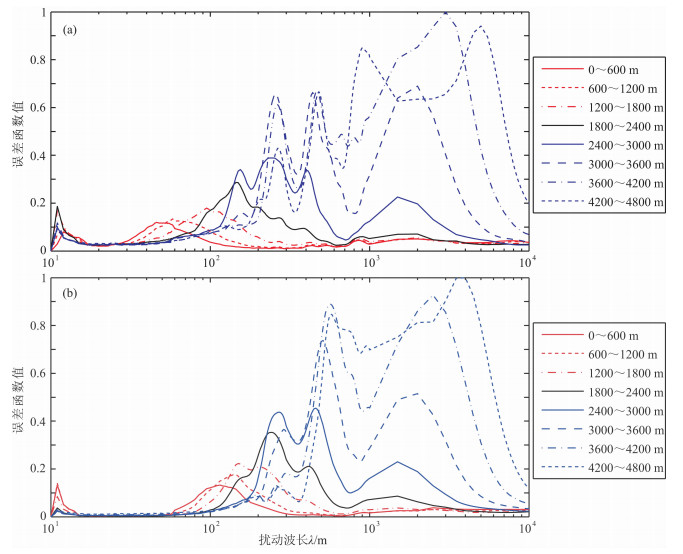
3.3 不同主频子波数据构造的目标函数随速度摄动尺度的变化关系图 12a、12b分别是子波主频为15 Hz和7 Hz时的L2范数目标函数随速度摄动尺度的变化曲线.与子波主频30 Hz(图 11)对比可以发现,随着震源子波主频的降低以及偏移距的增大,目标函数峰值向中长波长移动.因此,增大偏移距以及降低主频,有利于反演速度摄动的中长波长成分.
|
图 12 不同偏移距数据目标函数随速度摄动尺度的敏感曲线 (a)子波主频为15 Hz;(b)子波主频为7 Hz. Fig. 12 Dependence of the misfit functions (L2 norm) on the velocity perturbation scale according to different offset seismic data (a) Main frequency is 15 Hz; (b) Main frequency is 7 Hz. |
从以上分析可以看出,在波形反演时可以先利用低频数据反演速度摄动的低波数成分,并逐步提高数据的频率成分依次反演速度摄动的高波数成分.这种反演策略早在1995年Bunks就已提出[21],还有学者提出了频率域波形反演中的频率选择策略[22-24].这样做确实可以在一定程度上降低FWI的非线性程度.
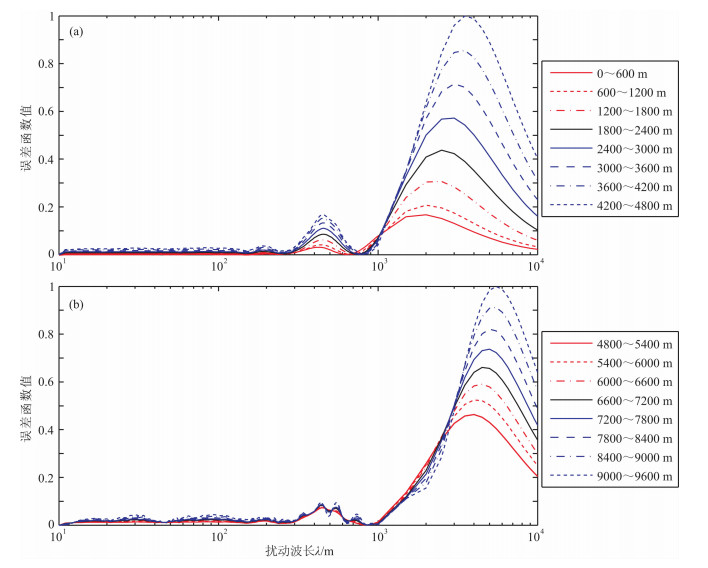
3.4 其它目标函数随速度摄动尺度的变化关系将地震数据进行Laplace变换后,同样可以利用不同偏移距的信息计算L2范数目标函数,其随速度摄动的曲线见图 13(子波主频为30 Hz).可以发现,Laplace变换后信息的目标函数主要反映了速度的大尺度摄动成分,而且非线性程度大幅度降低,反演的稳定性可以得到很大提高.Laplace变换的这种特征为更有效地反演速度变化的长波长成分(宏观速度模型)提供了保证,可以利用Laplace变换的这种特征,为全波形反演提供一个较好的初始模型[25].另外,Laplace变换后的目标函数在速度的小尺度扰动时基本为零,说明速度的小尺度扰动在地震道的Laplace变换信息上基本没有体现,也说明了Laplace变换无法反演速度变化的高频成分.
|
图 13 Laplace变换后不同偏移距数据的L2范数目标函数随速度摄动尺度的敏感曲线 Fig. 13 Dependence of the misfit functions (L2 norm) on the velocity perturbation scale according to the Laplace-transformed seismic data in different offset range |
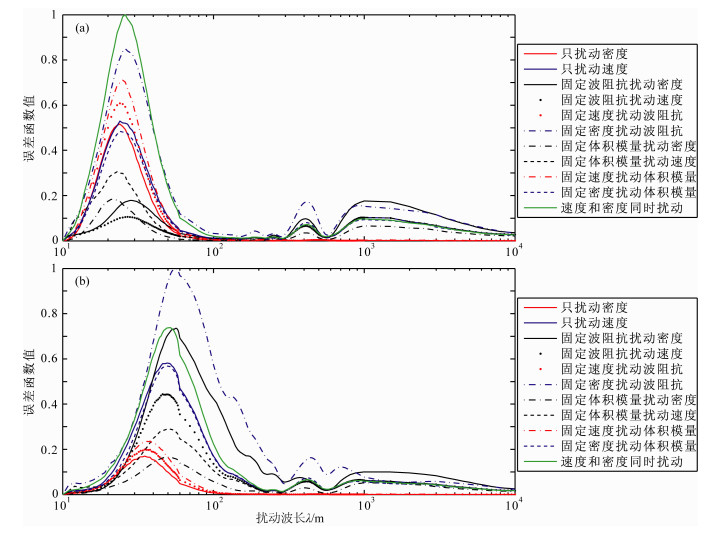
通过Hilbert变换可以计算地震道包络,利用包络信息也可以计算L2范数的目标函数随速度摄动尺度的变化曲线.图 14是分别利用0~600 m、600~1200 m偏移距地震数据的包络计算的L2范数目标函数随速度摄动尺度之间的变化曲线,将其与利用原始地震数据计算的目标函数随速度摄动尺度的变化曲线(图 5和图 8)进行比较可以发现,地震道包络与原始地震道随速度不同摄动成分的变化总体趋势基本一致,但利用地震道包络进行反演的非线性程度有所降低.我们可以利用地震道包络的这个特点,来反演非线性更强的速度变化的中长波长摄动成分,从而为传统的FWI提供一个更好的初始速度模型.
|
图 14 利用地震道包络计算的基于L2范数目标函数随速度摄动尺度的敏感曲线 (a)0~600 m偏移距;(b)600~1200 m偏移距. Fig. 14 Dependence of the misfit functions (L2 norm) on the velocity perturbation scale according to the envelop of the seismic trace (a) The offset range is 0~600 m; (b) The offset range is 600~1200 m. |
FWI对初始模型精度的要求与目标函数的非线性程度是密不可分的,目标函数的非线性程度越高,FWI对初始模型的要求就越高[26].因此,目前的基于梯度类的地震反演中对付强烈非线性问题,最直接的思路是建立一个更好的初始模型.由于长波长速度扰动成分主要体现在反射波走时的变化上,当然也可以利用走时信息,在数据域或成像域通过相关类目标函数的波形反演或偏移速度分析[27-28]、射线走时层析[29]或菲涅耳体走时层析[30-32]进行反演,为下一步的FWI提供具有更高精度的初始速度模型.
4 反演策略模型试验上述某些反演策略的有效性已经得到了试验证明,不再过多赘述.这里主要以前面分析得到的两个反演策略为例,说明目标函数性态分析的意义.这两个反演策略是:(1)分偏移距全波形反演策略;(2)在地震数据缺失低频情况下,通过地震道包络进行FWI反演,从而为传统的FWI提供一个更好的初始速度模型.
4.1 分偏移距全波形反演策略试验通过第3部分的目标函数性态分析可以看出,地下介质参数不同的摄动尺度在不同偏移距反射波上具有不同的体现.小炮检距地震数据更好地反映了地下介质速度的短波长变化,大炮检距地震数据更好地反映了地下速度的长波长变化,因此,可以通过分偏移距的策略分步骤地进行全波形反演.
进行以下两个试验:将前面的测井速度曲线扰动以后(扰动波长分别为800 m、1000 m),将其扩展为1.5维的实际地下模型(dx=dz=20 m),并利用地震模拟形成了480道的叠前地震数据,道距20 m,采用的子波主频为7 Hz.以扰动前的测井速度曲线扩展的1.5维模型作为初始模型,采用不同偏移距的地震数据进行全波形反演,来验证得到的分偏移距波形反演策略的有效性.
选取0~600 m、1200~1800 m和3000~3600 m这三段偏移距的地震数据进行全波形反演试验.从图 11的目标函数随速度摄动尺度的变化曲线上可以看到,在速度摄动波长为800 m和1000 m频段,0~600 m和1200~1800 m偏移距数据的目标函数值非常小,说明小偏移距数据不利于反演速度的中长波长摄动成分.而3000~3600 m偏移距数据的目标函数曲线在波长为800 m和1000 m的频段尽管呈现出更强的非线性,但目标函数值比较高,对中波长摄动成分比较敏感,应该更有利于反演速度摄动波长分别为800 m和1000 m的成分.
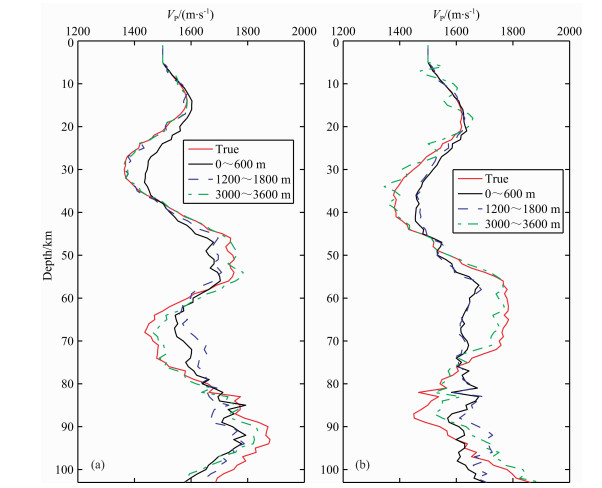
从反演结果(图 15)可以看出,对速度摄动波长分别为800 m和1000 m的模型,利用3000~3600 m大偏移距地震数据的反演结果(绿线)明显优于用0~600 m、1200~1800 m小偏移距地震数据的反演结果(黑线和蓝线),这也证明了前面目标函数性态分析得出的反演策略的正确性.
|
图 15 利用不同偏移距地震数据的全波形反演结果 (a)λ=800 m;(b)λ=1000 m. Fig. 15 Comparisons of FWI results with different offset seismic data (a) The perturbation wavelength is 800 m; (b) The perturbation wavelength is 1000 m. |
在实际地震资料波形反演中,低频成分缺失与初始模型较差是目前高度非线性FWI面临的难题之一[20].通过多尺度反演策略[21, 33]或者更多地利用走时信息[30]以及利用Laplace域反演[25]可以部分解决这个难题.从第3部分目标函数性态分析发现,利用地震道包络进行FWI反演的非线性程度有所降低,因此也可以利用这个特点通过地震道包络来反演非线性程度较高的速度变化的中长波长分量,从而为传统的FWI提供一个更好的初始速度模型.
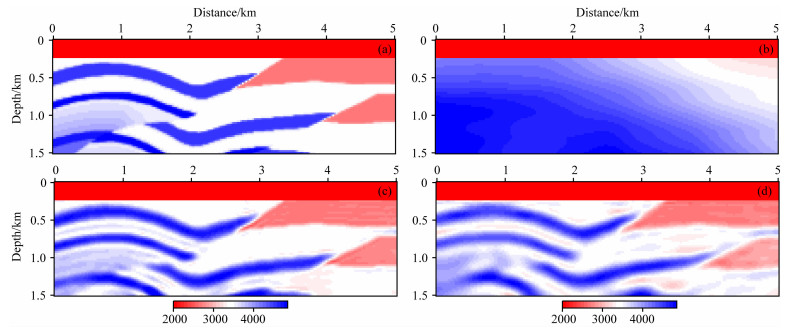
图 16a是Overthrust真实模型,共有48炮地震数据(炮间距100 m),每炮只在地表有201个检波器(道间距25 m),地震数据的主频为7 Hz.由于初始模型(图 16b)是对真实模型进行高斯平滑的结果,初始模型比较好,常规FWI以及利用地震道包络进行FWI均得到了较好的反演结果(图 16c和图 16d),只是前者的分辨率更高一点而已.
|
图 16 用高斯平滑初始模型和含低频数据的FWI反演结果 (a)Overthrust模型;(b)高斯平滑初始模型;(c)常规FWI反演结果;(d)基于包络的FWI反演结果. Fig. 16 The inverted results using Gauss smoothed initial model and seismic data with low frequency information (a) The real Overthrust model; (b) The Initial model for FWI after Gauss-window smoothed; (c) Inverted result with traditional FWI; (d) Inverted result with envelope-based FWI. |
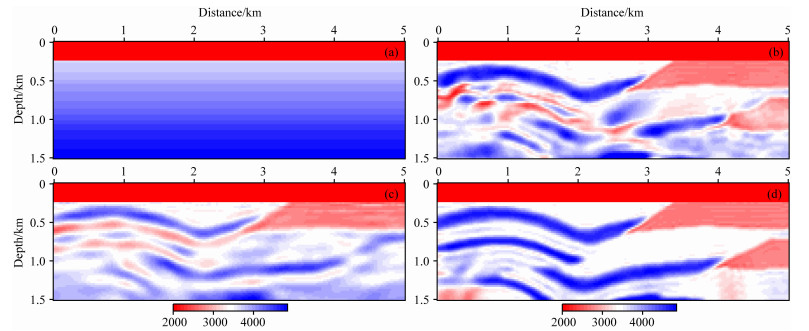
滤掉地震数据中5 Hz以下的频率成分,如果再采用一个速度沿深度呈梯度变化的模型(图 17a)作为FWI的初始模型,则常规的FWI的反演结果比较差(图 17b),明显可以看出在反演中局部极值问题比较严重.而利用地震道包络信息的反演结果(图 17c)在反映模型的宏观变化趋势方面明显优于图 17b,较好地反映了实际模型的低波数成分.以图 17c作为初始模型再进行常规的全波形反演,结果发现,即使在地震数据缺失低频成分、初始模型也很差的情况下,反演结果也非常理想(图 17d),反演模型的高低波数成分均比较好.这说明了通过目标函数性态分析得到的上述反演策略的正确性.
|
图 17 用梯度初始模型和不含低频数据的FWI反演结果 (a)梯度初始模型;(b)常规FWI反演结果;(c)基于包络的FWI反演结果;(d)用(c)作为初始模型的FWI反演结果. Fig. 17 The inverted results using initial gradient model and seismic data without low frequency in formation (a) Initial gradient model; (b) Inverted result of traditional FWI; (c) Inverted result of envelope-based FWI; (d) Inverted result of FWI with (c) being initial model. |
当然,利用地震道包络进行FWI反演在不同条件下的有效性,还需要进一步进行理论分析和数值试验.
5 结论与讨论地震数据和地下介质参数的变化关系是地震学中的核心问题,通过分析不同地震数据子集(如不同偏移距、地震道的包络、不同主频子波的地震数据)的目标函数随不同物性参数扰动的变化关系,可以得出以下结论:
(1) 不同物性参数的不同尺度摄动在地震数据上的反映是不同的,在FWI反演中具体就表现为目标函数的非线性程度差别很大,总体可以归为两大类(密度摄动和速度摄动).对目标函数性态的有效分析是更好地进行全波形反演的有效途径.
(2) 常规地震数据的L2范数目标函数对密度的较小尺度摄动具有较好的敏感度,而中长波长的密度摄动对地震反射波基本没有影响,FWI无法反演.
(3) 常规地震数据(特别是小偏移距数据)的L2范数目标函数对速度的较小尺度摄动成分有较好的反演能力,而在速度的中长波长摄动范围的非线性程度比较严重,FWI反演这些成分有一定难度.但速度的中长波长摄动在反射地震数据上还是有体现的,可以通过一定的反演策略来挖掘这些变化,进而反演速度的中长波长摄动,FWI并非对速度的中波长摄动无能为力.
(4) 不同目标函数的非线性程度不同,相对地震数据的L2范数目标函数,利用Laplace变换以及地震道包络构造的目标函数的非线性程度明显降低,可以通过它们来反演速度变化的中长尺度摄动,从而为常规FWI提供一个更好的初始模型.
(5) 地震数据的不同偏移距、不同频率等数据子集对应的目标函数的非线性程度不同,对不同物性参数的不同尺度摄动成分的反映也不同.例如,随着地震子波主频的降低,目标函数对短波长的敏感度降低,对中长波长的敏感度增强,有利于反演速度的中长波长摄动成分;大炮检距地震数据更好地反映了地下速度的长波长变化,而小炮检距地震数据则更好地反映了地下速度的短波长变化,地下速度的中波长变化在不同炮检距地震数据中也是有一定反映的.如何更好地利用不同数据子集进行分步骤、分尺度的全波形反演,是更好地解决全波形反演的高度非线性问题的主要思路.
| [1] | Lailly P. The seismic inverse problems as a sequence of before stack migration. Conference on Inverse Scattering Theory and Application, Society of Industrial and Applied Mathematics, Proceedings, 1983: 206-220. |
| [2] | Tarantola A. Inversion of seismic reflection data in the acoustic approximation. Geophysics , 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [3] | Tromp J, Tape C, Liu Q Y. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels. Geophys. J. Int. , 2005, 160(1): 195-216. |
| [4] | Plessix R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophys. J. Int. , 2006, 167(2): 495-503. DOI:10.1111/gji.2006.167.issue-2 |
| [5] | Fichtner A, Kennett B L N, Igel H, et al. Full seismic waveform tomography for upper-mantle structure in the Australasian region using adjoint methods. Geophys. J. Int. , 2009, 179(3): 1703-1725. DOI:10.1111/gji.2009.179.issue-3 |
| [6] | Chaiwoot B, Schuster G T, Paul V, et al. Applications of multiscale waveform inversion to marine data using a flooding technique and dynamic early-arrival windows. Geophysics , 2010, 75(6): R129-R136. DOI:10.1190/1.3507237 |
| [7] | Brossier R, Operto S, Virieux J. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion. Geophysics , 2009, 74(6): WCC105-WCC118. DOI:10.1190/1.3215771 |
| [8] | 单蕊, 卞爱飞, 於文辉, 等. 利用叠前全波形反演进行储层预测. 石油地球物理勘探 , 2011, 46(4): 629–633. Shan R, Bian A F, Yu W H, et al. Prestack full waveform inversion for reservoir prediction. Oil Geophysical Prospecting (in Chinese) , 2011, 46(4): 629-633. |
| [9] | Wang Y H, Rao Y. Reflection seismic waveform tomography. J. Geophys. Res. , 2009, 114. DOI:10.1029/2008JB005916 |
| [10] | Claerbout J F. Imaging the Earth's Interior. Blackwell Sci. Publ., 1985. |
| [11] | Snieder R, Xie M Y, Pica A, et al. Retrieving both the impedance contrast and background velocity: a global strategy for the seismic reflection problem. Geophysics , 1989, 54(8): 991-1000. DOI:10.1190/1.1442742 |
| [12] | 刘玉柱, 董良国.反射地震波形反演能力数值实验研究.//2003年中国地球物理年会论文集.南京:南京师范大学出版社, 2003. Liu Y Z, Dong L G. Numerical experimental research on inversion capability of seismic reflection waveform.//Annual of the Chinese Geophysical Society 2003 (in Chinese). Nanjing: Nanjing Normal University Press, 2003. |
| [13] | Hicks G J, Pratt R G. Reflection waveform inversion using local descent methods: estimating attenuation and velocity over a gas-sand deposit. Geophysics , 2001, 66(2): 598-612. DOI:10.1190/1.1444951 |
| [14] | Jannane M, Beydoun W, Crase E, et al. Wavelengths of Earth structures that can be resolved from seismic reflection data. Geophysics , 1989, 54(7): 906-910. DOI:10.1190/1.1442719 |
| [15] | Sears T J, Singh S C, Barton P J. Elastic full waveform inversion of multi-component OBC seismic data. Geophysical Prospecting , 2008, 56(6): 843-862. DOI:10.1111/gpr.2008.56.issue-6 |
| [16] | Pica A. On "Wavelengths of Earth structures that can be resolved from seismic reflection data". 80th Annual International Meeting, SEG, Expanded Abstracts, 2010: 3958-3959. |
| [17] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(1): 411–419. Dong L G, Ma Z T, Cao J Z, et al. Staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys (in Chinese) , 2000, 43(1): 411-419. |
| [18] | Tarantola A. Popper, Bayes and the inverse problem. Nature , 2006, 2: 492-494. |
| [19] | Beydoun W B, Tarantola A. First Born and Rytov approximation: Modeling and inversion conditions in a canonical example. Journal of the Acoustical Society of America , 1988, 83(3): 1045-1055. DOI:10.1121/1.396537 |
| [20] | Virieux J, Operto S. An overview of full-waveform inversion in exploration geophysics. Geophysics , 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [21] | Bunks C, Saleck F M, Zaleski S, et al. Multiscale seismic waveform inversion. Geophysics , 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
| [22] | Maurer H, Greenhalgh S, Latzel S. Frequency and spatial sampling strategies for crosshole seismic waveform spectral inversion experiments. Geophysics , 2009, 74(6): WCC79-WCC89. DOI:10.1190/1.3157252 |
| [23] | Kim Y, Cho H, Min D J, et al. Comparison of frequency-selection strategies for 2D frequency-domain acoustic waveform inversion. Pure and Applied Geophysics , 2010, 168(10): 1715-1727. |
| [24] | 刘国峰, 刘洪, 孟小红, 等. 频率域波形反演中与频率相关的影响因素分析. 地球物理学报 , 2012, 55(4): 1345–1353. Liu G F, Liu H, Meng X H, et al. Frequency related factors analysis in frequency domain waveform inversion. Chinese J. Geophys (in Chinese) , 2012, 55(4): 1345-1353. |
| [25] | Shin C, Cha Y H. Waveform inversion in the Laplace domain. Geophys. J. Int. , 2008, 173(3): 922-931. DOI:10.1111/gji.2008.173.issue-3 |
| [26] | Sirgue L, Pratt R G. Waveform inversion under realistic conditions: Mitigation of non-linearity. 73rd Annual International Meeting, SEG, Expanded Abstracts, 2003: 694-697. |
| [27] | Symes W W, Carazzonet J J. Velocity inversion by differential semblance optimization. Geophysics , 1991, 56(5): 654-663. DOI:10.1190/1.1443082 |
| [28] | van Leeuwen T, Mulder W A. Velocity analysis based on data correlation. Geophysical Prospecting , 2008, 56(6): 791-803. DOI:10.1111/gpr.2008.56.issue-6 |
| [29] | Zelt C A, Smith R B. Seismic traveltime inversion for 2-D crustal velocity structure. Geophys. J. Int. , 1992, 108(1): 16-34. DOI:10.1111/gji.1992.108.issue-1 |
| [30] | Luo Y, Schuster G T. Wave-equation traveltime tomography. Geophysics , 1991, 56(5): 645-653. DOI:10.1190/1.1443081 |
| [31] | 刘玉柱, 董良国, 李培明, 等. 初至波菲涅耳体地震层析成像. 地球物理学报 , 2009, 52(9): 2310–2320. Liu Y Z, Dong L G, Li P M, et al. Fresnel volume tomography based on the first arrival of the seismic wave. Chinese J. Geophys (in Chinese) , 2009, 52(9): 2310-2320. |
| [32] | Liu Y Z, Dong L G, Wang Y W, et al. Sensitivity kernels for seismic Fresnel volume tomography. Geophysics , 2009, 74(5): U35-U46. DOI:10.1190/1.3169600 |
| [33] | Sirgue L, Pratt R G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies. Geophysics , 2004, 69(1): 231-248. DOI:10.1190/1.1649391 |
 2013, Vol. 56
2013, Vol. 56