2. 中国科学院研究生院, 北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
2011 年3 月11 日5 时46 分,日本东北部(Tohoku)太平洋海域发生Mw9.0 特大地震,震源位置为38.322°N,142.369°E,位于仙台海岸约160km,东京的东北方向约400km 处(参见图 1).这次大地震是全球已观测到第5个9.0级特大地震.Tohoku地震为俯冲型浅源地震,其产生的原因是太平洋板块向西运动插入到欧亚板块下方,两个板块的相对运动造成的俯冲界面在日本本州岛下方破裂而引发地震.地震断层破裂长度达500km,震源深度20km左右,向西方向有微小倾角,滑行长达30m.日本精密GPS台网资料提供的地表同震应力场显示,地震导致的本州岛东海岸的水平位移和垂直位移分别达4m 和70cm.
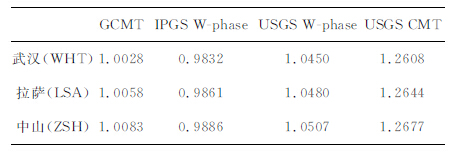
地震爆发后,国际上一些著名的地震研究机构,如the Global Centroid-Moment-Tensor Project(GCMT)[1-4],the United States Geological Survey(USGS)[5-9],Institut de Physique du Globe deStrasbourg (IPGS)[9-10],根据全球地震台网(GSN)的地震观测资料计算地震的震源机制解,并实时报道矩震级.USGS最早给出矩震级为7.9级.随着观测资料的进一步完善,GCMT、USGS、IPGS最终给出日本Tohoku 大地震的震级分别为Mw9.1、9.0(见表 1).
|
|
表 1 日本2011Tohoku大地震的震源机制解 Table 1 Focal mechanism solutions of the 2011 Tohoku earthquake |
地震的震源机制模型通常是将震源等效为双力偶点源.将震源近似看成点源时,双力偶点源与剪切元位错震源产生的远场地震波等价.因此利用远震体波和面波反演中小型地震的震源机制参数是可行的.但对于许多实际地震,尤其是特大地震的断层运动是极其复杂的,震源运动不仅包含剪切错动,还包含单向拉张或压缩、整体的膨胀或收缩,与双力偶点源模型相偏离[11-13].因此,对于特大地震,根据地震波观测资料反演得到的震源机制参数都有一定程度的不确定性.例如,2004 年苏门答腊大地震的震源机制解给出的震级为Mw9.0,而长周期自由振荡的观测结果却表明实际震级可能为Mw9.3[14].地球的长周期自由振荡可以约束地震的震源机制、地震大小及持续时间.观测和分析地球自由振荡简正模频率和振幅衰减可为地球内部动力学研究提供重要的约束,为观测地球的内部结构提供一个新的视角[14-19].
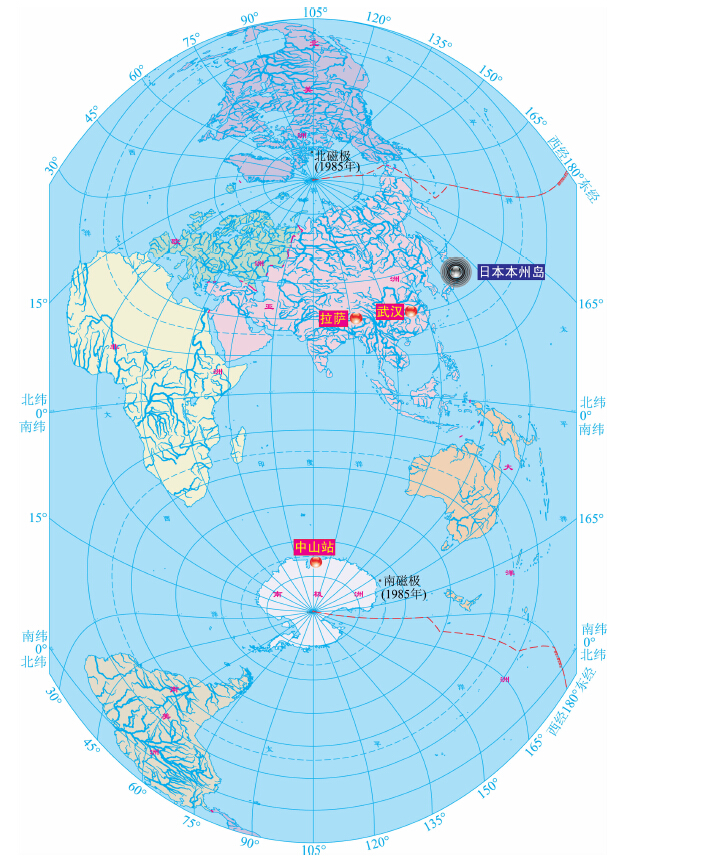
2 数据和方法 2.1 重力观测数据及预处理中国科学院测量与地球物理研究所在武汉、拉萨和南极中山站设有重力连续观测站(参见图 1),利用高精度重力仪监测地球的时变重力场.其中武汉和拉萨站为超导重力仪,南极中山站为ET 重力仪,各台站观测数据采样率均为1 Hz.超导重力仪具有高精度低噪声的特点,能够精密观测到地表垂直形变引起的重力场变化.前期研究成果表明:超导重力数据检测地球低频段自由振荡信号可以媲美宽频带地震仪.在1 mHz以下频段,超导重力仪观测自由振荡的信噪比更高[20].
|
图 1 重力观测站的位置及2011Tohoku大地震震源位置 Fig. 1 The hypocenter of the 2011 Tohoku earthquake and the locations of gravimeter stations |
地震爆发后,武汉、拉萨和南极中山站的重力仪均清楚记录到日本Tohoku大地震激发的地球自由振荡信号.首先对重力观测数据进行预处理:利用正交小波滤波方法消除观测记录中的固体潮信号和高频面波信号,然后消除气压变化对长周期自由振荡信号的影响[21-22],最后在重力观测记录中提取出地球自由振荡信号.由于此次地震释放能量太大,导致震后一段时间的波动信号超出重力仪的记录范围.从发震时刻开始,拉萨台和中山站有约1.8h 的数据“溢出".在观测数据的预处理过程中,我们将拉萨台和中山站的“溢出"数据剔除,以免影响分析结果.
2.2 利用震源机制解计算自由振荡地球的自由振荡是大地震激发的长周期波动,其简正模包括球型振荡nSml 和环型振荡nTml .球型振荡既有径向振动分量也有横向振动分量,可引起地球体积的变化,从而引起重力场的变化,因此重力仪可记录到球型振荡.而环型振荡仅有横向振动分量,其振动质点在以地轴为中心的纬度圈平面内运动,只引起地球的剪切变形,不产生体积的变化,因此不影响重力场的变化,通常情况下重力仪记录不到环型振荡.
地震的震源机制模型将震源等效为双力偶点源.根据双力偶地震矩心矩张量理论,地震矩张量6个独立分量为[23]

|
(1) |
其中r为径向方向;t为南北方向;p为东西方向;δ为断层的倾角dip,即断层面与水平面的夹角;λ 为断层的滑动方向角slip;φs 为断层走向strike;M0为矩张量的标量值,其大小决定了地震的矩震级.
由地球格林函数加权矩张量求和,可计算矩张量源激发产生的地球自由振荡的位移
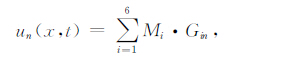
|
(2) |
其中,Mi为6个独立的矩张量分量;Gin为每个地震矩张量分量对应的格林函数.
表 1显示了国际上不同地震学术机构(GCMT、USGS、IPGS)提供的日本Tohoku大地震的震源机制解.数据分别来自于http://www.globalcmt.org/、http:// earthquake .usgs.gov/ earthquake s/eqinthenews/2011/usc0001xgp/scitech、http://eost.u-strasbg.fr/wphase/tohoku_oki_2011/UPDATED.
The Global Centroid-Moment-Tensor Project(GCMT,原Harvard CMT,2006 年更名)[1-4]通过应力分布来获得发震时间、震源位置和深度,并给出断层破裂半持续时间的估计值.对于中小型地震,通过分析长周期体波(T≥45s)得出震源机制解,而对于较大地震,GCMT 联合长周期面波(T≥135s)来求解[24].地震越大,选择周期越长的波段求解.2011Tohoku地震为特大型地震且持续时间较长,余震的影响较大.因此,GCMT 利用地球自由振荡(T>300s)反演计算震源机制解.
USGS Centroid Moment Tensor Solution (USGSCMT)[5-8]选择T≥15~20s的长周期体波为分析对象,首先计算单位矩张量元的阶跃函数响应(格林函数),然后将格林函数与源时间函数(地震矩率张量)做卷积,通过滤波与观测地震图比较,运用最小二乘法求得最优矩张量[24].USGS WPhase Moment Tensor Solution(USGSW-phase)和IPGS W-phase反演方法与USGSCMT反演方法类似,区别在于它们是选择周期范围为100~1000s的W-phase波形资料反演震源机制.W-phase反演震源机制参数是近年来出现的一种新型的求解方法,用于快速预报地震海啸[9-10].Hiroo Kanamori和Luis Rivera[25]对W-phase反演方法做了详细的介绍,并反演计算了几次大型地震的震源机制解.结果证明:当震中距小于10°范围内的宽频带地震资料可用时,利用W-phase反演方法,可以在发震6 min 内得出满意的震源机制解.由于W-phase波的传播受地球结构不均匀性的影响较小,地震激发产生的W-phase信号通常不易遭到其他信号的污染,受余震的影响很小,而体波和面波受这些影响较大.因此,W-phase反演可以提供体波和面波反演难以得到的信息.
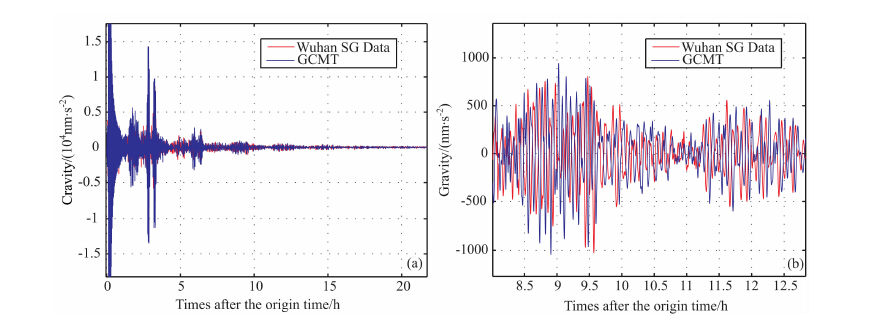
不同机构采用不同的震相和反演方法计算得出的震源机制结果也有所不同.表 1显示GCMT 给出的M0 最大,并由此给出日本Tohoku 地震的矩震级为Mw9.1,高于其前期报道的2004-12-26苏门答腊大地震的矩震级.根据表 1 中GCMT 的震源机制解和地球PREM 模型[26],我们计算了双力偶点源激发的地球自由振荡在武汉超导台站引起的重力变化(自由振荡模拟值),并与武汉台的重力观测值进行比较.图 2显示在自由振荡频段,模拟值和观测值在时间域符合较好.
|
图 2 (a)武汉超导台的重力观测数据和GCMT 震源机制解模拟数据在时间域的比较.(b)为(a)的局部放大 Fig. 2 (a)Comparison between observed data and the synthetic one based on the GCMT focal mechanism solution in the time domainat Wuhan SG station.(b)Partial blow-upof (a) |
我们以 0S0 为研究对象,利用 0S0 的重力观测对Tohoku大地震的震源机制进行分析. 0S0 是长周期径向简正模,根据地球PREM 模型,其频率为0.8143mHz,振幅在全球各处相同. 0S0 是球型自由振荡的一种特殊形式,其相应的质点振动只有径向运动而没有任何横向运动,在传播过程中受地球自转、地球介质横向不均匀和方位各向异性的影响较小.因此比较和分析 0S0 振幅变化得出的结果比较可靠.
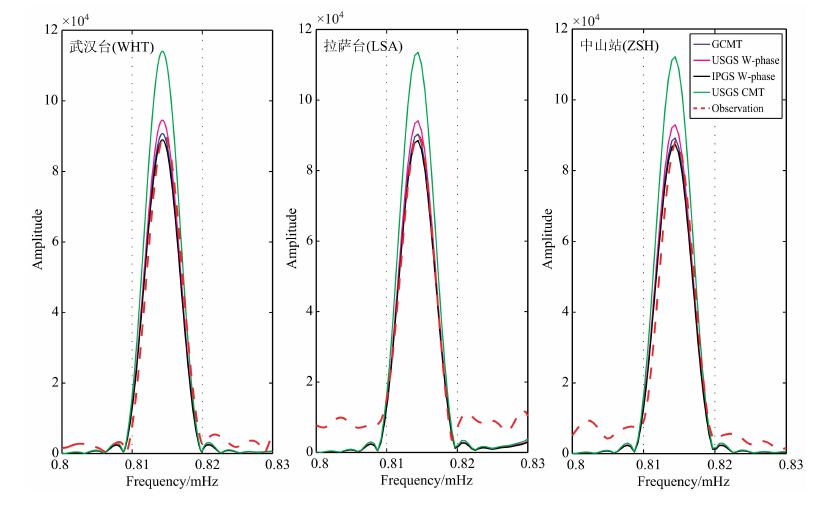
3.1 0S0 模拟值与观测值的比较由快速傅里叶变换(FFT)分别得到自由振荡模拟值和观测值的振幅谱.图 3 显示了武汉、拉萨、南极中山站 0S0 观测值和模拟值的振幅谱.武汉、拉萨和南极中山站地理位置相差甚远,但三个台站 0S0 的重力观测值几乎相等,其微小的差别主要由重力仪的标定系数引起.
|
图 3 不同震源机制解计算的2011Tohoku地震的 0S0 振幅与观测振幅的比较,时间窗均为100h Fig. 3 Comparisons among the observed 0S0 amplitude excited by 2011 Tohoku earthquake and synthetic ones based on different focal mechanism solutions.All time window length sare1 00h |
图 3还显示,由GCMT 震源机制解得到的 0S0 模拟值最接近观测值,而由美国USGSCMT 的震源机制解得到的结果明显大于观测值.表 2 列出了不同震源机制计算的 0S0 模拟值与观测值的比值.结果表明,USGSCMT 震源机制解得到的 0S0 模拟值是观测值的1.26倍,而由其他的震源机制解得到的模拟值都比较接近观测值.
|
|
表 2 武汉、拉萨、中山站记录的2011Tohoku地震的 0S0 振幅模拟值与观测值比值 Table 2 The ratio of synthetic 0S0 amplitude to observed one at WHT, LSA and ZSH after 2011 Tohoku earthquake |
由于 0S0 是长周期径向简正模,因此在矩心矩张量的6个独立分量中,只有矩心矩张量的径向分量Mrr对 0S0 振幅产生影响.Mrr与 0S0 振幅呈正比关系,两者之比为一常量.由表 1 可以看出,USGSCMT 的震源机制解给出的Mrr值最大.过大的Mrr值是导致 0S0 模拟值明显大于观测值的原因.但是,USGSCMT 的震源机制解给出的地震矩标量值M0却不是最大的,其值明显小于GCMT 的震源机制解的结果.
由矩张量径向分量的计算公式
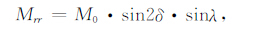
|
(3) |
除了地震矩标量值M0 以外,断层面倾角dip和断层滑动方向slip 也会影响Mrr的大小.表 1 显示GCMT 和USGSCMT 给出的dip和slip有较大的差别.
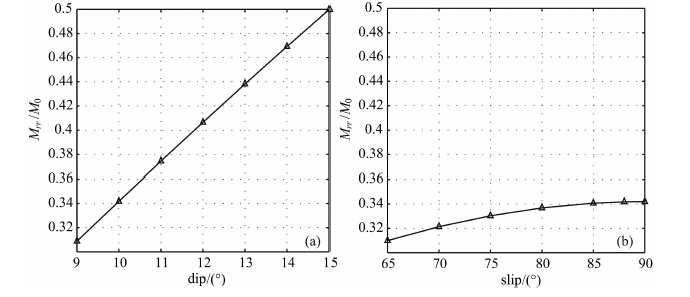
根据公式(3),我们分析逆冲型地震的断层倾角(dip)值和滑动方向角(slip)值对Mrr的影响.图 4直观反映了断层倾角和滑动方向角变化对Mrr变化的影响.在M0 和slip不变的情况下,Mrr随着dip的增大而线性递增.而在M0 和dip值不变的情况下,随着slip值的增大,Mrr增幅很小,且随着slip值不断增大,Mrr增值越缓慢.当dip值从10°增加到14°时,Mrr由0.34M0 激变为0.47M0,增幅为38%.而当slip值从68°增加到88°时,Mrr值由0.32M0 变为0.342M0,增幅仅为7%.尽管USGSCMT 的slip值与GCMT 的slip值相差多达20°,但这个差异对Mrr影响较小.二者的dip 值相差4°,是导致USGSCMT 的Mrr值过大的原因.
|
图 4 (a)倾角(dip)对Mrr的影响;(b)滑动角(slip)对Mrr的影响 Fig. 4 (a)The influence of dipon Mrr;(b)The influence of slipon Mrr |
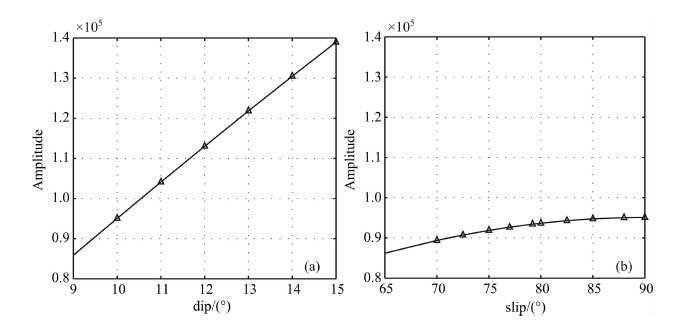
在自由振荡模拟计算中改变震源机制参数slip及dip的值,可分析二者对 0S0 振幅的影响.图 5 显示了 0S0 振幅与slip及dip值变化的关系.当dip值从10°增加到14°时, 0S0 振幅由95047 激变为13047,其增幅为38%.而当slip值从68°增加到88°时, 0S0 振幅由88107变为95047,增幅为7%.这些结果表明dip和slip值对 0S0 振幅的影响与其对Mrr的影响相同. 0S0 振幅的变化与Mrr的变化呈正比关系.因此,我们可以通过 0S0 振幅的重力观测值分析Mrr值的大小,进而约束slip及dip值.
|
图 5 (a)倾角(dip)对 0S0 振幅的影响;(b)滑动角(slip)对 0S0 振幅的影响 Fig. 5 (a)The influence of dipon 0S0 amplitude;(b)The influence of slipon 0S0 amplitude depth |
对于逆冲型大地震,断层面倾角dip 值较小(8°~15°),在此范围内,随着dip值的增大,sin(2×dip)快速递增;断层滑动方向角slip 值较大(65°~120°),随着slip值的增大,sin(slip)缓慢递增.因此断层面倾角对Mrr的影响较大,而断层滑动方向角对Mrr的影响较小.
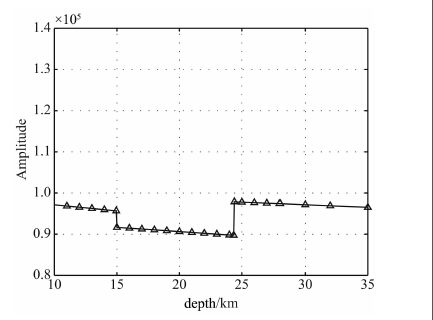
3.3 震源深度对 0S0 振幅的影响我们采用183 分层的径向各向异性PREM 模型分析不同震源深度对 0S0 振幅的影响.图 6表明,震源位于10~15km、15~24.4km、24.4~33km区间内时, 0S0 振幅随震源深度的增加而略微减小,即深度变化对 0S0 振幅的影响很小.但震源深度在15km 和24.4km 处时, 0S0 振幅出现突变.
我们注意到15km 和24.4km 是PREM 模型给出的地震波速度间断面(径向各向异性分层面).10~15km、15~24.4km、24.4~33km位于PREM模型的各向同性层.径向各向同性对 0S0 振幅的影响很小.因此,对于浅层地震,震源深度depth对 0S0 振幅的影响主要取决于depth 值相对于间断面(分层边界面)的位置.如果不同的震源机制模型给出的不同,但均在同一速度层内(径向各向同性层),这时depth的差异对 0S0 振幅影响很小,可以忽略.但如果depth 位于相邻的速度层,则会导致 0S0 振幅会有跳跃性的变化,其影响不可忽视.例如,在假定其他参数不变的情况下,当depth 从10km 变为20km, 0S0 振幅从97072 降为90570,下降幅度为6.6%.
在图 6 中,我们还注意到震源深度在15km处 0S0 振幅突然减小,而在24.4km 处 0S0 振幅却突然增大.对于地球的分层模型,整体上来说,随着深度的增加,密度、速度也随之变大, 0S0 振幅应呈现阶梯下降的趋势.在PREM 模型中,波速在24.4km 间断面处突然增大,但在随后的24.4~220km的范围内(软流圈低速区),波速和密度却随着深度的增加而减小,从而导致 0S0 振幅在24.4km 处增大.
|
图 6 震源深度对 0S0 振幅的影响.15km、24.4km 为PREM 模型的间断面 Fig. 6 The influence of the depth on 0S0 amplitude.The discontinuities are located at 15km,24.4km,respectively |
对于大型地震,断层的破裂通常要持续一段时间.破裂时间会影响标量地震矩M0 的大小,进而影响简正模振幅大小.假定大地震瞬间破裂产生的地震矩为M0,震源的破裂持续时间为t且破裂速度为一常量,地震矩M0 对频率为f的长周期自由振荡振幅的影响减小为[27-28]
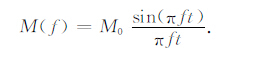
|
(4) |
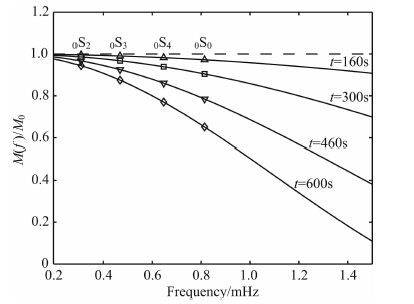
图 7显示不同破裂时间对长周期自由振荡振幅的影响.分析 0S0 振型,当破裂时间t=160s 时,M(f)/M0 =0.972,振幅下降为2.8%;t=300s时,M(f)/M0 =0.905,振幅下降9.5%;t=460s时,M(f)/M0 =0.785,振幅下降21.5%;t=600s时,M(f)/M0 =0.65,振幅下降达35%.图 7表明,破裂时间对 0S0 振幅有一定的影响.破裂时间越长,振幅下降幅度越大.因此,利用自由振荡信号分析大地震的震源机制,需要考虑破裂时间对自由振荡振幅的影响.
|
图 7 断层破裂时间造成简正模的振幅谱减小 Fig. 7 The duration of fault rupture results in a decrease of spectra lamp litudes of normal modes |
反演计算震源机制参数后,会根据地震矩M0 大小估计出震源的半破裂时间[24].例如GCMT 给出2004-12-26 苏门答腊大地震的震源破裂时间为190s.计算自由振荡简正模的观测值和模拟值的相位差,可以得到震源破裂时间[27-29].据此,Park等[28]计算得出苏门答腊大地震破裂时间为400~450s.Lambotte等[29]计算 0S0 振幅得出的破裂时间为460s,并由此推算出破裂长度约为1200km,这一结论比较符合观测结果.因此,对于大型地震,根据M0 得出的破裂时间不一定正确,可以通过自由振荡观测进行约束.
GCMT 给出的2011日本Tohoku大地震的震源破裂时间为140s.我们通过傅里叶变换得到 0S0 简正模的模拟值和观测值的相位谱,二者相减获得相位差.根据PREM 模型给出的 0S0 振幅的周期值,求得震源的破裂时间为160s,与GCMT 估值接近.此时M(f)/M0 约为0.972,即Tohoku地震的破裂时间(160s)造成 0S0 振幅下降2.8%,影响较小.
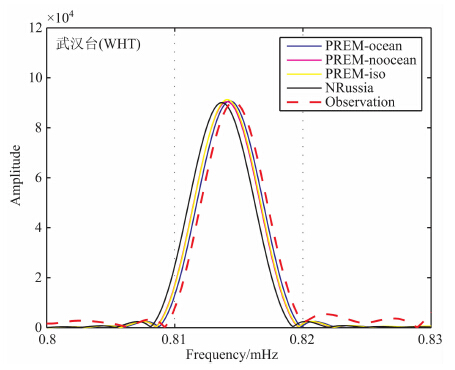
3.5 地球模型对 0S0 振幅的影响利用自由振荡约束震源机制解时,地球模型起着重要作用.本文研究采用的地球模型为考虑海洋影响的PREM 各向异性分层模型.该模型能比较准确地模拟地球长周期自由振荡,但也必须考虑模型的差异对 0S0 振幅的影响.我们采用GCMT 震源机制解和不同的地球模型计算 0S0 振幅,对比不同模型对其的影响.图 8 显示了由4 种不同的地球分层模型得到的 0S0 模拟值和观测值的比较.其中PREM-ocean模型的 0S0 振幅和频率与观测值最为接近,但不同模型的结果相差不大.表 3给出了不同地球模型 0S0 振幅与PREM-ocean 模型 0S0 振幅的比值,其差异十分微小.因此模型的差异对 0S0 振幅影响很小,可以忽略其对我们分析震源机制的影响.
|
图 8 不同地球模型计算的2011Tohoku地震的 0S0 振幅与观测振幅的比较 PREM-ocean为考虑海洋影响的PREM 各向异性模型,PREM-noocean为不考虑海洋影响的PREM 各向异性模型,PREM-iso为考虑海洋影响的PREM 各向同性模型,NRussia[30]为北俄罗斯的各向异性地球模型. Fig. 8 Comparisons among the observed 0S0 amplitude excited by 2011 Tohoku earthquake and synthetic ones based on different earth models PREM-ocean is the anisotropic PREM model with the oceanic influence,PREM-noocean is the anisotropic PREM model without the oceanic influence,PREM-iso is the isotropic PREM model with the oceanic influence,NRussia is the anisotropic North Russian model. |
|
|
表 3 其他地球模型的 0S0 振幅与PREM-ocean 0S0 振幅的比值 Table 3 The ratio of 0S0 amplitude based on other earth models to the one on PREM-ocean |
表 4详细给出了震源机制参数dip、slip、depth不同而导致的日本Tohoku大地震 0S0 振幅的差异.比较GCMT震源机制和USGSCMT震源机制激发的 0S0 振幅,三个参数的差异最终可导致USGSCMT 的 0S0 振幅增加36%.其中大部分的增益来自dip微小的增加.比较结果表明:对于逆冲型浅层大地震,断层面倾角dip 对 0S0 振幅的影响很大,断层滑动方向角slip和震源深度depth对 0S0 振幅的影响较小,USGSCMT 震源机制解中较大的断层倾角是导致其 0S0 振幅显著偏离观测值的原因.
|
|
表 4 变量dip、slip、depth对 0S0 振幅的影响 Table 4 The Influence of the variations of dip, slip and depth on 0S0 amplitude |
相对于USGS CMT 震源机制解,USGS W-phase震源机制解中的断层面倾角dip仍为14°,但地震矩M0 却下降13%(参见表 1).这一变化导致USGS W-phase 的 0S0 振幅接近观测值.IPGS W-phase的断层面倾角dip和地震矩M0 介于GCMT和USGS CMT 之间(表 1),这也导致IPGS W-phase的 0S0 振幅接近观测值.观测地球长周期自由振荡仅仅能约束震源机制解中dip和M0 的综合影响,但却无法分别约束其各自的影响.目前国际上对震源机制的约束也局限于两者的综合影响.自由振荡的观测结果只能说明USGSCMT 的结果显著偏离实际值,但是不能确切地判断GCMT、USGS W-phase和IPGS W-phase哪个结果更优.平衡dip与M0 的关系,是约束震源机制的关键[31].利用地球自由振荡对dip、M0 的独立约束遇到瓶颈.因此,如果能利用大地测量手段(如GPS 观测)约束地震断层倾角dip和地震断层滑动方向角slip[32-34],再结合地球自由振荡的观测和模拟,可对震源机制参数予以更强的约束,这也是我们下一步的研究目标.我们会另文分析大地测量手段与重力观测的联合约束.
致谢感谢武汉大地测量国家野外科学观测研究站提供的武汉、拉萨、南极中山站的重力观测数据.
| [1] | Nettles M, Ekstrom G, Koss H C. Centroid-moment-tensor analysis of the 2011 Tohoku earthquake and its larger foreshocks and aftershocks. Earth Planets Space , 2011, 99(1-9): 1-8. |
| [2] | Dziewonski A M, Chou T A, Woodhouse J H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. , 1981, 86(B4): 2825-2852. DOI:10.1029/JB086iB04p02825 |
| [3] | Arvidsson R, Ekstrom G. Global CMT analysis of moderate earthquake, Mw≥4.5, using intermediate-period surface waves. Bull. Seism. Soc. Am. , 1998, 88(4): 1003-1013. |
| [4] | Ekstrom G, Dziewoński A M, Maternovskaya N N, et al. Global seismicity of 2003: centroid-moment-tensor solutions for 1087 earthquakes. Phys. Earth Planet. Inter. , 2005, 148(2-4): 327-351. DOI:10.1016/j.pepi.2004.09.006 |
| [5] | Hayes G P, Earle P S, Benz H M, et al. 88 Hours: The U. S. geological survey national earthquake information center response to the 11 March 2011 Mw9.0 Tohoku earthquake. Seismol. Res. Lett. , 2011, 82(4): 481-493. DOI:10.1785/gssrl.82.4.481 |
| [6] | Sipkin S A. Estimation of earthquake source parameters by the inversion of waveform data: synthetic waveforms. Phys. Earth Planet. Inter. , 1982, 30(2-3): 242-259. DOI:10.1016/0031-9201(82)90111-X |
| [7] | Sipkin S A. Estimation of earthquake source parameters by the inversion of waveform data: Global seismicity, 1981—1983. Bull. Seism. Soc. Am. , 1986, 76(6): 1515-1541. |
| [8] | Sipkin S A. Rapid determination of global moment-tensor solutions. Geophys. Res. Lett. , 1994, 21(16): 1667-1670. DOI:10.1029/94GL01429 |
| [9] | Duputel Z, Rivera L, Kanamori H, et al. Real-time W phase inversion during the 2011 off the Pacific coast of Tohoku earthquake. Earth Planets Space , 2011, 63(7): 535-539. DOI:10.5047/eps.2011.05.032 |
| [10] | W Phase source inversion results 3/11/2011 (Mw9.0), Tohoku-oki, Japan. http://eost.u-strasbg.fr/wphase/tohoku_oki_2011/UPDATED. |
| [11] | Shao G F, Li X Y, Ji C, et al. Focal mechanism and slip history of the 2011 Mw9.1 off the Pacific coast of Tohoku earthquake, constrained with teleseismic body and surface waves. Earth Planets Space , 2011, 63(7): 559-564. DOI:10.5047/eps.2011.06.028 |
| [12] | Hayes G P. Rapid source characterization of the 2011 Mw9.0 off the Pacific coast of Tohoku earthquake. Earth Planets Space , 2011, 63(7): 529-534. DOI:10.5047/eps.2011.05.012 |
| [13] | 陈运泰. 地震参数:数字地震学在地震预测中的应用. 北京: 地震出版社, 2003 . Chen Y T. Parameters of Earthquake-Application of Digital Seismology in Earthquake Prediction (in Chinese). Beijing: Seismological Press, 2003 . |
| [14] | Stein S, Okal E A. Seismology: Speed and size of the Sumatra earthquake. Nature , 2005, 434(7033): 581-582. DOI:10.1038/434581a |
| [15] | Ammon C J, Ji C, Thio H K, et al. Rupture process of the 2004 Sumatra-Andaman earthquake. Science , 2005, 308(5725): 1133-1139. DOI:10.1126/science.1112260 |
| [16] | Lay T, Kanamori H, Ammon C J, et al. The great Sumatra-Andaman earthquake of 26 December 2004. Science , 2005, 308(5725): 1127-1133. DOI:10.1126/science.1112250 |
| [17] | Giardini D, Li X D, Woodhouse J H. Three-dimensional structure of the Earth from splitting in free-oscillation spectra. Nature , 1987, 325(6103): 405-411. DOI:10.1038/325405a0 |
| [18] | Laske G, Masters G. Limits on differential rotation of the inner core from an analysis of the Earth's free oscillations. Nature , 1999, 402(6757): 66-69. DOI:10.1038/47011 |
| [19] | Ishii M, Tromp J. Normal-mode and free-air gravity constraints on lateral variations in velocity and density of Earth's mantle. Science , 1999, 285(5431): 1231-1236. DOI:10.1126/science.285.5431.1231 |
| [20] | Hu X G, Liu L T, Sun H P, et al. Wavelet filter analysis of splitting and coupling of seismic normal modes below 1.5 mHz with superconducting gravimeters after the December 26, 2004 Sumatra earthquake. Science in China Series D: Earth Sciences , 2004, 49(12): 1259-1269. |
| [21] | Hu X G, Liu L T, Hinderer J, et al. Wavelet filter analysis of local atmospheric pressure effects on gravity variations. J. Geodesy , 2005, 79(8): 447-459. DOI:10.1007/s00190-005-0486-6 |
| [22] | Hu X G, Liu L T, Hinderer J, et al. Wavelet filter analysis of atmospheric pressure effects in the long-period seismic mode band. Phys. Earth Planet. Inter. , 2006, 154(1): 70-84. DOI:10.1016/j.pepi.2005.09.003 |
| [23] | Aki K, Richards P G. Quantitative Seismology: Theory and Methods. San Francisco: W. H. Freeman, 1980. http://www.oalib.com/references/18997245 |
| [24] | Helffrich G R. How good are routinely determined focal mechanisms? Empirical statistics based on a comparison of Harvard, USGS and ERI moment tensors. Geophys. J. Int. , 1997, 131(3): 741-750. DOI:10.1111/gji.1997.131.issue-3 |
| [25] | Kanamori H, Rivera L. Source inversion of W-phase: Speeding up seismic tsunami warning. Geophys. J. Int , 2008, 175(1): 222-238. DOI:10.1111/gji.2008.175.issue-1 |
| [26] | Dziewonski A M, Anderson D L. Preliminary reference Earth model. Phys. Earth Planet. Inter. , 1981, 25(4): 297-356. DOI:10.1016/0031-9201(81)90046-7 |
| [27] | Kedar S, Watada S, Tanimoto T. The 1989 Macquarie Ridge earthquake: Seismic moment estimation from long-period free oscillations. J. Geophys. Res. , 1994, 99(B9): 17893-17907. DOI:10.1029/94JB01251 |
| [28] | Park J, Song T A, Tromp J, et al. Earth's free oscillations excited by the 26 December 2004 Sumatra-Andaman earthquake. Science , 2005, 308(5725): 1139-1144. DOI:10.1126/science.1112305 |
| [29] | Lambotte S, Rivera L, Hinderer J. Rupture length and duration of the 2004 Aceh-Sumatra earthquake from the phases of the Earth's gravest free oscillations. Geophys. Res. Lett. , 2006, 33: L03307. DOI:10.1029/2005GL024090 |
| [30] | Shapiro N M, Ritzwoller M H. Monte-Carlo inversion for a global shear-velocity model of the crust and upper mantle. Geophys. J. Int. , 2002, 151(1): 88-105. DOI:10.1046/j.1365-246X.2002.01742.x |
| [31] | Tsai V C, Hayes G P, Duputel Z. Constraints on the long-period moment-dip tradeoff for the Tohoku earthquake. Geophys. Res. Lett. , 2011, 38: L00G17. DOI:10.1029/2011GL049129 |
| [32] | Banerjee P, Pollitz F F, Bürgmann R. The size and duration of the Sumatra-Andaman earthquake from far-field static offsets. Science , 2005, 308(5729): 1769-1772. DOI:10.1126/science.1113746 |
| [33] | Pollitz F F, Bürgmann R, Banerjee P. Geodetic slip model of the 2011 M9.0 Tohoku earthquake. Geophys. Res. Lett. , 2011, 38: L00G08. DOI:10.1029/2011GL048632 |
| [34] | Ammon C J, Lay T, Kanamori H, et al. A rupture model of the 2011 off the Pacific coast of Tohoku earthquake. Earth Planets Space , 2011, 63(7): 693-696. DOI:10.5047/eps.2011.05.015 |
 2012, Vol. 55
2012, Vol. 55