日落后,由于复合损失,赤道电离层F 区底部经常出现锐的电子密度梯度,导致赤道电离层不规则结构(等离子体泡)或赤道扩展F(ESF)的生成和发展,它们对跨电离层的无线电波传播存在极大的影响.自ESF 被发现以来,许多实验和理论研究都表明,ESF的生成和发展与广义瑞利-泰勒不稳定性(generalized Rayleigh-Taylorinstability)有关[1].ESF 表现出显著的随季节、经度变化的特征[1].也有研究者[2-4]注意到,电离层不规则结构活动在南北半球表现出不同的特征,沿磁力线也呈现出南-北半球分布不对称.不规则结构的不对称分布可能归因于触发不规则结构生成的物理机制不同[3],或等离子体不稳定性发展过程的差异,两者都与背景电离层的半球不对称有关[3].热层中性风场和磁偏角是导致电子密度及其梯度呈南北不对称的主要因素[5-6],可能影响瑞利-泰勒不稳定性和不规则结构的生成和演化,并影响不规则结构随季节和太阳活动的变化以及随地理经度和纬度的分布,这是一个值得深入研究的问题.
一系列研究指出,中性风场和磁偏角对ESF 的生成和发展有重要影响[1, 7-11].此外,中性风场的磁南北半球不对称分布,可能导致不同半球的等离子体不稳定性的发展过程存在差异,并影响低纬赤道区重力瑞利-泰勒不稳定性的发展.此前,许多研究者[12-14]曾利用通量管积分方法,分析瑞利-泰勒不稳定性的线性发展和演化过程.在这些研究中,都没有考虑磁偏角随经度变化的影响,也没有比较研究积分线性增长率和不规则结构出现率的经度变化,且通常用一个半球积分的两倍来代替沿整条通量管积分,这样将无法考查南-北半球不对称性对瑞利-泰勒不稳定性的影响.为了更有效地研究中性风场和磁偏角及其半球不对称对瑞利-泰勒不稳定性的影响,更好地反映赤道地区广义瑞利-泰勒不稳定性的发展过程,有必要分别对南北半球沿磁力线积分进行计算分析,并考查广义瑞利-泰勒不稳定性对不规则结构出现率经度变化的影响.
本文将利用通量管积分技术,对南北半球分别沿磁力线积分,研究热层中性风场和磁偏角所致背景电离层南-北半球不对称以及中性风场和磁偏角的共同作用随经度的变化对瑞利-泰勒不稳定性的影响,分析导致不规则结构呈南-北不对称分布的可能因素,并进一步探寻影响ESF经度效应的主要因素.
2 通量管积分电离层参量为考虑整条磁通量管对线性增长率的贡献,将粒子守恒和电荷守恒方程沿通量管积分,积分从一个半球通量管的根部通过磁通量管的顶点直到另一个半球通量管的根部,包括E 区和F 区.在偶极坐标系(q,s,l)中,$\hat{q}$在子午面内垂直于磁场,$\hat{l}$平行于磁场,$\hat{s}$满足$\hat{s}$=$\hat{l}$×$\hat{q}$.在赤道面内,偶极坐标系退化为极坐标系(L,φ),其中L为McIlwain参数,φ 为磁经度.假设磁力线为等势线[15].忽略复合率的影响,沿通量管积分之后,通量管积分粒子守恒和电荷守恒方程分别为
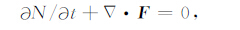
|
(1) |
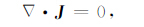
|
(2) |
式中N(L,φ,t)、F(L,φ,t)和J(L,φ,t)分别为通量管积分电子密度、数通量密度和电流密度,它们的定义分别为[15-16]
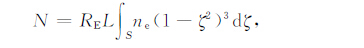
|
(3a) |
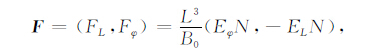
|
(3b) |

|
(3c) |
式中ne 是局地电离层电离密度,EL和Eφ 是电场垂直于磁力线的分量,RE 为地球半径,ζ =sinθ,θ 为磁纬.线积分(3a)从一个半球E 层底高度开始沿磁力线到另一半球E 层底高度.由于沿积分路径大部分高度上,Hall电导率远小于Pedersen 电导率,计算中忽略了Hall电导率的影响.符号UP,L和UP,φ分别表示Pedersen 电导率与磁偏角加权的积分中性风场垂直于磁力线的分量,UP,L向上为正,UP,φ向东为正;${{\tilde{\sum }}_{P}}$ 和${{\sum }_{P}}$ 为权因子不同的积分Pedersen电导率;OP 为Pedersen电导率加权的积分碰撞频率,它们分别定义为以下形式的线积分:
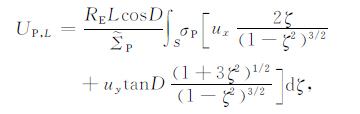
|
(4a) |
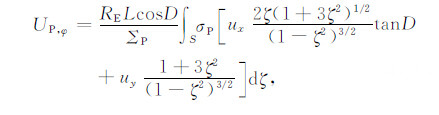
|
(4b) |
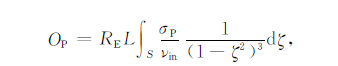
|
(4c) |
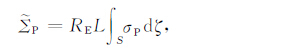
|
(4d) |
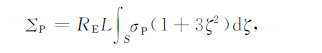
|
(4e) |
式中σP 是局地Pedersen电导率,ux和uy分别为局地热层子午风和纬圈风,D为磁偏角.式(3)和(4)的推导参见附录.
以往的研究在定义积分中性风场时,都没有考虑磁偏角的影响[12-15],实际上,热层风垂直于磁力线的分量是磁偏角D的函数,在导出(4a)和(4b)两式时,我们考虑了磁偏角的影响.此外,在以往的研究中,作为一种近似,都取一个半球通量管积分的两倍代替整条通量管的积分.考虑到南北半球电离层的不对称性,本文分别对南北半球积分,沿整条通量管积分的积分参量值为南半球积分值与北半球积分值之和,而不是一个半球通量管积分的两倍.
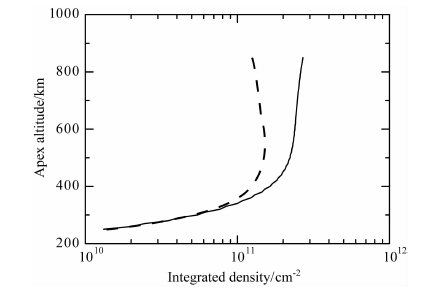
图 1给出磁南北半球的积分背景电离密度N0随磁力线顶点高度的变化.图 1 中的曲线由(3a)式计算得到,实线表示在北半球的积分值,虚线表示在南半球的积分值.计算所用的背景电离层和热层模型包括IRI2001[17],NRLMSIS00[18]和HWM07[19].由图 1可以看到,磁力线顶点高度较低时,南半球和北半球N0 相差很小,南-北半球基本对称;磁力线顶点较高时(约400km 以上),北半球的N0 明显大于南半球,随着磁力线顶点高度的增加,不对称性越来越显著.在南半球,磁力线顶点约600km 以上,随积分路径的增长,积分电离密度反而减小,这应该是电离赤道异常的效应.可以注意到,在南半球没有出现这种现象,这是电离赤道异常南北不对称的结果.
|
图 1 磁南(虚线)、北(实线)半球积分电离密度随磁力线顶点高度的变化 Fig. 1 (dashed-line)-north (solid line) hemisphere versus the apex height of the magnetic field line |
|
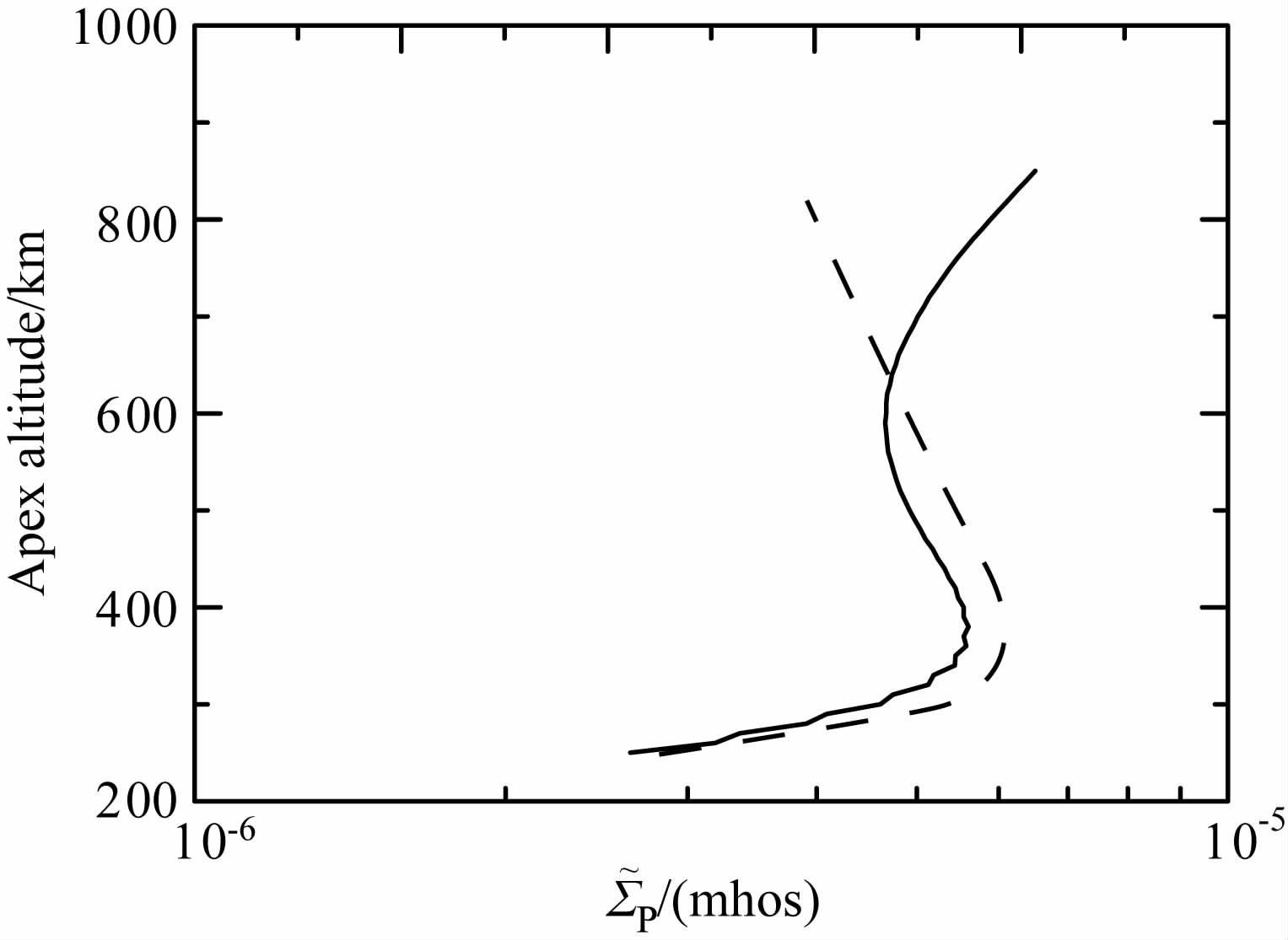
图 2 磁南(虚线)、北(实线)半球积分Pedersen电导率随磁力线顶点高度的变化 Fig. 2 (dashed-line)-north (solid line) hemisphere versus the apex height of the magnetic field line |
图 2给出磁南北半球积分Pedersen电导率${{\tilde{\sum }}_{P}}$随磁力线顶点高度的变化.图 2 中的曲线由(4d)式计算得到,实线表示在北半球的积分值,虚线表示在南半球的积分值.
由图 2可以看到,南半球积分Pedersen电导率${{\tilde{\sum }}_{P}}$ 的值随磁力线顶点高度变化,约370km 高度有一个极大值,370km 之下单调增大,370km 之上单调减小,意味着在此高度之上局地电导率随高度的减小比积分路径的增长更快;北半球的${{\tilde{\sum }}_{P}}$ 值随磁力线顶点高度的变化规律为,在约600km 高度以下,其形状与南半球类似,约370km 高度有一个极大值,600km 高度以下北半球的${{\tilde{\sum }}_{P}}$ 值稍低于南半球;在南半球,600km 高度上,${{\tilde{\sum }}_{P}}$ 有一个极小值,在600km以上,${{\tilde{\sum }}_{P}}$ 值随磁力线顶点高度升高而越来越大,其值很快超过南半球,南北半球不对称也越来越显著,说明南半球局地电导率沿磁力线随高度升高衰减较慢,积分路径长度变化对${{\tilde{\sum }}_{P}}$ 起控制作用.
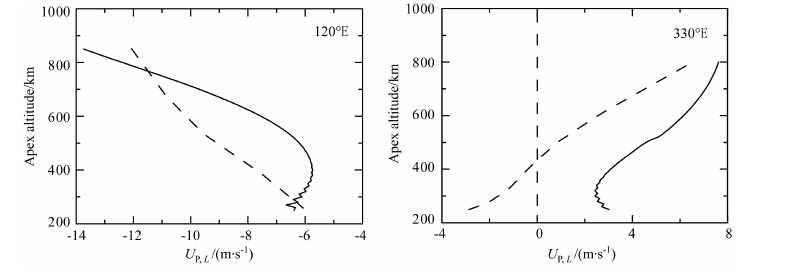
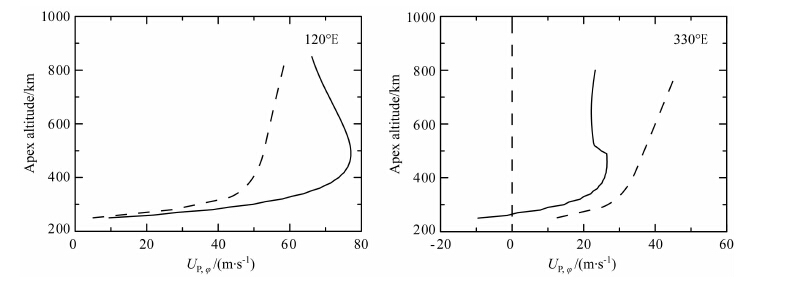
图 3给出120°E 和330°E 磁南北半球磁子午面内垂直磁力线的通量管积分垂直风场UP,L随磁力线顶点高度的变化.图 4给出120°E 和330°E 磁南北半球垂直磁子午面的通量管积分纬圈风场UP,φ随磁力线顶点高度的变化.实线表示在北半球的积分值,虚线表示在南半球的积分值.这两幅图中的曲线分别由(4a)和(4b)两式计算得到.
|
图 3 在南半球(虚线)、北半球(实线),磁子午面内垂直磁力线的积分中性风场(向上为正)随磁力线顶点高度的变化 Fig. 3 Integrated neutral wind perpendicular to the magnetic field line in the meridian in magnetic south (dashed-line)-north (solid line) hemisphere versus the apex height of the magnetic field line |
|
图 4 在南半球(虚线)、北半球(实线),垂直磁子午面的积分中性风场(向东为正)随磁力线顶点高度的变化 Fig. 4 Integrated neutral wind perpendicular to the meridian in magnetic south (dashed-line) -north (solid line) hemisphere versus the apex height of the magnetic field line |
由图 3和图 4可以看到,积分中性风场也表现出显著的南北半球不对称.同时,积分中性风场还存在随经度的变化.在120°E,南-北半球的垂直磁力线的积分垂直风场均指向下,磁力线顶点高度为450km,UP,LN=-5.9m/s,UP,φS =-8.4m/s.在330°E,磁力线顶点较低的高度,南半球的积分垂直风场向下;磁力线顶点较高的高度,南半球的积分垂直风场向上,北半球的积分垂直风场向上,磁力线顶点高度为450km,UP,LN=3.8m/s,UP,φS =0.2m/s.在120°E,北半球的积分纬圈风场大于南半球的积分纬圈风场,磁力线顶点高度为450km,UP,φN = 76 m/s,UP,φS =52m/s;在330°E,南半球的积分纬圈风场大于北半球的积分纬圈风场,磁力线顶点高度为450km,UP,φN =26m/s,UP,φS =35m/s.根据式(4a)和(4b),积分热层风场随磁力线顶点高度的变化对地理经度的依赖主要归因于热层中性风场自身随经度变化和磁偏角随经度的变化,也可能还与电导率的经度变化有关.
综上所述,通量管积分电离密度、热层子午和纬圈风以及Pedersen 电导率都存在不同程度的磁南北半球不对称性.因此,尽管取一个半球通量管积分的两倍代替整条通量管的积分作为一种近似有其合理性,但这种近似可能带来较大的误差,为了保证计算结果精确,分别对南北半球积分,用南半球积分值与北半球积分值之和代替一个半球通量管积分的两倍更可靠.此外,由于背景电离层参量影响等离子体不稳定性的发展演化过程,因此,沿磁力线积分的电离密度、热层子午和纬圈风以及Pedersen电导率的半球不对称可能导致不同半球的瑞利-泰勒不稳定性的生成和发展存在差异,影响不同半球的电离层不规则结构的生成和发展,对此后面将进一步讨论.
3 广义瑞利-泰勒不稳定性线性演化的半球不对称和随经度的变化下面将利用通量管积分电离层参量导出通量管积分瑞利-泰勒不稳定性增长率,通过数值计算,定量地分析南北半球不对称以及随经度变化的磁偏角和热层风场对广义瑞利-泰勒不稳定性线性演化的影响,并通过比较增长率和不规则结构出现率的经度变化来分析影响不规则结构出现率经度变化的主要控制因素.
3.1 通量管积分瑞利-泰勒不稳定性增长率考虑在平衡态参量上叠加一小扰动量,用下标0,1分别表示稳态量和扰动量,则N= N0 +N1,EL=EL,0 -∂φ1/RE∂L,Eφ =Eφ,0 -∂φ1/REL∂φ.
用A1 =A0exp[iωt-i(KL+mφ)]的形式表示扰动量.A0 是恒定的扰动幅度,K、m分别为沿L、φ方向的无量纲波数,K=REKL,m=RELKφ,KL、Kφ 分别为沿L、φ 方向的波数,则有∂/∂t=iω,∂/∂L=-iK,∂/∂φ =-im.
把以上形式的稳态量和扰动量代入方程(1)和(2),将方程线性化并进行通量管积分等离子体不稳定性分析,得到通量管积分广义瑞利-泰勒不稳定性线性增长率的表达式为
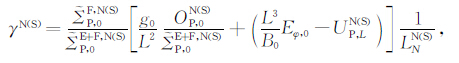
|
(5) |
式中LN为积分电子密度梯度的标度长度,上角标N 和S 分别表示北半球和南半球沿通量管积分的物理参量.$\tilde{\sum }_{P,0}^{F,N\left( S \right)}$ 分别表示北(南)半球F 区积分Pedersen电导率,$\tilde{\sum }_{P,0}^{F,N\left( S \right)}$(简写成${{\tilde{\sum }}_{P}}$,0)分别表示北(南)半球E 区和F区积分Pedersen电导率之和.沿整条通量管的积分线性增长率的表达式为
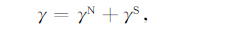
|
(6) |
在半球对称的条件下并假定磁偏角为零,沿整条通量管的积分线性增长率为(5)式的两倍,与以往得到的通量管积分线性增长率的表达式[13-14]相同.不过,由于${{N}_{0}},\tilde{\sum }_{P,0}^{E,F}$ 和中性风场都存在半球不对称,LN以及E 区电导率与E 区和F 区电导率之和的比值$\tilde{\sum }_{P,0}^{F},\tilde{\sum }_{P,0}^{E+F}$ 也在一定程度上呈半球不对称.因此,由(5)式对不同半球积分计算得到的线性增长率可能存在差异,即γN ≠γS.这意味着在利用通量管积分方法进行广义瑞利-泰勒不稳定性分析时,仅对一个半球进行积分,计算结果可能是不准确的;这也意味着瑞利-泰勒不稳定性在不同半球的发展过程可能存在差异,进而影响不同半球的不规则结构的形态特征,使不规则结构的分布呈半球不对称.我们将在下面对γN 和γS 进行比较验证.
3.2 电离层背景参量南北半球不对称对瑞利-泰勒不稳定性的影响如前所述,由于热层风场和磁偏角的作用[5-6],电离层背景参量沿磁赤道的南-北分布存在不对称.背景参量的不对称分布可能导致不稳定性在南-北半球的发展过程不同并影响广义瑞利-泰勒不稳定性的发展.下面通过比较在半球对称和半球不对称条件下得到的线性增长率,讨论背景电离层南北半球不对称对广义瑞利-泰勒不稳定性的影响.
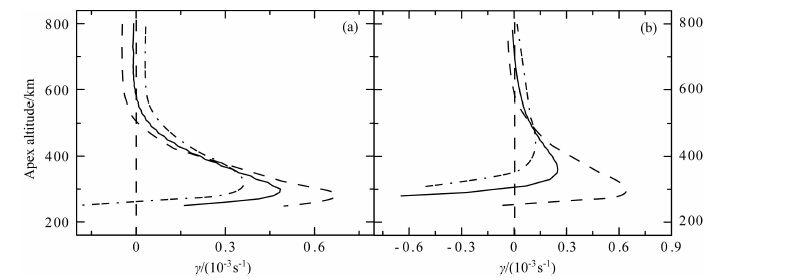
图 5给出120°E(图 3a)和330°E(图 3b)南-北半球通量管积分线性增长率2γN (点虚线)、2γS (虚线)以及沿整条通量管的积分增长率γN +γS (实线)随磁力线顶点高度的变化.图中曲线分别依据(5)和(6)式计算得到.
|
图 5 120°E(a)和330°E (b)通量管积分增长率随磁力线顶点高度的变化图中点虚线、虚线和实线分别表示为两倍北半球通量管积分增长率、两倍南半球通量管积分增长率和整条通量管积分增长率 Fig. 5 ine, dashed-lines and solid lines represent two times of the integrated growth rate in north hemisphere, two tmes of the integrated growth rate m south hemisphere and integrated growth rate along the total flux-tube. |
由图 5可以看到,磁南北半球通量管积分增长率存在明显的差别,两倍北半球通量管积分增长率小于整条通量管积分增长率,两倍南半球通量管积分增长率大于整条通量管积分增长率,因此,用一个半球积分的两倍来代替沿整条通量管积分是不准确的.此外,经度不同,通量管积分增长率的半球不对称特征也有差别.在120°E,北半球增长率在约320km高度上出现极大,量值为0.36×103s-1,南半球在约290km 高度上出现极大,量值为0.62×103s-1,整条通量管积分增长率在约300km 高度上出现极大,量值约为0.49×103s-1;在330°E,北半球增长率在约420km 高度上出现极大,量值为0.13×103s-1,南半球在约300km 高度上出现极大,量值为0.65×103s-1,整条通量管积分增长率在约360km高度上出现极大,量值约为0.25×103s-1.图 5的结果表明,半球不对称对瑞利-泰勒不稳定性的发展和不规则结构的生成有不可忽略的重要影响.为了精确地估计瑞利-泰勒不稳定性增长率,在利用通量管积分方法进行计算分析时,不能简单地选取一个半球积分的两倍代替沿整条通量管的积分,而应该沿整条通量管积分.选取一个半球积分的两倍引入的误差会降低线性增长率的应用价值,也会影响对瑞利-泰勒不稳定性分析的结果.
导致通量管积分瑞利-泰勒不稳定性增长率南北半球不对称主要归因于背景电离层参量存在南北半球不对称,比如南北半球不对称的中性风场、背景电子密度、电导率以及随经度变化的磁偏角.随经度变化的中性风场对背景电离层的影响存在半球不对称[20],因此,导致背景电子密度呈南北不对称的不对称中性风场和随经度变化的磁偏角可能是导致不规则结构呈南北分布不对称的重要因素.各种天基和地基的实验观测表明[2-4],电离层不规则结构及其所引起的电离层闪烁活动都呈现南北半球分布不对称.不同半球等离子体不稳定性发展过程存在的差异,可以在一定程度上解释实验观测到的现象.
3.3 随经度变化的磁偏角和中性风场对瑞利-泰勒不稳定性的影响由于中性风场和磁偏角随地理经度变化,在不同经度区,中性风场和磁偏角对瑞利-泰勒不稳定性的影响不同,可能导致瑞利-泰勒不稳定性增长率表现出随经度的变化.下面讨论随地理经度变化的磁偏角和中性风场对通量管积分广义瑞利-泰勒不稳定性线性增长率的影响.
图 6给出磁偏角(实线)和线性增长率(虚线)随地理经度的变化.图中线性增长率根据式(6)计算得到,磁偏角由IGRF模型得到.图中增长率随经度的变化由左边纵坐标和底部横坐标表示,磁偏角随经度的变化由右边纵坐标和顶部横坐标表示.注意顶部横坐标相对于底部横坐标向东移动了30°.
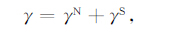
|
图 6 磁偏角(实线)和沿整条通量管的积分线性增长率(虚线)随地理经度的变化 Fig. 6 Flux-tube integrated growth rate (dashed-line) and declination (solid line) versus the geographic longitudes |
由图 6可以看到,增长率随地理经度变化的趋势与磁偏角随地理经度的变化趋势非常相似,但两者之间存在约30°的相位差.在180°E 至270°E(顶部横坐标),磁偏角为正,其值较大,变化较为平缓;与之相对应,在150°E 至240°E(底部横坐标),尽管增长率的值在210°E经度区出现一个极值,整体上看,通量管积分增长率的值相对较高,起伏变化也较小.在300°E 至330°E(顶部横坐标),磁偏角为负,其绝对值较大;对应地,在270°E 至300°E(底部横坐标),通量管积分增长率的值很小.在30°E 经度区(顶部横坐标),磁偏角的值较小;对应地,在0°E 经度区(底部横坐标),通量管积分增长率的值很大.这意味着磁偏角的变化对瑞利-泰勒不稳定性的发展有显著影响.较大的东向磁偏角有利于瑞利-泰勒不稳定性的发展,而较大的西向磁偏角抑制瑞利-泰勒不稳定性的发展.
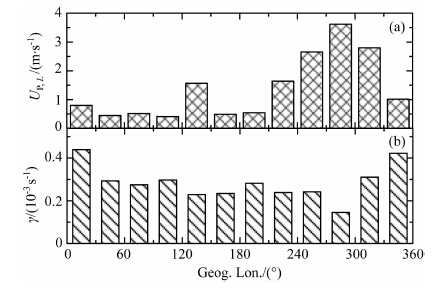
图 7给出沿整条通量管的磁子午面内垂直磁力线的积分垂直中性风场的大小UP,L(a)和线性增长率(b)随地理经度的变化.磁力线顶点高度为420km.图中UP,L和增长率分别根据式(4a)和(6)计算得到.
|
图 7 沿整条通量管的磁子午面内垂直磁力线的积分垂直风场UP,L(a)和线性增长率(b)随地理经度的变化 Fig. 7 Integrated neutral wind (a) and flux-tube integrated growth rate (b) versus the geographic longitudes |
由图 7可以看到,在大部分经度区,磁子午面内垂直于磁力线的热层风场绝对值随地理经度的变化趋势与增长率的变化趋势相反.随着积分中性风场的绝对值增大,增长率的值逐渐减小;随着中性风场的绝对值减小,增长率的值逐渐增大.增长率随地理经度的变化趋势与积分中性风场的变化趋势的这种相关性意味着,当垂直磁力线的中性风场的值较小时,促进瑞利-泰勒不稳定性的发展,不规则结构更易出现,这与文献[21]得到的结果一致.
增长率随地理经度的变化趋势与磁偏角和中性风场随地理经度的变化趋势存在相关性意味着,广义瑞利-泰勒不稳定性随经度的变化受到磁偏角和中性风场共同作用的影响.在增长率表达式(5)中,没有出现磁偏角,说明磁偏角对增长率没有直接的影响.而根据式(4a),磁偏角作为积分中性风场的权因子,对增长率有间接的影响,并且对子午风和纬圈风,权因子不同,这可能是磁偏角随经度变化和增长率随经度变化存在相位差的原因.
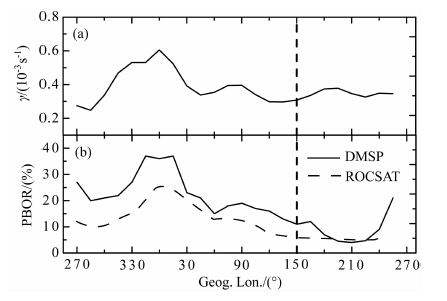
图 8比较了通量管积分增长率的经度变化与实测等离子体泡出现率的经度变化.图 8a给出沿整条通量管的积分线性增长率随地理经度的变化.图中增长率为1999—2004 年的3 月的平均值,根据式(6)计算得到.在计算增长率时,利用了ROCSAT卫星观测到的随经度变化的等离子体垂直漂移速度[22]所推算的电场.图 8b 给出两颗卫星观测到的等离子体泡的出现率(PlasmaBubble OccurrenceRate,简称PBOR)随经度的变化,实线为DMSP观测到的1989—2002年春季(3月)磁静期间,不规则结构的出现率随地理经度的变化;虚线为ROCSAT观测到的1999—2004 年春季(2—4 月)磁静期间,不规则结构的出现率随地理经度的变化.图 8b是基于文献[23]和[24]的结果重新制作.
由图 8b可以看到,尽管ROCSAT 与DMSP卫星轨道高度不同,整体上看,它们测量到的等离子体泡出现率随经度变化的特征基本一致,从330°E 至30°E,等离子体泡出现率较高,而从180°E 至240°E,等离子体泡出现率较低.比较图 8a和图 8b可以看到,理论计算得到的增长率随地理经度的变化趋势与卫星观测到的不规则结构出现率的经度变化存在一些类似的特征.从270°E 至150°E,增长率的变化趋势和不规则结构出现率的变化趋势基本相同,增长率的极大值和不规则结构出现率的极大均出现在0°E 附近,在210°E 和285°E 附近都出现极小.这表明广义瑞利-泰勒不稳定性是导致不规则结构出现的主要机制,通量管积分广义瑞利-泰勒不稳定性线性演化过程分析用于预测不规则结构的出现有指导性的意义,可以在一定程度上有效地反映包含非线性演化过程在内的电离层不规则结构的活动特征.
|
图 8 通量管积分增长率的经度变化(a)与实测等离子体泡出现率的经度变化(b)的比较 Fig. 8 Flux-tube integrated growth rate (a) and plasma bubble occurrence rate(b) versus the geographic longitudes |
不过,比较图 8a和图 8b也可以看到,有一些经度区域,增长率的变化趋势和不规则结构出现率的变化趋势不完全一致.这种不一致性表明,瑞利-泰勒不稳定性的线性增长率仅反映不稳定性的线性发展,而卫星观测到的不规则结构出现率包含瑞利-泰勒不稳定性的线性发展阶段和非线性演化阶段,过程很复杂,仅开展线性演化过程分析不足以描述电离层不规则结构出现的逐日变化.另外,增长率的变化趋势与不规则结构出现率的变化趋势之间的差异也可能意味着,不规则结构的经度变化还受到其他因素的影响,如随经度变化的磁场强度等[25].同时,瑞利-泰勒不稳定性在F 层底部触发的不规则结构不一定都会上升至F 层顶部[26],这也可能使瑞利-泰勒不稳定性的线性增长率的变化规律与卫星观测结果存在差异.
Iyer等[9]利用地基测量手段,比较分析地磁纬度相近的印度和巴西扩展F 的出现率,结果发现,印度(75°E)扩展F 出现率的极大出现在午夜前的两分点期间,巴西(38°W)扩展F出现率的极大出现在12月至点期间,两个不同经度扇区扩展F 出现率随季节变化的特征不同可能与磁偏角不同有关.通过比较南美洲东海岸的巴西(38°W)和西海岸的秘鲁(77°W)与阿根廷(64.5°W)的地基观测资料,Abdu等[8, 27]发现,同处于赤道异常区磁纬相近的这三个地点,扩展F 出现率和闪烁活动对地方时和季节的依赖呈现显著不同的特征,他们认为这是电离层不规则结构出现率受到磁偏角控制的结果.比较图 6 和图 8b,在磁偏角较大,即地理子午面与地磁子午面夹角较大的经度区,如180°E—270°E(磁偏角为正)和300°E—330°E(磁偏角为负),不规则结构的出现率均不高,处于中等或较低水平,通量管积分线性增长率也较低;在磁偏角较小的经度区,如345°E—30°E 附近,不规则结构的出现率较高,在0°E附近有极大值出现,对应的通量管积分线性增长率也较高.在磁偏角变化较为平缓的180°E—240°E 经度区,不规则结构出现率和通量管积分线性增长率的变化趋势均较为平缓.比较本文理论计算结果和地基与天基测量结果说明,磁偏角对电离层不规则结构出现率的控制作用,实际上反映它是促进还是抑制瑞利-泰勒不稳定性线性增长.
对于不规则结构出现率在不同经度区的差异,除了磁偏角的影响,还应考虑中性风场的作用[28].比较图 7 和图 8b,在不规则结构出现率较大的0°E—15°E经度区,中性风场的值较小;在不规则结构出现率相对较低的255°E—315°E 经度区,积分中性风场的值较大.在30°E—60°E 经度区,随着中性风场的值逐渐增大,不规则结构的出现率逐渐减小.这表明中性风场可能是影响不规则结构出现率的经度变化的另一重要控制因素,强中性风场会抑制不规则结构的生成和发展[21].
4 结 论本文利用通量管积分技术,考查了半球不对称对广义瑞利-泰勒不稳定性的影响,并讨论了影响广义瑞利-泰勒不稳定性经度变化的因素,将计算得到的线性增长率与卫星观测结果进行了对比分析.理论分析和数值计算结果表明:
(1) 通量管积分广义瑞利-泰勒不稳定性线性增长率存在显著的半球不对称.在利用通量管积分方法研究低纬-赤道电离层中的电动力学过程和等离子体不稳定性时,应对整条通量管积分,而不能用某一半球积分的两倍代替整条通量管积分.
(2) 通量管积分广义瑞利-泰勒不稳定性线性增长率存在对地理经度的依赖,广义瑞利-泰勒不稳定性是导致不规则结构出现的主要机制.磁偏角和中性风场可能是导致瑞利-泰勒不稳定性和不规则结构经度变化的重要控制因素.
对于中性风场和磁偏角对背景电离层和等离子体不稳定性的影响,包括对粒子运动过程和粒子的密度分布和温度变化等;对于影响瑞利-泰勒不稳定性和不规则结构经度变化的其他因素,如等离子体垂直漂移和磁场强度等,都有必要利用电离层理论模型对其中的动力学过程进行进一步研究.
附录 公式(3)和(4)的推导在偶极坐标系(q,s,l)中,垂直于磁力线的横向电流密度jq和js可以表示为[16]
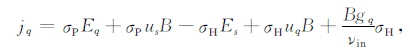
|
(A1) |
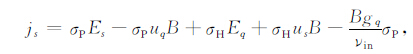
|
(A2) |
式中q在磁子午面内沿垂直地磁场B的方向(向外为正);s为磁子午面的法线方向(向东为正),l沿B的方向.Eq(s)和uq(s)为背景电场和中性风场在q和s方向的分量,σP 为Pedersen电导率,σH 为Hall电导率,νin 为离子-中性成分碰撞频率.
磁感应强度B和重力加速度gq由下式给出[15]:
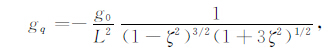
|
(A3) |
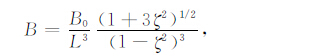
|
(A4) |
式中g0,B0 分别表示地表(L=1)磁赤道上的重力加速度和磁感应强度;ζ = sinθ,θ 为磁纬;L为McIlwain参数.
从极坐标系到偶极坐标系,电场的变换关系为
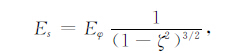
|
(A5a) |
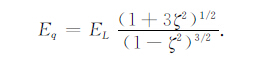
|
(A5b) |
定义等效到赤道面内沿磁力线积分的横向电流Jφ和JL为[15]
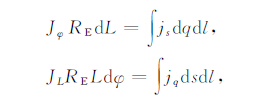
|
(A6) |
RE 为地球半径.考虑到南北半球不对称,沿通量管的积分将在南北半球分别进行.
积分长度变元为
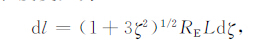
|
(A7a) |
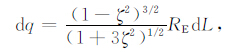
|
(A7b) |
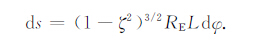
|
(A7c) |
把式(A7)代入式(A6),并利用定义式(A2)至(A5),整理后得到
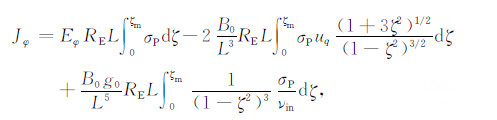
|
(A8) |
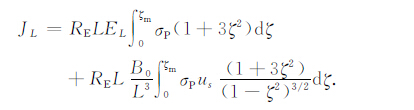
|
(A9) |
沿磁力线的积分路径从E 层底部(~100km,ζ=ζm)到磁力线顶点(赤道处,ζ=0).
定义通量管积分参量
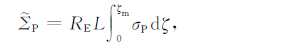
|
(A10a) |
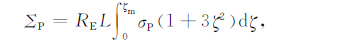
|
(A10b) |
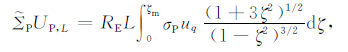
|
(A10c) |

|
(A10d) |
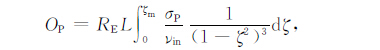
|
(A10e) |
利用定义式(A10),式(A8)和(A9)化为
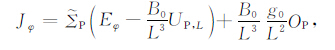
|
(EA11) |
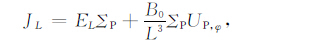
|
(A12) |
写成矢量的形式
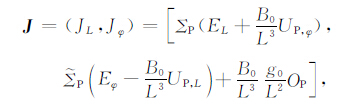
|
(A13) |
式(A13)即为文中式(3c),定义式(A10c)至(A10e)即文中式(4c)至(4e).注意,在导出式(A13)的过程中,应用了以下假设:Eq和Es是空间均匀的;σP、σH、uq、us和νin 不随φ 和L变化,仅仅是θ的函数;同时,忽略了含σH 的积分量.
考虑磁偏角和磁倾角的影响时,中性风场的表达式为
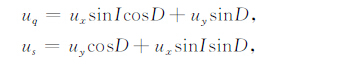
|
式中ux和uy分别为地理坐标系中的子午风和纬圈风,D和I分别为磁偏角和磁倾角.将其代入式(A10c)和(A10d)中,得到
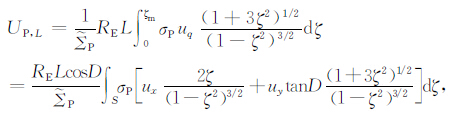
|
(A14a) |
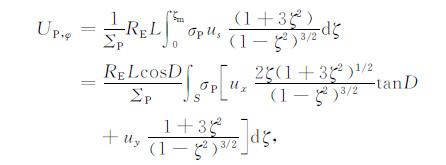
|
(EA14b) |
式(A14a)和(A14b)即为文中式(4a)和(4b).
定义粒子流通量为[15]
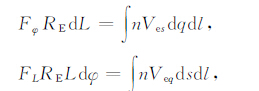
|
(A15) |
垂直于磁力线的横向电子速度分量为[16]
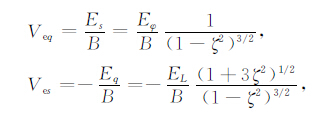
|
(A16) |
将式(A7b)和(A7c)分别代入式(A15)中,得到
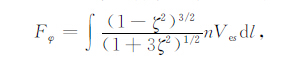
|
(A17a) |
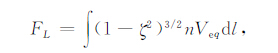
|
(A17b) |
将式(A16)分别代入式(A17a)和(A17b),并利用式(A4)、(A5)和(A7a),可得到
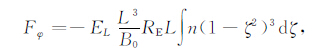
|
(A18) |
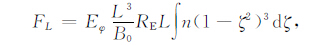
|
(A19) |
定义
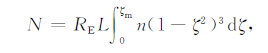
|
(A20) |
得到
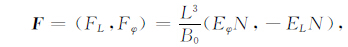
|
(A21) |
式(A20)即为文中式(3a).式(A21)即为文中的式(3b).
| [1] | Kelley M C. The Earth's Ionosphere: Plasma Physics and Electrodynamics (2nd ed). Elsevier, 2009. http://www.oalib.com/references/18986101 |
| [2] | Shimazaki T. A statistical study of world-wide occurrence probability of spread F, 1, Average state. J. Radio Res. Lab. , 1959, 6: 669-687. |
| [3] | Béghin C, Pandey R, Roux D. North-south asymmetry in quasi-monochromatic plasma density irregularities observed in night-time equatorial F-region. Adv. Space Res. , 1985, 5(4): 209-212. DOI:10.1016/0273-1177(85)90140-1 |
| [4] | Yokoyama T, Su S Y, Fukao S. Plasma blobs and irregularities concurrently observed by ROCSAT-1 and Equatorial Atmosphere Radar. J. Geophys. Res., 2007, 112: A05311, doi: 10.1029/2006JA012044. |
| [5] | Aydogdu M. North-south asymmetry in the ionospheric equatorial anomaly in the African and the West Asian regions produced by asymmetrical thermospheric winds. J. Atmos. Terr. Phys. , 1988, 50(7): 623-647. DOI:10.1016/0021-9169(88)90060-8 |
| [6] | Eyfrig R W. The effect of the magnetic declination on the F2 layer. J. Geophys. Res. , 1963, 68(9): 2529-2530. DOI:10.1029/JZ068i009p02529 |
| [7] | Tsundoa R T. Control of the seasonal and longitudinal occurrence of equatorial scintillations by the longitudinal gradient in integrated E region Pedersen conductivity. J. Geophys. Res. , 1985, 90(A1): 447-456. DOI:10.1029/JA090iA01p00447 |
| [8] | Abdu M A, Bittencourt J A, Batista I S. Magnetic declination control of the equatorial F region dynamo electric field development and spread F. J. Geophys. Res. , 1981, 86(A13): 11443-11446. DOI:10.1029/JA086iA13p11443 |
| [9] | Iyer K N, Jivani M N, Pathan B M, et al. Equatorial spread F: Statistical comparison between ionosonde and scintillation observations and longitude dependence. Adv. Space Res. , 2003, 31(3): 735-740. DOI:10.1016/S0273-1177(03)00047-4 |
| [10] | Abdu M A, Batista I S, Sobral J H A. A new aspect of magnetic declination control of equatorial spread F and F region dynamo. J. Geophys. Res. , 1992, 97(A10): 14897-14904. DOI:10.1029/92JA00826 |
| [11] | 肖佐, 张天华. 扩展F全球分布特点的理论分析. 科学通报 , 2001, 46(7): 597–599. Xiao Z, Zhang T H. A theoretical analysis of global characteristics of spread F. Chinese Sci. Bull. (in Chinese) , 2001, 46(7): 597-599. |
| [12] | Sultan P J. Linear theory and modeling of the Rayleigh-Taylor instability leading to the occurrence of equatorial spread F. J. Geophys. Res. , 1996, 101(A12): 26875-26891. DOI:10.1029/96JA00682 |
| [13] | Basu B. On the linear theory of equatorial plasma instability: Comparison of different descriptions. J. Geophys. Res. , 2002, 107(A8): 1199. DOI:10.1029/2001JA000317 |
| [14] | 罗伟华, 徐继生, 徐良. 积分电导率对广义R-T不稳定性的影响. 电波科学学报 , 2010, 25(5): 876–882. Luo W H, Xu J S, Xu L. Effects of flux tube integrated conductivity and its zonal gradient on the generalized R-T instability. Chinese J. Radio Sci. (in Chinese) , 2010, 25(5): 876-882. |
| [15] | Haerendel G, Eccles J V, Cakir S. Theory for modeling the equatorial evening ionosphere and the origin of the shear in the horizontal plasma flow. J. Geophys. Res. , 1992, 97(A2): 1209-1223. DOI:10.1029/91JA02226 |
| [16] | 罗伟华, 徐继生, 徐良. 赤道电离层R-T不稳定性发展的控制因素分析. 地球物理学报 , 2009, 52(4): 849–858. Luo W H, Xu J S, Xu L. Analysis of controlling factors leading to the development of R-T instability in equatorial ionosphere. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 849-858. |
| [17] | Bilitza D. International reference ionosphere 2000. Radio. Sci. , 2001, 36(2): 261-275. DOI:10.1029/2000RS002432 |
| [18] | Picone J M, Hedin A W, Drob D P, et al. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. , 2002, 107(A12): 1468. DOI:10.1029/2002JA009430 |
| [19] | Drob D P, Emmert J T, Crowley G, et al. An empirical model of the Earth′s horizontal wind fields: HWM07. J. Geophys. Res., 2008, 113: A12304, doi: 10.1029/2008JA013668. http://www.oalib.com/references/18990348 |
| [20] | McDonald S E, Dymond K F, Summers M E. Hemispheric asymmetries in the longitudinal structure of the low-latitude nighttime ionosphere. J. Geophys. Res., 2008, 113: A08308, doi: 10.1029/2007JA012876. |
| [21] | Mendillo M, Baumgardner J, Pi X Q, et al. Onset conditions for equatorial spread F. J. Geophys. Res. , 1992, 97(A9): 13865-13876. DOI:10.1029/92JA00647 |
| [22] | Kil H, Paxton L J, Oh S J. Global bubble distribution seen from ROCSAT-1 and its association with the evening prereversal enhancement. J. Geophys. Res., 2009, 114: A06307, doi: 10.1029/2008JA013672. |
| [23] | Burke W J, Gentile L C, Huang C Y, et al. Longitudinal variability of equatorial plasma bubbles observed by DMSP and ROCSAT-1. J. Geophys. Res., 2004, 109: A12301, doi: 10.1029/2004JA010583. http://www.oalib.com/references/18990335 |
| [24] | Su S Y, Chao C K, Liu C H. On monthly/seasonal/longitudinal variations of equatorial irregularity occurrences and their relationship with the postsunset vertical drift velocities. J. Geophys. Res., 2008, 113: A05307, doi: 10.1029/2007JA012809. http://www.oalib.com/references/18990337 |
| [25] | Vichare G, Richmond A D. Simulation study of the longitudinal variation of evening vertical ionospheric drifts at the magnetic equator during equinox. J. Geophys. Res., 2005, 110: A05304, doi: 10.1029/2004JA010720. |
| [26] | Hysell D L. An overview and synthesis of plasma irregularities in equatorial spread F. J. Atmos. Sol. Terr. Phys. , 2000, 62(12): 1037-1056. DOI:10.1016/S1364-6826(00)00095-X |
| [27] | Abdu M A, Sobral J H A, Batista I S, et al. Equatorial spread-F occurrence statistics in the American longitudes: Diurnal, seasonal and solar cycle variations. Adv. Space Res. , 1998, 22(6): 851-854. DOI:10.1016/S0273-1177(98)00111-2 |
| [28] | Maruyama T. A diagnostic model for equatorial spread F, 1, Model description and application to electric field and neutral wind effects. J. Geophys. Res. , 1988, 93(A12): 14611-14622. DOI:10.1029/JA093iA12p14611 |
 2012, Vol. 55
2012, Vol. 55


