基于GRACE 双星高精度感测中长波地球重力场的优秀表现，美国宇航局(NASA)提出了又一项专用于中短波地球重力场精密探测的GRACEFollow-On下一代卫星重力计划^[1-4].它预期采用近圆(轨道离心率0.001)、近极地(轨道倾角89°)和低轨道(轨道高度250km)设计，利用激光干涉测量系统高精度测量星间速度，利用高轨GPS卫星对低轨双星精密跟踪定位，利用高精度加速度计测量作用于双星的非保守力，利用无拖曳系统(Drag-free)高精度补偿双星受到的非保守力.GRACEFollow-On采用卫星跟踪卫星高低/低低飞行模式(SST-HL/LL)，既包含两组SST-HL，同时以差分原理测定低轨双星间的相互运动(星间距离约50km)，因此获得的全球重力场精度比GRACE 至少高一个数量级，同时为将来GOCEFollow-On卫星重力梯度测量计划的成功实施提供了借鉴价值.

早在20世纪60年代，Baker^[5]首次提出了利用卫星跟踪卫星技术(SST)测量地球重力场的重要思想.自此以后，国际大地测量学界的众多学者都积极投身于地球重力场反演方法的理论研究和模拟仿真之中.目前地球重力场反演方法主要包括6种类型:(1)轨道摄动法^[6-8]；(2)动力学法^[9-11]；(3)能量守恒法^[12-26]；(4)卫星加速度法^[27-30]；(5)半解析法^{[3， 31-35]}；(6)解析法^[4].但直到2000年以后，专用于地球重力场精密探测的重力卫星CHAMP(Challenging Minisatellite Payload)、GRACE (Gravity Recovery and Climate Experiment)和GOCE(Gravity Field and Steady-State Ocean Circulation Explorer)的成功发射及实测数据的有效处理应用，上述反演方法才真正进入实际操作阶段^[36-40].

卫星加速度法包括轨道加速度法和星间加速度法.由于GPS卫星定轨精度的限制，轨道加速度法较难建立高精度的地球重力场模型(如CHAMP 计划).星间加速度法的优点是观测方程形式简单、物理含义明确、易于重力场的敏感度分析、在保证求解精度的前提下计算量大大降低，通常采用PC 计算机可完成高阶地球重力场的快速求解；缺点是采用的数值微分算法在一定程度上损失了低频地球重力场的精度.文献^[27]于2005 年导出了星间加速度观测方程的简化形式，分别基于星间速度与星间加速度模拟计算了地球重力场；文献^[28]于2008年基于3点星间速度联合法(3RRC)解算了地球重力场；文献^[29]于2011 年基于星间加速度法反演了120阶GRACE 地球重力场；文献^[30]于2012年基于星间距离插值法，利用美国喷气推进实验室(JPL)公布的1 年的GRACE-Level-1B 实测数据，建立了120阶WHIGG-GEGM01S全球重力场模型.在上述研究建立的卫星观测方程中，由于引入了高精度的星间加速度观测量，因此地球重力场反演精度得到了大幅度地改善.由于星间加速度是地球重力场精度提高的关键因素，同时也是主要误差源，因此开展对星间加速度精度影响因素的分析研究是进一步提高地球重力场精度的重要保证.基于以上原因，本文利用星间加速度法开展了影响GRACEFollow-On星间加速度精度的插值公式、相关系数和采样间隔的优化选取论证，同时基于9点Newton插值公式、相关系数(K 波段测量系统星间距离和星间速度0.85、GPS轨道位置和轨道速度0.95、星载加速度计非保守力0.90)和采样间隔10s, 利用预处理共轭梯度法，精确和快速反演了120阶GRACEFollow-On地球重力场.

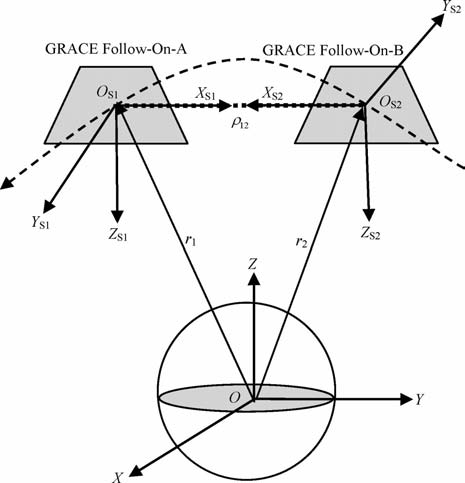
图 1表示星间距离、星间速度和星间加速度的测量原理，地心惯性坐标系O-XYZ的原点O位于地球的质心，X轴的正方向指向历元的平春分点，Z轴的正方向指向地球的北极，Y轴和X、Z轴成右手螺旋法则关系.星体坐标系O_S1(2)-X_S1(2)Y_S1(2)Z_S1(2)的原点O_S1(2)分别位于双星各自的质心，XS1和XS2(翻滚轴)的正方向反向共线，Z_S1(2)(偏航轴)垂直于X₁₍₂₎轴且位于同一轨道平面内，Y_S1(2)(倾斜轴)垂直于轨道平面且和X₁₍₂₎、Z₁₍₂₎轴成右手螺旋法则关系.

图 1

Fig. 1

图 1 GRACEFollow-On星间距离、星间速度和星间加速度的测量原理 Fig. 1 Measuring principle of intersatellite range, ranges rate and ranges acceleration from the GRACE Folk) w-On satellites

在地心惯性坐标系O-XYZ中，GRACEFollow-On星间加速度观测方程表示如下^[29]

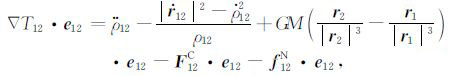
(1)

其中，ΔT₁₂ =Δ (T₂ -T₁)表示GRACE Follow-On-A/B相对扰动位梯度；ρ₁₂、$\dot{\rho }$₁₂ 和$\ddot{\rho }$₁₂ 分别表示星间距离、星间速度和星间加速度；GM表示地球质量M和万有引力常数G之积，r₁ 和r₂ 分别表示双星的绝对轨道位置矢量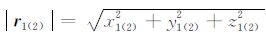，表示双星各自的地心半径，x₁₍₂₎，y₁₍₂₎，z₁₍₂₎ 分别表示双星各自位置矢量r₁₍₂₎的三个分量；r₁₂ =r₂-r₁和$\dot{r}$₁₂ =$\dot{r}$₂ -$\dot{r}$₁ 分别表示相对轨道位置矢量和相对轨道速度矢量，e12 = r₁₂/.r₁₂. 表示由GRACEFollow-On-A 指向GRACEFollow-On-B 的单位矢量；F₁₂^C=F₂^C-F₁^C 表示除地球引力之外的作用于双星的所有相对保守力之和(包括太阳引力、月球引力、地球固体、海洋、大气和极潮摄动力、广义相对论效应摄动力等)；f₁₂^N=f₂^N -f₁^N 表示作用于双星的所有相对非保守力之和(包括大气阻力、太阳光压、地球辐射压、卫星轨道高度及姿态控制力、经验摄动力等).

基于Newton插值模型，星间距离ρ₁₂ 的泰勒展开公式表示如下^[41]

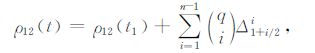
(2)

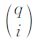
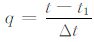
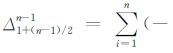
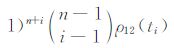
其中，表示二项式系数，，t表示插值点的时间，Δt表示采样间隔；表示差分算子，n表示插值的点数.

在(2)式两边同时对时间t求二阶导数可得星间加速度$\ddot{\rho }$₁₂ 的展开公式

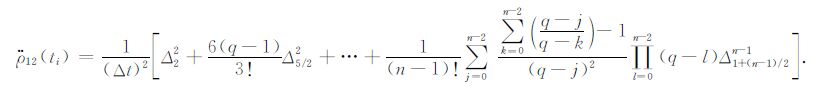
(3)

基于(3)式，3点、5点、7点和9点Newton插值公式表示如下:

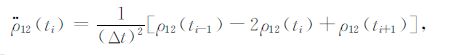
(4)

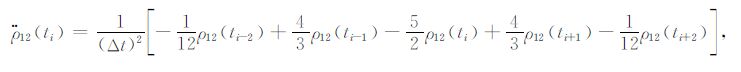
(5)

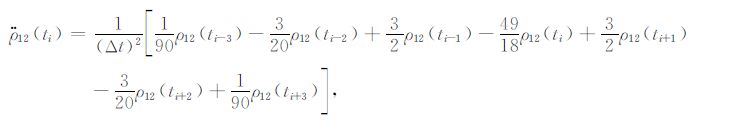
(6)

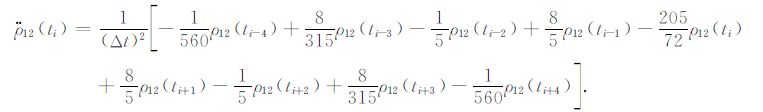
(7)

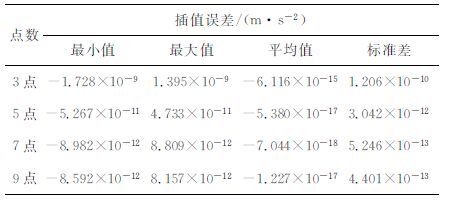
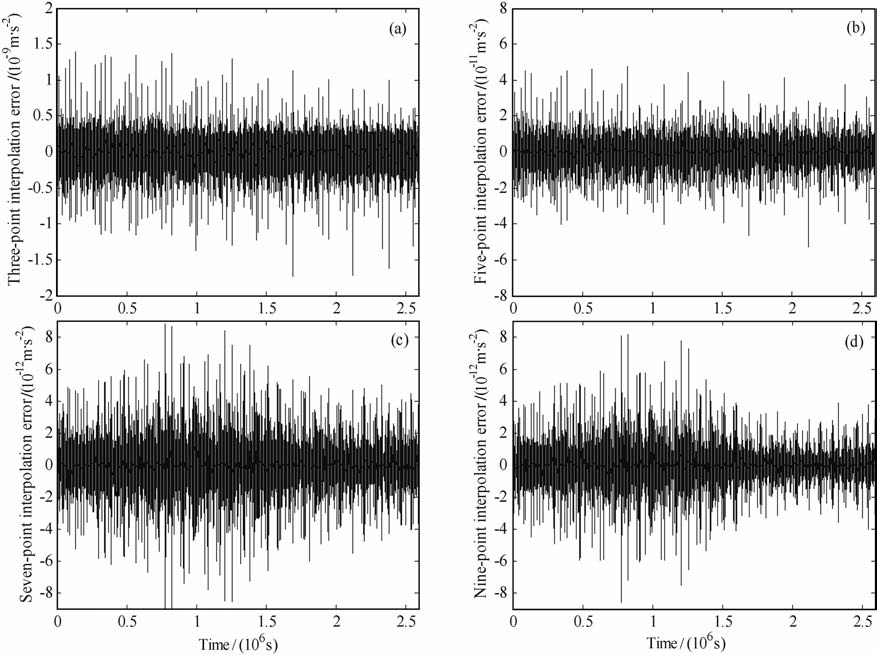
插值公式的优化选取是决定星间加速度精度的关键因素.基于$\dot{\rho }$12 =$\dot{r}$₁₂·e₁₂ +r₁₂·$\dot{e}$₁₂ 和(3)式计算得到的星间加速度分别为理论值和计算值，二者之差可有效评定Newton插值公式的插值精度.图 2表示基于采样间隔10s, 3 点、5 点、7 点和9 点Newton插值公式的插值精度，统计结果如表 1 所示.模拟结果表明:当采样间隔一定，随着Newton插值公式中插值点数的逐渐减少，星间加速度的插值误差逐渐增加.基于9 点Newton 插值公式，星间加速度的插值误差为4.401×10^-13 m·s^-2，分别基于7点、5点和3点Newton插值公式，插值误差增加了1.192倍、6.912倍和274.029倍.由于GRACEFollow-On星间加速度的测量精度约为10-12 m·s^-2量级，因此采用7 点和9 点Newton插值公式引入的插值误差将不会对GRACEFollow-On地球重力场的精度产生实质性影响.具体原因分析如下:

1) 当采用低阶插值公式(3 点和5 点)时，由于星间距离的插值点数较少，导致信号量较少，因此信噪比较低，不足以有效获得星间加速度信号.

2) 当采用高阶插值公式(7 点和9 点)时，随着星间距离插值点数增多，信号量逐渐增加，因此信噪比逐渐增高.但是，随着插值点数的增加，星间距离误差同时也逐渐增大，而且高阶微分公式易于放大观测误差，因此最优信噪比(插值点数)的选取是高精度获得星间加速度的关键所在.另外，优选7 点和9点高阶插值公式的详细计算和验证过程可具体参见文献^{[41， 42]}.综上所述，本文通过优化选取将采用9点Newton插值公式由星间距离插值得到星间加速度.

图 2

Fig. 2

图 2 不同点数Newton插值公式引人星间加速度的插值误差 (a)3点插值；(b)5点插值；(c)7点插值；(d)9点插值. Fig. 2 Interpolation errors of intersatellite range-acceleration based on Newton's interpolation formulaswith different number of interpolation points (a) Three-point； (b) Five-point； (c) Seven-point； (d) Nine-point.

表 1(Table 1)

表 1 星间加速度的插值误差统计 Table 1 Statistics of interpolation errors from intersatellite range-acceleration

表 1 星间加速度的插值误差统计 Table 1 Statistics of interpolation errors from intersatellite range-acceleration

星间加速度不是相互独立的，而是具有一定的相关性.因此，在插值的星间加速度中引入正态分布的随机白噪声不符合实际情况，应加入具有相关性的色噪声.星间加速度的色噪声可通过方差-协方差传播定律获得^[41]

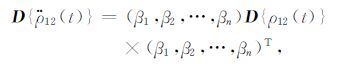
(8)

其中，D{ρ₁₂(t)}和D{$\ddot{\rho }$₁₂(t)}分别表示星间距离和星间加速度的方差-协方差矩阵，(β₁，β₂，…，βn)表示Newton插值公式(3)的系数.

假设卫星观测值是等精度测量，D{ρ₁₂(t)}表示如下

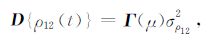
(9)

其中，σ_ρ12²表示星间距离的白噪声方差，Γ(μ)表示色噪声协方差转换阵:

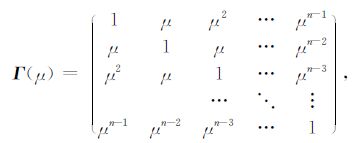
(10)

其中，μ=K^γ 表示相关系数(0<K<1)，K表示相关系数因子，.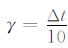

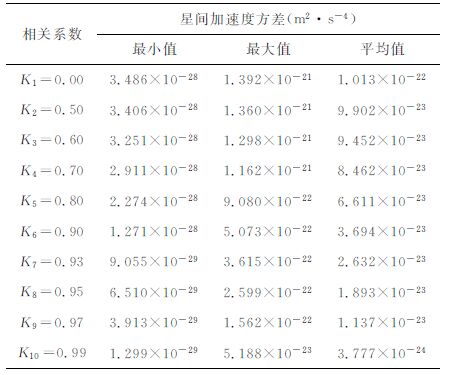
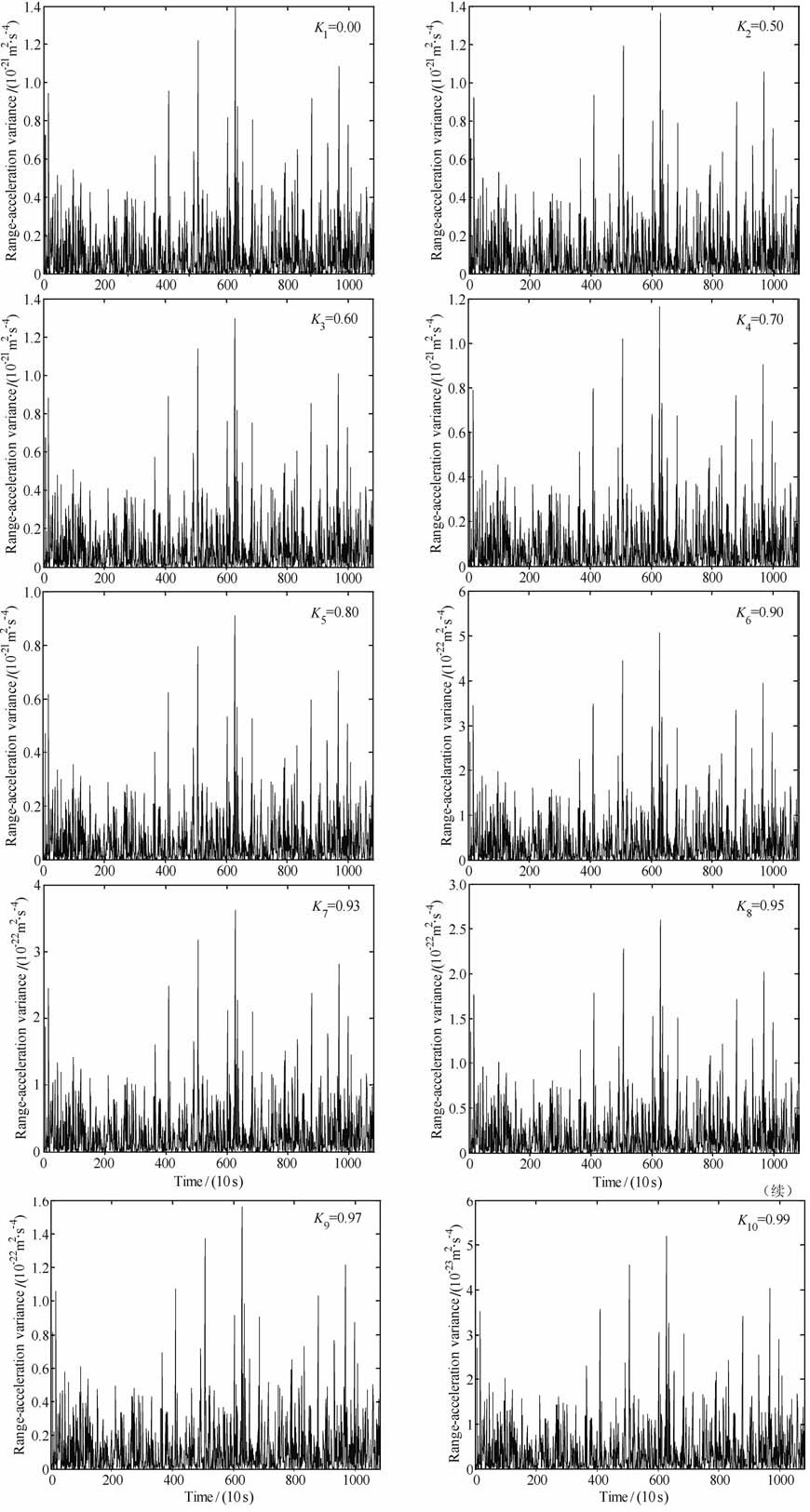
相关系数是影响星间加速度精度的重要因素.图 3表示基于9点Newton插值公式和采样间隔10s, 不同相关系数对星间加速度方差的影响，统计结果如表 2所示.模拟结果表明:当插值公式和采样间隔一定，随着相关系数逐渐增大，星间加速度的方差逐渐减小.基于相关系数0.99，星间加速度的方差为3.777×10^-24 m² ·s^-4，分别基于相关系数0.97、0.95、0.93、0.90、0.80、0.70、0.60、0.50和0.00，星间加速度的方差增加了3.011倍、5.102倍、6.968倍、9.780倍、17.503倍、22.404倍、25.025倍、26.217倍和26.820倍.在美国喷气推进实验室(JPL)公布的GRACELevellB实测数据中，K 波段测量系统星间距离和星间速度的相关系数约为0.85、GPS轨道位置和轨道速度的相关系数约为0.95、星载加速度计非保守力的相关系数约为0.90(see http://podaac.jpl.nasa.gov/grace).因此，本文将采用GRACE 卫星实测数据的相关系数计算星间加速度色噪声.

图 3

Fig. 3

图 3 不同相关系数对星间加速度方差的影响 Fig. 3 The impacts of correlation coefficients on variances of intersatellite range-acceleration

表 2(Table 2)

表 2 基于不同相关系数星间加速度方差统计 Table 2 Statistics of variances of intersatellite range-acceleration using different correlation coefficients

表 2 基于不同相关系数星间加速度方差统计 Table 2 Statistics of variances of intersatellite range-acceleration using different correlation coefficients

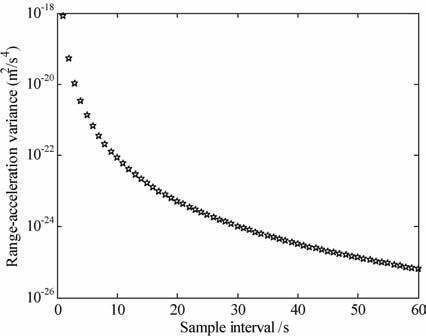
图 4表示基于9点Newton插值公式和相关系数因子K=0.99，不同采样间隔对星间加速度方差的影响.模拟结果表明:基于采样间隔1s, 星间加速度的方差为8.322×10^-19 m²·s^-4，分别基于采样间隔5s、10s、20s、30s和60s, 星间加速度的方差降低了6.228×10² 倍、9.929×10³ 倍、1.588×10⁵ 倍、8.004×10⁵ 倍和1.291×10⁷ 倍.当插值公式和相关系数因子一定，随着采样间隔的逐渐增大，星间加速度的方差逐渐降低，但同时卫星观测值的空间分辨率也随之降低.权衡利弊，本文将选取采样间隔10s计算星间加速度色噪声.

图 4

Fig. 4

图 4 不同采样间隔对星间加速度方差的影响 Fig. 4 Impacts of sampling interval on variances of intersatellite range-acceleration

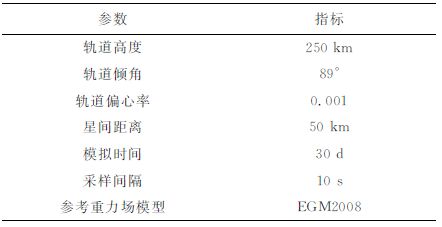
在卫星观测方程(1)建立之后，我们首先利用9阶Runge-Kutta 线性单步法结合12 阶Adams-Cowell线性多步法数值积分公式模拟了GRACEFollow-On-A/B的星历，轨道模拟参数如表 3所示.

表 3(Table 3)

表 3 GRACEFollow-On-A/B双星轨道模拟参数 Table 3 Orbital parameters from the GRACE Follow-On-A/B satellites

表 3 GRACEFollow-On-A/B双星轨道模拟参数 Table 3 Orbital parameters from the GRACE Follow-On-A/B satellites

基于Gauss-Markov 模型，卫星观测值的色噪声表示为^[41]

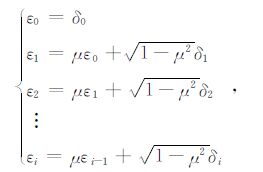
(11)

其中，δi(i=1，2，…，τ)表示正态分布的随机白噪声(μ=0)，i表示观测点的个数；ε_i(i= 1，2，…，τ)表示具有相关性的色噪声(0<μ<1).

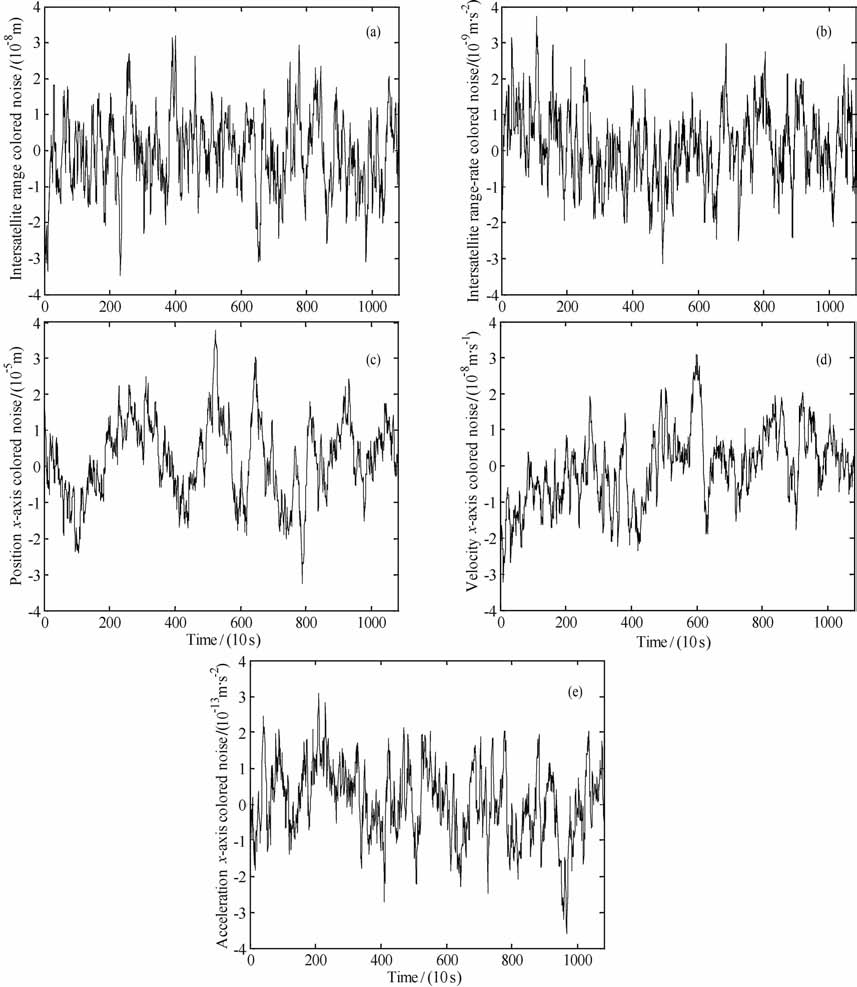
图 5 表示基于Gauss-Markov 色噪声模型，利用9点Newton插值公式、相关系数(K 波段测量系统星间距离和星间速度0.85、GPS轨道位置和轨道速度0.95、星载加速度计非保守力0.90)和采样间隔10s模拟的星间距离、星间速度以及轨道位置、轨道速度和非保守力x轴方向的色噪声(GPS轨道位置和轨道速度精度指标可通过高精度激光干涉星间测量系统辅助获得)，统计结果如表 4所示.

图 5

Fig. 5

图 5 星间距离、星间速度、轨道位置、轨道速度和非保守力色噪声模拟 Fig. 5 Colored noises of intersatellite range, intersatellite range-rate, orbital position, orbital velocity and non-conservative force

表 4(Table 4)

表 4 卫星观测值色噪声统计 Table 4 Statistics of colored noises from satellite observations

表 4 卫星观测值色噪声统计 Table 4 Statistics of colored noises from satellite observations

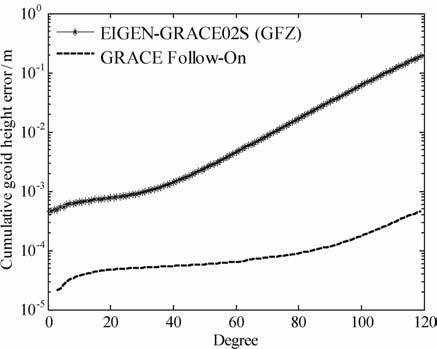
如图 6所示，星号线表示德国波兹坦地学研究中心(GFZ)公布的120阶EIGEN-GRACE02S地球重力场模型的实测精度，在120阶处累计大地水准面精度为1.894×10^-1 m；虚线表示基于9点Newton插值公式、相关系数(K 波段测量系统星间距离和星间速度0.85、GPS轨道位置和轨道速度0.95、星载加速度计非保守力0.90)和采样间隔10s, 利用Ditmar提出的卫星加速度平滑法^[43]结合预处理共轭梯度迭代法，反演GRACEFollow-On 地球重力场的模拟精度，在120 阶处累计大地水准面精度为4.602×10^-4 m, 统计结果如表 5所示.

图 6

Fig. 6

图 6 基于星间加速度法反演GRACE Follow-On 累计大地水准面精度 Fig. 6 Cumulative geoid height errors from GRACE Follow-On based on the intersatellite range-acceleration method

表 5(Table 5)

表 5 累计大地水准面精度统计 Table 5 Statistics of cumulative geoid height errors

表 5 累计大地水准面精度统计 Table 5 Statistics of cumulative geoid height errors

1) 当采样间隔一定，随着插值公式中插值点数的增多，信号量逐渐增加，但观测误差也同时增大，而且高阶微分公式易于放大观测误差，因此适当选择插值点数可有效优化信噪比进而提高插值精度.

2) 当插值公式和采样间隔一定，随着相关系数的逐渐增大，星间加速度的方差逐渐减小，因此适当增大相关系数可有效提高星间加速度的精度.

3) 当插值公式和相关系数一定，随着采样间隔逐渐增大，星间加速度的方差逐渐降低，但同时卫星观测值的空间分辨率也相应降低.因此，合理选取采样间隔有利于地球重力场精度的提高.

基于9 点Newton 插值公式、相关系数(K 波段测量系统星间距离和星间速度0.85、GPS轨道位置和轨道速度0.95、星载加速度计非保守力0.90)和采样间隔10s, 利用卫星加速度平滑法结合预处理共轭梯度迭代法反演了120 阶GRACEFollow-On地球重力场，在120阶处累计大地水准面精度为4.602×10^-4 m.

感谢编辑和评审专家、华中科技大学罗俊院士对本文的帮助.感谢美国宇航局(NASA)提供了GRACEFollow-On卫星的相关资料