2. 中国科学院研究生院,北京 100049
2. Graduate University, Chinese Academy of Sciences, Beijing 100049, China
岩石圈减薄是造山带演化过程的一个重要阶段,常被用来解释造山带后期演化过程的岩石圈伸展、地形抬升以及岩浆活动.根据前人的研究,造山带岩石圈减薄主要有两种可能机制:岩石圈拆沉作用和对流减薄作用.拆沉作用的概念是由Bird 在1978年和1979年发表的两篇文章中首次提出的,分别解释喜马拉雅造山带花岗岩岩浆作用和变质作用(可能是由于地壳和热的软流圈地幔接触产生)以及科罗拉多高原的隆升机制及伴随的岩浆作用机制[1, 2].1981 年,Houseman 等又提出,由于对流不稳定性,密度较大的岩石圈地幔沉入密度较小的软流圈从而导致岩石圈地幔减薄[3].
1996年,Seber等在Nature上撰文,从地震震源位置、地震波速及衰减、布格重力异常、地震反射波、钻井数据、地表地质学等各个方面的证据推测在AlboranSea及周围的西地中海区域的Betic和Rif造山带的下地幔中存在着高地震波速的刚性地质体,并指出该地质体很有可能是正在发生拆沉的大陆岩石圈[4],从而为岩石圈拆沉作用提供了很好的证据.有意思的是,Houseman 在同一期的Nature上指出该文提到的各种观测证据能更好地用对流减薄模型来解释[5].对于两种模式的区别,正如Houseman所指出的,Bird提出的拆沉作用的主要特点是发生拆沉的岩石圈沿着“拆沉轴"(axis of delamination)剥离(peel away)下沉[5],而对流减薄模型中,岩石圈发生连续变形,形成下降流从而导致减薄,与拆沉模型有三点不同:(1)对称,因而没有可移动的拆沉前(delamination front);(2)可能只有岩石圈地幔的下部参与减薄过程;(3)由于(2),软流圈并不会直接与地壳接触[3, 6].最新的研究也表明,这两种机制存在着明显的差别,适用于解释不同的地质构造现象[7~9].然而,由于这两种机制都能在较短的时间尺度内使岩石圈发生显著减薄,相关领域的学者们一般将它们统一称为拆沉作用[4, 5, 10].
碰撞造山带的演化可以分为三个阶段[11, 12]:(1)在板块构造力的作用下,地壳缩短增厚,地形升高;(2)地壳缩短停止,被抬升区域面积增加但抬升高度不再增加;(3)板块构造力消失,被抬升的区域发生重力垮塌.其中第二、三阶段的作用机制并不十分清楚.1991年,Nelson提出岩石圈拆沉是碰撞造山带演化的一个普遍存在的过程,并对大陆地壳的化学演化起着至关重要的作用[13, 14].1993 年,Kay等讨论了岩石圈拆沉作用和岩浆活动的关系[15],进一步肯定了拆沉作用在造山带演化研究中的作用.由此可见,岩石圈拆沉很可能是造山带第二、三阶段演化的一种作用机制.
尽管拆沉作用可以解释很多地质和地球物理现象,但是对于刚性岩石圈能否发生弱化却存在一些质疑.1998年,Meissner等通过合理的地温梯度和岩石圈组成估算了岩石圈的黏度深度曲线,指出岩石圈中有可能存在3 处低黏度区域,其中两处在地壳中,为下地壳和岩石圈地幔的拆沉提供了一定的支持[16].2001年,Jull等通过研究各种地壳地幔岩石在不同温度和压力下的流变性质和其他物性参数,结合数值模拟过程,指出在适当的条件下,Rayleigh-Taylor对流不稳定性可以导致下地壳在10 Ma的时间范围内沉入上地幔中[17].尽管如此,由于地球深部的不可入性,对于拆沉作用的触发及发生的形态的认识依旧处于很初步的阶段.
与此同时,一系列相应的数值模拟研究也极大地促进了人们对岩石圈减薄过程的认识[6, 12, 18~24].对于对流减薄机制而言,与Houseman的等黏度模型中大块岩石圈变形沉入上地幔不同,一些新的数值模拟研究认为,在温度压力相关的黏度模型中,只有处于刚性地幔岩石圈和软流圈之间的薄层会以drip off方式快速沉入上地幔中[20].在这种对流减薄机制中,加厚岩石圈是逐渐被底部对流侵蚀而减薄的,因此减薄所需的时间大为增加,甚至达到几十个Ma到上百个Ma.Pysklywec等人的数值模拟也显示,当岩石圈地幔的有效黏度较高时,只有极少部分底部的岩石圈地幔由于加热软化而沉入软流圈[24].为了区别这两种对流减薄机制,本文将Houseman 提出的对流减薄与Bird 提出的拆沉(delamination)归为一类,统称为拆沉作用,故如果不特别指明,本文后面提到的对流减薄均意指Morency等主张的对流减薄机制.
值得提出的是,起初国内地学界对于delamination的翻译有很多种,如拆沉作用、拆层作用、拆离作用等等[10].目前看来,以高山和金振民等主张的“拆沉作用"在很大程度上得到了国内地学界的认同.高山等综合分析了拆沉作用在地壳地幔演化过程中的重要意义,并提出拆沉作用是对经典板块构造理论的重要补充和完善.尽管对于拆沉作用存在各种各样的争论,但无可置疑的是,岩石圈拆沉作用的提出为我国大陆动力学研究提供了新的思路和方向.以秦岭-大别-苏鲁造山带为例,高山和李曙光等人的研究均认为该地区发生过岩石圈拆沉作用[10, 25, 26].在数值模拟方面,国内有许多学者从不同的角度研究了中国大陆和全球地球动力学过程的一些热点问题,取得了一些有意义的研究成果[27~35],有关岩石圈拆沉方面的数值模拟工作已成为近些年的研究重点之一.
本文基于非牛顿流体近似,用温度-压力-应变率相关的黏度模型对造山带岩石圈重力不稳定性的发展以及拆沉过程进行了二维数值模拟.通过不同的模型之间的比较,分析了岩石圈黏度结构对重力不稳定性的发展及拆沉作用的影响,展示并论述了岩石圈拆沉在造山带演化过程中的作用.
2 数值模型 2.1 控制方程目前研究岩石圈及其下覆地幔的动力演化问题时一般采用流体力学近似.在一定的边界条件和初始条件下,求解流体力学的Navier-Stokes方程组,即可模拟地壳和地幔的演化过程.假定该流体不可压缩,忽略惯性项,并采用Boussineqq近似,上述方程组一般可以表示为
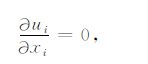
|
(1) |
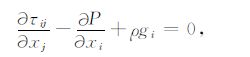
|
(2) |
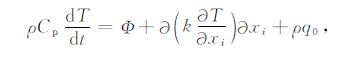
|
(3) |
其中,u,P,τ,g,Cp, T,t分别为速度、压力、偏应力、重力加速度、等压热容、温度和时间.
对于流体内部的偏应力τ,宏观上称为黏滞力,有如下本构方程:
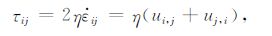
|
(4) |
其中η 是动力黏性系数,当η 与应变率无关,即黏滞力与剪切应变率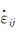
本文使用Ellipsis3D 对上述方程组进行二维数值模拟,流变关系采用非牛顿流体近似(如下文所示).Ellipsis3D 采用欧拉网格,同时以粒子追踪岩石的流变历史,并以粒子作为有限元单元的积分点,非常适合于模拟地质时间尺度下地球不同圈层介质的流变行为[36, 37].具体的算法描述及验证请参看文献[36].
2.2 流变关系地壳和地幔岩石的流变定律关系式为[38]
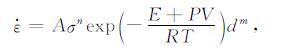
|
(5) |
其中\[{\dot{\varepsilon }}\] 为应变率,σ 为差应力,E为活化能,P为压力,V为活化体积,R为普适气体常数,T为温度,d为岩石粒度大小,m为粒度项指数(m<0).从(5)式可以看出,岩石的流变性质是与应变率、活化能、温度强烈相关的.由于在许多地球动力学过程中,应变率、温度是随时间变化的,所以岩石的流变性质具有非线性的、复杂的时空分布.为了便于处理,数值模拟中一般采用有效黏度来表征岩石的流变性质.若只考虑位错蠕变,则粒度项可忽略,即m=0,岩石的有效黏度可写为
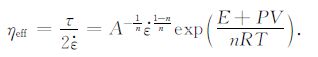
|
(6) |
除了上述流变定律之外,岩石在受力条件下的屈服机制及强度弱化机制也是岩石的流变性质非常重要的一个方面.数值模拟中一般采用如下屈服机制[12, 37, 38]:
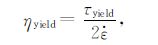
|
(7) |
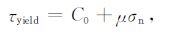
|
(8) |
其中公式(8)为Mohr-Coulomb 法则,C0 为内聚摩擦强度,μ 为摩擦系数.
采用如下应变相关的强度弱化机制[37]:
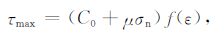
|
(9) |
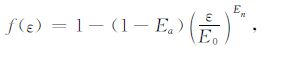
|
(10) |
其中应变ε为变量,其他为参数,取Ea=0.04,E0=0.2,En=1.
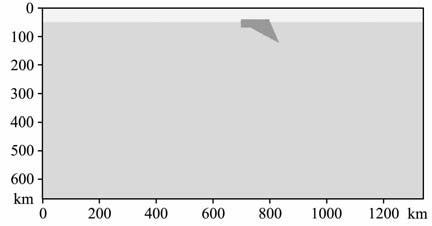
2.3 模型本文的主要研究目的是探讨造山带岩石圈由于重力不稳定性而发生拆沉减薄的过程,计算模型基于这样一个简单的假设:在造山过程中,岩石圈加厚产生重力上的不稳定性,在某种弱化机制下重力不稳定性逐步发展,部分岩石圈完全失稳发生拆沉作用进而沉入软流圈地幔.在模型设置过程中,采用笛卡儿二维直角坐标系,计算区域为1340km×670km, 在造山带内部设置一个低黏度区域以加速或引发拆沉作用的发生[8, 24],如图 1所示.
|
图 1 初始弱物质区域的设置:暗色区域为 弱区,黏度为5X1019Pa•s Fig. 1 The initial setup of weak material zone:The light area is weak zone, with viscosity of 5 X 1019 Pa•s |
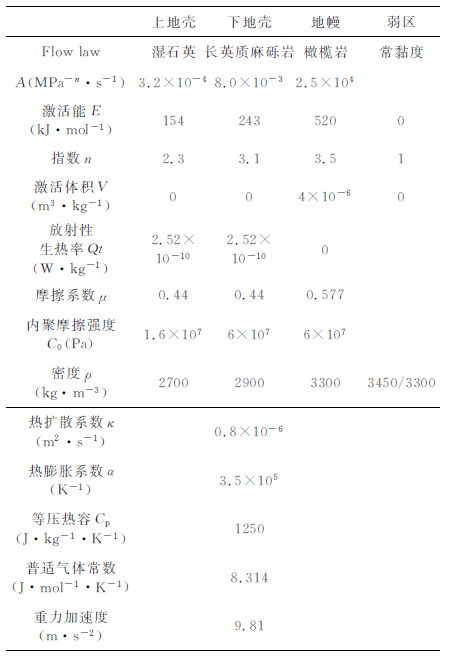
B.Schott等研究了地壳分层及厚度对拆沉过程的影响[12].参考他们的研究成果采取如下的地壳初始设置:34km 厚的上地壳,16km 厚的下地壳,其余为地幔.表 1是数值模拟过程中所采用的不同圈层物质的物性参数.
|
|
表 1 数值模拟过程中不同圈层物质的物性参数 Table 1 The physical parameters of different layers in the numerical simulation |
这里有必要引入数值模拟过程中的黏度截断温度的概念:在计算物质有效黏度时,若物质温度高于最低黏度截断温度,则以物质实际温度参与该物质的有效黏度计算;反之则以该物质最低黏度截断温度计算有效黏度.举个例子,如果某部分岩石温度为1000K,通过把该物质最低黏度截断温度设为1103K,就会导致该部分岩石的有效黏度降低.通过设置最低黏度截断温度,一方面可以防止有效黏度过大而导致计算难以收敛,另一方面可以有效调节不同圈层的黏度分布.这样,在有效地调节岩石圈的黏度结构的同时,也能保持黏度与温度、压力、应变率的函数关系.不仅如此,参与计算的有效黏度必须截断在一个范围,否则计算会很难收敛.计算模型的截断黏度取为1×1019~1×1024Pa·s.
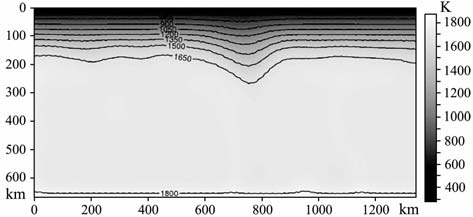
对于后碰撞造山阶段,我们采取与文献[12]相似的初始温度条件,如图 2 所示.在造山带下部,温度等值线向下弯曲,类似于余弦曲线,突出了加厚的岩石圈.温度边界条件为上下边界固定温度和侧边界热流为0,其中上边界273 K,下边界1873 K.速度边界条件为自由滑移边界条件,即垂直于界面的速度为0,且界面无切应力.从前面所提到的控制黏度的方法可以看出,该模型的初始温度条件一定程度上是与地壳地幔物质的最低黏度截断温度相关的.
|
图 2 初始温度条件 Fig. 2 Initial thermal condition |
从上述物质设置和热初始条件可以看出,模型中存在着初始的重力不稳定性.这个不稳定性也决定了整个模拟区域的初始应变力场.Ellipsis3D 采用反复迭代的方式处理非线性的流变关系(公式(6)),直到速度场收敛.为了防止局部区域由于应变率过小而导致收敛速度变慢,模型中设置了一个最低的应变率,即2×10-19s-1.
3 模拟结果及分析 3.1 拆沉过程图 3a~3e显示的是模型C1岩石圈拆沉作用过程中的温度场和速度场的演化过程.该过程大致分为三个阶段:
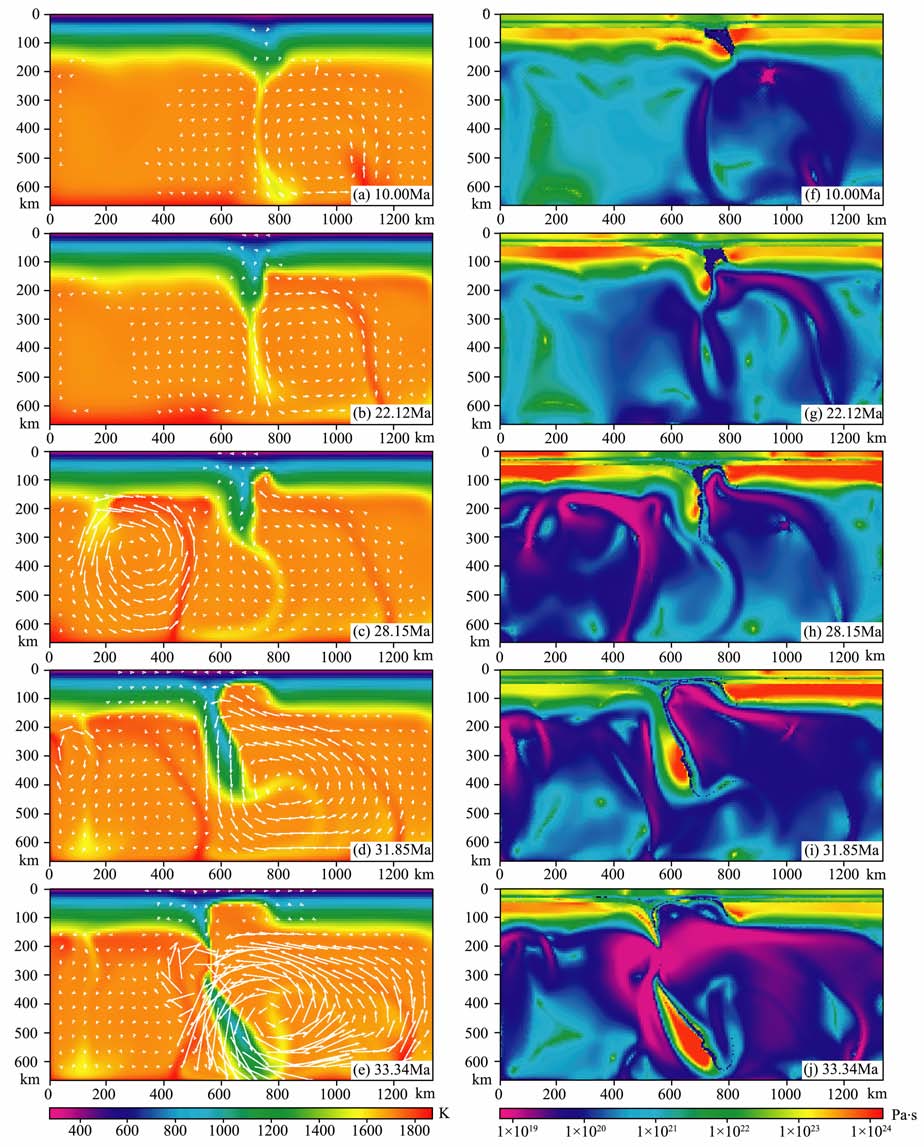
|
图 3 模型Cl岩石圈拆沉的温度速度(3a〜3e)和有效黏度(3f〜3j)演化过程 Fig. 3 丁he evolution of temperature-velocity (3a〜3e) and effective viscosity (3f〜3j) ofmodel Cl |
第一阶段:如图 3a~3b,加厚岩石圈的重力不稳定性逐步发展,岩石圈发生连续变形,这是一个相对而言较长的过程,约22 Ma.从地壳部分的速度场看,周围物质向造山带汇聚,故该过程对应造山带的挤压构造的后期.
第二阶段:如图 3b~3d,重力不稳定性发展到一定程度,岩石圈开始从最薄弱的地方撕裂剥离,软流圈物质沿撕裂处往上涌,并进一步加快撕裂过程,即开始拆沉,但此时拆沉的岩石圈仍然与上部岩石圈连在一起,拆沉块体的拖曳力与软流圈物质的上涌导致上部岩石圈发生一定程度的剥离(即Bird所谓的peel away).这一过程约5 Ma, 对应造山带挤压构造向伸展构造转化的时期.
第三阶段:如图 3d~3e,在岩石圈底部,拆沉块体的拖曳力使得其与上部岩石圈的连接处承受着巨大的拉力,最终导致拆沉块体与上部岩石圈完全解耦,快速沉入上地幔.同时由于软流圈物质的全面上涌,地壳部分的速度场变为发散型.这一过程比较短,约1 Ma, 该过程的发生标志着造山带正式进入伸展构造期.
图 3f~3j是分别对应图 3a~3e同时刻的黏度图像,从中可以看出拆沉过程中整个区域的有效黏度演化过程.在重力不稳定性发展的过程中,位于造山带中部的物质黏度减小,两侧物质黏度增大,岩石圈以下的上地幔黏度整体变小,如图 3f~3g;拆沉块体逐步下沉并在黏度弱区的作用下与右侧岩石圈解耦,导致右侧岩石圈受力变小,黏度增加(颜色变红),而左侧岩石圈受到极大的拖曳力,有效黏度降低1个数量级以上(颜色由红变黄),如图 3i;拆沉块体完全断离,应力释放,岩石圈受力变得均匀,黏度恢复到初始水平,如图 3j.
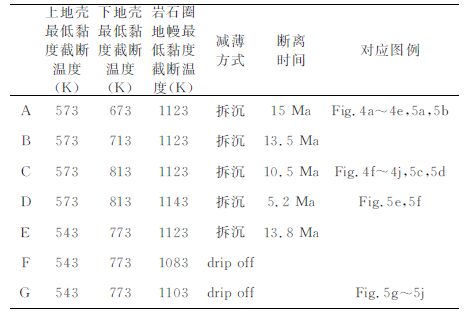
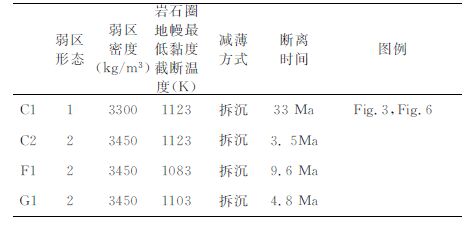
3.2 影响因素通过100多个算例的模拟计算,我们发现,相同模型设置、不同网格条件下的模型算例的结果有很好的相关性.为了统一对待,本文所有的图例及说明都针对160×80的网格精度而言.由于数值模拟的计算参数空间很大,本文选取下地壳和岩石圈地幔的最低黏度截断温度以及弱区的密度及形态作为主要可变参数,分析了岩石圈的黏度结构和密度结构对拆沉作用的发生及形态的影响.表 2 和表 3 展示了11个模型的参数设置及对应模拟结果的特征.需要说明的是,表中我们把大规模岩石圈沉入软流圈的过程都称为拆沉,而拆沉断离时间是指块体与上部岩石圈完全断离的时间,以此界定拆沉作用发生的时间.
|
|
表 2 各模型的参数设置及对应结果 Table 2 The parameter setup and corresponding result of our models 1 |
|
|
表 3 各模型的参数设置及对应结果2 Table 3 The parameter setup and corresponding result of our models 2 |
作为地壳与地幔的过渡形态,下地壳的流变性质在岩石圈变形及拆沉中起着非常重要的作用.如前所述,本文在模型中设置16km 厚的下地壳,通过调节黏度截断温度,可以有效控制下地壳的流变性质.表 2中,模型A,B,C 设置唯一的差别是下地壳的最低黏度截断温度.可以看出下地壳黏度越大(对应最低黏度截断温度越小),断离时间也就是拆沉发生的时间越长.这一点是显而易见的,因为下地壳黏度在一定程度上影响岩石圈不稳定性的发展.
然而下地壳的影响不仅如此.图 4 展示了模型A 与C 拆沉过程中的温度速度演化过程.通过比较可以发现两者之间存在着显著的差别:模型A 中,拆沉块体断离过程较为干脆,块体变形相对较小,如图 4d,4e,而在模型C 中拆沉块体像一个塑性体一样被拉长变细直至完全断离,块体变形相对较大,如图 4i,4j.图 5a和5c分别是模型A 和C 重力不稳定性发展时期的有效黏度分布图.比较可知,模型A的下地壳黏度的确比模型C 大,而这种差别正是造成上述不同拆沉形态的主要原因.不同的下地壳黏度影响了岩石圈的应力应变状态,从而导致了模型A和C的岩石圈黏度结构产生了更大的差异,如图 5b,5d.根据有效黏度的计算式,即公式(6),这种差异只可能是由温度场和应变率场的不同引起的.而从图 4中模型的温度场演化看,模型A 和C 的岩石圈温度结构并没有明显差异,故可以判断该差异主要是应变率的不同引起的.换句话说,模型A 相对于模型C 中发生了非常明显的局部应变集中现象.为什么模型A 和C 会产生这种差异呢?这与下地壳对岩石圈地幔的作用力有关.由于力学上的耦合,密度相对较低的下地壳物质的浮力对要拆沉的岩石圈地幔会施加一个向上的拉力.下地壳黏度越高,与岩石圈地幔耦合得越紧密,那么它施加给岩石圈地幔的拉力也就越大,因此局部应变集中现象会较早地出现,从而出现如图 4d,4e的断离现象.相反,下地壳黏度低,易于流动,它施加给岩石圈地幔的拉力小,拆沉块体被均匀拉伸,从而出现图 4i,4j的塑性拉伸断离现象.
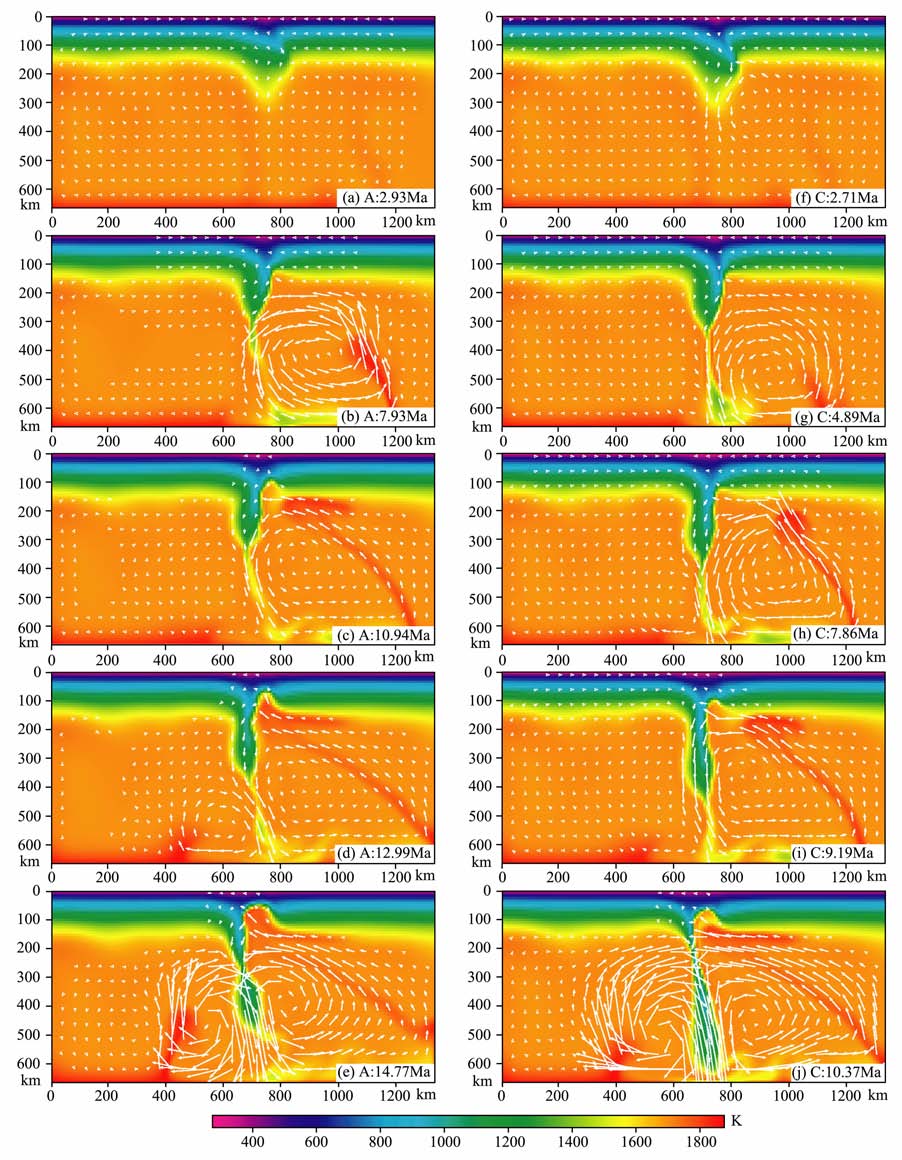
|
图 4 模型A (4a〜4e)与C (4f〜4j)的温度速度演化过程 Fig. 4 The evolution of temperature-velocity ofmodel A (a〜4e) and model C (4f〜4) |
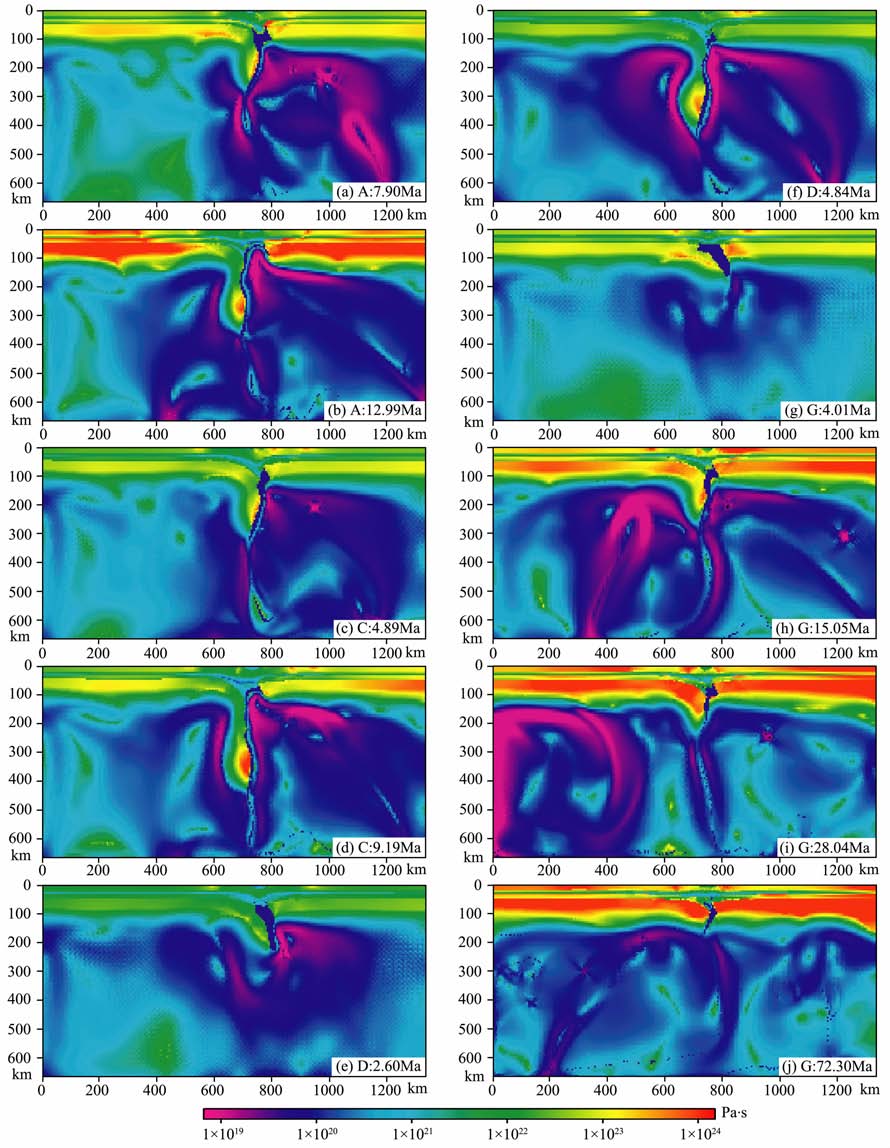
|
图 5 模型A,C,D,G的一些时间点的有效黏度分布图 Fig. 5 丁he effective viscosity distribution of some time points ofmodel A,C,D,G |
关于这一点,前人也有类似的结论,如B.Schott指出,分离(detachment)发生在下地壳高黏度和山根较厚时,因为上地壳施加给岩石圈地幔的张力是分离发生的一个重要因素[12].本文的研究肯定了下地壳流变性质在岩石圈拆沉断离过程中的影响,同时也认为岩石圈地幔塑性拉伸断离也是分离的一种方式.由此可见,下地壳的流变性质会影响岩石圈地幔的应力应变状态,进而影响拆沉过程的形态.
3.2.2 岩石圈地幔黏度的影响上文已有提及,下地壳的黏度在一定程度上影响着岩石圈拆沉过程发生的快慢.但是从表 2 中可以看出模型A,B,C 的断离时间的差距并不明显,尤其是对于下地壳最低黏度截断温度相差在100K 以上时而言.然而,比较模型C,D,岩石圈地幔的最低黏度截断温度提高20K(从C 到D),岩石圈拆沉的断离时间减少了5 Ma.再者,模型G 与E 相比,仅仅把该最低黏度截断温度降低了20K,岩石圈拆沉就不能发生.可以这样理解,截断温度降低20K,岩石圈地幔黏度增加,阻碍重力不稳定性的发展,使得拆沉发生的时间大幅延迟甚至不能发生.图 5a~5j分别是模型A,C,D,G 的一些时间点的有效黏度分布图.若比较各模型计算初期的岩石圈地幔黏度,可以发现:模型A≥1023Pa·s(图 5a),模型C≥1022Pa·s(图 5c),模型D≤1022Pa·s(图 5e),模型G≤1024Pa·s(图 5h),故D<C<A<G.这与表 2中的岩石圈拆沉的断离时间恰好对应,证明岩石圈地幔黏度越高,拆沉作用发生所需要的时间越长.这充分说明了岩石圈地幔的流变性质在岩石圈重力不稳定性的发展及拆沉过程中的主导性作用.
另外,值得注意的是,模型F,G 都是不能发生拆沉的,只有岩石圈底部物质以drip off(Morency所谓的对流减薄)方式飘入软流圈.图 5g~5j分别是模型G 在4.01,15.05,28.04,72.30 Ma时的有效黏度分布.从图中可以看出,尽管模型G 中岩石圈重力不稳定性有所发展,并在15.05 Ma时发展到顶峰,但是由于岩石圈的整体黏度比较高(大部分区域十分接近1024Pa·s),初始不稳定的岩石圈逐渐趋于稳定,仅在底界的对流作用下以dripoff方式发生缓慢地减薄,历时72.30 Ma还存着明显的岩石圈根.由此可见,若不发生拆沉作用,岩石圈很难发生大规模地减薄.Morency等指出,通过对流减薄方式,250km 厚的岩石圈完全减薄大约需要55~750Ma, 取决于岩石圈根的宽度[20],这与本文的数值模拟结果相互映证.
综合比较表 2中的算例,可以得出以下初步的结论:在一定的初始重力不稳定性条件下,当岩石圈地幔相关的有效黏度在1022~1024Pa·s时,拆沉作用有可能在5~30 Ma的时间范围内发生.而当有效黏度过高以致于重力不稳定性发展过于缓慢,岩石圈大规模减薄和拆沉作用则不能发生.同时,由于调节岩石圈地幔最低黏度截断温度与改变莫霍面温度有类似的效果,可以将该最低黏度截断温度看成是莫霍面温度.这样,从表 2 中的算例也可以看出,莫霍面温度对岩石圈重力不稳定性发展和拆沉过程有着很大的影响,即使是20K 的变化也能影响到拆沉作用的发生与否.
3.2.3 初始重力不稳定性的设置的影响岩石圈内部的重力不稳定性是拆沉作用发生的驱动力,而造成重力不稳定性的原因主要是不同圈层的密度差异.如前所述,本文在数值模拟中采用高密度的弱物质区来引发岩石圈拆沉作用.因此,改变弱物质区的密度大小及形态也就意味着改变了初始重力不稳定性的设置.表 2 中的模型使用的是同一种弱区形态设置(如图 1,不妨设为弱区设置1),表 3中的模型引入更大区域的弱区(设为弱区设置2)并改变弱区的密度.
首先看弱区密度的影响,模型C 与C1 的初始参数设置的差别仅在于弱物质区的密度,C 中密度为3450kg/m3,而C1 为3300kg/m3.计算结果显示,模型C 重力不稳定性发展很快,拆沉较早发生,并在10.5 Ma发生断离,而C1 经历了近20 Ma的重力不稳定性的发展才开始发生拆沉作用,在约33Ma发生断离.比较模型C 与C1在计算初期的岩石圈地幔黏度(图 5c和图 3f)发现,后者比前者高了近一个量级.这说明密度差异的减小通过应变率相关的黏度模型提高了岩石圈黏度,导致岩石圈重力不稳定性需要经过一定时间的积累才会发生拆沉.
同样,模型C2 在C 的基础上采用弱区设置2(即在图 1显示的弱区设置1 的基础上稍微加大弱区面积),模拟结果即产生显著差异,在3.5 Ma时即发生拆沉断离.根据前面分析可知,拆沉时间发生如此显著的变化,主要是由于高密度的弱区加大了初始重力不稳定性,并在应变率相关的黏度模型下软化了岩石圈,加速了重力不稳定性的发展.这种由弱区形态的变化引起的变化更明显地体现在模型F,G 与F1,G1的对比上:岩石圈地幔最低黏度截断温度为1103K 和1083K 时模型F,G 均不能发生拆沉,但一旦将弱区变大,模型F1,G1 重力不稳定性发展极快,拆沉断离时间甚至比A~D 都短.
4 讨论与应用通过不同模型算例的比较分析,前文已经论述了影响岩石圈拆沉过程的诸多因素.下面将综合讨论本文的数值模拟研究取得的认识,以及在造山带演化过程中的应用.
4.1 拆沉的触发及形态岩石圈拆沉是学者们研究造山带的演化时提出的一种假说,尽管这个假说能够解释很多的地学现象,但对于拆沉作用是怎样触发的这个问题却没有详细的研究.B.schott认为拆沉仅在加厚岩石圈的强度被极大地弱化(如水的弱化)时才能发生[12].本文基本上赞同这个观点,故而在模型设置中用弱物质区引发拆沉.但如模型结果所显示的,一旦围岩的有效黏度太高,弱物质区并不能引发拆沉.而Morency提出岩石圈拆沉发生在莫霍面温度超过800℃(1073K)的地方.尽管模型A~G 显示的拆沉临界莫霍面温度约为1123K 或更小,与上述观点基本一致.但本文认为这样一个临界值并没有太大意义,因为在数值模拟中影响有效黏度的重要因素还有岩石圈的流变参数的选取和背景应力应变状态.关于流变参数,影响最大的莫过于橄榄岩(上地幔的主要矿物)的活化能.根据橄榄岩的物性实验[38],干橄榄岩(dryolivine)的活化能为532±52kg/m3,湿橄榄岩(wetolivine)为471±31kg/m3.在上述范围内取不同的活化能参数进行模拟,所得到的临界值会有不小的差异.
应力应变状态是受板块构造力作用而改变的,其变化可能比温度变化更快,因而在某种程度上对岩石的流变性质的影响更为显著.本文的模型中并没有引入板块运动速度,加厚岩石圈的负浮力是造成应力应变状态改变的主导因素,关于板块运动速度的影响,相关研究已有论述[6, 22, 24].模型C1 与其他模型不同,经过了近20 Ma的重力不稳定性的发展才开始发生拆沉.图 3f~3j显示了模型C1 岩石圈拆沉过程中的有效黏度演化过程.从图中可以看出,重力不稳定性缓慢发展,同时局部区域的有效黏度逐步降低,在即将断离时黏度降低达到最高水平.分析可知,有效黏度的降低主要是由应变率升高导致的,因为热传导造成温度显著差异需要很长时间,而压力增加的效果是使黏度增加.在实际构造环境下,由于板块运动,岩石的应变率变化所导致的岩石圈的弱化效应应该比本文数值模拟的结果更为显著.
对比模型C1和模型C,我们发现提高弱区密度150kg/m3,拆沉作用的发生约提前了20 Ma.同样模型C2 在C 的基础上加大弱区面积,导致拆沉断离时间从10.5 Ma减少到3.5 Ma.由此可见,数值模拟过程中高密度物质对拆沉作用的触发具有非常重要和直接的作用.事实上,许多相关研究都认为相变所产生的高密度的榴辉岩下地壳触发了拆沉作用[13, 25, 26].因此本文从数值模拟的角度支持了这一观点.
根据前人的研究,Bird提出的拆沉作用有一个非常重要的特点:岩石圈地幔从上覆地壳剥离(peelaway)沉入软流圈[1, 2, 5].本文的数值模拟显示,岩石圈拆沉过程中的确存在着这种剥离,如图 3c~3e,3f~3i,3f~3i, 4c~4e所示.分析可知,剥离过程是由已沉入到软流圈的部分岩石圈地幔对与其相连的岩石圈地幔的拖曳力导致的,拖曳力越大越持久,剥离的范围越大.需要指出的是,本文模型中岩石圈地幔剥离的范围并不取决于模型设置中的弱区长度.如模型C1与A,C 比较具有相同的弱区长度,但C1的剥离长度约为A,C 的两倍以上.这是因为,C1中岩石圈有效黏度更高,重力不稳定性发展缓慢,剥离过程中拆沉块体的应力集中发生得较晚,使得更大范围的岩石圈地幔受到了影响,从而导致了更大范围的剥离.相反,若岩石圈地幔的黏度较小,如模型C 和D,则剥离范围很小以至于不发生剥离,如图 5d,5f.由此可见,在一定的岩石圈地幔有效黏度范围内(1022~1024Pa·s),若拆沉作用发生,黏度越大,重力不稳定性发展越慢,剥离范围越大.
4.2 应用挤压构造转化为伸展构造是造山作用的一个非常重要的过程.造山带前期的挤压构造是由板块汇聚所造成的,而后期的伸展构造常被简单归因于造山过程中积累的重力势能的释放.本文数值模拟所展示的拆沉作用有利于对造山带的这一过程的认识.
图 6展示了模型C1岩石圈拆沉过程中相关区域(x:400~800km, z:0~50km)的地壳速度场随时间的演化过程.从图中可以看出,在岩石圈重力不稳定性发展的过程中,地壳的汇聚中心会逐渐迁移,汇聚速度也有所减小,如图 6a~6d;紧接着,由于软流圈物质的上涌,地壳开始受到向上、向左的推力,中部地壳速度变大,周围地壳收敛速度趋于零,如图 6e~6g;最后中部地壳速度减小,随着拆沉块体完全断离,地壳开始进入全面的伸展时期,如图 6h,6i.
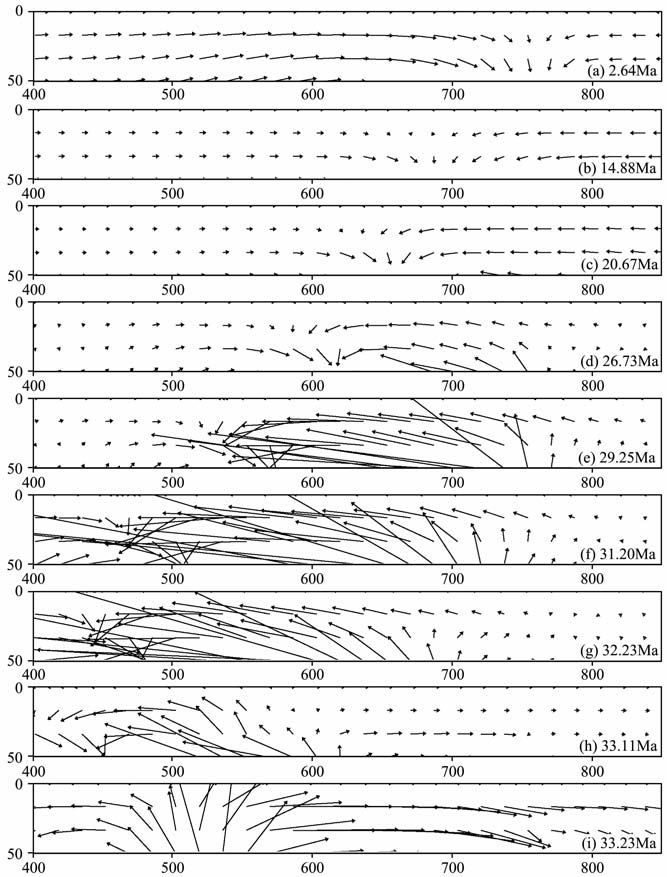
|
图 6 模型Cl相关区域(x:400〜800 km,:^:0〜50 km)的地壳速度场演化 Fig. 6 丁he evolution of crustal velocity in relative area (x:400〜800 km,之:0〜50 km) ofmodel C1 |
Houseman总结了一些以青藏高原为首的区域较宽的造山带的逆断层到正断层的转化时间,以此研究造山带从挤压构造到伸展构造的演化过程[6].结果发现,逆断层的终止到正断层的开始的间隔时间在数个Ma到50 Ma之间,其中大部分小于10 Ma, 个别甚至只有3 Ma左右.对于小型造山带似乎还没有相关研究,但是转化时间应该比上述时间还短.从图 6可以看出,模型C1 挤压构造转化为伸展构造的时间间隔约为4 Ma.因此,岩石圈拆沉作用是造山带由挤压构造转化为伸展构造的一种可能机制.
以秦岭-大别-苏鲁造山带为例,结合本文的数值模拟,我们发现拆沉作用能很好地解释造山带的地质构造现象及伴随的其他特征.许长海等对大别造山带的构造研究认为,140~85 Ma大别造山带进入热穹窿伸展作用时期[39].图 6h 显示了拆沉作用发生后造山带地壳的速度场,结合图 3e,3g,3i的岩石圈温度场,可以看出是软流圈物质的上涌导致了造山带的热穹窿伸展作用.事实上,李曙光等也认为早白垩世(130~110 Ma)大别山穹窿的迅速隆升及相对应的大规模岩浆事件需要一次岩石圈拆离(拆沉)[26].从本文图 3 所示的温度场看,拆沉作用过程中,高温的软流圈物质(红色)和低温的下地壳(蓝色)直接接触,如图 3c,3d,3e.这导致的一个直接结果是下地壳被软流圈侵蚀改造,引发地表的岩浆活动.因此,拆沉作用所导致的软流圈物质的上涌很好地解释了该地区的幔源岩浆活动.高山等建立了秦岭-大别造山带下地壳拆沉作用的化学地球动力学模型,认为大别苏鲁地区的榴辉岩是最可能被拆沉的物质[25].而本文数值模拟结果也表明,莫霍面附近的高密度物质(如榴辉岩)很有可能引发岩石圈拆沉作用.
另外,Davies等曾经提出一个模型解释同/后碰撞期岩浆活动和交代作用:大洋岩石圈俯冲导致陆陆碰撞,大洋岩石圈与大陆岩石圈的断裂(slabbreakoff)时,软流圈地幔沿裂口处上涌导致了岩浆活动和交代作用.但将该模型应用到大别山却发现,该地区大洋岩石圈与大陆岩石圈断裂深度在130km以上(由该地区的高压变质岩研究得出),无法产生大规模的岩浆活动[40].从本文前面的分析可以看出,在拆沉作用过程中,岩石圈开始撕裂,软流圈物质上涌即会引发岩浆活动,而块体断离与岩浆活动并没有直接关系.至于该地区的高压/超高压变质岩的形成和出露,则可能与拆沉块体的俯冲断离有关[25],但这不在本文的讨论范围之内,有待进一步研究.因此,相比Davies的模型,岩石圈拆沉作用能够更好地解释大别地区的岩浆事件.
5 结论本文从数值模拟的角度研究了造山带岩石圈由于重力上的不稳定性而发生拆沉作用的过程.通过不同模型分析比较及综合讨论,得出了以下几点认识:
(1) 下地壳的流变性质控制着地壳与岩石圈地幔的耦合程度,对岩石圈拆沉过程中断离的形态有很大的影响.当下地壳黏度较高时,耦合程度高,下地壳物质的浮力会施加较大向上的拉力从而使得断离较早发生,反之亦然.
(2) 岩石圈地幔的流变性质是影响重力不稳定性发展快慢的主要因素,在一定的初始重力不稳定性条件下,当岩石圈地幔相关的有效黏度在1022~1024Pa·s之间时,拆沉作用有可能在5~30 Ma内发生.莫霍面温度对岩石圈重力不稳定性发展和拆沉过程有着很大的影响,即使是20K 的变化也能影响拆沉作用的发生与否.
(3) 在非牛顿流体近似下,由于有效黏度与岩石应变率相关,高密度物质(如榴辉岩)对拆沉作用的触发有着很显著的作用.
(4) 岩石圈拆沉过程中的确存在着Bird 所描述的剥离(peel away)现象,这是由岩石圈的密度和黏度结构决定的.在一定的岩石圈地幔有效黏度范围内(1022~1024Pa·s),若拆沉作用发生,黏度越大,重力不稳定性发展越慢,剥离范围越大.
(5) 岩石圈拆沉过程中,软流圈物质上涌,会造成地表的岩浆活动,甚至热伸展作用.当拆沉块体完全断离时,造山带完成从挤压构造到伸展构造的转化过程.
致谢本成果使用了科学计算网格ScGrid, 开源程序Ellipsis3D,图例由GMT[41]绘制.感谢两位审稿人的建设性建议.
| [1] | Bird P. Initiation of intracontinental subduction in the Himalaya. J. Geophys. Res. , 1978, 83(B10): 4975-4987. DOI:10.1029/JB083iB10p04975 |
| [2] | Bird P. Continental delamination and Colorado Plateau. J. Geophys. Res. , 1979, 84(B13): 7561-7571. DOI:10.1029/JB084iB13p07561 |
| [3] | Houseman G A, McKenzie D P, Molnar P. Convective instability of a thickened boundary layer and its relevance for the thermal evolution of continental convergent belts. J. Geophys. Res. , 1981, 86: 6135-6155. |
| [4] | Seber D, Barazangi M, Ibebrahim A, et al. Geophysical evidence for lithospheric delamination beneath the Alboran Sea and Rif-Betic mountains. Nature , 1996, 379(6568): 785-790. DOI:10.1038/379785a0 |
| [5] | Houseman G A. From mountains to basin. Nature , 1996, 379(6568): 771-772. DOI:10.1038/379771a0 |
| [6] | Houseman G A, Molnar P. Gravitational (Rayleigh-Taylor) instability of a layer with non-linear viscosity and convective thinning of continental lithosphere. Geophys. J. Int. , 1997, 128(1): 125-150. DOI:10.1111/gji.1997.128.issue-1 |
| [7] | Gogus O H, Pysklywec R N. Near-surface diagnostics of dripping or delaminating lithosphere. J. Geophys. Res. , 2008, 113: B11404. DOI:10.1029/2007JB005123 |
| [8] | Gogus O H, Pysklywec R N. Mantle lithosphere delamination driving plateau uplift and synconvergent extension in eastern Anatolia. Geology , 2008, 36(9): 723-726. DOI:10.1130/G24982A.1 |
| [9] | West J D, Fouch M J, Roth J B, et al. Vertical mantle flow associated with a lithospheric drip beneath the Great Basin. Nature Geosciences , 2009, 2(6): 439-444. DOI:10.1038/ngeo526 |
| [10] | 高山, 金振民. 拆沉作用(Delamination)及其壳-幔演化动力学意义. 地质科技情报 , 1997, 16(1): 1–9. Gao S, Jin Z M. Delamination and its geodynamical significance for the crust mantle evolution. Geological Science and Technology Information (in Chinese) (in Chinese) , 1997, 16(1): 1-9. |
| [11] | Froidevaux C, Ricard Y. Tectonic evolution of high plateaus. Tectonophysics , 1987, 134(1-3): 227-238. DOI:10.1016/0040-1951(87)90259-9 |
| [12] | Schott B, Schmeling H. Delamination and detachment of a lithospheric root. Tectonophysics , 1998, 296(3-4): 225-247. DOI:10.1016/S0040-1951(98)00154-1 |
| [13] | Nelson K D. A unified view of craton evolution motivated by recent deep seismic reflection and refraction results. Geophys. J. Int. , 1991, 105(1): 25-35. DOI:10.1111/gji.1991.105.issue-1 |
| [14] | Nelson K D. Are crustal thickness variations in old mountain belts like the Appalachians a consequence of lithospheric delamination?. Geology , 1992, 20(6): 498-502. DOI:10.1130/0091-7613(1992)020<0498:ACTVIO>2.3.CO;2 |
| [15] | Kay R W, Kay S M. Delamination and delamination magmatism. Tectonophysics , 1993, 219(1-3): 177-189. DOI:10.1016/0040-1951(93)90295-U |
| [16] | Meissner R, Mooney W. Weakness of the lower continental crust: a condition for delamination, uplift, and escape. Tectonphysics , 1998, 296(1-2): 47-60. DOI:10.1016/S0040-1951(98)00136-X |
| [17] | Jull M, Kelemen P B. On the conditions for lower crustal convective instability. J. Geophys. Res. , 2001, 106(B4): 6423-6446. DOI:10.1029/2000JB900357 |
| [18] | Marotta A M, Fernàndez M, Sabadini R. Mantle unrooting in collisional settings. Tectonophysics , 1998, 296(1-2): 31-46. DOI:10.1016/S0040-1951(98)00134-6 |
| [19] | Marotta A M, Fernàndez M, Sabadini R. The onset of extension during lithospheric shortening: a two-dimensional thermomechanical model for lithospheric unrooting. Geophys. J. Int. , 1999, 139(1): 98-114. DOI:10.1046/j.1365-246X.1999.00922.x |
| [20] | Morency C, Doin M P, Dumoulin C. Convective destabilization of a thickened continental lithosphere. Earth Planet. Sci. Lett. , 2002, 202(2): 303-320. DOI:10.1016/S0012-821X(02)00753-7 |
| [21] | Morency C, Doin M P. Numerical simulations of the mantle lithosphere delamination. J. Geophys. Res. , 2004, 109: B03410. DOI:10.1029/2003JB002414 |
| [22] | Molnar P, Houseman G A, Conrad C P. Rayleigh-Taylor instability and convective thinning of mechanically thickened lithosphere: effects of non-linear viscosity decreasing exponentially with depth and of horizontal shortening of the layer. Geophys. J. Int. , 1998, 133(3): 568-584. DOI:10.1046/j.1365-246X.1998.00510.x |
| [23] | Molnar P, Jones C H. A test of laboratory based rheological parameters of olivine from an analysis of late Cenozoic convective removal of mantle lithosphere beneath the Sierra Nevada, California, USA. Geophys. J. Int. , 2004, 156(3): 555-564. DOI:10.1111/gji.2004.156.issue-3 |
| [24] | Pysklywec R N, Gogus O, Percival J, et al. Insights from geodynamical modeling on possible fates of continental mantle lithosphere: collision, removal, and overturn. Canadian Journal of Earth Sciences , 2010, 47(4): 541-563. DOI:10.1139/E09-043 |
| [25] | 高山, 张本仁, 金振民, 等. 秦岭—大别造山带下地壳拆沉作用. 中国科学 (D辑) , 1999, 29(6): 532–541. Gao S, Zhang B R, Jin Z M, et al. Lower crustal delamination in the Qinling-Dabie orogenic belt. Science in China (Series D) (in Chinese) (in Chinese) , 1999, 29(6): 532-541. |
| [26] | 李曙光, 黄方, 李晖. 大别—苏鲁造山带碰撞后的岩石圈拆离. 科学通报 , 2001, 46(17): 1487–1491. Li S G, Huang F, Li H. Post-collisional lithosphere delamination of the Dabie-Sulu orogen. Chinese Science Bulletin (in Chinese) (in Chinese) , 2001, 46(17): 1487-1491. |
| [27] | Bai W M, Vigny C, Ricard Y, et al. On the origin of deviatoric stresses in the lithosphere. J. Geophys. Res. , 1992, 97(B8): 11729-11737. DOI:10.1029/91JB00292 |
| [28] | 黄金水, 钟时杰. 牛顿流体小尺度地幔对流对海底地形与热流的影响. 科学通报 , 2004, 49(22): 2354–2361. Huang J S, Zhong S J. Effects on the seafloor topography and heat flux of Newtonian fluid small scale mantle convection. Chinese Science Bulletin (in Chinese) (in Chinese) , 2004, 49(22): 2354-2361. |
| [29] | Cai Y E, Wang C Y. Fast finite-element calculation of gravity anomaly in complex geological regions. Geophys. J. Int. , 2005, 162(3): 696-708. DOI:10.1111/gji.2005.162.issue-3 |
| [30] | 刘洁, 刘启元, 宋惠珍. 非均匀介质热蠕变流动的数值求解. 地球物理学报 , 2006, 49(4): 1029–1036. Liu J, Liu Q Y, Song H Z. Numerical method of modeling thermal creeping flow in heterogeneous medium. Chinese J. Geophys. (in Chinese) , 2006, 49(4): 1029-1036. |
| [31] | 朱涛, 马宗晋, 冯锐. 三维地震波速结构约束下的变黏度地幔对流及其动力学意义. 地球物理学报 , 2006, 49(5): 1347–1358. Zhu T, Ma Z J, Feng R. 3-D lateral variable viscosity mantle convection constrained by seismic wave velocity and its geodynamic implications. Chinese J. Geophys. (in Chinese) , 2006, 49(5): 1347-1358. |
| [32] | 傅容珊, 韩力波, 黄建华, 等. 现代板块运动驱动地幔块体置换度及地幔混合的研究. 地球物理学报 , 2007, 50(5): 1409–1417. Fu R S, Han L B, Huang J H, et al. Study of the mantle mixing driving by plate motions. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1409-1417. |
| [33] | 陈建业, 杨晓松, 石耀霖. 热-流-固耦合方法模拟岩石圈与软流圈相互作用. 地球物理学报 , 2009, 52(4): 939–949. Chen J Y, Yang X S, Shi Y L. A coupled thermal-fluid-solid approach for modeling the lithosphere-asthenosphere interactions. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 939-949. |
| [34] | 熊熊, 单斌, 王继业, 等. 蒙古—贝加尔地区上地幔小尺度对流及地球动力学意义. 地球物理学报 , 2010, 53(7): 1594–1604. Xiong X, Shan B, Wang J Y, et al. Small-scale upper mantle convection beneath the Mongolia-Baikal Rift Zone and its geodynamic significance. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1594-1604. |
| [35] | Li Z H, Gerya T V. Polyphase formation and exhumation of high- to ultrahigh-pressure rocks in continental subduction zone: numerical modeling and application to the Sulu ultrahigh-pressure terrane in eastern China. J. Geophys. Res. , 2009, 114: B09406. DOI:10.1029/2008JB005935 |
| [36] | Moresi L, Dufour F, Mühlhaus H B. A Lagrangian integration point finite element method for large deformation modeling of viscoelastic geomaterials. J. Comput. Acoust. , 2003, 184: 476-497. |
| [37] | O'Neill C, Moresi L, Müller D, et al. Ellipsis 3D: a particle-in-cell finite element hybrid code for modelling mantle convection and lithospheric deformation. Comput. Geosci. , 2006, 32(10): 1769-1779. DOI:10.1016/j.cageo.2006.04.006 |
| [38] | Ranalli G. Rheology of the Earth. Boston: Allen & Unwin , 1995. |
| [39] | 许长海, 周祖翼, 马昌前, 等. 大别造山带140-85.Ma热窿伸展作用——年代学约束. 中国科学 (D辑) , 2001, 31(11): 925–937. Xu C H, Zhou Z Y, Ma C Q, et al. The arch-like thermal extension of Dabie orogen in 140-85Ma—limited from chronology. Science in China (Series D) (in Chinese) (in Chinese) , 2001, 31(11): 925-937. |
| [40] | Davies J H, von Blanckenburg F. Slab breakoff: A model of lithosphere detachment and its test in the magmatism and deformation of collisional orogens. Earth Planet. Sci. Lett. , 1995, 129(1-4): 85-102. DOI:10.1016/0012-821X(94)00237-S |
| [41] | Wessel P, Smith W H F. New, improved version of generic Mapping Tools released. Eos Trans. AGU , 1998, 79(47): 579. DOI:10.1029/98EO00426 |
 2011, Vol. 54
2011, Vol. 54