2. 中国地质大学(武汉)构造与油气资源教育部重点实验室,武汉 430074
2. Key Laboratory of Tectonics and Petroleum Resources (China University of Geosciences), Ministry of Education, Wuhan 430074, China
应用地球物理资料进行地质体边界的精确定位是地质-地球物理解释中的一项重要工作,它不仅可以刻划岩性的变化,还可以提供有关构造体系、变形样式等丰富的地下地质信息.另外,我们将边界位置信息与地球物理场资料、地质资料的联合使用可以大大提高单一资料的解释能力,得到更加丰富、全面的地下地质信息,提高解释的质量.
近几十年来,学者提出了多种基于位场梯度的边界定位方法[1~5],几乎都是对位场数据进行某种形式的梯度运算.传统的方向导数、水平总梯度模以及Euler反褶积[6]等确定重磁源位置的方法,在地球物理资料分析解释中得到了广泛深入的应用.但是由于重磁异常导数是一个高通滤波器,处理过程易受噪声的影响而产生振荡,压制甚至丢失有用信号.Euler反褶积是以Euler齐次方程为理论基础,利用方程中的构造指数来反演场源的位置,Euler齐次方程是一个灵敏度极高的方程式,其中异常的导数计算也使得该方法容易受噪声的影响,导致反演结果产生偏差,并且还需要根据先验信息确定构造指数,影响了方法的使用.另外,对于一些复杂的深源异常或区域异常,由于梯度平缓,异常微弱,传统方法计算边界效果不理想,或者根本无法确定边界信息.2006~2007 年,张凤旭等提出利用余弦变换计算重磁异常的方向导数[7, 8],实现在保证计算效率的前提下,获得比Fourier变换计算导数更高的精度;2007年,张凤旭等提出了三方向小子域滤波方法检测断裂构造[9],获得了更为清晰丰富的断裂信息;2004年,Verduzco等提出利用Tilt水平导数[10]可以准确地探测场源边界,该方法需要计算异常的高阶导数,因此对数据的噪声更加敏感;2005年,Chris Wijns等人提出使用Thet amap分析磁源边界[11],另辟蹊径,尤其对低纬度磁源边界可以获得比较好的结果.2008 年,Gordon R J Cooper 和Duncan R Cowan 提出了利用位场梯度的归一化标准差方法[12],该方法主要思想是借用标准差来衡量位场的局部变异性,对不同强度的异常都有不错的探测效果.
基于梯度的边界分析方法运算简单,物理意义明确,缺点是对区域边界信息不敏感,还容易受高频噪声的影响.另外在复杂构造区的异常分析中,常规的算法具有各向同性的特点,即都是一视同仁地对数据采用统一处理,比如方向导数、水平总梯度模等边界分析方法,往往在弱异常、叠加异常处会丢失信息,处理效果不理想.我们从梯度检测的角度出发,针对传统微分算法的不足,力求一种稳定有效的边界分析方法,使之不仅能够处理低信噪比的异常数据,而且对于微弱异常、叠加异常,也能够有效地识别.
本文提出基于各向异性标准化方差(Anisotropy Normalized Variance, ANV)计算重磁源边界的方法,文章首先通过坐标旋转构造了各向异性高斯函数,给出了各向异性标准化方差的计算公式,并从理论上阐明了方法的物理意义.笔者描述了本文算法的核心流程,通过对理论数据及加噪模型的分析,证实了算法的有效性与稳定性,表明该方法可以获得丰富的边界信息,尤其对微弱异常以及复杂异常都能够实现边界分析.
2 方法原理分析 2.1 各向异性标准化方差在重磁源边界分析中,梯度算法是普遍使用的一类方法,常规的微分算法受噪声的干扰比较严重,另外基于各向同性的算法都很难识别不同方向的边界信息,虽然采用不同方向的方向导数可以一定程度上突出特定方向的边界,但是这些方法对旁侧叠加异常、弱异常达不到满意的识别效果,往往会模糊边界信息.
基于此,本文利用一种各向异性的高斯函数,在其二阶导数的基础上提出了“各向异性标准化方差"分析重磁源边界的方法.
考虑方向θ ,令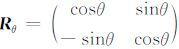
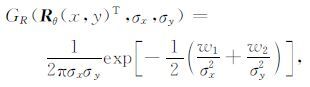
|
(1) |
其中
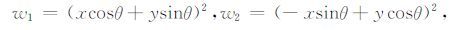
|
σx、σy分别为长轴、短轴方向的方差.
可以看出,函数GR具有明显的方向性,如图 1所示,分别反映 [0,π/16,2π/16,…,π)方向的GR函数,体现了其各向异性的特征,可以自适应地分析不同方向的重磁源边界.

|
图 1 不同方向的GR函数示意图(坐标单位为数据点) Fig. 1 Different directions of GR function |
根据(1)式,推导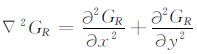
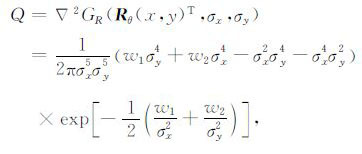
|
(2) |
对(M+1)×(M+1)大小的Q,定义位场数据f(x,y)的各向异性标准化方差如下:
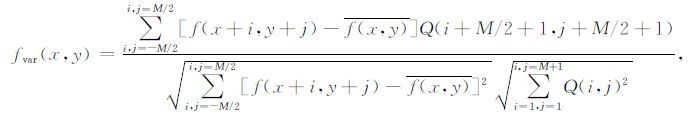
|
(3) |
其中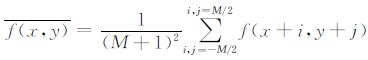
对于(3)式,其分子部分是一个离散的褶积计算形式,我们假设用fs*Q来表示这个过程,考虑到Q=∇2G,根据褶积的微分性质,fs*Q可以表示成如下形式:
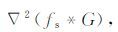
|
可以发现,fvar(x,y)实质上就是一种广义化的二阶导数的计算形式.据此分析,对位场数据而言,其场源边界位置对应于fvar(x,y)的零值点位置.
根据上文分析知,构造各向异性函数Q需要确定参数σx、σy(它们的大小决定Q的作用范围与各向异性尺度)以及方向θ,计算方法如下:
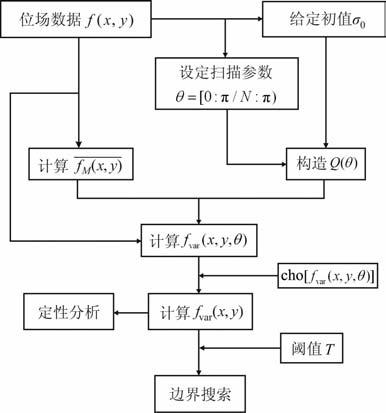
首先根据先验信息给定初值σ0,计算σx=σ0,σy=σx/cof.其中cof表示比例系数,在场源边界处,cof值大,即函数Q的各向异性尺度大,有利于边界分析,在非边界处,cof 的取值对结果影响不大,本文取cof=1,体现各向同性特征.另外,本文采用全方位扫描确定θ 值,具体计算流程如图 2.
|
图 2 本文算法流程 Fig. 2 Flow chart of algorithm |
(1) 根据先验信息给定位场异常的初值σ0,设定全方位扫描参数θ=[0:π/N:π),N为正整数;
(2) 计算σx、σy,构造各向异性函数Q(θ);
(3) 根据(3)式计算fvar(x,y,θ);
(4) 计算fvar(x,y)=cho[fvar(x,y,θ)](cho为选择算法,即选择经过全方位扫描后得到的最可能的边界值),得到扫描后的各向异性标准化方差;
(5) 可以利用fvar(x,y)定性分析重磁源边界,也可以选择阈值,自动搜索边界位置,得到定量的解释图件.
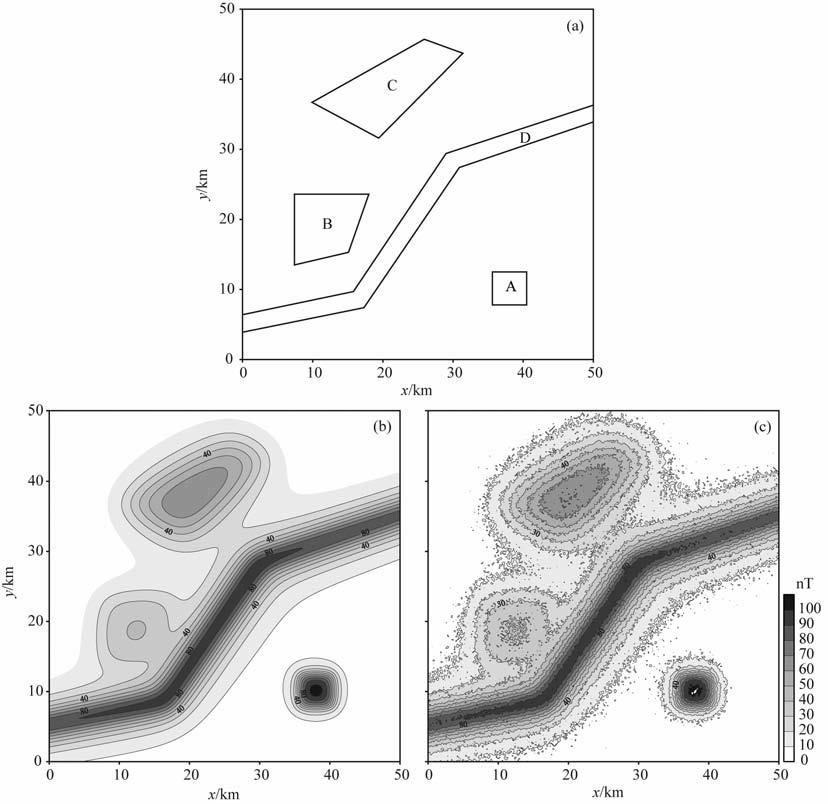
3 理论模型分析为对本文方法进行验证,我们做了模型数值实验,并在此基础上做了算法稳定性分析.首先设计了一个组合模型(模型位置见图 3a所示),4个形体均为向下无限延深,磁化倾角I取90°,其他参数如表 1所示.正演得到的磁异常如图 3b所示,图 3c是在原始异常的基础上加了随机干扰的结果.
|
图 3 (a)理论模型位置;(b)理论模型正演磁异常;(c)正演磁异常加20%随机干扰 Fig. 3 (a) Theoretical model location; (b) Forward magnetic anomaly; (c) Forward magnetic anomaly adds 20% random noise |
|
|
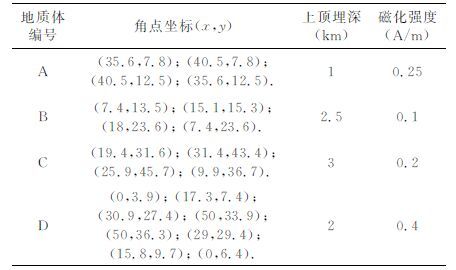
表 1 模型参数 Table 1 The model parameters |
从图 3b可以看出,地质体A、D 产生的是强磁异常,边界位置明确,地质体B、C 由于埋深大磁化强度小,异常梯度平缓、幅值相对微弱,边界位置不易确定.此外由于地质体B 和D 相邻,异常叠加,增加了地质体B 的边界确定难度.我们首先采用水平总梯度模方法来进行边界定位:通过计算
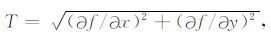
|
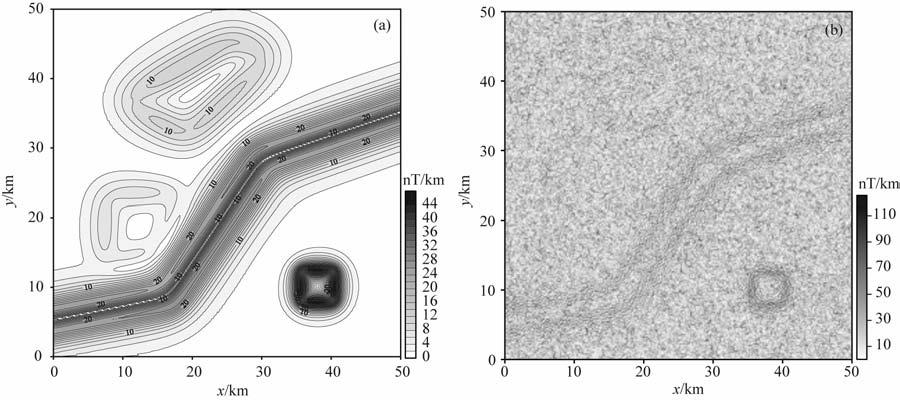
T的极大值处表示场源边界.对该方法而言,随着地质体变深,总磁场强度异常会变宽缓,异常幅值降低,一阶水平方向导数强度也会降低,造成深部地质体的边界难以识别,另外,相邻异常的叠加也会对边界的识别造成影响.从图 4a可以看出,水平总梯度模将地质体A、D 的边界较好地反映出来,而对地质体B、C 的边界反映的相对模糊,尤其对地质体B,受异常叠加的影响,水平总梯度模反映的边界有缺失现象.另外图 4b是对加了噪声干扰的磁异常计算水平总梯度模的结果,受干扰的影响,该方法已经很难识别出边界信息,除了地质体A 的边界有模糊的反映外,其他三个地质体几乎没有信息反映.
|
图 4 (a)图 3b的水平总梯度模;(b)图 3c的水平总梯度模 Fig. 4 (a) The horizontal total gradient mode of Fig.3b; (b) The horizontal total gradient mode of Fig.3c |
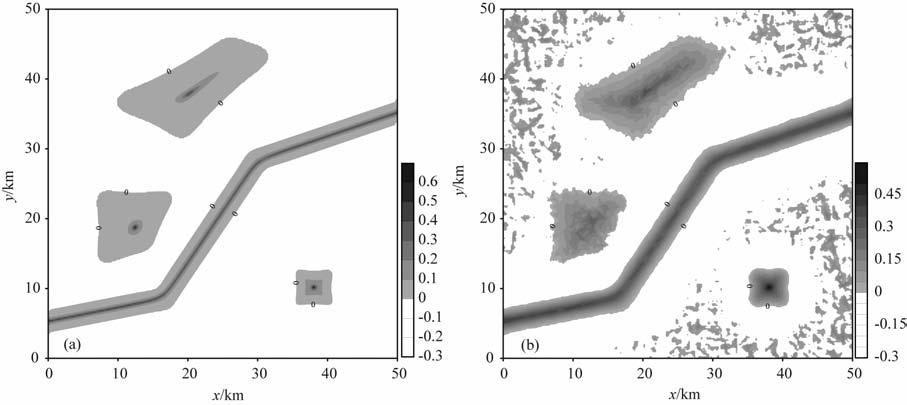
图 5a是采用本文提出的方法计算场源边界的结果,其中σ0=0.5,N=16.可以看出,各向异性标准化方差清晰地反映出了各个场源边界,尤其对深部的地质体B、C 的边界也有很明确的反映,没有发生诸如图 4a出现的地质体B的边界模糊缺失现象.
|
图 5 (a)图 3b的各向异性标准化方差;(b)图 3c的各向异性标准化方差 Fig. 5 (a) Anisotropy normalized variance of Fig.3b; (b) Anisotropy normalized variance of Fig.3c |
为了检验方法的稳定性,我们对图 3c的加噪异常同样计算各向异性标准化方差,如图 5b 所示(σ0=3,N=16),在高频干扰的情况下,该方法还是能有效地反映出四个地质体的边界信息,尤其对地质体B、C 的弱异常边界,都得到比较客观的反映,场源边界两侧各向异性标准化方差值正负差异明显,很容易判别.值得注意的是,地质体B 和D 相邻部分的边界也被较好地反映出来,边界形状没有发生严重的扭曲,表明了本文方法在识别弱异常、叠加异常边界的有效性.
4 实例应用利用位场资料进行构造区块的划分和解释对于油气勘探远景预测具有重要的科学意义.2005 年,在完成中石化南方公司的项目时,为了探讨大巴山、米仓山及前缘地区区域构造特征,评价工区油气勘探前景,我们对该区的重磁数据做了大量的边界分析工作1);2006年至今,在完成中国石化“十一五"科技攻关项目时,为了研究中扬子南北缘盆山构造系统的结构,划分构造区块以及了解中扬子地区结晶基底残块,也需要利用重磁资料进行构造分析解释.
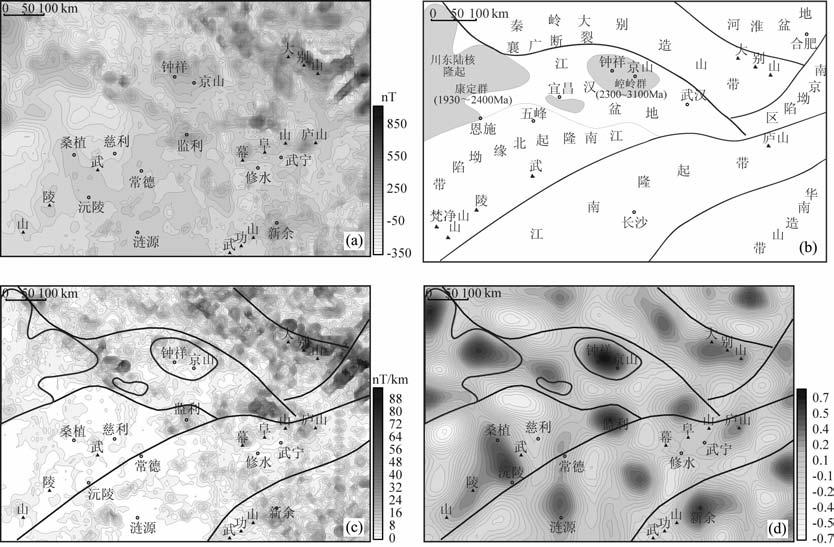
图 6a是中扬子地区航磁化极异常图,其中东北角大别山地区存在一条明显的北西向强磁异常带,四川盆地与钟祥、京山地区的结晶基底残块也依稀可辨.利用本区的地球物理资料结合区域地质资料综合解释得到图 6b的构造分区2),包括秦岭大别造山带、江汉盆地、江南隆起带以及华南造山带等一系列构造区块.图 6c是计算得到的航磁异常水平总梯度模,可以看出,水平总梯度模反映出了秦岭大别造山带,对华南造山带也有一定的反映,但是在其他区域由于异常强度低,异常梯度变化不大,水平总梯度模没有明显的信息反映,尤其是对该区研究有重要意义的结晶基底残块基本没有指示.
|
图 6 (a)中扬子地区航磁化极异常图;(b)中扬子地区构造分区图(图中阴影部分表示川东及钟祥、京山地区的结晶基底残块);(c)水平总梯度模;(d)各向异性标准化方差 Fig. 6 (a) Reduction-to-the-pole of the total magnetic intensity anomaly of mid Yangtze region; (b) Sketch map showing geology of mid Yangtze region (the shaded areas express crystalline basement debris of eastern Sichuan, Zhongxiang and Jing shan) ; (c) The horizontal total gradient mode according to Fig.6a; (d) Anisotropy normalized variance according to Fig.6a |
图 6d是利用本文方法计算得到的航磁异常各向异性标准化方差,它不仅可以反映具有强磁异常信息的秦岭大别造山带,同时对与之相邻的河淮盆地及南京坳陷区、有微弱异常的江南隆起带都有一定的反映.此外,该结果比较客观地反映出了钟祥、京山地区的结晶基底残块.由于该方法可以识别微弱异常,受相邻异常的影响小,图 6d反映了丰富的构造边界信息,对中扬子地区的构造与基底划分的深入研究将提供重要的指导信息.
5 结论与讨论从20世纪70年代初至今,学者们提出了多种基于位场梯度的边界定位方法,大部分方法都与异常的振幅有密切的联系,对微弱异常的边界计算效果欠佳,在相邻异常处也容易丢失信息.本文基于微分算法的思想,构造了各向异性高斯函数,利用各向异性标准化方差分析重磁源边界,具有以下特点:
(1) 本文方法与二阶导数有相似的物理意义,计算结果的零值线位置对应重磁源边界,比一阶导数等采用极大值方法更容易识别微弱异常源边界;
(2) 采用全方位扫描的计算思想,有利于识别不同方向的边界,避免传统计算多个方向导数的繁琐;
(3) 算法稳定,受噪声干扰的影响小,计算结果的分辨率高.
与以往方法不同的是,各向异性标准化方差提供的边界与非边界信息差异显著,一定程度上克服了传统方法“一视同仁"的缺点,实现强、弱异常自适应检测.通过理论模型及实际算例,表明了该方法的有效性,同时可以实现对微弱异常以及相邻叠加异常的边界识别,将有重要的实际应用价值.该方法可以提供准确丰富的边界信息,对区域异常的精细解释也有一定的指导意义,可以为位场数据边界分析提供一种新的计算途径.
致谢笔者对两位匿名评审专家中肯的建议表示衷心的感谢!
| [1] | Hsu S K, Sibuet J C, Shyu C T. High-resolution detection of geologic boundaries from potential-field anomalies: An enhanced analytic signal technique. Geophysics , 1996, 61(2): 373-386. DOI:10.1190/1.1443966 |
| [2] | Fedi M, Florio G. Detection of potential field source boundaries by enhanced horizontal derivative method. Geophysical Prospecting , 2001, 49(1): 40-58. DOI:10.1046/j.1365-2478.2001.00235.x |
| [3] | Boschetti F. Improved edge detection and noise removal in gravity maps via the use of gravity gradients. Journal of Applied Geophysics , 2005, 57(3): 213-225. DOI:10.1016/j.jappgeo.2004.12.001 |
| [4] | Pilkington M. Locating geologic contacts with magnitude transforms of magnetic data. Journal of Applied Geophysics , 2007, 63(2): 80-89. DOI:10.1016/j.jappgeo.2007.06.001 |
| [5] | Phillips J D, Hansen R O, Blakely R J. The use of curvature in potential-field interpretation. Exploration Geophysics , 2007, 38(2): 111-119. DOI:10.1071/EG07014 |
| [6] | 管志宁. 地磁场与磁力勘探. 北京: 地质出版社, 2005 . Guan Z N. Geomagnetic Field and Magnetic Exploration (in Chinese). Beijing: Geological Publishing House, 2005 . |
| [7] | 张凤旭, 孟令顺, 张凤琴, 等. 重力位谱分析及重力异常导数换算新方法——余弦变换. 地球物理学报 , 2006, 49(1): 244–248. Zhang F X, Meng L S, Zhang F Q, et al. A new method for spectral analysis of the potential field and conversion of derivative of gravity-anomalies: cosine transform. Chinese J. Geophys. (in Chinese) , 2006, 49(1): 244-248. |
| [8] | 张凤旭, 张凤琴, 孟令顺, 等. 基于离散余弦变换的磁位谱分析及磁异常导数计算方法. 地球物理学报 , 2007, 50(1): 297–304. Zhang F X, Zhang F Q, Meng L S, et al. Magnetic potential spectrum analysis and calculating method of magnetic anomaly derivatives based on discrete cosine transform. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 297-304. |
| [9] | 张凤旭, 张凤琴, 刘财, 等. 断裂构造精细解释技术——三方向小子域滤波. 地球物理学报 , 2007, 50(5): 1543–1550. Zhang F X, Zhang F Q, Liu C, et al. A technique for elaborate explanation of faulted structures: three-directional small subdomain filtering. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1543-1550. |
| [10] | Verduzco B, Fairhead J D, Green C M, et al. New insights into magnetic derivatives for structural mapping. The Leading Edge , 2004, 23(2): 116-119. DOI:10.1190/1.1651454 |
| [11] | Wijns C, Perez C, Kowalczyk P. Theta map: Edge detection in magnetic data. Geophysics , 2005, 70(4): L39-L43. DOI:10.1190/1.1988184 |
| [12] | Cooper G R J, Cowan D R. Edge enhancement of potential field data using normalized statistics. Geophysics , 2008, 73(3): H1-H4. DOI:10.1190/1.2837309 |
 2011, Vol. 54
2011, Vol. 54