2. 长安大学计算地球物理研究所, 西安 710054
2. Institute of Computing Geophysics, Chang'an University, Xi'an 710054, China
自Aki和Lee的奠基性研究工作开始[1], 地震层析成像技术已成为研究地球内部结构及各向异性行之有效的方法之一.其成像尺度小到岩石组分, 大至全球构造.经过30多年的探索, 无论是成像方法种类(如:体波成像、面波成像、全波型反演成像、地震噪声成像等), 还是成像技术本身都有了长足的进展[2, 3].但也存在不少技术难点, 如:全波型反演成像技术尽管其空间分辨率要明显高于体波成像, 然而由于正演模拟时模型的过度简化, 使得正演理论地震图与实际观测记录相距甚远, 加之非线性程度较高, 使得反演解对初始模型的依赖程度较高.另外, 受计算机内存及计算速度的制约, 全波型反演成像技术主要用于较小尺度(如:井间、垂直地震剖面VSP等)结构成像.鉴于此, 目前应用较多的依然是体波成像, 而且主要是单一震相的走时成像, 即射线成像, 如:初至波P (Pn, Pg), 或S (Sn, Sg), 反射波(PmP, PcP等)成像.
高频近似下的射线类成像的主要缺点是空间分辨率较低, 加之受地震分布、地震台网间距的制约, 理论上来讲采用单一震相走时进行成像不可能获得高分辨率的地质构造图像.目前全球地震台网分布密度最好的台网间距也只能达到20~30 km.换句话说, 假设地震分布是理想的, 那么使用单一震相走时资料进行成像的空间分辨率最多也只能达到20~30 km.而实际情况并非这样乐观, 地震层析成像的空间分辨率除了与地震台网的间距有关外, 还与地震分布、射线路径直接相关.例如:使用远震走时资料进行地壳结构成像时, 台站下方近乎垂直的地震射线很难保证较高的垂向分辨率; 同样利用宽角折(反)射波走时进行成像时横向分辨率就不可能太高.另一方面, 除了上述影响成像分辨率的因素外, 异常体的锁定还与震相种类有关, 即增加不同种类射线路径的交叉对异常体空间位置的锁定也至关重要.而目前提高走时成像分辨率主要有两种可能的途径:其一是减小地震观测台站的间距, 但这样做常受到经费的限制; 其二是引入后续震相资料, 即进行多震相走时资料的联合反演.美国学者C A Zelt等人在这方面做了许多很有价值的讨论[4~8].较为典型的多震相走时资料提高成像分辨率的例子是赵大鹏等(2005)利用美国Landers地震余震进行的多波走时(震相S、SmS、sSmS)成像试验, 成像试验中仅用了相距200km的两个观测台站和其间发生的180个余震, 结果表明使用多波走时成像技术其空间分辨率可提高至台站间距的1/8~1/6, 本例中为25~35 km[9].
目前使用多波走时联合反演成像的主要困难在于:其一是缺少实用性强的多波射线正演计算程序; 其二是欠缺多震相到时数据.然而后者由于宽频带数字地震仪的广泛使用, 已积累了大量的宽频带地震记录, 若有实用性强的多震相到时自动拾取技术, 则收集多震相到时数据指日可待.而实用性强的多次波射线追踪算法业已实现.例如:Rawlinson和Sambridge (2004)提出了分区多步计算技术, 采用有限差分解程函方程的快速行进法实现了二维层状介质中多次波的追踪计算[10], 随后又将该算法推广到三维层状介质中[11].白超英和唐小平(2009)实现了分区多步最短路径算法下2D/3D复杂层状介质中多次波射线路径的追踪计算[12~14].随后又将该算法推广, 实现了不规则最短路径算法下多次波的追踪计算, 可有效处理地表及反射界面起伏时的情形[15, 16].
本文在上述多波正演算法的基础上, 利用共轭梯度法求解带约束的阻尼最小二乘问题, 探讨了二维复杂层状模型中地震多震相走时的联合成像方法技术.其中包括:(1) 层间速度分布已知时, 逐层(或同时)进行反射界面的精确定位; (2) 反射界面已知时多震相走时联合反演成像技术; (3) 多震相走时联合同时确定速度模型和反射界面起伏.最后, 对该反演算法抗噪声能力进行了评价.结果表明:无论是成像的空间分辨率, 还是成像深度, 多波走时成像均明显好于单一震相时的情形.同时该反演算法对走时、模型中的随机噪声并不敏感.
2 正、反演方法简介 2.1 正演算法本文采用的多次波射线追踪正演算法是新近研发的, 所以有必要进行简单的介绍.在改进型最短路径算法的基础上[17], 引入分区多步计算技术, 采用不规则最短路径算法可实现复杂模型中多次波的射线追踪及相应走时的计算[15, 16].其中分区多步计算技术的原理如下:所谓"分区"就是将速度模型按照地表起伏和速度界面的具体情况分成相对独立的层状区域(如图 1a所示), 相邻区域由速度界面相连接.模型参数化时, 起伏界面附近采用不规则网格单元(如图 1b所示), 而远离起伏界面的区域依然用规则网格单元.速度采样在主节点上进行, 次级节点上的速度则由二次线性插值函数确定[15, 16].而所谓"多步计算"就是从炮点所在的区域开始, 沿着目标射线所要通过的区域, 逐区进行波前扫描.由于本文中存在规则和不规则的网格单元, 所以波前扩展时分两种情况分别进行计算.若当前区域内所有网格单元内节点都计算完毕后, 波前停留在该区的速度离散界面上, 此时程序暂停, 并同时保存速度界面上各离散点的走时和相应的射线路径.然后视所要追踪射线的类型自该界面上走时最小的点继续新区的波前扫描.举例来说(如图 1a所示), 如果是追踪透射波P1P2(约定:上标代表上行波, 下标代表下行波, 数字1、2表示区号), 则调用2区速度模型(如是透射转换波P1S2则调用2区S波速度模型), 从所保存的速度界面上走时最小的点开始, 继续2区内波前扩展和射线追踪.如果是计算反射波P1P1(或者是反射转换波P1S1), 则调用1区相应的速度模型, 按照上述步骤重复则可实现多次波的追踪计算, 有关详细内容可参阅文献[12~16].
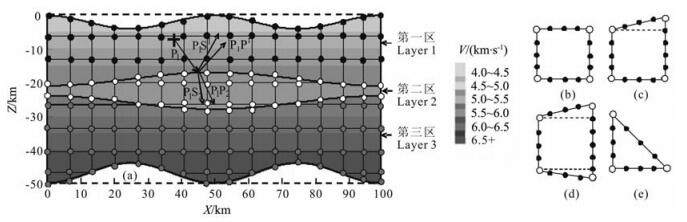
|
图 1 含有起伏界面及低速夹层的二维层状速度模型中分区多步ISPM算法计算透射、反射及转换波的示意图(a, 模型中次级节点没有给出).(b), (c), (d), (e)为模型参数化时采用的四种规则网格及不规则网格(白色球表示主节点, 黑色球表示所加入的次级节点) Fig. 1 A schematic explanation for computing the transmitted, reflected and converted arrivals using the multistage ISPM in 2-D layeredmediawith irregular interfaces and lowvelocity layer involved (diagrama, note that the secondary nodes are not shown for clarity). Diagrams (b, c, d and e) are 4 different kinds of regular and irregular cels used in the model parameterization (white and black circles indicate primary and secondary nodes, respectively) |
对于多参数的联合反演同时更新速度和反射界面位置, 目前局部线性化的反演方法主要有:(1) 刘福田等采用的参数分离法[18~21]; (2) BLNKennett等提出的Subspace反演算法[22]; (3) CAZelt等提出的加权算法[4~8]; (4) 各参数归一化法[23, 24]; 以及上述四种方法的改进型, 如:与正则化、滤波、平滑等相结合.上述四种方法各有其优缺点, 这里就不再评述.有兴趣的读者请参阅文献[25].方法(1)、(2)均是基于参数分离的算法; 而方法(3)、(4)则是基于不同权系数的算法.CAZelt等提出的加权算法中, 引入了两个权系数, 用来平衡速度模型与界面更新的权重问题.然而, 权系数的选择则需要通过试算(或经验性)得到, 因此, 或多或少的带有人为因素.为了避免这种人为因素对反演结果的影响, 本文采用第四种算法, 即:两种不同反演参数归一化处理的算法.并根据多次波的特点引入了不同观测数据的权系数, 以及射线密度的概念.一般而言, 非线性多波走时(含反射或折射波)联合进行同时反演问题, 可归结为下列带约束的阻尼最小二乘最优化问题, 其反演问题的2范数目标函数为
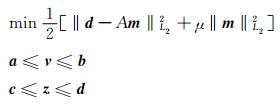
|
(1) |
式中:d=[p1(δt11, δt21, …, δtM11); p2(δt12, δt22, …, δtM22), …, pn(δtn1, δt2n, …, δtMnn)]是n种震相实际观测数据和理论数据的残差向量, 其中:p1, p2, …, pn为反演中考虑各震相所占的权重(或相应震相走时拾取时误差的精度类别), M1, M2, …, Mn则为各震相的射线条数; m=[λ1(δv1, δv2, …, δvN1); λ2(Δz1, Δz2, …, ΔzN2)]是模型空间参数的相对改变量, 其中:(δv1, δv2, …, δvN1)为速度模型的相对改变量, (Δz1, Δz2, …, ΔzN2)则为离散反射界面位置的相对改变量(注:可以是一个反射界面或多个反射界面), (λ1, λ2)则为考虑两种不同量纲模型参数的归一化因子.A是雅克比矩阵, μ是阻尼因子; a和b是反演解中速度模型可容许的上下边界值, 而c和d则为离散反射界面深度可容许的上下边界值.Menke (1984)得到公式(1)的解的一般形式为[26]
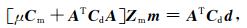
|
(2) |
其中(Cm, Cd)为模型和数据空间的协方差矩阵.(2)式是非线性问题局部线性化的基本反演公式, 其解具有局域解的特征, 为了得到具有实际物理意义的解, 可采用Cm, Cd及Zm的先验信息.因此, 选择不同组合的(Cm, Cd)可得到不同形式的反演解; 若μ=0, Cd=I; 则(2)式变为经典的最小二乘问题; 若Cd=Cm=I, Zm=W, A=GW, 这里W是表征射线宽度的带宽矩阵, 则(2)式转化成Meyerholtz和Szpakowski (1989)提出的卷积压制法[27]; 若Cd=I, Cm=DTD, 这里D是一阶或二阶差分算子, 则(2)式转化成由Shaw和Orcutt (1985)提出的一阶或二阶正则化方法[28].本文主要采用Tarantola和Valette (1982)提出的广义带约束的阻尼最小二乘反演解, 即(Cm, Cd)分别取模型和数据空间的协方差矩阵的逆阵, 则解为[29]
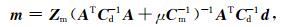
|
(3) |
其解的约束为
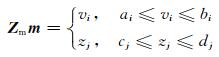
|
上述矩阵方程可采用迭代的共轭梯度算法求解[30, 31].目前关键的问题是如何求解具有偏导性质的Jacobi矩阵中的元素.
2.3 偏导Jacobi矩阵二维情形下根据射线理论, 沿某一射线路径Rj的走时tj可表述为下列积分:
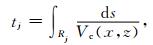
|
(4) |
其中ds为沿路径Rj上的线积分元, 而Vc(x, z)则为沿射线路径上的速度分布函数.当模型网格单元参数化后, 沿该射线路径Rj上的走时可写成求和形式:
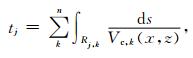
|
(5) |
其中: n为射线穿过的单元总数, Rj, k、Vc, k(x, z)分别为射线穿过第k个单元的长度和速度分布.
当界面与速度同时反演时, Jacobi偏导矩阵中包含了两部分的内容:其一是走时关于速度变化的偏导数; 其二是走时关于反射点深度变化的偏导数.
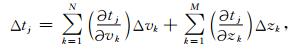
|
(6) |
式中tj是第j条射线Rj的走时; vk是长度为N的模型空间中的第k个单元的速度分布; zk是离散界面点中第k个点的深度值.
当射线穿过某个单元时, 走时对速度的一阶导数可用射线两端点导数的平均值代替[31]:
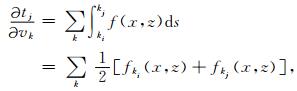
|
(7) |
其中:
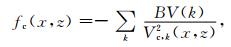
|
ki, kj是穿过第k个单元射线段的两个端点; BV(k)则是该单元上主节点的速度值.
反射及透射情形时, 二维介质中走时对界面位置的一阶偏导数的计算公式推导如下, 界面处p点走时关于界面位置的导数为[21]
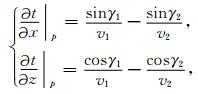
|
(8) |
式中:γ1, γ2分别为p点的入射角和透射角(反射时有γ1=γ2), 而v1, v2则分别是界面p点入射和透射时的速度(反射时有v1=v2).
作为一种近似, 即只考虑z方向情形, (8)式就简化为Zelt等人推导的反射波走时对界面深度的偏导数公式[4]:
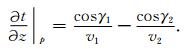
|
(9) |
当只考虑反射时, (9)式可进一步简化为Bishop等人推导的反射波走时对界面反射点的偏导数公式[32]:
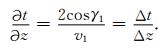
|
(10) |
本文中走时对速度的一阶偏导数可以用公式(7)计算, 走时关于反射点深度变化((10)式)可由射线追踪正演后利用有限差分法求得, 这里我们采用更为便捷的方法, 仿照地震精定位中的做法[33], 即正演时在初始反射界面上下引入两条平行的辅助离散界面, 这样(10)式中走时关于反射点深度变化的导数在正演过程中即可求出.即
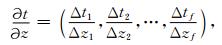
|
(11) |
其中f为离散反射界面上反射点的总数.
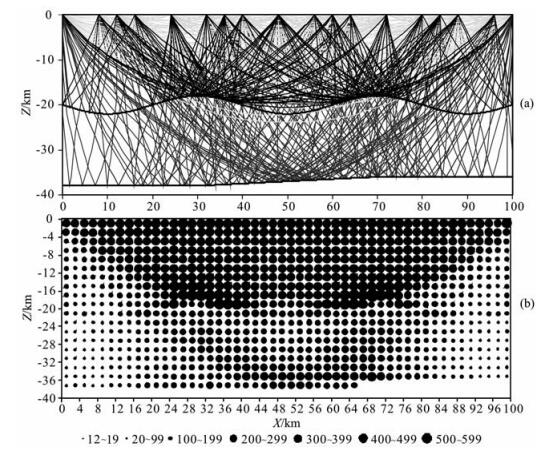
为了避免射线密度过大(或过小)区域速度模型的过度(或欠)更新, 我们引入了等权射线密度的概念, 其基本思路是某单元内通过一条射线和n条射线时走时残差对速度模型更新的贡献相等, 当单元k中有n条射线通过时, 定义其倒数为等权射线密度, 即1/n.具体做法是:正演计算完成后统计模型参数化下穿过每个单元内的射线条数ni(图 3b), 然后在Jacobi偏导矩阵元素(走时关于速度的偏导数)的求取时对不同的单元引入相应的等权射线密度1/ni, 也即当某条射线穿过第i个单元时求取的偏导矩阵元素乘以1/ni.
|
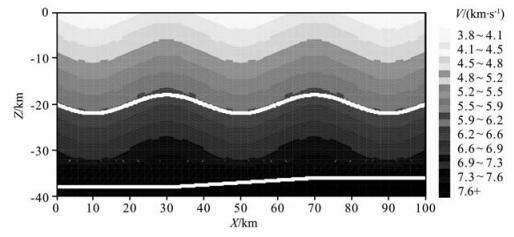
图 2 二维变化速度模型 其中白色粗线为反射界面. Fig. 2 2-D varied velocity model In figure the thin white lines are the reflected interfaces. |
|
图 3 三种震相地震射线路径(a)和模型各单元内穿过地震射线的条数分布图(b) Fig. 3 Ray paths for three different arrivals (a) and the numbers of rays crossing each element (b) |
本文中采用较为复杂的二维速度模型(图 2).X方向速度以cosx函数形式变化, 且随深度线性变化至Z=32.0 km, 在Z=32~40 km间速度只随深度线性变化, 但有一台阶式构造.根据速度模型变化特征引入两个反射界面, 上反射界面是一个与速度分布相应的cosx曲线; 而下反射界面则为倾斜台阶界面.模型参数化采用2 km×2 km的单元, 而在界面附近则采用尺度相应的三角形单元, 所加次级节点的间距为0.2 km.模型顶界面等间距放置35个炮点, 51个检波器.图 3给出了本文中所用的三种震相(初至P波、界面一的反射P1P波、界面二的反射P2P波)的相应地震射线路径(图 3a)及各单元内穿过的所有三种地震射线条数的统计分布图(图 3b).从中可以看出在界面一的两个峰值和界面二的中心及邻近区域产生了地震射线的汇集现象.
3.1 层速度已知时反射界面起伏的精确定位地震勘探的主要目的就是确定不同波阻抗(反射)界面的位置及起伏细节, 用地震射线进行偏移成像时, 首先要确定(或估计)层间波速, 然后进行叠加或偏移成像.这里假定用地震勘探的方法已初步得到了层间波速分布, 则可用上述反演算法进行反射界面的逐层(或同时)精确定位.图 4a, 4b给出了分别利用反射P1P、P2P波走时对界面一、二进行逐层精确定位的结果; 图 4c, 4d则是利用反射P1P和P2P波走时联合对界面一、二同时精确定位的结果.从图中可看出, 无论是逐层还是同时定位其结果是十分相近的, 几乎看不出有什么差别.该反演算法的优势在于:无论初始反射界面的位置在哪里, 一般经过3~4个迭代循环后均能够唯一的确定反射界面的位置与起伏细节.这也是我们在地震勘探及深地震测深时所需要的.
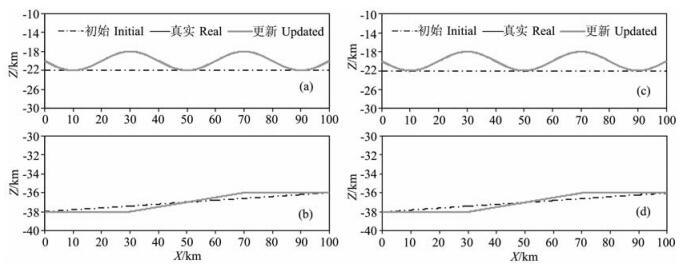
|
图 4 层速度分布已知时利用反演算法进行反射界面的逐层精确定位(a, b)和同时精确定位(c, d) 图中(a, c)是界面一的结果; (b, d)是界面二的结果. Fig. 4 The accurate reflector location with inversion method one interface by one interface (diagrams a, b) and smultaneously (diagram c, d) when the mternal velocity fields are known In figure (a, c) are the results of reflector 1, and (c, d) are the results of reflector 2. |
为了分析讨论多震相走时联合成像的空间分辨率及其优越性, 此模拟实验对三种波的不同组合方式进行了成像, 反演过程中反射界面不更新, 而只更新速度模型.这样做的理由是检验反演算法的能力, 为后面速度和反射界面的同时更新提供参考模型.选用一维线性速度模型作为初始模型, 图 5给出了仅用直达P波(图 5a)、直达P波和P1P反射波(图 5b)、直达P波和P2P反射波(图 5c)、以及直达P波、P1P、P2P反射波(图 5d)的成像结果.从中可看出:仅用直达P波走时资料进行成像, 由于受炮检距的制约, 其成像深度较浅, 但最为主要的是成像的空间分辨率较低(图 5a所示).加上反射波P1P走时资料后, 其空间分辨率明显好于仅用直达P波走时成像的情形(图 5b所示).成像分辨率的提高, 不仅是增加了射线条数, 更重要的是增加了两种不同射线的交叉概率, 从而有利于速度异常体空间位置的锁定.另一方面, 由于反射波资料的使用, 成像的深度显然也就增加了, 当然这取决于反射界面的深度.使用直达P波和界面二的反射P2P波走时的组合, 或是利用直达P波、界面一反射P1P波和界面二反射P2P波走时的组合, 其成像结果直观来看几乎一样(见图 5c和5d), 但从反演解与实际模型的差别来看, 图 5d的结果更接近真实速度模型(图略).从这个模拟实例可以得到这样的结论:采用不同震相的走时资料进行联合反演成像的优势是明显的, 即:(1) 由于增加了射线的覆盖率, 故而可显著提高成像的空间分辨率; (2) 由于增加了交叉射线的概率, 因而可减少重建速度分布中的畸变.当然, 对于局域地震成像而言, 成像的深度也明显加深.
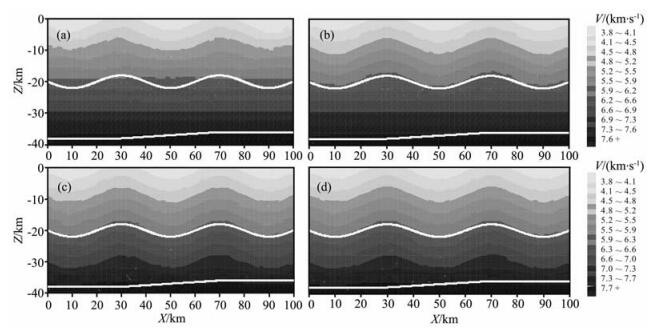
|
图 5 利用三种不同震相走时组合进行联合成像结果 (a) 仅用直达P波; (b) 直达P +反射波P1P; (c) 直达P +反射波P2P; (d) 直达P +反射波P1P.反射波P2P. Fig. 5 Seismic tomography with different combination of three different arrivals (a) Direct P arrival only; (b) Direct P arrival + reflected arrival PiP; (c) Direct P arrival+reflected arrival P2P; (d) Direct P arrival + reflected arrival PiP+reflected arrival P2P. |
在同时反演中, 考虑到不同模型参数的量纲不同, 且两者扰动对走时的影响程度也不同, 故反演中对Jacobi偏导矩阵元素中走时对速度的偏导数和走时对反射点深度位置的偏导数分别进行了归一化处理(见2.2节所述), 同时引入了等权射线密度的概念.初始速度模型的选用与3.2节相同, 上下初始反射界面均置于水平.为了对比这里仅就单一界面和速度进行同时反演, 图 6a, 6c为利用直达波P和反射波P1P, 以及直达波P和反射波P2P分别对速度和界面一、速度和界面二的反演结果(其中未引入等权射线密度); 而图 6b, 6d则是引入等权射线密度后相应的反演结果.从图 6a, 6c中明显可看出, 部分区域速度异常有所放大(失真), 如:界面一峰值附近的速度异常形态过度放大, 且反射界面起伏幅度也未完全恢复; 同样界面二的中心区域附近也存在速度异常形态过度更新问题.这主要是由于反射界面一的形态所造成, 即:在反射界面的两个峰值附近造成了地震射线的汇集(散射)现象, 而在谷底则发散.由图 3可直观地看出, 反射界面一两个峰值及附近的射线密度远大于其他区域.从这个例子可看出, 射线密度大的区域有可能造成重建速度模型局部的失真(过度放大).解决的方法是, 可引入等权射线密度(或因子), 见图 6b, 6d所示.引入等权射线密度后, 这种速度异常过度放大(失真)现象消失, 且界面起伏形态的更新也有显著改善.
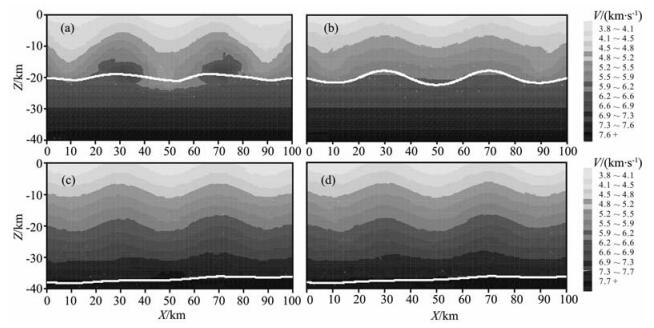
|
图 6 利用直达波和反射波走时同时反演模型速度和反射界面起伏形态 (a, b)为直达P +反射波P1P的结果; (c, d)为直达P +反射波P2P. (a, c)为常规反演结果; (b, d)为引人等权射线密度时的结果. Fig. 6 Recovered velocity fields with (b, d) or without (a, c) the equal weighted ray density in the simultaneous inversion by using combined the direct P and the reflected PP arrivals times (a, b) Direct P+reflected PP from the upper interface; (c, d) Direct P +reflected PP from the lower interface. |
图 7给出了考虑等权射线密度后利用直达P波、反射P1P和P2P波进行速度模型和两个界面同时反演更新的结果, 从图 6、7中可看出无论是速度和单一界面的同时更新、还是速度和两个界面的同时更新, 均能够较好地反演速度场分布和界面起伏细节.另一方面由于在反演中引入了等权射线密度的概念, 所得到的速度模型没有出现明显过度更新的区域, 这也从侧面验证了此方法的有效性.
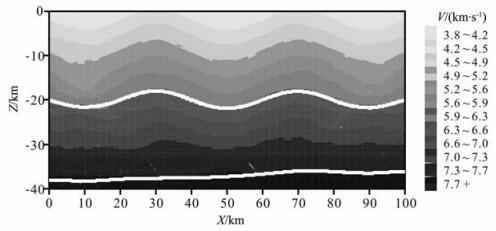
|
图 7 利用直达波P、反射波P1P和P2P对速度模型和两个界面的同时反演成像结果 图中白线为更新后的反射界面. Fig. 7 Simultaneous inversion for velocity and two interfaces using direct P, reflected P1P and P2P In figure the white lines are the updated rnterfaces. |
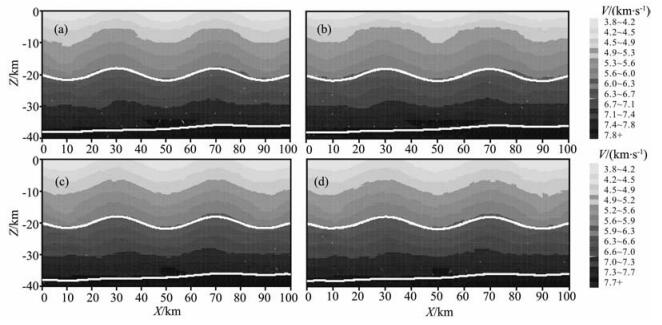
由于各震相到时拾取时存在一定的误差, 特别是后续震相到时拾取的误差就更大一些, 因此, 实际反演的走时资料中存在一定误差是不可避免的, 所以有必要进行反演算法的噪声敏感性分析.另一方面, 噪声除了来自走时资料外, 还有速度模型扰动引起的误差, 这是因为无论怎样, 我们对速度模型的估计总是近似或粗略的.从这点上来说, 好的反演算法应对走时中不可避免的误差或模型中小的扰动引起的误差不十分敏感, 否则该反演算法在实际应用中是无效的.基于上述分析讨论, 本实验中我们对上述两种误差均进行了模拟.采用直达P波、反射P1P和P2P波走时对速度分布和两个界面起伏进行了同时反演.其中速度模型扰动误差, 我们以随机相对扰动强度分别为±2.5%(结果见图 8a)和±5.0%(结果见图 8b)给出.走时误差的模拟, 我们引入绝对走时误差, 即在模拟观测走时中加入强度分别为±0.1s (结果见图 8c)和±0.2s (结果见图 8d)的随机误差.与无噪声时的结果(图 7)相比可以看出, 已基本反演出速度分布的主要特征及反射界面的起伏细节.当随机噪声继续增强时(如:走时中随机噪声强度增至±0.3s, 或速度模型中相对扰动增至±10.0%), 其成像结果中还可以大体反映速度模型及反射界面的基本特征, 但局部速度分布失真(图略).因此, 可以得出结论:该反演算法在走时中随机误差强度不大时(≤0.2 s), 或速度模型中随机相对扰动强度不大(≤5.0%)时反演结果是有效的, 其结果与我们先前有关初至波成像中所得敏感性试验结果相符[31].
|
图 8 反演算法噪声敏感性实验 (a) 速度模型±2.5%随机相对扰动; (b) 速度模型±5.0%随机相对扰动; (c) 走时±0.1 s绝对随机误差; (d) 走时±0.2 s绝对随机误差. Fig. 8 Sensitive tests for inversion algorithm (a)±2.5% random perturbation in velocity model; (b)±5.0% random perturbation in velocity model; (c) Absolute random error with strength level of±0.1 s in travel times; (d) Absolute randomerrorwith strength level of±0.2 s in travel times. |
本文利用新近提出的多次波射线追踪正演算法技术, 结合共轭梯度求解带约束的阻尼最小二乘问题的反演算法, 分析讨论了多震相走时联合同时反演成像技术.为了兼顾各种震相走时的拾取误差不同, 反演中引入了不同震相种类数据的权系数; 为了平衡两种不同模型参数对走时贡献的不同, 反演中引入了模型参数的归一化因子; 为了克服射线密度过大(或过小)区域速度值的过度(或欠)更新问题, 反演算法中引入了等权射线密度, 从而有效地解决了速度成像的失真问题.数值模拟结果表明:多波走时联合成像是一种提高走时成像空间分辨率, 进而降低重建模型失真度行之有效的途径.加之, 宽频带数字地震仪的大范围使用, 该算法更具有广泛的实际应用价值.另一方面, 多波走时联合同时反演成像技术也是地震测深首选的算法.目前工作的重点是如何在反演算法中引入射线交叉概率, 并将其推广至三维情形, 以满足利用天然地震资料进行精细结构成像的实际需要.
| [1] | Aki K, Lee W H K. Determination of three dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes. J Geophys Res , 1976, 81: 4381-4399. DOI:10.1029/JB081i023p04381 |
| [2] | Rawlinson N, Sambridge M. Seismic traveltime tomography of the crust and lithosphere. Adv in Geophys , 2003, 46: 81-198. DOI:10.1016/S0065-2687(03)46002-0 |
| [3] | Zhao D, Kayal J R. Impact of seismic tomography on Earth sciences. Current Science , 2000, 79: 1208-1214. |
| [4] | Zelt C A, Smith R B. Seismic traveltime inversion for 2-D crustal velocity structure. Geophys J Int , 1992, 108: 16-34. DOI:10.1111/gji.1992.108.issue-1 |
| [5] | Zelt C A, White D J. Crustal structure and tectonics of the southeastern Canadian Cordillera. J Geophys Res , 1995, 100: 24255-24273. DOI:10.1029/95JB02632 |
| [6] | Zelt C A, Hojka A M, Flueh E R, et al. 3D simultaneous seismic refraction and reflection tomography of wide-angle data from the central Chilean margin. Geophys Res Lett , 1999, 26: 2577-2580. DOI:10.1029/1999GL900545 |
| [7] | Zelt C A, Sain K, Naumenko J V, et al. Assessment of crustal velocity models using seismic refraction and reflection tomography. Geophys J Int , 2003, 153: 609-626. DOI:10.1046/j.1365-246X.2003.01919.x |
| [8] | Zelt C A, Ellis R M, Zelt B C. Three-dimensional structure across the Tintina strike-slip fault, northern Canadian Cordillera, from seismic refraction and reflection tomography. Geophys J Int , 2006, 167: 1292-1308. DOI:10.1111/gji.2006.167.issue-3 |
| [9] | Zhao D, Todo S, Lei S. Local earthquake reflection tomography of the Landers aftershock area. Earth Planet Sci Lett , 2005, 235: 623-631. DOI:10.1016/j.epsl.2005.04.039 |
| [10] | Rawlinson N, Sambridge M. Multiple reflection and transmission phases in complex layered media using a multistage fast marching method. Geophysics , 2004, 69: 1338-1350. DOI:10.1190/1.1801950 |
| [11] | De Kool M, Rawlinson N, Sambridge M. A practical grid-based method for tracking multiple refraction and reflection phases in three-dimensional heterogeneous media. Geophys J Int , 2006, 167: 253-270. DOI:10.1111/gji.2006.167.issue-1 |
| [12] | Bai C Y, Tang X P, Zhao R. 2D/3D multiply transmitted, converted and reflected arrivals in complex layered media with the modified shortest path method. Geophys J Int , 2009, 179: 201-214. DOI:10.1111/gji.2009.179.issue-1 |
| [13] | 唐小平, 白超英. 最短路径算法下三维层状介质中多次波追踪. 地球物理学报 , 2009, 52(10): 2635–2643. Tang X P, Bai C Y. Multiple ray tracing within 3-D layered media with the shorted path method. Chinese J Geophys (in Chinese) , 2009, 52(10): 2635-2643. |
| [14] | 唐小平, 白超英. 利用改进后的最短路径法追踪二维复杂层状介质中的多次波. 地球物理学进展 , 2009, 24(6): 2087–2096. Tang X P, Bai C Y. Multiple ray tracing within 2D layered media with the shorted path method. Progress in Geophys (in Chinese) , 2009, 24(6): 2087-2096. |
| [15] | 赵瑞, 白超英. 复杂层状模型中多次波快速追踪--一种基于非规则网格的最短路径算法. 地震学报 , 2010, 32(4): 433–444. Zhao R, Bai C Y. Fast multiple ray tracing within complex layered media:the shortest path method based on irregular grid cells. Acta Seismologica Sinica (in Chinese) , 2010, 32(4): 433-444. |
| [16] | Bai C Y, Huang G J, Zhao R. 2D/3D irregular shortest-path ray tracing for multiple arrivals and its applications. Geophys J Int , 2010, 183: 1596-1612. DOI:10.1111/j.1365-246X.2010.04817.x |
| [17] | Bai C Y, Greenhalgh S A, Zhou B. 3-D ray tracing by using a modified shortest-path method. Geophysics , 2007, 72: T27-T36. DOI:10.1190/1.2732549 |
| [18] | 刘福田. 震源位置和速度结构的联合反演(I)--理论和方法. 地球物理学报 , 1984, 27(2): 167–175. Liu F T. Simultaneous inversion of earthquake hypocenters and velocity structure (I)-Theory and method. Chinese J Geophys (in Chinese) , 1984, 27(2): 167-175. |
| [19] | 华龙标, 刘福田. 界面和速度反射联合成像--理论与方法. 地球物理学报 , 1995, 38(6): 750–756. Hua L B, Liu F T. Joint reflection imaging of velocity and interface-theory and method. Chinese J Geophys (in Chinese) , 1995, 38(6): 750-756. |
| [20] | 李松林, 吴宁远, 宋占隆, 等. 速度分布和界面位置的联合反演. 地震学报 , 1997, 19(4): 383–392. Li S L, Wu N Y, Song Z L, et al. Simultaneous inversion of velocity distribution and interface positions. Acta Seismologica Sinica (in Chinese) , 1997, 19(4): 383-392. |
| [21] | 周龙泉, 刘福田, 陈晓非. 三维介质中速度结构和界面的联合成像. 地球物理学报 , 2006, 49(4): 1062–1067. Zhou L Q, Liu F T, Chen X F. Simultaneous tomography of 3-D velocity structure and interface. Chinese J Geophys (in Chinese) , 2006, 49(4): 1062-1067. |
| [22] | Kennett B L N, Sambridge M S, Williamson P R. Subspace methods for large inverse problem with multiple parameter classes. Geophysical Journal , 1988, 94: 237-247. DOI:10.1111/j.1365-246X.1988.tb05898.x |
| [23] | McCaughey M, Satish S C. Simultaneous velocity and interface tomography of normal-incidence and wide-aperture seismic traveltime data. Geophys J Int , 1997, 131: 87-99. DOI:10.1111/gji.1997.131.issue-1 |
| [24] | Hobro J W D, Satish S C, Minshull T A. Three-dimensional tomographic inversion of combined reflection and refraction seismic traveltime data. Geophys J Int , 2003, 152: 79-93. DOI:10.1046/j.1365-246X.2003.01822.x |
| [25] | Greenhalgh S A, Zhou B, Green A. Solutions, algorithms and inter-relations for local minimization search geophysical inversion. J Geophys Eng , 2006, 3: 101-113. DOI:10.1088/1742-2132/3/2/001 |
| [26] | Menke W. Geophysical Data Analysis:Discrete Inverse Theory. San Diego, California:Academic Press Inc., 1984 |
| [27] | Meyerholtz K A, Szpakowski S A. Convolutional quelling in seismic tomography. Geophysics , 1989, 54: 570-580. DOI:10.1190/1.1442684 |
| [28] | Shaw P R, Orcutt J A. Waveform inversion of seismic refraction data and applications to young Pacific crust. Geophys J R Astr Soc , 1985, 82: 375-414. DOI:10.1111/j.1365-246X.1985.tb05143.x |
| [29] | Tarantola A, Valette B. Generalized non-linear inverse problems solved using the least squares criterion. Rev Geophys Space Phys , 1982, 20: 219-232. DOI:10.1029/RG020i002p00219 |
| [30] | Zhou B, Sinadinovski C, Greenhalgh S A. Iterative algorithm for the damped minimum norm, least-squares and constrained problem in seismic tomography. Exploration Geophysics , 1992, 23: 497-505. DOI:10.1071/EG992497 |
| [31] | Bai C Y, Greenhalgh S A. 3-D non-linear travel time tomography:imaging high contrast velocity anomalies. Pure Appl Geophys , 2005, 162: 2029-2049. DOI:10.1007/s00024-005-2703-x |
| [32] | Bishop T N, Bube R T, Cutler R T, et al. Tomographic determination of velocity and depth in laterally varying media. Geophysics , 1985, 50: 903-923. DOI:10.1190/1.1441970 |
| [33] | Bai C Y, Greenhalgh S A. 3-D local earthquake hypocenter determination with an 'irregular' shortest-path method. Bull Seism Soc Am , 2006, 96: 2257-2268. DOI:10.1785/0120040178 |
 2010, Vol. 53
2010, Vol. 53


