2. 中国科学院研究生院,北京 100039
2. Graduate University of Chinese Academy of Sciences, Beijing 100039, China
振幅随偏移距变化(AVO)技术广泛应用于储层反演、预测岩石物性,提高了储层预测准确性. AVO技术理论基础是振幅随入射角变化(AVA),二者仅在地下反射层为水平界面情况下等价[1].偏移距向入射角/反射角转换是AVO关键步骤.国内工业界俗称的角度道集(CAG)是将NMO校正后共中心点道集(CMP)或叠前偏移后偏移距域共像点道集(CIG)/共反射点道集(CRP)映射到角度域.偏移距域到角度域映射较少采用对层速度要求较高的射线追踪方法,通常利用Walden近似[2],该公式基于水平层状介质假设,无法得到相对于倾斜地层法线的入射角.Resnick[3]等分析了NMO后、DMO后以及叠前时间偏移后CRP道集AVO效应,建议Kirchhoff偏移同AVO分析一起使用;Mosher等[4]导出平面波叠前时间偏移射线参数p道集,并与CMP道集相比较,展示了叠前时间偏移对于改善地层分辨率、AVO目标局部精度等方面的价值.
近年来,用于速度以及AVA分析的角度域共像点道集(ADCIG)引起学者广泛关注[5~10],ADCIG相对于偏移距共像点道集(ODCIG)可以很大程度上减少假象.这些研究多基于叠前深度偏移(PSDM),与叠前时间偏移(PSTM)地表偏移距近似得到的入射角相比,前者在速度精确情况下求得入射角为地下局部入射角;但由于PSDM速度建模困难、计算成本昂贵等原因,基于此的ADCIG尚未见到应用于三维AVA反演实例.Kirchhoff积分法叠前时间偏移对观测系统适应性强、计算成本低等特点使得该方法一直在实际应用中占主导地位,以此输出的角度道集适用于AVA分析.Zheng[11]、Perez[12]提出一种基于直射线近似Kirchhoff叠前时间偏移角度域成像方法,并在高分辨成像和裂缝分析(方位AVAZ)得到应用;程玖兵提出走时计算基于射线追踪的表驱Kirchhoff叠前时间偏移角度域算法[13]以及非双曲时差方位/角度域叠前时间偏移[14],走时计算考虑射线弯曲效应以及等效横向各向同性,可以获得相对准确的入射角、走时.Wang等[15]分析了基于平面波分解叠前时间偏移所产生的射线参数p道集,并用于AVO分析,但推广到三维尚存在难度.
本文首先分析传统算法偏移距域转换角度域所存在问题;提出新的三维Kirchhoff叠前时间偏移角度道集提取算法,计算走时采用适应长偏移距(大入射角)优化六阶NMO方程[16],或者对线性横向变速介质有更好聚焦性的非对称走时算法[17, 18],采用相对保真的加权因子以及覆盖次数校正技术;理论模型和实际数据表明Kirchhoff叠前时间偏移角度道集,可更准确获得偏移距与入射角映射关系,其振幅相对保真,适于AVA反演.
2 叠前时间偏移角度道集与CMP、CRP道集对比实际生产中,CMP、CRP/CIG向角度道集转化较多采用公式(1)[2]:
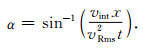
|
(1) |
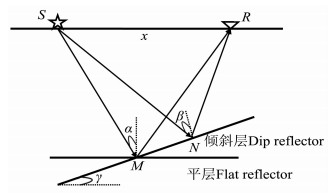
如图 1所示,α为入射射线与时间轴之间夹角,vint为层速度,vRms为均方根速度,t为双程走时,x为炮检距,该公式仅在二维水平层状介质下成立,地层倾斜时转化的角度不准确.图 1中,地下界面水平时,共深度点M即为反射点,但当地层倾斜时,反射点在N处,分选CMP道集将来自N处反射信息归为M处CMP道集,N点入射角β与水平层入射角α不相同,随着地层倾角γ值增大,二者偏离增大,M点振幅值也将受到影响.Muerdter等[19]数值分析了不同地层倾角下偏移距与反射角变化,表明AVA分析必须考虑地层倾斜.除了角度因素外,在CMP道集上,断层等横向不连续所产生断面波、绕射波与目的层反射波互相干涉,以此基础上的AVO/AVA分析不可信.因此,基于叠前偏移的AVA分析变得十分必要.叠前偏移使倾斜反射归位到真正地下界面的位置,并使绕射波收敛,改善了地震资料的横向分辨率和信噪比,消除界面曲率、倾角对地震波相位与振幅的影响,为属性处理和反演提供振幅相对保真的基础资料[20~23].
|
图 1 CMP、CRP、CAG道集示意图 Fig. 1 Contrast between CMP, CRP and CAG gathers |
CRP道集转化角度道集存在如下问题:地下构造较复杂时会出现射线阴影区,阴影区中CRP道集存在假象[7];CRP道集不记录炮检点坐标,分选叠加不考虑方位因素,当地层倾角较大时,根据Walden公式转换入射角与真实值偏离较大;CRP道集按不同偏移距进行分选,近、中、远偏移距参与叠加次数、偏移距分选间隔处理不当,都将造成振幅异常假象,使AVA走向误区.角度域叠前偏移算法在偏移同时记录入射角/反射角信息,既保留CRP道集优势,又避开CRP道集转化角度道集对水平层状假设的依赖,合适的振幅加权因子、角度域覆盖次数纠正技术使得偏移后的角度道集可应用于AVA反演;另外,角度道集上拉伸因子不变,可以较好地消除影响成像分辨率、影响AVA分析效果的远道拉伸效应[24].
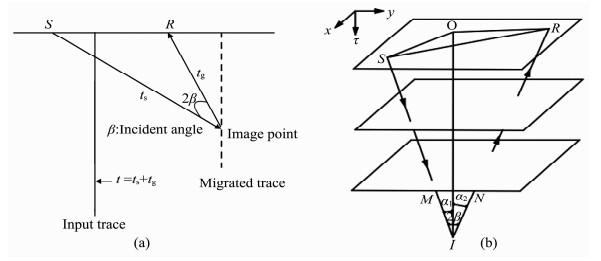
3 叠前时间偏移角度道集提取算法叠前时间偏移提取角度道集就是将偏移距改为入射角/反射角作为分选单位,同一偏移距地震数据被映射到不同角度中.图 2a为直射线PSTM射线路径图,计算走时采取DSR双曲走时:
|
图 2 直射线(a)与考虑射线弯曲射线(b)路径、入射角示意图 Fig. 2 Raypath and incident angle of (a) straight-ray and (b) bending-ray |
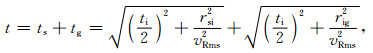
|
(2) |
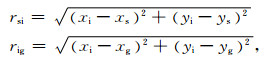
|
(3) |
其中,ti为零炮检距双程走时,rsi,rig分别为炮点、检波点到成像点水平距离,炮点S坐标为(xs,ys,0),检波点R坐标为(xg,yg,0),成像点I坐标为(xi,yi,ti).
入射角β为入射射线SI与反射射线IR夹角一半,二者夹角可由余弦定理求出[12],该算法克服公式(1)对水平层状介质假设依赖,可求得入射射线与倾斜地层法线之间夹角.直射线法PSTM有如下不足:采用双曲走时公式(2)仅保留偏移距r的2次项,随着r增加,所计算走时与真实值偏差增大,使得大偏移距/大入射角无法拉平;由于未考虑射线弯曲效应,该算法所计算入射角范围对目的层照明不足,严重影响大倾角成像以及AVA反演精度.工业界多采用大偏移距采集,陆上最大偏移距一般可达到5000~6000m,甚至更高,直射线法在走时以及入射角计算精度上都不能达到要求.Ross[25]、Bale等[26]提出使用非双曲走时进行NMO校正与AVO相结合,可以提高AVO反演的精度.我们将以上思路结合,拓展到Kirchhoff叠前时间偏移中,计算走时采用非双曲走时方程,如优化6阶NMO方程,适应线性横向变速的非对称走时算法等,根据射线参数法并考虑偏移距高阶项计算入射角,因此大角度处理更精确.
我们以优化6阶NMO方程为例[16],说明非双曲走时(弯曲射线)角度道集提取策略,公式(4)为双平方根(DSR)优化6阶NMO走时方程:
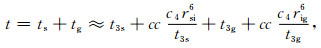
|
(4) |
其中,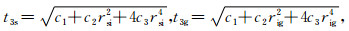
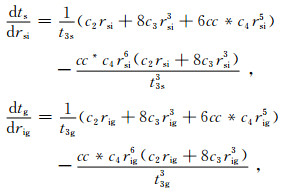
|
(5) |
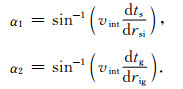
|
(6) |
实际计算α1、α2时,公式(5)保留到r的5次项即可,可节约计算量,而该方法对以度为计量单位的入射角精度影响甚微,本文模型以及实际数据都采用这种截断,角度之间采用交替叠加以提高信噪比.如图 2b所示,由公式(6)分别求得射线MI与时间轴t0夹角α1以及射线NI与时间轴夹角α2,入射角β可由空间向量法则求得[29]:
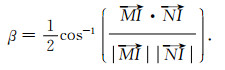
|
(7) |
其中,·代表向量点积,射线与时间轴夹角的单位向量记为(8)式,其模为1:
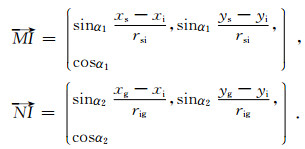
|
(8) |
振幅保真的Kirchhoff叠前时间偏移中,采取与射线弯曲效应相适应的权因子[30~32]:
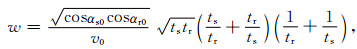
|
(9) |
其中,coss0,cosr0分别为地表处入射射线、出射射线与时间轴夹角,v0为地表速度.采集不均匀导致对地下反射点照明不均,是三维AVA主要问题,偏移前对数据进行规则化只能消除地表覆盖不均,还需进行角度域覆盖次数校正,以减弱地下照明不均所造成的AVA假象[33],其思路是计算入射角同时记录成像点每个角度有效叠加次数,再通过角度域正则化除法[8],最终得到纠正后角度道集.
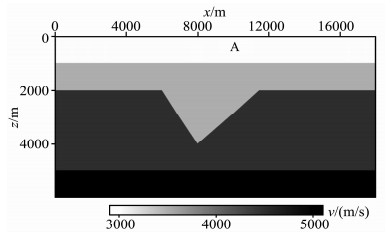
4 模型测试为了检验本文算法正确性,设计一个二维模型,如图 3所示,速度模型包含三个分界面,第一层纵波速度3000m/s,第二层速度3500m/s,第三层速度4500m/s,第四层速度为5000m/s,最大深度6000m,横向1700个CMP点,间隔10m.采用声波方程高阶有限差分法模拟,最大偏移距6000m,记录长度4s,采样时间4ms,炮间距40m,道间距20m,单边接收.
|
图 3 凹陷模型速度示意图 Fig. 3 Velocity profile of depression model |
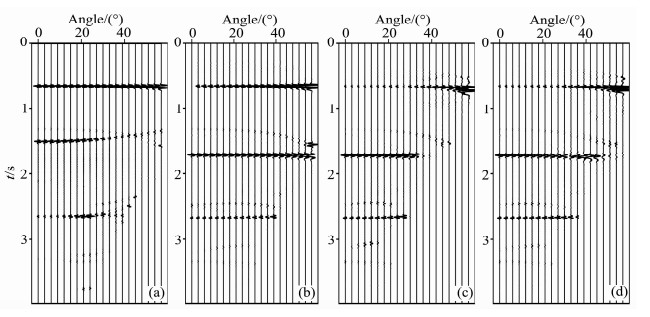
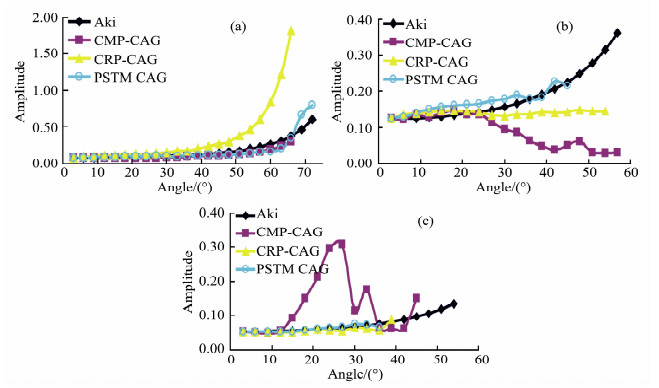
对正演数据进行Kirchhoff叠前时间偏移,并输出A点(图 3)CRP道集以及直射线、本文算法角度道集,使用Hampson-Russell(HRS)软件将A点NMO后CMP道集、CRP道集转化成角度道集,该软件根据公式(1)计算入射角,如图 4所示.将CMP、CRP道集转化以及本文方法所得角度道集各层振幅峰值与Aki公式计算的理论反射系数归一化后进行比较,检验各种方法AVA效果,如图 5所示.
|
图 4 各种方法所得凹陷模型中A点角度道集显示 (a)CMP道集转化角度道集;(b)CRP道集转化角度道集;(c)直射线叠前时间偏移角度道集;(d)本文方法所得角度道集. Fig. 4 CAG at location A in depression model extracted by different algorithms (a) CAG transformed with CMP gathers; (b) CAG transformed with Kirchhoff PSTM CRP gathers; (c) CAG extracted with straight-ray Kirchhoff PSTM; (d) CAG extracted with non-hyperbolic traveltime Kirchhoff PSTM. |
|
图 5 各反射层理论Aki公式与CMP、CRP以及本文方法所得角度道集振幅变化曲线 (a)第一层;(b)第二层;(c)第三层. Fig. 5 Contrast between Amplitude variation with angle, extracted with CMP, CRP, our PSTM-CAG method, and theoretical reflection coefficient curve using Aki formula (a) The first reflector; (b) The second reflector; (c) The third reflector; Aki: the theoretical reflection coefficient curve; CMP-CAG、CRP-CAG: Common-angle gather transformation based on CMP、CRP gathers; PSTM CAG: CAG gathers extracted by our PSTM mehod. |
图 4a中,由CMP道集转化的角度道集信噪比低,第二层斜层不能将断层绕射波归位,从振幅与理论反射系数对比图来看,第一层平层振幅与理论反射系数较好吻合(图 5a),第二层断层产生的绕射波影响第二层及第三层振幅,导致这两层振幅与理论反射系数曲线背离(图 5b、5c);图 4b为偏移CRP道集所转化的角度道集,从道集上看,反射归位,绕射收敛,信噪比高,第一层、三层平层振幅曲线与理论值匹配相对较好,第二层倾斜层不能与理论曲线吻合(图 5b),如前文所述,这是由公式(1)忽略地层倾斜导致;图 4c是直射线法叠前时间偏移角度道集;图 4d为本文方法计算角度道集,具有CRP道集优点,振幅变化也克服CRP道集AVA缺陷,无论第一层、第二层倾斜层以及第三层平层都与理论曲线基本相符(图 5);与直射线PSTM比较,本文方法获得入射角范围增大,中深层入射角范围增大15°左右(图 4c,4d),大角度信息保留对目标层成像及AVA反演都十分重要.因此,从模型测试来看,本文提出的叠前时间偏移角度道集算法具有更准确的入射角以及相对保真的振幅,适合AVA叠前反演.
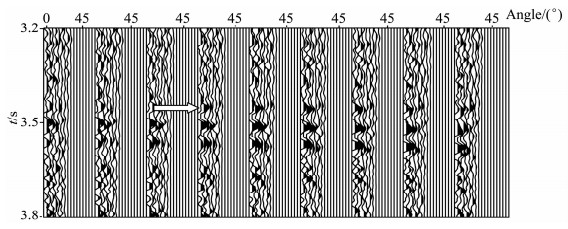
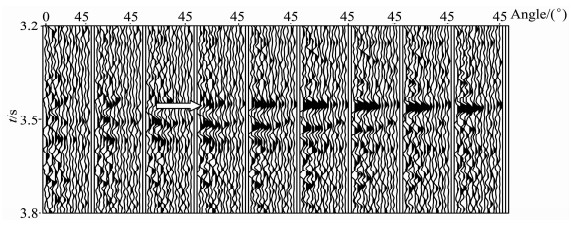
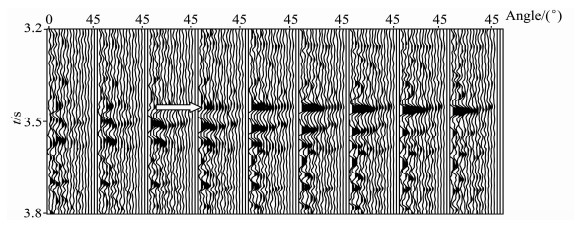
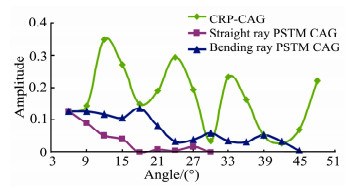
5 实际数据我们对西部某工区进行叠前AVA反演,该工区目的层碳酸盐储层位于5000~5700m奥陶系.西部地区地表衰减吸收强,地震数据信噪比低,目的层碳酸盐储层为杂乱反射,给地震成像、叠前反演带来困难.该区CMP道集信噪比低,不适合AVO反演;Kirchhoff叠前时间偏移可以对缝洞较好地成像,因此通常做法是将CRP道集转化成角度道集,以此为基础进行AVA反演.图 6为直射线叠前时间偏移输出角度道集,图 7是弯曲射线叠前时间偏移输出的CRP道集利用HRS软件转化所得角度道集,图 8是本文方法输出角度道集.比较图 6、7、8,直射线法PSTM入射角范围小,在目的层最大入射角约30°,其他两种方法目的层角度达到42°,适合两项AVA分析.我们对比井旁道3452ms附近三种角度道集AVA曲线(图 9),将该时刻附近振幅峰值归一化比较.从图 9可看出,CRP转化角度道集振幅变化起伏较大,直射线PSTM角度道集入射角范围较窄,而本文方法得到角度道集达到反演要求,振幅随入射角递减趋势变化平缓.另外,CRP转化角度道集最大角度处出现振幅异常值,给AVA反演带来误差,因此,实际操作中需限制参与反演最大、最小角度.
|
图 6 井旁直射线叠前时间偏移输出角度道集 Fig. 6 Section of common-angle gather extracted by Straight ray PSTM |
|
图 7 井旁CRP道集转化角度道集 Fig. 7 Section of common-angle gather (transformed CRP with HRS Software) |
|
图 8 井旁本文方法叠前时间偏移角度道集 Fig. 8 Section of common-angle gather extracted by bending-ray Kirchhoff PSTM |
|
图 9 井旁道3452ms时刻附近CRP转化、直射线以及弯曲射线叠前时间偏移角度道集AVA对比 Fig. 9 AVA curve contrast between CAG transformed based on CRP, by straight ray PSTM and bending ray PSTM at 3452 ms |
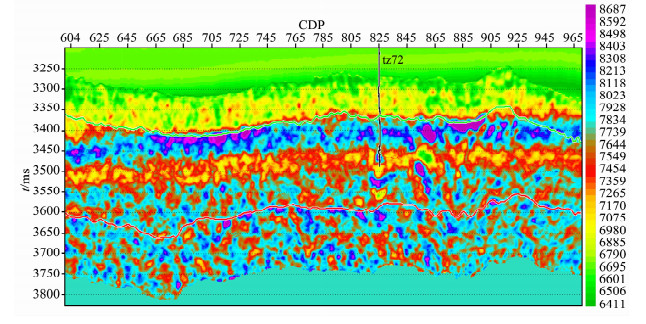
以本文方法所得角度道集为基础,结合本工区测井资料,进行叠前AVA同步反演.图 10为横波阻抗过井剖面,图中串珠状储层横向、纵向分布得到较好描述,结果表明本文算法所得角度道集更适于AVA反演.
|
图 10 本文方法角度道集反演横波阻抗过井剖面 tz72为井号,色标表示横波阻抗值,单位为(m·s-1)·(g·cm-3). Fig. 10 Section of shear wave impedance inversion with CAG extracted by our method |
本文提出角度域非双曲走时Kirchhoff叠前时间偏移方法,与传统转化角度道集方法比较,具有角度相对精确、角度范围广、振幅相对保真等特点,计算量增加有限,更适于叠前AVA分析及反演.文中覆盖次数纠正技术在简单地质情况下是可行的,一旦地质构造复杂导致反射点覆盖次数统计出现误差,将给振幅带来新的误差,因此,如何在角度域更好消除成像点照明/覆盖不均匀以提高三维AVA准确性,需进一步研究.
振幅保真包括地震数据的保真处理以及保真偏移,二者缺一不可,如果处理中振幅出现异常,将影响后续保幅偏移.常规处理、偏移导致振幅出现畸变,将使AVA分析、反演走向误区.因此,地震数据保真处理解释定量化,对于岩性油气藏的描述,变得尤为迫切.
PSTM适用于横向缓变速介质,如果地质构造复杂、横向变速剧烈,Kirchhoff叠前时间偏移角度道集用于AVA分析也将不适合,真振幅叠前深度偏移角度道集是AVA反演发展方向.
致谢感谢中石化南京物探技术研究院张兵提供模型正演数据;感谢Cgg公司“大学捐助计划”提供HRS软件.
| [1] | Shang Z, Mcdonald J A, Gardner G H F. Automated extraction of AVA information in the presence of structure. 63th Annual International Meeting. SEG, Expanded Abstracts , 1993: 713-715. |
| [2] | Walden A T. Making AVO sections more robust. Geophysical Prospecting , 1991, 39(7): 915-942. DOI:10.1111/gpr.1991.39.issue-7 |
| [3] | Resnick J R, Ng P, Larner K. Amplitude versus offset analysis in the presence of dip. 57th Annual International Meeting. SEG, Expanded Abstracts , 1987: 617-620. |
| [4] | Mosher C C, Keho T H, Weglein A B, et al. The impact of migration on AVO. Geophysics , 1996, 61(6): 1603-1615. DOI:10.1190/1.1444079 |
| [5] | Prucha M L, Biondi B L, Symes W W. Angle-domain image gathers by wave-equation migration: Angle-domain common image gathers by wave equation. 69th Annual Meeting. SEG, Expanded Abstracts , 1999: 824-827. |
| [6] | Mosher C C, Jin S, Foste D J. Migration velocity analysis using common angle image gathers. 71st Annual International Meeting. SEG, Expanded Abstracts , 2001: 889-892. |
| [7] | Xu S, Chauris H, Lambare G, et al. Common-angle migration: A strategy for imaging complex media. Geophysics , 2001, 66(6): 1877-1894. DOI:10.1190/1.1487131 |
| [8] | Sava P C, Fomel S. Angle-domain common-image gathers by wavefield continuation methods. Geophysics , 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078 |
| [9] | Stolk C C, de Hoop M V, Symes W W. Kinematics of prestack shot-geophone migration. 75th Annual International meeting. SEG, Expanded abstracts , 2005: 1866-1869. |
| [10] | 陈凌, 吴如山, 王伟君. 基于Gabor-Daubechies小波束叠前深度偏移的角度域共成像道集. 地球物理学报 , 2004, 47(5): 876–885. Chen L, Wu R S, Wang W J. Common angle image gathers obtained from Gabor daubechies beamleat prestack depth migration. Chinese J. Geophys. (in Chinese) , 2004, 47(5): 876-885. |
| [11] | Zheng Y. Seismic azimuthal anisotropy and fracture analysis from PP reflection data [Ph. D. thesis]. Calgary: University of Calgary, 2006 http://www.crewes.org/ResearchLinks/GraduateTheses/2006/Zheng-PhD-2006.pdf |
| [12] | Perez G, Marfurt K J. Improving lateral and vertical resolution of seismic images by correcting for wavelet stretch in common-angle migration. Geophysics , 2007, 72(6): 94-104. |
| [13] | 程玖兵, 王楠, 马在田. 表驱三维角度域Kirchhoff叠前时间偏移成像方法. 地球物理学报 , 2009, 52(3): 792–800. Cheng J B, Wang N, Ma Z T. Table-driven 3-D angle-domain imaging approach for Kirchhoff prestack time migration. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 792-800. |
| [14] | 程玖兵, 王楠.非双曲时差方位/角度域叠前时间偏移.CPS/SEG Beijing 2009 International Geophysical Conference & Exposition. 2009. ID1179. Cheng J B, Wang N Azimuth/angle-domain imaging in prestack time migration using non-hyperbolic moveout. CPS/ SEG Beijing 2009 International Geophysical Conference & Exposition. 2009. ID1179 |
| [15] | Wang D, Zheng X D, Chen J B. Amplitude-preserving planewave prestack time migration for AVO analysis. Applied Geophysics , 2008, 5(3): 212-218. DOI:10.1007/s11770-008-0023-5 |
| [16] | Sun C W. Optimized 6th NMO correction for long-offset seismic data. 72th Annual International Meeting. SEG, Expanded Abstracts , 2002. |
| [17] | 刘洪, 王秀闽, 曾锐, 等. 单程波算子积分解的象征表示. 地球物理学进展 , 2007, 22(2): 463–471. Liu H, Wang X M, Zeng R, et al. Symbol description to integral solution of one-way wave operator. Progress in Geophysics (in Chinese) , 2007, 22(2): 463-471. |
| [18] | 李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形提速实现方法. 地球物理学报 , 2009, 52(1): 1–8. Li B, Liu G F, Liu H. A method of using GPU to accelerate seismic pre-stack time migration. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 1-8. DOI:10.1002/cjg2.v52.1 |
| [19] | Muerdter D, LLC L, Kelly M, et al. The effect of reflector dip on AVO analysis. 75th Annual International Meeting. Expanded Abstracts , 2005. |
| [20] | 刘洪林, 朱秋影. 基于叠前深度偏移的AVO反演及解释. 地球物理学进展 , 2007, 22(3): 905–913. Liu H L, Zhu Q Y. AVO inversion and interpretation based on prestack depth migration. Progress in Geophysics (in Chinese) , 2007, 22(3): 905-913. |
| [21] | 胡贤根, 尚新民, 石林光, 等. 基于叠前时间偏移资料的AVO处理技术. 石油物探 , 2002, 41(3): 343–346. Hu Y G, Shang X M, Shi LG, et al. AVO process techniquebased on prestack time migration data. Geophysical Prospeding for PeLroleum (in Chinese) , 2002, 41(3): 343-346. |
| [22] | Tygel M, Santons L T, Schleich r J. Kirchhoff imaging as a tool for AVO/AVA. The Leading Edge , 1999, 18(8): 940-945. DOI:10.1190/1.1438413 |
| [23] | Avseth P, Mukerji T, Mayko G. Quantitative Seismic Interpretation. Cambridge University Press. 2005 : 190 -200. |
| [24] | Roy B, ANmo P D, Baumel R, et al. Analytic correction for wavelet stretch due to imaging. 75th Annual International Meeting. SEG, Expanded Abstracts , 2005: 234-237. |
| [25] | Ross C. AVO and nonhyperbolic moveout: A practical example. First Break , 1997, 15: 43-48. |
| [26] | Bale R, Leaney S, Dumitru G. Offset-to-angle transformations for PP and PS AVO analysis. 71th Annual International Meeting. SEG, Expanded Abstacts , 2001: 235-238. |
| [27] | Taner M T, Koehler F. Velocity spectra-digital computer derivation and applications of velocity functions. Geophysics , 1969, 34(6): 859-881. DOI:10.1190/1.1440058 |
| [28] | Castal R J. A theory of norml moveout. Geophysics , 1994, 59(6): 983-999. DOI:10.1190/1.1443658 |
| [29] | Zou Z, Liu H, Liu W H. 3-D angle-domain common imaging gathers during Kirchhoff PSTM. 79th Annual International Meeting. SEG, Expanded Abstracts , 2009: 326-330. |
| [30] | Zhang Y, Gray S, Yong J. Exact and approximate weights for Kirchhoff migration. 70th Annual International Meeting. SEG, Expanded Abstacts , 2000: 1039-1039. |
| [31] | Lee S, King D, Lin S. Efficient true-amplitude weights in Kirchhoff time migration. 74th Annual International Meeting. SEG, Expanded Abstracts , 2004: 1089-1092. |
| [32] | Dellinger J A, Gray S H, Mu phy G E, et al. Efficient 2. 5-D true-amplitude migration. Geophysics , 2000, 65(3): 943-950. DOI:10.1190/1.1444790 |
| [33] | Audebert F, Nicoletis L, Froidevaux P. Regularization of illumination in angle domains-A key to true amplitude migration. The Leading Edge , 2005, 24(6): 643-654. DOI:10.1190/1.1946222 |
 2010, Vol. 53
2010, Vol. 53

