2. 中国地震局地质研究所, 北京 100029;
3. 北京市地震局, 北京 100080
2. Institute of Geology, China Earthquake Administration, Beijing, 100029, China;
3. Earthquake Administration of Beijing City, Beijing 100080, China
由于地质系统本身的固有属性[1]或实际研究障碍[2], 依据目前的知识, 通常认为地震、火山喷发以及滑坡等灾害的预报是不可能的.目前, 大地震的预测是世界性的科学难题.其中, 孕震区几何与地质条件的复杂性、断裂带应力的不可量测性、地球介质的非均匀性以及孕震过程的非线性是最重要的影响因素[1~3].但为了有效减轻大地震及巨震带来的严重灾害, 地震预测问题必须解决.
尽管人们在地震科学研究中已做出了巨大努力[4~48], 但世界上许多灾难性地震无法预测的严酷现实表明, 我们对地震机制的认识远远不够.目前, 对地震三要素(时间、地点和震级)的预测研究主要集中于两个方面:
(1)基于地震学观测以及统计物理学、试验和力学理论进行失稳演化机理分析, 并利用这些成果做出进一步预测.然而, 由于孕震过程的强烈非线性作用, 描述地震孕育过程的动力学方程[11]还不能准确约束.即使这些方程能够可靠地写出, 确定诸多的几何与力学参数仍十分困难.Tang[12]指出, 在非线性和不连续问题的理论研究方面有一种越来越复杂且难以实际应用的趋势.
(2)通过经验和统计模型(例如时间-破坏模型[13]和对数周期时间-破坏模型[14])预测地震的发生时间与震级.然而, 除个别巧合的情况[3, 9]外, 难以证明这些模型具有实际地震预测的可靠性. Coral[15]曾指出, 从规则的周期模型、特征地震到地震随机发生模型角度来看, 这些预测结果是相互矛盾的.因此, 要解决地震的预测问题, 尤其是地震的时间和震级预测, 也需要有新的理念和新的研究方法.
现已发现[16, 17], 累积Bemoff应变[9](序列地震释放能量的平方根之和)可作为大地震的前兆现象, 在较大区域内中等强度预震(preshock)的加速应变能释放与较小区域内的减速应变能释放是一种明显的前兆模式, 对大地震或主震中期预测研究非常有用.然而, 它们的物理机制仍需完全破解.
许多地震学家[38~40]认为2008年5.12汶川大地震没有明显的前兆, 并且可能是一个水库诱发地震的实例.这些观点正确吗?该地震能否被预报? 2010年1月13日海地Mw7. 0级地震发生在Etang de Miragoane断层与Jacmel-Fauchedepression断层的交汇处(还有一些没被探明的隐伏断层), 死亡人数已经超过了20万人.像汶川和海地大地震等灾难性地震存在有地震加速活动性前兆吗?能不能被提前预测?本文首先根据孕震断层多锁固段脆性破裂行为, 建立相应的理论方法, 通过对历史地震的回溯和分析, 期望对大地震能否预测预报给出一定程度解答.
2 理论地震源自于沿断层的滑动.已有研究发现[18], 断层的运动模式和相关的地震活动性受断层面上一个或多个锁固段所控制."锁固段"(诸如断层中所谓的岩桥(Rock bridge)、障碍(Barrier)或凸起体(Aspenty))可定义为在断层面上具有较高强度且在地震中释放较大地震矩的结构部位.例如, 在断层面上不同类型、尺寸不一的凸起体, 包括两断层面之间的非均匀接触体、不连续断层之间的未破裂区段、或蠕滑受阻区域.一旦所有的锁固段被突破, 主震将不可避免地发生.
2.1 锁固段的临界破坏概率将断层两盘间的一个锁固段分为N个子段, 每一个子段称为一个基本块体(一级块体).将N个基本块体组成N/2个集团(二级块体), 每一个包含两个块体, 构建一个分等级模型(图 1).当集团中的两个块体都破坏了, 可认为该集团破坏.通过限制一个集团内部的应力转移[10, 19], 使得复杂的破坏问题可解.一个集团有两种破坏模式.第一种是两个块体同时破坏; 第二种是一个块体先破坏, 然后由于应力转移导致另一个块体破坏.

|
图 1 锁固段破坏过程的分等级模型 Fig. 1 Illustration of the hierarchical model for the failure process of a locked patch, in which each of two adjacent blocks is regarded as a group and so on |
这里我们选用经典的Weibull分布[20]表示一个块体的破坏强度σf小于应力ασ时的概率Pα, 可表示为
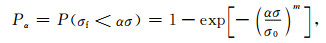
|
(1) |
式中, σ为应力, α为尺度参数, σ0为平均应力, m是形状参量, 表示局部强度变化的测度.
当α=1时基本块体的破坏概率可表示为
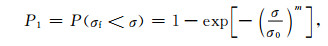
|
(2) |
联合式(1)和式(2), 可得
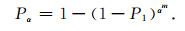
|
(3) |
当应力(a-b)σ传递给一个承担应力为bσ的未破坏块体时, 其破坏将发生的条件概率Pa, b[19]可表示为

|
(4) |
对于含有破坏或未破坏两个块体的集团, 可能有四种状态: [b, b], [b, un], [un, b]和[un, un], 其中b和un分别表示破坏和未破坏.显然[b, un]和[un, b]表示相同的状态.当附加应力从相邻的破坏块体传递到一个未破坏块体时, 以前的状态将改变为[b, b], [un, b]→[b, b], [un, b]和[un, un].不难理解, 仅[b, b]+{[un, b]→[b, b]}状态对二级块体的破坏概率P1(2)有影响.块体与集团之间应力相互作用的概率P1(2)[19]为
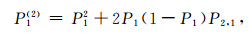
|
(5) |
式中, P2, 1可由方程(4)解得, 为

|
(6) |
将式(6)代入式(5), 得
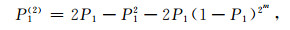
|
(7) |
对于更高级的块体, 式(7)的通式为
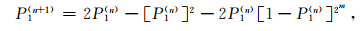
|
(8) |
其中, n为块体的级别.
令P1(n+1)=P1(n)=P*, 可解得三个不动点, 分别为0, 1, 以及
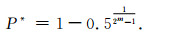
|
(9) |
根据重正化群理论[21]可确定, P*=0和P*=1都是稳定不动点, 式(9)表示的P*是一个非稳定不动点.P*=0和P*=1分别表示系统处于稳定状态和完全破坏状态.对于P1 < P*或P1>P*(式(9)中的P*), 系统将分别向稳定状态P1(∞)→0或不稳定状态P1(∞)→1演化.因此, 满足式(9)的破坏概率P*是一个临界值, 对应于一个锁固段的临界破坏点.
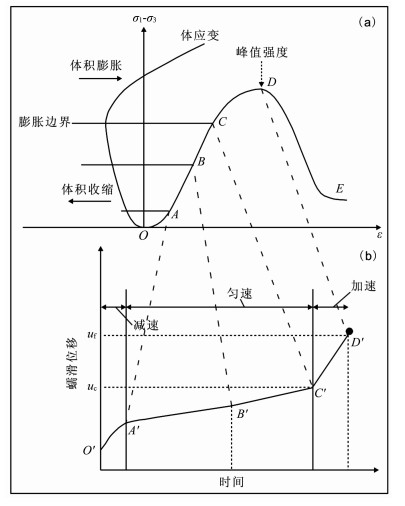
2.2 锁固段破坏机理与其蠕滑行为的关系通常, 在三轴压缩条件下岩石或类岩石材料的变形与破坏过程呈现5个明显不同的阶段[22], 如图 2a所示.可看出, 对应于体膨胀界限的C点是稳定与不稳定破坏的分界点, C点以后的应变率将远高于C点之前的应变率.在CD阶段, 即使施加的差应力保持不变, 破裂仍会不断地累进性发展直至最终破坏.因此, 可以合理地推断点C对应着锁固段临界破坏点(膨胀界限)和加速蠕变起点C', 如图 2b所示.这里, 我们定义峰值强度点为锁固段断裂点, 表示主震的临界失稳点.当一个断层系统处于此临界失稳点时, 主震随时可被适当的扰动触发.
|
图 2 锁固段变形破坏过程与发震断层蠕滑阶段的对应关系 (a)三轴压缩下岩石的典型应力应变曲线(OA, AB, BC, CD, DE分别表示裂纹闭合、弹性、稳定破裂、非稳定破裂、宏观破坏阶段); (b)对应锁固段变形破坏过程的蠕滑特征(O′A′, A′B′, B′C′和C′D′分别对应于应力应变曲线上OA, AB, BC和CD阶段; A′B′和B′C′均属于等速蠕变阶段, 但由于裂纹传播效应, B′C′阶段的位移速率略高于A′B′阶段; 黑点表示主震发生. Fig. 2 Corresponding relationship between the process of deformation and failure and the creep phase for a locked patch on a seismogenic fautt (a) A typical stress-strain curve of rock under triaxial compression with compaction stage (OA), elastic stage (AB), the stage of crack initiation and stable crack growth (BC), the stage of progressive failure (CD) and the stage of macroscopic rupture (DE); (b) The characteristics of creep displacement corresponding to the process of deformation and failure of the locked patch, where O′A′, A′B′, B′C′ and C′D′ on the time-displacement curve corresponds to OA, AB, BC and CD on the stress-strain curve, respectively |
根据Weibull分布微元体的弹性假设[43], 式(1)也可表示为蠕滑位移的函数, 即
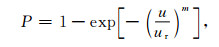
|
(10) |
式中, u为沿断层面的蠕滑位移; ur是平均位移的测度.
由式(10)可得具有应变软化属性的锁固段剪切本构模型[23]为

|
(11) |
式中, Gs为初始剪切模量, h为断层面厚度.Weibull分布引人注意的一点是形状参数m的存在.例如, 当m=1时, 为指数分布; 当m=2时, 为二次方函数分布, 在地震学研究中常用; 当m=3时, 很接近于正态分布.因为m是材料局部强度变化的量度, 可称m值为材料的均匀性指标.
求解式(1)关于位移u的一阶导数, 得到与峰值强度相对应的位移值为

|
(12) |
将式(9)代入式(10), 锁固段的临界破坏点C的位移可表示为
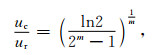
|
(13) |
将式(12)与式(13)做比值, 可得

|
(14) |
通过上述类比分析可知, 应力应变曲线上uc和uf表示的位移对应于时间-位移曲线上加速蠕变起点和锁固段断裂点的位移.若uc和m值分别由时间-位移曲线和力学试验确定, 则uf可解.
通过计算可知, 当m≥1时, 式(14)对参数m并不敏感.根据剪切试验[24]可知, 在缓慢加载作用下, 岩样的m值通常为1~3.当m=1~3时, 式(14)右边的平均值为1.48.因此, 式(14)可近似表示为
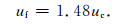
|
(15) |
由于沿断层面的深部滑动位移不能直接测量, 我们应寻求位移的替代量.幸运的是, Benioff应变提供了这一参量的测度.假设Benioff应变与位移成正比, 则有
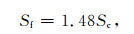
|
(16) |
式中, Sf和Sc分别为与uf和uc相对应的应变.
2.4 多锁固段临界应变准则实际上, 一个孕震断层可能包含多个锁固段.在此我们以两个锁固段为例做进一步分析.在构造荷载作用下, 大量的应变能积聚在锁固段处.假设第一个锁固段的强度低于第二个锁固段, 在剪应力集中作用下, 在某一应变值时第一个锁固段将破坏.因此根据式(6), 第一个锁固段断裂点的应变值可表示为
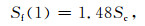
|
(17) |
随后, 剪应力将施加于第二个锁固段上, 以连锁反应的方式导致第二个锁固段破坏.同理, 第二个锁固段断裂点的应变表达式为
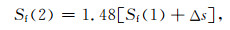
|
(18) |
式中, Δs为第一个锁固段断裂与第二个锁固段临界破坏开始前的应变增量.通常认为, 第二个锁固段临界破坏前的应变能释放率很低, 故Δs为一小量, 可忽略不计.因此, 式(8)可写为
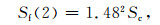
|
(19) |
同样, 对于k个锁固段, 可得
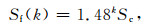
|
(20) |
式中, Sf(k)为对应于第k个锁固段断裂点(即将发生的中等强度预震或大预震)的临界应变.在最后一个锁固段破坏后, 主震将发生.
式(20)表明, 失稳点的临界应变与加速应变始点值和锁固段的数目有关, 而与锁固段的尺寸和强度无关.
3 回溯性预测验证给出几个典型地震实例以验证式(20)的潜在科学意义.首先, 需要在时间-应变曲线上找出一个明显的应变速率加速点, 对应于一个地震目录中的中等强度预震或在短时间内在同一区域的地震活动性加速(震群)事件, 然后利用式(0)进行预测.如果我们不能从该曲线中判断该预震事件, 我们建议在曲线上选择一个明显的台阶形状的加速应变开始点, 作为加速应变能释放的起点.
印度尼西亚苏门答腊2004年12月26日Mw=9. 0~9.3级地震引发了一场灾难性的海啸, 使地震学家们认识到地震预测预报的巨大难度.然而根据式(16), 从图 3可见, 对单锁固段情况, 预测的该地震Sf值接近于失稳点的实际应变值(对应地震震级), 预测的地震发生时间较实际发震时间提前了大约一年.可以预料, 如果在一个地震周期内1965年以前的数据能够得到, 该地震时间与震级的预测精度将大大提高.这说明监测越早, 预测效果越好.据报道[8]根据时间一破坏模型取得较好预报结果的一个地震实例是1989.10.17Ms=7.1Loma Prieta地震, 从图 4可看出, 根据我们提出的预测方法, 时间与震级预测效果也很理想.从图 5和图 6知, 对多锁固段情况, 正如预期的一样, 每一步Sf(k)的预测值均十分接近估计的锁固段断裂点的应变值, 且最后一步的预测值接近或几乎等于实际主震发生时刻对应的应变值.

|
图 3 2004年12月26日印度尼西亚Sumatra地震前(Mw=9.0~9.3)观测的累积Benioff应变随时间变化曲线 图中数据点(十字)[25]为主震前观测的累积Benoff应变值.曲线表示用时间-破坏模型对观测数据的拟合值.垂直虚线和红线分别表示预测与实际的主震发生时间. Fig. 3 Time variation of the observed cumulative Benioff strain for the great Sumatra earthquake on 26 December, 2004 (Mw=9. 0~9. 3) in Indonesia Data points[25] (crosses) are observed cumulative Benioff strains prior to major earthquake. The observations are fitted by a power-law time-to-failure model (solid curve). The dashed and red vertical lines denote the predicted and actual occurrence time of the mainshock, respectively. |
|
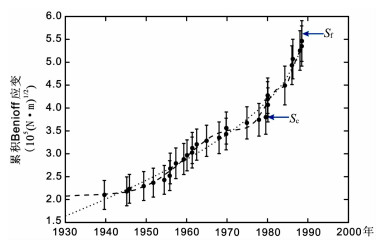
图 4 1989年10月17日Loma Prieta Mw=7. 1地震前累积Benioff应变与时间关系 图中数据点(黑圈)[8]为主震前观测的累积Benoff应变值.曲线表示用两种时间-破坏模型对观测数据的拟合值.误差棒表示震级的精度为上下0.3个单位. Fig. 4 A plot of accumulated Benioff strain as a function to time before the Mw=7.1 Loma Prieta earthquake occurred in the San Francisco California of central California on October 17, 1989 The two smooth curves represent the two types of time-to-failure models. Error bars are assigned on the assumption that magnitudes are accurate to 0. 3 units. |
|
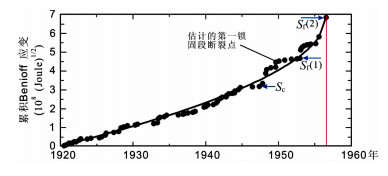
图 5 1956年7月9日希腊Amorgos地震(M=7.5)前震区观测的累积Benioff应变随时间变化曲线. 图中数据点(黑圈)[26]是观测的主震前累积Benioff应变值.曲线表示用时间-破坏模型对观测数据的拟合值.垂直红线表示主震发生时间 Fig. 5 Time variation of the observed cumulative Benioff strain in the preshock region of theM=7.5 Amorgos earthquake on 9 July, 1956 in Greece Data points[26](black circles) are observed cumulative Benioff strains prior to major earthquake. The observations are fitted by a power-law time-to-failure model (solid curve). The redvertical line denotes the occurrence time of the mainshock. |
|
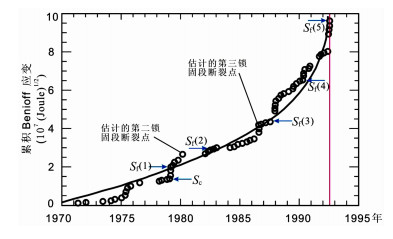
图 6 1992年6月28日加利福尼亚Landers地震(M=7. 3)前震区观测的累积Bemoff应变随时间变化曲线 图中数据点(黑空心圈)[27]是观测的主震前累积Benoff应变值, 曲线表示用时间-破坏模型对观测数据的拟合值.垂直红线表示主震发生时间. Fig. 6 Time variation of the observed cumulative Benioff strain in the preshock region of the M=7.3 Landers earthquake on June 28, 1992 in California Data points [27] (open circles) are observed cumulative Benioff strains prior to major earthquake. The observations are fitted by a power-law time-to-failure model (solid curve). The red vertical line denotes the occurrence time of the mainshock. |
一个累积应变-时间曲线提供了判断地震活动性的丰富信息.在曲线上一个明显的台阶形状意味着应变速率的迅速增长与一个锁固段的临界破坏和断裂错动过程有关, 之后低速的应变增长(通常接近于零)归于下一个锁固段承载力的施加.在最后一个锁固段破坏前, 每一个锁固段的临界破坏一断裂过程表示一个中级或大级别预震的产生过程; 在最后一个锁固段破坏之后, 主震将发生.
4 误差修正方法需注意的是, Benioff应变计算依赖于特定孕震构造区一个地震周期内完整且准确的地震目录以及对孕震区域的准确识别, 故观测和计算误差不可避免.为此我们提出一种估算Benoff应变误差的方法.
若考虑应变误差Δ那么加速应变起点和第一个锁固段断裂点的实际应变值分别为Sc*+Δ和Sf*+Δ其中Sc*和Sf*为观测值.由式(16)可求得误差的表达式:
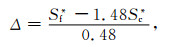
|
(21) |
给出三个实例说明该误差修正方法的效果.由图 7~9可看出, 预测结果令人满意.此外, 我们还分析了文献中其他55个具有长期观测周期的地震实例, 均得到了与观测结果一致的满意的预测结果.

|
图 7 2000年1月15日中国姚安6.5级地震前时间-应变关系曲线 观测数据点[8]以黑圈表示, 曲线表示用时间-破坏模型对观测数据的拟合值.垂直红线表示主震发生时间.误差修正已被考虑. Fig. 7 Time-strain relation before the 15 January 2000 Ms=6.5 earthquake in Yaoan, China The curve of power-law fitting is shown in the figure. The black circles and red line denote observed data [8] and the occurrence time of the mainshock, respectively. The error correction is also considered. |
|
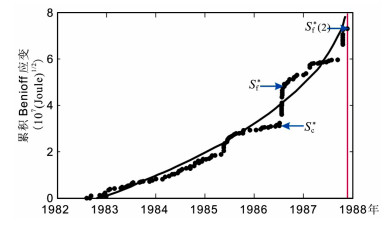
图 8 1987年11月24日圣地亚哥Superstition Hills地震(M=6. 6)前观测的累积Beniof应变随时间变化曲线 图中观测数据(黑圈)[29]表示累积Benoff应变, 曲线表示用时间-破坏模型对观测数据的拟合值, 垂直红线表示主震发生时间.误差修正已被考虑. Fig. 8 Time variation of the observed cumulative Benioff strain before the 24 November 1987 M=6.6 Superstition Hills earthquake in San Diego The observational data[29] (black circles) are fitted by a power-law time-to-failure model (solid c^urve). The red line indicates the occurrence time of themainshock. The error correction is also considered. |
|
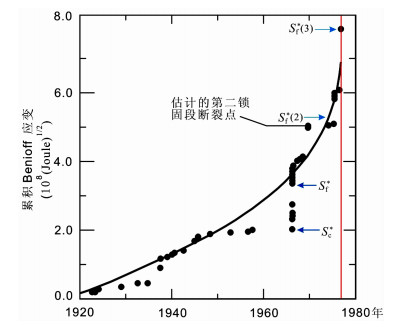
图 9 1976年7月28日唐山M=7.8地震前观测的累积Beniof应变随时间变化曲线 图中观测数据(黑圈)[6]表示累积Benoff应变, 曲线表示用时间-破坏模型对观测数据的拟合值, 垂直红线表示主震发生时间.误差修正已被考虑. Fig. 9 Time variation of the observed cumulative Benioff strain before the 28 July 1976 M=7.8 Tangslian earthquake in China Solid smooth lines represent fitting to the data [6](black circles) of a power law and red vertical lines denote the occurrence time ofmainshocks. The error correction is also considered. |
对存在多个锁固段的一条地震断裂带, 地震序列主要来自于一个锁固段破坏与另一个未破坏的锁固段阻挡地震断裂的相互作用过程, 这相当于一个地震活跃期、一个地震平静期, 如此等等, 从时间上看将产生一个交替的地震周期现象.
Mogi[30]、Kelleher和SZvino[31]发现, 在日本西南部、旧金山湾区以及环太平洋地带, 主震前的地震活动丛集在即将到来的主震区的外围, 且主震区本身的地震活动性是相对平静的, 构成地震空区.我们对这种现象的合理解释如下:对多个锁固段情况, 每一个锁固段的累进性破坏都将产生中等强度预震或更大震级预震, 这些地震应该发生在最后一个未破裂的锁固段(震中区)周围, 主震震中区本身在最后一个锁固段临界破坏前其地震活动性应该是相对平静的, 即未来主震区断层是闭锁的, 积累弹性应变能.因为锁固段[18]可能控制着前震、主震和余震的位置.需强调的是, 只有当最后一个锁固段破坏后, 主震才能发生.
Bufe等[32]和Steven等[9]也观察到, 一些地震的前震事件丛集在主震的成核域而不是分散在周边地带.Scholz[33]曾解释这种现象为震前滑移引起的膨胀硬化与应力松弛.然而, 我们认为这些情况与一个锁固段有关.可以预料, 锁固段外围的地震活动性将是相对平静的, 而在该锁固段临界破坏开始后, 即将发生的大地震震中域将呈现出地震活动性逐步增强的特征, 即大地震前存在中小地震加速活动性前兆.
5.2 地震孕育过程有自组织临界性吗?自组织临界性(SOC)[42]指的是, 一个具有持续的能量供给、由很多基本单元组成、组成系统的基本单元之间具有(非线性的)相互作用的系统, 会自发地演化到一个类似于临界状态的状态.目前国际上围绕地震预测问题的争论, 很大程度上与地震的自组织临界性(SOC)模型有关.根据地震的SOC模型, 地震预测被认为是不可能的.Geller等[1](1997)认为:"地球是处在一种自组织临界状态上的, 其中任何小地震都有可能级联式地发展成一个大地震.这一想法得到除特大地震之外的所有地震的尺度不变性的观测事实的支持".如果地球总是处于自组织临界状态, 那么地震真的不能被预测.但根据我们上述的实例分析, 在某个锁固段变形到临界破坏(膨胀)-断裂阶段, 在此处的地质体处于自组织临界状态; 在其断裂后下一个锁固段临界破坏前, 系统又脱离了临界状态, 其演化过程的自组织临界状态是间断出现的, 不是总处于临界状态.
5.3 地震孕育过程有混沌性吗?1963年, Lorenz[24]在研究大气对流的稳定性时, 发现了著名的混沌效应.混沌系统的最大特点是对初值的极其敏感性, 如著名的"蝴蝶效应"指出:巴西的一只蝴蝶拍拍翅膀, 就可能导致美国德克萨斯州的一场龙卷风.根据混沌动力学理论, 不少学者推断地质系统如斜坡系统、孕震系统在其演化过程中存在着混沌性, 因此得到了地质灾害的长期预测是不可能准确的, 甚至是不可能预测的片面结论.由上述分析知, 在锁固段开始膨胀前, 系统可能有混沌性, 其未来的演化路径可能有多种选择; 但在其膨胀开始后, 除非发生大幅的减载作用, 否则系统肯定向失稳态演化, 但其失稳时间受控于动力环境条件与触发因素.这说明在所关注的地质体演化到膨胀点后, 系统的演化将遵循确定性的规律, 没有混沌现象出现.
5.4 地震的可预报性地震可以预报吗?对这个问题有着广泛的争议与辩论[4].对于含多个锁固段的孕震断层, 即使锁固段的数目未知, 结合地震活动性观测, 我们仍可以利用式(20)进行逐步的大地震发生时间与震级大小预测; 通过动态追踪沿孕震断层的预震活动性区域, 推测较大震级预震与主震的发生地点.应该注意对单锁固段情况, 用式(20)不能预测前震, 但可把第一个中级前震或震群作为地震前兆(加速应变增长)预测未来的主震.我们建议在未来的地震预测研究中, 为了识别锁固段的个数且尽早预测主震, 地震学家应多关注锁固段的地质和地球物理调查研究.
尽管从现有技术角度看, 地球是不可人的且某些物理参量难以直接测定, 但主震前的每次中、小地震活动都是对沿断层面滑动位移的一次测度, Benoff应变是反映深部位移的一个可靠参量, 因此我们可以不去测定地球深部的其他物理细节和指标; 再者在锁固段演化到膨胀点后, 孕震系统将遵循确定性的规律, 即没有混沌性.因此, 我们可以确认, 至少在理论上和现有的技术层面大地震或特大地震是可以预测的.
5.5 慢地震与寂静地震近年来, 在许多地壳俯冲带上, 如日本南海沟、卡斯卡底古陆及墨西哥格雷罗, 发现了一系列异常的地震现象[34~37], 包括深部幕式颤动、低频地震、极低频地震、慢滑以及寂静地震.与常规地震一样, 这些异常现象都被证明是由剪切滑动引起的, 但其具有相对长的持久特征且释放较少的地震能量.
这些异常的地震与常规地震是类似的还是完全不同的, 是一个有趣的科学问题.流体的存在和其扩散作用以及依赖于速率和状态的摩擦律[34]被认为是这些异常事件的机理.然而, 我们认为这些异常事件来自于锁固段的稳定破裂(图 2a中的BC阶段).在高孔隙水压力作用下[35], 随着沿孕震断层的慢滑开始, 当达到锁固段的弹性极限后, 锁固段的局部破坏开始并稳定扩展.这些稳态的破裂能够释放较少的地震能量, 导致小的颤动, 也就是慢地震或寂静地震.随后, 在稳态破裂过程达到膨胀界限后, 一个强震的加速产生过程将开始.因此, 在相同的俯冲地带, 慢地震或寂静地震提供了一个未来强震发生的前兆线索.在卡斯卡底古陆俯冲带[36], 这个前兆线索尤其重要, 此地区历史上的强震均有详细记录, 且类似的强震一定会重演.
尽管慢地震与快地震的表现方式不同, 但都遵循着如岩石力学试验[22]所揭示的基本变形和破坏原理, 这些貌似迥异的现象容易用我们现有的知识解释.
5.6 汶川大地震是人类活动触发的吗?2008年5月12日汶川7.9级大地震发生于龙门山断裂带上[47], 此次地震摧毁了四川盆地西北边缘的汶川映秀镇、北川曲山镇等乡镇, 造成近10万人伤亡和巨大的财产损失.一些研究人员[38]认为距地震断层仅500 m、距震中5.5 km的紫平铺水库可能触发了灾难性汶川地震.然而, 没有人能提供充分证据证实汶川地震是一个水库诱发的地震实例[39].紫平铺水库于2004年12月开始蓄水, 两年时间内, 水位迅速上升到了120 m.从图 10可见, 其加速应变能释放(锁固段临界破坏)以在1999年9月14日发生的一次Ms=5.0地震(汶川地震前兆)为标志开始, 在经过了短暂的地震平静期后, 以在同年11月30日发生的另一次Ms=5.0地震事件为标志结束.9月14日5.0级地震位于龙门山主中央断裂, 11月30日5.0级地震位于龙门山前山的隐伏断裂上, 该双震分别位于绵竹县清平乡和汉旺乡.这意味着在一个锁固段的情况下主震将不可避免地发生我们也观察到, 在该Mw=7.9级地震发生以前, 与1999年9月14日前的地震活动性对比, 水库蓄水前后地震活动性总体上是平静的和稳态的, 这证据表明汶川地震与紫平铺水库蓄水基本无关, 与文献[48]的观点一致.

|
图 10 1977.1.1~2008.5.12期间观测的龙门山断裂带累积Beniof应变曲线[40] 数据统计采用了ML≥2.5的地震目录, 垂直虚线与红线分别表示预测与实际的主震发生时间. Fig. 10 Temporal distribution of cumulative Benioff strain[40] for the Wenchuan earthquake using earthquakes with ML≥2.5 for the period from 1 January 1977 to 12 May 2008 along the Longmen Shan fautt The dashed and red vertical lines denote the predicted and actual occurrence time of the mainshock, respectively. |
我们还注意到, 该地震与文中提及的其他地震情况不同.原理上, 在构造加载作用下一个锁固段达到了膨胀界限, 在恒定或增长的应力水平下, 其累进性的破坏将迅速发展而不会长期中途停止.然而, 汶川地震并不遵循这一常规模式, 这表明至少在1999年11月之后, 施加于龙门山断裂带上的构造应力较之前是减小的.预测的该地震破坏时间为实际地震发生前3. 5月, 震级预测值也与实际震级接近.如果在一个地震周期内1977年前的观测数据能得到, 可以期望得到更好的时间与震级预报结果.如果根据该双震的发生地点推测未来的主震震中, 那么预测的汶川大地震震中应该在绵竹县清平乡和汉旺乡附近.实际上, 对主震震中的预测应该进行动态追踪判断, 在加速应变开始后, 不断追踪预震的地点并予以修正以逼近实际震中位置, 如追踪汶川地震前2008年2~3月发生在都江堰附近的大于3级的事件.
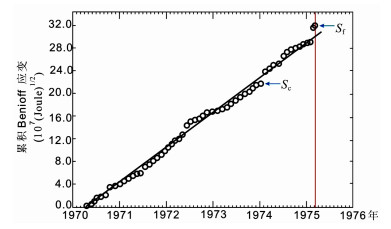
5.7 关于主震一余震型地震序列我们认为主震-余震型地震序列是不存在的, 因为即使对一个锁固段, 在其膨胀开始前, 会有小震发生; 在膨胀开始后, 会有一个或多个中级事件发生.只是这些中级事件可能会发生在主震前的早期阶段(如汶川大地震)或邻近阶段(如1975年2月4日海城地震(图 11), 临震前的小地震群及2月3日的Ms=4.6事件).
|
图 11 1975年2月4日中国海城地震(Ms=7. 3)前观测的累积Benof f应变随时间变化曲线.图中观测数据(黑圈)[41]表示累积Bemoff应变, 直线表示用时间-破坏模型对观测数据的拟合值, 垂直红线表示主震发生时间. Fig. 11 Time variation of the observed cumulative Benioff strain before the 4 February 1975 M=7. 3 Haicheng earthquake in China.Solid smooth lines represent fitting tothe data [41] (black circles) of a power law and red vertical lines denote the occurrence time of mainshock. |
海地地震发生时间为海地当地时间1月12日16时53分, 地点为北纬18.5°西经72.5°地震震级为:中国国家台网M7.3级, 美国国家台网Mw7.0级, 震源深度约10 km.地震目录数据引自美国地震信息中心(NEIS)网站, 数据时段为1973年到2010年1月12日主震发生的时间范围内的所有事件. Benioff应变计算时, 先把不同的震级单位统一换算为地方震级ML, 然后根据Bowman[29]等建议的公式和方法计算累积Benoff应变值.以震中为圆心, 根据Bufe与Varnes[13]建议的孕震区域临界半径与震级的统计关系:
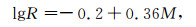
|
(22) |
计算孕震区域临界尺度, 然后根据此区域的地震目录计算Benioff应变.海地地震震级如按7.0~7.3考虑, 则计算的R值分别为209 km和268 km.实际分析发现, R值在200~300 km范围内取值, 都能得到好的预测结果.
图 12示出了不同半径的预测结果.对海地地震, 预测的锁固段断裂点的应变值对应着主震前最后一次mb=4.4前震事件, 为2009年9月4日, 为主震前4. 3月.这说明在2009年9月4日, 海地孕震断裂系统已处于临界失稳状态, 主震随时可被适当的扰动触发.根据1973年以来累积的地震能量反算得到的震级为6. 8~6. 9级, 略低于实际震级, 这是因为在一个地震周期内1973年以前的数据缺失导致的结果.根据加速事件发生的地点推测未来的震中域约为北纬19. 7°西经70. 7°震源深度为10 km, 这都与实际的震中位置和震源深度接近.
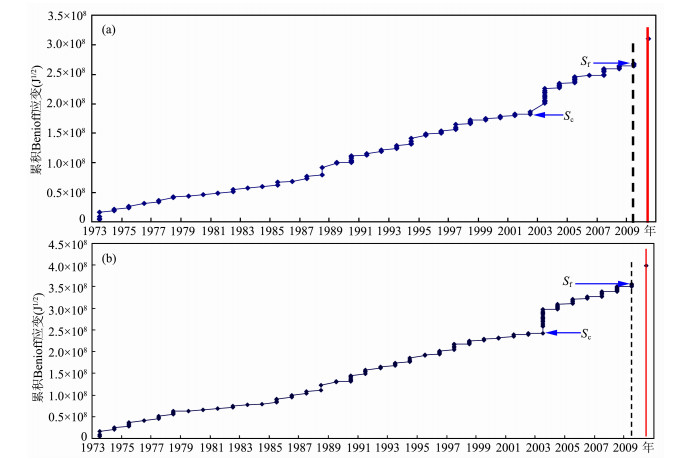
|
图 12 不同搜索半径的海地地震前累积Benoff应变随时间的变化 (a)R=250 km; (b)R=300 km.垂直红线为主震发生时间, 垂直虚线为预测的主震发生时间. Fig. 12 Time variation of the observed cumulative Benioff strain before the 13 January 2010 Haiti earthquake for the radius of searching area (a)R=250 km and (b)R=300 km. The dashed and red vertical lines denote the predicted and actual occurrence time of the mainshock, respectively. |
对比图 12和图 10可看出, 海地地震与汶川地震的应变能释放曲线相似, 都是在锁固段经过加速破裂后但未破裂完全的情况下发生的.这也说明, 地震都是有加速性活动前兆的, 是可以认识和预测的.
实际上, 将以上方法用于实际地震预测时, 实际地震震中位置难以定位, 则孕震临界区域的圆心坐标不易确定.我们建议结合对孕震断层的地质判断, 根据第一个中级事件出现的地点先初步定位, 然后用式(22)及该中级事件发生区域的历史最大地震震级估算搜索区域范围, 用式(16)进行初步预测.若搜索范围内明显的地震活动性加速特征或更大的地震事件出现后, 且其出现的位置与初始位置有大的差别, 则改变原搜索圆心坐标并调整搜索半径, 进行下一轮的搜索与预测.
5.9 为什么预期中的Parkfield 6.0级地震姗姗来迟?在San Andreas断层带上的Parktield段, 大约每隔22年就发生一次震级约为6级的中级地震[44], 前几次地震分别发生在1857年、1881年、1901年、1922年、1934年和1966年.根据这一规律, Parktield应于1988年发生一次6. 0级地震, 最迟也不应超过1993年.但直到2004年9月28日, 等待了11年之久的6. 0级地震才终于发生了.为什么预期中的该地震姗姗来迟?地震学家对此百思不得其解.我们试图根据本文提出的方法探索这一科学之谜.
由于该断层带的孕震区域[44]明确, 因此计算Benoff应变时搜索区域为一沿断层带的矩形区域, 长度为实际地震发生后断层破裂长度, 宽度为垂直断层走向两侧各20~40km (在此范围内取值都能得到同样的分析结果).地震目录引自美国地震信息中心(NEIS)网站提供的数据, 数据时段为1975年到2004年9月28日主震发生的时间范围内的所有事件.
从地震目录和图 13知, 在1993年3月14日至1993年11月14日间, 发生了一串2. 7~4. 9级中小地震事件, 表明第一锁固段已破裂完毕.在短暂的平静后, 于1994年12月12日至1994年12月20日间, 发生了一系列3~5级地震事件, 经计算表明第二锁固段经过加速破裂后未破裂完毕, 之后必有更大的事件发生.预测的该6. 0级地震发生时间为2001年11月26日, 之后地震活动趋于平静.这说明在2001年11月26日, Parktield孕震断裂系统已处于临界失稳状态, 但主震何时发生取决于扰动因素的的触发.
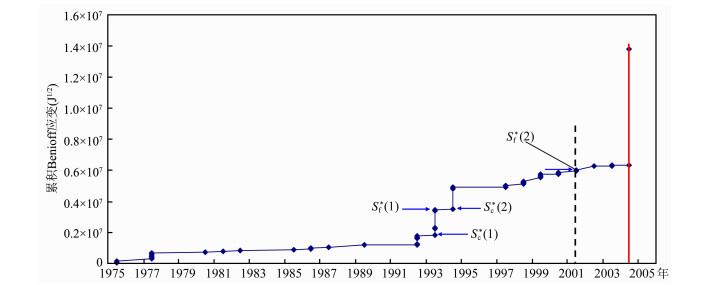
|
图 13 1975-05-01~2004-09-28期间观测的沿San Andreas断层Parkfileld段累积Benioff应变曲线 垂直虚线与红线分别表示预测与实际的主震发生时间.误差修正已被考虑. Fig. 13 Temporal distribution of cumulative Benioff strainngu [40] for the Parkfield earthquake for the period from 1 May 1975 to 28 September 2004 along the Parkiield section of the SanAndreas fault. The dashed and red vertical lines denote the predicted and actual occurrence time of the mainshock, respectively.The error correction is also considered. |
由以上分析知, 实际上预期中的1993年地震事件已经发生了, 但不是震级为6.0的事件, 而是最大震级为4. 9的事件.由于第二锁固段的存在, 我们预测到的6. 0级事件尽管已在2001年11月底已处于临界失稳状态, 但由于触发因素的影响, 直到2004年9月28日该地震才最终发生.
5.10 智利8.8级巨震预测验证分析2010年2月27日, 智利发生了该地区自1960年9. 5级地震以来的又一次大震, 也是1900年以来全球第5大地震.地震参数如下:发震时刻: 2010年02月27日, 地点为南纬35.8°西经72. 7°震源深度为33 km, 震级为8. 8级.该地震能根据我们提出的方法进行预测吗?我们将对此进行验证分析.
智利8. 8级地震发生在纳斯卡板块和南美板块的交汇的消减带上, 由于缺乏该地区的相关地质资料, 我们依据震后反演得到的地震断层滑动分布投影图(王卫民, 赵连锋, 姚振兴, 2010年2月27日智利8. 8级地震震源破裂过程初步结果, 中国地震信息网), 对长约为650 km、宽约为220 km的矩形孕震区域内的地震事件进行累积Benioff应变计算, 地震目录引自美国地震信息中心(NEIS)网站提供的数据, 数据时段为1973年到2010年2月27日主震发生的时间范围内的所有事件.从图 14可看出, 该地震断层有两个锁固段, 可能由于两个锁固段距离较近, 第一锁固段的断裂直接导致了第二锁固段的累进性破坏开始, 第二锁固段的临界破裂起点为一震级7. 5事件.根据前述的方法, 预测的该地震震级为8. 6, 发生时间为2009年12月底, 约为实际地震发生前2个月, 地点为南纬34°西经72°震源深度为33~37 km.
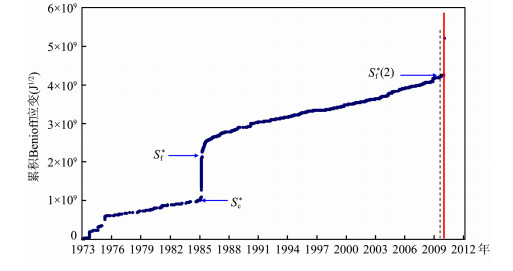
|
图 14 1973-01-07~2010-02-27期间观测的智利8.8级地震累积Benioff应变曲线 垂直虚线与红线分别表示预测与实际的主震发生时间.误差修正已被考虑. Fig. 14 Temporal distribution of cumulative Benioff strain[40]for the Chili earthquake for the period from 17 January 1973 to 27 February 2010. The dashed and red vertical lines denote the Predicted and actual occurrence time of the mainshock, respectively. The error correction is also considered. |
从图 15可看出, 不管地震序列总体是加速的还是减速的, 亦即在适当的临界区域与主震孕震区域范围内, 都能得到同样好的预测结果.这说明, 只要计算Benoff应变时统计范围选取得当, 都可以应用式(20)进行预测分析.
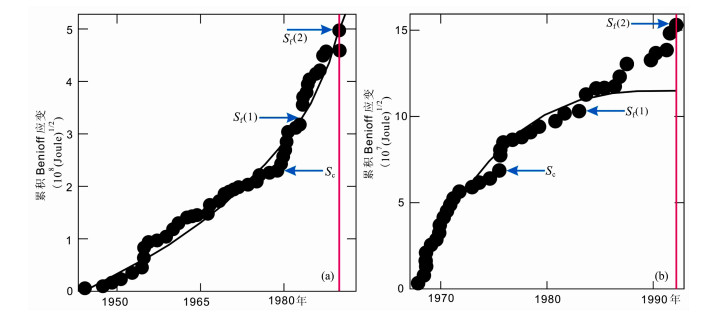
|
图 15 1992年4月25日M=7.1加利福尼亚地震加减速地震序列 图中数据点(黑圈)[45]为主震前观测的累积Benioff应变值.曲线表示用时间-破坏模型对观测数据的拟合值.垂直红线表示主震发生时间. Fig. 15 Accelerating-decelerating seismic sequences for the 25 April 1992 (M=7.1) mainshock in central California The time variation of the cumulative Benioff strain is given for the accelerating sequence (a) and decelerating sequence (b).Solid smooth lines represent fitting to the data (black circles)[45] of a power law and red vertical lines denote the occurrence time of mainshock. |
本文提出的理论方法可以改进我们对滑坡和火山喷发等灾害预测问题的理解.另一个有趣的发现是, 通过分析35个滑坡、崩塌实例的时间一位移曲线, 本文提出的方法也能可靠用于滑坡和崩塌灾害的预测.这说明, 滑坡、崩塌与地震一样, 遵循着统一的失稳演化规律.我们的研究表明, 虽然大地震和特大地震的孕震过程千差万别且十分复杂, 但它们的孕震过程仍遵循着一个基本、确定乃至简单的力学规律, 大地震是可以预测的.
本文提出的理论方法若应用于实际地震预测实践, 还需解决孕震区域的判识[46]、触发因素与发震时间的关系等问题.在解决地震预测预报的征途上, 我们还面临着诸多科学难题[49, 50]的挑战, 需要坚持不懈的努力探索.衷心希望本拙作的发表, 能起到抛砖引玉的作用.
致谢感谢刘光鼎院士、滕吉文院士、朱日祥院士、吴福元研究员对第一作者的鼓励, 感谢王思敬院士、张倬元教授和第一作者的有益讨论, 感谢中国科学院知识创新工程(编号: KZCX2-YW-113和KZCX2-YW-Q03-02113)对研究工作的资金支持.
| [1] | Geller R J, Jackson D D, Kagan Y Y, et al. Earthquakes cannot be predicted. Science , 1997, 275: 1616. DOI:10.1126/science.275.5306.1616 |
| [2] | Karplus W J. The Heavens are Falling:the Scientific Prediction of Catastrophes in Our Time. New York: Plenum Press, 1992 . |
| [3] | Wyss M. Why is earthquake prediction research not progressing faster?. Tectonophysics , 2001, 338: 217-223. DOI:10.1016/S0040-1951(01)00077-4 |
| [4] | Rundle J B, Gross S, Klein W, Ferguson C, et al. The statistical mechanics of earthquakes. Tectonoophysics , 1997, 277: 147-164. DOI:10.1016/S0040-1951(97)00083-8 |
| [5] | Mora P, Place D. Stress correlation function evolution in lattice solid elasto-dynamic models of shear and fracture zones and earthquake prediction. Pure Appl.Geophys. , 2002, 159: 2413-2427. DOI:10.1007/s00024-002-8741-8 |
| [6] | Yin X C, Mora P, Peng K Y, et al. Load-unload response ratio and accelerating moment/energy release critical region scaling and earthquake prediction. Pure Appl.Geophys. , 2002, 159: 2511-2523. DOI:10.1007/s00024-002-8745-4 |
| [7] | Ben-Zion Y. Dynamic ruptures in recent models of earthquake faults. Journal of the Mechanics and Physics of Solids , 2001, 49: 2209-2244. DOI:10.1016/S0022-5096(01)00036-9 |
| [8] | Gross S, Rundle J. A systematic test of time-to-failure analysis. Geophys.J.Int. , 1998, 133: 57-64. DOI:10.1046/j.1365-246X.1998.1331469.x |
| [9] | Steven C J, Lynn R S. Evolving towards a critical point:a review of accelerating seismic moment/energy release prior to large and great Earthquakes. Pure Appl.Geophys , 1999, 155: 279-306. DOI:10.1007/s000240050266 |
| [10] | Allegre C J, Mouel J L Le, Provost A. Scaling rules in rock fracture and possible implications for earthquake prediction. Nature , 1982, 297: 47-49. DOI:10.1038/297047a0 |
| [11] | González A, Vázquez-Prada M, Gómez J B, et al. A way to synchronize models with seismic faults for earthquake forecasting:Insights from a simple stochastic model. Tectonophysics , 2006, 424: 319-334. DOI:10.1016/j.tecto.2006.03.039 |
| [12] | Tang C A. Numerical simulation of progressive rock failure and associated seismicity. Int.J.Rock Mech.Min.Sci. , 1997, 34: 249-261. DOI:10.1016/S0148-9062(96)00039-3 |
| [13] | Bufe C G, Varnes D J. Predictive modeling of the seismic cycle of the greater San Francisco bay region. J.Geophys.Res. , 1993, 98: 9871-9883. DOI:10.1029/93JB00357 |
| [14] | Sornette D, Sammis C G. Complex critical exponents from renormalization group theory of earthquakes:implications for earthquake predictions. J.Phys.I France , 1995, 5: 607-619. DOI:10.1051/jp1:1995154 |
| [15] | Corral á. Dependence of earthquake recurrence times and independence of magnitudes on seismicity history. Tectonophysics , 2006, 424: 177-193. DOI:10.1016/j.tecto.2006.03.035 |
| [16] | Papazachos B C, Scordilis E M, Papazachos C B, et al. A forward test of the precursory decelerating and accelerating seismicity model for Califomia. Journal of Seismology , 2006, 10: 213-224. DOI:10.1007/s10950-005-9009-4 |
| [17] | Ben-Zion Y, Lyakhovsky V. Accelerated seismic release and related aspects of seismicity patterns on earthquake faults. Pure Appl.Geophys. , 2002, 159: 2385-2412. DOI:10.1007/s00024-002-8740-9 |
| [18] | Lei X. How do asperities fracture? an experimental study of unbroken asperities. Earth and Planetary Science Letters , 2003, 213: 347-359. DOI:10.1016/S0012-821X(03)00328-5 |
| [19] | Smalley R F, Turcotte D L, Solla S A. A renormalization group approach to the stick slip behavior of faults. J.Geophys.Res. , 1985, 90: 1894-1900. DOI:10.1029/JB090iB02p01894 |
| [20] | Hudson J A, Fairhurst C. Tensile strength, Weibull's theory and a general statistical approach to rock failure. The Proceedings of the Southampton 1969 Civil Engineering Materials Conference , 1969: 901-914. |
| [21] | Wilson K G. Problems in physics with many scales of length. Sci.Am. , 1979, 241: 158-179. |
| [22] | Bieniawski Z T. Time-dependent behaviour of fractured rock. Rock Mech. , 1970, 2: 123-137. DOI:10.1007/BF01239744 |
| [23] | Qin S Q, Jiao J J, Li Z G. Nonlinear evolutionary mechanisms of instability of plane-shear slope:catastrophe, bifurcation, chaos and physical prediction. Rock Mechanics and Rock Engineering , 2006, 39: 59-76. DOI:10.1007/s00603-005-0049-4 |
| [24] | 秦四清, 王思敬, 孙强, 等. 非线性岩土力学基础. 北京: 地质出版社, 2008 . Qin S Q, Wang S J, Sun Q. Nonlinear Mechanics Fundaments for Rock and Soil (in Chinese). Beijing: Geological Publishing House, 2008 . |
| [25] | Mignan A, King G, Bowman D, Lacassin R., et al. Seismic activity in the Sumatra-Java region prior to the December 26.2004(Mw=9.0-9.3) and March 28, 2005(Mw=8.7) earthquakes. Earth and Planetary Science Letters , 2006, 244: 639-654. DOI:10.1016/j.epsl.2006.01.058 |
| [26] | Papazachos B, Papazachos C. Accelerated preshock deformation of broad regions in the Aegean area. Pure Appl.Geophys. , 2000, 157: 1663-1681. DOI:10.1007/PL00001055 |
| [27] | Rundel J B, Klein W, Turcotte D L, et al. Precursory seismic activation and critical-point phenomena. Pure Appl.Geophys. , 2000, 157: 2165-2182. DOI:10.1007/PL00001079 |
| [28] | 彭克银, 尹祥础, 和锐. 用临界点理论讨论应变能加速释放现象和孕震区尺度. 中国地震 , 2003, 19(4): 425–430. Peng K Y, Yin X C, He R. Accelerating strain release and earthquake genesis scaling exponents from critical point hypothesis. Earthquake Research in China (in Chinese) , 2003, 19(4): 425-430. |
| [29] | Bowman D D, Ouillon G, Sammis C G, et al. An observational test of the critical earthquake concept. J.Geophys.Res. , 1998, 103: 359-372. |
| [30] | Mogi K. Earthquake Prediction. Tokyo: Academic Press, 1985 . |
| [31] | Kelleher J, Savino J. Distribution of seismicity before large strike-slip and thrust-type earthquakes. J.Geophys.Res. , 1975, 80: 260-271. DOI:10.1029/JB080i002p00260 |
| [32] | Bufe C G, Nishenko S P, Varnes D J. Seismicity trends and potential for large earthquakes in the Alaska-Aleutian region. Pure Appl.Geophys. , 1994, 142: 83-99. DOI:10.1007/BF00875969 |
| [33] | Scholz Ch H. Mechanism of seismic quiescences. Pure Appl.Geophys. , 1988, 26: 701-718. |
| [34] | Ide S, Beroza G C, Shelly D R, et al. A scaling law for slow earthquakes. Nature , 2007, 447: 76-79. DOI:10.1038/nature05780 |
| [35] | Ito Y, Obara K, Shiomi K, et al. Slow earthquakes coincident with episodic tremors and slow slip events. Science , 2007, 315: 503-506. DOI:10.1126/science.1134454 |
| [36] | Kanamori H. Earthquake physics and real-time seismology. Nature , 2008, 451: 271-273. DOI:10.1038/nature06585 |
| [37] | Segall P, Desmarais E K, Shelly D, et al. Earthquakes triggered by silent slip events on Kilauea volcano, Hawaii. Nature , 2006, 442: 71-74. DOI:10.1038/nature04938 |
| [38] | 雷兴林, 马胜利, 闻学泽, 等. 地表水体对断层应力与地震时空分布影响的综合分析-以紫坪铺水库为例. 地震地质 , 2008, 30(4): 1046–1064. Lei X L, Ma S L, Wen X Z, et al. Integrated analysis of stress and regional seismicity by surface loading-a case study of Zipingpu reservoir. Seismotogy and Geology (in Chinese) , 2008, 30(4): 1046-1064. |
| [39] | Richard A K, Richard S. A human trigger for the great quake of Sichuan?. Science , 2009, 323: 322. DOI:10.1126/science.323.5912.322 |
| [40] | 赵祎喆, 吴忠良, 蒋长胜, 等. 用地震资料估计的龙门山断裂深部形变及其对于汶川地震成因的意义. 地质学报 , 2008, 82(12): 1778–1787. Zhao Y Z, Wu Z L, Jiang C S, et al. Present deep deformation along the Longmenshan fault by seismic data and implications for the tectonic context of the Wenchuan earthquake. Aata GeoLogica Sinica (in Chinese) , 2008, 82(12): 1778-1787. |
| [41] | 苗青壮.中国大陆强震前应变释放特征[硕士学位论文].兰州:中国地震局兰州地震研究所, 2008.1~62. Miao Q Z.Strain release characteristics before strong earthquakes in Chinese mainland[Master's degree thesis].Lanzhou:Lanzhou Institute of Seismology, 2008.1~62 http://cdmd.cnki.com.cn/Article/CDMD-85403-2008130676.htm |
| [42] | 吴忠良. 自组织临界性与地震预测-对目前地震预测问题争论的评述(之一). 中国地震 , 1998, 14(4): 1–9. Wu Z L. Self-organization criticality and earthquake prediction-a review on the current discussions about earthquake prediction (I). Earthquake Research in China (in Chinese) , 1998, 14(4): 1-9. |
| [43] | Tang C A, Xu X H. Evolution and propagation of material defects and Kaiser effect function. Journat of Seismological Research , 1990, 13(2): 203-213. |
| [44] | Bakun W H, Aagaard B, Dost B, et al. Implications for prediction and hazard assessment from the 2004 Parkfield earthquake. Nature , 2005, 473: 969-974. |
| [45] | Papazachos C B, Karakaisis G F, Scordilis E M, Papazachos B C. New observational information on the precursory accelerating and decelerating strain energy release. Tectonophysics , 2006, 423: 83-96. DOI:10.1016/j.tecto.2006.03.004 |
| [46] | Xu X W, Deng Q D. Nonlinear characteristics of paleoseismicity in China. Journal of Geophysical Research , 1996, 101(B3): 6209-6231. DOI:10.1029/95JB01238 |
| [47] | 陈章立, 赵翠萍, 王勤彩, 等. 汶川Ms8.0级地震发生背景与过程的研究. 地球物理学报 , 2009, S2(2): 455–463. Chen Z L, Zhao C P, Wang Q C. A study on the occurrence background and process of Wenchuan Ms8. 0.Chinese J.Geophys. (in Chinese) , 2009, S2(2): 455-463. |
| [48] | 陈顒. 汶川地震是由水库蓄水引起的吗?. 中国科学D辑:地球科学 , 2009, 52(2): 257–259. Chen Y. Is Wenchuan earthquake caused by the reservoir water?. Science in China (Earth Science) (in Chinese) , 2009, 52(2): 257-259. DOI:10.1007/s11430-009-0010-6 |
| [49] | 滕吉文, 张永谦, 闫雅芬. 强烈地震震源破裂和深层过程与地震短临预测探索. 地球物理学报 , 2009, 52(2): 428–443. Teng J W, Zhang Y Q, Yan Y F. Deep process of the rupture of strong earthquakes and exploration for the impending earthquake prediction. Chinese J.Geophys. (in Chinese) , 2009, 52(2): 428-443. |
| [50] | 傅容珊, 万柯松, 崇加军, 等. 地震前兆还是其他因素?-与"汶川大地震宽带地震仪短临异常及成因初探"作者商榷. 地球物理学报 , 2009, 52(2): 584–589. Fu R S, Wan K S, Chong J J, et al. Earthquake auspice or other factor-Discuss with authors of the paper"The short term anomalies detected by broadband seismographs before the May 12 Wenchuan earthquake, Sichuan, China. Chinese J.Geophys. (in Chinese) , 2009, 52(2): 584-589. |
 2010, Vol. 53
2010, Vol. 53


