地球物理学报  2010, Vol. 53 Issue (4): 994-1000   PDF    
引用本文
邓少贵, 李智强, 范宜仁 等. 斜井泥浆侵入仿真及其阵列侧向测井响应数值模拟. 地球物理学报, 2010, 53(4): 994-1000, doi: 10.3969/j.issn.0001-5733.2010.04.024.  
Deng S G, Li Z J, Fan Y R, et al. Numerical simulation of mud invasion and its array laterolog response in deviated wells. Chinese J. Geophys. (in Chinese), 2010, 53(4): 994-1000, doi: 10.3969/j.issn.0001-5733.2010.04.024.  
斜井泥浆侵入仿真及其阵列侧向测井响应数值模拟
邓少贵1 , 李智强1 , 范宜仁1 , 陈华2     
1. 中国石油大学(华东)地球资源与信息学院, 青岛 266555;
2. 中国石油大学(华东) CNPC测井重点实验室, 青岛 266555
收稿日期 2009-02-16, 2010-01-18 收修定稿
基金项目: 国家科技重大专项(2008ZX05035-02)、山东省自然科学基金(Y2007F25)、中石油中青年创新基金(06E1020)和中央高校基本科研业务费专项资金（09CX04001A）资助
通讯作者: 邓少贵, 男, 1970年生, 博士, 副教授, 主要从事电测井理论计算及岩石物理的教学和科研工作, E-mail:dengshg@upc.edu.cn
摘要: 为了研究斜井泥浆侵入储层的井周岩石物理特征，采用广义曲线坐标系统模拟斜井泥浆侵入特性，进而研究泥浆侵入过程的阵列侧向测井响应.数值仿真表明，采用广义曲线坐标系消除了笛卡儿坐标系统在斜井边界处网格划分的锯齿现象；储层非均质造成泥浆侵入不均匀，储层渗透性越好，泥浆滤液侵入越深；泥浆滤液侵入使得井周地层饱和度、孔隙水矿化度的分布发生变化，进而造成斜井井周岩石电阻率分布剖面复杂变化；泥浆侵入过程中阵列侧向视电阻率变化以及深浅视电阻率的幅度差异，有效反映了斜井泥浆侵入特性；文中采用了基于Marquardt方法的阵列侧向测井四参数反演，有效恢复了斜井储层侵入剖面，得到了原状地层电阻率.斜井泥浆侵入特征及其阵列侧向测井响应模拟分析，有助于正确认识斜井井周岩石物理特征和利用阵列侧向测井进行斜井储层评价.
关键词: 曲线坐标      斜井      泥浆侵入      阵列侧向      测井响应     
Numerical simulation of mud invasion and its array laterolog response in deviated wells
DENG Shao-Gui1, LI Zhi-Jiang1, FAN Yi-Ren1, CHEN Hua2     
1. College of Geo-resources & Information, China University of Petroleum, Qingdao 266555, China;
2. CNPC Well Logging Laboratory, China University of Petroleum, Qingdao 266555, China
Abstract: In order to study the petrophysical properties of mud-invaded formation in deviated well, a generalized curvilinear coordinate system is used to simulate the characteristics of mud invasion, and then the array laterolog response during mud invasion is researched. Numerical simulation shows that the phenomena of saw tooth in mesh generation on the border of dip borehole, which is unavoidable in Cartesian coordinate system, can be effectively eliminated in curvilinear coordinate system. The heterogeneity of formation results in non-uniform mud invasion, the better the reservoir permeability is, the more deeply mud filtrate invades. And mud invasion changes the distribution of both fluid saturation and salinity around borehole, thus leading to the complexity of rock resistivity distribution around the deviated well. The variation of apparent resistivity from array laterolog and the difference between its deep and shallow resistivity during mud invasion reflect the characteristics of mud invasion. In this paper a four-parameter inversion of array laterolog based on Marquardt method is adopted to effectively recover the invasion profile and then obtain the original formation resistivity in deviated well. The analysis of invasion characteristics and array laterolog response simulation in deviated well contributes to the correct understanding of petrophysical properties around the well and reservoir evaluation with array laterolog in deviated well..
Key words: Curvilinear coordinate      Deviated well      Mud invasion      Array laterolog      Log response     
1 引言

随着石油工业的不断发展, 大斜度井、水平井勘探技术正逐步成为高效率、高效益的油气田勘探开发技术[1].斜井的泥浆侵入形状和侵入体积复杂, 泥浆侵入造成了井周储层岩石物理性质发生复杂变化, 影响着电测井的响应特征[2~6].双侧向或双感应测井只提供两种探测深度的电阻率信息, 且受相对井斜、薄层等因素影响, 无法描述斜井泥浆侵入造成的复杂的井周地层电阻率分布特征, 因此, 难以满足斜井储层流体精细评价的要求.

阵列化是测井仪器发展趋势, 斯伦贝谢公司1998年推出高分辨率新型阵列侧向测井仪(HRLA), 能提供6种不同探测深度电阻率信息[7~10], 阿特拉斯1998年推出高分辨率阵列侧向测井仪(HDLL), 能提供8种不同探测深度电阻率[11], 与前者不同, 后者采用软聚焦方式确定地层电阻率.由于阵列侧向测井具有较强的纵向分辨率, 提供了不同探测深度的多条视电阻率曲线, 可用于反映斜井泥浆的侵入特征.因此, 进行斜井泥浆侵入特性模拟, 研究孔隙流体、岩石电阻率分布及泥浆侵入过程的阵列侧向测井响应, 进而利用阵列侧向测井进行斜井泥浆侵入剖面反演, 对斜井储层测井评价具有重要的意义.

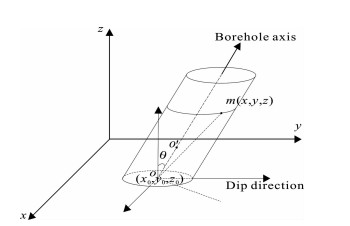
2 斜井模型的曲线坐标系统

目前, 通常采用有限差分方法求解用于描述泥浆侵入特征的油水两相渗流方程[12].在笛卡儿坐标系下, 对于斜井地层模型来说, 如图 1经典的正交矩形网格采用阶梯近似来模拟, 如图 2, 只有在网格无限小时才能达到精确模拟.Stratton (1941)为了解决不规则边界提出了广义曲线坐标系理论[13], 它可以有效消除"阶梯"效应, Avis等人(1981)、Hoang和Kleppe (2006)就将曲线坐标系统用于复杂油藏数值模拟[14, 15].

图 1 斜井模型 Fig. 1 The deviated well model
图 2 正交坐标下斜井纵剖面网格 Fig. 2 Longitudinal grid of deviated well in orthogonal coordinate system

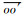
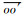
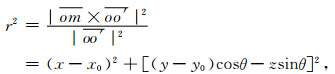
根据斜井模型, 假设o(x0, y0, 0)为井轴上某一点, 井轴方向向量可以表示为(0, sinθ, cosθ), θ为井斜角.斜井井壁边界处各点可用向量om表示, 写成(x-x0), y-y0, z), om和的关系可写成

(1)

其中, r为井眼半径.引入广义坐标, 令ξ=ξ(x, y, z)=x-x0, η=η(x, y, z)=(y-y0) cosθ-zsinθ, ζ=ζ(x, y, z)=z, 式(1)变成

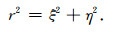
(2)

3 曲线坐标系统中斜井泥浆侵入理论依据 3.1 泥浆侵入过程的油水两相渗流方程

假设泥浆滤液对地层流体的驱替过程是非混溶的, 在泥浆侵入过程中流体渗流遵循Dacy定律, 油水两相流体的流动方程为

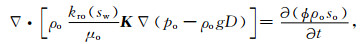
(3)

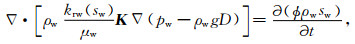
(4)

式中, pw、po分别为水相和油相压力so、sw分别为含油、水饱和度, μo、μw分别为油、水黏度kro、krw分别为油、水两相的相对渗透率, ϕ为地层孔隙度, D为地层深度, g为重力加速度, ρw、ρo分别为水和油的密度, t为侵人时间, K为渗透率张量, 用于描述地层的渗透性各向异性,

考虑简单情况, 沿层面方向渗透率为kh, 垂向渗透率为kv, kxx=kyy=k h, kzz=kv, kxy=kxz=kyx=kyz=kzx=kzy=0.将油水两相渗流方程(3)和(4)改写为

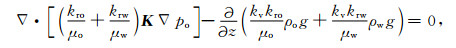
(5)

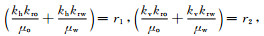
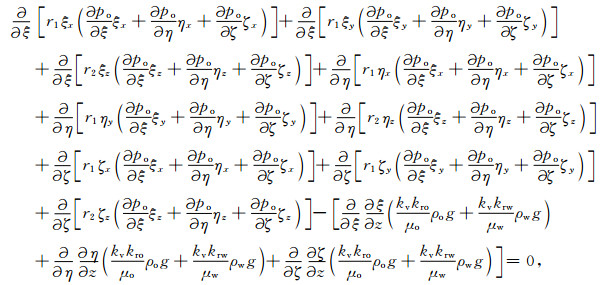
令得曲线坐标油水两相渗流方程，

(6)

含油饱和度的确定，

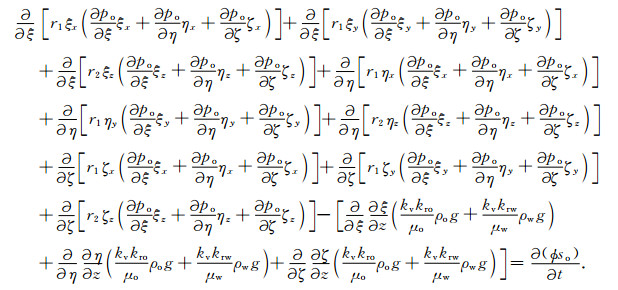
(7)

3.2 泥浆侵入过程水的对流扩散方程

泥浆侵人过程中, 由于泥浆滤液和地层水的矿化度不同, 离子发生对流扩散, 并遵循如下方程:

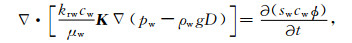
(8)

式中, Cw为地层孔隙水矿化度.式(8)改写为

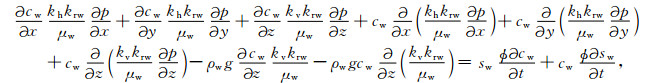
(9)

在曲线坐标系统下, 式(9)改写为

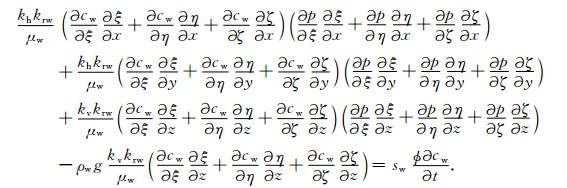
(10)

本文根据式(6)(7)(10), 利用三维有限差分方法, 并采用超松弛迭代法进行泥浆侵人过程井周岩石孔隙流体饱和度、孔隙水矿化度分布的数值模拟.实际模拟时采用径向非均匀、纵向均匀网格划分, 在算例中的2m×6m×6 m计算区域内, 得到50×150×150个网格.泥浆侵人过程岩石电阻率分布由阿尔奇公式确定,

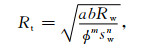
(11)

式中, Rw是孔隙水电阻率, a、b为岩性系数, m、n分别为孔隙度和饱和度指数, 它们均为经验常数.

4 斜井泥浆侵人特征数值模拟 4.1 计算条件

井斜45°目的层为砂岩, 层厚6 m, 考虑地层的非均质, 不考虑渗透率各向异性, 目的层由三层组成, 渗透率分别为100×10-3 μm2、300×10-3μm2和100×10-3μm2.地层含油饱和度60%, 束缚水饱和度20%, 残余油饱和度20%, 孔隙度为24%, 地层温度85℃, 原油黏度为3mPas, 孔隙水黏度1mPas, 孔隙水密度为1g/cm3, 油的密度为0. 8g/cm3, 重力加速度为9. 8m/s2.井眼与地层压力差2 MPa, 井径30 cm, 井内泥浆电阻率1 Ωm, 上下泥岩电阻率为2 Ωm, 式(11)中a、b均取1, m、n均取2.除特殊说明外, 本文算例均以此为计算条件.

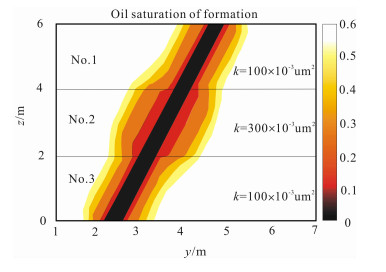
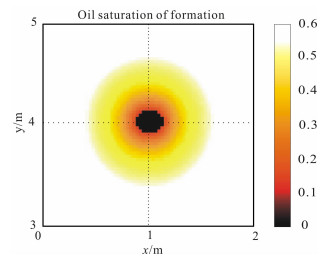
4.2 孔隙流体分布特征

泥浆滤液侵人油层, 含油饱和度降低, 随远离井眼, 含油饱和度逐渐升高到原始状态, 且由于储层渗透性的差异, 泥浆侵人显示明显的"单层突进"特征, 如图 3; 而泥浆侵人剖面显示轴对称性, 如图 4, 这是由于该计算条件下的重力影响较小且未考虑渗透率各向异性影响之缘故, 相关渗透性各向异性和重力对斜井泥浆侵人的影响可参见文献[3].

图 3 斜井泥浆滤液侵入剖面 Fig. 3 Mud filtrate invasion profile in deviated well
图 4 斜井泥浆侵入储层含油饱和度分布 Fig. 4 Oil saturation of mud-invaded reservoir m deviated well
4.3 泥浆侵入过程井周岩石电阻率分布特征

分别模拟淡水泥浆和盐水泥浆侵人情况, 假设地层水矿化度为8g/L, 目的层原状地层电阻率为71 Ωm.泥浆滤液矿化度分别为3g/L和30g/L, 侵人时间为5天.结果显示, 盐水泥浆侵人油层呈现明显的"低侵"特征, 且目的层中部泥浆侵人较深, 如图 5a, 目的层上、中、下三部分井眼附近地层电阻率分别为20.9 Ωm、17.7 Ωm、20.9 Ωm, 离开井眼, 侵人带电阻率逐渐增加到71 Ωm, 它们的差异是由于中间部分渗透率较高而受泥浆侵人程度较深所致; 淡水泥浆侵人油层, 如图 5b, 目的层上、中、下三层井眼附近电阻率分别为49. 7 Ωm、42. 2 Ωm、49. 7 Ωm, 侵人带电阻率分布较复杂, 有低阻环带显示.

图 5 泥浆侵入地层井周岩石电阻率分布特征 (a)盐水泥浆侵入地层; (b)淡水泥浆侵入地层. Fig. 5 Borehole-circumferential resistivity distribution of mud-invaded formation (a) Salty mud-invaded formation; (b) Fresh mud-invaded formation.
4.4 泥浆侵入过程斜井阵列侧向测井响应特征

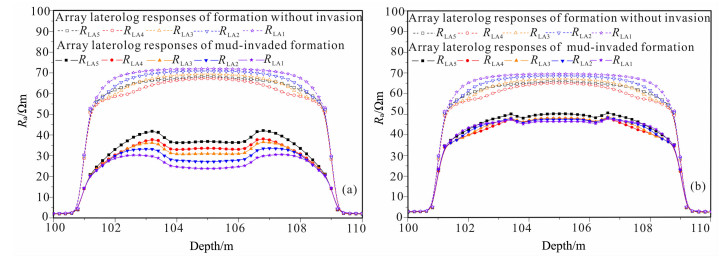
泥浆侵人过程井周岩石电阻率的分布决定了地层的阵列侧向电阻率测井响应, 而阵列侧向提供了多条不同探测深度的视电阻率曲线, 可以用于反映斜井泥浆的侵人特性, 进而揭示地层的真实特征.针对图 5的泥浆侵人条件, 以斯伦贝谢高分辨率阵列侧向测井仪为例, 采用三维有限元方法计算其阵列侧向测井响应[16], 如图 6, RLA1, …, RLA5分别表示探测深度由浅到深的地层视电阻率, 由于RLA0只反映泥浆电阻率, 文中不予考虑.受井斜的影响, 根据曲线确定地层视厚度要大于真实厚度.没有侵人时, 探测深度较浅的阵列侧向视电阻率RLA1为60. 9 Ωm, 接近原状地层电阻率71 Ωm, 探测深度较深的视电阻率偏小是由于受围岩影响较大所致.和淡水泥浆侵人相比, 盐水泥浆侵人使视电阻率降低更明显, 远低于无侵测井响应值, 呈现明显的泥浆低侵特征, 即深浅视电阻率呈现正幅度差.同时受渗透性差异造成的不均匀侵人影响, 阵列侧向测井响应呈现三层指示, 渗透性好的中间储层电阻率降低更多, 深浅电阻率差异更明显.

图 6 斜井泥浆侵入地层的阵列侧向测井响应特征 (a)盐水泥浆侵入地层; (b)淡水泥浆侵入地层. Fig. 6 Array laterolog responses of mud-invaded formation in deviated well (a) Salty mud-invaded formation; (b) Fresh mud-invaded formation.
5 斜井阵列侧向测井反演 5.1 反演方法概述

针对斜井盐水泥浆侵人情况, 采用多层整体反演原则, 进行阵列侧向测井响应反演.由于阵列侧向测井分辨率较高, 本文利用其曲线拐点并经垂深转换确定地层界面参与反演.构造井周电阻率分布模型:令r1是冲洗带半径, Rxo是冲洗带电阻率, r1和r2(r2>r1)之间为过渡带, Ri是过渡带电阻率, Rt是原状地层电阻率, 反演时假设Ri随侵入深度线性变化, Ri=(Rt-Rxo)/(r2-r1)×(r-r1)+Rxo.阵列侧向测井响应函数表示为

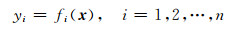
(11)

其中, x=(r2, r1, Rxo, Rt)为地层参数向量, yi为第i个探测深度的阵列侧向响应, 一组特定地层参数可确定5个不同探测深度的测井响应值.由于是四参数反演, 故取n≥4, 将问题归结为一个优化的最小二乘问题,

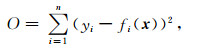
(12)

采用Marquardt方法对方程(12)求解[16].为提高反演的计算效率, 在多层反演中每层只取部分响应值参与反演, 对5.2节中算例, 每层取2个采样点, 3层的四参数反演耗时11 min (计算机内存为4 G, CPU处理器主频为2.39 GHz).

5.2 计算实例分析

针对图 6a中盐水泥浆侵入算例的阵列侧向测井响应进行反演, 得到的地层侵入剖面(图 7)与正演计算的泥浆侵入剖面(图 5a)具有较好的一致性.将二者计算结果进一步对比, 如图 8, 目的层中间部分反演冲洗带电阻率为17.7Ωm, 上下部分反演冲洗带电阻率为20.9 Ωm, 反演原状地层电阻率为71 Ωm, 均和地层模型吻合.中间过渡带的差异是由于反演中采用线性模型, 而实际地层电阻率非线性分布所致.

图 7 阵列侧向测井响应反演电阻率剖面 Fig. 7 Inverted resistivity profile of array laterolog response
图 8 实际地层电阻率与阵列侧向反演结果对比 Fig. 8 Actual formation resistivity & inversion results of array laterolog
6 结论

本文依据广义坐标理论, 将曲线坐标系统引入斜井泥浆侵入环境, 巧妙解决了数值模拟过程中由于井轴与地层相对倾斜造成的网格划分出现的"锯齿"情况, 有助于模拟井周岩石物理性质变化规律.

斜井泥浆侵入造成井周岩石流体饱和度、孔隙水矿化度、岩石电阻率复杂变化, 储层渗透性非均质造成了泥浆非均匀侵入.

斜井泥浆侵入特性影响着阵列侧向测井响应特征及其深浅电阻率的幅度差异, 阵列侧向测井较好揭示了斜井泥浆侵入特性, 正反演有效结合, 有助于提升斜井条件利用电测井评价储层的可靠性.

致谢

对两位匿名评审专家提出的宝贵意见深表敬意!

参考文献
[1] Passey Q R, Yin H, Rendeir C M, et al. Overview of highangle and horizontal well formation evaluation:issues, learning, and future directions. Well Logging Technology , 2006, 30(1): 1-10.
[2] Peeters M, Kovats J, Moita C, et al. Monitoring and modeling invasion using ground penetrating radar and flow simulation programs.43rd Annual Logging Symposium, Society of Petrophysicists & Well Log Analysts. Expanded Abstracts , 2002, VV: 1-10.
[3] 汪宏年, 陶宏根, 王桂萍, 等. 双感应测井资料的快速近似迭代反演. 地球物理学报 , 2007, 50(5): 1614–1622. Wang H N, Tao H G, Wang G P, et al. A fast approximate iterative inversion technique of dual induction logging data. Chinese J.Geophys. (in Chinese) , 2007, 50(5): 1614-1622.
[4] 邓少贵, 杨震, 李智强, 等. 大斜度井/水平井复杂介质双侧向测井响应数值模拟. 测井技术 , 2009, 33(1): 32–36. Deng S G, Yang Z, Li Z Q. Numerical simulation of dual laterolog response of complex media in high deviated and horizontal well. Well Logging Technology (in Chinese) , 2009, 33(1): 32-36.
[5] Proett M A, Chin W C, Wu J H, et al. Sample quality prediction with integrated oil and water-based mud invasion modeling. Proceedings SPE Asia Pacific Oil and GasConference and Exhibition, Society of Petroleum Engineer Inc..Expanded Abstracts , 2002: 1081-1094.
[6] Yao C Y, Holditch S A. Reservoir permeability estimation from time-lapse log data. SPE Formation Evaluation , 1996, 11(2): 69-74. DOI:10.2118/25513-PA
[7] Smits J W, Dubourg I, Luling M G, et al. Improved resistivity interpretation utilizing a new array laterolog tool and associated inversion processing. Annual Technical Conference and Exhibition, Society of Petroleum Engineers Inc..Expanded Abstracts , 1998: 831-843.
[8] Chen Y H, Chew W C, Zhang H J. A novel array laterolog method. The Log Analyst , 1998, 39(3): 23-32.
[9] 刘振华, 张霞. 阵列侧向测井响应的多参数反演. 西安石油大学学报(自然科学版) , 2005, 20(1): 30–33. Liu Z H, Zhang X. Multi-parameter inversion of array laterolog responses. Journal of Xi'an Shiyou University (in Chinese) , 2005, 20(1): 30-33.
[10] 仵杰, 谢尉尉, 解茜草, 等. 阵列侧向测井仪器的正演响应分析. 西安石油大学学报(自然科学版) , 2008, 23(1): 73–76. Wu J, Xie W W, Xie X C, et al. Forward response analysis of array lateral logging tool. Journal of Xi'an Shiyou University (in Chinese) , 2008, 23(1): 73-76.
[11] Rabinowitz P D, Zhou Z Q. Array processing-a new method to detect and correct errors on array resistivity logging tool measurements. Chinese Journal of Oceanology and Limnology , 2007, 25(1): 51-58. DOI:10.1007/s00343-007-0051-7
[12] 韩大匡, 陈钦雷. 油藏数值模拟基础. 北京: 石油工业出版社, 2001 . Han D K, Chen Q L. The Reservoir Numerical Simulation (in Chinese). Beijing: Petroleum Industry Press, 2001 .
[13] Stratton J A. Electromagnetic Theory. New York: McGrawHill, 1941 .
[14] Avis D, Toassaint T A. An efficient algorithm for decomposing a polygon into star-shaped polygons. Pattern Recognition , 1981, 13(6): 395-398. DOI:10.1016/0031-3203(81)90002-9
[15] Hoang H M, Kleppe J.A parallel adaptive finite difference algorithm for reservoir simulation.SPE 99572, in SPE Europec/EAGE Annual Conference and Exhibition, Society of Petroleum Engineers Inc..Expanded Abstracts, 2006
[16] 张庚骥. 电法测井. 北京: 石油工业出版社, 1984 . Zhang G J. Electrlog (in Chinese). Beijing: Petroleum Industry Press, 1984 .