2. School of Earth and Space Sciences, University of Science and Technology of China, Hefei 230026, China
2. 中国科学技术大学地球与空间科学学院, 合肥 230026
Since the discovery of seismoelectric pheno-menon[1, 2], many researchers have been focused on the theoretical and experimental study of seismo-electric phenomenon[3~15]. It should be stressed that Pride[9] derived a set of macroscopic dynamic governing equations describing the propagation of coupled seismic and electromagnetic wave-tields in porous media, which has been widely adopted in the study of seismoelectric effect from then on.
Chen[16~18] developed a method to calculate synthetic seismograms for layered media, decom-posing every vector using a set of orthogonal and complete basis vectors in a cylindrical coordinate system before applying the generalized reflection and transmission coefficients method. Ge and Chen[19] developed a new efficient approach for simulating wave propagation in multi-layered media with irregular interfaces, introducing a more straightforward evaluation of the generalized reflection and transmission coefficients.
Based on the model described by the macro-scopic dynamic governing equations of Pride[9], the above method of calculating theoretical seismo-grams[16~18] is extended to the numerical simulation of seismoelectric wave-fields in porous media[20]. In this new numerical emulation method, a set of scalar and vector wave-function basis is applied to decompose the concerned scalar and vector fields in the governing equations. Then two sets of governing equations corresponding to PSVTM (PSV waves generate electrical currents in the PSV particle motion plane coupling to the electro-magnetic (EM)-wavefield components with tran-sverse magnetic (TM) polarization) and SHTE (SH waves generate electrical currents in the SH particle motion plane that couple to the EM-wavefield components with transverse electric (TE) polarization) models respectively are obtained. Finally the equations are solved by the generalized reflection and transmission coefficients method, during which the straightforward evaluation of the generalized reflection and transmission coefficients developed by Ge and Chen[19] is applied.
Compared with the previously introduced method on the numerical simulation of coupled seismic and EM waves in layered porous media[11, 13], the new technique by Ren et al. [20] is quite transparent for a theoretical understanding and easy on programming. Furthermore, this method provides a straightforward evaluation of the generalized reflection and transmission coefficients as well as the evaluation of the vertical component of EM waves.
However, in the evaluation of the integral of the source terms, an exponential growth factor in the integrand of integral may lead to numerical instability. The numerical calculation is stable when the source layer is thin compared with the seismic wavelength (in other words, low-frequency). However, if the source layer is thick (or at high-frequency), the numerical instability problem will emerge and prevent us from obtaining the correct results. A natural regularization approach is to introduce a fictitious thin flat source layer which includes the source point in numerical calculations. In such a numerical regularization procedure the thickness of the fictitious thin source layer is finite, which cannot always be adequate for all cases, because an appropriate thickness of fictitious layer depends on the particular situation of each case. Moreover, the introduction of fictitious source layer would result in a certain amount of extra computation. This high-frequency instability problem also exists in the calculation of theoretical seismograms. Chen[17] introduced an analytical regularization approach which works well for any case without sacrificing any computational efficiency. In this article, we extend the analytical regularization approach of Chen[17] to deal with the high-frequency instability problem in the numerical simulation of seismoelectric wave-fields in layered porous media. It turns out this analytical regularization approach completely solves the high-frequency instability problem. A numerical example is used to investigate the high-frequency instability problem.
2 High-Frequency InstabilityThe multi-layered model is assumed to have N homogeneous layers over a half-space. The j-th layer is bounded by horizontal flat interfaces, z=z(j-1) and z=z(j).The source placed in the s-th layer is at depth of z=zs.
Decomposing the concerned seismoelectric fields with the scalar and vector wave-function basis, we obtain the fundamental equation given as[20]
where j=1, 2, ···, N+1, δj, s is Kronecker delta function, y and F are the displacement-stress-EM matrix and source matrix respectively, and A is the coefficient matrix including the media properties and the electrokinetic coupling coefficient.
The general solution of equation (1) is written as
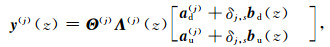
|
(2) |
where
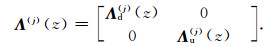
|
(3) |
Θ(j) and Λ(j) (z) are the matrices related to the eigen-vectors and eigen-values of A(j). The diagonal matrix Λ(j) (z) contains exponential decay terms only. The wave-amplitude ad(j) and au(j) are unknown vectors corresponding to down-going and up-going waves respectively. bd(z) and bu(z) relate to the source as follows
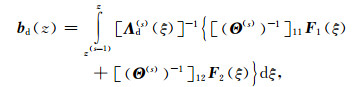
|
(4) |
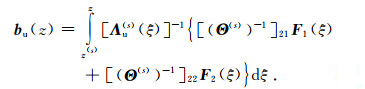
|
(5) |
Through the generalized reflection and transmission coefficients 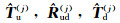
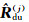
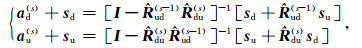
|
(6) |
and
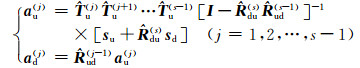
|
(7) |
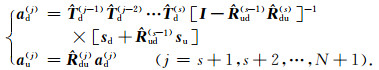
|
(8) |
where sd and su are source terms corresponding to down-going and up-going waves respectively, and they are written as

|
(9) |
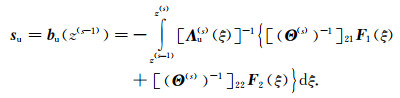
|
(10) |
To obtain the explicit value of wave-amplitude vector, we have to determine the source term according to equations (9) and (10). Since matrices Λd(s) (ξ) and Λu(s) (ξ) contain exponential decay terms only, matrices [Λd(s) (ξ)]-1 and [Λu(s) (ξ)]-1 contain exponential growth terms only, which will lead to numerical instability for high-frequency or thick source layer.
3 Analytical Regularization ApproachAn efficient way to solve the high-frequency instability problem is the analytical regularization approach which creates an infinite thin fictitious source layer within the original source layer (Fig. 1).
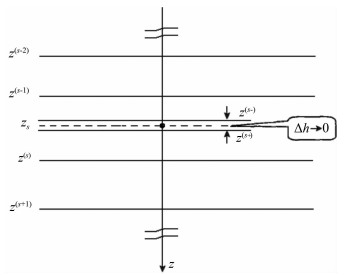
|
Fig. 1 Illustration of infinitely thin fictitious source layer inside the original source layer |
The fictitious upper and lower interfaces are denoted by s- and, s+ respectively. The correspon-ding generalized reflection and transmission coefficients at the two fictitious interfaces are given as
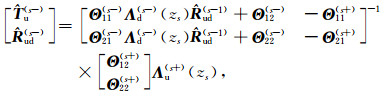
|
(11) |
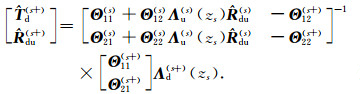
|
(12) |
In obtaining the equations (11) and (12), we have used the fact that the thickness of the fictitious layer Δh→0 and

|
Matrix A(j) stands for the properties in j-th layer, thus we have A(s-)=A(s+)=A(s), which yields Θ(s-)=Θ(s+)=Θ(s), and γi(s-)=γi(s+)=γi(s).(13) According to the definition of Λ(j)(z), we have

|
(14) |
where
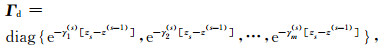
|
(15) |
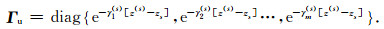
|
(16) |
Substitution of equations (13)~(14) into (11) and (12) yields
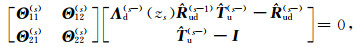
|
(17) |
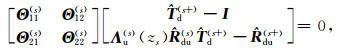
|
(18) |
which means
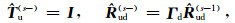
|
(19) |

|
(20) |
Under the "new" structure, the source terms sd and su become

|
(21) |

|
(22) |
where
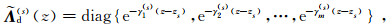
|
(23) |

|
(24) |
Since the thickness of fictitious source layer is infinitely small, the new source terms defined by equations (21) and (22) will not contain any exponential growth factors, thus the solution in frequency-wavenumber domain will be regular for any wavenumber.
According to the new generalized reflection and transmission coefticients and the new source terms, the general solutions can be rewritten as

|
(25) |

|
(26) |
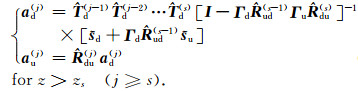
|
(27) |
The high-frequency instability problem is now resolved. The regularization solution given by equations (25)~(27) works well for any case.
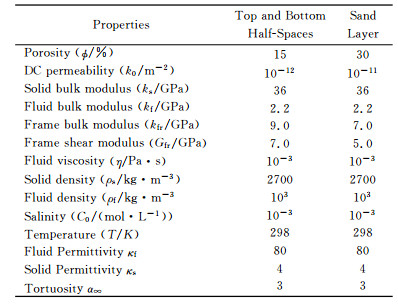
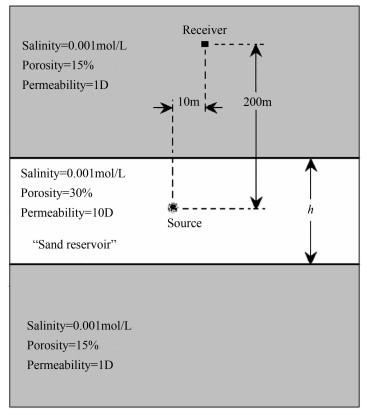
4 Numerical Example of High-Frequency InstabilityIn the calculation of seismoelectric wave-fields in layered porous media, the numerical simulation is stable at low-frequencies. However, the high-frequency instability problem emerges at high-frequencies or when the source layer is thick. For each frequency, there is a critical thickness of the source layer, which separates stability from instability in numerical simulations. Now we use a three-layer-model to investigate the critical thick-ness at different frequencies.
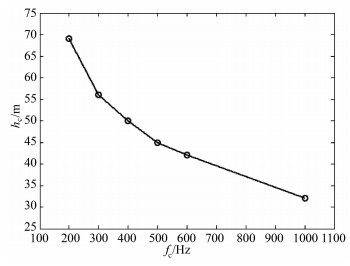
The model is a sand layer sandwiched between two identical half-spaces (see Fig. 2). The media properties used in the numerical simulation are given in Table 1. An explosion source is positioned in the middle of the source layer whose thickness is alterable. One receiver is positioned in the top half-space 200 m above the source with horizontal offset x=10 m. The Ricker wavelet as applied as source time function. Several different center frequencies are chosen from 200 to 1000 Hz. The variation of the critical thickness of the source layer is shown in Fig. 3. The results indicated that the critical thickness decreases as the center frequency increases.
|
Fig. 2 Three-layer-model used to investigate the critical source layer thickness (hc) at different center frequency (fc). The thickness of the sand layer (h) is alterable |
|
Fig. 3 Variation of the critical source layer thickness (hc) at different center frequencies (fc) |
|
|
Table 1 Media properties of the three-layer model in the numerical sample |
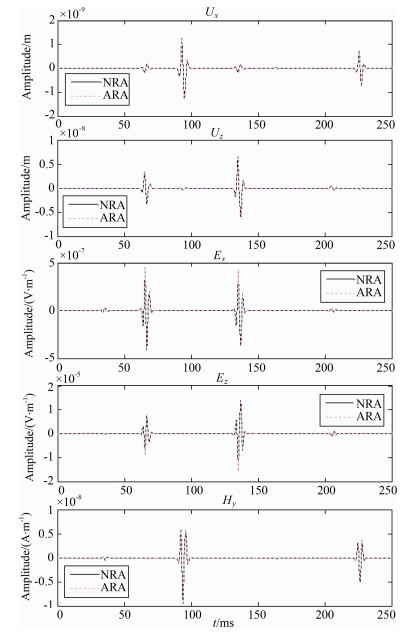
We now consider the three-layer-model with source layer thickness of 200 m and center frequency of 200 Hz. This is a thick source layer configuration. The exponential growth factor w il resuit in instability in numerical calculation. The natural regularization approach (NRA), which is introducing a fictitious thin flat source layer with finite small thickness, and the analytical regularization approach (ARA) described in this paper are respectively applied to eliminate the high-frequency instability. While using the NRA, we choose several different thickness of the fictitious source layer. It turns out we can not obtain the numerical results until the thickness is less than the critical source layer thickness (which is approximate 69 m for this configuration). The comparisons of nonzero waves in numerical results given by both approaches are displayed in Fig. 4. The amplitudes of direct P waves and accompanying electric waves are multiplied by a small factor of 0.03 to make other waves more visible. There is no significant difference between these two results. However, the computation time of ARA is less than the computation time of NRA by approximately 30%.
|
Fig. 4 Comparisons of numerical results between the natural regularization approach (NRA) and the analytical regularization approach (ARA) |
We discuss the high-frequency instability problem in the numerical smulation of seismoelectric wave-fields in multi-layered porous media and analyze the cause of this problem. A natural regularization approach is to introduce a fictitious thin flat source layer with a finite small thickness. In such a numerical regularization procedure, we have to find out an appropriate thickness for each case. Moreover, the introduction of a fictitious source layer would result in a certain amount of extra computation. We present an analytical regularization approach, which is creating an infinitely thin source layer within the original source layer, to eliminate the exponential growth factors in the integrand of integral of source terms. This regularization procedure does not sacrifice any computational efficiency. The results showed that the analytical regularization solution works well for any case. The technique presented in this paper may have potential applications in oll exploration[8] and earthquake-related electromagnetic studies[21~27].
AcknowledgmentsWe thank R.Robinson for reading the manuscript. This research was supported by the National R & D Special Fund for Public Welfare Industry of Earthquakes (200808069) and the National Natural Science Foundation of China (40974038, 40774028, 40821062).
| [1] | Blau L W, Statham L. Method and apparatus for seismic electric prospecting. U.S.Patent, 1936: No.2054067. |
| [2] | Thompson R R. The seismic electric effect. Geophysics, 1936, 1: 327-335. DOI:10.1190/1.1437119 |
| [3] | Ivanov A G. Effect of electrization of earth layers by elastic waves passing through them. Dokl.Akad.Nauk SSSR, 1939, 24: 42-45. |
| [4] | Frenkel J. On the theory of seismic and seismoelectric phenomena in a moist soil. J.Phys., 1944, 8: 230-241. |
| [5] | Biot M A. Mechanics of deformation and acoustic propagation in porous media. J.Appl.Phys., 1962, 33: 1482-1498. DOI:10.1063/1.1728759 |
| [6] | Revil A, Leroy P. Governing equations for ionic transport in porous shales. J.Geophys.Res., 2004, 109: B03208. DOI:10.1029/2006JB002755 |
| [7] | Revil A, Linde N. Chemico-electromechanical coupling in microporous media. J.Coll.Interf.Sci., 2006, 302: 682-694. DOI:10.1016/j.jcis.2006.06.051 |
| [8] | Thompson A H, Gist G A. Geophysical applications of electrokinetic conversion. The Leading Edge, 1993, 12: 1169-1173. DOI:10.1190/1.1436931 |
| [9] | Pride S R. Governing equations for the coupled electro-magnetics and acoustics of porous media. Phys.Rev.B, 1994, 50: 15678-15696. DOI:10.1103/PhysRevB.50.15678 |
| [10] | Pride S R, Haartsen M W. Electroseismic wave properties. J.Acoust.Soc.Am., 1996, 100: 1301-1315. DOI:10.1121/1.416018 |
| [11] | Haartsen M W, Pride S R. Electroseismic waves from point sources in layered media. J.Geophys.Res., 1997, 102: 24745-24769. DOI:10.1029/97JB02936 |
| [12] | Zhu Z, Haartsen M W, Toksoz M N. Experimental studies of seismoelectric conversions in fluid-saturated porous media. J.Geophys.Res., 2000, 105: 28055-28064. DOI:10.1029/2000JB900341 |
| [13] | Garambois S, Dietrich M. Full waveform numerical simulations of seismoelectromagnetic wave conversions in fluid-saturated stratified porous media. J.Geophys.Res., 2002: 107. DOI:10.1029/2001JB000316 |
| [14] | Pride S R, Moreau F, Gavrilenko P. Mechanical and electrical response due to fluid-pressure equilibration following an earthquake. J.Geophys.Res., 2004: 109. DOI:10.1029/2003JB002690 |
| [15] | Haines S S, Pride S R. Seismoelectric numerical modeling on a grid. Geophysics, 2006, 71: N57-N65. DOI:10.1190/1.2357789 |
| [16] | Chen X F. A systematic and efficient method for computing seismic normal modes in layered half-space. Geophys.J.Int., 1993, 115: 391-409. DOI:10.1111/gji.1993.115.issue-2 |
| [17] | Chen X F. Seismogram synthesis in multi-layered half-space part I. Theoretical formulations.Earthquake Research in China, 1999, 13: 149-174. |
| [18] | Chen X F. Generation and propagation of seismic SH waves in multi-layered media with irregular interfaces. Advances in Geophysics, 2007, 48: 191-264. DOI:10.1016/S0065-2687(06)48004-3 |
| [19] | Ge Z, Chen X F. An Efficient Approach for Simulating Wave Propagation with the Boundary element Method in Multilayered Media with Irregular Interfaces. Bulletin of the Seismological Society of America, 2008: 98. DOI:10.1785/0120080920 |
| [20] | Ren H X, Huang Q H, Chen X F. A new numerical technique for simulating the coupled seismic and electromagnetic waves in layered porous media. Earthquake Science, 2010, 23(2). DOI:10.1007/s11589-009-0071-9 |
| [21] | Johnston M J S. Review of electric and magnetic fields accompanying seismic and volcanic activity. Surv.Geophys., 1997, 18: 441-475. DOI:10.1023/A:1006500408086 |
| [22] | Huang Q H. One possible generation mechanism of co-seismic electric signals. Proc.Japan Acad., 2002, 78: 173-178. |
| [23] | Huang Q H. Controlled analogue experiments on propagation of seismic electromagnetic signals. Chinese Science Bulletin, 2005, 50: 1956-1961. DOI:10.1360/982004-312 |
| [24] | Huang Q, Liu T. Earthquakes and tide response of geoelectric potential field at the Niijima station. Chinese J.Geophys., 2006, 49: 1745-1754. |
| [25] | Zhao G Z, Zhan Y, Wang L F, et al. Electromagnetic anomaly before earthquakes measured by electromagnetic experiments. Earthquake Science, 2009, 22: 395-402. DOI:10.1007/s11589-009-0395-5 |
| [26] | Huang Q H, Ikeya M. Seismic electromagnetic signals (SEMS) explained by a simulation experiment using electromagnetic waves. Phys.Earth Planet.Inter., 1998, 109(3-4): 107-114. DOI:10.1016/S0031-9201(98)00135-6 |
| [27] | Huang Q H, Lin Y F. Selectivity of seismic electric signal (SES) of the 2000 Izu earthquake swarm:a 3D FEM numerical simulation model. Proc.Japan Acad.B, 2010, 86(3): 257-264. DOI:10.2183/pjab.86.257 |
 2010, Vol. 53
2010, Vol. 53