2. 中国科学院研究生院, 北京 100049;
3. 中国电波传播研究所青岛分所, 青岛 266107
2. Graduate University of the Chinese Academy of Sciences, Beijing 100049, China;
3. Qingdao Branch of China Research Institute of Radio Wave Propagation, Qingdao 266107, China
利用GPS探测数据获得的电离层电子浓度总含量(Total Electronic Content,TEC),已成为当前电离层观测与研究的一种重要参量.但必须注意,由GPS测量数据估算的是沿电波路径的斜向TEC(记为TECS),实际的研究和应用中,常常需要将其转换为垂直TEC(记为TECV),这种转换通常要通过映射函数(Mapping Function)实现[1~4].不同形式的电离层电子浓度高度剖面,对应于不同的映射函数形式,因此,采用正确形式的映射函数,是保证垂直TEC换算精度的关键所在[5~7].
当前的TECV换算中,使用最多的是薄层模型(Single Layer Model,SLM)[8~10],该模型的映射函数有较为简单的解析表达式[1].在研究中有时也采用具有Chapman函数等解析形式的电子浓度高度剖面,通过数值积分估算相应的映射函数,并研究映射函数随剖面参量(高度、标高等)的变化[10].此外,在实际应用中,曾经使用过Klobuchar的广播映射函数[10, 11]和Clynch等提出的Q-factor函数等[12].分析结果表明,在较小的卫星天顶角情况下,上述不同映射函数可以对垂直TEC和斜向TEC的关系进行较好的描述,但是在卫星天顶角较大时候各不相同,且误差较大.因此,为了保持垂直TEC的换算精度,实际应用中常常人为地将卫星天顶角较大时的测量数据舍弃不用,从而造成了数据资源的浪费.
本文针对垂直TEC的换算问题,提出了一种源于实际观测的实验映射函数的概念与估算方法.下面首先分析常用的两种模型映射函数的特性,特别是电离层高度对模型映射函数的控制作用.然后对2006年全球GPS台站的观测结果得出的实验映射函数进行统计分析,着重讨论实验映射函数与模型映射函数之间的差异.结果表明,实验映射函数可用于大天顶角时从斜向TEC到垂直TEC的换算中,在理论研究和实际应用中具有重要意义.
2 垂直TEC换算的模型映射函数映射函数定义为TE C S与TE CV之间的比值[6]:
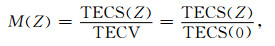
|
(1) |
其中,Z为卫星相对地面接收站的天顶角.可见,TECV可视为Z=0时TECS.忽略电子密度的水平梯度后,M(Z)由电子浓度的高度剖面N(h)确定.下面讨论两种简单N(h)模型情况下的映射函数特性.
首先讨论当前广泛采用的薄层模型(SLM),该模型的电子浓度剖面可以描述为
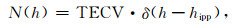
|
(2) |
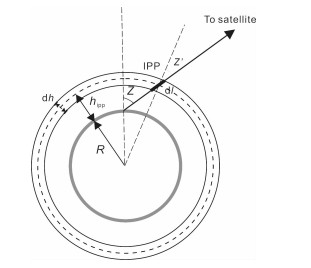
这里hipp为电离层的穿透点(Ionospheric Pierce Point, IPP)所在高度,应当使用电子浓度的质心高度,而通常采用经验公式hipp=hmF2+80 km来近似估算穿透点高度.实际上,穿透点高度常常被经验地固定为350~450 km之间的某一个高度.图 1是薄层模型的示意图,图中Z和Z′分别是地面台站和穿透点处的卫星天顶角,Re是地球半径.利用式(2)可以导出SLM的映射函数为
|
图 1 电离层薄层模型(SLM)示意图 Fig. 1 The diagram of single layer model |
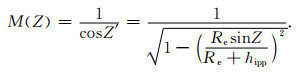
|
(3) |
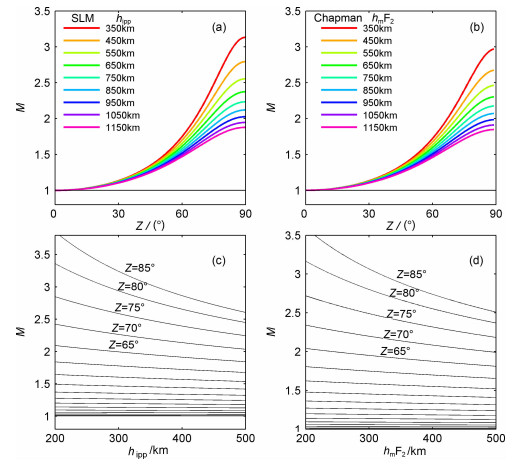
图 2(a,c)给出了不同穿透点高度时映射函数随天顶角的变化.
|
图 2 (a)不同hipp对应的SLM模型映射函数随地面上卫星天顶角Z的变化曲线;(b)不同hmF2对应的Chapman模型映射函数随Z的变化曲线;(c)不同Z对应的SLM模型映射函数随hipp的变化曲线;(d)不同Z对应的Chapman模型映射函数随hmF2的变化曲线 Fig. 2 (a) A cluster of curves calculated from SLM.Every curve indicate mapping function of different hipp, the abscissa is the zenith distance at the receiver location; (b) Calculated from Chapman model.The mapping function of different hmF2; (c) A cluster of curves calculated from SLM.Every curve indicate mapping function of different zenith distance at the receiver location (Z), the abscissa is the hipp; (d) Calculated from Chapman model.The abscissa is the hmF2 |
其次,在实际研究中也常常用到具有Chapman函数形式的电子浓度剖面,
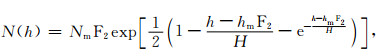
|
(4) |
其中H是标高,hmF2和NmF2分别是电离层(F2层)的峰值高度和峰值电子浓度.在这种电子浓度分布剖面上计算,即把(4)式代入(1)式,可以得到映射函数:
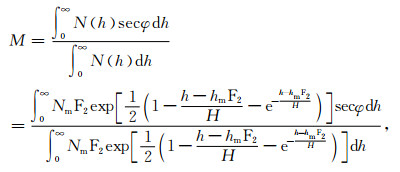
|
(5) |
式中secφ可以利用图 1的几何关系求得,
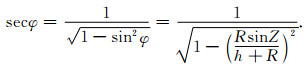
|
(6) |
此处M的解析形式不易求出,通常通过数学软件数值积分求出.在式(5)中代入secφ后,M实际上是卫星地面天顶角Z,标高H和峰值高度hmF2共同的函数,采用数值积分方法,可以得到相应不同的Z,H,hmF2的Chapman模型映射函数(图 2b,2d).计算表明,在常用的标高变化范围内,标高对Chapman模型映射函数影响比起hmF2的影响要小得多,因此图中只给出了标高为典型值(50 km,其他取值情况与此十分类似)的情况.
在上述两种模型映射函数中,最为明显的特征是映射函数值随卫星天顶角的增大而增加,并且受到电离层高度的控制.从图 2a和2b中首先可以看出,两种模型映射函数随Z的增加而单调增大,即M(Z)从Z=0°时的1增加到Z=90°时的1.5~3.5.其次,当Z较小时,映射函数随电离层高度参量(hipp和hmF2)的变化较小;但当Z较大,特别是卫星接近地平面附近时,两种模型映射函数都明显受到高度参量的控制,即M(Z)随高度参量的增加而快速减小.
为了进一步说明M(Z)随高度参量的变化,我们在图 2c和2d中给出了不同天顶角Z时的映射函数M(Z)随电离层高度参量的变化曲线.由图可见,当Z大于65°时,M(Z)的单调减小十分显著,且卫星天顶角越大,M(Z)的单调减小越明显.需要说明的是,电离层高度参量在这里一般取具有物理意义的典型值:在使用SLM模型时,通常取hipp在hmF2加80 km的高度,hipp常常被经验地固定为350~450 km之间的某一个高度,而Chapman模型中的高度参量是具有实际意义的hmF2,通常不超过350 km.画出电离层高度参量在400 km以上的模型映射函数图像是为了后面的讨论,在现今的相关研究中使用SLM和Chapman模型时并没有取到400 km以上的高度.而且,薄层和Chapman模型事实上都是单层模型,Chapman模型可以看作一个具有数千米层厚的单层模型,从图 2a和2b可以看出它们的曲线形态也很接近.
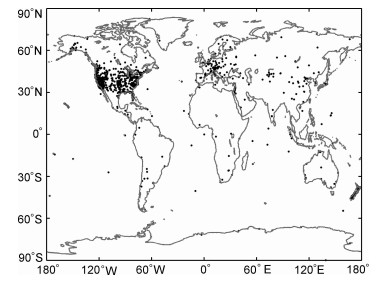
3 实验映射函数及其与模型映射函数的比较使用电子浓度的理论剖面获得的模型映射函数能够在一定程度上反映映射函数的主要特征,但为了获得更为可靠的映射函数分布,我们也可以用观测的TECS和TECV数据获得实验意义上的映射函数,本文称之为实验映射函数.在本文的分析中,TECS来自2006年期间全球IGS(International GPS Service)台站的GPS观测数据;TECV来自JPL(Jet Propulsion Laboratory)的全球电离层TEC地图(Global Ionospheric Maps)数据.JPL数据在处理时舍弃了大卫星天顶角数据,只保留了卫星天顶角较小情况,这种情况下可以使用薄层模型来计算垂直TEC而不至于产生较大偏差(图 2). TECS为直接的测量结果,TECV则来自JPL的计算.JPL使用的IGS台站数目众多,在它的分辨率范围内只使用小的卫星天顶角数据进行计算,因而对整体结果影响不大,使用这些数据可以获得全球电离层电子浓度的真实分布.为了使数据分布更加均匀,在全部IGS台站中,我们只选取经纬度间隔大于1°的台站数据,所选台站位置分布如图 3所示.而对于较小的范围,或者接收机分布比较稀疏的地区,如中国地区或者大洋区域,为了更好地研究电离层的变化,更多的数据变得更加重要.利用统计得出的实验映射函数,能够充分利用较大卫星天顶角时候的数据,增加数据,提高图像质量.
|
图 3 实验映射函数计算中所选的部分IGS台站 Fig. 3 Permanent ground GPS receivers of IGS network used in the calculation of experimental mapping function |
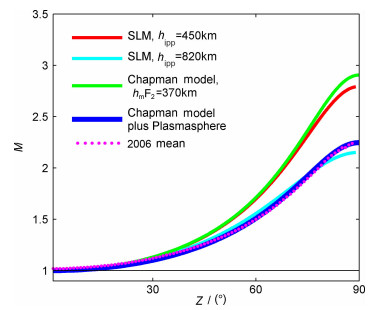
通过消除TECS中的硬件误差,利用(1)式可估算不同时间不同地点的实验映射函数.图 4给出了平均的实验映射函数随卫星天顶角Z的变化情况(品红点线).为了比较,图 4中同时给出了两种高度的SLM模型映射函数(hipp分别为450 km和820 km,注意450 km是典型值,820 km是拟合实验映射函数曲线时所需要的高度),hmF2=370 km的Chapman模型映射函数,以及相同高度的Chapman模型加等离子体层模型(将在后面说明)的模型映射函数.图 4表明,实验映射函数随卫星天顶角Z单调增加,在Z较小时增长比较缓慢,Z较大时增长较快,当Z接近90°时增速有明显减缓.可见实验映射函数随Z的变化与模型映射函数完全相同.但是,与典型电离层高度参数(即hipp=450 km,hmF2=370 km)下的模型映射函数相比,实验映射函数在Z较大时明显偏低.例如,在Z=80°时,实验映射函数值较SLM和Chapman映射函数值分别小0.4821和0.5551.但当SLM中的电离层穿透点高度大幅度增加(如hipp=820 km,这用薄层模型理论是无法解释的),或者在Chapman电子浓度剖面模型上叠加一个等离子体层模式电子浓度剖面(如Gallagher模式[13]),模型映射函数值均可降低到与实验映射函数值相当的水平,如图 4中的相应曲线所示.
|
图 4 SLM模型映射函数、Chapman模型映射函数以及通过考虑等离子体层电子浓度剖面改进后的Chapman模型映射函数与实验映射函数的比较 Fig. 4 A comparison of the observational mapping function (2006 mean) with those calculated from the electron density models, SLM and Chapman. And the Chapman model modified by plus protonosphere electron density calculated by Gallagher plasma model |
在Birch等人对位于英国西部的Lancaster(53°52′N,2°45′W)台站1993年10月至1994年2月TEC数据的研究中[14],记录了类似的情形:由于对映射函数的高估,导致对此台站上空垂直TEC的推算存在高达15%~30%的误差.他们给出的SLM可用薄层高度在600~1200 km之间.在文献[14~16]里也提到过使用薄层模型映射函数估算TECV的误差问题,通常认为这种误差较大.但是对电离层薄层模型的使用范围和薄层高度的选择,仍然存在许多不同的标准,SLM模型中使用较多的仍然是前面的经验公式hipp=hmF2+80 km,Chapman模型则主要使用的是电离层高度参量取hmF2时对应的情况,如图 4中的红线和绿线所示.在本文中统计了2006年度全球的情况,我们也证明了这种典型模型映射函数在大卫星天顶角处的偏高现象,不仅仅是某地特殊的电离层状况所致,而是具有普遍意义的现象.
图 4还表明,使用等离子体层来修正大卫星天顶角时典型参数的映射函数是一种有效的方法.由于电离层之外等离子体层的存在,由GPS观测的TEC必然会反映等离子体层的贡献.Lunt等人[17, 18]曾指出,在太阳活动低年,等离子体层对垂直TEC的贡献在白天约为10%~20%,在晚上可高达50%.这导致了我们实验映射函数的曲线比只将电离层当作一个单层处理而不考虑等离子体层的典型模型映射函数曲线(SLM:hipp=450 km;Chapman: hmF2=370 km)要低.总之,等离子体层对TEC的贡献明显[14~16, 19],在GPSTEC测量中,特别是使用模型映射函数进行大卫星天顶角数据垂直TEC转换时,必须加以考虑.
至于用薄层模型或者Chapman模型来数值逼近实验映射函数,使用较大的电离层高度参数也可以较好接近.但是这么做就失去了使用该模型的物理意义,仅仅是作为一个形状近似的曲线.我们认为,这种方法可以在快速估算大卫星天顶角时映射函数时使用,就2006年的数据,本文给出一个可用的经验公式(SLM)hipp=hmF2+450 km.
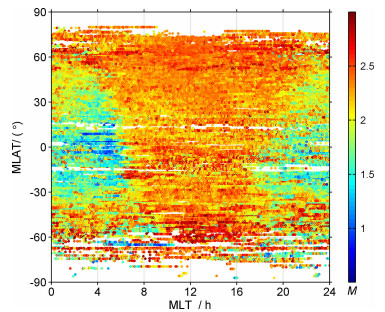
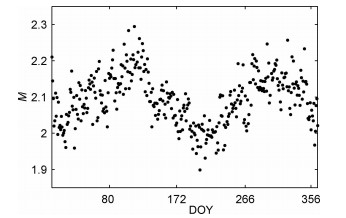
4 映射函数的统计分析结果与讨论利用上述方法获得的实验映射函数随时间和地理分布而变,而我们所说的模型映射函数一般只是受控于电离层高度参数的时间空间变化,在实际应用中无法随时随地地获得随时间空间变化的电离层高度参数,但是通过统计分析以获得实验映射函数时空分布特征不失为一种合理的处理方法.我们更为关心的是卫星天顶角较大时候映射函数的分布情况.作为例子,图 5给出了北半球夏至附近1个月期间在固定天顶角(Z=80°)处的实验映射函数值随地磁纬度(MLAT)和磁地方时(MLT)的分布.图 6给出的是天顶角Z=80°时中低纬度(|MLAT|<30°)实验映射函数的日平均值在一年内的变化.由图 5可见,实验映射函数在夜晚较小,在白天较大,在晨昏线附近有明显的快速变化.此外,实验映射函数在中低纬度地区较小,在高纬及中高纬度地区较大.而图 6表明,实验映射函数具有明显的半年变化,即在春夏与秋冬交接处具有峰值,在夏秋与冬春交接处具有谷值.
|
图 5 地面上卫星天顶角Z=80°时,006年北半球夏至附近1个月期间的实验映射函数随地磁纬度MLAT与磁当地时MLT的分布 Fig. 5 Examples of experimental mapping functions during the month around the Summer Solstice of the northern hemisphere during 2006, when Z=80° |
|
图 6 地面上卫星天顶角Z=80°时,中低纬(-30° < MLAT < 30°)地区实验映射函数的半年变化 Fig. 6 Experimental mapping functions ofthe low magnetic latitude (-30° < MLAT < 30.), when Z=80° |
在图 4中我们使用了一个简单的等离子体层模式Gallagher模式,与传统的Chapman电离层模型结合,得到了与实验映射函数吻合很好的映射函数曲线.由此我们认为造成常用参数范围内的简单模型映射函数与实验映射函数的差异主要是因为现有模型映射函数中没有考虑到等离子体层的贡献.利用等离子体层与电离层时空分布的相对大小和变化的强弱可以定性地解释实验映射函数时空分布的一些特征.考虑到当地面上的卫星天顶角固定后,实验映射函数的大小取决于电子浓度剖面的质心高度,为了讨论的直观,可将电离层和等离子体层看作两个分离的薄层,具有各自的质心高度.求两个同心薄球壳层共同的质心高度即求它们密度的比值,因此GPS卫星高度以下电子浓度分布的质心高度基本上取决于等离子体层的电子浓度积分含量(记为TECP)和电离层的电子浓度积分含量(记为TECI)的相对大小,即TECP相对较大(TECI相对较小)时映射函数相对较小,反之亦然.
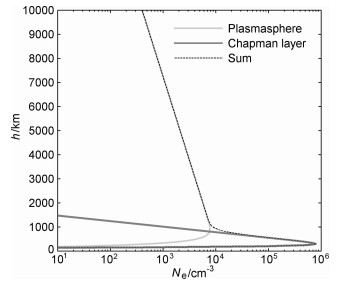
等离子体层是位于地球内磁层的冷等离子体层,其粒子主要来自电离层上行粒子,主要存在于中低纬区域,在高纬稀薄到可以忽略不计.其浓度随纬度的增加而减少,减少的速度较电离层要快得多,且在高中纬地区迅速消失.图 7给出了使用模式计算的[9]中纬地区夜间等离子体层电子浓度与Chapman电子浓度的高度剖面.在1000 km之下,电离层(Chapman层)构成了电子浓度的大部分,到1000 km以上电子浓度总和基本上跟等离子体层的曲线重合,电离层(Chapman层)迅速消失,只剩下等离子体层.从图中也可以清楚看到,虽然等离子体层的峰值高度远小于电离层F2层峰高,但是由于它在空间向上延伸到很远的范围,因此积分结果是很可观的.例如,取高度上限为20000 km时计算得到的TECP为27.3TECU,TECI为40.6TECU,TECP能够占到总电子浓度的40.19%之多.这与Lunt等人[13, 14]指出的,在太阳活动低年的晚上等离子体层对TEC的影响可高达50%是一致的.
|
图 7 使用Gallagher模式得到的一个典型等离子体层电子浓度分布剖面(中纬30°,MLT=12:00)和Chapman型典型电离层电子浓度剖面(hmF2=300 km,NmF2=8×105cm-3) Fig. 7 A typical electron concentration profile calculated by Gallagher plasmasphere model (LAT=30°, MLT=12:00), and a typical Chapman electron concentration profile (hmF2=300 km, NmF2=8×105cm-3) |
电离层和等离子体层都具有季节(年度)变化、地方时变化以及(磁)纬度变化.一般说来,电离层的季节/年度变化和日变化幅度要比等离子体层大得多,但等离子体层在纬度方向的变化是很明显的,这些可以用来解释图 5、图 6中实验映射函数的变化特征.
(1)在图 5中,低纬地区的实验映射函数明显小于中高纬地区的实验映射函数,这与TECP随纬度的增加较TECI增加更快是一致的.
(2)在图 5中,白天的实验映射函数明显大于夜晚的实验映射函数,这是因为TECP的日变化较TECI小得多.
(3)图 6中实验映射函数的半年变化应主要来自电离层的半年变化,因为等离子体层的半年变化较电离层要弱得多.图 6中映射函数半年变化的峰值位于春秋分附近,谷值位于夏冬至附近,这与电离层TEC的半年变化基本符合.
5 结论电离层垂直TEC精确换算中映射函数的选取非常关键.本文中我们考察了不同电子浓度剖面的模型映射函数,在此基础上,又提出了一种源于实际观测的实验映射函数的估算方法.我们利用IGS全球GPS观测站的斜向TEC和JPL提供的垂直TEC数据,估算了2006年期间的实验映射函数,并统计分析了实验映射函数的地理分布与季节变化.分析证明,实验映射函数与典型电离层高度参数下的模型映射函数之间存在明显差异.典型的电离层高度参量下模型映射函数值要比实验映射函数高,而且模型映射函数值随所取的“电离层高度”的升高有下降的趋势.另外,实验映射函数具有明显的纬度变化、周日变化和季节变化.本文认为,这种差异和变化主要来自于等离子体层的作用.若在应用中采用基于实验映射函数的模式,或者考虑等离子体层的贡献,对现有模型映射函数进行改进,可以有效提高电离层TEC的估算精度,增加可以使用的数据量,获得更好的局域电离层图像.等离子体层对映射函数的影响及作用机制,是我们下一步研究的方向.
| [1] | Mannucci A J, Wilson B D, Yuan D N, et al. A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Science , 1998, 33(3): 565-582. DOI:10.1029/97RS02707 |
| [2] | Bilitza D.International Reference Ionosphere 1990.National Space Science Data Center/World Data Center A for Rockets and Satellites, Greenbelt, Md., USA, 90-22, Nov.1990 |
| [3] | Lanyi G E, Roth T. A comparison of mapped and measured total ionospheric electron content using global positioning system and beacon satellite observations. Radio Science , 1988, 23(4): 483-492. DOI:10.1029/RS023i004p00483 |
| [4] | 张东和, 萧佐. 利用GPS计算TEC的方法及其对电离层扰动的观测. 地球物理学报 , 2000, 43(4): 451–458. Zhang D H, Xiao Z. A method of calculating TEC with GPS data and its application to the ionospheric disturbances. Chinese J.Geophys. (in Chinese) , 2000, 43(4): 451-458. |
| [5] | 萧佐, 王劲松, 张东和, 等. 当前的电离层气候学研究. 中国科学(A辑) , 2000, 30(Z1): 9–11. Xiao Z, Wang J S, Zhang D H, et al. The current study work of ionospheric climate. Science in China (Series A) (in Chinese) , 2000, 30(Z1): 9-11. |
| [6] | 熊波, 万卫星, 宁百齐, 等. 海南三亚地区S4指数与C/N、ROTI的比较分析. 地球物理学报 , 2007, 50(6): 1639–1648. Xiong B, Wan W X, Ning B Q, et al. A comparison and analysis of the S4 index, C/N and ROTI over Sanya. Chinese J.Geophys. (in Chinese) , 2007, 50(6): 1639-1648. |
| [7] | 赵晓峰, 李征航. 有关电离层映射函数问题的探讨. 测绘通报 , 2003(9): 8–10. Zhao X F, Li Z H. A study of some problems pertinent to ionosphere mapping function. Bulletin of Surveying and Mapping (in Chinese) , 2003(9): 8-10. |
| [8] | Komjathy A, Langley R B.The effect of shell height on high precision ionospheric modelling using GPS.Proceedings of the 1996 IGS Workshop International GPS Service for Geodynamics (IGS), 1996.193~203 |
| [9] | Orús R, Hernández-Pajares M, Juan J M, et al. Performance of different TEC models to provide GPS ionospheric corrections. Journal of Atmospheric and Solar-Terrestrial Physics , 2002, 64(18): 2055-2062. DOI:10.1016/S1364-6826(02)00224-9 |
| [10] | Schaer S.Mapping and predicting the Earth's ionosphere using the Global Positioning System[Ph.D.thesis]. Berne, Switzerland:Astronomical Institute, University of Berne, 25 March 1999.54~64 |
| [11] | Klobuchar J A.Ionospheric time-delay algorithm for single-frequency GPS Users.IEEE Transactions on Aerospace and Electronic Systems, May 1987, AES-23, Issue 3:325~331 |
| [12] | Clynch J R, Coco D S, Coker C, et al.A versatile GPS ionospheric monitor-High latitude measurements of TEC and scintillation.Institute of Navigation Satellite Division. International Technical Meeting, 2nd, Colorado Springs, CO, Sept.27~29, 1989, Proceedings (A90-4367619-17). Washington D C:Institute of Navigation, 1989.445~450 |
| [13] | Gallagher D L, Craven P D, Comfort R H, et al. An empirical model of the Earths plasmasphere. Adv.Space Res. , 1988, 8(8): 15-24. DOI:10.1016/0273-1177(88)90258-X |
| [14] | Birch M J, Hargreaves J K, Bailey G J. On the use of an effective ionospheric height in electron content measurement by GPS reception. Radio Science , 2002, 37(1): 1015. DOI:10.1029/2000RS002601 |
| [15] | Breed A M, Goodwin G L, Silby J H. Total electron content measurements in the southern hemisphere using GPS satellites, 1991 to 1995. Radio Science , 1998, 33(6): 1705-1726. DOI:10.1029/98RS01856 |
| [16] | Smith D A, Araujo-Pradere E A, Minter C, et al. A comprehensive evaluation of the errors inherent in the use of a two-dimensional shell for modeling the ionosphere. Radio Science , 2008, 43: RS6008. DOI:10.1029/2007RS003769 |
| [17] | Lunt N, Kersley L, Bailey G J. The influence of the protonosphere on GPS observations:model simulations. Radio Science , 1999, 34(3): 725-732. DOI:10.1029/1999RS900002 |
| [18] | Lunt N, Kersley L, Bishop G J, et al. The effect of the protonosphere on the estimation of GPS total electron content:validation using model simulations. Radio Science , 1999, 34(5): 1261-1271. DOI:10.1029/1999RS900043 |
| [19] | Miguel J, Antonio Rius, Hern'andez-Pajares, et al. A two-layer model of the ionosphere using Global Positioning System data. Geophysical Research Letters , 1997, 24(4): 393-396. DOI:10.1029/97GL00092 |
 2010, Vol. 53
2010, Vol. 53


