2. Guangdong Power Grid Development Research Institute Co. Ltd., Guangzhou 510030, China;
3. Suzhou Huatian Power Technology Co. Ltd., Suzhou 215000, China
With the acceleration of social and economic growth and the vigorous development of emerging industries, there will emerge more and more types of power users. At the same time, the differences of typical daily load curve characteristics of different power consumers in the same industry are also increasing. Taking traditionally simple and crude analysis methods based on user-reported categories as load classifications are no longer suitable for the development of next-generation power systems and energy Internet. The refined daily load curve characteristic analysis can help the grid to perform real-time optimization scheduling, formulate reasonable demand response management measures, the expansion planning and distribution network planning [1].
At present, many clustering analysis methods have been used to extract typical daily load characteristics of power users [2, 3], such as Fuzzy C-Means Algorithm (FCM) [4], K-MEANS algorithm [5], DBSCAN algorithm [6] and self-organizing map neural network(SOM) [7], etc. Among them, FCM algorithm performs excellent in operational efficiency, clustering effect and robustness of the algorithm.However, there are two disadvantages to performing daily load curve clustering directly using the traditional FCM algorithm:
(1) Clustering analysis was performed directly using the distance between the original daily load curve data as a similarity criterion. This will lead to a poorer clustering performance and ignore the intrinsic characteristics of the load curve.
(2) The clustering effect of FCM algorithm is susceptible to the initial point position.
To solve the above problems, this paper firstly selects the load characteristic index to reduce the dimension of the original daily load curve data, and proposes a fuzzy mean clustering algorithm based on GWO to perform the clustering analysis of daily load curve. The proposed algorithm combines the advantages of the GWO algorithm and the FCM algorithm. It can use GWO's global search capability to search the optimal initial clustering center for FCM algorithm quickly, reduce the sensitivity of FCM algorithm to the initial clustering point, obtain the approximate global optimal clustering and improve the clustering effect of daily load curve. In a word, the proposed method can solve two shortcomings of traditional cluster analysis mentioned above.
2 Dimensionality Reduction of Daily Load Curve DataIn a traditional clustering method, the similarity of data samples is usually judged by the distance between the original sample data. However, as a kind of time series data, the daily load curve data is greatly affected by factors, such as user type, weather and time-sharing price policy. As a result, the power consumption characteristics of user data cannot be directly reflected by the distance. Under high-dimensional raw samples, data may exhibit undesirable equidistance. The daily load clustering analysis not only needs to pay attention to the equidistance of the daily load curve data, but also analyzes the similarity of its shape and contour to understand the user's electricity habits and characteristics.
The load characteristic index can comprehensively reflect the user's power consumption characteristics [8]. Five characteristic indexes are selected according to the division plan of the peak and valley period of Guangdong Power Grid for data dimensionality reduction. The definitions and calculation methods of indexes are shown in Table 1.
| Table 1 Daily load characteristic indexes |
In Table 1, P represents the power load; the subscripts av, max and min represent the mean, the maximum and the minimum respectively; the subscripts peak, val and sh represent the peak period, the valley period and the shoulder period, respectively.
The daily load characteristics of the load users can be described from the time scales of the whole day, the peak period, the shoulder period and the valley period using the indexes I1 − I5. The physical meanings of each indexes are different, which can describe the internal characteristics of the daily load curve more comprehensively.
3 Fuzzy C-Means Clustering Algorithm Based on GWO 3.1 Fuzzy C-Means Clustering AlgorithmFCM is a clustering classification algorithm that ultimately makes the similarity between the samples classified into the same class as high as possible, while making the difference between the samples classified into the different class as high as possible. FCM is improved on the basis of ordinary C-means clustering, and the concept of fuzzy set is introduced to realize flexible fuzzy clustering [9].
3.2 GWOThe GWO is a group search intelligent algorithm proposed by Mirjalili S et al. The algorithm treats each feasible solution as a wolf and treats the optimal solution as a prey. By referring to the wolf group level and hunting habit, each solution is graded and searched to find the optimal solution [10].
3.3 GWO-FCM Clustering AlgorithmAs a gradient-based search algorithm, FCM clustering algorithm has the advantages of rapid convergence and excellent local search ability. The traditional FCM algorithm starts from the initial cluster center matrix or the fuzzy partition matrix. Since the initial matrix is randomly generated, if the initial values are different, the clustering results may be different. Therefore, if the initial value is not properly selected, the clustering result may fall into local optimum. This problem is particularly prominent when the number of samples is large. The GWO has excellent global search ability, rapid convergence speed, and is not easy to fall into local optimum. Therefore, considering the combination of GWO and FCM algorithm to fully utilize the advantages of global optimization of GWO and strong local convergence of FCM algorithm, reduce the dependence of FCM algorithm on initial value selection, and obtain better clustering effect.
Coding of Grey Wolf Particle. It can be seen from the above analysis that the FCM algorithm can select the fuzzy partition matrix U or the cluster center matrix P for initialization. For the clustering analysis problem in daily load curve of power users, it is usually necessary to process and analyze the load curve data of a large number of users, which will result in that the data number n of the data sample set is too large. If the elements in the fuzzy partition matrix U are used to form the code of the grey wolf, the coding dimension reaches the c × n dimension, and the high dimension will affect the efficiency of the GWO. After the data reduction operation on the original data, the feature quantity m of a single piece of data is often much smaller than the number of its data pieces n. Therefore, the element structure of the cluster center matrix P is selected as the encoding of the grey wolf particles, and the particle dimension can be reduced to c × m dimension. Then the particle code can be expressed as:
| $ {\mathit{\boldsymbol{p}}_i} = \left( {{p_{11}}, .{\rm{ }}.{\rm{ }}.;{p_{1m}}, .{\rm{ }}.{\rm{ }}., {p_{c1}}, .{\rm{ }}.{\rm{ }}., {p_{cm}}} \right) $ | (1) |
Fitness Function. The FCM algorithm needs to construct a suitable fitness function to evaluate the quality of each grey wolf particle. The fitness function defined in this paper is as follows:
| $ \min \mathit{J}\left( {\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{P}}} \right) = \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^{\rm{c}} {u_{ij}^g} } d_{ij}^2 $ | (2) |
| $ f\left( {{\mathit{\boldsymbol{p}}_i}} \right) = \frac{1}{{\mathit{J}\left( {\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{P}}} \right)}} $ | (3) |
For an individual grey wolf, the smaller the corresponding target value J(U, P), the higher the fitness value f(pi), indicating that the clustering effect is better.
The position of each grey wolf in the wolves represents a feasible solution in the problem space, indicating a method for selecting the initial cluster center. Therefore, the position of wolves α, β and δ in each iteration of the GWO. The update of information only needs to correspond to each initial clustering center according to the fitness value.
Conversion conditions between GWO and FCM algorithm. The GWO-FCM algorithm is mainly divided into two parts: the first part uses the GWO to search for a better initial clustering center in the feasible domain, and the second stage uses the local search ability of the FCM algorithm. Based on the optimal initial clustering center, the iterative calculation performs local optimization and completes cluster analysis.
The variance of the wolf population fitness is defined as follows:
| $ {\sigma ^2} = \frac{1}{z}{\sum\limits_{i = 1}^z {\left[ {f\left( {{\mathit{p}_i}} \right) - {f_{avg}}} \right]} ^2} $ | (4) |
where z is the wolf number; favg is the average of all grey wolf individuals. The magnitude of fitness variance σ2 characterizes the degree of convergence of grey wolf individuals. When the value of σ2 is small, the degree of dispersion of the wolf group's fitness value is not high, the GWO tends to converge, and its global search ability begins to decline. Therefore, when the value of σ2 is less than the set threshold ξ, the GWO-FCM algorithm is switched from the first stage to the second stage, that is, the clustering analysis is performed by using the FCM, so that the later convergence is faster.
The algorithm flow of GWO-FCM. The flow chart of GWO-FCM algorithm are shown in Fig. 1.
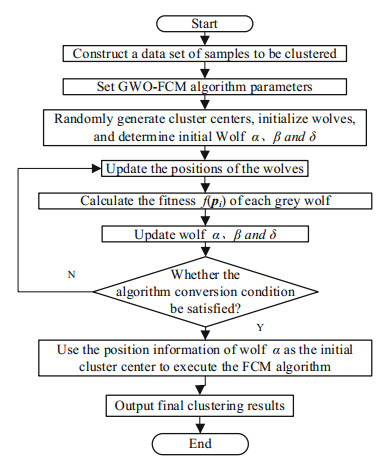
|
Fig.1 Flow chart of GWO-FCM algorithm |
The GWO-FCM algorithm is described as follows:
Step(1): Initialize the wolves. Set the required clustering number c, randomly generate c clustering centers to encode the grey wolf position, and then initialize the position of a grey wolf; repeat S times to obtain the initial wolf composed of S initial grey wolf group. Then calculate the fitness degree of each wolf in the wolves, and select the top three grey wolf individuals, which are recorded as wolf α, β and δ in order;
Step(2): Update the wolf position. Updating the positions of the wolves in the wolves;
Step(3): Calculate the fitness value of each grey wolf f(pi);
Step(4): Update the wolf rank. Select three grey wolves with the best fitness value, and update the positions of wolf α, β and δ in order;
Step(5): Determine the conversion conditions. If the wolf group fitness variance σ2 is less than the threshold ξ or the number of algorithm loop iterations reaches the maximum number of iterations, the GWO iterative global search phase is stopped, and the wolf α position is set as the initial cluster center of the FCM algorithm; otherwise, go to Step(2);
Step(6): Use the result of step(5) as the initial clustering center and execute FCM algorithm. The final clustering center P and the fuzzy partition matrix U are output according to the principle of maximum membership.
4 Implementation Method 4.1 Dataset PreprocessingData Cleaning. First, remove the load curve data with abnormal or missing data. Then use the smoothing formula or other interpolation algorithm to change or fill the daily load curve data with a small amount of abnormal or missing data.
Input sample set construction. The daily load curve data of the completed data cleaning is subjected to data dimensionality reduction using the daily load characteristic indicators listed in Table 1. The load data in the existing metrology automation system is usually 96 sampling points per day, and the sampling interval is 15 min. After data cleaning has been completed, the number of remaining daily load data is N, the dimension of the original data sample set is reduced from the original N × 96 dimension to N × 5 dimension by data dimension reduction.
4.2 Evaluation Index of Clustering EffectivenessThe silhouette coefficient can be used to reflect the tightness and separability of the class. This index can determine the optimal cluster number and evaluate the clustering effect when the number of clusters is unknown. For the profile x, the profile coefficient characteristic index is defined as shown in Eqs. (5)–(7):
| $ SIL\left( x \right) = \frac{{{D_a}\left( x \right){\rm{ }} - {D_b}\left( x \right)}}{{{\rm{max}}\left( {{D_a}\left( x \right), {D_b}\left( x \right)} \right)}} $ | (5) |
| $ {D_a}\left( x \right) = \frac{{\sum {_{s \in {C_k}, s \ne x}} d\left( {x, s} \right)}}{{\left| {{C_k}} \right| - 1}} $ | (6) |
| $ {D_b}\left( x \right) = {\min _{{C_j}:1 \le j \le c, j \ne k}}\left\{ {\frac{{\sum {_{s \in {C_k}}} d\left( {x, s} \right)}}{{\left| {{C_j}} \right|}}} \right\} $ | (7) |
where SIL(x) represents the silhouette coefficient of the sample x; x represents the sample belonging to the class Ck; Da(x) and Db(x) represent the average distance between the x and Ck internal residual objects, and the minimum average distance of x and non-Ck class objects, respectively.
The silhouette coefficient varies between [−1, 1]. When the silhouette coefficient is closer to 1, indicating that the tightness of Ck class and class separability to which x belongs are better, and so is the clustering effect. If the silhouette factor is less than 0, the clustering fails.
The average of the overall clustering was evaluated using the mean of the silhouette coefficients of all data samples. It is expressed as Eq. (8):
| $ SLIMEAN = \frac{1}{N}\sum\limits_{i = 1}^N {SIL\left( {{x_i}} \right)} $ | (8) |
The larger the SLIMEAN, the better the overall clustering effect. The maximum number of clusters c that make SLIMEAN is the optimal number of clusters.
5 Experimental Results and Analysis 5.1 Input Dataset ConstructionThe clustering study selected the actual daily load curve data of 1536 users in a normal working day in May 2017 in a city of Guangdong. The data collection upload interval is 15 min, and the amount of single-day load data per user is 96 points. The original daily load curve data is preprocessed using the construction method of the input data set described in Sect. 4. After processing, the final example contains 1498 data strips, and the matrix to be clustered falls from 1498 × 96 dimensions to 1498 × 5 dimensions. Compare the clustering analysis of the processed matrix to be clustered by the algorithm proposed in this paper with the clustering results of the FCM algorithm after normalizing the data with 96 sampling points as the input.
The specific parameters are set as follows: the maximum cluster number cmax = 8; the minimum clustering number cmin = 2; the fuzzy degree coefficient g = 2; the wolf group size is 25; the maximum iteration number takes lmax = 300. The parameters of the traditional FCM algorithm are as follows: the degree of fuzzification is g = 2; the maximum number of iterations is tmax = 100, and the threshold of the objective function is 10−7.
5.2 Results of ClusteringTable 2 shows the clustering effectiveness index calculation results of the two methods in the case of setting different cluster numbers. Figure 2 shows the trend of the mean value of the contour coefficients of the two methods under different clustering numbers. Combined with Table 2 and Fig. 2, the SLIMEAN mean value of both algorithms is maximized when the number of clusters is 4. Therefore, the optimal number of clusters for both algorithms is 4. At the same time, the SLIMEAN mean value index using the clustering result of this method is larger than the SLIMEAN mean value obtained by the traditional FCM method when the clustering number takes any other value, and the clustering effect is better. This also shows that the proposed method combines the global search ability of GWO with the local search ability of FCM algorithm, and reduces the possibility that the clustering result converges to local optimum.
| Table 2 Calculation results of clustering effectiveness index |
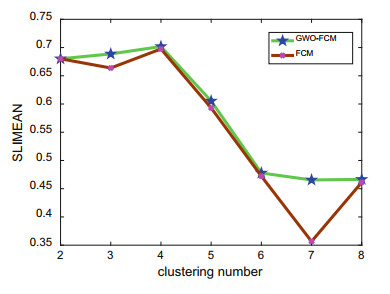
|
Fig.2 Variation trend of clustering effectiveness index |
Figure 3 shows the clustering results of the daily load curve of the clustering algorithm, where the red curve is the average of the overall load of the class. Since the algorithm has the process of data dimensionality reduction, the clustering center of each dimensionality reduction index can be obtained, and various typical load curves cannot be directly obtained. This paper considers that the daily load curve averaged as the same type of load is the typical daily load curve for this type of load. In the clustering results obtained by the algorithm of this paper, the number of curves belonging to each category are 384, 354, 362 and 398, respectively. The traditional clustering algorithm is used to obtain the clustering results, and the number of curves belonging to each category are 375, 365, 372 and 386, respectively the number of classifications and classification results are basically the same.
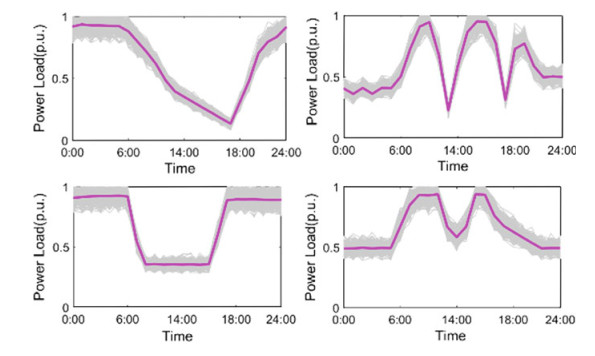
|
Fig.3 Daily load curve clustering result based on the proposed algorithm |
5.3 Robustness Test of Algorithm
Select the 6 types of daily load curves known in [11]. Based on the known correct clustering results, random noise with a ratio r is added to each data point of each typical curve to obtain The daily load curves of 6 categories and 200 strips of each class are used as cluster samples to verify the robustness of the clustering algorithm.
The robustness of the algorithm is analyzed by using the optimal clustering number, clustering validity index and accuracy. In this paper, the ratio of the total number of correctly classified load curve data to the number of all load curves is taken as the accuracy rate. The results of the comparison of the robustness test results are shown in Table 3.
| Table 3 Comparison of algorithm robustness |
It can be seen from Table 3 that when the noise ratio r is increased, the optimal clustering numbers of the two clustering algorithms are changed, and the clustering effectiveness index and the accuracy rate are both decreased. When the noise ratio r is less than 25%, the optimal clustering number is always 6 and the accuracy is close to 100%. For the traditional FCM algorithm, when the noise ratio r increases to 10%, the optimal clustering number changes, the classification accuracy begins to decrease, and the robustness is poor. Although the noise ratio r is greater than 25%, the optimal clustering number of the two algorithms is not 6, the clustering effectiveness index and accuracy of the proposed method are slightly higher than the traditional FCM algorithm. Therefore, the robustness of the proposed method is better than the traditional FCM algorithm.
6 ConclusionIn this paper, a daily load curve reduction dimension clustering method based on grey wolf optimization and fuzzy mean clustering algorithm is proposed. Firstly, the load characteristic index is used to reduce the data of the original daily load curve data, and the proposed algorithm is used to perform the daily load curve reduction dimension clustering analysis. The example shows that this method can improve the global search ability of traditional FCM clustering algorithm and reduce the possibility that the clustering result falls into local optimum. It has engineering feasibility and good robustness.
With the continuous development of smart grids, the requirements for refined power grid planning and grid operation management are constantly improving. How to combine multi-source data fusion, select typical load characteristic index system, and establish a more refined clustering method is the future research direction.
| 1. |
Bofeng L, Yunfei M, Hongjie J, et al (2018) Decision method of power supply access for large consumers based on load feature library. Autom Electr Power Syst
42(6): 66-72. (  0) 0) |
| 2. |
Al-Otaibi R, Jin N, Wilcox T, et al (2017) Feature construction and calibration for clustering daily load curves from smart-meter data. IEEE Trans Industr Inform
12(2): 645-654. (  0) 0) |
| 3. |
Zigui J, Rongheng L, Fangchun Y, et al (2018) A fused load curve clustering algorithm based on wavelet transform. IEEE Trans Industr Inf
14(5): 1856-1865. DOI:10.1109/TII.2017.2769450 (  0) 0) |
| 4. |
Kong X, Hu Q, Dong X, Zeng Y, et al (2017) Load data identification and repair method based on improved fuzzy C-means clustering. Autom Electr Power Syst
41(09): 90-95. (  0) 0) |
| 5. |
Tzortzis L (2009) The global Kernel K-Means algorithm for clustering in feature space. IEEE Trans Neur Netw
20(7): 1181-1194. DOI:10.1109/TNN.2009.2019722 (  0) 0) |
| 6. |
Guilan W, Guoliang Z, Hongshan Z, et al (2016) Fast clustering and anomaly detection technique for large-scale power data stream. Autom Electr Power Syst
40(24): 27-33. (  0) 0) |
| 7. |
Kohonen T (1982) Self-organized formation of topologically correct feature maps. Biol Cybern
. (  0) 0) |
| 8. |
Xiaodi W, Junyong L, Youbo L, et al (2019) Typical load curve shape clustering algorithm using adaptive piecewise aggregation approximation. Autom Electr Power Syst
43(01): 110-121. (  0) 0) |
| 9. |
Phu VN, Dat ND, Ngoc Tran VT, et al (2017) Fuzzy C-means for english sentiment classification in a distributed system. Appl Intell
46(3): 717-738. DOI:10.1007/s10489-016-0858-z (  0) 0) |
| 10. |
Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw
69(3): 46-61. (  0) 0) |
| 11. |
Chicco G, Napoli R, Piglione F (2006) Comparisons among clustering techniques for electricity customer classification. IEEE Trans Power Syst
21(2): 933-940. (  0) 0) |
 2020 : 661-671 DOI: 10.1007/978-981-13-9783-7_54
2020 : 661-671 DOI: 10.1007/978-981-13-9783-7_54



