2. State Grid Hunan Electric Power Company Limited, 398 Xinshao East Road, Changsha 410004, Hunan, China
With the deepening of power market reform, the formulation of market risk prevention countermeasures become a vital research contents. PSC has become more complicated from the power purchase side or the power sales side. In recent years, researching on the purchase and sale of electricity risks of PSC has emerged in an endless stream. Reference [1] studied the risk of power purchase portfolio strategy of PSC earlier in China, and researched the mathematical model of power purchase in the spot market and contract market under the single purchase mode of PSC considering the load forecasting error. Reference [2] innovatively applied the value at risk (VaR) assessment method of the financial sector to the calculation of the risk combination strategy of the electricity market, and established a VaR-based optimal power purchase combination plan and a risk assessment model. Later, some scholars found that the CVaR theory can reflect the essential characteristics of risk better. Therefore, the CVaR theory was used to evaluate the risk of the power purchase market and make power purchase optimization decisions [3, 4].
Initially, the focus of research on risk decision-making is to study the risk of purchasing power side [1-5]. As the power market sales side gradually liberalizes, some papers consider both the power purchase side and sale side to study the purchase-sale risk decision and evaluation [6-8]. Reference [9] focused on the impact of peak-valley TOU electricity price on purchase-sale electricity income risks which evaluated by two indicators of yield and standard deviation, and analyzes the impact of TOU price on user load. In Ref. [10], the CVaR method was used to study the influence of peak-valley TOU price on power purchase combination strategy of PSC, but the impact of TOU price on users load was not considered. Generally speaking, the implementation of peak-valley TOU price will play the role of cutting peaks and filling valleys, and the peak load reduction or trough load increase under different electricity prices will be different. Therefore, this paper considers the impact of peak-valley TOU price on users load, and the price elasticity of electric energy demand is used to quantify the change of peak, flat and valley power consumption after the implementation of peak-valley TOU price. The objective function which based on the CVaR theory to assess the risk of the purchase and sale of electricity is established. The results show that an appropriate peak-valley TOU price policy can effectively reduce the income risk of the PSC.
2 The Trade Model 2.1 Power Consumption Under TOU Electricity Price PolicyIn power demand side, changes in prices will cause users to change their demand for electrical energy. Under usual conditions, the user's reaction to the price of electricity is that the higher the price of electricity, the lower the user's electricity consumption. However, when the price of electricity changes within a certain period of time, the user not only simply increases or decreases the amount of electricity used, but transfers the load to other time periods according to the schedule [11]. This article uses the more common formula called demand price elasticity to reflect the degree of response of demand changes to price changes. Electricity can be seen as a commodity in the electricity market, and its price elasticity for electricity demand is expressed as:
| $ {{e}_{ii}}=\frac{\partial {{Q}_{i}}/{{Q}_{i}}}{\partial {{\text{p}}_{i}}/{{p}_{i}}} $ | (1) |
| $ {{e}_{ij}}=\frac{\partial {{Q}_{i}}/{{Q}_{i}}}{\partial {{\text{p}}_{j}}/{{p}_{j}}} $ | (2) |
eii is the self-elastic coefficient which represents the electricity demand elasticity of the i-period for the current period, and eij is the cross-elastic coefficient which represents the electricity demand elasticity of the i-period for the j-period. ∂Qi and Qi represents relative increments of the electricity consumption and the electricity consumption in the i period, respectively. ∂pi and pi represent relative change in sales price and the sales price in i period, respectively. Thus, the price elasticity of the user at different time periods can be represented by the E matrix which is expressed as:
| $ {{\mathit{\boldsymbol{E}}}_{\left( ij \right)}}=\left[ \begin{matrix} {{e}_{11}} & {{e}_{12}} & \cdots & {{e}_{1j}} \\ {{e}_{21}} & {{e}_{22}} & \cdots & {{e}_{2j}} \\ \vdots & \vdots & {} & \vdots \\ {{e}_{i1}} & {{e}_{i2}} & \cdots & {{e}_{ij}} \\ \end{matrix} \right] $ | (3) |
Therefore, the relationship between the user's power consumption and the TOU price at different times is [12]:
| $ \left( \begin{matrix} {{q}_{1}} \\ {{q}_{2}} \\ {{q}_{i}} \\ \end{matrix} \right)=\left( \begin{matrix} q_{1}^{\left( 0 \right)} \\ q_{2}^{\left( 0 \right)} \\ q_{i}^{\left( 0 \right)} \\ \end{matrix} \right)+\left( \begin{matrix} q_{1}^{\left( 0 \right)} & 0 & 0 & 0 \\ 0 & q_{2}^{\left( 0 \right)} & 0 & 0 \\ \vdots & \vdots & {} & \vdots \\ 0 & 0 & \cdots & q_{i}^{\left( 0 \right)} \\ \end{matrix} \right){{\mathit{\boldsymbol{E}}}_{\left( ij \right)}}\left( \begin{matrix} \left( {{p}_{1}}-p_{1}^{\left( 0 \right)} \right)/p_{1}^{\left( 0 \right)} \\ \left( {{p}_{2}}-p_{2}^{\left( 0 \right)} \right)/p_{2}^{\left( 0 \right)} \\ \left( {{p}_{i}}-p_{i}^{\left( 0 \right)} \right)/p_{i}^{\left( 0 \right)} \\ \end{matrix} \right) $ | (4) |
In the formula, qi(0) and qi represent the load of the user in i-period before and after the implementation of the TOU electricity price, respectively. and pi(0) and pi represent the unit price of the power sold by the PSC before and after the implementation of the TOU price, respectively.
2.2 Revenue Estimation of the PSCBy learning from the electricity market trading mechanism in developed countries, the electricity purchase mode of the PSC is roughly as follows: PSC stipulates the price of electricity and settles electricity through long-term market contracts, and settles all electricity in the spot market, then balances the deviation between the current output and actual electricity demand in real-time trading market [13]. This article assumes that the trading market of a PSC is divided into three types: contract market (long-term market), spot market and real-time trading market. Assume that X = (x1, x2, x3)T is electricity purchase combination vector of the PSC, and xi(i = 1, 2, 3) are the electrical energy purchased in contract market, spot market and real-time market. S = (s1, s2, s3)T is the electricity purchase unit price vector, and μ = (μ1, μ2, μ3)T is the expected value of unit purchase price.
The selling price to the user is assumed to be p0, the peak, flat and valley electricity prices after the implementation of the peak-valley TOU price can be expressed as: p0(1 + γ), p0, p0(1 - γ).γ is the spread ratio, the user's purchase vector is P = ((1 + γ)p0, p0, (1 - γ)p0)T. Assume that Q = (qf, qp, qg)T is the power consumption combination vector of users on the demand side, qf, qp, qg indicate the power consumption of the user in the peak, flat, and valley segments, respectively. If λi(i = 1, 2, 3) represent the weights of electricity consumption in peak, flat and valley periods, the electricity sales vector Q can be expressed as (λ1Q, λ2Q, λ3Q)T. Q is the total amount of electricity.
The load will change correspondingly due to the user's response to the fluctuation of the electricity price. Then, the power load of the user in the peak, flat and valley periods can be obtained by the formula (4), as shown in (5).
| $ \mathit{\boldsymbol{Q}}=\left( \begin{matrix} {{q}_{f}} \\ {{q}_{p}} \\ {{q}_{g}} \\ \end{matrix} \right)=\left( \begin{matrix} q_{f}^{\left( 0 \right)} \\ q_{p}^{\left( 0 \right)} \\ q_{g}^{\left( 0 \right)} \\ \end{matrix} \right)+\left( \begin{matrix} q_{f}^{\left( 0 \right)} & 0 & 0 \\ 0 & q_{p}^{\left( 0 \right)} & 0 \\ 0 & 0 & q_{g}^{\left( 0 \right)} \\ \end{matrix} \right)\mathit{\boldsymbol{E}}\left( \begin{matrix} \left( {{p}_{1}}-p_{1}^{\left( 0 \right)} \right)/p_{1}^{\left( 0 \right)} \\ \left( {{p}_{2}}-p_{2}^{\left( 0 \right)} \right)/p_{2}^{\left( 0 \right)} \\ \left( {{p}_{3}}-p_{3}^{\left( 0 \right)} \right)/p_{3}^{\left( 0 \right)} \\ \end{matrix} \right) $ | (5) |
In the formula, qf(0), qp(0), qg(0) represent the electricity price during peak, flat, and valley periods before using the TOU electricity price. p1, p2, and p3 represent the electricity price during peak, flat, and valley periods after using the TOU power consumption, respectively. In summary, the revenue of PSC can be defined as:
| $ \mathit{\boldsymbol{R}}={{\mathit{\boldsymbol{Q}}}^{\text{T}}}\mathit{\boldsymbol{P}}-{{\mathit{\boldsymbol{X}}}^{\text{T}}}\mathit{\boldsymbol{S}} $ | (6) |
VaR and CVaR are two methods commonly used by the financial community to measure risk [14]. When x is the decision variable and y is the uncertainty variable, for a certain x, the distribution function of the loss function f (x, y) with respect to the critical value α is:
| $ \psi \left( x, \alpha \right)=\int\limits_{f\left( x, y \right)}{p\left( y \right)dy} $ | (7) |
β ∈ (0, 1) is the confidence level, then the value of α at the confidence level β is defined as:
| $ {{\alpha }_{\beta }}=\min \left\{ \alpha \in R;\psi \left( x, \alpha \right)\ge \beta \right\} $ | (8) |
CVaR is the conditional expectation of loss greater than α. Since the value of CVaR is difficult to obtain directly, it is generally simulated the sample data by Monte Carlo method, then the approximation of CVaR is generally expressed as:
| $ \begin{align} \begin{array} [c]{c} & F{{\left( x, \alpha \right)}_{\text{CVaR}\text{. }{\rm{ \mathsf{ β} }}\text{ }}}=\alpha +\frac{1}{m\left( 1-\beta \right)}\sum\limits_{k=1}^{m}{{{\left[ {{f}_{k}}\left( x, y \right)-\alpha \right]}^{+}}} \\ & {{\left[ {{f}_{k}}\left( x, y \right)-\alpha \right]}^{+}}=\max \left( 0, {{f}_{k}}\left( x, y \right)-\alpha \right) \\ \end{array} \end{align} $ | (9) |
fk(x, y) is the loss function, x is the decision variable, and y is the uncertainty factor. Assume Zk = [fk(x, y)-α]+, i.e. Zk ≥[fk(x, y)- α≥ and Zk ≥ 0, F(x, α)CVaR.β can be defined as:
| $ F{{\left( x, \alpha \right)}_{\text{CVaR}\text{. }{\rm{ \mathsf{ β} }}\text{ }}}=\alpha +\frac{1}{m\left( 1-\beta \right)}\sum\limits_{k=1}^{m}{{{Z}_{k}}} $ | (10) |
This article uses CVaR method to measure the profit risk of the sales company in the trading market, and defines the risk loss function of the sales company as:
| $ f\left( x, y \right)=\left[ E\left( R \right)-R \right]={{\mathit{\boldsymbol{Q}}}^{\text{T}}}\left( {{\mathit{\boldsymbol{P}}}_{0}}-\mathit{\boldsymbol{P}} \right)+{{\mathit{\boldsymbol{X}}}^{T}}\left( \mathit{\boldsymbol{S}}- \mathit{\boldsymbol{\mu}} \right) $ | (11) |
E(R) is the expected value of R, and E(R) = QTP0- XTμ, P0 = (p0, p0, p0)T. The objective function thus established is as follows:
| $ \begin{align} & \min F{{\left( x, \alpha \right)}_{CVaR.\beta }}=\alpha +\frac{1}{m\left( 1-\beta \right)}\sum\limits_{k=1}^{m}{{{Z}_{k}}} \\ & s.t.\ \ \ \ \ \ \sum\limits_{i=1}^{3}{{{x}_{i}}\text{=}Q} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{i=1}^{3}{{{\lambda }_{i}}\text{=}1}\ \ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}_{i}}\ge 0\ \ \ \ \left( i=1, 2, 3 \right) \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{z}_{k}}\ge 0\ \ \ \ \left( k=1, 2, \cdots m \right) \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{z}_{k}}\ge {{\mathit{\boldsymbol{Q}}}^{\text{T}}}\left( {{\mathit{\boldsymbol{P}}}_{0}}-\mathit{\boldsymbol{P}} \right)+{{\mathit{\boldsymbol{X}}}^{T}}\left( \mathit{\boldsymbol{S}}- \mathit{\boldsymbol{\mu}}\text{ } \right)-\alpha \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{X}}}^{\rm T}} \mathit{\boldsymbol{\mu}}\le M \\ \end{align} $ | (12) |
x is the electricity purchased by the electricity company, y is the uncertainty of the electricity price fluctuation on the electricity purchase side and the TOU price on the electricity sales side.
4 Case StudyAssuming that the electricity prices of the three electricity purchase markets are subject to a normal distribution, this paper uses the Monte Carlo simulation method to generate 200 sets of electricity prices, and the electricity price parameters are imputed through the forecasted date given by the literature [15], as shown in Table 1.
| Table 1 Price expectation and variance for three markets |
Assuming that the electricity sold by PSC is a constant value, for the convenience of calculation, set up Q = 1, then xi(i = 1, 2, 3) respectively represent the power purchase weights of the three markets. Assume that the upper limit of the cost of purchasing electricity M = 38 $/MW · h, Then calculate the revenue risk loss of PSC in the following different cases.
Case 1: Before implementing the peak-valley TOU price policy.
The optimal combination of purchasing and selling electricity prices by solving the linear programming function formula (10) is shown in the following Table 2.
| Table 2 Optimal portfolio of purchased power at different confidence levels |
When the PSC does not consider the peak-valley TOU price policy, It can be seen in Table 2 that VaR and CVaR increases correspondingly with the increase of the β, and When β = 95%, CVaR is significantly larger than VaR. PSC will increase its purchases in the long-term market to avoid risks when its risk increases, while reducing the purchase of electricity in uncertain spot and real-time markets, this also verifies the rationality of this method.
Case 2: After implementing the peak-valley TOU price policy.
According to common sense, the greater the electricity price difference ratio, the greater the absolute value of the user's demand price elasticity, and the corresponding peak-filling effect is more obvious. For the values of the elastic coefficients corresponding to different γ, this paper refers to the data of paper [12] and makes appropriate adjustments, as shown in Table 3.
| Table 3 Elastic coefficient values under different γ |
In this case, β = 0.95 and λ0 = (0.4, 0.35, 0.25)T. The weights of power purchase and sale of the PSC can be calculated according to formulas (5) and (12), compare the calculation results in the above five situations, as shown in Table 4.
| Table 4 Optimal portfolio of electricity and VaR and CVaR in different situations |
Comparing the values of VaR and CVaR in Tables 2 and 4 at the same confidence level, it can be seen that after the peak-valley TOU price, when γ is 0.2 and 0.3, VaR and CVaR are higher than before at the same confidence level, but when γ exceeds 0.4, the result is just the opposite. The results can be explained as follows: when γ is small, the peak-clipping and valley-filling effect of TOU electricity price is not obvious enough, on the contrary, the risk of loss of PSC is increased due to the change of demand-side electricity price. However, with the increase of γ, the user's price elasticity of electric energy demand and the degree of response to "Peak clipping and valley filling" increase, thus the PSC's risk of loss of is reduced, and greater profits are obtained.
As can be seen from the relationship between γ and VaR and CVaR in Fig. 1, when the electricity price difference ratio increases. VaR and CVaR are reduced, that is, the smaller the risk that the sales company bears, and the smaller the minimum expected return that can be achieved. Therefore, PSC can reduce the risk of loss of purchase and sale of electricity transactions by formulating appropriate peak-valley TOU tariff policies.
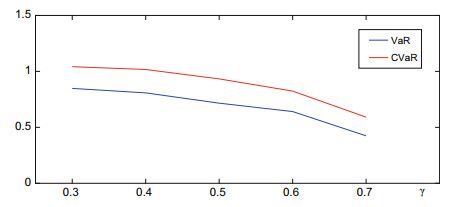
|
Fig.1 The relationship of γ and VaR, CVaR |
In Fig. 2, as the γ increases, λ1 decline, and λ2 basically remains the same, while λ3 increases, which indicates that when the electricity price difference ratio increases, the user will prevent the increase in the cost of purchasing electricity by reducing the peak-purchase while increasing the valley-purchase, moreover, the degree of user response to the TOU price policy is positively correlated with γ.
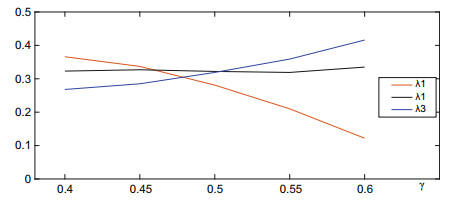
|
Fig.2 The relationship γ and λ |
But it should be noted that although the results of the example can be seen that the risk loss of PSC's income decreases with the increase of the price spread ratio, the formulation of the electricity price policy needs to consider multiple factors in practice, The maximum profit of users is not taken into account in this paper, so the conclusions of this paper are for reference only. And what value does γ take for the best return of PSC and user at the same time is a question worthy of further study.
5 ConclusionsThis paper establishes a risk loss decision model based on the volatility of the electricity price on the power purchase side, the impact of the implementation of the peak-valley TOU price on the user load, and the impact of the TOU price spread ratio on the PSC purchase and sale risk loss. Finally, the validity of the model is illustrated by the case studies, and the conclusions can be drawn as follows:
(1) The CVaR-based risk assessment model established in this paper can be used as a method to measure the risk of power trading, and it will be a good reference for PSC's decision-making on power procurement and sales.
(2) The use of peak-valley TOU price policy can help PSC reduce its risk of purchasing and selling electricity, thereby increasing its sales revenue.
(3) Introducing the E matrix, which represents the price elasticity of user demand, can better analyze the impact of the implementation of TOU electricity price on PSC and accurately quantify the "Peak clipping and valley filling" effect of users.
(4) PSC can appropriately increase the value of price spread ratio γ to reduce the risk loss because the increase of γ will reduce the risk loss and conditional risk loss. But blindly increasing the value of γ to get smaller losses will not be realistic, PSC must also consider the interests of users and other constraints.
| 1. |
Wang J (2005) Analysis of power purchase risk model in electricity market. Power Grid Technol
9: 46-49. (  0) 0) |
| 2. |
Zhou M, Nie Y, Li G, Ni Y (2006) Long-term power purchase plan and risk assessment in power market. Proc CSEE
6: 116-122. (  0) 0) |
| 3. |
Zhang Q, Wang X, Wang J (2010) Risk decision of power suppliers purchasing and selling electricity under real-time electricity price on demand side. Autom Electr Power Syst
34(03): 22-27+ 43. (  0) 0) |
| 4. |
Huang H, Yan Z, Hou Y (2008) A novel CVaR based portfolio optimization model for LDC electricity procurement. IEEE Trans
12-15(2008). (  0) 0) |
| 5. |
Zhang J, Xia Y, Duan D, Zhang Z, Li W, Liu J (2017) Energy market benefits of virtual power plant based on WCVaR evaluation-risk model. Autom Electr Power Syst
41(09): 77-83. (  0) 0) |
| 6. |
Wang L, Zhang G, Zhang F, Jin D (2018) Decision-making and risk assessment of electricity sales and purchase of electricity sales companies. Autom Electr Power Syst
42(01): 47-54+143. (  0) 0) |
| 7. |
Meng Yang, Xin Ai, Liang Tang, Shuai Guo, Gengyu Luo (2016) Research on balanced market optimization trading strategy of power distribution companies considering risk avoidance. Power System Technol
40(11): 3300-3309. (  0) 0) |
| 8. |
Luo S, Jiang C, Xu W, Yang M, Wang J, Yin S (2019) The power purchase strategy and risk assessment of power sales companies under the background of new electricity reform. Power System Technol
43(03): 944-953. (  0) 0) |
| 9. |
Song Y, Tan Z, Yu C, Jiang H (2010) Analysis model of influence of demand-side peak-to-valley time-sharing electricity price on power supply company's purchase and sale risk. Trans China Electrotech Soc
25(11): 183-190. (  0) 0) |
| 10. |
Zhu W, Xie P (2015) Analysis of the influence of peak-to-valley time-of-use electricity price based on CVaR on power supply company's power purchase combination strategy. Power Syst Prot Control
43(14): 16-21. (  0) 0) |
| 11. |
Yao J, Fu Q, Ye L, Peng Z, Hanyu Yang, Yang H (2017) Substation capacity planning method considering the influence of peak and valley time-sharing electricity price. Autom Electr Power Syst
41(13): 53-61. (  0) 0) |
| 12. |
Tan Z, Hou J, Wang C, Cao F, Wang M, Guan Y (2007) The risk control model of power supply enterprises' purchase and sale under the time-of-use price system. Power Grid Technol
8: 17-21+26. (  0) 0) |
| 13. |
Zhou M, Yan Y, Ding Q, Wu Z, He Y, Long S (2017) Transaction and settlement mechanism of typical foreign electricity market and its enlightenment to China. Autom Electr Power Syst
41(20): 1-8+ 150. (  0) 0) |
| 14. |
Wang G, Luo J (2019) Financing strategy of risk aversion supplier based on CVaR criterion. Ind Eng Manag
, 1-17. (  0) 0) |
| 15. |
Woo CK, Horowitz I, Olson A, Horii B, Baskette C (2006) Efficient frontiers for electricity procurement by an LDC with multiple purchase options. Omega
34(1): 70-80. DOI:10.1016/j.omega.2004.07.022 (  0) 0) |
 2020 : 907-916 DOI: 10.1007/978-981-13-9779-0_74
2020 : 907-916 DOI: 10.1007/978-981-13-9779-0_74



