文章编号: 2096-3203(2024)05-0122-09 中图分类号: TM732
随着“双碳”进程推进,风电、光伏等出力波动性较大的电力电子化微源在电力系统中的比重逐渐增加,致使电力系统惯量特性下降,系统频率失稳[1-4]。火电机组难以满足系统调频需求,而储能具有快速、精准响应的优势,可以用于辅助系统调频,二者相结合,可有效提高系统调频能力[5-9]。
针对新能源场站并网一次调频能力改造,以锂电池为代表的电化学储能应用最为广泛。文献[10]提出一种提升电网频率暂态稳定性的储能容量配置方法。文献[11]从风电场自身的一次调频能力出发,提出风储联合调频中储能的容量优化配置,可降低系统一次调频总成本。但锂电池属于能量型储能,随着放电倍率增加,寿命和可靠性将显著降低[12-15]。飞轮储能在放电深度以及使用寿命方面远远优于电池储能。文献[16-17]提出飞轮储能参与电网一次调频协调控制策略与容量优化配置方法,能够有效改善机组调频性能且运行经济性良好。提供电网频率调节辅助服务的储能系统的理想特性是高功率密度、高能量密度、低成本和更长的循环寿命[18]。文献[19]分析对比单一储能与混合储能的容量配置结果,得到混合储能系统比单一储能系统更经济的结论。文献[20]研究表明飞轮能够缓解电池储能在电网频率调节中加速老化的问题。因此,在一次调频方面,飞轮和锂电池相配合具有提高经济性及延长电池寿命的发展潜力。
正虚拟惯性、负虚拟惯性以及虚拟下垂控制是储能一次调频的典型控制方式。文献[21]考虑正虚拟惯性控制与虚拟下垂控制相互配合,未考虑负虚拟惯性控制,频率恢复较慢。文献[22-23]均采用正、负虚拟惯性控制及虚拟下垂控制相互组合的方法,实现系统一次调频,但未引入各控制方法的调节权重因子,不利于充分发挥各控制方法的优势。
国内外已有大量文献对储能电池荷电状态(state of charge, SOC)的限制与变化进行研究。在一次调频过程中,考虑储能SOC快速变化,避免储能过充过放,可以提高循环寿命和经济性。文献[24]基于S型函数根据储能设备的SOC对传统调频控制策略进行改进,提高储能设备的调频能力。文献[25]以SOC为约束控制飞轮的充放电功率,对传统调频控制策略进行改进,有利于提高飞轮储能容量的持续性。
但上述文献均只针对单一储能,无法直接应用于混合储能,充分利用各储能的优势。针对混合储能,文献[26]基于Logistic函数,建立混合储能SOC与下垂系数的关系,可避免储能过充过放。文献[27]考虑不同种类电池在混合储能系统中的协同运作,设计一种基于蓄电池SOC的改进电压下垂法,但未考虑飞轮SOC的影响,电池与飞轮配合不紧密。
目前关于混合储能的一次调频策略大多缺少正、负虚拟惯性及虚拟下垂控制策略的权重因子考虑,在调频过程中各单一控制策略出力没有侧重,不利于充分发挥三者的调频优势。且仅考虑2种不同类型储能的简单组合,未充分利用不同储能特性从而发挥混合储能调频优势。
因此,文中针对电池-飞轮混合储能,首先根据频率变化建立含正、负虚拟惯性控制和虚拟下垂控制的权重分配一次调频模型。其次为使飞轮和锂电池相互配合,发挥各自调频优势,提高混合储能在SOC阈值附近的充放电调频能力,提出双馈飞轮和锂电池根据实时SOC变化的自适应调频方法。最后仿真对比文中控制策略与其他控制策略的调频能力,验证了在各调频场景下文中控制策略的有效性。
1 混合储能一次调频综合控制策略为充分发挥虚拟下垂控制和虚拟惯性控制各自的优势,文献[28]提出二者出力比重随频率变化而调节的综合控制方法,在相同储能出力下,减小电网频率波动。但是虚拟下垂控制和虚拟惯性控制的配合,在频率开始恢复时,会阻止频率的恢复,最终造成系统频率二次跌落[29]。而负虚拟惯性控制可以在频率恢复时提高频率恢复速率,充分发挥储能调频的积极作用。
文中建立含负虚拟惯性控制的权重分配一次调频模型,得到混合储能一次调频总出力ΔPH,虚拟惯性控制出力ΔPMH,虚拟下垂控制出力ΔPKH。
考虑电池和飞轮SOC快速变化对混合储能寿命及经济性的影响,以现有的电池储能的SOC变系数一次调频控制为基础,以电池-飞轮的SOC对虚拟惯性控制系数Mb、虚拟下垂控制系数Kb 进行修正,最终提出完整的基于自适应SOC的电池-飞轮混合储能一次调频控制策略。
1.1 调频策略权重分配文中提出的综合调频策略包含虚拟下垂控制和正、负虚拟惯性控制,其在不同场景下具有不同的权重分配。在频率跌落时,正虚拟惯性控制和负虚拟惯性控制不能同时存在,当dΔf/dt<0时(Δf为频率变化量),采用正虚拟惯性控制;当dΔf/dt>0时,采用负虚拟惯性控制。
按式(1)对各基本调频策略进行权重分配。其中,α1为虚拟惯性控制的权重系数,α2为虚拟下垂控制的权重系数,α1+α2=1。
| $ \Delta P_{\mathrm{H}}=-\alpha_1 \Delta P_{\mathrm{MH}}-\alpha_2 \Delta P_{\mathrm{KH}} $ | (1) |
其中:
| $ \Delta P_{\mathrm{MH}}= \begin{cases}M_{\mathrm{b}} \mathrm{d} \Delta f / \mathrm{d} t & (\mathrm{~d} \Delta f / \mathrm{d} t) \cdot \Delta f>0 \\ -M_{\mathrm{b}} \mathrm{d} \Delta f / \mathrm{d} t & (\mathrm{~d} \Delta f / \mathrm{d} t) \cdot \Delta f<0\end{cases} $ | (2) |
| $ \Delta P_{\mathrm{KH}}=K_{\mathrm{b}} \Delta f $ | (3) |
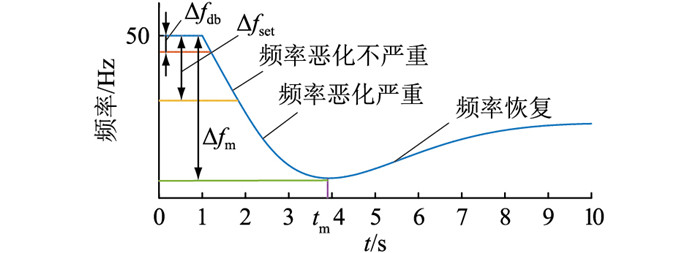
图 1为负荷突增时频率变化曲线。其中,Δfdb为死区阈值;Δfset为区分以虚拟下垂控制为主或以虚拟惯性控制为主的额定频率偏差界限,考虑频率不应超过0.3 Hz,故取Δfset =0.2 Hz;tm为频率最低时所对应的时刻;Δfm为最低频率与额定频率的偏差值。
|
图 1 负荷突增时频率变化曲线 Fig. 1 Frequency change curve during load surge |
(1) 频率恶化阶段,(dΔf/dt) ·Δf >0。
频率恶化不严重,|Δfdb|<|Δf| ≤ |Δfset|时,令α1≥α2,且随时间推移,|Δf|增大,α1减小,α2增大,即虚拟惯性出力为主但出力比重逐渐减小,虚拟下垂出力比重逐渐增大。表达式如下:
| $ \left\{\begin{array}{l} \alpha_1=\mathrm{e}^{-10|\Delta f|} \\ \alpha_2=1-\mathrm{e}^{-10|\Delta f|} \end{array}\right. $ | (4) |
频率恶化严重,|Δfset|<|Δf| ≤ |Δfm|时,令α2≥α1,且随时间推移,|Δf|继续增大,α1继续减小,α2继续增大,即虚拟下垂出力为主且出力比重逐渐增大,虚拟惯性出力持续减小。表达式如下:
| $ \left\{\begin{array}{l} \alpha_1=\frac{1}{1+\mathrm{e}^{5\;000|\Delta f|}} \\ \alpha_2=1-\frac{1}{1+\mathrm{e}^{5\;000|\Delta f|}} \end{array}\right. $ | (5) |
(2) 频率上升阶段,(dΔf/dt) ·Δf < 0。
令α2≥α1,且随时间推移,|Δf|减小,α1减小,α2增大,以虚拟下垂出力为主,负虚拟惯性出力为辅。表达式如下:
| $ \left\{\begin{array}{l} \alpha_1=-\frac{1}{1+\mathrm{e}^{1\;000|\Delta f|}} \\ \alpha_2=1+\frac{1}{1+\mathrm{e}^{1\;000|\Delta f|}} \end{array}\right. $ | (6) |
由于混合储能SOC在长时间扰动中易快速殆尽或饱和,文中提出电池-飞轮混合储能的基于SOC的变系数调频方法。设计虚拟下垂控制系数Kb受储能SOC实时控制,且虚拟惯性控制系数Mb与虚拟下垂控制系数Kb成一定比例对电网频率进行调节。
| $ \left\{\begin{array}{l} K_{\mathrm{b}}=K_{\mathrm{d}} \\ M_{\mathrm{b}}=\lambda K_{\mathrm{b}} \end{array} \quad \Delta f \leqslant-\Delta f_{\mathrm{db}}\right. $ | (7) |
| $ \left\{\begin{array}{l} K_{\mathrm{b}}=K_{\mathrm{c}} \\ M_{\mathrm{b}}=\lambda K_{\mathrm{b}} \end{array} \quad \Delta f>\Delta f_{\mathrm{db}}\right. $ | (8) |
式中:Kc、Kd分别为储能系统充电、放电时虚拟下垂系数;λ为比例系数,取λ=0.5。
设定SOC阈值Smax、Shigh、Slow、Smin,将储能电池SOC分为5个区间,Smax、Shigh、Slow、Smin的选取不唯一,不同电池取值不同,取决于电池自身特性[18]。为定量分析SOC恶化时混合储能各自的出力问题,文中设定锂电池的SOC阈值为SB, min=0.2,SB, max=0.8,SB, low=0.4,SB, high=0.6;飞轮储能的SOC阈值为SF, min=0.1,SF, max=0.9, SF, low=0.3,SF, high =0.7。
以储能系统放电为例,设储能系统SOC值为S:S < Smin时,为防止过放,应设置储能系统出力为0,即虚拟下垂系数为0;Smin≤S≤Shigh时,虚拟下垂系数应随SOC的增大而增大,储能系统出力增加;S>Shigh时,可增加储能系统出力,适度增大虚拟下垂系数,使SOC尽快处于[Slow,Shigh]。Logistic函数符合对SOC控制的需求,初始阶段大致呈指数增长,后逐渐饱和,最终稳定在某一值。故文中基于Logistic函数设计充、放电虚拟下垂系数,见式(9)、式(10)。其中,取最大下垂系数Kmax=40, 调整系数β=0.2,根据储能系统的功率容量配置进行适当调整。
| $ \begin{gathered} K_{\mathrm{c}}= \\ \left\{\begin{aligned} & (1+\beta) K_{\max } \quad 0 \leqslant S \leqslant S_{\min } \\ & \frac{(1+\beta) K_{\max }^2 \mathrm{e}^{\frac{n\left(S_{\mathrm{low}}-S\right)}{0.1}}}{(1+\beta) K_{\max }+K_{\max }\left(\mathrm{e}^{\frac{n\left(S_{\mathrm{low}}-S\right)}{0.1}}-1\right)} \quad S_{\min }<S \leqslant S_{\text {low }} \\ & K_{\text {max }} \quad S_{\text {low }}<S \leqslant S_{\text {high }} \\ & \frac{0.01 K_{\max } \mathrm{e}^{\frac{n\left(S_{\max }-S\right)}{0.1}}}{K_{\max }+0.01\left(\mathrm{e}^{\frac{n\left(S_{\max }-S\right)}{0.1}}-1\right)} \quad S_{\text {high }}<S \leqslant S_{\max } \\ & 0 \quad S_{\max }<S \leqslant 1 \end{aligned}\right. \end{gathered} $ | (9) |
| $ \begin{gathered} K_{\mathrm{d}}= \\ \left\{\begin{aligned} & 0 \quad 0 \leqslant S \leqslant S_{\min } \\ & \frac{0.01 K_{\max } \mathrm{e}^{\frac{n\left(S-S_{\min }\right)}{0.1}}}{K_{\max }+0.01\left(\mathrm{e}^{\frac{n\left(S-S_{\min }\right)}{0.1}}-1\right)} \quad S_{\min }<S \leqslant S_{\text {low }} \\ & K_{\text {max }} \quad S_{\text {low }}<S \leqslant S_{\text {high }} \\ & \frac{(1+\beta) K_{\max }^2 e^{\frac{n\left(S-S_{\text {high }}\right)}{01}}}{(1+\beta) K_{\max }+K_{\max }\left(\mathrm{e}^{\frac{n\left(S-S_{\text {high }}\right)}{0.1}}-1\right)} \quad S_{\text {high }}<S \leqslant S_{\max } \\ & (1+\beta) K_{\max } \quad S_{\max }<S \leqslant 1 \end{aligned}\right. \end{gathered} $ | (10) |
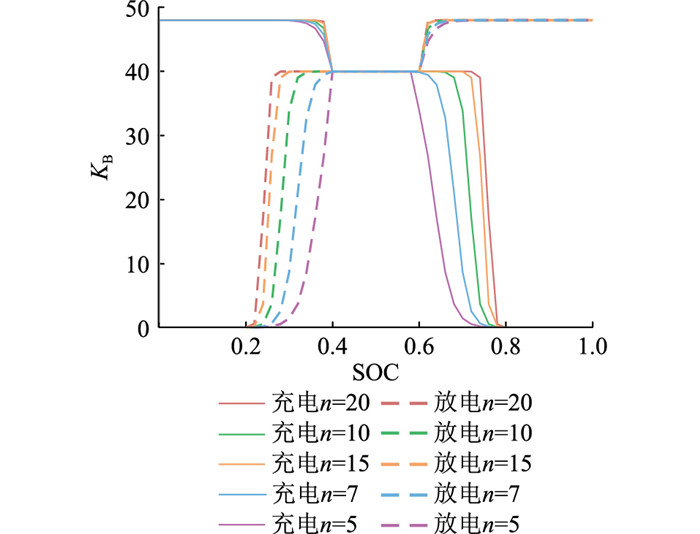
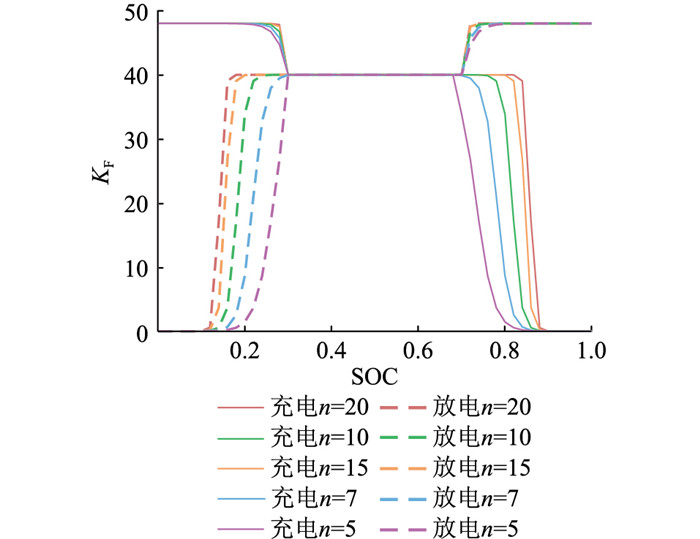
式中:n为曲线的自适应因子,通过实验确定合适的取值。取不同n值根据式(9)、式(10)分别得到锂电池虚拟下垂系数KB与飞轮虚拟下垂系数KF关于SOC的曲线, 如图 2、图 3所示。
|
图 2 电池虚拟下垂系数KB关于SOC的曲线 Fig. 2 Curves of battery sag coefficient KB with respect to SOC |
|
图 3 飞轮虚拟下垂系数KF关于SOC的曲线 Fig. 3 Curves of flywheel sag coefficient KF with respect to SOC |
n=7时,在[SB, min,SB, low]、[SB, high, SB, max]中,下垂系数随SOC变化较为明显,当电池的荷电状态SB =0.32时,KB=Kmax/2,故综合考虑,选择n=7。
同理,n=7时,在[SF, min,SF, low],[SF, high,SF, max]中,下垂系数随SOC变化较为明显,当飞轮的荷电状态SF=0.22时,KF=Kmax/2,综合考虑,选择n=7。
2 仿真分析 2.1 混合储能一次调频频率响应系统模型混合储能系统一次调频功率分配原则一般为:低频功率成分(0.01~0.1 Hz)由能量型储能电池平抑,高频功率成分(超过0.1 Hz)由功率型储能飞轮吸收。
采取上述功率分配原则,基于MATLAB/Simulink仿真平台,在阶跃扰动、连续秒级扰动以及24 h等效负荷扰动下,仿真对比不同综合调频策略下电网频率波动以及储能系统SOC情况,以验证文中所提方案,即方案Ⅲ的调频能力以及SOC维持效果。
方案Ⅰ:含虚拟下垂控制与虚拟惯性控制,且二者权重一致,均为0.5,不考虑SOC影响;
方案Ⅱ:含虚拟下垂控制与正、负虚拟惯性控制,采取文中权重分配策略,不考虑SOC影响;
方案Ⅲ:含虚拟下垂控制与正、负虚拟惯性控制,采取文中权重分配策略,考虑SOC影响。
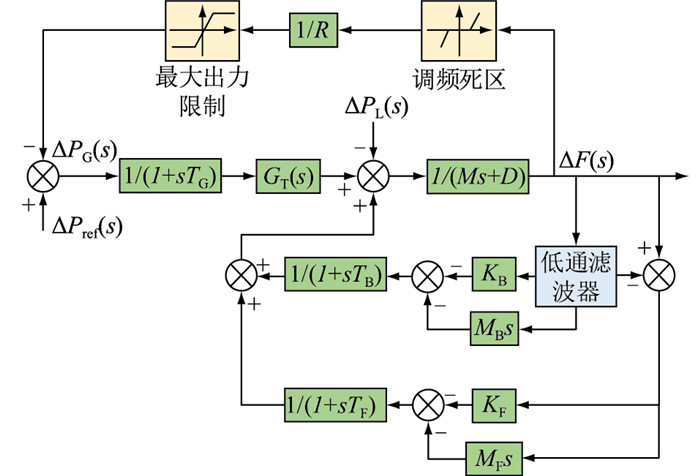
混合储能一次调频频率响应模型如图 4所示,仿真系统参数见表 1。系统频率波动时,由电池-飞轮混合储能系统配合传统火电机组进行一次调频。其中,MB、MF分别为电池、飞轮的虚拟惯性系数;GT(s)为火电机组调频传递函数模型;ΔPref (s)为发电机设定发电指令,当发电机仅参与电网一次调频时,功率设定值为0;ΔPG (s)为发电机出力;ΔPL (s)为负荷调整功率;R为火电机组下垂系数;TG为液压放大器的时间常数;M为发电机转子转动惯量;D为负载阻尼系数;TF为飞轮储能时间常数;TB为锂电池储能时间常数;ΔF(s)为一次调频响应量。
|
图 4 一次调频频率响应模型 Fig. 4 Frequency response model of primary frequency modulation |
|
|
表 1 仿真系统参数 Table 1 Parameters of simulation system |
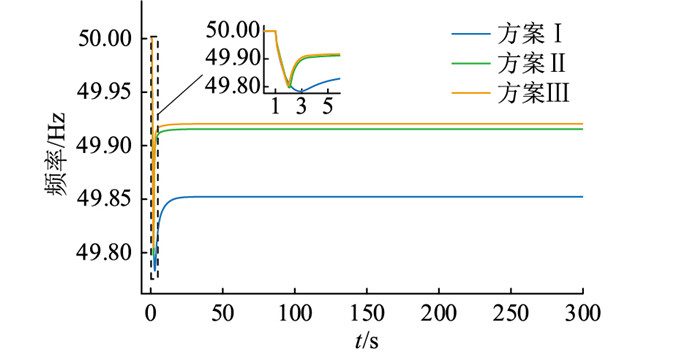
电网实际运行过程中,会因为负荷突增或者风光出力突然减小导致系统频率阶跃扰动。为验证阶跃扰动下,文中所提一次调频策略的调频效果,在仿真模型中投入幅值为0.1 p.u.的阶跃负荷扰动,此工况下频率、SOC波形如图 5、图 6所示。
|
图 5 阶跃扰动系统频率 Fig. 5 Step disturbance system frequency |
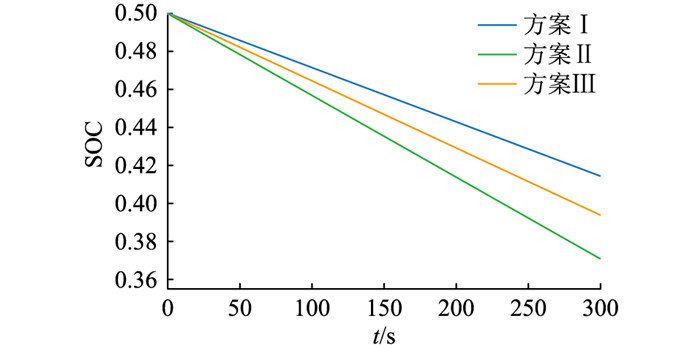
|
图 6 阶跃扰动电池SOC Fig. 6 Step disturbance battery SOC |
针对阶跃扰动工况,选取最大频率偏差Δfm、频率恶化速度Δ|fm/tm|、最终频率偏差Δfend及300 s长时充放电后SOC偏差ΔQSOC作为控制策略的评价指标[30]。
| $ \Delta Q_{\mathrm{SOC}}=Q_{\text {soc-end }}-Q_{\text {soc-start }} $ | (11) |
式中:Qsoc-end为300 s时SOC值;Qsoc-start为0 s时SOC值。
表 2为不同方案在阶跃扰动下的频率评价指标对比,可见,方案Ⅲ的Δfm相较方案Ⅰ减小10.1%,相较方案Ⅱ减小3.9%;方案Ⅲ的Δfend相较方案Ⅰ减小45.9%,相较方案Ⅱ减小5.9%。可得,文中所提控制策略能够有效减小最大频率偏差和最终频率偏差。
|
|
表 2 不同方案阶跃扰动频率评价指标 Table 2 Evaluation index of step disturbance frequency of different schemes |
结合图 5可知,在混合储能相同出力情况下,方案Ⅲ调频效果最好,频率偏差最小。由图 6可见,方案Ⅱ和方案Ⅲ的SOC下降更多,更加积极地参与了系统频率调节,且方案Ⅲ的ΔQSOC为0.107,相较方案Ⅱ减小17.1%,SOC维持效果较好。故在SOC处于正常区间的前提下,自适应SOC的控制策略能够在相同出力下,更好地维持系统的频率稳定。
2.3 连续秒级扰动由于造成发电机组进行一次调频的频率波动一般是由连续无规律的小幅度负荷快速波动引起的,因此,须进一步在连续扰动情况下分析文中所提一次调频策略的调频效果。
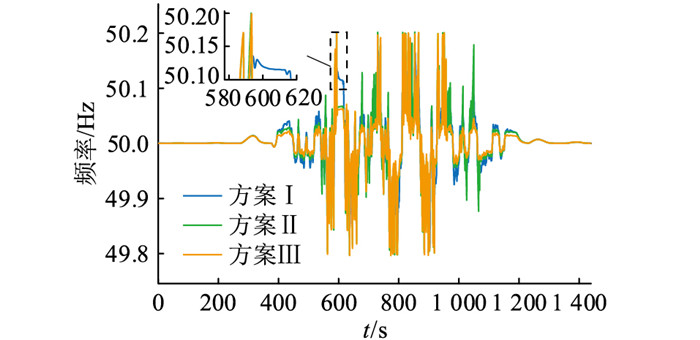
设置扰动范围在±0.1 p.u.之间、扰动持续时长1 440 s、频繁扰动集中于400~1 200 s的连续秒级扰动,此工况下频率、SOC波形如图 7、图 8所示。
|
图 7 连续秒级扰动系统频率 Fig. 7 Continuous second-order disturbance system frequency |
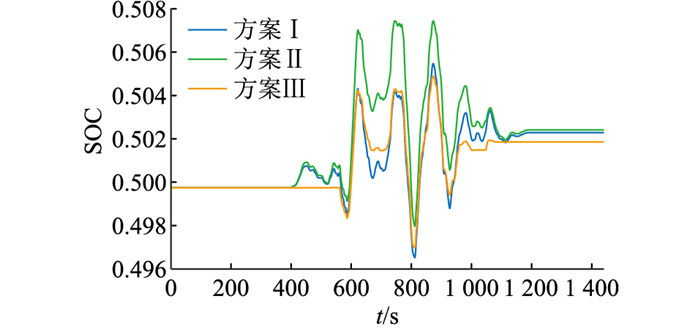
|
图 8 连续秒级扰动电池SOC Fig. 8 Continuous second-order disturbance battery SOC |
针对连续负荷扰动,选取频率偏差的均方根值Δfrms和SOC偏差的均方根值ΔSrms作为评价指标[31]。
| $ \Delta f_{\mathrm{rms}}=\sqrt{\frac{1}{N} \sum\limits_{j=1}^N \Delta f_j^2} $ | (12) |
| $ \Delta S_{\mathrm{rms}}=\sqrt{\frac{1}{N} \sum\limits_{j=1}^N\left(S_j-S_{\mathrm{tr}}\right)^2} $ | (13) |
式中:Δfj为采样点j的频率偏差;Sj为采样点j的SOC值;Str为SOC理想值,取0.5;N为采样点个数。
表 3为不同方案在连续秒级扰动下的频率评价指标对比,可见,方案Ⅲ的Δfrms相较方案Ⅰ减小12.3%,相较方案Ⅱ减小11.5%,在连续秒级扰动下,方案Ⅲ使得电网频率波动最小;方案Ⅲ的ΔSrms相较方案Ⅰ减小9%,相较方案Ⅱ减小35.5%,方案Ⅲ的SOC维持效果最好且储能SOC值最接近储能SOC理想值。
|
|
表 3 不同方案连续秒级扰动频率评价指标 Table 3 Evaluation index of continuous second-order disturbance frequency of different schemes |
结合图 7、图 8可知,在连续秒级扰动下,方案Ⅲ相较其他方案频率波动最小,调频效果最好,减少了储能系统SOC偏低或偏高时储能充放电调频能力降低的情况,SOC恢复效果最好。
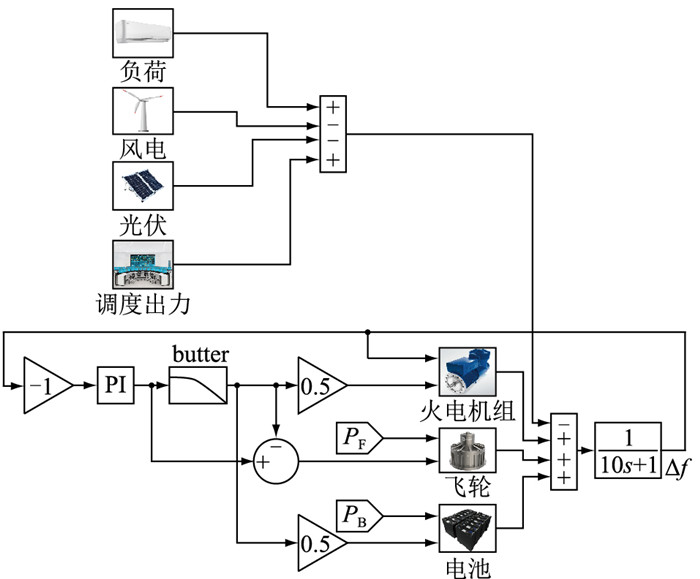
2.4 24 h等效负荷扰动为验证文中所提一次调频策略在长时间尺度的实际工况下的调频效果,建立图 9所示仿真模型。
|
图 9 地区频率波动控制分析仿真模型 Fig. 9 Simulation model of regional frequency fluctuation control analysis |
图 9中,风电机组额定容量为40 MW,光伏发电额定容量为200 MW, PI为比例积分调节模块,butter为滤波模块。PB, PF分别为电池储能和飞轮储能参与二次调频的功率指令,若不计二次调频,则为0。
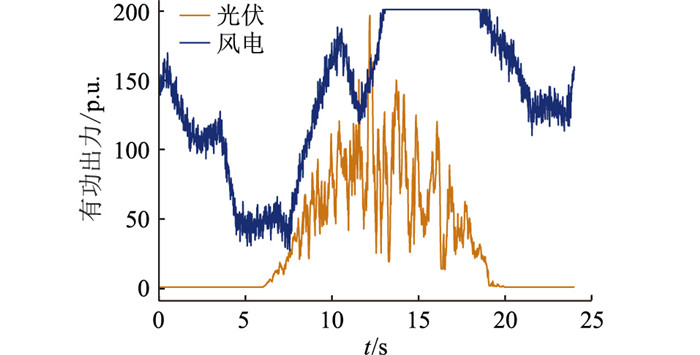
利用Meteonorm软件选取新疆某地的太阳辐射量数据、气温数据、风速数据,根据典型年历史气象数据计算出光伏、风机输出功率,用以模拟光伏发电系统和风机发电系统的出力。风光出力曲线如图 10所示。
|
图 10 风光出力曲线 Fig. 10 Wind-solar output curves |
风光接入电网后向电网输出功率。为了便于分析电网有功功率平衡关系,可以将风电和光伏功率等效为“负”的负荷,通过负荷功率与风电光伏功率作差得到系统的等效负荷功率。
| $ \Delta P_{\mathrm{E}}=P_{\mathrm{L}}-P_{\mathrm{W}}-P_{\mathrm{S}}-P_{\text {plan }} $ | (14) |
式中:ΔPE为含有风电和光伏的系统等效负荷功率;PL为全网负荷功率;PW为风电出力;PS为光伏出力;Pplan为根据日前数据预测的调度计划出力。
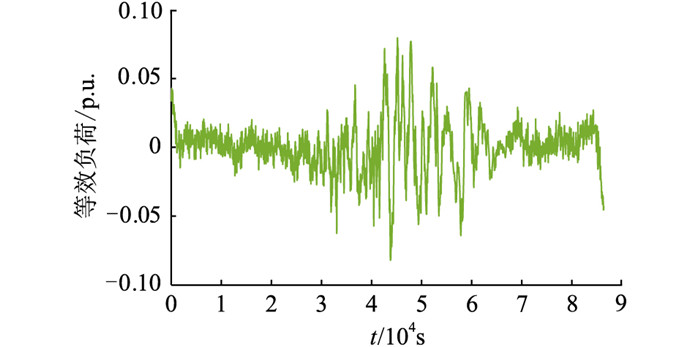
等效负荷波动曲线如图 11所示。
|
图 11 系统等效负荷波动曲线 Fig. 11 System equivalent load fluctuation curve |
在24 h调频过程中考虑二次调频对系统的影响,采用同一种二次调频策略,对比不同一次调频策略。PI控制器追踪电网频率误差,生成二次调频参考功率,根据二次调频功率分配策略将调频指令分配给调频机组和调频储能单元,文中火电机组和混合储能分配系数均为0.5。
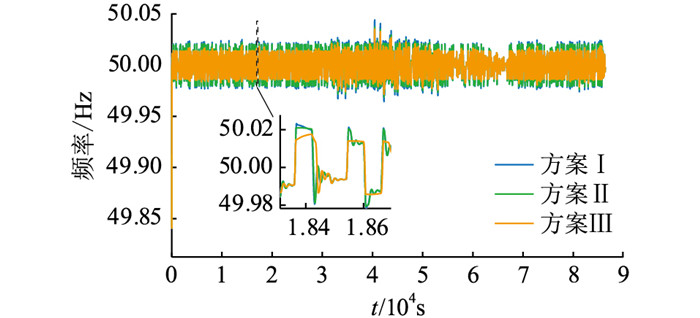
24 h等效负荷扰动的评价指标与连续秒级扰动评价指标一致,如表 4所示。不同控制策略下系统频率和电池储能SOC曲线如图 12、图 13所示。
|
|
表 4 不同方案24 h等效负荷扰动评价指标 Table 4 Evaluation index of 24 h equivalent load disturbance of different schemes |
|
图 12 某地区24 h等效负荷扰动系统频率 Fig. 12 24 h equivalent load disturbance system frequency in a certain area |
|
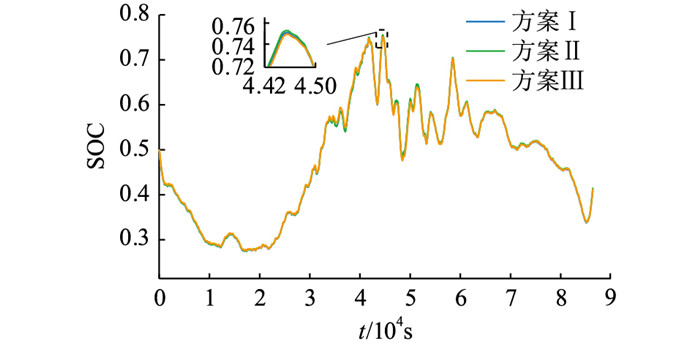
图 13 某地区24 h等效负荷扰动电池SOC Fig. 13 24 h equivalent load disturbs battery SOC in a certain area |
结合表 4,由图 12可知,方案Ⅲ的Δfrms相较方案Ⅰ减小28.5%,相较方案Ⅱ减小4.8%。相比于其他控制策略,方案Ⅲ能够更好地维持系统频率稳定。
由图 13可知,方案Ⅲ相比于其他控制策略,能较好地将电池的SOC控制在0.27~0.75之间,电池储能SOC波动范围最小,且电池储能充放电深度最小。
综合来看,方案Ⅲ在某地区24 h等效负荷波动情况下,以电池与飞轮的SOC控制在正常范围内为前提,能够有效控制系统频率的稳定,且防止了储能系统过充过放,能有效延长电池的使用寿命。
2.5 混合储能配置比的影响为验证混合储能配置比对文中所提一次调频策略的影响,以24 h等效负荷扰动为例,设置飞轮与电池储能配置比分别为10 ∶1、2 ∶1、0.4 ∶1,锂电池额定功率为10 MW,容量为10 MW ·h。各混合储能配置比下方案Ⅲ的评价指标如表 5所示。
|
|
表 5 不同配置比下方案Ⅲ的24 h等效负荷扰动评价指标 Table 5 Evaluation index for 24 h equivalent load disturbance of scheme Ⅲ with different configuration ratios |
混合储能配置比越高,即飞轮配置容量越大,系统频率更加稳定,电池SOC波动越小。在一定的配置比变化下,相比方案Ⅰ、方案Ⅱ,采用方案Ⅲ参与一次调频,电池不会发生过充过放且能保持系统频率波动不超过±0.2 Hz,体现了文中所提一次调频策略的优越性。
3 结论文中针对电池-飞轮混合储能系统参与电网一次调频的问题,考虑储能系统SOC对电池寿命的影响,提出一种基于自适应SOC的混合储能一次调频综合控制策略。仿真结果表明,该策略具有以下优势:
(1) 在阶跃扰动、连续秒级负荷扰动以及24 h等效负荷扰动下,相比不考虑权重分配的控制方法及不考虑SOC的控制方法,文中所提基于自适应SOC的一次调频综合控制策略的系统频率稳定性最好,储能系统SOC波动范围最小。
(2) 当配置比变化时,相比不考虑权重分配的控制方法及不考虑SOC的控制方法,文中所提基于自适应SOC的一次调频综合控制策略的电池不会发生过充过放,且能够保持系统频率波动不超过±0.2 Hz。
混合储能配置比对文中所提控制策略有一定影响,配置比越高,即飞轮配置容量越大,系统频率越稳定,电池SOC波动越小。相应地,飞轮配置容量越大,储能初始投资成本越高。调频场景下,配置合适的混合储能可作为后续研究重点。
| [1] |
张桂红, 刘飞, 王世斌, 等. 高比例新能源电力系统频率稳定性的惯量需求分析[J]. 电力系统及其自动化学报, 2022, 34(7): 81-87. ZHANG Guihong, LIU Fei, WANG Shibin, et al. Inertia requirement analysis of frequency stability of renewable-dominant power system[J]. Proceedings of the CSU-EPSA, 2022, 34(7): 81-87. (  0) 0) |
| [2] |
TENG Y T, DENG W, PEI W, et al. Review on grid-forming converter control methods in high-proportion renewable energy power systems[J]. Global Energy Interconnection, 2022, 5(3): 328-342. DOI:10.1016/j.gloei.2022.06.010 (  0) 0) |
| [3] |
ZARE M, MALEKPOUR M, AZIZIPANAH-ABARGHOOEE R, et al. Stochastic unit commitment to determine frequency response ramp rate including wind turbines with synthetic inertia and virtual synchronous generator[J]. International Journal of Electrical Power & Energy Systems, 2023, 152: 109272. (  0) 0) |
| [4] |
苏鹏, 陈璐, 吴坚, 等. 新型电力系统多能源能量惯性动态优化控制模型[J]. 电力建设, 2022, 43(9): 87-93. SU Peng, CHEN Lu, WU Jian, et al. Dynamic optimal control model of multi-energy inertia in new power system[J]. Electric Power Construction, 2022, 43(9): 87-93. (  0) 0) |
| [5] |
孙玉树, 杨敏, 师长立, 等. 储能的应用现状和发展趋势分析[J]. 高电压技术, 2020, 46(1): 80-89. SUN Yushu, YANG Min, SHI Changli, et al. Analysis of application status and development trend of energy storage[J]. High Voltage Engineering, 2020, 46(1): 80-89. (  0) 0) |
| [6] |
谢惠藩, 王超, 刘湃泓, 等. 南方电网储能联合火电调频技术应用[J]. 电力系统自动化, 2021, 45(4): 172-179. XIE Huifan, WANG Chao, LIU Paihong, et al. Application of joint frequency regulation technology of energy storage and thermal power in China southern power grid[J]. Automation of Electric Power Systems, 2021, 45(4): 172-179. (  0) 0) |
| [7] |
朱晓荣, 韩啸. 储能电池与常规机组配合参与一次调频的自适应控制策略[J]. 电测与仪表, 2023, 60(9): 34-42. ZHU Xiaorong, HAN Xiao. The adaptive control strategy of energy storage battery cooperating with conventional generating units to participate in primary frequency regulation[J]. Electrical Measurement & Instrumentation, 2023, 60(9): 34-42. (  0) 0) |
| [8] |
沈子伦, 尹忠东, 陈俊晔, 等. 基于SOC预测的火储联合调频控制策略[J]. 电力建设, 2023, 44(9): 129-136. SHEN Zilun, YIN Zhongdong, CHEN Junye, et al. Joint frequency modulation control method for energy storage thermal power units based on SOC prediction[J]. Electric Power Construction, 2023, 44(9): 129-136. (  0) 0) |
| [9] |
高嵩, 李军, 宋辉, 等. 提升火电机组一次调频性能的火电-储能一体化系统研究[J]. 电力系统保护与控制, 2023, 51(21): 116-125. GAO Song, LI Jun, SONG Hui, et al. An integrated thermal power-energy storage system for improving primary frequency regulation performance of thermal power units[J]. Power System Protection and Control, 2023, 51(21): 116-125. (  0) 0) |
| [10] |
杨丘帆, 王琛淇, 魏俊红, 等. 提升电网惯性与一次调频性能的储能容量配置方法[J]. 电力建设, 2020, 41(10): 116-124. YANG Qiufan, WANG Chenqi, WEI Junhong, et al. Capacity allocation of energy storage system for improving grid inertia and primary frequency regulation[J]. Electric Power Construction, 2020, 41(10): 116-124. (  0) 0) |
| [11] |
石基辰, 周云海, 崔黎丽, 等. 风储联合调频中储能的容量优化配置[J]. 水电与新能源, 2023, 37(9): 24-28. SHI Jichen, ZHOU Yunhai, CUI Lili, et al. Optimization configuration of the energy storage capacity in wind power and storage combined frequency regulation[J]. Hydropower and New Energy, 2023, 37(9): 24-28. (  0) 0) |
| [12] |
庞轶, 尚丽平, 屈薇薇. 不同SOC区间及倍率下锂电池老化分析[J]. 电子元件与材料, 2022, 41(2): 143-148. PANG Yi, SHANG Liping, QU Weiwei. Aging analysis of lithium battery under different SOC range and discharge rate[J]. Electronic Components and Materials, 2022, 41(2): 143-148. (  0) 0) |
| [13] |
COLLATH N, TEPE B, ENGLBERGER S, et al. Aging aware operation of lithium-ion battery energy storage systems: a review[J]. Journal of Energy Storage, 2022, 55: 105634. DOI:10.1016/j.est.2022.105634 (  0) 0) |
| [14] |
薄利明, 郑惠萍, 张世锋, 等. 锂电池健康状态均衡技术综述[J]. 电测与仪表, 2023, 60(4): 11-18. BO Liming, ZHENG Huiping, ZHANG Shifeng, et al. Review on health state equalization technology for lithium batteries[J]. Electrical Measurement & Instrumentation, 2023, 60(4): 11-18. (  0) 0) |
| [15] |
王佳蕊, 李德鑫, 张家郡, 等. 微电网储能系统控制对电能质量的保障[J]. 哈尔滨理工大学学报, 2021, 26(6): 87-93. WANG Jiarui, LI Dexin, ZHANG Jiajun, et al. The control of microgrid energy storage system guarantees the power quality[J]. Journal of Harbin University of Science and Technology, 2021, 26(6): 87-93. (  0) 0) |
| [16] |
罗耀东, 田立军, 王垚, 等. 飞轮储能参与电网一次调频协调控制策略与容量优化配置[J]. 电力系统自动化, 2022, 46(9): 71-82. LUO Yaodong, TIAN Lijun, WANG Yao, et al. Coordinated control strategy and optimal capacity configuration for flywheel energy storage participating in primary frequency regulation of power grid[J]. Automation of Electric Power Systems, 2022, 46(9): 71-82. (  0) 0) |
| [17] |
张继红, 崔天祥, 熊伟, 等. 飞轮储能参与风场调频控制研究[J]. 浙江电力, 2022, 41(8): 49-56. ZHANG Jihong, CUI Tianxiang, XIONG Wei, et al. Research on participation of flywheel energy storage in wind farm frequency regulation control[J]. Zhejiang Electric Power, 2022, 41(8): 49-56. (  0) 0) |
| [18] |
AKRAM U, NADARAJAH M, SHAH R, et al. A review on rapid responsive energy storage technologies for frequency regulation in modern power systems[J]. Renewable and Sustainable Energy Reviews, 2020, 120: 109626. DOI:10.1016/j.rser.2019.109626 (  0) 0) |
| [19] |
AKRAM U, MITHULANANTHAN N, SHAH R, et al. Sizing HESS as inertial and primary frequency reserve in low inertia power system[J]. IET Renewable Power Generation, 2021, 15(1): 99-113. DOI:10.1049/rpg2.12008 (  0) 0) |
| [20] |
DAMBONE SESSA S, TORTELLA A, ANDRIOLLO M, et al. Li-ion battery-flywheel hybrid storage system: countering batery aging during a grid frequency regulation service[J]. Applied Sciences, 2018, 8(11): 2330. DOI:10.3390/app8112330 (  0) 0) |
| [21] |
马智慧, 李欣然, 谭庄熙, 等. 考虑储能调频死区的一次调频控制方法[J]. 电工技术学报, 2019, 34(10): 2102-2115. MA Zhihui, LI Xinran, TAN Zhuangxi, et al. Integrated control of primary frequency regulation considering dead band of energy storage[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2102-2115. (  0) 0) |
| [22] |
吴启帆, 宋新立, 张静冉, 等. 电池储能参与电网一次调频的自适应综合控制策略研究[J]. 电网技术, 2020, 44(10): 3829-3836. WU Qifan, SONG Xinli, ZHANG Jingran, et al. Study on self-adaptation comprehensive strategy of battery energy storage in primary frequency regulation of power grid[J]. Power System Technology, 2020, 44(10): 3829-3836. (  0) 0) |
| [23] |
邓霞, 孙威, 肖海伟. 储能电池参与一次调频的综合控制方法[J]. 高电压技术, 2018, 44(4): 1157-1165. DENG Xia, SUN Wei, XIAO Haiwei. Integrated control strategy of battery energy storage system in primary frequency regulation[J]. High Voltage Engineering, 2018, 44(4): 1157-1165. (  0) 0) |
| [24] |
王铭岐. 电池储能系统参与系统一次调频控制策略研究[D]. 吉林: 东北电力大学, 2022. WANG Mingqi. Research on control strategy of battery energy storage system participating in primary frequency regulation of power system[D]. Jilin: Northeast Dianli University, 2022. (  0) 0) |
| [25] |
罗耀东. 飞轮储能参与电网一次调频控制方法研究[D]. 济南: 山东大学, 2021. LUO Yaodong. Research on control strategy of flywheel energy storage participating in primary frequency regulation of power grid[D]. Jinan: Shandong University, 2021. (  0) 0) |
| [26] |
方红艳, 马平. 考虑混合储能调频死区的自适应下垂控制策略[J]. 电气工程学报, 2021, 16(4): 213-222. FANG Hongyan, MA Ping. Adaptive droop control strategy considering frequency modulation dead band of hybrid energy storage[J]. Journal of Electrical Engineering, 2021, 16(4): 213-222. (  0) 0) |
| [27] |
刘宇宸. 飞轮-蓄电池混合储能系统调频特性研究[D]. 北京: 华北电力大学, 2021. LIU Yuchen. Research on frequency modulation characteristics of flywheel-battery hybrid energy storage system[D]. Beijing: North China Electric Power University, 2021. (  0) 0) |
| [28] |
李军徽, 侯涛, 穆钢, 等. 基于权重因子和荷电状态恢复的储能系统参与一次调频策略[J]. 电力系统自动化, 2020, 44(19): 63-72. LI Junhui, HOU Tao, MU Gang, et al. Primary frequency regulation strategy with energy storage system based on weight factors and state of charge recovery[J]. Automation of Electric Power Systems, 2020, 44(19): 63-72. (  0) 0) |
| [29] |
傅质馨, 张晶晶, 崔晓丹, 等. 储能支撑光伏参与电网一次调频的优化控制策略研究[J]. 可再生能源, 2021, 39(11): 1530-1540. FU Zhixin, ZHANG Jingjing, CUI Xiaodan, et al. Research on optimal control strategy of photovoltaic system supported by energy storage participating in primary frequency regulation of power grid[J]. Renewable Energy Resources, 2021, 39(11): 1530-1540. (  0) 0) |
| [30] |
刘英培, 田仕杰, 梁海平, 等. 考虑SOC的电池储能系统一次调频策略研究[J]. 电力系统保护与控制, 2022, 50(13): 107-118. LIU Yingpei, TIAN Shijie, LIANG Haiping, et al. Control strategy of a battery energy storage system considering SOC in primary frequency regulation of power grid[J]. Power System Protection and Control, 2022, 50(13): 107-118. (  0) 0) |
| [31] |
严干贵, 王铭岐, 段双明, 等. 考虑荷电状态恢复的储能一次调频控制策略[J]. 电力系统自动化, 2022, 46(21): 52-61. YAN Gangui, WANG Mingqi, DUAN Shuangming, et al. Primary frequency regulation control strategy of energy storage considering state of charge recovery[J]. Automation of Electric Power Systems, 2022, 46(21): 52-61. (  0) 0) |

 王俊月(2000), 女, 硕士在读, 研究方向为储能系统控制及应用(E-mail:
王俊月(2000), 女, 硕士在读, 研究方向为储能系统控制及应用(E-mail: