文章编号: 2096-3203(2024)02-0011-10 中图分类号: TM732
2. 东南大学电气工程学院, 江苏 南京 210096
化石能源的大量使用不断加剧全球变暖,导致气候变化。因此,国内外启动了能源转型计划,为后化石时代做准备。加快发展氢能产业,是应对全球气候变化,实现碳达峰、碳中和目标,保障国家能源安全和实现经济社会高质量发展的战略选择。据中国氢能联盟预测,预计到2060年,氢能在终端能源消费中比重约为20%[1]。在技术经济效益双重刺激下,氢能作为可再生能源存储利用的介质,在新型电力系统中发挥着重要的作用。文献[2]全面阐述了氢能产业在我国能源转型中的作用,指出氢能在各行业的应用前景;文献[3-5]以新型电力系统为背景,提出氢能应用的若干挑战性问题;文献[6-10]以电氢储能为载体,验证了其在综合能源系统中的应用潜力。
目前,关于氢储能的研究大都以综合能源系统为背景。文献[11]以提高风-氢互补系统的经济性为目标,提出风电、电解槽-储氢罐-燃氢燃气轮机的优化配置模型。文献[12]以一次性投资最小为目标,以风电100%消纳为约束,构建了风电-氢储-煤化工多能耦合系统设备优化规划模型,给出了多类型能源的配置方案。文献[13]提出无废充能服务区多源微网(zero-waste charging service area multi-energy microgrid, ZWSA-MEMG)优化运行方法,提高了以氢储能为基础的多源微网的经济性和电网调节的灵活性。文献[14]以可再生能源为基础,提出一种利用高温进行运输的电氢一体化系统最优运行策略,通过数值实例验证了电力系统和氢能系统之间的协同效应,并强调了灵活性在氢气生产、运输和需求方面的影响。文献[15]提出一种考虑个体利益的风力发电和加氢站合作运营模型,利用纳什均衡理论解决了合作过程中的能源交易和利益共享问题,大大降低了加氢站的制氢成本。
针对氢储能在多能联储联供方面的深远意义,国内外研究机构在电氢互补系统方面进行了初步研究。文献[16]针对风-光-氢多能互补微电网的经济性,提出一种计及需求侧响应的优化配置方法。文献[17]主要研究风-光-氢多主体能源系统的协同运行,并基于纳什均衡理论,提出风-光-氢多主体能源系统的合作运行模型。文献[18]提出考虑电氢耦合的混合储能容量优化方法,以度电成本、供电可靠性和能源利用率为目标,证实了该方法的有效性,提高了光伏发电利用率。文献[19-22]为减少独立型微网弃风弃光,将电转氢作为灵活性资源,建立了以微网经济性最优和静态灵活性水平最高为目标的多目标优化模型。文献[23-25]考虑热负荷需求不足和商业电制氢效率低下的问题,采用在生产氢气的同时向区域供热网络提供热量的综合解决方案,验证了电-氢-热方案通过提高系统经济性和安全性所带来的整体效益。文献[26]将制得氢气掺入天然气管网,建立电-氢经济分析模型。上述文献对电氢耦合模型及其有效性进行了比较详细的研究,但未充分考虑氢储能电制氢过程中的热效应和已储存氢能再供电供热以提高系统经济性和效率的优势。
文中考虑某地自然资源、电热负荷需求的特点,以提高经济性、供电可靠性和可再生能源利用率为目标,提出电-氢-热多能互补的控制策略,建立一种面向电-氢-热多能互补的独立微网容量优化配置模型。通过算例验证了该优化配置方案的可行性,并分析了文中所提方案在提高多能互补效率和系统经济性方面的有效性。
1 电-氢-热多能互补独立微网结构图 1为独立型电-氢-热多能互补独立微网结构示意,主要由分布式电源(distributed generation,DG)、储能装置、电-氢-热装置和负荷组成。其中,DG主要包括风电机组(wind turbine,WT)、光伏机组(photovoltaic cell,PV),储能装置主要包括化学储能电池(storage battery,SB)、储氢罐(hydrogen storage tank,HST)、储热罐(thermal storage tank,TST),电-氢-热装置主要包括电解槽(electrolyzer,ELE)、质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)、氢锅炉(hydrogen boiler,HB)。
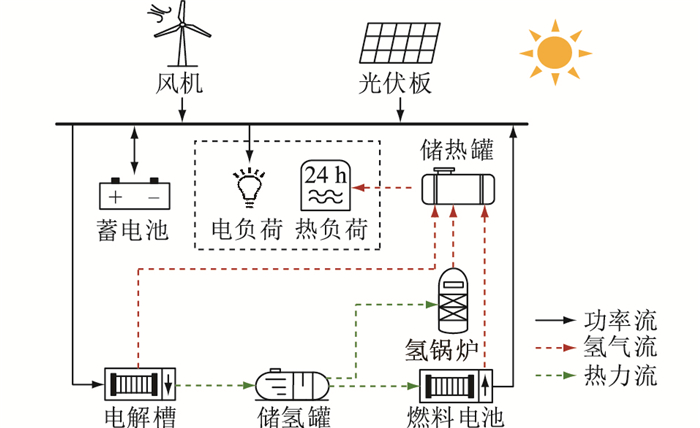
|
图 1 独立型电-氢-热多能互补系统结构示意 Fig. 1 Schematic diagram of the islanded electricity-hydrogen-thermal multi-energy complementary system structure |
独立微网的工作模式为:风机、光伏发电优先满足用户用电负荷,当发电系统功率大于用电负荷功率时,储能系统吸收剩余部分功率并将其分配给电解槽或蓄电池,电能以氢能或化学能的方式储存,其中氢能既可以在必要时通过燃料电池转换为电能,在此过程中又可以供给用户热负荷,同时当热负荷高峰时,氢能也可以通过氢锅炉转换为热能;当发电系统功率无法满足用电负荷所需功率时,储能系统释放能量,蓄电池组或燃料电池放电,实现系统功率实时平衡。
2 考虑电-氢-热多能互补的独立微网多目标优化配置模型 2.1 目标函数文中以微网中风电、光伏、储能装置和电-氢-热装置的容量为决策变量,以系统的年均总费用f1、负荷失电率f2以及可再生能源利用率f3为目标,构建多目标优化函数。
| $ \left\{\begin{array}{l} \min f_{1}=C_{\text {init }}+C_{\text {oper }}+C_{\text {rep }} \\ \min f_{2}= \\ \sum\limits_{t=1}^{n_{1}}\left(P_{\text {load }}(t)-\sum\limits_{i=1}^{g} P_{i}(t)-P_{\mathrm{bd}}(t)-P_{\mathrm{fc}}(t)\right) / \\ \sum\limits_{t=1}^{n} P_{\text {load }}(t)=\sum\limits_{t=1}^{n} P_{\text {drump }}(t) / \sum\limits_{t=1}^{n} P_{\text {load }}(t) \\ \max f_{3}= \\ 1-\sum\limits_{t=1}^{n_{2}}\left(\sum\limits_{i=1}^{g} P_{i}(t)-P_{\text {load }}(t)-P_{\mathrm{bc}}(t)-P_{\text {ele }}(t)\right) / \\ \sum\limits_{t=1}^{n} P_{\text {load }}(t)=1-\sum\limits_{t=1}^{n} P_{\text {loss }}(t) / \sum\limits_{t=1}^{n} P_{\text {load }}(t) \end{array}\right. $ | (1) |
式中:Cinit、Coper、Crep分别为考虑电-氢-热耦合系统下的规划配置成本、运行维护成本以及替换成本,Cinit主要考虑待配置设备的固有安装成本,Coper主要考虑待配置设备的运行维护成本、可再生能源补贴成本和电-氢-热耦合系统带来的年收益,Crep主要考虑待配置设备的置换成本和折旧收入;n1为规划建设周期内不满足用电负荷需求的采样点数量;g为系统中可再生能源类型数目;n为规划建设周期内总的采样点数量;Pload(t)为t时刻电负荷功率;Pi(t)为第i种类型可再生能源t时刻的输出功率;Pbd(t)为t时刻蓄电池放电功率;Pfc(t)为t时刻燃料电池输出电功率;Pdrump(t)为t时刻系统的失电功率;n2为规划建设周期内存在弃风弃光的采样点数量;Pbc(t)为t时刻蓄电池充电功率;Pele(t)为t时刻电解槽输入功率;Ploss(t)为t时刻系统的可再生能源损失功率。
| $ \left\{\begin{array}{l} C_{\text {init }}=\eta_{\mathrm{CRF}}\left(r, N_{\text {age }}\right) \sum\limits_{l \in \varGamma} N_{l} \pi_{l} \\ C_{\text {rep }}=\eta_{\mathrm{CRF}}\left(r, N_{\text {age }}\right) \sum\limits_{l \in \varGamma}\left(C_{l, \text { rep }}-C_{l, \text { rem }}\right) \\ \eta_{\mathrm{CRF}}\left(r, N_{\text {age }}\right)=\frac{r(1+r)^{N_{\text {age }}}}{(1+r)^{N_{\text {age }}}-1} \\ r=\frac{r_{1}-\delta}{1+\delta} \end{array}\right. $ | (2) |
式中:ηCRF(r,Nage)为待配置设备的资金回收系数;r为实际贴现率;Nage为待配置设备的工作年限;Γ为由各待配置设备构成的集合;Nl、πl分别为待配置设备l的数量、单价;Cl, rep、Cl, rem分别为待配置设备l在Nage年后的置换成本和折旧收入;r1为长期贴现率;δ为通货膨胀率。
| $ \begin{equation*} C_{\text {oper }}=C_{\text {om }}-C_{\text {sub }}-C_{\text {ex }} \end{equation*} $ | (3) |
式中:Com为待配置设备的维护成本;Csub为风光发电国家补贴年收益;Cex为电-氢-热多能互补系统运营年收益。
| $ \left\{\begin{array}{l} C_{\mathrm{om}}=\sum\limits_{l \in \varGamma} C_{l, \mathrm{om}} \\ C_{\mathrm{sub}}=\sum\limits_{q \in\{\mathrm{WT}, \mathrm{PV}\}} \pi_{q, \mathrm{sub}} E_{q, \mathrm{sub}} \\ C_{\mathrm{ex}}=\pi_{\mathrm{el}}(t) \sum\limits_{t=1}^{8760} P_{\mathrm{el}}(t)+\pi_{\mathrm{hl}}(t) \sum\limits_{t=1}^{8760} Q_{\mathrm{hl}}(t) \end{array}\right. $ | (4) |
式中:Cl, om为待配置设备l的维护成本;πq, sub、Eq, sub分别为可再生能源q出力单位补贴标准和年发电总量;Pel(t)、Qhl(t)分别为t时刻系统提供的用户电负荷、热负荷功率;πel(t)为t时刻用户用电电价,文中采用分时电价进行计算;πhl(t)为t时刻用户用热单价,文中取0.255元/(kW ·h)。
2.2 设备运行模型由于可再生能源的模型研究已较为成熟,不再详细敷述。下面构建微网其余设备模型,包括蓄电池、储热罐、储氢罐、电解槽、燃料电池及氢锅炉。
2.2.1 蓄电池模型蓄电池充放电模型如下:
| $ \left\{\begin{array}{l} W_{\mathrm{bt}}(t)=W_{\mathrm{bt}}(t-1)\left(1-\mu_{\mathrm{bt}, \text { loss }}\right)+ \\ \quad\left(\eta_{\mathrm{bt}, \mathrm{ch}} P_{\mathrm{bc}}(t)-P_{\mathrm{bd}}(t) / \eta_{\mathrm{bt}, \mathrm{dis}}\right) \\ 0 \leqslant U_{\mathrm{bt}, \mathrm{ch}}(t) P_{\mathrm{bc}}(t) \leqslant P_{\mathrm{bc}}^{\max } \\ 0 \leqslant U_{\mathrm{bt}, \mathrm{dis}}(t) P_{\mathrm{bd}}(t) \leqslant P_{\mathrm{bd}}^{\max } \\ U_{\mathrm{bt}, \mathrm{ch}}(t)+U_{\mathrm{bt}, \mathrm{dis}}(t) \leqslant 1 \end{array}\right. $ | (5) |
式中:Wbt(t)为t时刻蓄电池电量;μbt, loss为蓄电池自损率;ηbt, ch、ηbt, dis分别为蓄电池充、放电效率;Ubt, ch(t)、Ubt, dis(t)为0-1变量,分别表征t时刻蓄电池的充、放电状态,Ubt, ch(t)=1表示蓄电池充电,Ubt, dis(t)=1表示蓄电池放电;Pbcmax、Pbdmax分别为蓄电池最大充、放电功率。
2.2.2 储热罐模型与蓄电池充放电模型类似,储热罐模型如下:
| $ \left\{\begin{array}{l} W_{\mathrm{tst}}(t)=W_{\mathrm{tst}}(t-1)\left(1-\mu_{\mathrm{tst}, \mathrm{loss}}\right)+ \\ \quad\left(\eta_{\mathrm{tst}, \mathrm{ch}} Q_{\mathrm{tst}, \mathrm{ch}}(t)-Q_{\mathrm{tst}, \mathrm{dis}}(t) / \eta_{\mathrm{tst}, \mathrm{dis}}\right) \\ 0 \leqslant U_{\mathrm{tst}, \mathrm{ch}}(t) Q_{\mathrm{tst}, \mathrm{ch}}(t) \leqslant Q_{\mathrm{tst}, \mathrm{ch}}^{\max } \\ 0 \leqslant U_{\mathrm{tst}, \mathrm{dis}}(t) Q_{\mathrm{tst}, \mathrm{dis}}(t) \leqslant Q_{\mathrm{tst}, \mathrm{dis}}^{\max } \\ U_{\mathrm{tst}, \mathrm{ch}}(t)+U_{\mathrm{tst}, \mathrm{dis}}(t) \leqslant 1 \end{array}\right. $ | (6) |
式中:Wtst(t)为t时刻储热罐存储的热能;μtst, loss为储热罐的自损率;ηtst, ch、ηtst, dis分别为储热罐吸、放热效率;Qtst, ch(t)、Qtst, dis(t)分别为t时刻储热罐的吸、放热功率;Utst, ch(t)、Utst, dis(t)为0-1变量,分别表征t时刻储热罐的吸、放热状态,Utst, ch(t)=1表示储热罐吸热,Utst, dis(t)=1表示储热罐放热;Qtst, chmax、Qtst, dismax分别为储热罐的最大吸、放热功率。
2.2.3 储氢罐储氢罐是必要的储运氢气的设备,在气路的应用中,储氢罐的作用是缓冲、降温、除水和储能,确保输出气体连续。储氢罐的具体模型如下:
| $ \left\{\begin{array}{l} W_{\mathrm{hst}}(t)=W_{\mathrm{hst}}(t-1)+V_{\mathrm{cs}}(t-1)-V_{\mathrm{dcs}}(t-1) \\ 0 \leqslant U_{\mathrm{cs}}(t) V_{\mathrm{cs}}(t) \leqslant V_{\mathrm{cs}}^{\max } \\ 0 \leqslant U_{\mathrm{dcs}}(t) V_{\mathrm{dcs}}(t) \leqslant V_{\mathrm{dcs}}^{\max } \\ U_{\mathrm{cs}}(t)+U_{\mathrm{dcs}}(t) \leqslant 1 \end{array}\right. $ | (7) |
式中:Vhst(t)为t时刻储氢罐的储氢量;Vcs(t)、Vdcs(t)分别为t时刻储氢罐的充气速率和供气速率;Vcsmax、Vdcsmax分别为储氢罐的最大充气速率和最大供气速率;Ucs(t)、Udcs(t)为0-1变量,分别表征t时刻储气罐的充、供气工作状态,Ucs(t)=1表示储氢罐处于充气状态,Udcs(t)=1表示储氢罐处于供气状态。
2.2.4 碱性电解槽模型碱性电解槽产氢速率如下:
| $ \begin{equation*} V_{\mathrm{h}}=\eta_{\mathrm{ele}} P_{\mathrm{ele}} / H_{\mathrm{hv}} \end{equation*} $ | (8) |
式中:Vh为碱性电解槽的产氢速率;ηele为碱性电解槽的效率;Pele为输入碱性电解槽的电功率;Hhv为氢气热值,文中取3.509 kW ·h/Nm3。当碱性电解槽正常运行时,电解槽的产氢速率和输入功率呈现近似线性关系,因此可以假设ηele恒定,此时采用电解槽电耗量来表示其输入输出特性,如式(9)所示。
| $ \begin{equation*} V_{\mathrm{h}, s}=P_{\mathrm{h}, s} \Delta s / \mu_{\mathrm{h}} \end{equation*} $ | (9) |
式中:Vh, s为s时段内碱性电解槽的产氢体积;Ph, s为s时段内碱性电解槽的平均耗电功率;Δs为s时段的时间长度;μh为碱性电解槽的耗电量,受目前工艺和技术条件限制[19],其取值范围一般为4.50~5.04 kW ·h/Nm3。
2.2.5 质子交换膜燃料电池模型作为高效环保的能源转换装置,经过多年发展研究,质子交换膜燃料电池已成为适用性最广的燃料电池。质子交换膜燃料电池的输出功率为:
| $ \left\{\begin{array}{l} P_{\mathrm{fc}}=V_{\mathrm{fc}} H_{\mathrm{hv}} \eta_{\mathrm{fc} \_\mathrm{e}} \\ Q_{\mathrm{fc}}=V_{\mathrm{fc}} H_{\mathrm{hv}} \eta_{\mathrm{fc} \_\mathrm{h}} \end{array}\right. $ | (10) |
式中:Pfc、Qfc分别为燃料电池输出电功率、热功率;Vfc为燃料电池每小时的氢气耗量;ηfc_e、ηfc_h分别为燃料电池的发电效率与发热效率,其与燃料电池自身容量、负载率有关[27-28]。
| $ \left\{\begin{array}{l} \eta_{\mathrm{fc} \_\mathrm{e}}=a_{1} X_{\mathrm{fc}}^{2}+b_{1} X_{\mathrm{fc}}+c_{1} \\ \eta_{\mathrm{fc} \_\mathrm{h}}=a_{2} X_{\mathrm{fc}}^{2}+b_{2} X_{\mathrm{fc}}+c_{2} \\ X_{\mathrm{fc}}=P_{\mathrm{fc}} / P_{\mathrm{fc}}^{\mathrm{rate}} \end{array}\right. $ | (11) |
式中:a1、b1、c1、a2、b2、c2为燃料电池效率系数,具体数值见表 1;Xfc为燃料电池的负载率;Pfcrate为燃料电池的额定功率。
|
|
表 1 燃料电池特性参数 Table 1 Fuel cell characteristic parameters |
当系统设备满足电负荷需求,氢气仍有盈余,且此时无法满足用户热需求时,需要氢锅炉补燃,实现热能的供需平衡。
| $ \begin{equation*} Q_{\mathrm{hb}}=V_{\mathrm{hb}} H_{\mathrm{hv}} \eta_{\mathrm{hb}} \end{equation*} $ | (12) |
式中:Qhb为氢锅炉的输出热功率;Vhb为氢锅炉每小时的氢气耗量;ηhb为氢锅炉发热效率。
2.3 运行约束条件基于上述设备运行模型,文中建立微网各设备运行约束及系统运行约束条件。
(1) 决策变量约束。
| $ \begin{equation*} 0 \leqslant S_{l} \leqslant S_{l, \max } \quad l \in \varGamma \end{equation*} $ | (13) |
式中:Sl、Sl, max分别为待配置设备l的容量及其上限值,可根据实际投资预算及安装占地面积等因素来进行设置,并且根据负荷情况划定数量上限值可提高求解效率。
(2) 储能状态约束。蓄电池荷电状态(state of charge,SOC)一般采用剩余容量与额定容量的比值来表示,其取值范围为0~1。类似地,定义储氢罐、储热罐储能状态,考虑到储能水平值对储能寿命的影响,须设定储能水平的上下限值。
| $ \left\{\begin{array}{l} S_{\mathrm{SOC}}(t)=W_{\mathrm{bt}}(t) / C_{\mathrm{ESS}} \\ S_{\mathrm{LOT}}(t)=W_{\mathrm{tst}}(t) / C_{\mathrm{TSS}} \\ S_{\mathrm{LOH}}(t)=W_{\mathrm{hst}}(t) / C_{\mathrm{HSS}} \\ S_{\mathrm{SOC}, \min } \leqslant S_{\mathrm{SOC}}(t) \leqslant S_{\mathrm{SOC}, \text { max }} \\ S_{\mathrm{LOT}, \min } \leqslant S_{\mathrm{LOT}}(t) \leqslant S_{\mathrm{LOT}, \max } \\ S_{\mathrm{LOH}, \text { min }} \leqslant S_{\mathrm{LOH}}(t) \leqslant S_{\mathrm{LOH}, \max } \end{array}\right. $ | (14) |
式中:SSOC(t)、SLOT(t)、SLOH(t)分别为t时刻蓄电池、储热罐、储氢罐的储能状态;CESS、CTSS、CHSS分别为蓄电池、储热罐、储氢罐的总容量;SSOC, max、SSOC, min、SLOT, max、SLOT, min、SLOH, max、SLOH, min分别为蓄电池、储热罐、储氢罐的储能水平的上、下限值。
(3) 设备出力约束。文中具有出力约束的设备包括风光电源、蓄电池、燃料电池及电解槽,其约束条件如下:
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{pv}} \leqslant P_{\mathrm{pv}, 0} S_{\mathrm{pv}} \\ 0 \leqslant P_{\mathrm{wt}} \leqslant P_{\mathrm{wt}, 0} S_{\mathrm{wt}} \\ P_{\mathrm{bt}, \text { min }} \leqslant P_{\mathrm{bc}}+P_{\mathrm{bd}} \leqslant P_{\mathrm{bt}, \text { max }} \\ P_{\mathrm{fc}, \text { min }} \leqslant P_{\mathrm{fc}} \leqslant P_{\mathrm{fc}, \text { max }} \\ P_{\mathrm{ele, min}} \leqslant P_{\mathrm{ele}} \leqslant P_{\mathrm{ele}, \max } \end{array}\right. $ | (15) |
式中:Ppv, 0、Pwt, 0分别为光伏和风机单位容量Ppv、Pwt的最大出力值;Spv、Swt分别为光伏和风机的配置容量;Pbt, max、Pbt, min分别为蓄电池的出力上、下限值;Pfc, max、Pfc, min分别为燃料电池输出电功率的上、下限值;Pele, max、Pele, min分别为电解槽的用能上、下限值。
(4) 功率平衡约束。
| $ \left\{\begin{array}{c} P_{\mathrm{pv}}(t)+P_{\mathrm{wt}}(t)-P_{\mathrm{bc}}(t)+P_{\mathrm{bd}}(t)- \\ P_{\mathrm{ele}}(t)+P_{\mathrm{fc}}(t)=P_{\mathrm{el}}(t) \\ Q_{\mathrm{fc}}(t)+Q_{\mathrm{hb}}(t)+Q_{\mathrm{tst}, \mathrm{dis}}(t)=Q_{\mathrm{hl}}(t) \end{array}\right. $ | (16) |
式中:Qfc(t)、Qhb(t)、Qtst, dis(t)分别为t时刻燃料电池、氢锅炉输出热功率以及储热罐放热功率。
(5) 氢气供需平衡约束。
| $ \begin{equation*} V_{\mathrm{fc}}(t)+V_{\mathrm{hb}}(t)+V_{\mathrm{cs}}(t)=V_{\mathrm{dcs}}(t)+V_{\mathrm{h}}(t) \end{equation*} $ | (17) |
式中:Vhb(t)为t时刻氢锅炉的耗氢速率;Vh(t)为t时刻电解槽产氢速率。
值得注意的是,文中独立微网的应用场景一般为小区、办公楼等供电范围较小的区域,因此文中未考虑电网和热网的网架结构和潮流约束。
2.4 电-氢-热多能互补系统控制策略在优先满足电负荷需求的基础上,为了提高系统效率,满足部分热负荷需求,此时储能装置须根据风光输出功率与电热负荷需求的关系来不断调整储能状态。文中定义系统t时刻的净输出功率为Pnet,如式(18)所示。
| $ \begin{equation*} P_{\mathrm{net}}(t)=\sum\limits_{i=1}^{g} P_{i}(t)-P_{\mathrm{load}}(t) \end{equation*} $ | (18) |
当风光发电功率大于微网内电负荷时,Pnet(t)>0,此时电解槽工作,多余的电量被转化为氢气并储存起来,并通过氢锅炉供给部分热需求,表达式如下:
| $ \left\{\begin{array}{l} V_{\mathrm{h}}(t)=\min \left\{P_{\mathrm{net}}(t) \eta_{\mathrm{ele}} / H_{\mathrm{hv}}, V_{\mathrm{h}, \max }\right\} \\ Q_{\mathrm{hb}}(t)=\min \left\{V_{\mathrm{h}}(t), V_{\mathrm{hb}, \max }\right\} \times H_{\mathrm{hv}} \eta_{\mathrm{hb}} \end{array}\right. $ | (19) |
式中:Vh, max为电解槽允许最大产氢速率;Vhb, max为氢锅炉允许最大耗氢速率。
当t时刻风光发电输出功率小于电负荷需求时,Pnet(t) < 0,燃料电池工作,储存的氢气被转化为电能来供应电负荷不足的部分,此过程产生的热能来供给部分热需求,表达式如下:
| $ \left\{\begin{array}{l} P_{\mathrm{fc}}(t)=\min \left\{\left|P_{\mathrm{net}}(t)\right|, P_{\mathrm{fc}, \max }\right\} \\ Q_{\mathrm{fc}}(t)=P_{\mathrm{fc}}(t) \eta_{\mathrm{fc} \_\mathrm{h}} / \eta_{\mathrm{fc} \_\mathrm{e}} \end{array}\right. $ | (20) |
当t时刻风光发电和燃料电池的输出电功率总和仍不能满足电负荷需求,则Pfc(t) < |Pnet(t) |,此时负荷失电功率Pdrump(t)如式(21)所示。
| $ \begin{equation*} P_{\text {drump }}(t)=\left|P_{\text {net }}(t)\right|-P_{\mathrm{fc}}(t) \end{equation*} $ | (21) |
传统粒子群算法表现出鲁棒性强、收敛速度快、优化效率高、易实现等优势,但其存在搜索精度不高、易陷入局部最优等缺陷。而模拟退火算法在搜索过程中引入了随机因素,当算法迭代更新可行解时,以一定的概率接受比当前解差的解,因此可以跳出局部最优解而达到全局最优解。考虑到电-氢-热多能互补系统复杂性,文中将粒子群算法和模拟退火算法相结合,采用基于模拟退火的粒子群优化(simulated annealing particle swarm optimization,SAPSO)算法对各待配置设备的容量进行寻优。为了同时保证目标函数负荷失电率f2<8%,可再生能源利用率f3>95%,文中目标函数表达式如下:
| $ \begin{equation*} \min f=f_{1}+l_{1}\left(f_{2}-0.08\right) \lambda_{1}+l_{2}\left(0.95-f_{3}\right) \lambda_{2} \end{equation*} $ | (22) |
式中:λi∈{0, 1},i=1, 2,λi=0表示该项目标未越限,λi=1表示该项目标越限;li(i=1,2)为对应项的惩罚因子,通常惩罚因子为正数,且随着迭代次数k增加而增大,文中项目惩罚因子li取
基于SAPSO算法的模型求解步骤如下。
(1) 初始化参数,包括种群退火温度T,温度冷却系数C,交叉概率Pc,变异概率Pm,学习因子p1和p2。读取系统待配置设备基本参数、负荷情况以及区域自然资源等参数。
(2) 随机产生N个初始粒子种群。
(3) 根据式(23)—式(25)对种群中粒子进行操作。
| $ \begin{gather*} v_{i d, k+1}=\varphi\left[v_{i d, k}+p_{1} r_{1, k}\left(p_{i d, k}-x_{i d, k}\right)+\right. \\ \left.p_{2} r_{2, k}\left(g_{i d, k}-x_{i d, k}\right)\right] \end{gather*} $ | (23) |
| $ x_{i d, k+1}=x_{i d, k}+v_{i d, k} $ | (24) |
| $ \left\{\begin{array}{l} \varphi=\frac{2}{\left|2-p-\sqrt{p^{2}-4 p}\right|} \\ p=p_{1}+p_{2} \quad p>4 \end{array}\right. $ | (25) |
式中:d为搜索空间维数,此处取3;vid, k、xid, k分别为粒子i在第k次迭代中第d维的速度和位置;pid, k、gid, k分别为粒子i在第k次迭代中第d维的当前和全局最优位置;r1, k、r2, k为0~1之间的随机值;φ为压缩因子。
(4) 对步骤(3)产生的种群以交叉概率Pc进行交叉操作:从子种群随机选取个体xj、xm,按步骤(2)、步骤(3)进行交叉操作,产生新个体x′j、x′m,计算适应度函数f(xj)、f(xm)、f(x′j)和f(x′m)。若min{1, exp(-(f(x′j)-f(xj))/T}>Rr,则把x′j作为新个体;若min{1, exp(-(f(x′m)-f(xm))/T}>Rr,则把x′m作为新个体,其中Rr为0~1之间的随机值。
(5) 对交叉后的新种群以变异概率Pm进行变异操作:从子种群随机选取个体xj进行高斯变异操作,产生新个体x″j,计算适应度函数f(xj)和f(x″j)。若min{1, exp(-(f(x″j)-f(xj))/T}>Rr,则把x″j作为新个体。
(6) 选取交叉、变异后新种群的整数变量粒子,将其位置规格化为整数。
(7) 若当前最优个体已满足收敛条件,则终止运算,输出最优结果。
(8) 若未达到最大迭代次数,则修改种群退火温度,令T为TC,转到步骤(3)同时迭代次数加1。具体求解流程如图 2所示。
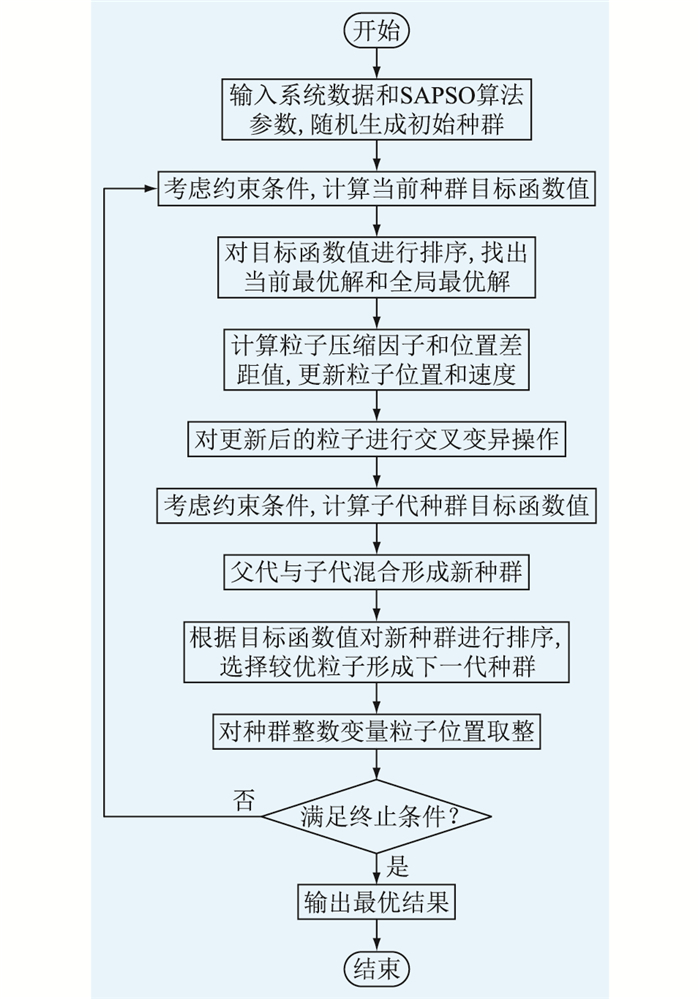
|
图 2 基于SAPSO算法的电-氢-热多能互补微网求解流程 Fig. 2 Flow chart for solving electric-hydrogen-thermal multi-energy complementary microgrid based on SAPSO algorithm |
我国东北地区自然资源丰富,但有较大的季节和时间差异性。冬季风电资源丰富,风力发电高峰期主要集中在夜间,电力负荷较低,热负荷高峰期间如果不合理调度风电输出将导致大量风电弃电;夏季热量需求低,而电力需求高。
文中以东北某地区为例,风速、光照强度、温度及负荷年变化曲线如图 3所示,各待配置设备参数如表 2所示[29]。
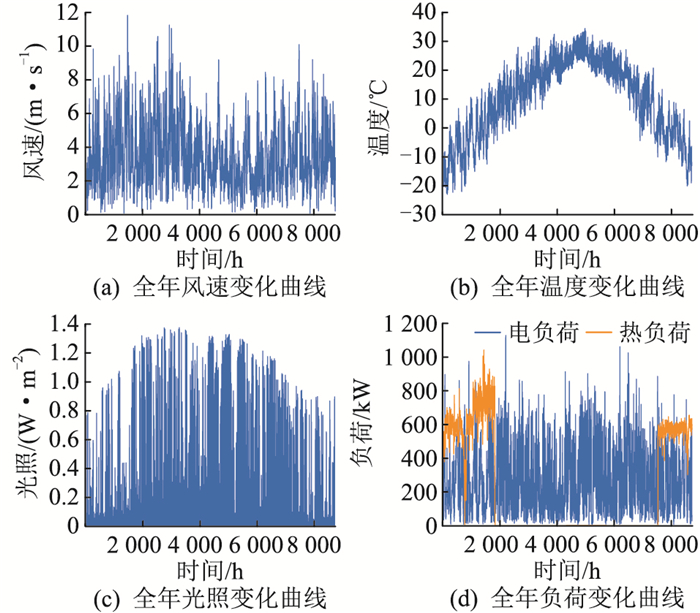
|
图 3 北方某地区自然资源及负荷年变化曲线 Fig. 3 Annual variation curve of natural resources and load in a certain area in the north |
|
|
表 2 各待配置设备参数 Table 2 Parameters of each device to be configured |
模型参数如下:储能SOC取值区间为[0.1, 0.9],长期贴现率为6%,通货膨胀率为3%,系统规划周期设置为20 a,其中光伏和风机的生命周期设置为20 a,储氢罐和储热罐的生命周期设置为10 a,氢锅炉的生命周期设置为8 a,电解槽的生命周期设置为5 a,蓄电池和质子交换膜燃料电池的生命周期设置为3 a,可再生能源的补贴为0.1元/(kW ·h)。SAPSO算法的参数设置为:种群规模取200,迭代次数取100,变异率为0.05,交叉率为0.1,惯性系数取值区间为[0.4, 0.9]。
3.2 算例设置文中设计对比方案来证明电-氢-热多能互补系统的经济性和可靠性,主要分为3个方案。
方案1:仅考虑蓄电池作为系统储能元件。
方案2:考虑蓄电池和氢储能混合储能作为系统储能元件。
方案3:考虑蓄电池、氢储能和热储能混合储能作为系统储能元件,即文中所提出的电-氢-热多能互补系统。
各方案的待配置设备组成如表 3所示。
|
|
表 3 各方案设备组成 Table 3 Equipment composition of each program |
以微网年均总费用、负荷失电率和可再生能源利用率为优化目标,对上述3个方案进行求解,得到3种方案的优化配置结果如表 4所示。
|
|
表 4 3种方案优化配置结果 Table 4 Optimization configuration results of three schemes |
对比方案1和方案2可知,配置一定量的氢储能对提高独立微网的供电可靠性和可再生能源利用率都有显著作用,且方案2蓄电池配置数量明显比方案1少,不难得出氢储能有效缓解了蓄电池储能压力。但由于购置了电解槽、储氢罐和质子交换膜燃料电池等设备,方案2的成本有所增加。对比方案2和方案3可知,在不增加微网负荷失电率的前提下,方案3进一步提高了可再生能源利用率,且蓄电池数量进一步减少,其原因在于剩余的可再生能源转化成热能,为热负荷提供补充。对比方案1和方案3可知,所提多能互补方案3较传统电储能配置方案1负荷失电率降低了3.18%,可再生能源利用率提高了8.37%。由此可以得出,文中提出的考虑电-氢-热多能互补的独立微网优化配置方法,对提高独立微网供电可靠性、促进可再生能源消纳和提升终端能源利用效率具有积极作用。
选取该地区冬季、夏季典型100 h分析电-氢-热多能互补的独立微网优化配置结果,其电力电量平衡如图 4所示。

|
图 4 考虑电-氢-热多能互补的独立微网优化配置的电量平衡结果 Fig. 4 Electric balance results of optimized configuration of independent microgrid considering electricity-hydrogen-heat multi-energy complementation |
在风光出力充裕的时段,电解槽工作,将原本的“弃风弃光”转化为氢气储存,作为电热备用。在风光出力不足的时段,质子交换膜燃料电池工作,将氢能转换为电能弥补电负荷缺额。图 5为该时段内独立微网配置的风光电源与电负荷间的差值(净功率),由数据可知,该时段内净功率维持在较小范围内,可由氢储能存储消耗,该地区基本可以实现100%可再生能源供电。
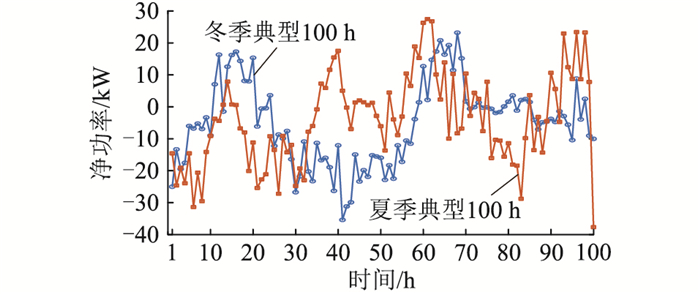
|
图 5 电量平衡结果 Fig. 5 Electricity balance results |
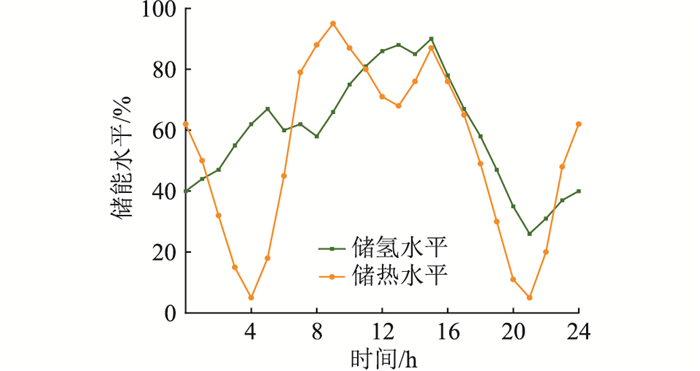
为了分析热备用工况下的氢储能运行特性,选取热负荷需求最高的冬季典型日为例,此时氢储能优势最为明显。其储氢水平、储热水平曲线如图 6所示。此过程对应氢储能供热功率变化曲线如图 7所示。
|
图 6 冬季典型日储能水平特性曲线 Fig. 6 Typical daily energy storage level characteristic curves in winter |

|
图 7 冬季典型日供热功率曲线 Fig. 7 Typical daily heating power curve in winter |
由图 6可知,储氢水平的变化与风光出力和电负荷需求之间的关系高度相关,0时—5时为风电出力较高时段,8时—13时为光伏出力较高时段,这2个时段可再生能源出力高于电负荷需求,此时电解槽持续电解水制氢并进行储存,储氢水平快速上升,同时此时段也是热负荷需求较高、需要供热的主要时段。16时—21时为电负荷需求高峰时段,此时可再生能源出力低于电负荷需求,质子交换膜燃料电池持续耗氢供电,储氢水平快速下降,此后由于风电出力上升,电负荷需求下降,储氢水平逐渐回升。储热水平不仅与风光出力和电负荷需求之间存在关系,还与热负荷需求高度相关,0时—4时、10时—13时这2个时段可再生能源出力高于电负荷需求,且此时热负荷需求较高,储热罐放热供应部分热负荷,储热快速下降。16时—21时电热负荷需求均高峰,储热罐快速放热满足热负荷,且持续时间较长,储热水平随之快速下降。其余时段储热罐处于吸热状态。
由图 7可知,考虑电-氢-热多能互补的独立微网中燃料电池耗氢产热、氢锅炉燃氢供热、储热罐吸放热这3种方式可灵活配合来供应部分热负荷。0时—4时、9时—13时这2个时段可再生能源出力高于电负荷需求,燃料电池不工作,但热负荷需求仍较高,此时热负荷由氢锅炉和储热罐供应。4时—5时、8时—9时这2个时段可再生能源出力高于电负荷需求,燃料电池不工作,热负荷需求较低,此时电解槽产氢部分用于储存,其余部分用于氢锅炉燃烧储热。16时—21时电热负荷需求均处于高峰,可再生能源出力低于电负荷需求,燃料电池持续耗氢供电供热,氢锅炉和储热罐同时工作供应剩余热负荷。其余时段电热负荷都较低,储热罐吸热作为热备用。
4 结论文中结合氢储能跨季节长周期大规模存储特性和多能联储联供特点,考虑当地自然资源和负荷需求特点,以风光发电、氢储能、蓄电池、氢锅炉等设备为基础,提出电-氢-热多能互补的热电联供独立微网系统,以经济性、供电可靠性、可再生能源利用率为目标对系统容量进行优化配置。通过设置3个方案进行算例验证对比:对比方案1和方案2可知,氢储能有利于提高微网的供电可靠性和可再生能源利用率;对比方案2和方案3可知,考虑电-氢-热多能互补的联合配置对提高独立微网供电可靠性、促进可再生能源消纳和提升终端能源利用效率都具有积极作用。所提方案较传统电储能配置方案负荷失电率降低了3.18%,可再生能源利用率提高了8.37%,可有效促进可再生能源消纳,保证独立微网的供电可靠性。
致谢
本文得到江苏省气电互联综合能源工程研究中心及江苏省高校自然科学研究项目(21KJB470024)资助,谨此致谢!
| [1] |
闫华光, 韩笑, 康建东. 电氢耦合助力构建新型电力系统[N/OL]. 中国能源报, 2021-08-16(8)[2023-03-20]. http://paper.people.com.cn/zgnyb/html/2021-08/16/content_3063957.htm. YAN Huaguang, HAN Xiao, KANG Jiandong. Electric hydrogen energy system assisted to construct the new power system[N/OL]. China Energy News, 2021-08-16(8)[2023-03-20]. http://paper.people.com.cn/zgnyb/html/2021-08/16/content_3063957.htm. (  0) 0) |
| [2] |
巩聪聪. 《中国氢能源及燃料电池产业白皮书》发布[J]. 山东国资, 2019(6): 14. GONG Congcong. ″White paper on China's hydrogen energy and fuel cell industry″ released[J]. State-Owned Assets of Shandong, 2019(6): 14. (  0) 0) |
| [3] |
周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205. ZHOU Xiaoxin, CHEN Shuyong, LU Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904, 2205. (  0) 0) |
| [4] |
PFENNINGER S, HAWKES A, KEIRSTEAD J. Energy systems modeling for twenty-first century energy challenges[J]. Renewable and Sustainable Energy Reviews, 2014, 33: 74-86. DOI:10.1016/j.rser.2014.02.003 (  0) 0) |
| [5] |
舒印彪, 薛禹胜, 蔡斌, 等. 关于能源转型分析的评述(一)转型要素及研究范式[J]. 电力系统自动化, 2018, 42(9): 1-15. SHU Yinbiao, XUE Yusheng, CAI Bin, et al. A review of energy transition analysis part one elements and paradigms[J]. Automation of Electric Power Systems, 2018, 42(9): 1-15. (  0) 0) |
| [6] |
邵志芳, 吴继兰, 赵强. 城市电网耦合氢储能系统投资决策方法研究[J]. 电力工程技术, 2017, 36(5): 45-51. SHAO Zhifang, WU Jilan, ZHAO Qiang. Investment decision method of coupled hydrogen energy storage system in urban power grid[J]. Electric Power Engineering Technology, 2017, 36(5): 45-51. (  0) 0) |
| [7] |
PAN G S, GU W, LU Y P, et al. Optimal planning for electricity-hydrogen integrated energy system considering power to hydrogen and heat and seasonal storage[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2662-2676. DOI:10.1109/TSTE.2020.2970078 (  0) 0) |
| [8] |
WEN T, ZHANG Z Y, LIN X N, et al. Research on modeling and the operation strategy of a hydrogen-battery hybrid energy storage system for flexible wind farm grid-connection[J]. IEEE Access, 2020, 8: 79347-79356. DOI:10.1109/ACCESS.2020.2990581 (  0) 0) |
| [9] |
TENG Y, WANG Z D, LI Y, et al. Multi-energy storage system model based on electricity heat and hydrogen coordinated optimization for power grid flexibility[J]. CSEE Journal of Power and Energy Systems, 2019, 5(2): 266-274. (  0) 0) |
| [10] |
蒋东方, 贾跃龙, 鲁强, 等. 氢能在综合能源系统中的应用前景[J]. 中国电力, 2020, 53(5): 135-142. JIANG Dongfang, JIA Yuelong, LU Qiang, et al. Application prospect of hydrogen energy in integrated energy systems[J]. Electric Power, 2020, 53(5): 135-142. (  0) 0) |
| [11] |
马榕谷, 陈洁, 赵军超, 等. 非并网风氢互补系统的容量多目标优化[J]. 太阳能学报, 2019, 40(2): 422-429. MA Ronggu, CHEN Jie, ZHAO Junchao, et al. Multi-objective optimization for capacity of non-grid-connected wind/hydrogen hybrid power system[J]. Acta Energiae Solaris Sinica, 2019, 40(2): 422-429. (  0) 0) |
| [12] |
袁铁江, 李国军, 张增强, 等. 风电-氢储能与煤化工多能耦合系统设备投资规划优化建模[J]. 电工技术学报, 2016, 31(14): 21-30. YUAN Tiejiang, LI Guojun, ZHANG Zengqiang, et al. Optimal modeling on equipment investment planning of wind power-hydrogen energy storage and coal chemical pluripotent coupling system[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 21-30. (  0) 0) |
| [13] |
滕云, 闫佳佳, 回茜, 等. "无废" 电-氢充能服务区多源微网优化运行模型[J]. 中国电机工程学报, 2021, 41(6): 2074-2088. TENG Yun, YAN Jiajia, HUI Qian, et al. Optimization operation model of ″zero-waste″ electricity-hydrogen charging service area multi-energy microgrid[J]. Proceedings of the CSEE, 2021, 41(6): 2074-2088. (  0) 0) |
| [14] |
SHAO C C, FENG C J, SHAHI DEHPOUR M, et al. Optimal stochastic operation of integrated electric power and renewable energy with vehicle-based hydrogen energy system[J]. IEEE Transactions on Power Systems, 2021, 36(5): 4310-4321. DOI:10.1109/TPWRS.2021.3058561 (  0) 0) |
| [15] |
WU X, LI H Y, WANG X L, et al. Cooperative operation for wind turbines and hydrogen fueling stations with on-site hydrogen production[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2775-2789. DOI:10.1109/TSTE.2020.2975609 (  0) 0) |
| [16] |
陈维荣, 傅王璇, 韩莹, 等. 计及需求侧的风-光-氢多能互补微电网优化配置[J]. 西南交通大学学报, 2021, 56(3): 640-649. CHEN Weirong, FU Wangxuan, HAN Ying, et al. Optimal configuration of wind-solar-hydrogen multi-energy complementary microgrid with demand side[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 640-649. (  0) 0) |
| [17] |
马腾飞, 裴玮, 肖浩, 等. 基于纳什谈判理论的风-光-氢多主体能源系统合作运行方法[J]. 中国电机工程学报, 2021, 41(1): 25-39, 395. MA Tengfei, PEI Wei, XIAO Hao, et al. Cooperative operation method for wind-solar-hydrogen multi-agent energy system based on Nash bargaining theory[J]. Proceedings of the CSEE, 2021, 41(1): 25-39, 395. (  0) 0) |
| [18] |
李奇, 赵淑丹, 蒲雨辰, 等. 考虑电氢耦合的混合储能微电网容量配置优化[J]. 电工技术学报, 2021, 36(3): 486-495. LI Qi, ZHAO Shudan, PU Yuchen, et al. Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 486-495. (  0) 0) |
| [19] |
李鹏, 韩建沛, 殷云星, 等. 电转氢作为灵活性资源的微网容量多目标优化配置[J]. 电力系统自动化, 2019, 43(17): 28-35, 139. LI Peng, HAN Jianpei, YIN Yunxing, et al. Multi-objective optimal capacity configuration of microgrid with power to hydrogen as flexible resource[J]. Automation of Electric Power Systems, 2019, 43(17): 28-35, 139. (  0) 0) |
| [20] |
黄福荣, 许方园, 刘国中, 等. 计及负荷需求响应的风光储氢系统容量优化配置[J]. 供用电, 2023, 40(2): 45-51. HUANG Furong, XU Fangyuan, LIU Guozhong, et al. Optimal capacity allocation of wind solar hydrogen storage system considering load demand response[J]. Distribution & Utilization, 2023, 40(2): 45-51. (  0) 0) |
| [21] |
李彬, 潘雨情, 文华杰, 等. 基于碳减排的氢电资源耦合发展现状及展望[J]. 供用电, 2023, 40(10): 106-113. LI Bin, PAN Yuqing, WEN Huajie, et al. Current status and prospects of hydrogen electricity resource coupling developmentbased on carbon emission reduction[J]. Distribution & Utilization, 2023, 40(10): 106-113. (  0) 0) |
| [22] |
尤石, 郑艺, 黄纯军. 电解水制氢在丹麦能源系统中的发展与应用[J]. 供用电, 2022, 39(1): 2-7. YOU Shi, ZHENG Yi, HUANG Chunjun. Converting green electricity to green hydrogen: the status and prospects of water electrolyser development and applications in Denmark[J]. Distribution & Utilization, 2022, 39(1): 2-7. (  0) 0) |
| [23] |
LI J R, LIN J, SONG Y H, et al. Operation optimization of power to hydrogen and heat (P2HH) in ADN coordinated with the district heating network[J]. IEEE Transactions on Sustainable Energy, 2019, 10(4): 1672-1683. DOI:10.1109/TSTE.2018.2868827 (  0) 0) |
| [24] |
XU Y, XU Y, HUANG Y. Generation of typical operation curves for hydrogen storage applied to the wind power fluctuation smoothing mode[J]. Global Energy Interconnection, 2022, 5(4): 353-361. DOI:10.1016/j.gloei.2022.08.002 (  0) 0) |
| [25] |
LU J, HUANG D, REN H. Data-driven source-load robust optimal scheduling of integrated energy production unit including hydrogen energy coupling[J]. Global Energy Interconnection, 2023, 6(4): 375-388. DOI:10.1016/j.gloei.2023.08.001 (  0) 0) |
| [26] |
严思韵, 王晨, 周登极. 含氢能气网掺混输运的综合能源系统优化研究[J]. 电力工程技术, 2021, 40(1): 10-16, 49. YAN Siyun, WANG Chen, ZHOU Dengji. Optimization of integrated electricity and gas system considering hydrogen-natural-gas mixture transportation[J]. Electric Power Engineering Technology, 2021, 40(1): 10-16, 49. (  0) 0) |
| [27] |
王珺. 区域综合能源系统规划及优化运行[D]. 南京: 东南大学, 2017. WANG Jun. Planning and operating of regional integrated energy system[D]. Nanjing: Southeast University, 2017. (  0) 0) |
| [28] |
许剑, 刘松阳, 卢建生, 等. 基于递阶模型的综合能源系统多时间尺度运行优化研究[J]. 供用电, 2023, 40(1): 73-79. XU Jian, LIU Songyang, LU Jiansheng, et al. Research on multi-time scale operation optimization of integrated energy system based on hierarchical model[J]. Distribution & Utilization, 2023, 40(1): 73-79. (  0) 0) |
| [29] |
王侃宏, 赵政通, 刘欢, 等. 基于HOMER和SA-PSO算法的风光氢储系统的优化匹配[J]. 水电能源科学, 2020, 38(5): 207-210. WANG Kanhong, ZHAO Zhengtong, LIU Huan, et al. Optimization matching analysis of wind-photovoltaic-hydrogen-storage system based on HOMER and SA-PSO algorithm[J]. Water Resources and Power, 2020, 38(5): 207-210. (  0) 0) |
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China

 吕振宇(1989), 男, 博士, 讲师, 研究方向为微电网运行控制、新型储能应用(E-mail:
吕振宇(1989), 男, 博士, 讲师, 研究方向为微电网运行控制、新型储能应用(E-mail: