文章编号: 2096-3203(2023)04-0023-08 中图分类号: TM72; U469.72
2. 国网江苏省电力有限公司靖江市供电分公司,江苏 泰州 214500;
3. 南方电网科学研究院有限责任公司,广东 广州 510663
石油资源短缺和环境污染问题日渐突出,电动汽车(electric vehicle, EV)因具有低碳环保、舒适安静等显著优势,对社会经济可持续发展具有重要意义[1-4]。公共快充站(fast charging station, FCS)是EV的主要能源供给设施[5-7],随着EV的推广应用,FCS也得到快速建设与发展。截至2022年底,我国EV保有量为1 045万辆[8],充电基础设施累计数量为521万台[9],随之而来的充电负荷也快速攀升,易造成配电网局部过载以及低电压等问题[10]。而充电负荷作为一种灵活的需求侧响应资源,可直接或间接对其充电过程进行有序控制,即控制、引导充电负荷的时空分布,缓解EV接入给配电网运行带来的冲击与不良影响,进一步提升配电网可容纳的充电负荷。
针对电力交通的融合交互,国内外学者在充电引导方面开展了探索与分析,其中文献[11-14]通过分析电力与交通之间的交互,构建充电引导框架,实现对用户充电行为的引导,文献[11-14]考虑的主体行为略有差异。文献[11]考虑交通和配电网的运行情况,假设用户在充电导航下选择总时间最小的FCS进行充电,进而分析充电负荷分布情况;文献[12]构建基于“车-网-路-站”的有序充电导航系统,考虑多方诉求, 构建“车-网-路-站”多目标引导优化模型,实现充电策略综合最优;文献[13]考虑电网运行和实时交通信息,提出EV快速充电导航优化策略,以用户出行时间和充电费用的综合成本最小为目标;文献[14]在路-电耦合网络下构建交通流-能量流-信息流的交互框架,提出路径规划与交通网信息更新同周期的动态导航。上述研究主要侧重多方主体交互的充电引导,分析多方信息融合下的用户充电行为,但未精细刻画交通出行过程对充电行为的影响,影响充电引导过程的精确性。
充电价格是影响用户充电行为的另一重要因素。在采用价格激励引导EV充电行为方面,国内外学者开展了充电价格制定方面的研究,间接灵活控制、引导负荷分布。文献[15-19]通过制定充电电价,引导调整用户充电计划,以价格激励实现有序充电控制,但侧重略有不同。其中文献[15]设计削峰填谷定价机制,引导充电负荷合理分布;文献[16]基于边际成本制定随机出行行为模型,以车辆充电成本优化模型和基于代理的市场均衡模型确定电价,进而抑制负荷峰值;文献[17]讨论不同主体利益最大和多方共赢下的定价模型优缺点,提出多目标充电定价优化模型;文献[18]提出以方差评估调峰水平以及考虑用户充电等待时间的博弈模型,进而优化EV充电行为;文献[19]提出将虚拟电厂作为售电运营商的主从博弈模型,通过制定合理的售电价格引导EV有序充电。上述研究主要利用价格激励间接控制、引导充电负荷在时间上的分布,未考虑交通网络、充电设施分布在空间上的差异。
在考虑充电负荷时空灵活性的定价方面,国内外学者也开展了相关研究。文献[20]通过制定拥塞水平、节点电压偏差和能量损失率作为节点指标,优化节点电价和道路交通拥堵价格,并从空间和时间上转移负荷;文献[21]通过考虑用户与FCS之间的博弈,优化FCS的充电价格,使得FCS之间的服务率达到平衡;文献[22]针对充电决策行为路径规划,利用图论中的扩展图模型描述,考虑电网和交通运营商等作为单独个体,以社会运行最优为目标,制定时空充电价格。上述研究针对引导充电负荷时空分布进行了初步探讨,而针对多主体行为也已有相关文献开展研究。文献[23]利用动态路网模型和主从博弈模型,以“车-路-网”3个主体的利益最大为目标,提出多目标充电负荷时空优化调度;文献[24]面向“代客加电”场景,主要考虑用户、司机以及充电网运营商的利益,提出多目标优化的充电引导策略。但上述研究对于用户决策行为的刻画较为理想,未精细化考虑不同用户对于充电决策方案的反应程度和权衡过程,影响充电时空分布的评估精度。
为解决上述问题,文中建立EV出行链移动模型,分析EV出行剩余电量时空分布。进而综合考虑剩余电量、充电设施分布、充电电价等因素,提出基于后悔理论的充电决策模型,分析不同因素对充电负荷时空分布的影响。最终建立以配电网经济运行为目标的充电价格优化模型,实现最优充电价格的制定。
1 考虑用户充电决策行为的EV充电引导策略模型 1.1 EV充电引导策略框架考虑用户在不同FCS的选择、剩余电量以及充电服务价格等对充电决策行为的影响,文中所提EV充电引导策略框架如图 1所示。该策略主要包括EV移动模型、用户充电决策模型和充电服务价格优化模型。其中, EV移动模型利用出行链刻画用户的出行需求,并考虑动态交通路况获取充电需求的时空分布。在此基础上,利用后悔理论,构建用户充电决策模型,在剩余电量支撑下,确定用户选择的FCS。进而建立充电服务价格优化模型,通过分析用户充电决策行为,确定充电负荷分布,以配电网网损最小为目标,优化FCS的充电服务价格,引导用户的充电行为,改变充电负荷空间分布,提升配电网运行经济性。

|
图 1 EV充电引导策略框架 Fig. 1 EV charging guidance strategy framework |
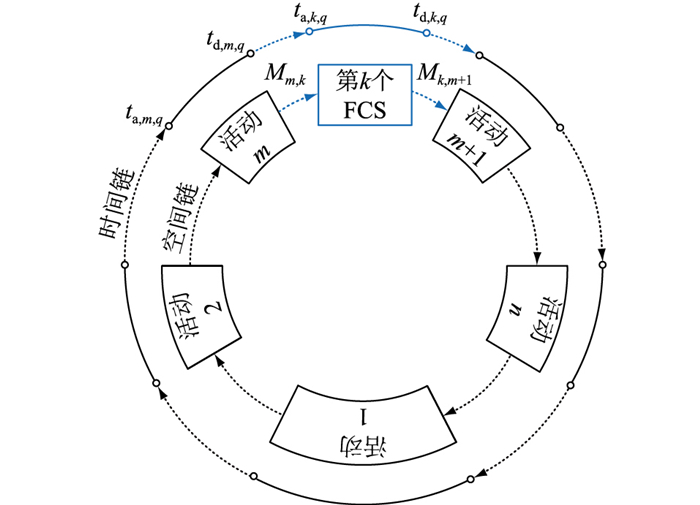
针对EV充电负荷时空分布特点,建立EV移动模型,确定EV剩余电量的时空分布。首先,采用出行链法描述EV一天的出行需求,文中出行需求为每个活动的类型、地点和出发时间。然后,根据出行需求和历史交通状况,利用Dijkstra最短路径算法规划出行时间最少的行车路径。第q辆EV的出行链如图 2所示。
|
图 2 第q辆EV的出行链 Fig. 2 Trip chain of the q-th EV |
图 2中,活动1、2、…、m-1、m、m+1、…、n-1、n为用户每次出行的活动地点;ta, m, q、td, m, q分别为第q辆EV到达和离开活动地点m的时间;ta, k, q、td, k, q分别为第q辆EV到达和离开第k个FCS的时间;Mm, k为活动地点m到第k个FCS路径中设置的路段集合;Mk, m+1为第k个FCS到活动地点m+1路径中设置的路段集合;Mm, m+1为活动地点m到活动地点m+1路径中设置的路段集合。
利用上述模型,可考虑在活动地点慢充,在FCS快充。在离开活动地点m时,如果第q辆EV的荷电状态(state of charge, SOC)不能满足未来到达活动地点m+1的路径规划需求,则第q辆EV将放弃原规划路径,绕行至第k个FCS,如图 2中蓝线所示。文中所述用户充电决策行为可选择出最优FCS以及到达该FCS的最优绕行路径。
根据出行需求、行车路径和交通状况,第q辆EV到达活动地点m的时间为:
| $ t_{\mathrm{a}, m, q}=t_{\mathrm{d}, m-1, q}+\sum\limits_{(i, j) \in M_{m-1, m}} t_{\mathrm{r}, i, j} $ | (1) |
式中:td, m-1, q为第q辆EV离开活动地点m-1的时间;Mm-1, m为活动地点m-1到活动地点m路径中设置的路段集合;tr, i, j为节点i到节点j路段的行程时间。
| $ t_{\mathrm{r}, i, j}=d_{i, j} / v_{i, j} $ | (2) |
式中:di, j为节点i到节点j的距离,可由Dijkstra算法确定;vi, j为EV在节点i到节点j路段的平均通行速度,具体表达见式(3)。
| $ \left\{\begin{array}{l} v_{i, j}=v_{i, j}^{\max } /\left[1+\left(\frac{Q_{i, j}}{C_{i, j}}\right)^w\right] \\ w=a+b\left(\frac{Q_{i, j}}{C_{i, j}}\right)^\gamma \end{array}\right. $ | (3) |
式中:vi, jmax为节点i到节点j路段的通行速度最大值;Qi, j为节点i到节点j路段的车流量;Ci, j为节点i到节点j路段的道路通行能力;a、b、γ为道路等级自适应系数。
确定第q辆EV到达活动地点m的剩余电量为:
| $ E_{\mathrm{A}, m, q}=E_{\mathrm{F}, m-1, q}-\sum\limits_{(i, j) \in M_{m-1, m}} E_{\mathrm{c}} d_{i, j} $ | (4) |
式中:EF, m-1, q为第q辆EV离开活动地点m-1的剩余电量;Ec为EV行驶每千米的耗电量。
EV起始充电时间是影响充电负荷时空分布的关键因素,而EV起始充电时间受用户出行需求的影响。据统计,用户出行分布具有早、晚高峰等多峰分布,而正态分布无法准确描述多峰现象。因此,文中假设第q辆EV离开活动地点1的时间td, 1, q服从高斯混合模型分布,具体概率分布函数p(td, 1, q|Θ)为:
| $ p\left(t_{\mathrm{d}, 1, q} \mid \Theta\right)=\sum\limits_{\vartheta=1}^J x_{\vartheta} N_{\vartheta}\left(t_{\mathrm{d}, 1, q} ; \mu_{\vartheta}, D_{\vartheta}\right) $ | (5) |
| $ \begin{aligned} & N_{\vartheta}\left(t_{\mathrm{d}, 1, q} ; \mu_{\vartheta}, D_{\vartheta}\right)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} D_{\vartheta}}} \times \\ & \exp \left(-\left(t_{\mathrm{d}, 1, q}-\mu_{\vartheta}\right)^2 /\left(2 D_{\vartheta}\right)\right) \end{aligned} $ | (6) |
式中:N∂(td, 1, q; μ∂, D∂)为第∂个高斯分量函数, μ∂为平均值, D∂为方差;J为高斯分量的个数;x∂为第∂个高斯分量的权重;Θ={θ1, θ2, …, θ∂, …, θJ}为元素集合。
EV初始SOC概率密度函数Pd(E0; φ, D)为:
| $ \begin{gathered} P_{\mathrm{d}}\left(E_0 ; \varphi, D\right)=\frac{\tau}{d_{\mathrm{R}}\left(1-E_0\right) \sqrt{2 {\rm{ \mathsf{ π} }} D}} \times \\ \exp \left(-\left(\ln \left(1-E_0\right)-\left(\varphi-\ln \left(d_{\mathrm{R}} / \tau\right)\right)\right)^2 /(2 D)\right) \end{gathered} $ | (7) |
式中:E0为EV的初始SOC;φ为日行驶里程值;D为概率密度函数方差;τ为EV充电后可行驶天数;dR为EV续航里程。
1.3 用户充电决策模型该模型首先考虑充电绕行,并计算出行消耗总时间;然后针对站内等待时间,利用双队列集合,枚举确定用户等待时间;最后利用后悔理论,在给定价格方案下,结合充电费用和消耗时间,考虑用户充电行为的主观判断与决策,确定EV选择充电的FCS,进而确定充电负荷分布。
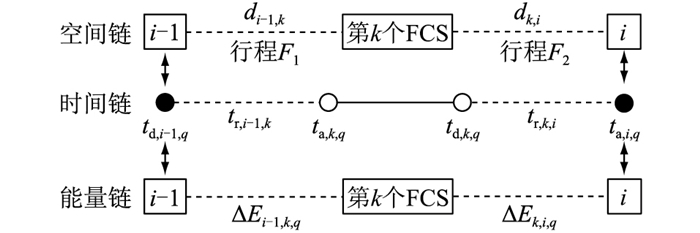
1.3.1 充电绕行在行驶过程中若电池电量无法支撑EV到达目的地,用户会选择途中充电。例如,当第q辆EV的电量无法支撑其从第i-1个目的地到第i个目的地,EV需要绕行到第k个FCS进行充电,则第q辆EV的此次出行将包括2个行程。一是从第i-1个停留地行驶到第k个FCS,即图 3中的行程F1;二是从第k个FCS行驶到第i个停留地,即图 3中的行程F2。图 3中,ΔEi-1, k, q为第q辆EV从第i-1个目的地到第k个FCS的耗电量;ΔEk, i, q为第q辆EV从第k个FCS到第i个目的地的耗电量。
|
图 3 EV途中充电出行示意 Fig. 3 Schematic diagram of EV on-the-way charging travel |
假设服从先到先服务的规则,第q辆EV在FCS的活动情况如图 4所示。

|
图 4 EV在FCS的活动情况 Fig. 4 EV activities at FCS |
根据EV到达时间、FCS内EV数量和充电桩数量,可利用2个队列描述站内EV用户等待和充电情况。利用集合A={ta, k, q|q∈[1, NFC]}、B={td, k, q|q∈[1, NFC]}分别表示EV到达和离开第k个FCS的时间,其中NFC为需要充电的EV数量。可确定时刻t第k个FCS的EV数量为:
| $ n_{\text {ev }, k, t}=f_{\text {size }}(A, t)-f_{\text {size }}(B, t) $ | (8) |
式中: fsize(A, t)、fsize(B, t)分别为时刻t前累计到达和离开的EV数量。
以第q辆EV在第k个FCS的具体活动为例。当第q辆EV在时刻ta, k, q到达第k个FCS时,第q辆EV前面排有nev, k, t辆EV。如果nev, k, t小于第k个FCS处的充电桩数量Ck,则第q辆EV在第k个FCS的等待时间tw, k, q等于0;否则tw, k, q取式(9)中tw的最小值。
| $ \left\{\begin{array}{l} \min t_{\mathrm{w}} \\ \text { s.t. } f_{\mathrm{size}}\left(B, t_{\mathrm{a}, k, q}+t_{\mathrm{w}}\right)+C_k>f_{\text {size }}\left(A, t_{\mathrm{a}, k, q}\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ t_{\mathrm{a}, k, q}+t_{\mathrm{w}} \in B \end{array}\right. $ | (9) |
受限于自身心理因素和认知水平,用户并非能够选择整体或个体利益效用最大的方案。若用户所选方案效用低于其他备选方案效用,可能会产生后悔状态;反之,则产生欣喜状态。用户习惯通过反复权衡不同方案之间的效用差,倾向选择具有折衷效应的方案。考虑到上述用户行为状态,文中利用后悔理论描述用户的后悔规避状态[23]。
将全部备选FCS即剩余电量可到达的FCS作为方案集。每个备选方案中主要采用时间消耗以及充电费用刻画备选方案效用,如式(10)所示。通过比较全部备选方案的效用,用户将选择综合成本最小的FCS完成充电。
| $ \begin{aligned} U_{\mathrm{c}}= & \sum\limits_{j_{\mathrm{c}} \neq k_{\mathrm{c}}} \ln \left(1+\exp \left(\xi_1\left(t_{\mathrm{c}, j \mathrm{c}}-t_{\mathrm{c}, k \mathrm{c}}\right)\right)\right)+ \\ & \ln \left(1+\exp \left(\xi_2\left(C_{j \mathrm{c}}-C_{k \mathrm{c}}\right)\right)\right)+\sigma_{\mathrm{c}} \end{aligned} $ | (10) |
| $ t_{\mathrm{c}, k \mathrm{c}}=t_{\mathrm{c}}+t_{\mathrm{w}}+t_{\mathrm{r}} $ | (11) |
式中:Uc为考虑充电时间消耗和充电费用的综合成本;jc、kc为备选FCS的编号;ξ1、ξ2分别为决策者对时间消耗和充电费用的等效折算系数;tc, jc为EV选择第jc个FCS的时间消耗;tc, kc为EV选择第kc个FCS的时间消耗,其由充电时间tc、等待时间tw和充电绕行时间tr三部分构成;Cjc、Ckc分别为选择第jc个、第kc个FCS的充电费用;σc为随机误差。
1.4 充电服务价格优化模型配电网网损SL最小的目标函数如式(13)所示,可利用内敛法求解该模型。
| $ \min\ S_{\mathrm{L}}=\sum\limits_{l=1}^{N_{\mathrm{LI}}} \sum\limits_{t_1=1}^T s_{l, t_1} $ | (13) |
式中:sl, t1为支路l在时段t1的网损;NLI为配电网线路条数;T为总时段数。
(1) FCS收入约束。假设优化充电价格之前,所有FCS充电价格相同且不变,设为p0。假设所有FCS隶属于同一运营商,从而FCS收入在优化前后保持不变,即用户充电成本保持不变,具体表示为:
| $ \sum\limits_{k=1}^{N_{\mathrm{fcs}}} p_k \times \sum\limits_{q \in {\mathit{\Omega}}\left(k, p_k\right)} \Delta F_{k, q}=\sum\limits_{k=1}^{N_{\mathrm{fcs}}} p_0 \times \sum\limits_{q \in {\mathit{\Omega}}\left(k, p_0\right)} \Delta F_{k, q} $ | (14) |
式中:Nfcs为FCS的数量;pk为第k个FCS调整后的充电价格;Ω(k, pk)、Ω(k, p0)分别为以充电价格pk、p0选择第k个FCS的EV用户集合;ΔFk, q为第q辆EV在第k个FCS充电的充电量。
(2) 充电服务价格上下限边界约束。
| $ p_{\min } \leqslant p_k \leqslant p_{\max } $ | (15) |
式中:pmax、pmin分别为充电服务价格的上、下限。
(3) 电压约束。
| $ U_{\min } \leqslant U_n \leqslant U_{\max } $ | (16) |
式中:Un为配电网节点n的电压;Umax、Umin分别为配电网节点的最大、最小电压。
(4) 电流约束。
| $ I_{l, \min } \leqslant I_l \leqslant I_{l, \max } \quad l \in {\mathit{\Omega}}_{\mathrm{L}} $ | (17) |
式中:Il为支路l中的电流;Il, max、Il, min分别为支路l的最大、最小电流;ΩL为支路集合。
(5) 潮流约束。
| $ \left\{\begin{array}{l} P_{\mathrm{D}, f}+P_f=U_f \sum\limits_{g=1}^{N_{\mathrm{D}}} U_g\left(G_{f, g} \cos \theta_{f, g}+B_{f, g} \sin \theta_{f, g}\right) \\ Q_{\mathrm{D}, f}+Q_f=U_f \sum\limits_{g=1}^{N_{\mathrm{D}}} U_g\left(G_{f, g} \sin \theta_{f, g}-B_{f, g} \cos \theta_{f, g}\right) \end{array}\right. $ | (18) |
式中:PD, f、QD, f分别为无充电负荷接入时,节点f的有功和无功功率;Pf、Qf分别为节点f的充电负荷有功和无功功率;ND为配电网节点数;Ug为配电网节点g的电压;Gf, g、Bf, g分别为节点f和节点g间线路的电导、电纳;θf, g为节点f与节点g处电压的相角差。
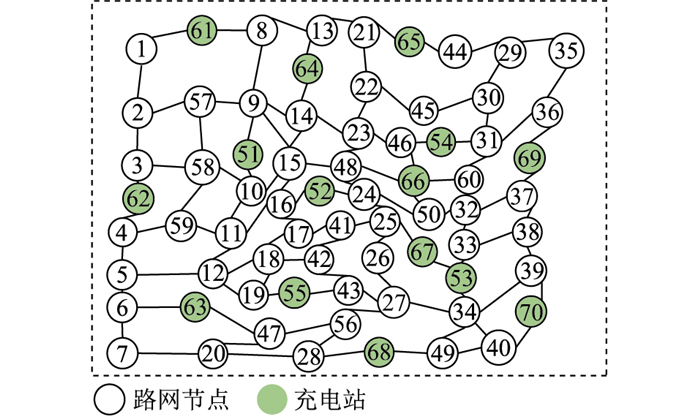
2 实例分析 2.1 算例设置算例设置15个FCS,分别位于路网中的节点51—55、61—70,路网结构如图 5所示,具体参数可参考文献[23]。
|
图 5 路网结构 Fig. 5 Road network structure |
算例采用3个IEEE 33节点配电网,其中位于路网节点51—55的充电站分别接入配电网1的节点10、20、24、17、12,位于路网节点61—65的充电站分别接入配电网2的节点10、20、24、17、12,位于路网节点66—70的充电站分别接入配电网3的节点10、20、24、17、12。改进后IEEE 33节点配电网的负荷线路等信息可参考文献[25]。
假设每个FCS的EV运营商相同,且充电桩规格相同。位于路网节点51—55、61—70的FCS,站内充电桩数分别为10、15、20、30、10、20、20、15、25、10、10、12、12、15、15,每个充电桩的充电功率最大值为90 kW。设置EV为1 200辆,共设置4种车型,各车型的电池额定容量及Ec见表 1。pmax=2元/(kW ·h),pmin=1元/(kW ·h);每个站充电服务价格初始值均设为1.6元/(kW ·h);配电网节点电压的上、下限分别为节点额定电压的1.1倍和0.9倍;ξ1、ξ2分别设置为17和1。
|
|
表 1 主要EV类型 Table 1 Main EV types |
参考文献[25],考虑7种类型的停留,分别为临时返回家、工作、购物、娱乐、接送某人、就餐和返回家,具体停留时间参考文献[25]。路网中各节点的活动类型如表 2所示。
|
|
表 2 路网节点类型 Table 2 Road network node types |
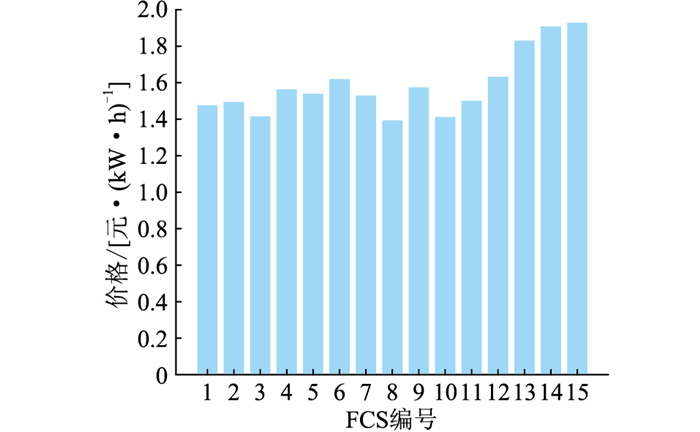
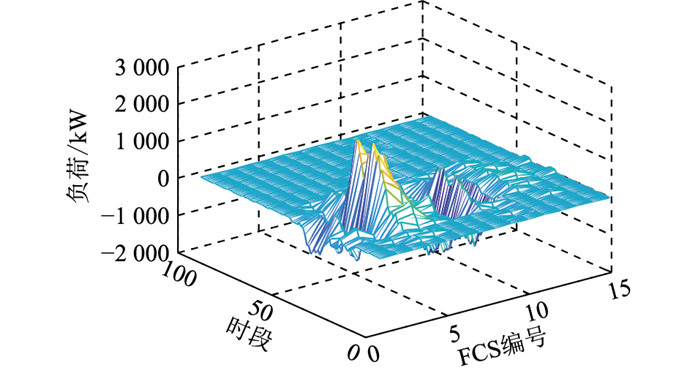
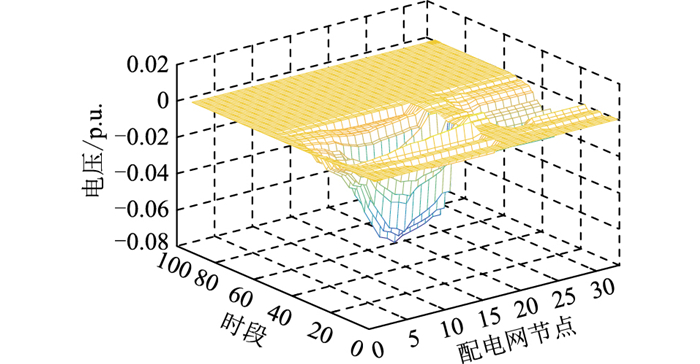
在初始充电服务费下,利用内敛法寻找优化解,经8次迭代后,网损从优化前的710.4 kW减少到47.5 kW。优化后的充电服务费方案见图 6,其中将位于路网节点51—55、61—70的FCS编号为1号—15号。13号—15号FCS充电服务费高于原始价格1.6元/(kW ·h),而其余FCS的充电服务费略低于1.6元/(kW ·h)。6号FCS与其他相邻FCS相比,充电服务费略高。优化前后FCS充电负荷差见图 7,在充电服务费引导下,13号—15号FCS由于充电服务费较高,充电负荷略有所降低。而6号FCS的充电价格较高,原充电用户将在距离和时间等因素可接受的FCS中,选择折衷方案。用户改变充电选择后,充电负荷发生时空转移,6号FCS的充电负荷明显降低,进而引起配电网节点10的电压变化见图 8。文中方法通过优化后的充电服务费引导负荷分布,进而改善电压分布,减少配电网总网损。
|
图 6 优化后的充电服务费方案 Fig. 6 Optimized charging service fee pricing scheme |
|
图 7 优化前后FCS充电负荷差 Fig. 7 FCS charging load difference before and after optimization |
|
图 8 优化前后配电网电压差值 Fig. 8 Voltage difference of distribution network before and after optimization |
为分析EV总数量与各车型比例对引导结果的影响,文中设置场景1—场景4,不同场景的EV分布如表 3所示。场景1—场景4的EV总数量分别为1 200、1 200、1 200、800。
|
|
表 3 不同场景EV分布 Table 3 EV distribution under different scenarios |
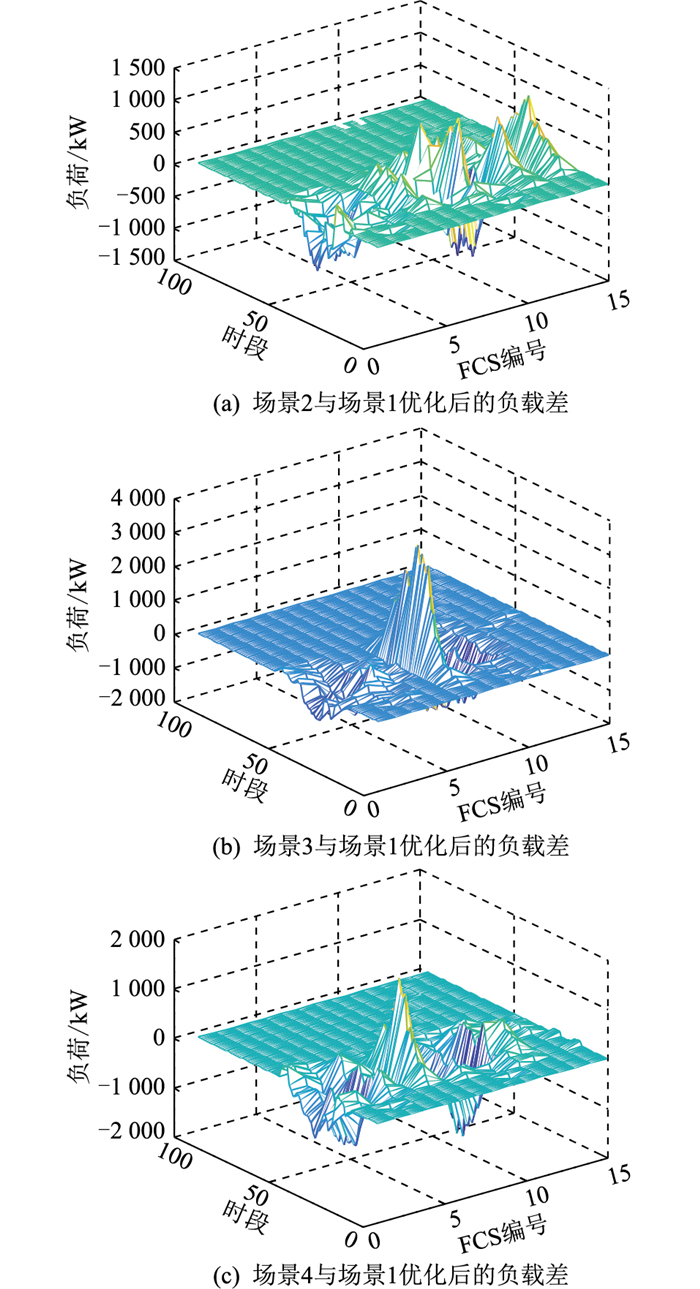
各场景优化后与场景1优化后的负荷差如图 9所示。小容量EV车型增加时,各FCS的充电负荷均有所增加,如图 9(a)所示。而大容量EV车型增加时,充电负荷变化主要集中在某个FCS,如图 9(b)所示。这表示小容量EV车型占比较多时,文中方法更易全局进行充电负荷调整;而大容量EV车型占比较多时,更容易调整某个FCS负荷。由图 9(c)可知,场景4与场景1相比,车辆总数减少时,各FCS充电负荷整体有增有减,网损变化不大,可见EV总数对整体调整效果影响不大。
|
图 9 优化后各场景FCS负荷差 Fig. 9 FCS load difference of each scene after optimization |
为分析充电决策模型中参数ξ1、ξ2对引导结果的影响,文中设置场景5—场景7,如表 4所示。再结合场景1—场景4,所有场景优化后的总网损如表 5所示。对比场景1—场景3的总网损,车型容量整体越小时,利用充电服务费引导的效果越好;对比场景1与场景4的总网损,EV总数量对网损的影响较小。对比场景1与场景5—场景7的总网损,用户时间消耗等效折算系数越低,引导时充电服务费对用户充电选择的影响越大,越需要降低充电服务费以引导充电负荷。
|
|
表 4 等效折算系数设置 Table 4 Equivalent conversion coefficient setting |
|
|
表 5 各场景优化后的总网损 Table 5 Total network loss after optimization in each scenario |
文中针对城市公共FCS,综合考虑剩余电量、充电设施分布、充电电价等因素,提出基于后悔理论的充电决策模型,以配电网网损最小为目标,优化各FCS的充电服务价格,从而实现用户充电行为引导。通过算例对比分析可知:文中所提方法可有效改变充电负荷空间分布,且对小容量车型的引导效果更好;FCS可参与电力市场获取额外收益,用较低的充电服务费引导负荷分布。
文中目前主要从用户角度刻画其决策行为,暂未考虑影响EV电量消耗的因素以及其他主体利益,这些将是下一步工作的研究重点。
| [1] |
王明深. 面向多应用场景的电动汽车集群控制与日前竞价策略研究[D]. 天津: 天津大学, 2020. WANG Mingshen. Control and day-ahead bidding strategies of electric vehicle aggregator for multiple application scenarios[D]. Tianjin: Tianjin University, 2020. (  0) 0) |
| [2] |
贺瑜环, 杨秀媛, 陈麒宇, 等. 电动汽车智能充放电控制与应用综述[J]. 发电技术, 2021, 42(2): 180-192. HE Yuhuan, YANG Xiuyuan, CHEN Qiyu, et al. Review of intelligent charging and discharging control and application of electric vehicles[J]. Power Generation Technology, 2021, 42(2): 180-192. (  0) 0) |
| [3] |
李龙, 贺瀚青, 张钰声, 等. 配电网接纳电动汽车充电负荷能力的评估方法[J]. 电网与清洁能源, 2022, 38(11): 107-116. LI Long, HE Hanqing, ZHANG Yusheng, et al. Evaluation of electric vehicle charging load capacity of distribution networks[J]. Power System and Clean Energy, 2022, 38(11): 107-116. (  0) 0) |
| [4] |
程杉, 赵子凯, 陈诺, 等. 计及耦合因素的电动汽车充电负荷时空分布预测[J]. 电力工程技术, 2022, 41(3): 194-201, 208. CHENG Shan, ZHAO Zikai, CHEN Nuo, et al. Prediction of temporal and spatial distribution of electric vehicle charging load considering coupling factors[J]. Electric Power Engineering Technology, 2022, 41(3): 194-201, 208. (  0) 0) |
| [5] |
李东东, 段维伊, 林顺富, 等. 实时电价条件下基于用户引导的电动汽车-充电桩匹配策略[J]. 电力系统自动化, 2020, 44(8): 74-82. LI Dongdong, DUAN Weiyi, LIN Shunfu, et al. User guidance based matching strategy for electric vehicle-charging pile in condition of real-time electricity price[J]. Automation of Electric Power Systems, 2020, 44(8): 74-82. (  0) 0) |
| [6] |
LIU X, FENG T. Energy-storage configuration for EV fast charging stations considering characteristics of charging load and wind-power fluctuation[J]. Global Energy Interconnection, 2021, 4(1): 48-57. DOI:10.1016/j.gloei.2021.03.005 (  0) 0) |
| [7] |
曹一帆, 郝思鹏. 基于充电差异性的电动汽车充电设施优化配置[J]. 供用电, 2022, 39(5): 96-103. CAO Yifan, HAO Sipeng. Optimal configuration of electric vehicle charging facilities based on charging difference[J]. Distribution & Utilization, 2022, 39(5): 96-103. (  0) 0) |
| [8] |
我国新能源汽车保有量达1 310万辆呈高速增长态势[EB/OL]. (2023-01-11)[2023-03-29]. https://www.gov.cn/xinwen/2023-01/11/content_5736281.htm. China's new energy vehicle ownership reached 13.1 million, showing a high-speed growth trend[EB/OL]. (2023-01-11)[2023-03-29]. https://www.gov.cn/xinwen/2023-01/11/content_5736281.htm. (  0) 0) |
| [9] |
2022年全国电动汽车充换电基础设施运行情况[EB/OL]. (2023-01-12)[2023-03-29]. https://mp.weixin.qq.com/s?__biz=MzUyMzAzMjcwNQ==&mid=2247509293&idx=1&sn=4a1abe8c8ba8461ecf97629230f0847e&chksm=f9c024c3ceb7add5774df1e3bee30b95f417ae7b2b1896c69ef31ed10d86b9e429235477bbe4&scene=27. Operation of national electric vehicle charging and replacing infrastructure in 2022[EB/OL]. (2023-01-12)[2023-03-29]. https://mp.weixin.qq.com/s?__biz=MzUyMzAzMjcwNQ==&mid=2247509293&idx=1&sn=4a1abe8c8ba8461ecf97629230f0847e&chksm=f9c024c3ceb7add5774df1e3bee30b95f417ae7b2b1896c69ef31ed10d86b9e429235477bbe4&scene=27. (  0) 0) |
| [10] |
WU F Z, YANG J, ZHAN X P, et al. The online charging and discharging scheduling potential of electric vehicles considering the uncertain responses of users[J]. IEEE Transactions on Power Systems, 2021, 36(3): 1794-1806. (  0) 0) |
| [11] |
GUO Q L, XIN S J, SUN H B, et al. Rapid-charging navigation of electric vehicles based on real-time power systems and traffic data[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1969-1979. (  0) 0) |
| [12] |
侯慧, 樊浩, 苏舒, 等. 多方互利共赢的电动汽车智能充电服务策略[J]. 电力系统自动化, 2017, 41(19): 66-73. HOU Hui, FAN Hao, SU Shu, et al. Multilateral win-win strategy for smart charging service of electric vehicle[J]. Automation of Electric Power Systems, 2017, 41(19): 66-73. (  0) 0) |
| [13] |
MO W Y, YANG C, CHEN X, et al. Optimal charging navigation strategy design for rapid charging electric vehicles[J]. Energies, 2019, 12(6): 962. (  0) 0) |
| [14] |
傅质馨, 朱韦翰, 朱俊澎, 等. 动态路-电耦合网络下电动出租车快速充电引导及其定价策略[J]. 电力自动化设备, 2022, 42(4): 9-17. FU Zhixin, ZHU Weihan, ZHU Junpeng, et al. Fast charging guidance and pricing strategy for electric taxis based on dynamic traffic-grid coupling network[J]. Electric Power Automation Equipment, 2022, 42(4): 9-17. (  0) 0) |
| [15] |
HU Z C, ZHAN K Q, ZHANG H C, et al. Pricing mechanisms design for guiding electric vehicle charging to fill load valley[J]. Applied Energy, 2016, 178: 155-163. (  0) 0) |
| [16] |
DALLINGER D, WIETSCHEL M. Grid integration of intermittent renewable energy sources using price-responsive plug-in electric vehicles[J]. Renewable and Sustainable Energy Reviews, 2012, 16(5): 3370-3382. (  0) 0) |
| [17] |
崔金栋, 罗文达, 周念成. 基于多视角的电动汽车有序充放电定价模型与策略研究[J]. 中国电机工程学报, 2018, 38(15): 4438-4450, 4644. CUI Jindong, LUO Wenda, ZHOU Niancheng. Research on pricing model and strategy of electric vehicle charging and discharging based on multi view[J]. Proceedings of the CSEE, 2018, 38(15): 4438-4450, 4644. (  0) 0) |
| [18] |
马英姿, 马兆兴. 基于博弈算法的电动汽车有序充电优化及效益分析[J]. 电力工程技术, 2021, 40(5): 10-16. MA Yingzi, MA Zhaoxing. Orderly charging optimization and benefit analysis of electric vehicles based on game algorithm[J]. Electric Power Engineering Technology, 2021, 40(5): 10-16. (  0) 0) |
| [19] |
李强, 朱丹丹, 黄地, 等. 虚拟电厂运营商与电动汽车用户的主从博弈定价策略[J]. 电力工程技术, 2022, 41(4): 183-191. LI Qiang, ZHU Dandan, HUANG Di, et al. Stackelberg game pricing strategy between virtual power plant operators and electric vehicle users[J]. Electric Power Engineering Technology, 2022, 41(4): 183-191. (  0) 0) |
| [20] |
TANG D F, WANG P. Nodal impact assessment and alleviation of moving electric vehicle loads: from traffic flow to power flow[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4231-4242. (  0) 0) |
| [21] |
BAYRAM I S, MICHAILIDIS G, DEVETSIKIOTIS M. Unsplittable load balancing in a network of charging stations under QoS guarantees[J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1292-1302. (  0) 0) |
| [22] |
ALIZADEH M, WAI H T, CHOWDHURY M, et al. Optimal pricing to manage electric vehicles in coupled power and transportation networks[J]. IEEE Transactions on Control of Network Systems, 2017, 4(4): 863-875. (  0) 0) |
| [23] |
郑远硕, 李峰, 董九玲, 等. "车-路-网"模式下电动汽车充放电时空灵活性优化调度策略[J]. 电力系统自动化, 2022, 46(12): 88-97. ZHENG Yuanshuo, LI Feng, DONG Jiuling, et al. Optimal dispatch strategy of spatio-temporal flexibility for electric vehicle charging and discharging in vehicle-road-grid mode[J]. Automation of Electric Power Systems, 2022, 46(12): 88-97. (  0) 0) |
| [24] |
金志刚, 胡怡, 李根, 等. 面向"代客加电"服务的电动汽车充电引导策略[J]. 电力系统保护与控制, 2022, 50(14): 76-84. JIN Zhigang, HU Yi, LI Gen, et al. Charging guiding strategy for electric vehicles oriented to a valet charging service[J]. Power System Protection and Control, 2022, 50(14): 76-84. (  0) 0) |
| [25] |
董晓红. 考虑交通行为的电动汽车快充站协同规划与时空引导策略[D]. 天津: 天津大学, 2019. DONG Xiaohong. Collaborative planning of electric vehicle fast charging stations and spatial-temporal guidance strategy considering the traffic behavior[D]. Tianjin: Tianjin University, 2019. (  0) 0) |
2. State Grid Jingjiang Power Supply Company of Jiangsu Electric Power Co., Ltd., Taizhou 214500, China;
3. Electric Power Research Institute of China Southern Power Gird, Guangzhou 510663, China

 范宏(1978),女,博士,副教授,研究方向为综合能源系统、实时仿真(E-mail:
范宏(1978),女,博士,副教授,研究方向为综合能源系统、实时仿真(E-mail: