文章编号: 2096-3203(2022)05-0040-10 中图分类号: TM722
2. 上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240
模块化多电平换流器型高压直流输电(modular multilevel converter based high voltage direct-current, MMC-HVDC)具有控制方便、谐波小、可模块化设计等优势,在高电压等级输电[1—2]、无源网络供电[3]以及海上风电并网[4]等场景中广泛应用。架空线是MMC-HVDC实现大功率电能输送的主要方式。当长距离线路直接暴露于环境中时,故障概率会增加[5—6]。若故障后保护迅速动作,限制电流上升率和峰值水平,直流断路器开断并清除故障[7],则能避免换流站闭锁[8],因此MMC闭锁前的故障暂态分析具有工程意义。短路电流水平是电路参数和绝缘配合设计的重要依据,且有助于故障定位和制定保护策略[9—10]。
MMC子模块(sub-module,SM)投切具有非线性特征,故障电磁暂态过程复杂,采用仿真软件模拟计算存在局限性[11—12]:(1) 直流工程复杂度高,建模困难,应用不便;(2) 须针对不同故障类型和故障位置分别进行仿真,耗时长,效率较低。因此,高效剖析故障后暂态过程,便捷且准确地解析计算故障电流成为控制保护领域关注的重点。
文献[13]基于两端MMC-HVDC极间短路机理建立了等值电路模型,求解故障电流解析表达式,并在此基础上讨论了系统参数对故障过程的影响;文献[14]研究经大、小电阻短路2类场景下故障电流解析计算,提出了一种桥臂旁路保护方法;文献[15—16]以故障电流解析解为依据,分析了直流故障清除方法;文献[17]则针对多端系统中单极接地、单极接中性线和双极短路等不同故障类型,构建了故障阶段直流电网等值电路模型,通过建立修正矩阵方程定量分析计算暂态短路电流。上述故障电流计算的相关研究中,基本思路都是将换流站表示为等值电路,输电线表示为RL支路,进而将故障后直流系统等效为线性电路,通过电路理论列方程求解[11—17],但忽略了输电线路分布参数特性,无法体现实际的故障行波传播过程。实际工程中,行波原理是故障定位[18]和保护设计(例如线路保护)[19]的重要依据。鉴于此,为精细化分析架空线路故障后的详细暂态过程,在MMC-HVDC系统故障电流计算过程中引入传输线分布式参数模型。
描述传输线特性的偏微分方程组是故障暂态分析的出发点,而该方程组只在极少数情况下有解析解(如均匀无损输电线)。为克服此限制,文中在复频域中展开分析。首先,将故障阶段MMC等效为RLC串联电路,分布式参数传输线表示为两端口网络,并基于节点分析法列写方程求得直流系统故障电流表达式。然后,通过数值拉普拉斯逆变换(numerical inversion of Laplace transform, NILT)[20—22]将复频域中分析结果转换为相应的时域暂态。最后,在PSCAD/EMTDC中建模仿真验证并进行理论分析。文中所提算法能反映完整行波过程,且具有较高精度,对MMC-HVDC系统进行故障分析以及保护设计具有工程价值。
1 MMC-HVDC故障过程分析 1.1 MMC短路电流通路以对称双极结构MMC-HVDC为研究对象分析直流故障暂态特性,典型的MMC拓扑结构见图 1,Rg为接地极电阻。MMC正、负极结构完全一致,换流站中性点连接金属回线, 直流线路两端连接平波电抗器Lfw。换流器每相上、下桥臂分别由N个半桥SM与桥臂电抗Larm串联构成,每个SM包含2个绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)、续流二极管组和1个储能电容CSM。
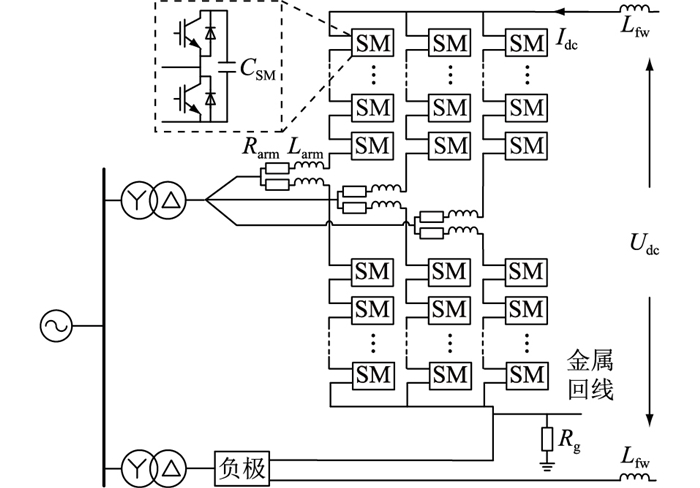
|
图 1 MMC拓扑结构 Fig. 1 MMC topology |
正常运行时,直流侧电压、电流分别为Udc,Idc,且保持稳定。任意时刻MMC中每相上、下桥臂投入SM总数不变,均为N,将电阻Rarm等效为桥臂SM开关导通损耗。通过控制N个投入SM在上、下桥臂间分配得到相应的输出交流电压。
文中重点讨论直流线路短路后、MMC闭锁前的故障电流计算。为降低故障暂态过程的分析复杂度,对这一阶段短路电流通路进行讨论并建立等值电路,如图 2所示。
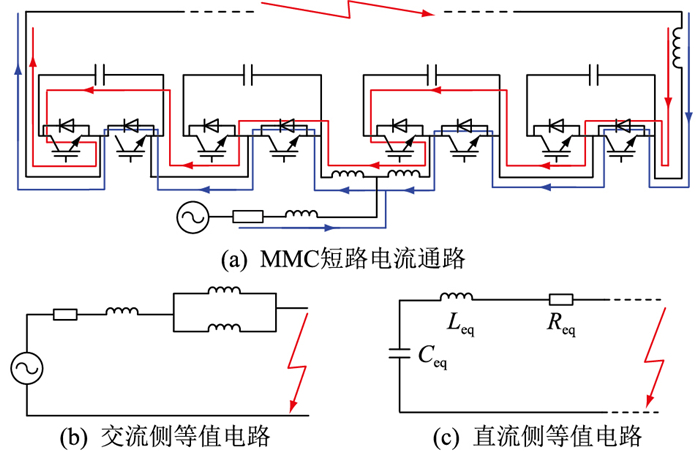
|
图 2 短路后MMC闭锁前短路电流通路及等值电路 Fig. 2 Short-circuit current path and equivalent circuits of MMC before being blocked after fault |
根据现有研究[13—14],MMC闭锁前一段时间内(约10 ms)桥臂投入SM数量保持不变,处于投入状态的SM电容经IGBT向故障点放电,图 2(a)中以红色线表示,直流侧可等效为RLC串联电路,其中Leq,Ceq,Req分别为等值电路中的电感、电容和电阻值。同时,交流系统通过SM中的二极管向短路点注入电流,图 2(a)中以蓝色线表示,相当于发生三相短路。但由于换流站交流侧系统三相对称,因此交流故障电流只流经各相桥臂,对直流侧故障电流无贡献。分析直流线路故障暂态时,可直接将交流侧断开。线路故障电流解析计算即为已知初始条件情况下的线性电路响应求解问题,该过程并不涉及控制系统[8, 23—24]。
1.2 极间短路故障MMC-HVDC发生极间短路时,金属回线上无电流经过。两端换流站正、负极MMC中SM电容经过正、负极线路同时向故障点放电。传输线极间短路故障后换流站闭锁前MMC-HVDC系统等值电路如图 3所示,其中Rf为短路过渡电阻。
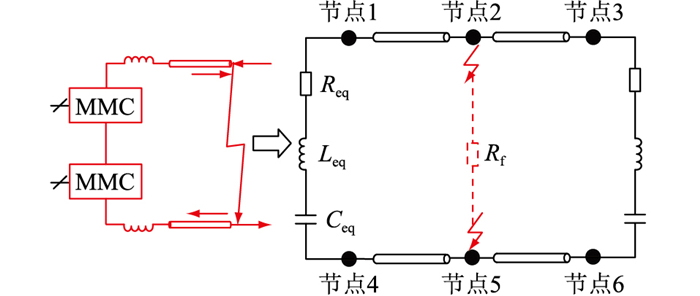
|
图 3 MMC-HVDC传输线极间短路等值电路 Fig. 3 Equivalent circuit of short circuit between transmission lines in MMC-HVDC |
等值电路中Req,Leq,Ceq分别为:
| $ \left\{\begin{array}{l} R_{\mathrm{eq}}=4 R_{\mathrm{arm}} / 3 \\ L_{\mathrm{eq}}=4 L_{\mathrm{arm}} / 3+2 L_{\mathrm{fw}} \\ C_{\mathrm{eq}}=3 C_{\mathrm{SM}} /(2 N) \end{array}\right. $ | (1) |
MMC闭锁前等值电路放电过程初始条件为:
| $ \left\{\begin{array}{l} u_C\left(0_{+}\right)=u_C\left(0_{-}\right)=U_{\mathrm{dc}} \\ i_L\left(0_{+}\right)=i_L\left(0_{-}\right)=I_{\mathrm{dc}} \end{array}\right. $ | (2) |
式中:uC(0+),uC(0-)分别为短路前、后瞬间等值电路中的电容电压;iL(0+),iL(0-)分别为短路前、后瞬间等值电路中的电感电流。
1.3 单极短路故障单极短路故障分为单极接地和单极接金属回线2类,两者的区别在于故障电流是否流经接地极。以正极线路接地为例进行分析,故障后两端换流站正极MMC电容放电,故障电流依次流经正极线路、故障点以及接地极,由金属回线返回MMC,形成通路。传输线单极短路故障后换流站闭锁前MMC-HVDC系统等值电路如图 4所示。
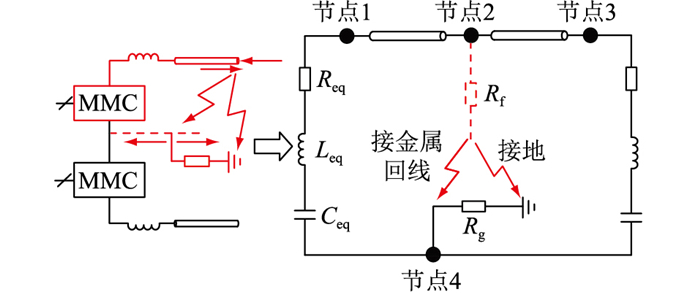
|
图 4 MMC-HVDC传输线单极故障等值电路 Fig. 4 Equivalent circuit of single-pole fault of transmission line in MMC-HVDC |
等值电路中Req,Leq,Ceq分别为:
| $ \left\{\begin{array}{l} R_{\text {eq }}=2 R_{\mathrm{arm}} / 3 \\ L_{\text {eq }}=2 L_{\mathrm{arm}} / 3+L_{\mathrm{fw}} \\ C_{\mathrm{eq}}=3 C_{\mathrm{SM}} / N \end{array}\right. $ | (3) |
MMC闭锁前等值电路放电过程初始条件为:
| $ \left\{\begin{array}{l} u_C\left(0_{+}\right)=u_C\left(0_{-}\right)=U_{\mathrm{dc}} / 2 \\ i_L\left(0_{+}\right)=i_L\left(0_{-}\right)=I_{\mathrm{dc}} \end{array}\right. $ | (4) |
直流系统中传输线连接换流站。分布式参数有损传输线的等值电路见图 5,首末端节点记为m,n;时域中两端电压、电流分别记为um,un和im,in;传输线长度为Lline;R0,L0,G0,C0分别为单位长度电阻、电感、电导及电容。
|
图 5 分布式参数有损传输线的等值电路 Fig. 5 Equivalent circuit of distributed parameter lossy transmission line |
传输线时域模型的偏微分方程组表示为:
| $ \left\{\begin{array}{l} -\frac{\partial u(x, t)}{\partial x}=R_0 i(x, t)+\frac{L_0 \partial i(x, t)}{\partial t} \\ -\frac{\partial i(x, t)}{\partial x}=G_0 u(x, t)+\frac{C_0 \partial u(x, t)}{\partial t} \end{array}\right. $ | (5) |
对式(5)进行拉氏变换,复频域下传输线模型用常微分方程表示为:
| $ \left\{\begin{array}{l} -\mathrm{d} U(x, s) / \mathrm{d} x=\left(s L_0+R_0\right) I(x, s) \\ -\mathrm{d} I(x, s) / \mathrm{d} x=\left(s C_0+G_0\right) U(x, s) \end{array}\right. $ | (6) |
其通解为:
| $ \left\{\begin{array}{c} U(x, s)=U_{\mathrm{f}}(s) \mathrm{e}^{-\gamma x}+U_{\mathrm{b}}(s) \mathrm{e}^{\gamma x} \\ I(x, s)=I_{\mathrm{f}}(s) \mathrm{e}^{-\gamma x}+I_{\mathrm{b}}(s) \mathrm{e}^{\gamma x}= \\ \frac{1}{Z}\left(U_{\mathrm{f}}(s) \mathrm{e}^{-\gamma x}-U_{\mathrm{b}}(s) \mathrm{e}^{\gamma x}\right) \end{array}\right. $ | (7) |
其中:
| $ \left\{\begin{array}{l} \gamma=\sqrt{\left(s L_0+R_0\right)\left(s C_0+G_0\right)} \\ Z=\sqrt{\left(s L_0+R_0\right) /\left(s C_0+G_0\right)} \end{array}\right. $ | (8) |
式中:Uf,Ub分别为电压前行、反行波;If,Ib分别为电流前行、反行波。则有:
| $ \left\{\begin{array}{l} U(x, s)+Z I(x, s)=2 U_{\mathrm{f}}(s) \mathrm{e}^{-\gamma x} \\ U(x, s)-Z I(x, s)=2 U_{\mathrm{b}}(s) \mathrm{e}^{\gamma x} \end{array}\right. $ | (9) |
文中仅关心传输线两端电气特性,分别取输电线位置x=0,x=Lline,得到两端电流、电压关系为:
| $ \left\{\begin{array}{l} U(0, s)+Z I(0, s)= \\ \quad\left(U\left(L_{\text {line }}, s\right)+Z I\left(L_{\text {line }}, s\right)\right) \mathrm{e}^{\gamma L_{\text {line }}} \\ U(0, s)-Z I(0, s)= \\ \quad\left(U\left(L_{\text {line }}, s\right)-Z I\left(L_{\text {line }}, s\right)\right) \mathrm{e}^{-\gamma L_{\text {line }}} \end{array}\right. $ | (10) |
因此复频域下传输线可视为两端口网络,其端口特性由导纳矩阵Y表示为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\boldsymbol{I}=\left[\begin{array}{c} I_m \\ I_n \end{array}\right]=\boldsymbol{Y} \boldsymbol{U}=\left[\begin{array}{ll} Y_1 & Y_2 \\ Y_3 & Y_4 \end{array}\right]\left[\begin{array}{l} U_m \\ U_n \end{array}\right]=\\ \left[\begin{array}{cc} \frac{\cosh \left(\gamma L_{\text {line }}\right)}{Z \sinh \left(\gamma L_{\text {line }}\right)} & -\frac{1}{Z \sinh \left(\gamma L_{\text {line }}\right)} \\ -\frac{1}{Z \sinh \left(\gamma L_{\text {line }}\right)} & \frac{\cosh \left(\gamma L_{\text {line }}\right)}{Z \sinh \left(\gamma L_{\text {line }}\right)} \end{array}\right]\left[\begin{array}{c} U_m \\ U_n \end{array}\right] \end{array} $ | (11) |
式中:I为支路电流向量;U为节点电压向量;Im,In分别为复频域中首末端节点m,n处电流;Um,Un分别为复频域中首末端节点m,n处电压;Yk为矩阵Y中第k个元素。
故基于描述传输线特性的电报方程,在复频域下建立传输线端口数学分析模型,如图 6所示。

|
图 6 传输线等效两端口网络 Fig. 6 Equivalent two-port network of transmission line |
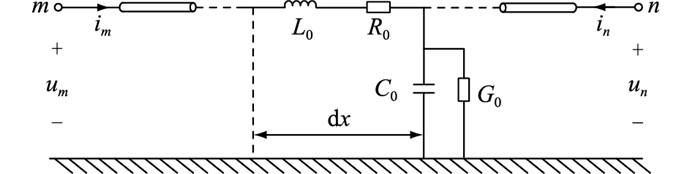
在MMC-HVDC故障等值电路中,MMC表示为RLC串联电路。电感、电容的时域表达式经拉氏变换后变为:
| $ U_L(s)=L s I_L(s)-L i_L\left(0_{-}\right) $ | (12) |
| $ I_C(s)=C s U_C(s)-C u_C\left(0_{-}\right) $ | (13) |
式中:UL(s),UC(s)分别为复频域下等值电路中电感、电容的电压;IL(s),IC(s)分别为复频域下等值电路中电感、电容的电流。
则电感和电容分别采用诺顿等值电路和戴维南等值电路表示,如图 7所示。
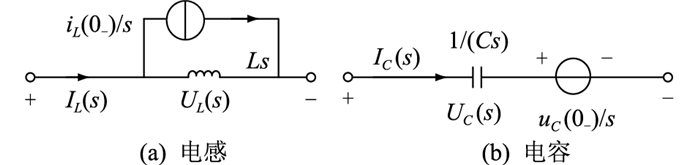
|
图 7 复频域下电感和电容等值电路 Fig. 7 The equivalent circuit of indutor and capacitor in complex frequency domain |
MMC的等效RLC串联电路是传输线的端接网络。记端口电压、电流分别为UMMC(s),IMMC(s),则复频域下MMC等值电路的电气特性表示为:
| $ U_{\mathrm{MMC}}(s)=Z_{\mathrm{eq}} I_{\mathrm{MMC}}(s)-L_{\mathrm{eq}} i_L\left(0_{-}\right)+u_C\left(0_{-}\right) / s $ | (14) |
其中,Zeq为等值电路阻抗,即:
| $ Z_{\mathrm{eq}}=R_{\mathrm{eq}}+s L_{\mathrm{eq}}+1 /\left(s C_{\mathrm{eq}}\right) $ | (15) |
记故障点距左、右两端换流站距离分别为lL,lR。对图 3、图 4中故障等值电路各节点编号,节点电压记为Uj(s),下标j为节点编号;将支路电流记为Inm(s)。
采用节点分析法求解直流系统传输线故障等值电路,即可得到各支路电流。式(11)中传输线等效端口特性方程通过导纳矩阵反映复频域下传输线两端电流和电压关系。根据实际电路信息,在单一传输线导纳矩阵Ynm的基础上得到等值电路的节点导纳矩阵YTrans,并建立如下方程:
| $ \boldsymbol{I}=\boldsymbol{Y}_{\text {Trans }} \boldsymbol{U} $ | (16) |
图 3中极间短路等值电路的节点导纳矩阵YTrans为:
| $ \begin{gathered} {\boldsymbol{Y}_{\mathrm{Trans}}=} \\ {\left[\begin{array}{cccccc} Y_{12, 1} & Y_{12, 2} & 0 & 0 & 0 & 0 \\ Y_{12, 3} & Y_{12, 4}+Y_{23, 1}+\frac{1}{R_{\mathrm{f}}} & Y_{23, 2} & 0 & -\frac{1}{R_{\mathrm{f}}} & 0 \\ 0 & Y_{23, 3} & Y_{23, 4} & 0 & 0 & 0 \\ 0 & 0 & 0 & Y_{45, 1} & Y_{45, 2} & 0 \\ 0 & -\frac{1}{R_{\mathrm{f}}} & 0 & Y_{45, 3} & Y_{45, 4}+Y_{56, 1}+\frac{1}{R_{\mathrm{f}}} & Y_{56, 2} \\ 0 & 0 & 0 & 0 & Y_{56, 3} & Y_{56, 4} \end{array}\right]} \end{gathered} $ | (17) |
图 4中单极故障等值电路的节点导纳矩阵YTrans为:
| $ \boldsymbol{Y}_{\text {Trans }}=\left[\begin{array}{cccc} Y_{12, 1} & Y_{12, 2} & 0 & 0 \\ Y_{12, 3} & Y_{12, 4}+Y_{23, 1}+\frac{1}{R_{\mathrm{f}}} & Y_{23, 2} & 0 \\ 0 & Y_{23, 3} & Y_{23, 4} & 0 \\ 0 & 0 & 0 & \frac{1}{R_{\mathrm{g}}} \end{array}\right] $ | (18) |
式中:Ynm, k为传输线导纳矩阵Ynm中第k个元素。式(18)导纳矩阵针对单极接地故障建立,若为单极接金属回线故障,则相应YTrans中YTrans(2, 4)替换为-1/Rf,YTrans(4, 2)替换为-1/Rf,YTrans(4, 4)替换为1/Rg+1/Rf即可。
针对极间短路故障和单极故障2类情况,可根据式(14)分别引入如式(19)、式(20)所示的边界条件。
| $ \left\{\begin{array}{l} I_{14}(s)=-I_{41}(s)=I_{\mathrm{MMC}, \mathrm{L}}(s) \\ I_{36}(s)=-I_{63}(s)=I_{\mathrm{MMC}, \mathrm{R}}(s) \\ U_1(s)-U_4(s)=U_{\mathrm{MMC}, \mathrm{L}}(s) \\ U_3(s)-U_6(s)=U_{\mathrm{MMC}, \mathrm{R}}(s) \end{array}\right. $ | (19) |
| $ \left\{\begin{array}{l} I_{14}(s)=-I_{41}(s)=I_{\mathrm{MMC}, \mathrm{L}}(s) \\ I_{34}(s)=-I_{43}(s)=I_{\mathrm{MMC}, \mathrm{R}}(s) \\ U_1(s)-U_4(s)=U_{\mathrm{MMC}, \mathrm{L}}(s) \\ U_3(s)-U_4(s)=U_{\mathrm{MMC}, \mathrm{R}}(s) \end{array}\right. $ | (20) |
式中:UMMC, L(s),UMMC, R(s)为两端换流站MMC等值电路端口电压;IMMC, L(s),IMMC, R(s)为两端换流站MMC等值电路端口电流。其中,电气量的下标L,R分别表示其位于MMC等值电路中的左端、右端。
将式(19)、式(20)分别代入式(16)中得到式(21)、式(22)。
复频域下,求解式(21)得到极间故障等值电路节点电压响应,求解式(22)得到单极故障等值电路节点电压响应,进一步将求解结果代入式(16)既可获得各支路电流。上述计算过程可通过计算机编程可简易实现。
3.3 NILT计算方法频域分析方法克服了传输线方程组在时域中无法获得解析解的限制,因此对于3.2节中在复频域下计算得到的直流故障电流表达式,其关键点在于如何转换为时域动态响应。
NILT作为一种简单易行的数值计算方法,容易编程实现,可以高效、方便地将复频域中分析结果F(s)转换为时域中f(t)。
拉普拉斯逆变换定义如式(23)所示。
| $ \left[ {\begin{array}{*{20}{c}} {{Y_{12, 1}}}&{{Y_{12, 2}}}&0&{{Y_{45, 1}}}&{{Y_{45, 2}}}&0\\ 0&{{Y_{23, 3}}}&{{Y_{23, 4}}}&0&{{Y_{56, 3}}}&{{Y_{56, 4}}}\\ {{Y_{12, 3}}}&{{Y_{12, 4}} + {Y_{23, 1}} + \frac{1}{{{R_{\rm{f}}}}}}&{{Y_{23, 2}}}&0&{ - \frac{1}{{{R_{\rm{f}}}}}}&0\\ 0&{ - \frac{1}{{{R_{\rm{f}}}}}}&0&{{Y_{45, 3}}}&{{Y_{45, 4}} + {Y_{56, 1}} + \frac{1}{{{R_{\rm{f}}}}}}&{{Y_{56, 2}}}\\ {1 + {Z_{{\rm{eq, L }}}}{Y_{12, 1}}}&{{Z_{{\rm{eq, L}}}}{Y_{12, 2}}}&0&{ - 1}&0&0\\ 0&{{Z_{{\rm{eq }}, {\rm{R}}}}{Y_{23, 3}}}&{1 + {Z_{{\rm{eq }}, {\rm{R}}}}{Y_{23, 4}}}&0&0&{ - 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{U_1}}\\ {{U_2}}\\ {{U_3}}\\ {{U_4}}\\ {{U_5}}\\ {{U_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ {\frac{{{u_{C, {\rm{L}}}}\left( {{0_ - }} \right)}}{s} - {L_{{\rm{eq}}, {\rm{L}}}}{i_{14}}\left( {{0_ - }} \right)}\\ {\frac{{{u_{C, {\rm{R}}}}\left( {{0_ - }} \right)}}{s} - {L_{{\rm{eq}}, {\rm{R}}}}{i_{36}}\left( {{0_ - }} \right)} \end{array}} \right] $ | (21) |
| $ \left[\begin{array}{cccc} Z_{\mathrm{eq}, \mathrm{L}} Y_{12, 1}+1 & Z_{\mathrm{eq}, \mathrm{L}} Y_{12, 2} & 0 & -1 \\ Y_{12, 3} & Y_{12, 4}+Y_{23, 1}+\frac{1}{R_{\mathrm{f}}} & Y_{23, 2} & 0 \\ 0 & Z_{\mathrm{eq}, \mathrm{R}} Y_{23, 3} & Z_{\mathrm{eq}, \mathrm{R}} Y_{23, 4}+1 & -1 \\ Y_{12, 1} & Y_{12, 2}+Y_{23, 3} & Y_{23, 4} & \frac{1}{R_{\mathrm{g}}} \end{array}\right]\left[\begin{array}{c} U_1 \\ U_2 \\ U_3 \\ U_4 \end{array}\right]=\left[\begin{array}{c} \frac{u_{C, \mathrm{~L}}\left(0_{-}\right)}{s}-L_{\mathrm{eq}, \mathrm{L}} i_{14}\left(0_{-}\right) \\ 0 \\ \frac{u_{C, \mathrm{R}}\left(0_{-}\right)}{s}-L_{\mathrm{eq}, \mathrm{R}} i_{34}\left(0_{-}\right) \\ 0 \end{array}\right] $ | (22) |
| $ \begin{gathered} f(t)=\frac{1}{2 \pi \mathrm{j}} \int_{\sigma-\mathrm{j} \infty}^{\sigma+\mathrm{j} \infty} F(s) \mathrm{e}^{s t} \mathrm{~d} t= \\ \frac{1}{2 \pi \mathrm{j} t} \int_{\sigma-\mathrm{j} \infty}^{\sigma+\mathrm{j} \infty} F\left(\frac{z}{t}\right) \mathrm{e}^z \mathrm{~d} z \end{gathered} $ | (23) |
式中:s=σ+jω为拉普拉斯算子;σ为任意正常数;z=st。
利用有理函数ξα, β(z)对ez进行Pade逼近[20—21],使得两者泰勒展开式的前α+β+1项相等。ξα, β(z)表达式如式(24)所示,其中Pα(z),Qβ(z)分别为α,β阶多项式;zi为ξα, β(z)极点,ki为极点对应留数,两者均可为复数。当α,β给定,可确定有理函数ξα, β(z)。
| $ \begin{gathered} \mathrm{e}^z \approx \xi_{\alpha, \beta}(z)=\frac{P_\alpha(z)}{Q_\beta(z)}= \\ \frac{\sum\limits_{i=0}^\alpha(\beta+\alpha-i)! \;C_\alpha^i z^i}{\sum\limits_{i=0}^\beta(-1)^i(\beta+\alpha-i)! \;C_\beta^i z^i}=\sum\limits_{i=1}^\beta \frac{k_i}{z-z_i} \end{gathered} $ | (24) |
用ξα, β(z)替代式(23)中ez得到f(t)的近似表达
| $ \hat{f}(t)=\frac{1}{2 \pi \mathrm{j} t} \int_{\sigma^{\prime}-\mathrm{j} \infty}^{\sigma^{\prime}+\mathrm{j} \infty} F\left(\frac{z}{t}\right) \xi_{\alpha, \beta}(z) \mathrm{d} z $ | (25) |
变量置换后积分范围σ′亦为任意正常数。将式(25)中积分路径连接右半平面上半径无限远的半圆弧形成顺时针闭合路径c,如图 8所示。
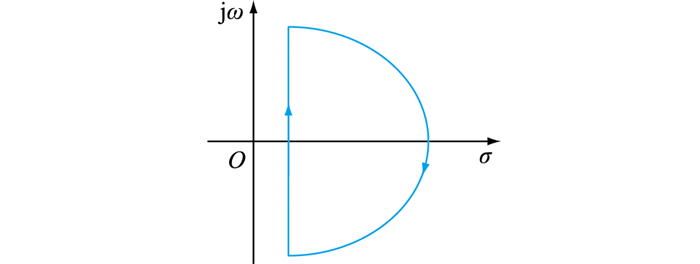
|
图 8 复频域下积分路径 Fig. 8 Integration path in complex frequency domain |
适当选择α,β满足β-α>2,使得被积函数G(z)=F(z/t)ξα, β(z)的极点数至少比零点数多2,此时沿半圆弧路径的积分值趋于零,原积分路径由路径c代替。积分可根据留数定理计算如下:
| $ \oint\limits_c {G(z){\rm{d}}z = - 2{\rm{ \pi j}}\sum {{\mathop{\rm Res}\nolimits} } \left[ {G(z)} \right]} $ | (26) |
式中:Res[G(z)]为被积函数G(z)在闭合路径中极点对应留数。ξα, β(z)所有极点均可包含在闭合路径中;而函数F(z/t)作为无源线性系统的响应函数,其极点必在左半平面,即G(z)包含在闭合积分路径中的极点全部为ξα, β(z)极点。式(26)可改写为:
| $ \oint\limits_c {F\left( {\frac{z}{t}} \right){\xi _{\alpha , \beta }}(z){\rm{d}}z = - 2{\rm{ \pi j}}\sum\limits_{i = 1}^\beta F \left( {\frac{{{z_i}}}{t}} \right){k_i}} $ | (27) |
将式(27)代入式(25)得到
| $ \hat{f}(t)=-\frac{1}{t} \sum\limits_{i=1}^\beta F\left(\frac{z_i}{t}\right) k_i $ | (28) |
由于极点分布及相应留数具有共扼性质,则式(28)为关于t的实函数。由上述推导过程可以看出,zi和ki根据Pade逼近得到,与时域响应函数f(t)无关,计算过程独立进行,故NILT方法具有普遍性。文中计算采用有理函数ξ6, 8(z)和ξ12, 16(z)对ez逼近。两函数的极点和相应的留数分别由表 1、表 2给出,且极点和留数以共轭复数的形式成对出现。
|
|
表 1 ξ6, 8(z)的极点和对应的留数 Table 1 The poles and the corresponding residues of ξ6, 8(z) |
|
|
表 2 ξ12, 16(z)的极点和对应的留数 Table 2 The poles and the corresponding residues of ξ12, 16(z) |
文中采用主频2.50 GHz的Intel(R) Core(TM) i5-7300HQ中央处理器、内存16 GB的4核计算机,运行64位Windows 10操作系统,基于NLIT的故障暂态计算方法则通过Matlab编程实现。此外,在商业电磁暂态仿真平台PSCAD/EMTDC中搭建两端MMC-HVDC系统作为算例,如图 9所示,直流侧接地点设置在送端,接地电阻Rg=20 Ω,受端中性点由金属回线连接接地极。传输线采用Bergeron模型表示,主要工程参数如表 3所示。
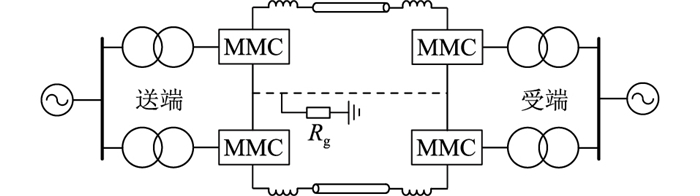
|
图 9 两端MMC-HVDC系统仿真模型 Fig. 9 Simulation model of two-terminal MMC-HVDC system |
|
|
表 3 两端MMC-HVDC系统主要参数 Table 3 Main parameters of two-terminal MMC-HVDC system |
文中重点考察直流侧线路故障电流,忽略MMC内部态过程,因此在满足精度要求的前提下为兼顾效率,电磁暂态仿真采用平均值模型[25],仿真步长设定为20 μs。
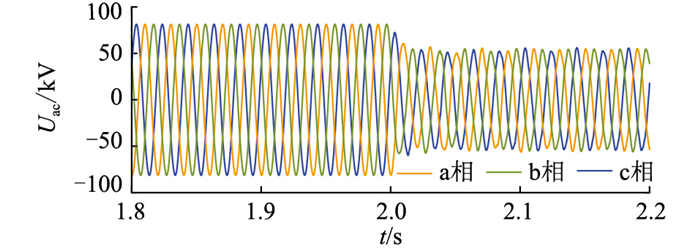
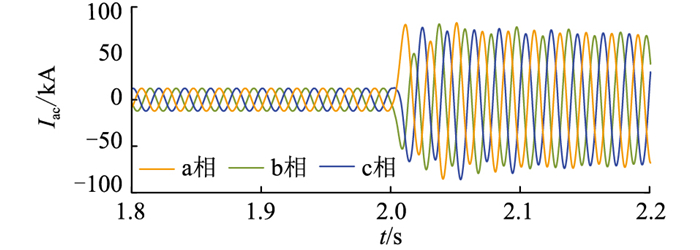
4.1 故障电流计算方法仿真验证仿真场景中,MMC-HVDC系统运行至稳态后,设定t在2.0 s时刻,直流线路中点位置发生故障,过渡电阻Rf为5 Ω。针对极间短路、单极接地和单极接金属回线3类故障工况分别进行仿真验证,以送端正极MMC为例,交流侧电压、电流的电磁暂态仿真结果如图 10、图 11所示。
|
图 10 送端MMC交流侧电压 Fig. 10 The AC side voltage of the sending end MMC |
|
图 11 送端MMC交流侧电流 Fig. 11 The AC side current of the sending end MMC |
可以发现,直流侧故障后,交流侧相当于发生三相短路,电压跌落,电流增大,验证了1.1节中对短路电流通路的分析。
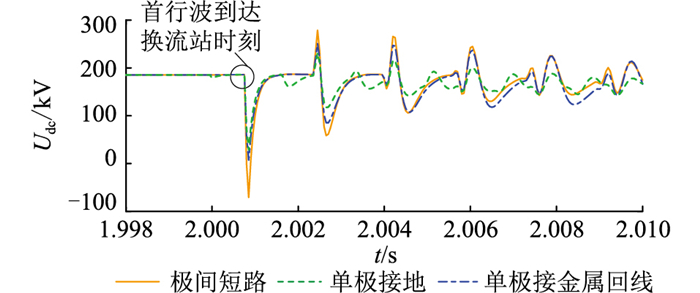
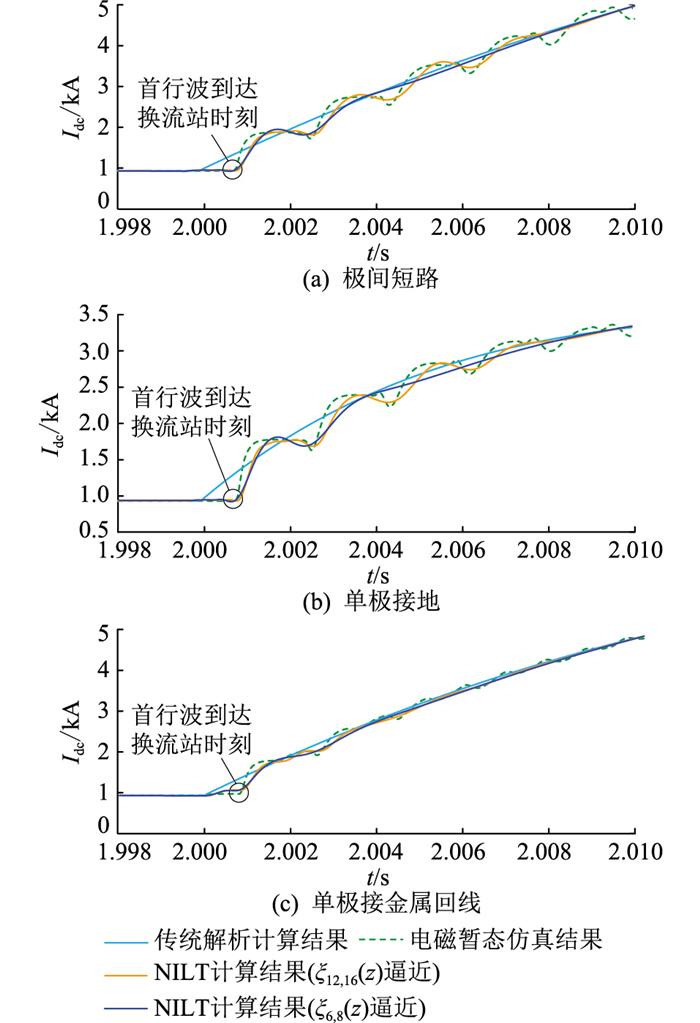
记录故障后10 ms内直流侧电流、电压暂态波形,这也是保护设计重点关注的阶段。图 12为直流侧电压的电磁暂态仿真结果。以电磁暂态仿真结果为参考给出了以ξ6, 8(z)和ξ12, 16(z)逼近时NLIT方法的计算结果,并与传统解析算法结果对比如图 13所示。
|
图 12 送端MMC直流侧电压 Fig. 12 The DC side voltage of the sending end MMC |
|
图 13 送端MMC直流侧故障电流对比 Fig. 13 Comparison of fault currents on the DC side of the sending end MMC |
可以看出,文中算法计算的波形与仿真波形基本重合,整体发展趋势高度一致,且Pade逼近时选用有理函数ξα, β(z)的阶数越高,波形吻合程度越高。若以ξ12, 16(z)进行逼近,故障后5 ms内最大误差小于6%,10 ms内最大误差小于8%。其原因是采用Pade逼近的NILT的截断误差正比于tα+β+1,误差随着时间推移逐渐扩大[22]。
由理论分析和计算结果可知,故障后SM电容放电导致直流侧产生过电流。所有故障类型中极间短路危害最大,故障电流同时流经正、负极线路,且快速上升。由于文中研究对象为对称双极结构的MMC-HVDC,因此单极故障不影响非故障极正常运行。单极接金属回线故障时,故障极过电流水平接近极间短路;而单极接地故障时,由于故障电流流经接地极电阻,因此其过电流水平较低。
传统解析算法中,2.0 s时刻传输线中点位置发生故障后,距离故障点200 km处的送端MMC直流侧电流立刻上升,且几乎呈线性增长。这是因为传输线采用集中参数模型,描述为RL串联支路,线路上不存在波过程,因此电气量变化与空间位置无关。根据电磁暂态仿真结果,短路后送端MMC直流侧电流、电压并没有立刻发生变化。0.8 ms后电流才开始上升,并且出现电压跌落。这是因为在实际过程中,速度为v的故障行波沿线路传播200 km后首次到达换流站需要0.8 ms。此后线路上各处电流、电压即为所有折、反射波的叠加。当行波再次到达换流站,故障电流继续上升,直流侧电压再次出现跌落,因此故障电流呈阶梯状上升。文中所提算法考虑行波的传播特性,计算中引入传输线分布式参数模型,能详尽描述故障电流暂态过程的发展趋势和上述故障特征,相比于传统解析算法,准确度更高,过程更完整,分析结论更可靠。
MMC-HVDC模型拓扑结构复杂,PSCAD仿真过程中须建立高阶节点导纳矩阵并求解,因此计算量大。而文中所提算法只须在复频域中求解2次低阶矩阵方程(极间故障为6阶,单极故障为4阶),后续的NILT计算只涉及基本的四则运算,计算复杂度大幅度降低。记录该算例的计算用时,PSCAD仿真需要39.40 s,而基于NLIT的算法通过Matlab实现需要1.08 s。较电磁暂态仿真而言,文中所提算法在计算速度方面有明显优势,这将极大提升研究效率。
4.2 故障电流暂态特性分析借助NLIT方法选用ξ12, 16(z)逼近进一步讨论不同故障位置、过渡电阻情况下故障电流暂态特性。为进一步说明文中算法的普适性,分析中同时给出电磁暂态仿真结果,用于对比参考。
对于不同过渡电阻,传输线中点位置发生各类型短路时的故障电流计算波形见图 14。过渡电阻Rf分别设定为0.001 Ω、2 Ω及20 Ω,分别表示金属性短路、经小电阻短路和经大电阻短路的情况。
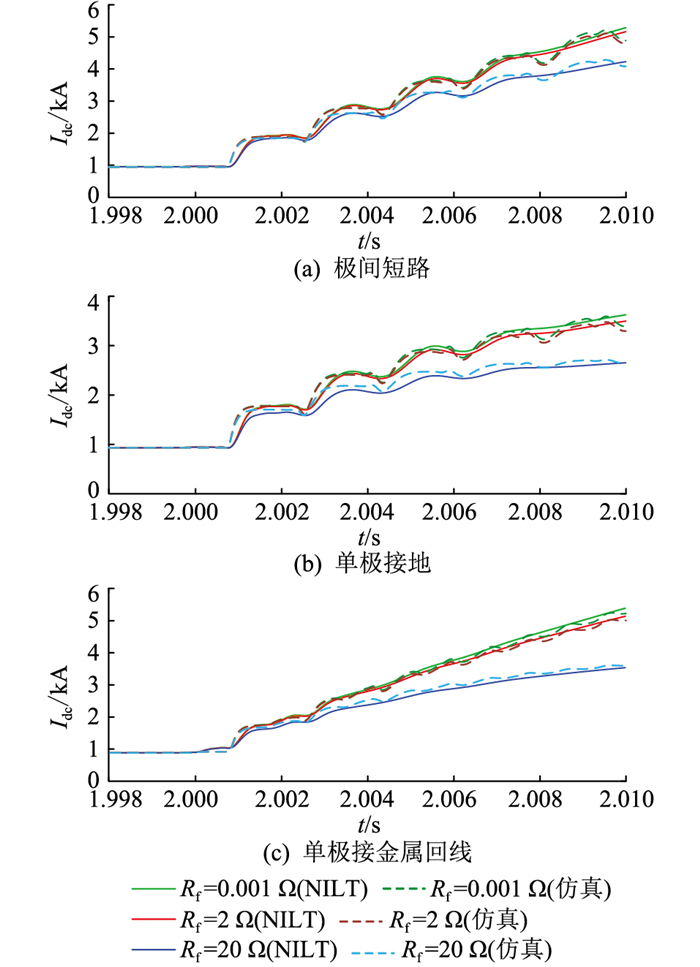
|
图 14 过渡电阻不同时的送端MMC直流侧故障电流 Fig. 14 The fault current on the DC side of the sending end MMC with different short-circuit resistances |
由图 14可知,各类型故障中, 发生金属性短路时故障电流最大。短路过渡电阻只影响故障电流上升速率和大小,并不影响行波到达换流站的时间,并且随着短路过渡电阻增大,故障电流逐渐减小。
对于不同故障位置,不同短路位置时的故障电流计算波形见图 15。在距离送端换流站50 km(近端)、200 km(中点)以及350 km(远端)处分别设置故障,过渡电阻Rf设定为5 Ω。
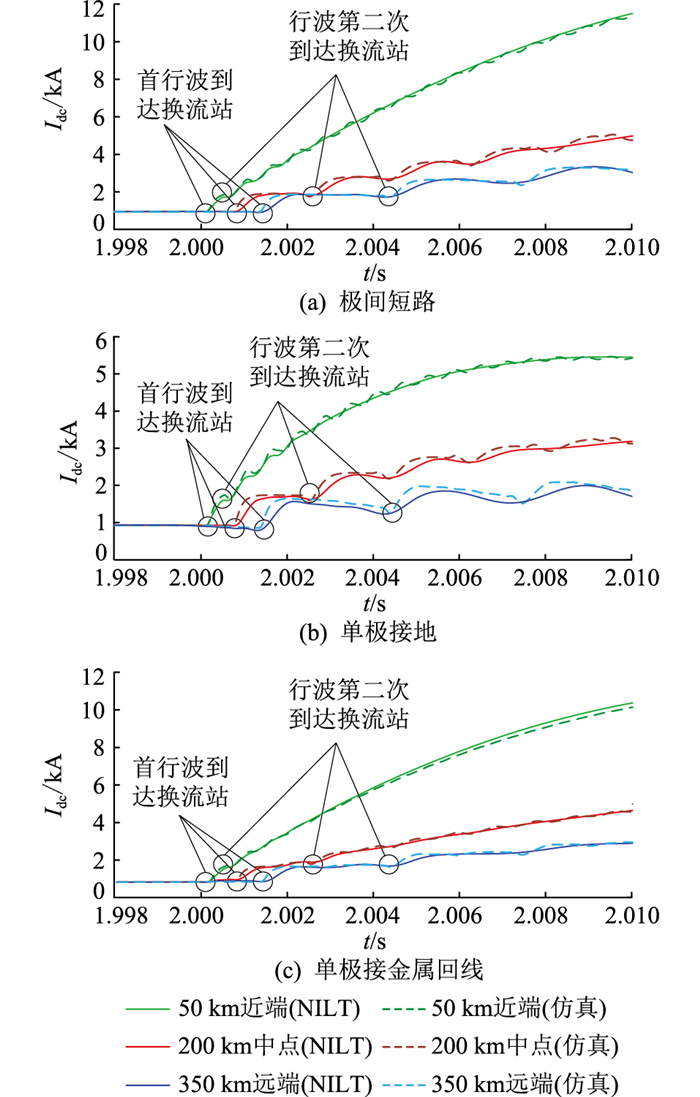
|
图 15 短路位置不同时的送端MMC直流侧故障电流 Fig. 15 The fault current on the DC side of the sending end MMC with different short-circuit positions |
由图 15可知,短路位置距离换流站越近,故障电流越大,上升越快。t0=2.0 s时刻故障发生,由于行波传输需要时间,t1时刻首行波到达换流站,保护安装处可检测到电流开始上升。50 km、200 km和350 km处发生故障时,t1分别为2.000 2 s、2.000 8 s和2.001 4 s。此后故障点处反射波于t2时刻再次到达换流站,故障电流继续上升。50 km、200 km和350 km处发生故障时,t2分别为2.000 6 s、2.002 5 s和2.004 4 s。故障类型不影响行波沿到达换流站时间。
由理论分析可知,若故障位置越远,首行波到达时刻t1越晚。即对于速度为v的行波,故障点至换流站距离x可计算为:
| $ x=v\left(t_1-t_0\right) $ | (29) |
并且行波2次抵达换流站间传播经过路程为2倍故障位置距离,则x还可以表示为:
| $ x=v\left(t_2-t_1\right) / 2 $ | (30) |
以上性质可用于故障定位以及行波保护设计。
针对不同故障位置和过渡电阻情况下各种类型故障工况,对比分析了故障暂态电流的仿真结果和基于NILT的计算结果。结果表明两者高度吻合,能准确表达故障电流暂态特性,从而进一步验证了文中所提算法的有效性和普适性。
5 结论针对MMC-HVDC系统的保护策略设计,需要重点考察架空线路故障后暂态过程。文中提出了基于NILT的短路电流计算方法,所得结论如下:
(1) 文中所提算法的计算结果与电磁暂态仿真结果高度吻合,能够精确表达故障电流整体发展趋势,验证了算法的有效性。但由于该数值算法的固有特性,其分析结果误差随时间推移而扩大,方法主要适用于故障后短时间内暂态分析。
(2) 计算中引入传输线分布式参数模型,能够反映架空线路上波过程,详尽描述暂态故障电流发展趋势和特征,例如波形、上升率以及行波到达时间等。其结果准确度更高,过程更加完整,对直流系统故障分析、定位和保护设计具有参考价值。
(3) 基于MMC-HVDC系统拓扑结构,构建等值电路分析故障暂态。其计算过程简单,规避了繁琐复杂的仿真过程,具有便捷性;且可以实现对任意故障位置、任意过渡电阻情况下的短路电流定量分析,具有通用性和普适性。
本文得到智能电网保护和运行控制国家重点实验室项目“基于数值拉普拉斯变换和架空线路频率相关参数的混合直流电网故障定位方法与保护优化研究”资助,谨此致谢!
| [1] |
杜晓磊, 郭庆雷, 吴延坤, 等. 张北柔性直流电网示范工程控制系统架构及协调控制策略研究[J]. 电力系统保护与控制, 2020, 48(9): 164-173. DU Xiaolei, GUO Qinglei, WU Yankun, et al. Research on control system structure and coordination control strategy for Zhangbei demonstration project of MMC-HVDC grid[J]. Power System Protection and Control, 2020, 48(9): 164-173. (  0) 0) |
| [2] |
胡宏, 陈浩, 丁浩寅, 等. 特高压混合级联多端直流输电系统的协调控制策略研究[J]. 电力工程技术, 2021, 40(4): 42-51. HU Hong, CHEN Hao, DING Haoyin, et al. Coordinated control strategy for hybrid cascaded UHVDC system[J]. Electric Power Engineering Technology, 2021, 40(4): 42-51. (  0) 0) |
| [3] |
周保荣, 李选平, 杨健, 等. 向无源电网供电的MMC-HVDC稳态运行区域分析[J]. 智慧电力, 2020, 48(6): 98-104. ZHOU Baorong, LI Xuanping, YANG Jian, et al. Analysis of steady operation region of MMC-HVDC connected to passive network[J]. Smart Power, 2020, 48(6): 98-104. DOI:10.3969/j.issn.1673-7598.2020.06.016 (  0) 0) |
| [4] |
蔡旭, 杨仁炘, 周剑桥, 等. 海上风电直流送出与并网技术综述[J]. 电力系统自动化, 2021, 45(21): 2-22. CAI Xu, YANG Renxin, ZHOU Jianqiao, et al. Review on off-shore wind power integration via DC transmission[J]. Automation of Electric Power Systems, 2021, 45(21): 2-22. (  0) 0) |
| [5] |
杨海倩, 王玮, 荆龙, 等. MMC-HVDC系统直流侧故障暂态特性分析[J]. 电网技术, 2016, 40(1): 40-46. YANG Haiqian, WANG Wei, JING Long, et al. Analysis on transient characteristic of DC transmission line fault in MMC based HVDC transmission system[J]. Power System Technology, 2016, 40(1): 40-46. (  0) 0) |
| [6] |
王渝红, 傅云涛, 曾琦, 等. 柔性直流电网故障保护关键技术研究综述[J]. 高电压技术, 2019, 45(8): 2362-2374. WANG Yuhong, FU Yuntao, ZENG Qi, et al. Review on key techniques for fault protection of flexible DC grids[J]. High Voltage Engineering, 2019, 45(8): 2362-2374. (  0) 0) |
| [7] |
董新洲, 汤兰西, 施慎行, 等. 柔性直流输电网线路保护配置方案[J]. 电网技术, 2018, 42(6): 1752-1759. DONG Xinzhou, TANG Lanxi, SHI Shenxing, et al. Configuration scheme of transmission line protection for flexible HVDC grid[J]. Power System Technology, 2018, 42(6): 1752-1759. (  0) 0) |
| [8] |
汤兰西, 董新洲. MMC直流输电网线路短路故障电流的近似计算方法[J]. 中国电机工程学报, 2019, 39(2): 490-498, 646. TANG Lanxi, DONG Xinzhou. An approximate method for the calculation of transmission line fault current in MMC-HVDC grid[J]. Proceedings of the CSEE, 2019, 39(2): 490-498, 646. (  0) 0) |
| [9] |
XIANG W, YANG S Z, XU L, et al. A transient voltage-based DC fault line protection scheme for MMC-based DC grid embedding DC breakers[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 334-345. DOI:10.1109/TPWRD.2018.2874817 (  0) 0) |
| [10] |
彭宇锋, 张英敏, 李俊松, 等. 考虑线路电容的MMC-HVDC系统直流接地故障电流计算方法[J]. 电力系统保护与控制, 2020, 48(23): 57-63. PENG Yufeng, ZHANG Yingmin, LI Junsong, et al. Ground fault current calculation method for an MMC-HVDC system considering line capacitance[J]. Power System Protection and Control, 2020, 48(23): 57-63. (  0) 0) |
| [11] |
郝亮亮, 李伟杰, 王卓雅, 等. MMC-HVDC电网输电线路双极短路故障电流的实用计算[J]. 电力系统自动化, 2020, 44(5): 68-76. HAO Liangliang, LI Weijie, WANG Zhuoya, et al. Practical calculation for bipolar short-circuit fault current of transmission line in MMC-HVDC grid[J]. Automation of Electric Power Systems, 2020, 44(5): 68-76. (  0) 0) |
| [12] |
李俊松, 张英敏, 曾琦, 等. MMC-MTDC系统单极接地故障电流计算方法[J]. 电网技术, 2019, 43(2): 546-555. LI Junsong, ZHANG Yingmin, ZENG Qi, et al. Pole-to-ground fault current calculation method for MMC-MTDC systems[J]. Power System Technology, 2019, 43(2): 546-555. (  0) 0) |
| [13] |
张国驹, 祁新春, 陈瑶, 等. 模块化多电平换流器直流双极短路特性分析[J]. 电力系统自动化, 2016, 40(12): 151-157, 199. ZHANG Guoju, QI Xinchun, CHEN Yao, et al. Characteristic analysis of modular multilevel converter under DC pole-to-pole short-circuit fault[J]. Automation of Electric Power Systems, 2016, 40(12): 151-157, 199. (  0) 0) |
| [14] |
郭晓茜, 崔翔, 齐磊. 架空线双极MMC-HVDC系统直流短路故障分析和保护[J]. 中国电机工程学报, 2017, 37(8): 2177-2185. GUO Xiaoqian, CUI Xiang, QI Lei. DC short-circuit fault analysis and protection for the overhead line bipolar MMC-HVDC system[J]. Proceedings of the CSEE, 2017, 37(8): 2177-2185. (  0) 0) |
| [15] |
吴婧, 姚良忠, 王志冰, 等. 直流电网MMC拓扑及其直流故障电流阻断方法研究[J]. 中国电机工程学报, 2015, 35(11): 2681-2694. WU Jing, YAO Liangzhong, WANG Zhibing, et al. The study of MMC topologies and their DC fault current blocking capacities in DC grid[J]. Proceedings of the CSEE, 2015, 35(11): 2681-2694. (  0) 0) |
| [16] |
李斌, 李晔, 何佳伟. 具有直流故障清除能力的MMC子模块关键性能研究[J]. 中国电机工程学报, 2016, 36(8): 2114-2122. LI Bin, LI Ye, HE Jiawei. Research on the key properties of MMC sub-modules with DC fault eliminating capability[J]. Proceedings of the CSEE, 2016, 36(8): 2114-2122. (  0) 0) |
| [17] |
裴翔羽, 汤广福, 张盛梅, 等. 双极柔性直流电网短路电流暂态特性分析[J]. 全球能源互联网, 2018, 1(4): 403-412. PEI Xiangyu, TANG Guangfu, ZHANG Shengmei, et al. Analysis on transient characteristics of short-circuit current for bipolar VSC-based DC grid[J]. Journal of Global Energy Interconnection, 2018, 1(4): 403-412. (  0) 0) |
| [18] |
邢志杰, 田行军, 刘宇晰, 等. 电缆-架空线混合线路行波故障测距算法研究[J]. 电网技术, 2020, 44(9): 3540-3546. XING Zhijie, TIAN Xingjun, LIU Yuxi, et al. Research of traveling wave fault location algorithm for the overhead line-cable hybrid line[J]. Power System Technology, 2020, 44(9): 3540-3546. (  0) 0) |
| [19] |
张晨浩, 宋国兵, 李洋, 等. 基于故障电压行波传播项指数系数的柔性直流输电线路单端行波保护原理[J]. 中国电机工程学报, 2021, 41(24): 8424-8437. ZHANG Chenhao, SONG Guobing, LI Yang, et al. Principle of non-unit traveling wave protection for VSC-HVDC grids based on index of fault voltage traveling wave propagation term[J]. Proceedings of the CSEE, 2021, 41(24): 8424-8437. (  0) 0) |
| [20] |
GRIFFITH J R, NAKHLA M S. Time-domain analysis of lossy coupled transmission lines[J]. IEEE Transactions on Microwave Theory and Techniques, 1990, 38(10): 1480-1487. (  0) 0) |
| [21] |
JEONG J, NEVELS R. Time-domain analysis of a lossy nonuniform transmission line[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2009, 56(2): 157-161. (  0) 0) |
| [22] |
鲁跃军, 卢斌先, 孙曰生, 等. 基于故障输电线分布参数节点导纳方程的带分支的配电线故障分析[J]. 电网技术, 2003, 27(5): 40-42. LU Yuejun, LU Binxian, SUN Yuesheng, et al. Fault analysis of branched transmission line based on distributed-parameter nodal admittance equation[J]. Power System Technology, 2003, 27(5): 40-42. (  0) 0) |
| [23] |
ZHANG Z R, XU Z. Short-circuit current calculation and performance requirement of HVDC breakers for MMC-MTDC systems[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2016, 11(2): 168-177. (  0) 0) |
| [24] |
LI C Y, ZHAO C Y, XU J Z, et al. A pole-to-pole short-circuit fault current calculation method for DC grids[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4943-4953. (  0) 0) |
| [25] |
喻悦箫, 刘天琪, 王顺亮, 等. 基于平均值模型的双端MMC-HVDC系统小信号建模[J]. 中国电机工程学报, 2018, 38(10): 2999-3006, 3150. YU Yuexiao, LIU Tianqi, WANG Shunliang, et al. Small signal modeling of two-terminal MMC-HVDC based on AVM model[J]. Proceedings of the CSEE, 2018, 38(10): 2999-3006, 3150. (  0) 0) |
2. Key Laboratory of Control of Power Transmission and Conversion, Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

 吴通华(1977),男,博士,研究员级高级工程师,从事交直流电力系统的保护与控制工作(E-mail:
吴通华(1977),男,博士,研究员级高级工程师,从事交直流电力系统的保护与控制工作(E-mail: