文章编号: 2096-3203(2023)01-0218-08 中图分类号: TM471
随着新型电力系统的构建,分布式电源、数据中心、电动汽车等新型直流源荷比重将进一步增大,配电网的直流特征愈发明显[1-2]。新型直流源、荷主要以微电网的形式接入配电网[3],然而,直流微电网为小惯量系统,在离网状态下,发电功率波动、负荷投切等不确定性扰动均会导致直流母线电压波动,影响整个微电网的稳定运行[4-5]。因此,如何提高直流微电网的惯性特性,抑制微电网的电压波动是目前亟须解决的问题。
针对微电网的低惯量问题,国内外学者从换流器控制方式出发,提出多种虚拟惯性控制方法[6-9]。其中,虚拟直流电机(virtual direct current motor,VDCM)利用虚拟惯量模拟直流电机的转动惯量,可有效提升微电网的惯性特性,获得了广泛关注。文献[10-11]分别针对储能与光伏侧换流器,在双环控制的基础上引入虚拟角速度,实现了VDCM控制。文献[12]则在能量路由器中采用VDCM,保证了不同工作模态下电网的惯性。但上述文献均未对VDCM惯性特性展开分析。文献[13]提出一种基于扩张状态观测器的VDCM控制,可有效削弱直流母线电压超调量,但该控制下虚拟惯量的变化规律须进一步分析。文献[14]提出一种简化的VDCM控制,利用简化的控制结构提升VDCM虚拟惯量,但虚拟惯量提升对等效惯量的影响仍有待探究。文献[15]指出VDCM控制思想等价于增加直流母线侧电容,即等效惯量,但该文献并未对虚拟惯量与等效惯量间的对应关系展开分析。文献[16]提出一种基于有功调节效果的等效电容计算方法,但在新能源独立供电条件下,该计算方法并不适用。
基于此,文中提出一种基于改进弗雷歇算法的VDCM等效惯量计算方法。首先,基于虚拟惯量与等效惯量的小信号模型,确立惯量等效关系。然后,利用弗雷歇算法度量虚拟惯量与等效惯量的电压阶跃响应曲线相似度,建立两者数值的对应关系。最后,采用基于方差、决定系数、标准差的最优拟合方式,实现惯量等效关系的函数化。针对弗雷歇算法的局部性与准确性问题,提出基于相关性约束与曲线特征约束的改进弗雷歇算法,综合考虑系统的稳态与暂态特征,提高等效惯量计算的准确性。
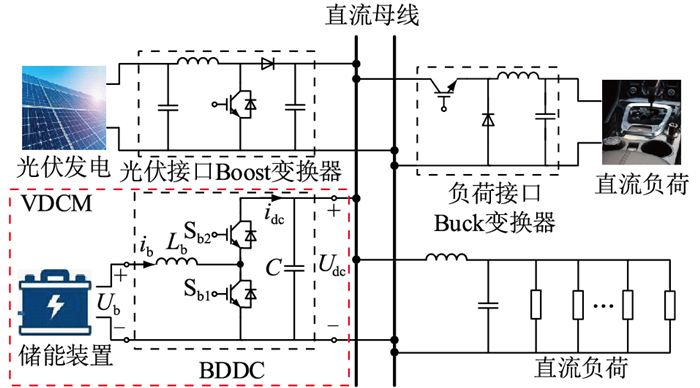
1 VDCM模型建立文中针对图 1所示直流微电网展开研究,其中光伏系统采用最大功率点跟踪控制,提取光伏最大功率;储能装置通过双向DC-DC换流器(bi-directional DC-DC converter,BDDC)接入直流母线。
|
图 1 直流微电网架构 Fig. 1 Architecture of DC microgrid |
VDCM由BDDC、直流母线电容C和储能装置构成。BDDC包括2个双向开关器件Sb1、Sb2和连接在支路中点的滤波电感Lb,可等效为一个二端口网络,与直流电机模型结构相似[17]。图 1中Ub为BDDC输入电压;ib为BDDC输入电流;Udc为BDDC输出电压,即直流母线电压;idc为BDDC输出电流。
为模拟直流电机的惯性特性,提升微电网电压稳定性,针对上述BDDC,在双环控制的基础上,引入虚拟角速度ω,实现VDCM控制。其中VDCM电磁转矩Tev[18]的表达式为:
| $ T_{\mathrm{ev}}=\frac{e I_{\mathrm{ref}}}{\omega} $ | (1) |
其中:
| $ e=C_{\mathrm{t}} \mathit{\Phi} \omega $ | (2) |
式中:e为VDCM电枢电动势;Iref为输出电流参考值;Ct为转矩常数;Φ为磁通。
VDCM电枢方程为:
| $ e-U_{\mathrm{b}}=I_{\mathrm{ref}} R $ | (3) |
式中:R为VDCM电枢电阻。
VDCM机械方程为[19]:
| $ T_{\mathrm{mv}}-T_{\mathrm{ev}}=J_{\mathrm{v}} \frac{\mathrm{d} \omega}{\mathrm{d} t}+D_{\mathrm{v}}\left(\omega-\omega_0\right) $ | (4) |
式中:Tmv为VDCM机械转矩;Jv为虚拟惯量;Dv为虚拟阻尼系数;ω0为额定角速度。
VDCM控制电路如图 2所示[20]。图 2中Uref为直流母线电压参考值;s为拉普拉斯算子;Ibref为电感电流参考值;Pm为VDCM机械功率;S1、S2分别为Sb1、Sb2的触发信号;PWM为脉冲宽度调制。

|
图 2 VDCM控制框图 Fig. 2 Block diagram of VDCM control |
VDCM控制分为3个目标:电压调节、惯性仿真和电流调节。首先,将直流母线电压Udc与Uref的偏差量引入电压比例积分(proportional integral,PI)控制器,利用PI控制器的调节能力,实现电压调节;其次,将外环PI控制器输出与Uref的乘积作为机械功率Pm,利用虚拟角速度ω与Pm构建直流电机的机械方程和电枢回路方程,实现惯性仿真;将惯性环节的输出经Uref/Ub环节转换为电流调节环节输入Ibref,最后将Ibref与ib的偏差量引入电流PI控制器,实现电流调节。
2 惯量等效关系分析 2.1 虚拟惯量与等效惯量由于直流微电网的惯性主要由电容提供,而直流微电网中母线侧电容受制于体积与成本,容量较小,母线电压无法获得有效的惯性支撑[21],因此VCDM控制所虚拟出的虚拟电容Cv直接影响直流微电网的惯性支撑作用。依据电容充放电特性, 得到Cv的动力学方程为:
| $ i_{\mathrm{v}}=C_{\mathrm{v}} \frac{\mathrm{d} U_{\mathrm{dc}}}{\mathrm{d} t}+G_{\mathrm{v}} U_{\mathrm{dc}} $ | (5) |
式中:iv为流入Cv的虚拟电流;Gv为Cv的寄生电导。分别对Udc与iv添加扰动信号Δudc和Δiv,得出Δudc和Δiv间的小信号模型为:
| $ G_1(s)=\frac{\Delta u_{\mathrm{dc}}}{\Delta i_{\mathrm{v}}}=\frac{1}{C_{\mathrm{v}} s+G_{\mathrm{v}}} $ | (6) |
从式(6)可以看出,Cv的小信号模型近似于一阶惯性环节,其中Cv等价于惯性环节中惯性时间常数,反映了VCDM提供的惯量大小,为VDCM的等效惯量。
结合图 2中的惯性仿真模块与式(1)—式(4)可得:
| $ T_{\mathrm{mv}}-\frac{\left(C_{\mathrm{t}} \mathit{\Phi}\right)^2 \omega}{R}=J_{\mathrm{v}} \frac{\mathrm{d} \omega}{\mathrm{d} t}+D_{\mathrm{v}}\left(\omega-\omega_0\right) $ | (7) |
对ω与Tmv,分别添加扰动信号Δω和ΔTmv,得到Δω和ΔTm间的小信号模型为:
| $ G_{{\rm{ \mathsf{ ω} }}\mathrm{T}}(s)=\frac{\Delta \omega}{\Delta T_{\mathrm{mv}}}=\frac{1}{J_{\mathrm{v}} s+\left(C_{\mathrm{t}} \mathit{\Phi}\right)^2 / R+D_{\mathrm{v}}} $ | (8) |
从式(6)、式(8)可以看出,惯量仿真模块的小信号模型与Cv的小信号模型在结构上具有一致性,其中Jv与Cv均可反映VDCM中惯量大小,具有一定的等效关系。
2.2 小信号模型分析为验证Jv与Cv的等效关系,对VDCM的小信号模型展开分析,其中ib的扰动信号Δib与Δudc对占空比D的扰动信号Δd的传递函数[22]分别为:
| $ G_{\mathrm{id}}(s)=\frac{\Delta i_{\mathrm{b}}}{\Delta d}=\frac{s C U_{\mathrm{dc}}+(1-D) i_{\mathrm{b}}}{s^2 C L_{\mathrm{b}}+s C R_{\mathrm{b}}+(1-D)^2} $ | (9) |
| $ G_{\mathrm{ud}}(s)=\frac{\Delta u_{\mathrm{dc}}}{\Delta d}=-\frac{\left(s L_{\mathrm{b}}+R_{\mathrm{b}}\right) i_{\mathrm{b}}-(1-D) U_{\mathrm{dc}}}{s^2 C L_{\mathrm{b}}+s C R_{\mathrm{b}}+(1-D)^2} $ | (10) |
式中:Rb为电感内阻。VDCM控制策略中,Δudc对e的扰动信号Δe的传递函数[23]为:
| $ G_{\mathrm{ue}}(s)=\frac{\Delta u_{\mathrm{dc}}}{\Delta e}=\frac{U_{\mathrm{ref}} C_{\mathrm{t}} \mathit{\Phi} R\left(s k_{\mathrm{pu}}+k_{\mathrm{iu}}\right)}{s \omega_0\left[J_{\mathrm{v}} R s+\left(C_{\mathrm{t}} \mathit{\Phi}\right)^2+D_{\mathrm{v}} R\right]} $ | (11) |
式中:kpu、kiu分别为电压PI控制器的比例系数和积分系数。Δe对Δib的传递函数为:
| $ G_{\mathrm{ei}}(s)=\frac{\Delta e}{\Delta i_{\mathrm{b}}}=\frac{U_{\mathrm{ref}}}{R U_{\mathrm{b}}} $ | (12) |
依据上述传递函数,可建立图 3所示VDCM小信号模型。

|
图 3 VDCM小信号模型 Fig. 3 Small signal model of VDCM |
其中GPIi(s)为电流控制器函数。由图 3得出Uref的扰动信号Δuref对Δudc的传递函数为:
| $ \begin{gathered} G(s)=\frac{\Delta u_{\mathrm{ref}}}{\Delta u_{\mathrm{dc}}}=G_{\mathrm{ue}}(s) G_{\mathrm{ei}}(s) G_{\mathrm{PIi}}(s) G_{\mathrm{ud}}(s) / \\ \left(1+G_{\mathrm{PIi}}(s) G_{\mathrm{id}}(s)+G_{\mathrm{ei}}(s) G_{\mathrm{PIi}}(s) G_{\mathrm{ud}}(s)+\right. \\ \left.G_{\mathrm{ue}}(s) G_{\mathrm{ei}}(s) G_{\mathrm{PIi}}(s) G_{\mathrm{ud}}(s)\right) \end{gathered} $ | (13) |
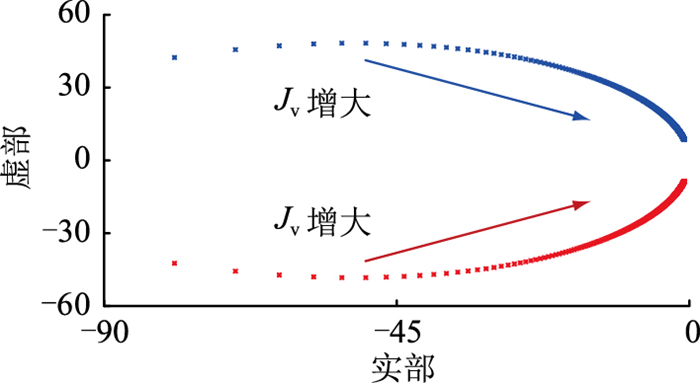
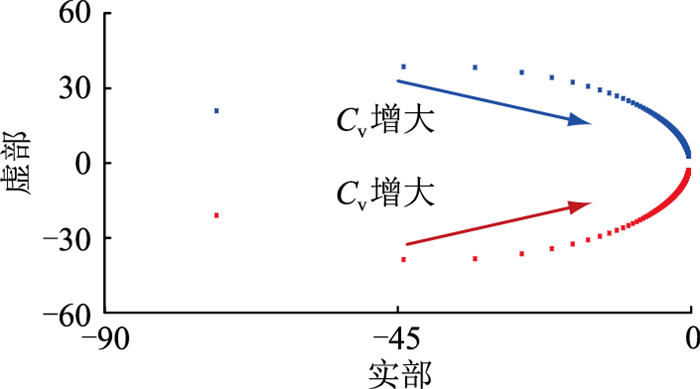
表 1为VDCM参数。依据表 1与式(13),分别绘制Jv在1×10-4~3×10-2 kg · m2内,Jv与Cv以相同变化率增长过程中系统的特征根轨迹,结果分别如图 4、图 5所示。
|
|
表 1 VDCM参数 Table 1 VDCM parameters |
|
图 4 Jv对系统特征根的影响 Fig. 4 Influence of Jv on the characteristic root of system |
|
图 5 Cv对系统特征根的影响 Fig. 5 Influence of Cv on the characteristic root of system |
由图 4可知,随着Jv数值的增加,VDCM的特征根向虚轴移动,系统惯性提升,但稳定性裕度与动态特性裕度逐步降低。从图 5可以发现,随着Cv数值的增加,系统特征根的整体变化规律与Jv具有一致性,表明Cv与Jv具有等效关系,可以通过改变Jv的大小调节系统的惯量特性。但在初始期间,Jv增加时系统特征根更密集,表明在Jv与Cv增长过程中,特征根移动速度存在差异性,即Jv与Cv在相同数值下系统特征根不具有一致性,因此Jv与Cv间不存在直接等价关系。
此外,分析图 4发现,Jv数值选取不当会影响整个系统的稳定裕度与动态特性裕度。因此,考虑稳定性及动态特性约束[24],最终确定Jv阈值约束范围,即:
| $ J_{\mathrm{vmin} } \leqslant J_{\mathrm{v}} \leqslant J_{\mathrm{vmax}} $ | (14) |
式中:Jvmax、Jvmin分别为Jv阈值约束的最大值与最小值。
依据文献[24]所提出的稳定运行边界计算方法,以稳定性与动态响应为约束集,利用传递函数的主导特征根,最终确定阈值约束的最小值与最大值分别为2.6×10-3 kg · m2与5.8×10-3 kg · m2。
3 等效惯量计算方法 3.1 改进的弗雷歇算法为明确VDCM控制所虚拟出的Cv大小,参考文献[25]中户变关系识别中弗雷歇算法对电表电压曲线相似度的度量方法,以Jv与Cv对应关系为基础,提出一种通过度量电压曲线相似度计算等效惯量的方法。弗雷歇算法是一种用于描述曲线空间相似度的算法,具体求解过程[26]为:
假设曲线LC和LD分别具有m与n个特征点,特征点集分别表示为LC{p1, ⋯, pm}和LD{q1, ⋯, qn},第i次循环下2条曲线间特征点对如式(15)所示。
| $ \begin{gathered} \boldsymbol{L}_i\left\{\left(p_1, q_i\right), \left(p_2, q_i\right), \cdots, \left(p_m, q_i\right)\right\} \\ i=1, 2, \cdots, n \end{gathered} $ | (15) |
度量函数下2条曲线在第i次循环下的相对距离为‖Li‖,表达式如式(16)所示。
| $ \left\|\boldsymbol{L}_i\right\|=\max\limits _{k=1, 2, \cdots, m} d\left(p_k, q_i\right) $ | (16) |
可以得出最终弗雷歇距离为:
| $ F\left(L_{\mathrm{C}}, L_{\mathrm{D}}\right)=\min \left\|\boldsymbol{L}_i\right\| $ | (17) |
由式(15)—式(17)发现,弗雷歇距离将部分匹配点之间的距离作为相似性结果的一部分,是一种局部匹配度量法,未考虑系统的稳态与暂态特征。
为提高弗雷歇距离的准确性与全局性,在计算‖Li‖之前引入相关性约束与曲线特征约束,实现弗雷歇算法的改进。
相关性约束:为了保证2条曲线的全局相关性,引入皮尔逊相关系数P,利用相关程度对2条曲线之间总体变化趋势进行衡量,并通过限制P的取值范围,实现相关性约束。
曲线特征约束:电压偏差是衡量电能质量的一项基本指标,电压偏差一般用电压偏差值与系统标称电压的百分比表示。此外,面对风、光等间歇性能源输出功率波动、负荷投切等常见扰动时,直流配电系统将会面临更多快速的功率波动,因此换流器输出电压须尽量避免电压超调,保证系统的暂态特性。
综上,通过规定曲线相对超调量Δσp与电压偏差ΔU′的取值范围,实现曲线特征约束,提高曲线间的特征相似度。ΔU′与Δσp的计算公式为:
| $ \Delta U^{\prime}=\left|\Delta U_1-\Delta U_2\right| $ | (18) |
| $ \Delta \sigma_{\mathrm{p}}=\left|\frac{U_{\mathrm{pp} 1}-U_{\mathrm{pp} 2}}{U_{\mathrm{pp} 1}}\right| \times 100 \% $ | (19) |
式中:ΔU1、ΔU2分别为曲线LC和曲线LD的电压偏差;Upp1、Upp2分别为曲线LC和曲线LD的最大峰值或最小谷值。
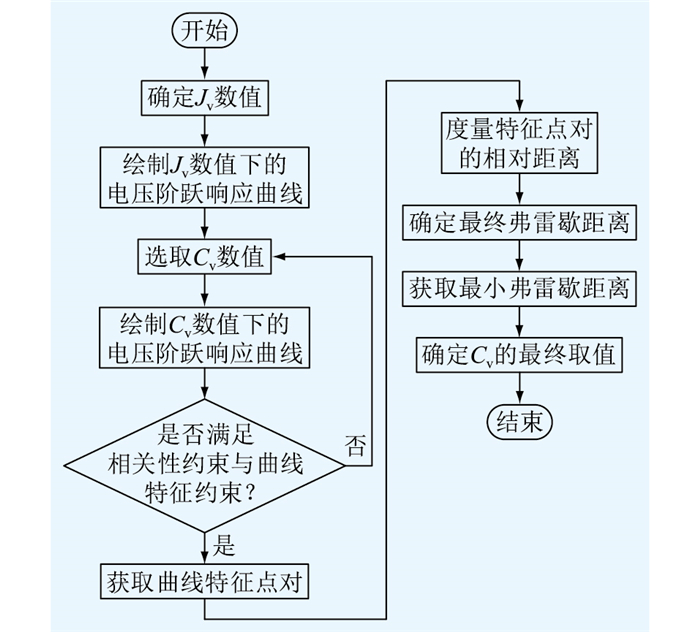
3.2 基于改进弗雷歇算法的等效惯量计算基于改进弗雷歇算法与Jv和Cv间的等效关系,最终确定等效惯量计算方法为:首先,确定阈值约束范围内Jv的数值,依据传递函数G(s)构建固定Jv与不同Cv下电压阶跃响应曲线;其次,利用相关性约束与曲线特征约束,筛选Cv的取值大小;最后,度量固定Jv与不同Cv下电压阶跃响应曲线的弗雷歇距离,弗雷歇距离最小值即为该Jv下VDCM所对应Cv,从而实现VDCM惯性特性的量化分析。具体流程如图 6所示。
|
图 6 基于改进弗雷歇算法的等效惯量计算流程 Fig. 6 Equivalent inertia calculation flow based on improved Frecher algorithm |
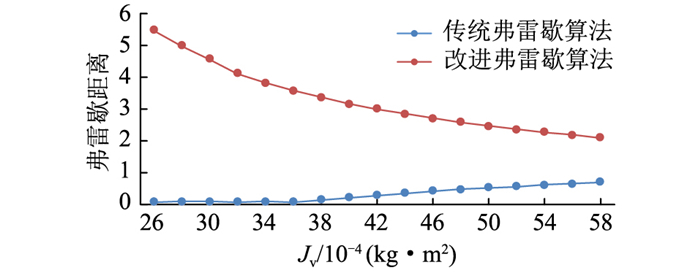
为验证改进弗雷歇算法在VDCM等效惯量计算中的有效性,依据上述等效惯量计算流程,分别对比传统弗雷歇算法与改进弗雷歇算法的弗雷歇距离、相对超调量、电压偏差与相关系数,其结果分别如图 7—图 10所示。
|
图 7 弗雷歇距离对比 Fig. 7 Comparison of Frecher distance |
|
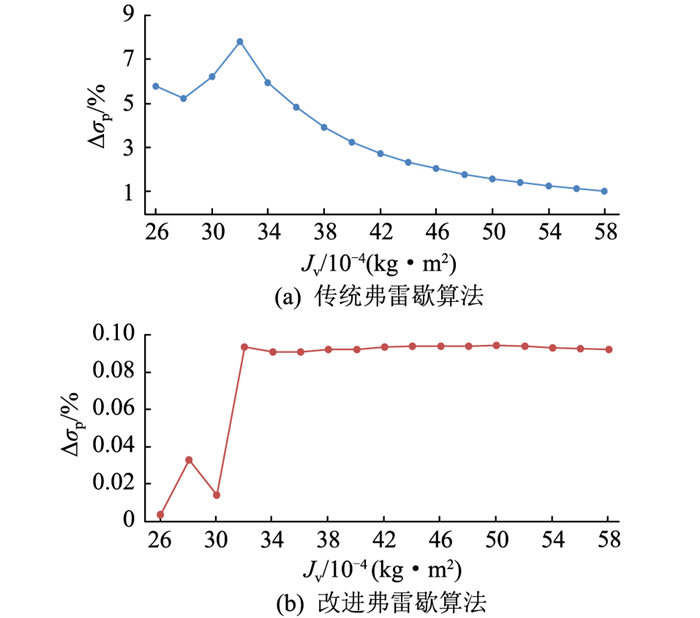
图 8 相对超调量对比 Fig. 8 Comparison of relative overshoot |
|
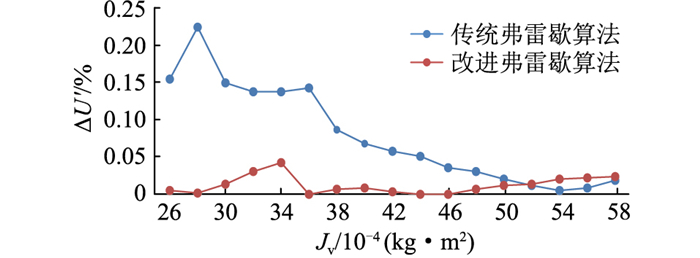
图 9 电压偏差对比 Fig. 9 Comparison of relative voltage deviation |
|
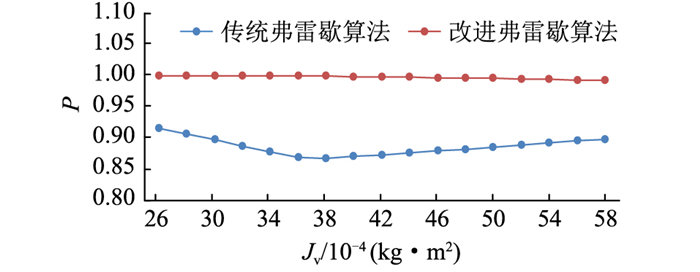
图 10 相关系数对比 Fig. 10 Comparison of correlation coefficient |
从图 7可以看出,引入相关性与曲线特性约束后,弗雷歇距离数值明显上升。图 8、图 9中相比于传统弗雷歇算法,改进弗雷歇算法的曲线相对超调量、电压偏差量明显下降,表明改进弗雷歇算法可以有效抑制相对超调量的增长与电压偏差量的提升,保持相对超调量与电压偏差量的稳定,增加电压曲线的特征相似度。从图 10可以发现,通过引入皮尔逊相关系数约束,可以有效提升曲线相关性,保证曲线变化趋势的一致性。
综上,相对于传统弗雷歇算法,改进后弗雷歇算法虽然扩大了2条曲线间的弗雷歇距离,但增加了曲线相关性与曲线特征相似度,提高了电压曲线对比的准确性,保证了等效惯量计算的正确性。
3.3 惯量等效关系基于改进弗雷歇算法获取的Jv与Cv对应数值,分别选取幂指数逼近法、有理数逼近法、多项式逼近法对Jv与Cv的等效关系进行拟合。针对拟合结果,分别从和方差、决定系数、标准差对3种方式进行对比,选取最优的拟合方式。其中和方差与标准差可以衡量拟合数据与拟合结果之间的偏离度,数值越小,拟合结果越精确。决定系数可以衡量拟合数据与拟合结果之间的契合度,数值越接近1,拟合程度越好。拟合方式对比结果如表 2所示。
|
|
表 2 拟合方式对比 Table 2 Comparison of fitting methods |
由表 2可知,相比幂函数逼近法与有理数逼近法,多项式逼近法拟合结果精度最高,拟合效果最好。因此将多项式逼近法中的一元三次式作为最优拟合方式,最终确定Cv与Jv的函数关系为:
| $ C_{\mathrm{v}}=p_1 J_{\mathrm{v}}^3+p_2 J_{\mathrm{v}}^2+p_3 J_{\mathrm{v}}+p_4 $ | (20) |
其中p1=-833.7,p2=15.18,p3=0.014 67,p4=2.169×10-5。由式(20)可知,在虚拟惯量阈值约束范围内Jv与Cv之间存在非线性关系,Cv随着Jv的增大而增大。该函数关系实现了Jv和Cv数值变换,定量描述了VDCM控制在负荷波动时所提供的惯量大小,表征了VDCM控制的惯性支撑作用,便于直流微电网系统惯量的调节。
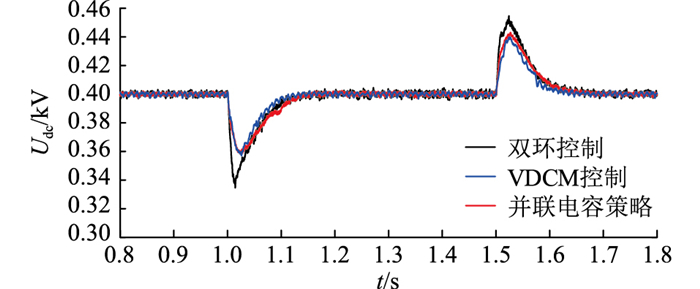
4 仿真验证 4.1 VDCM控制有效性验证为验证VDCM控制的有效性以及所提等效惯量计算方式的正确性,在PSCAD/EMTDC中搭建图 1所示直流微电网仿真模型。其中,直流母线电压为400 V,光伏阵列输出电压为124 V,VDCM参数选择见表 1。图 11为双环控制、VDCM控制与并联电容策略下母线电压响应的对比。
|
图 11 不同控制方式下的直流母线电压 Fig. 11 DC bus voltage under different control modes |
由图 11可知,相比于双环控制策略,VDCM控制策略可以有效抑制电压突变,降低直流母线电压超调量。对比VDCM控制与并联电容策略下直流母线电压的变化曲线,可以看出2条曲线的变化趋势、超调量、稳态误差基本一致。
因此,相比于双环控制,VDCM控制与并联电容策略可以有效抑制电压突变,提高系统的稳定性。此外,VDCM控制与并联电容策略在改善电压质量、增强直流系统惯性能力方面具有类似性,验证了VDCM控制中Jv与Cv间的等效性。
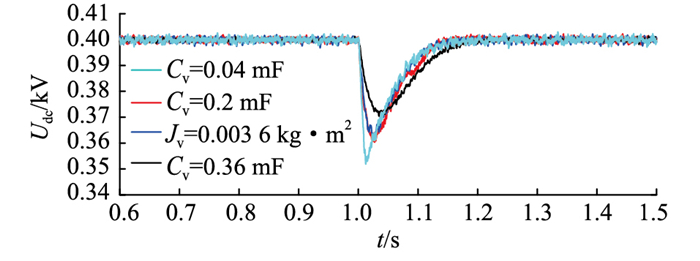
4.2 等效惯量计算方法正确性验证通过对比不同Cv与固定Jv下直流母线电压波形,观察曲线的相似程度,确立Cv的取值范围,并利用弗雷歇算法确定两者的对应数值,对等效惯量计算方法的正确性进行验证。图 12为不同等效惯量下母线电压波形。
|
图 12 不同等效惯量下母线电压波形 Fig. 12 Bus voltage waveforms at different kinds of equivalent inertia |
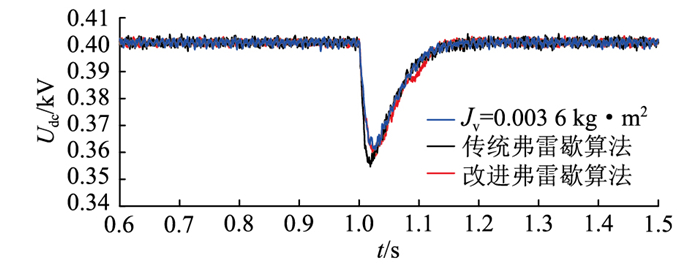
对比图 12中电压曲线,可知当Cv为0.04 mF时,母线电压超调量偏大,响应时间偏短;而当Cv为0.36 mF时,超调量偏小,响应时间偏长;仅当Cv为0.2 mF时,Jv与Cv的电压超调量与响应时间具有相似性,因此初步确定Cv的取值范围为0.04~0.36 mF。其次,分别采用传统弗雷歇算法与改进弗雷歇算法获取Jv为3.6×10-3 kg · m2时Cv的对应数值,结果分别为0.08 mF与0.2 mF。图 13为不同算法下母线电压波形。
|
图 13 不同算法下母线电压波形 Fig. 13 Bus voltage waveforms under different algorithms |
依据图 13中传统弗雷歇算法与改进弗雷歇算法下母线电压波形和式(18)、式(19),最终得出传统弗雷歇算法下Jv与Cv两者母线电压波形之间的Δσp与ΔU′分别为4.8%、0.11%,改进弗雷歇算法下Δσp与ΔU′分别为0.095%、0.01%,与阶跃响应曲线分析结果具有一致性,验证了改进弗雷歇算法在VDCM等效惯量计算方法上的有效性。
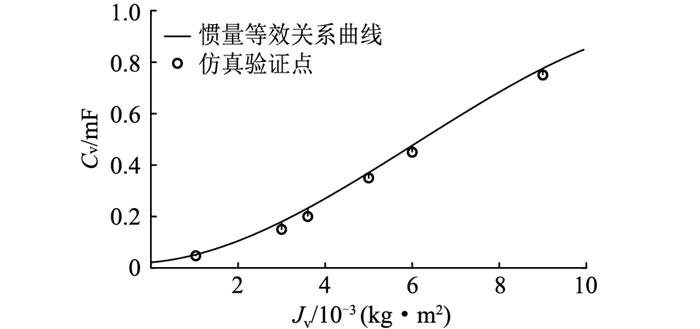
为充分验证惯量等效关系的准确性,文中采用上述计算方法分别在阈值约束范围内、外各取3组等效惯量的对应数据,对惯量等效关系曲线进行验证,结果如图 14所示。
|
图 14 惯量等效关系验证结果 Fig. 14 Verification results of equivalence relation of inertia |
由图 14可知,验证数据基本落在惯量等效关系曲线附近,其中验证数据与拟合曲线间的决定系数、相关系数与显著水平均为1,表明两者具有强相关性,且无显著性差异。此外验证点的残差平方和仅为0.054,而残差平方和数值越小,则文中得出的惯量等效关系和Jv与Cv间实际关系的相似程度越高,从而验证了该计算方法的正确性。
5 结论文中提出一种基于改进弗雷歇算法的VDCM控制惯量等效关系计算方法,并以直流微电网为应用场景对该方法进行了验证,得出以下结论:
(1) 与双环控制相比,VDCM控制能够抑制直流母线电压突变,降低母线电压超调量,提高系统惯量,且通过小信号模型分析以及仿真结果发现Jv与Cv在改善电压质量、增强直流系统惯性方面具有一致性,表明了Jv与Cv间的对应关系。
(2) 与传统弗雷歇算法相比,文中提出的基于相关性约束与曲线特征约束的改进弗雷歇算法充分考虑了系统的稳态与暂态特征,提高了弗雷歇算法准确性,保证了等效惯量计算结果的有效性。
(3) 等效惯量计算方法以函数形式具现了Jv与Cv的非线性等效关系,明确了VDCM控制在负荷波动时提供的惯量大小,便于直流微电网惯量的调节。
致谢
本文得到江苏省研究生科研与实践创新计划项目(SJCX22_1083),南京工程学院校级基金项目(CKJB202114)资助,谨此致谢!
| [1] |
GUO Q, TU C M, JIANG F, et al. Improved dynamic voltage restorer with reduced capacity of power inverter and energy storage for voltage sag mitigation[J]. IET Power Electronics, 2021, 14(5): 958-968. DOI:10.1049/pel2.12078 (  0) 0) |
| [2] |
王植, 俞子聪, 张泉, 等. 光伏参与直流微电网调压控制策略[J]. 高电压技术, 2020, 46(11): 3762-3770. WANG Zhi, YU Zicong, ZHANG Quan, et al. Voltage regulation control strategy for DC microgrid with photovoltaic participation[J]. High Voltage Engineering, 2020, 46(11): 3762-3770. DOI:10.13336/j.1003-6520.hve.20200227001 (  0) 0) |
| [3] |
田艳军, 彭飞, 朱晓荣, 等. 直流微网储能单元的灵活类虚拟同步发电机控制[J]. 高电压技术, 2020, 46(7): 2316-2328. TIAN Yanjun, PENG Fei, ZHU Xiaorong, et al. Flexible analogous virtual synchronous generator control for energy storage units in DC microgrid[J]. High Voltage Engineering, 2020, 46(7): 2316-2328. DOI:10.13336/j.1003-6520.hve.20200306 (  0) 0) |
| [4] |
朱珊珊, 汪飞, 郭慧, 等. 直流微电网下垂控制技术研究综述[J]. 中国电机工程学报, 2018, 38(1): 72-84, 344. ZHU Shanshan, WANG Fei, GUO Hui, et al. Overview of droop control in DC microgrid[J]. Proceedings of the CSEE, 2018, 38(1): 72-84, 344. (  0) 0) |
| [5] |
杨金文, 吴杰康, 庄仲, 等. 基于小区源-储-荷协同的微网多能协调控制策略[J]. 电力工程技术, 2021, 40(1): 40-49. YANG Jinwen, WU Jiekang, ZHUANG Zhong, et al. Multi-energy coordinated control strategy based on source-storage-load micro network in community[J]. Electric Power Engineering Technology, 2021, 40(1): 40-49. (  0) 0) |
| [6] |
王毅, 黑阳, 付媛, 等. 基于变下垂系数的直流配电网自适应虚拟惯性控制[J]. 电力系统自动化, 2017, 41(8): 116-124. WANG Yi, HEI Yang, FU Yuan, et al. Adaptive virtual inertia control of DC distribution network based on variable droop coefficient[J]. Automation of Electric Power Systems, 2017, 41(8): 116-124. (  0) 0) |
| [7] |
WANG Y, WANG C, XU L, et al. Adjustable inertial response from the converter with adaptive droop control in DC grids[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 3198-3209. DOI:10.1109/TSG.2018.2820160 (  0) 0) |
| [8] |
兰征, 涂春鸣, 姜飞. 基于虚拟电机技术的直流微电网与主电网柔性互联策略[J]. 电工技术学报, 2019, 34(8): 1739-1749. LAN Zheng, TU Chunming, JIANG Fei. The flexible interconnection strategy between DC microgrid and AC grid based on virtual electric machinery technology[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1739-1749. (  0) 0) |
| [9] |
朱晓荣, 蔡杰, 王毅, 等. 风储直流微网虚拟惯性控制技术[J]. 中国电机工程学报, 2016, 36(1): 49-58. ZHU Xiaorong, CAI Jie, WANG Yi, et al. Virtual inertia control of wind-battery-based DC micro-grid[J]. Proceedings of the CSEE, 2016, 36(1): 49-58. (  0) 0) |
| [10] |
GUO Y, MENG J H, WANG Y, et al. A virtual DC machine control strategy for dual active bridge DC-DC converter[C]//IEEE Innovative Smart Grid Technologies-Asia. Chengdu, China. IEEE, 2019: 2384-2388.
(  0) 0) |
| [11] |
程启明, 杨小龙, 褚思远, 等. 基于虚拟直流发电机的光伏系统控制策略[J]. 高电压技术, 2017, 43(7): 2097-2104. CHENG Qiming, YANG Xiaolong, CHU Siyuan, et al. Research on control strategy of PV system based on virtual DC generator[J]. High Voltage Engineering, 2017, 43(7): 2097-2104. (  0) 0) |
| [12] |
盛万兴, 刘海涛, 曾正, 等. 一种基于虚拟电机控制的能量路由器[J]. 中国电机工程学报, 2015, 35(14): 3541-3550. SHENG Wanxing, LIU Haitao, ZENG Zheng, et al. An energy hub based on virtual-machine control[J]. Proceedings of the CSEE, 2015, 35(14): 3541-3550. (  0) 0) |
| [13] |
崔健, 吕志鹏, 盛万兴, 等. 一种新型虚拟直流电机控制技术[J]. 中国电机工程学报, 2019, 39(10): 3029-3038. CUI Jian, LYU Zhipeng, SHENG Wanxing, et al. A new control technology based on virtual DC motor[J]. Proceedings of the CSEE, 2019, 39(10): 3029-3038. (  0) 0) |
| [14] |
张祥宇, 李浩, 付媛. 含新型虚拟电机的直流微网动态稳定性分析与自适应电压惯性控制[J]. 高电压技术, 2021, 47(8): 2865-2874. ZHANG Xiangyu, LI Hao, FU Yuan. Dynamic stability analysis and self-adaptive voltage inertia control of DC microgrids with novel virtual machine[J]. High Voltage Engineering, 2021, 47(8): 2865-2874. (  0) 0) |
| [15] |
张辉, 谭树成, 肖曦, 等. 具有直流电机特性的储能接口变换器控制策略[J]. 高电压技术, 2018, 44(1): 119-125. ZHANG Hui, TAN Shucheng, XIAO Xi, et al. Control strategy of energy storage converter with DC machine characteristics[J]. High Voltage Engineering, 2018, 44(1): 119-125. (  0) 0) |
| [16] |
孟建辉, 张赟, 范莹, 等. 基于直流微网虚拟电容控制的等效电容计算方法[J]. 电力建设, 2020, 41(7): 25-32. MENG Jianhui, ZHANG Yun, FAN Ying, et al. Equivalent capacitance calculation method based on virtual capacitance control of DC microgrid[J]. Electric Power Construction, 2020, 41(7): 25-32. (  0) 0) |
| [17] |
SAMANTA S, MISHRA J P, ROY B K. Virtual DC machine: an inertia emulation and control technique for a bidirectional DC-DC converter in a DC microgrid[J]. IET Electric Power Applications, 2018, 12(6): 874-884. (  0) 0) |
| [18] |
刘玲, 林刚, 焦世青, 等. 充电站直流微网虚拟直流电机控制策略及其动态特性分析[J]. 电力系统保护与控制, 2020, 48(11): 28-35. LIU Ling, LIN Gang, JIAO Shiqing, et al. Virtual DC generator control strategy and its dynamic analysis of DC charging station microgrid[J]. Power System Protection and Control, 2020, 48(11): 28-35. (  0) 0) |
| [19] |
孟建辉, 郭禹, 王毅, 等. 双有源全桥DC-DC变换器的自适应虚拟直流电机控制方法[J]. 高电压技术, 2020, 46(5): 1497-1507. MENG Jianhui, GUO Yu, WANG Yi, et al. Adaptive virtual DC machine control strategy for dual active bridge DC-DC converter[J]. High Voltage Engineering, 2020, 46(5): 1497-1507. (  0) 0) |
| [20] |
WANG P Y, ZHAO J F, LIU K L. Parameter-adaptation-based virtual DC motor control method for energy storage converter[J]. IEEE Access, 2021(9): 90795-90804. (  0) 0) |
| [21] |
尹英龙, 刘宝泉. DC/DC变换器虚拟直流电机控制稳定机理研究[J]. 陕西科技大学学报, 2021, 39(2): 146-152. YIN Yinglong, LIU Baoquan. Research on stabilizing mechanism of distributed DC/DC converter virtual DC motor control[J]. Journal of Shaanxi University of Science & Technology, 2021, 39(2): 146-152. (  0) 0) |
| [22] |
支娜, 丁可, 黄庆辉, 等. 基于P-U下垂特性的虚拟直流电机控制策略[J]. 电工技术学报, 2021, 36(6): 1238-1248. ZHI Na, DING Ke, HUANG Qinghui, et al. A virtual DC motor control strategy based on P-U drooping characteristics[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1238-1248. (  0) 0) |
| [23] |
TAN S C, DONG G, ZHANG H, et al. Virtual DC machine control strategy of energy storage converterin DC microgrid[C]//IEEE Electrical Power and Energy Conference. Ottawa, ON, Canada. IEEE, 2016: 1-5.
(  0) 0) |
| [24] |
孟建辉, 宋美琪, 王毅, 等. 虚拟电容控制下并网型直流微网VSC多约束稳定运行边界[J]. 电力系统自动化, 2019, 43(15): 172-179, 199. MENG Jianhui, SONG Meiqi, WANG Yi, et al. Multi-constraint stable operation boundary of grid-connected voltage source converter of DC microgrid with virtual capacitance control[J]. Automation of Electric Power Systems, 2019, 43(15): 172-179, 199. (  0) 0) |
| [25] |
唐冬来, 倪平波, 张捷, 等. 基于离散弗雷歇距离的户变关系识别方法[J]. 电力系统自动化, 2021, 45(6): 223-230. TANG Donglai, NI Pingbo, ZHANG Jie, et al. Identification method for relationship between household transformers based on discrete Frechet distance[J]. Automation of Electric Power Systems, 2021, 45(6): 223-230. (  0) 0) |
| [26] |
黄世泽, 陈威, 张帆, 等. 基于弗雷歇距离的道岔故障诊断方法[J]. 同济大学学报(自然科学版), 2018, 46(12): 1690-1695. HUANG Shize, CHEN Wei, ZHANG Fan, et al. Method of turnout fault diagnosis based on Fréchet distance[J]. Journal of Tongji University (Natural Science), 2018, 46(12): 1690-1695. (  0) 0) |

 王书征(1983),男,博士,副教授,研究方向为直流配电网运行与控制(E-mail:
王书征(1983),男,博士,副教授,研究方向为直流配电网运行与控制(E-mail: