文章编号: 2096-3203(2022)06-0154-09 中图分类号: TM247
2. 福州大学电气工程与自动化学院, 福建 福州 350108;
3. 天津大学电气自动化与信息工程学院, 天津 300072
超高压海底电缆输电具有远距离、大容量以及低损耗电能跨海传输的优势,是实现我国海岛与海上平台供电、海上风电并网以及电网国际化互联的有效途径[1-3]。海底电缆导体所允许的最高运行温度通常为90 ℃,当电缆运行温度长期高于该值时将对电缆造成损伤,降低海底电缆运行寿命;而当电缆运行温度长期小于该值时将造成能源的不完全利用[4]。因此,分析计算海底电缆载流量对于充分发挥海底电缆输送效率以及提高海底电缆输电线路的安全稳定性等具有重要意义。
目前,针对海底电缆稳态载流量分析的方法主要包括基于IEC 60287[5]建立稳态热路模型的计算方法以及基于有限元的仿真计算方法[6]。IEC 60287建立的海底电缆热路模型运用传热学原理计算海底电缆导体达到最高允许工作温度时的载荷能力[7]。有限元仿真计算方法则将理论分析与数值计算相结合,建立海底电缆多物理场耦合仿真模型,计算复杂工况下海底电缆的载荷能力[8]。国内外学者利用这2种计算方法对海底电缆载流量进行了分析计算。文献[9]建立电磁-热-流多物理场耦合的海底电缆有限元仿真模型,对不同敷设方案下220 kV三芯交联聚乙烯(cross linked polyethylene,XLPE)海底电缆载流量进行计算分析。文献[10]则分别建立基于IEC 60287的热路模型与有限元仿真模型对三芯XLPE海底电缆载流量进行计算分析。
以往研究主要针对220 kV及以下等级的海底电缆。近几年随着我国海底电缆技术不断发展,海缆电压等级已达到500 kV,因此关于500 kV海缆的研究已逐渐成为热点。文献[6]采用三维电-热耦合仿真模型对比研究不同冷却方式对提升500 kV XLPE海底电缆登陆段载流能力的影响。文献[11]则通过构建500 kV充油海底电缆暂态热路模型,对不同敷设环境下的海底电缆过负荷能力进行分析。
海底电缆运行环境复杂多变,且目前缺乏对典型敷设环境下500 kV交流XLPE海底电缆稳态载流量的研究。在此背景下,文中针对500 kV交流XLPE超高压海底电缆在典型敷设环境下的稳态载流量展开研究,建立考虑不同线路敷设环境、不同海缆敷设方式、不同海缆敷设深度以及外界环境温度变化的海底电缆稳态热路模型,并通过有限元仿真验证热路模型计算结果的准确性。
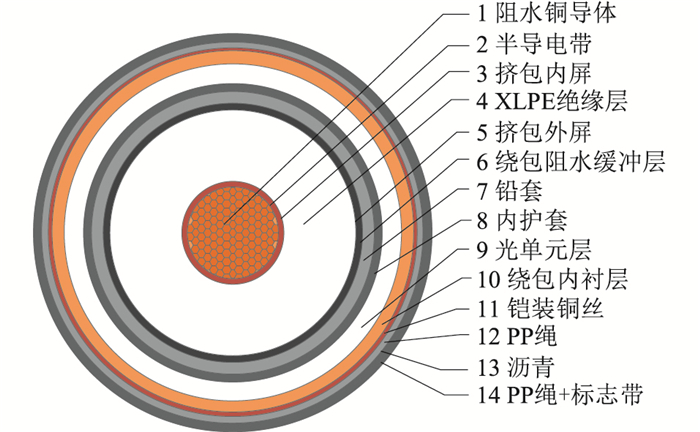
1 500 kV交流XLPE海底电缆稳态热路模型 1.1 海缆结构及参数文中研究的500 kV交流XLPE海底电缆,主要结构由阻水导体、导体屏蔽、XLPE绝缘、绝缘屏蔽、阻水层、合金铅护套、聚丙烯(polypropylene,PP)绳、铜丝铠装并内嵌光单元层等组成,具体截面结构如图 1所示,结构参数如表 1所示。
|
图 1 500 kV XLPE海底电缆截面结构 Fig. 1 Cross-section structure of 500 kV XLPE submarine cable |
|
|
表 1 500 kV XLPE海底电缆结构参数 Table 1 Structure parameters of 500 kV XLPE submarine cable |
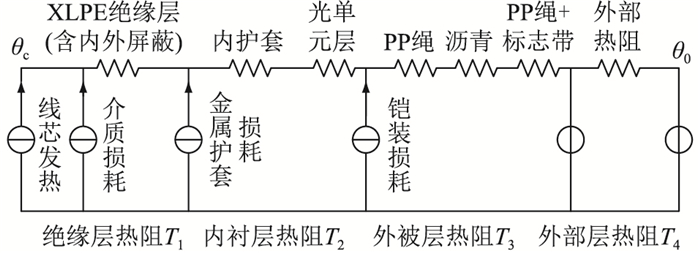
当交流电流通过海缆时,在阻水导体层、绝缘介质层、金属护套层和铠装层中都将产生损耗,形成热流,由于各部分热阻的存在,热流流经海缆各部分时产生温度降,海缆从内到外形成温差。文中500 kV XLPE海底电缆结构共由14层组成,且各层材料导热系数存在一定差异。在建立海缆稳态热路模型时,需要根据各层材料的损耗因数及导热系数对海缆结构进行分层。然而,如果对海缆从内向外逐层进行热阻计算,得到的热路模型较为复杂,可能影响计算准确性。为简化热路模型,文中将导热系数相近的材料归于同一等效层。将海缆热路分为绝缘层、内衬层、外被层、外部媒质层四部分。海缆稳态热路模型如图 2所示,海缆采用双回路平行排列方式。
|
图 2 500 kV XLPE海底电缆等效稳态热路模型 Fig. 2 Equivalent steady state thermal circuit model of 500 kV XLPE submarine cable |
图 2中,T1,T2,T3,T4分别为单位长度海缆的绝缘层、内衬层、外被层和外部媒质层热阻;θc,θ0分别为海缆线芯及环境温度。由于线芯铜导体、金属铅护套、铠装铜丝均为金属材质,导热性能好,温度降小,故在建立等效稳态热路模型时其热阻可忽略不计[12-13]。
1.3 海底电缆稳态热路模型损耗计算线芯发热损耗可由I2R计算得到。根据IEC 60287,导体交流电阻R计算公式为:
| $ R=R^{\prime}\left(1+Y_{\mathrm{s}}+Y_{\mathrm{p}}\right) $ | (1) |
式中:R为工作温度下导体的交流电阻;R′为工作温度下导体的直流电阻;Ys为集肤效应系数;Yp为邻近效应系数。
Ys与Yp计算公式为:
| $ Y_{\mathrm{s}}=\frac{X_{\mathrm{s}}^4}{192+0.8 X_{\mathrm{s}}^4} $ | (2) |
| $ X_{\mathrm{s}}^2=\frac{8 \pi f}{R^{\prime}} \times 10^{-7} k_{\mathrm{s}} $ | (3) |
| $ \begin{gathered} Y_{\mathrm{p}}=\frac{X_{\mathrm{p}}^4}{192+0.8 X_{\mathrm{p}}^4}\left(-\frac{d_{\mathrm{c}}}{s}\right)^2 \times 0.312\left(\frac{d_{\mathrm{c}}}{s}\right)^2+ \\ 1.18 /\left(\frac{X_{\mathrm{p}}^4}{192+0.8 X_{\mathrm{p}}^4}+0.27\right) \end{gathered} $ | (4) |
| $ X_{\mathrm{p}}^2=\frac{8 \pi f}{R^{\prime}} \times 10^{-7} k_{\mathrm{p}} $ | (5) |
式中:dc为海缆导体层外径;ks, kp对于干燥的圆绞铜线分别取0.435 Ω/(m ·Hz),0.37 Ω/(m ·Hz);s为平行敷设海缆间距。
最高工作温度下导体直流电阻R′计算公式为:
| $ R^{\prime}=R_0\left[1+\alpha_{20}\left(T_{\mathrm{c}}-20\right)\right] $ | (6) |
式中:R0为导体在20 ℃下直流电阻率,文中取7.3×10-6 Ω ·m;α20为导体温度系数,文中取3.93×10-3;Tc为电缆最高允许工作温度,500 kV交流XLPE海缆最高允许工作温度为90 ℃[14]。
单位长度单芯海缆的介质损耗Wd计算公式为:
| $ W_{\mathrm{d}}=\omega C U_0^2 \tan \delta $ | (7) |
| $ C=\frac{\varepsilon}{18 \ln \left(D_{\mathrm{i}} / d_{\mathrm{c}}\right)} \times 10^{-9} $ | (8) |
式中:ω=2πf,f为频率;U0为对地电压,文中取为288.7 kV;tan δ为在电源系统和工作温度下的介质损耗角正切值,取5×10-4;C为单位长度海缆电容;ε为绝缘材料相对介电系数,取2.3;Di为绝缘层直径;dc为导体直径。
护套中的损耗主要分为金属护套功率损耗和铠装层损耗两部分。这两部分损耗通常用其相对于线芯损耗的损耗因数表示。文中使用λ1表示金属护套功率损耗,使用λ2表示铠装层损耗。λ1是由环流λ′1和涡流λ″1所引起的损耗。
对于单芯海缆,通常采取双点接地方式,文中根据IEC 60287,对环流损耗λ′1取经验值[15],直接敷设时λ′1=0.03,敷设于管道中时λ′1=0.05。
金属套涡流损耗因数λ″1计算公式为[15]:
| $ \lambda_1^{\prime \prime}=\frac{R_{\mathrm{s}}}{R}\left[g_{\mathrm{s}} \lambda_0 H N J+\frac{\left(\beta_1 t_{\mathrm{il}}\right)^4}{12 \times 10^{12}}\right] $ | (9) |
| $ R_{\mathrm{s}}=\frac{\rho_{\mathrm{s}}}{A_{\mathrm{s}}}\left[1+\alpha_{\mathrm{s}}\left(\theta_{\mathrm{s}}-20\right)\right] $ | (10) |
| $ \beta_1=\sqrt{\frac{4 \pi \omega}{\rho_{\mathrm{s}} \times 10^7}} $ | (11) |
| $ g_{\mathrm{s}}=1+\left(\frac{t_{\mathrm{i} 1}}{D_1}\right)^{1.74}\left(\beta_1 D_1 \times 10^{-3}-1.6\right) $ | (12) |
| $ \lambda_0=C\left(\frac{m^2}{1+m^2}\right)\left(\frac{D_1}{2 S}\right)^2 $ | (13) |
| $ m=\left(\omega / R_{\mathrm{s}}\right) \times 10^{-7} $ | (14) |
| $ \theta_{\mathrm{s}}=\theta_c-\left(I^2 R+0.5 W_{\mathrm{d}}\right) T_1 $ | (15) |
式中:ρs为铅护套在20 ℃下的电阻率,文中取为2.068 4×10-7 Ω ·m;αs为铅的电阻温度系数,取3.76×10-3;θs为护套工作温度,其与载流量互相影响,故设定其初始温度为60 ℃,多次计算迭代得到最终稳态温度值[15];D1为铅护套外径,为133.98 mm;ti1为铅护套厚度,为4.5 mm;S为海缆轴间距。假定导体以逆序连接,海缆共有A、B、C三相,由于B相温升最高[16],故取海缆的B相计算载流量,则H=1.027,N=1.266 2,J=1.002。
海缆金属铠装的功率损耗因数λ2的计算公式为[14]:
| $ \lambda_2=1.23 \frac{R_{\mathrm{s}}}{R}\left(\frac{2 d_{\mathrm{c}}}{d_{\mathrm{A}}}\right)^2 \frac{1}{\left(\frac{2.77 R_{\mathrm{s} 1} \times 10^6}{\omega}\right)^2+1} $ | (16) |
| $ R_{\mathrm{s} 1}=\frac{\rho_{\mathrm{s}}}{A_{\mathrm{s}}}\left[1+a_{\mathrm{s}}\left(\theta_{\mathrm{s}}-20\right)\right] $ | (17) |
式中:Rs1为工作温度下铠装铜丝的电阻值;dA为铠装层的平均直径;ρs为20 ℃时铠装金属的电阻率,取7.3×10-6 Ω ·m;αs为铠装铜丝的电阻温度系数,取3.93×10-3。
1.4 海底电缆稳态热路模型热阻计算 1.4.1 绝缘层热阻计算海缆等效绝缘层是指线芯铜导体与金属护套之间的部分,主要材料为XLPE绝缘,半导电带、挤包内屏蔽、挤包外屏蔽的厚度较薄,且导热系数高,其温降可以忽略不计,因此绝缘层热阻的计算公式为:
| $ T_1=\frac{\rho_{T_1}}{2 \pi} \ln \left(1+\frac{2 t_{\mathrm{i}}}{d_{\mathrm{c}}}\right) $ | (18) |
式中:ρT1为绝缘材料热阻系数,文中取3.5 K ·m/W;ti为铜导体与金属套之间的绝缘层厚度。
1.4.2 内衬层热阻计算等效内衬层主要有5层材料,分别是铅护套、内护套、光单元层、绕包内衬层和铠装铜丝。由于铅护套与铠装铜丝均为金属材料,导热性能良好,故其对温度的影响可以忽略不计。光单元层绝大部分材料为PE,故可近似视为PE层。内衬层热阻的计算公式为:
| $ T_2=\frac{\rho_{T_2}}{2 \pi} \ln \left(1+\frac{2 t_2}{D_1}\right) $ | (19) |
式中:ρT2为等效内衬层热阻系数,取3.5 K ·m/W;D1为金属套外径;t2为等效内衬层各层厚度。
1.4.3 外被层热阻计算等效外被层是指海缆铠装之外至护套内径之间的部分,其具体计算公式为:
| $ T_3=\frac{\rho_{T_3}}{2 \pi} \ln \left(1+\frac{2 t_{\mathrm{e}}}{D_2}\right) $ | (20) |
式中:ρT3为等效外被层热阻系数,取3.5 K ·m/W;D2为铠装外径;te为等效外被层厚度。
1.4.4 外部热阻计算超高压海缆在不同敷设环境下的外部热阻不同。海缆在海水中的敷设方式主要为土壤直埋方式,在登陆段的敷设方式主要为土壤直埋与管道敷设方式,在空气段的敷设方式主要为电缆沟埋设方式。各敷设环境下的热阻计算方法如下。
(1) 土壤直埋外部热阻计算。在深海段与浅海段敷设时,海缆周围热阻T4为:
| $ T_4=\frac{\rho_{T_4}}{2 \pi} \ln \left(u+\sqrt{u^2-1}\right) $ | (21) |
| $ u=2 L / D_{\rm e} $ | (22) |
式中:ρT4为介质土壤热阻系数,由于不同埋深的土壤成分不同,故热阻系数也不同;L为海缆埋深;De为海缆外径。
在海缆登陆段附近,平行排列的三相海缆轴间距较小,仅为0.4 m,此时海缆间的散热对海缆载流量影响较为显著,不可忽略。故针对登陆段海缆,外部热阻计算采用修正公式[17]:
| $ T_4=\frac{\rho_{T_4}}{2 \pi}\left(\ln \left(u+\sqrt{u^2-1}\right)+\ln \left(1+\frac{2 L}{S}\right)\right) $ | (23) |
(2) 管道敷设外部热阻计算。海缆敷设在PE管道底部,管道外部为土壤直埋环境,其外部热阻主要由以下三部分组成:
| $ T_4=T_4^{\prime}+T_4^{\prime \prime}+T_4^{\prime \prime \prime} $ | (24) |
式中:T′4为海缆表面和管道内表面之间空间热阻;T″4为管道本身热阻;T'''4为管道外部热阻。
T′4的计算公式为:
| $ T_4^{\prime}=\frac{U D_{\rm{e}}}{1+0.1\left(V+Y \theta_{\mathrm{m}}\right)} $ | (25) |
式中:U,V,Y与海缆敷设条件有关[18],文中U=5.2,V=0.91,Y= 0.01;θm为海缆与管道之空间介质的平均温度,文中取40 ℃。
T″4的计算公式为:
| $ T_4^{\prime \prime}=\rho_{\mathrm{t}} \frac{\ln \left(D_{\mathrm{o}} / D_{\mathrm{d}}\right)}{2 \pi} $ | (26) |
式中:ρt为管道材料的热阻系数,取3.5 K ·m/W;Do为管道外径,取280 mm;Dd为管道内径,取250 mm。
T'''4的计算公式为:
| $ T_4^{\prime \prime \prime}=\rho_{T_4}(0.475 \ln (2 u)-0.346) $ | (27) |
| $ u=2 L / D_{\mathrm{d}} $ | (28) |
(3) 空气敷设外部热阻计算。假设陆上段海缆埋设在电缆沟内,不受阳光直接照射,海缆周围热阻T4为:
| $ T_4=\frac{1}{\pi D_{\mathrm{e}} h \Delta \theta_{\mathrm{s}}^{0.25}} $ | (29) |
| $ h=\frac{Z}{D_{\mathrm{e}}^g}+E $ | (30) |
式中:h为散热系数;Z=0.62;E=1.95;g=0.25;Δθs0.25根据Ka可查表得到[18]。
| $ \begin{gathered} K_{\mathrm{a}}=\frac{\pi D_{\mathrm{e}} h}{1+\lambda_1+\lambda_2} \times \\ {\left[\frac{T_1}{n}+T_2\left(1+\lambda_1\right)+T_3\left(1+\lambda_1+\lambda_2\right)\right]} \end{gathered} $ | (31) |
结合以上各部分热阻和损耗的计算,500 kV交流XLPE海底电缆的载流量计算公式为:
| $ \begin{gathered} I= \\ \sqrt{\frac{\Delta \theta_{\mathrm{c}}-W_{\mathrm{d}}\left[0.5 T_1+n\left(T_2+T_3+T_4\right)\right]}{R T_1+n R\left(1+\lambda_1\right) T_2+n R\left(1+\lambda_1+\lambda_2\right)\left(T_3+T_4\right)}} \end{gathered} $ | (32) |
式中:I为所求海缆的载流量值;n为海缆芯数,取1;Δθc为海缆线芯铜导体温度与敷设环境稳态温度差值。
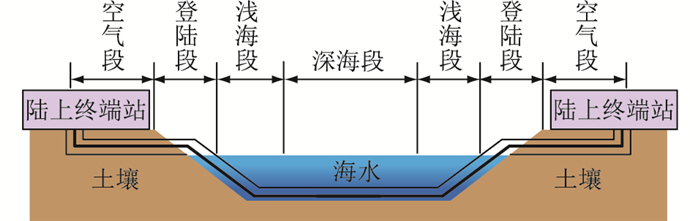
1.6 等效稳态热路模型热阻计算结果根据500 kV交流XLPE海底电缆运行线路的设计与工作环境,将敷设环境主要分为深海段、浅海段、登陆段、空气段[19-20]。敷设环境如图 3所示,不同敷设环境下,海底电缆热路模型所考虑的外界环境参数不尽相同。因此,对应不同敷设环境,给出不同敷设环境下的环境温度、土壤埋深以及土壤热阻系数,如表 2所示。根据表 2数据,给出500 kV海底电缆热阻计算结果,如表 3所示。
|
图 3 500 kV XLPE海底电缆敷设环境 Fig. 3 Layout environment of 500 kV XLPE submarine cable |
|
|
表 2 不同敷设环境下环境参数 Table 2 Environment parameters under different layout environments |
|
|
表 3 500 kV XLPE海底电缆热阻计算结果 Table 3 Thermal resistance calculation results of 500 kV XLPE submarine cable |
为验证文中所建立的500 kV交流XLPE海缆稳态热路模型的准确性,针对所用海缆结构,在有限元仿真软件中建立海底电缆磁-热-流多物理场耦合仿真模型,采用双回路平行排列,各层材料的材料参数如表 4所示。
|
|
表 4 500 kV XLPE海底电缆材料参数 Table 4 Material parameters of 500 kV XLPE submarine cable |
海缆在不同的敷设环境中海缆轴间距也会发生变化,根据GB/T 51190—2016[21]要求,平行敷设海底电缆应避免交叉重叠,电缆间距不宜小于该处最大水深的1.2倍,登陆段间距可适当缩小,但应满足电缆载流量和保护的要求。假设敷设区域最大水深为40 m,故将深海段海缆间距设为50 m,浅海段海缆间距设为5 m,登陆段与空气段海缆较短,且采取降温措施,故登陆段与空气段海缆间距设为0.4 m。
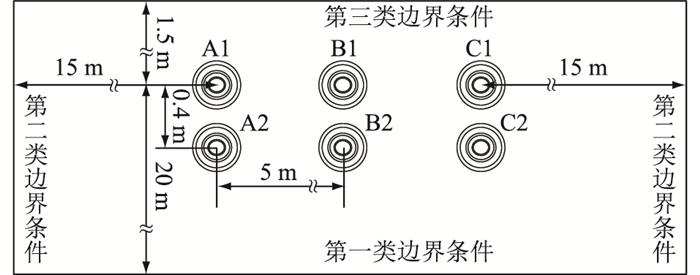
双回路海底电缆采用平行排列时,采用有限元仿真软件建立多物理场耦合模型拓扑如图 4所示,图中以浅海段土壤直埋敷设为例。
|
图 4 500 kV XLPE海底电缆有限元仿真拓扑 Fig. 4 Finite element simulation topology of 500 kV XLPE submarine cable |
图 4中海缆敷设条件为:相邻海缆等间距,间距为5 m,上下平行海缆间隔为0.4 m,上层海缆距离地面埋设深度为1.5 m,与深层土壤距离20 m,左右土壤边界距离海缆15 m。空气段模型中电缆直接与开放空间自然对流,对流换热系数为5 W/(m2·K),外部温度为26 ℃。
海缆传热的边界条件可以归结为3类边界条件[19]。第一类边界条件为确定的边界温度,计算公式为:
| $ \left\{\begin{array}{l} \frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0 \\ \left.T(x, y)\right|_{\Gamma}=\left.f(x, y)\right|_{\Gamma} \end{array}\right. $ | (33) |
第二类边界条件为法向热流密度,计算公式为:
| $ \left\{\begin{array}{l} \frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0 \\ -\left.k \frac{\partial T}{\partial n}\right|_{\Gamma}=\left.f(x, y)\right|_{\Gamma}=q_2 \end{array}\right. $ | (34) |
式中:q2为热流密度;k为导热系数。
第三类边界条件为对流边界条件,即对流换热系数和流体温度,计算公式为:
| $ \left\{\begin{array}{l} \frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0 \\ -\left.k \frac{\partial T}{\partial n}\right|_{\Gamma}=\left.\alpha\left(T-T_{\mathrm{f}}\right)\right|_{\Gamma} \end{array}\right. $ | (35) |
式中:Tf为流体温度;α为对流换热系数。
文中对不同敷设环境下边界条件的设置如表 5所示。采用物理场控制网格对整个求解域进行网格划分,以浅海段土壤直埋为例,部分区域的网格剖分如图 5所示。
|
|
表 5 不同敷设环境下边界条件设置 Table 5 Setting of boundary conditions under different layout environments |

|
图 5 500 kV XLPE海底电缆网格划分局部示意 Fig. 5 Partial schematic diagram of grid division of 500 kV XLPE submarine cable |
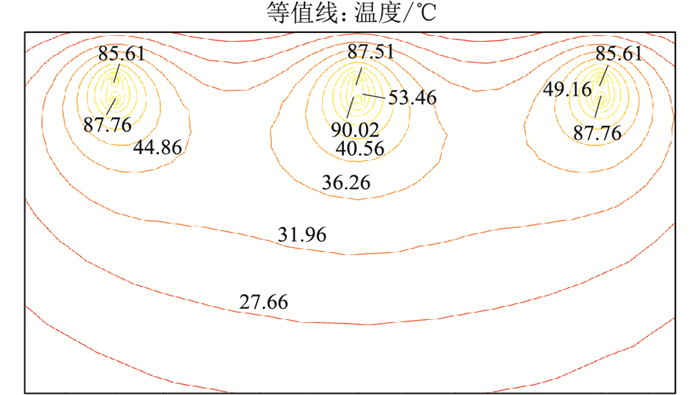
建立模型并完成参数和边界条件设置,对仿真模型进行计算,当海缆导体最高温度达到90 ℃时,海缆温度场等温线分布如图 6所示。上层海缆从左至右设为A1相、B1相以及C1相海缆,下层海缆从左至右设为A2相、B2相以及C2相海缆。最高温度出现在下层中间的海缆,即B2相海缆,C2相、A2相与B1相海缆温度次之,比B2相海缆温度低2.34 ℃,A1相与C1相海缆导体温度最低,上层海缆温度比相同位置的下层海缆温度低1.6 ℃,当B2相海缆导体最高温度达到90 ℃时,载流量为2 066 A。
|
图 6 500 kV XLPE海底电缆等温线局部示意 Fig. 6 Partial schematic diagram of isotherm of 500 kV XLPE submarine cable |
将稳态热路模型计算结果与有限元仿真模型计算结果进行对比分析,计算不同敷设段海缆载流量变化情况,结果如表 6所示。由表 6可知,海底电缆在空气段的载流量最大,有限元计算海缆在空气段载流量达到2 568 A,热路法计算海缆空气段载流量为2 385.5 A,误差为7.65%;登陆段海缆载流量远小于其他敷设段,土壤直埋敷设时,有限元计算海缆在登陆段载流量为1 276 A,热路法计算海缆登陆段载流量为1 399.5 A,误差为8.82%。因此,登陆段海缆为整条线路载流量瓶颈段。登陆段海缆通常采用土壤直埋或管道敷设方案,文中也针对管道敷设时海缆在登陆段的载流量进行了计算,有限元计算得到海缆管道敷设时登陆段载流量为1 170 A,热路法计算结果为1 219.2 A,误差为4.04%。该结果表明,管道敷设时,由于管道内散热条件较差,海缆载流量要比土壤直埋时降低约150 A。
|
|
表 6 不同敷设环境下载流量计算结果对比 Table 6 Comparison of calculation results of ampacity under different layout environments |
以上对比分析表明,文中所建立的海缆稳态热路模型与有限元分析所得到的载流量计算结果误差均控制在9%以内。除此之外,表 6的误差表明,浅海段、登陆段、登陆段(管道)以及空气段的误差明显大于深海段误差,文中推测是因为海缆由深海段进入浅海段及陆上段时,间距逐渐减小,海缆间的散热对载流量影响逐渐显著,而文中提出的稳态热路模型与有限元计算方法对海缆间散热影响的处理存在一定差异,故误差增大。
3 登陆段载流量影响因素从上文分析结果可知,登陆段海底电缆是整条线路载流量的瓶颈段,因此采用文中所建立的稳态热路模型对登陆段海缆载流量影响因素进行详细分析[20]。
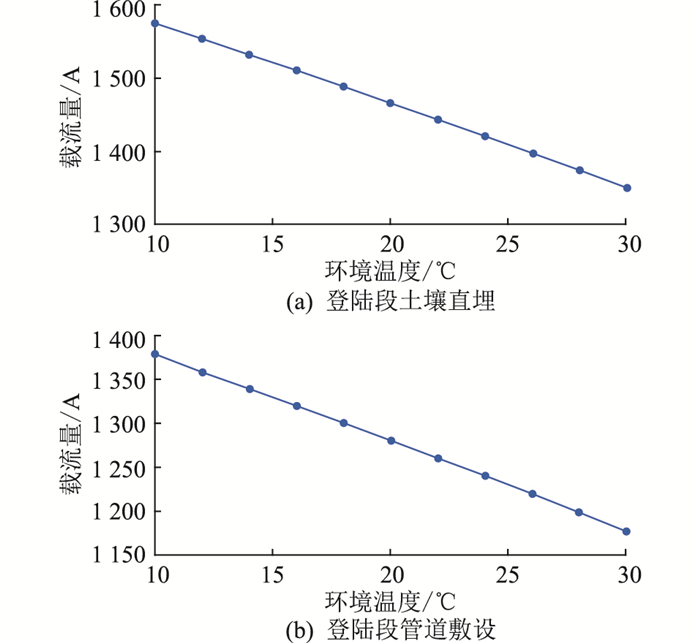
3.1 环境温度对海缆载流量的影响由于海缆敷设线路较长,我国沿江沿海地域分布较广,南至南海诸岛,北至渤海各港口。各地气候差异较大,气温变化范围也较大,因此需要考虑环境温度对海缆载流量的影响[22-24]。基于此,文中利用所建立的海缆稳态热路模型计算当环境温度在10~30 ℃变化时,土壤直埋敷设与管道敷设2种情况下登陆段海底电缆载流量随环境温度的变化规律,结果如图 7所示。随着环境温度的上升,登陆段海底电缆载流量几乎呈线性下降的趋势,环境温度每增加10 ℃,海缆载流量降低约100 A。
|
图 7 500 kV XLPE海底电缆载流量随环境温度变化情况 Fig. 7 The relationship between the ampacity of 500 kV XLPE submarine cable and the ambient temperature |
当环境温度达到30 ℃时,土壤直埋敷设时海缆载流量约为1 350 A,管道敷设时海缆载流量约为1 170 A。因此在夏季气温较高时期,须降低海缆输送容量,以免对海缆造成损伤,降低运行寿命。
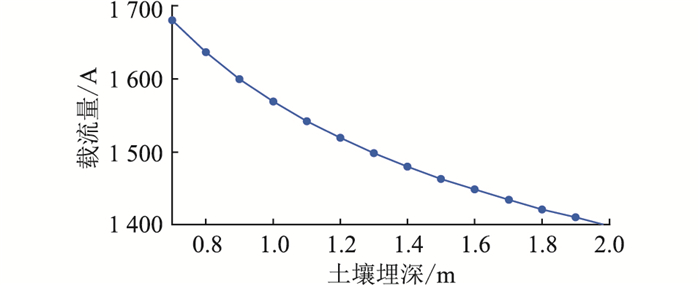
3.2 土壤埋深对海缆载流量的影响根据GB 50217—2018,电力电缆在土壤内埋设深度不得低于0.7 m[25],而海缆在登陆段的埋设深度则根据实际工程需要确定,土壤埋设深度的变化将影响海缆外界环境参数,进而影响海缆载流量。基于此,文中利用所建立的海缆热路模型计算当海缆埋设深度从0.7 m增加到2 m时载流量的变化关系,结果见图 8,其中土壤热阻系数为1.25 K ·m/W。从图中可以看出,随着土壤埋设深度的增大,海缆载流量逐渐减小。当埋设深度从0.7 m增大到2 m,海缆载流量从1 680 A下降到1 400 A。此外,随着埋设深度的增大,载流量下降趋势逐渐趋于平缓。
|
图 8 500 kV XLPE海底电缆载流量随土壤埋深变化情况 Fig. 8 The relationship between the ampacity of 500 kV XLPE submarine cable and the soil buried depth |
文中按照IEC 60287建立了500 kV交流XLPE超高压海底电缆稳态热路模型,对不同敷设环境下海缆载流量的变化规律进行分析,并通过超高压海底电缆磁-热-流多物理场耦合有限元仿真模型对稳态热路模型计算结果进行验证。2种方法得到的载流量计算结果相差不大,5种经典敷设环境下的计算误差均在9%以内。结果表明:登陆段海底电缆为整条线路的载流量瓶颈段,当登陆段海缆采用土壤直埋敷设时载流量为1 350 A,而当登陆段海缆采用管道敷设时载流量则降为1 200 A;外界环境温度每上升10 ℃,登陆段海缆载流量下降约100 A;登陆段海缆采用土壤直埋敷设时,当埋设深度从0.7 m增加到2 m时,海缆载流量下降约300 A。
| [1] |
梁正波, 徐明忠, 陈锋, 等. 典型敷设环境下超高压海底电缆的热特性[J]. 高电压技术, 2019, 45(11): 3452-3458. LIANG Zhengbo, XU Mingzhong, Chen Feng, et al. Thermal characteristics of EHV submarine cable in typical layout environments[J]. High Voltage Technology, 2019, 45(11): 3452-3458. (  0) 0) |
| [2] |
吕安强, 李永倩, 李静, 等. 基于BOTDR的光纤复合海底电缆应变/温度监测[J]. 高电压技术, 2014, 40(2): 533-539. LYU Anqiang, LI Yongqian, LI Jing, et al. Strain and temperature monitoring of 110 kV optical fiber composite submarine power cable based on brillouin optical time domain reflectometer[J]. High Voltage Technology, 2014, 40(2): 533-539. (  0) 0) |
| [3] |
郭宜果, 魏鑫, 于秋雨, 等. 220 kV光纤复合三芯海底电缆线路电气参数的计算[J]. 山东电力技术, 2020, 47(11): 28-33. GUO Yiguo, WEI Xin, YU Qiuyu, et al. Electrical parameters calculation of 220 kV optical fiber composited three-core submarine cable[J]. Shandong Electric Power, 2020, 47(11): 28-33. (  0) 0) |
| [4] |
卞佳音, 李永兰, 单鲁平, 等. 500 kV电力电缆稳态热路模型分析及载流量计算[J]. 绝缘材料, 2019, 52(9): 96-101. BIAN Jiayin, LI Yonglan, SHAN Luping, et al. Analysis of steady-state heat path model and calculation of current carrying capacity for 500 kV power cable[J]. Journal of Insulation Materials, 2019, 52(9): 96-101. (  0) 0) |
| [5] |
Calculation of the current rating of electric cables, part3: sections on operating conditions, section 1: reference operating conditions and selection of cable type IEC 60287-3-1[S].
(  0) 0) |
| [6] |
胡列翔, 欧阳本红, 刘宗喜, 等. 交流500 kV海底电缆登陆段载流能力提升[J]. 高电压技术, 2019, 45(11): 3421-3428. HU Liexiang, OUYANG Benhong, LIU Zongxi, et al. Improvement in current carrying capacity of landing section of AC 500 kV submarine cable[J]. High Voltage Technology, 2019, 45(11): 3421-3428. (  0) 0) |
| [7] |
雷成华, 刘刚, 阮班义, 等. 根据导体温升特性实现高压单芯电缆动态增容的实验研究[J]. 高电压技术, 2012, 38(6): 1397-1402. LEI Chenghua, LIU Gang, RUAN Banyi, et al. Experimental research of dynamic capacity based on conductor temperature-rise characteristic of HV single-core cable[J]. High Voltage Technology, 2012, 38(6): 1397-1402. (  0) 0) |
| [8] |
刘英, 张申冬, 曹俊平, 等. 500 kV直流XLPE海缆的热场及电场仿真研究[J]. 高压电器, 2020, 56(12): 7-15. LIU Ying, ZHANG Shendong, CAO Junping, et al. Thermal field and electric field simulation of 500 kV DC XLPE cable[J]. High voltage apparatus, 2020, 56(12): 7-15. (  0) 0) |
| [9] |
陆莹, 范明明, 郑明, 等. 基于电磁-热-流耦合场的非开挖敷设方案的海底电缆载流量计算[J]. 广东电力, 2020, 33(5): 117-124. LU Ying, FAN Mingming, ZHENG Ming, et al. Calculation of ampacity for submarine cables under trenchless laying method based on electromagnetic-therma-flow coupled field[J]. Guangdong electric power, 2020, 33(5): 117-124. (  0) 0) |
| [10] |
张巍伟. 基于解析法和有限元法的海底电缆温度场分析[J]. 船电技术, 2020, 40(10): 40-44. ZHANG Weiwei. Temperature field analysis of submarine cable based on analytic method and finite element method[J]. Ship Electric Technology, 2020, 40(10): 40-44. (  0) 0) |
| [11] |
陈玉, 李涵之, 姚凯, 等. 500 kV充油海底电缆过负荷能力分析[J]. 电工电能新技术, 2021, 40(10): 1-9. CHEN Yu, LI Hanzhi, YAO Kai, et al. Analysis on overload capacity of 500 kV oil-filled submarine cable[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(10): 1-9. (  0) 0) |
| [12] |
杨帆. 110 kV电缆线路载流量关键技术研究[D]. 广州: 华南理工大学, 2019. YANG Fan. Research on key technology of carrying capacity of 110 kV cable line [D]. Guangzhou: South China University of Technology, 2019. (  0) 0) |
| [13] |
雷成华. 高压单芯电缆动态增容的理论分析与实验研究[D]. 广州: 华南理工大学, 2012. LEI Chenghua. Theoretical analysis and experimental research on dynamic capacity enhancement of high voltage single core cable [D]. Guangzhou: South China University of Technology, 2012. (  0) 0) |
| [14] |
马国栋. 电线电缆载流量[M]. 北京: 中国水利水电出版社, 2003. MA Guodong. Load capacity of wire and cable[M]. Beijing: China Water and Power Press, 2003. (  0) 0) |
| [15] |
LIU Gang, FAN Mingming, WANG Pengyu, et al. Study on reactive power compensation strategies for long distance submarine cables considering electro-thermal coordination[J]. Journal Marine Science and Engineering, 2021, 9(1): 1-17. (  0) 0) |
| [16] |
BENATO R, DAMBONE S, DE Z R, et al. Different bonding types of scilla-villafranca 43 km double-circuit AC 380 kV submarine-land cables[J]. IEEE Transactions on Industry Applications, 51(6): 5050-5057. (  0) 0) |
| [17] |
国网浙江省电力有限公司. 500 kV交联聚乙烯(XLPE)绝缘海底电缆工程技术[M]. 北京: 中国电力出版社, 2020. State Grid Zhejiang Electric Power Co., Ltd. 500 kV XLPE insulated submarine cable engineering technology[M]. Beijing: China Electric Power Press, 2020. (  0) 0) |
| [18] |
国家机械工业局. 电缆载流量计算第2部分: 热阻第1节: 热阻的计算: JB/T 10181.3—2000[S]. 北京: 机械科学研究院, 2000. State Bureau of Machinery Industry. Calculation of the current rating of electric cables, part 2: thermal resistance, section 1: calculation of thermal resistance: JB/T 10181.3-2000[S]. Beijing: Institute of Mechanical Science, 2000. (  0) 0) |
| [19] |
邱超. 双回路单芯电力电缆不同敷设与排列方式下温度场与载流量计算[D]. 广州: 华南理工大学, 2013. QIU Chao. Calculation of temperature field and ampacity of dual-circuit single core power cable with different laying modes and arrangement modes [D]. Guangzhou: South China University of Technology, 2013. (  0) 0) |
| [20] |
游磊. 海上风电场送出海缆载流量瓶颈区段与提升方法研究[D]. 广州: 华南理工大学, 2018. YOU Lei. Research on the bottleneck section and lifting method of the current carrying capacity of the submarine cable sent by the off shore wind farm [D]. Guangzhou: South China University of Technology, 2018. (  0) 0) |
| [21] |
海底电力电缆输电工程设计规范: GB/T 51190—2016[S]. 北京: 中国计划出版社, 2017. Code for design of submarine power cable project: GB/T 51190-2016[S]. Beijing: China Planning Press, 2017. (  0) 0) |
| [22] |
康强, 钱森, 徐阳, 等. 高压直流XLPE海缆现场试验方法综述[J]. 绝缘材料, 2015, 48(8): 8-14. KANG Qiang, QIAN Sen, XU Yang, et al. Review of field test methods of high voltage direct current XLPE submarine cable[J]. Insulation Materials, 2015, 48(8): 8-14. (  0) 0) |
| [23] |
刘恒. 岸电电缆多物理场耦合模型研究及复杂环境实时载流量计算[D]. 重庆: 重庆大学, 2020. LIU Heng. Research on multiphysics coupling model of shore power cable and calculation method of real-time ampacity in complex environment [D]. Chongqing: Chongqing University, 2020. (  0) 0) |
| [24] |
WORZYK Thomas. Submarine power cables: design, installation, repair, environmental aspects[M]. Beijing: China Machine Press, 2011.
(  0) 0) |
| [25] |
电力工程电缆设计标准: GB 50217—2018[S]. 北京: 中国计划出版社, 2018. Cable design standard for power engineering: GB 50217-2018[S]. Beijing: China Planning Press, 2018. (  0) 0) |
2. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108, China;
3. School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China

 张皓(1986), 男, 硕士, 高级工程师, 从事高压电缆状态评价及海缆运维检修工作(E-mail:
张皓(1986), 男, 硕士, 高级工程师, 从事高压电缆状态评价及海缆运维检修工作(E-mail: