文章编号: 2096-3203(2023)01-0154-08 中图分类号: TM854
交联聚乙烯(cross linked polyethylene,XLPE)电缆因其大容量和地下埋设的特点被广泛应用于配网电力传输[1-3]。而电缆接头结构相对复杂,其内部缺陷会影响绝缘性能[4],因此需要一种有效的缺陷检测和老化推测手段来维护电缆接头的正常运行。
电缆接头缺陷一般产生于制造和安装过程,常位于XLPE层与硅橡胶层之间,目前已有多种手段对电缆接头缺陷进行检测[5-7]。文献[8]借助超声波对电缆接头中的空间电荷进行测量,以判断缺陷位置。文献[9]采用光纤测温方法对电缆故障进行预警。目前已有的方法大多是凭借热效应和超声波来确定接头内部缺陷,这些手段只有在电缆接头内部产生明显缺陷后才能起到检测效果。而电缆接头附近电场对缺陷敏感度高,因此可通过检测电缆接头周围的电场分布来判断其内部缺陷种类[10]。文献[11-12]分别在有限元软件ANSYS和三维电磁场软件CST Studio中建立电缆中间接头的三维模型,分析电缆中间接头存在硅脂涂抹不均匀、主绝缘划伤、气隙、杂质及接头受潮等施工缺陷时的电场分布规律。文献[13]建立电缆中间接头XLPE绝缘片状模型,探究了XLPE表面划伤、附着污染颗粒和表面受潮缺陷对电场及击穿电压的影响程度。上述文献分析了缺陷对电场的影响,但对电缆缺陷造成的电场畸变可能引发的电树枝生长情况讨论甚少。文中着重分析配网XLPE电缆接头附近电场,确定典型缺陷附近电场强度的分布特征。
电缆接头缺陷引发的电场畸变会导致接头内绝缘材料生成电树枝,使得XLPE层出现导电通道,增加击穿风险。目前已有多种用来预测电树发展的电树枝发展轨迹模拟方法[14]。国外学者陆续建立了分形介质击穿模型[15]、威斯曼-泽勒(Wiesman-Zeller,WZ)模型[16]、诺斯科夫-库赫塔-洛帕汀(Noskov-Kukhta-Lopatin,NKL)模型[17]。上述模型利用电场强度计算电树枝生长的概率,实现对电场生长的随机性模拟。文献[18]提出一种同时考虑电场和机械应力的电树生长的热动力学模型,使电树模拟发展到更深入的阶段。文献[19]提出微逾渗理论,建立电树枝的微逾渗模型,有助于从微观层面理解电树枝的引发及生长过程。
模拟电荷法是一种计算电场分布的方法,对于轴对称几何结构的电场数值计算问题,模拟电荷法可以显著降低计算量[20-21]。此外,电树枝轨迹与瞬时电场分布密切相关,而电树枝的生长具有随机性,因此适合将模拟电荷法与随机漫步理论结合来描述电树枝的生长过程。
文中采用模拟电荷法,对气隙、水膜、金属碎屑和金属外破4种典型缺陷下的电缆接头周围电场进行计算,同时对带有缺陷的电缆接头周围电场进行测量,并与计算结果相比较。将电场计算与随机漫步理论相结合来模拟电缆接头内电树枝的生长过程,确定4种典型缺陷所引发的电树枝的生长规律。同时研究了4种典型缺陷下电缆接头周围电场的分布特征,并提出相应的故障预防策略。
1 电缆接头模型及其分析方法配网XLPE电缆接头结构如图 1所示,尺寸如表 1所示。采用铜芯交联聚乙烯绝缘聚氯乙烯护套电力电缆,型号为YJV-10 1×70,额定电压为10 kV,单芯,标称截面积为70 mm2;采用冷缩中间接头,型号为JLS-10/1.4,适用电缆截面积300~400 mm2。

|
图 1 配网XLPE电缆接头结构 Fig. 1 Structure of a distributed networkXLPE cable joint |
|
|
表 1 电缆和中间接头的尺寸 Table 1 Sizes of cable and intermediate joint |
电缆接头周围的电场分布符合泊松方程及其边界条件。
泊松方程:
| $ \nabla^2 \varphi=-\frac{\rho}{\varepsilon} $ | (1) |
第一类边界条件:
| $ \left.\varphi\right|_{\Gamma}=f_1 $ | (2) |
第二类边界条件:
| $ \left.\frac{\partial \varphi}{\partial n}\right|_{\Gamma}=f_2 $ | (3) |
式中:φ为电位;ρ为自由电荷密度;ε为介电常数;Γ为求解区域的边界;n为边界法向分量。
电场采用模拟电荷法计算,即在接头内部及周围区域放置若干模拟电荷,并在不同介质的边界处放置若干匹配点,根据边界条件求解出各个模拟电荷的电荷量。根据求得的离散模拟电荷,计算场域中的电场分布,即:
| $ \mathit{\boldsymbol{Pq}} = \mathit{\boldsymbol{\varphi }} $ | (4) |
式中:P为系数矩阵;q为待求解电荷所构成的矩阵;φ为各匹配点的电位构成的矩阵。
电缆接头内模拟电荷的放置如图 2所示。考虑到电缆接头的轴对称性,在电缆芯中放置线电荷,而接头中不同绝缘材料的交界面附近放置若干环形电荷。其中线电荷48个,环形电荷432个,线电荷与环形电荷均放置于介质分界面附近以准确描述边界条件。材料的相对介电常数取值如下:空气为1,硅橡胶为3.6,应力锥为2.78,XLPE为2.3,水膜缺陷为80。金属缺陷视为悬浮等电位体处理。

|
图 2 电缆接头内模拟电荷示意 Fig. 2 Schematic diagram of simulation charges in cable joint |
对于电缆芯(即导体)与XLPE(即电介质)的交界面而言,有:
| $ \sum\limits_{i=1}^{n_{\mathrm{C}}} p_i q_{\mathrm{C}, i}+\sum\limits_{i=1}^{n_{\mathrm{SI}}} p_i q_{\mathrm{SI}, i}=\varphi_{\mathrm{C}} $ | (5) |
式中:pi为交界面上匹配点与相应位置第i个电荷的电位系数;qC, i、qSI, i分别为电缆芯、硅橡胶内侧第i个电荷;nC、nSI分别为电缆芯、硅橡胶内侧的模拟电荷数量;φC为电缆芯的电位。
接头内XLPE与硅橡胶的交界面、硅橡胶与空气的交界面的电位连续边界条件和电场边界条件如下:
| $ \sum\limits_{i=1}^{n_{\mathrm{XO}}} p_i q_{\mathrm{X} 0, i}-\sum\limits_{i=1}^{n_{\mathrm{SI}}} p_i q_{\mathrm{SI}, i}=0 $ | (6) |
| $ \sum\limits_{i=1}^{n_{\mathrm{SO}}} p_i q_{\mathrm{S} 0, i}-\sum\limits_{i=1}^{n_{\mathrm{A}}} p_i q_{\mathrm{A}, i}=0 $ | (7) |
| $ \varepsilon_{\mathrm{X}} E_{\mathrm{Xn}}-\varepsilon_{\mathrm{S}} E_{\mathrm{Sn}}=\sum\limits_{i=1}^{n_{\mathrm{SI}}} \varepsilon_{\mathrm{X}} f_i q_{\mathrm{S}, i}-\sum\limits_{i=1}^{n_{\mathrm{XO} }} \varepsilon_{\mathrm{S}} f_i q_{\mathrm{X} 0, i}=0 $ | (8) |
| $ \varepsilon_{\mathrm{S}} E_{\mathrm{Sn}}-\varepsilon_{\mathrm{A}} E_{\mathrm{An}}=\sum\limits_{i=1}^{n_{\mathrm{A}}} \varepsilon_{\mathrm{S}} f_i q_{\mathrm{A}, i}-\sum\limits_{i=1}^{n_{\mathrm{SO}}} \varepsilon_{\mathrm{A}} f_i q_{\mathrm{SO}, i}=0 $ | (9) |
式中:
处理边界条件时,为了简化计算,仅利用边界附近的模拟电荷计算。完成边界条件的处理后,可根据上述方程求得离散电荷q,按照叠加原理可求得空间中的电场分布。
1.2 典型缺陷附近的模拟电荷布置如图 3所示,文中研究4种典型缺陷:气隙、水膜、金属碎屑和金属外破。其中,气隙、水膜属于不导电缺陷,金属碎屑和金属外破属于导电缺陷。图 3(a)为前3种缺陷在电缆接头的位置;图 3(b)为前3种缺陷的形状;图 3(c)、(d)、(e)为前3种缺陷的具体尺寸;图 3(f)、(g)为金属外破的位置和尺寸。

|
图 3 电缆接头4种典型缺陷 Fig. 3 Four types of typical defects of cable joint |
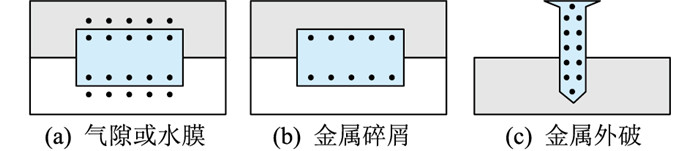
由于缺陷附近的电场分布对电树枝的生成十分重要,因此在使用模拟电荷法时,在缺陷表面附近密集地放置多个模拟点电荷,如图 4所示(图 4中的黑色实心圆点代表点电荷)。根据模拟电荷法,放置更多的模拟电荷有利于得到更精确的缺陷附近的电场分布。
|
图 4 缺陷附近模拟电荷放置示意 Fig. 4 Schematic diagram of placement of simulation charges close to the defects |
图 4中灰色区域为硅橡胶,白色区域为XLPE,中间的蓝色区域为缺陷。缺陷上边界(硅橡胶和缺陷交界面)、缺陷下边界(XLPE和缺陷交界面)的电位连续方程和场强边界条件为:
| $ \sum\limits_{i=1}^{n_{\mathrm{DS}}} p_i q_{\mathrm{DS}, i}-\sum\limits_{i=1}^{n_{\mathrm{SD}}} p_i q_{\mathrm{SD}, i}=0 $ | (10) |
| $ \sum\limits_{i=1}^{n_{\mathrm{DX}}} p_i q_{\mathrm{DX}, i}-\sum\limits_{i=1}^{n_{\mathrm{XD}}} p_i q_{\mathrm{XD}, i}=0 $ | (11) |
| $ \varepsilon_{\mathrm{D}} E_{\mathrm{Dn}}-\varepsilon_{\mathrm{S}} E_{\mathrm{Sn}}=\sum\limits_{i=1}^{n_{\mathrm{SD}}} \varepsilon_{\mathrm{D}} f_i q_{\mathrm{SD}, i}-\sum\limits_{i=1}^{n_{\mathrm{DS}}} \varepsilon_{\mathrm{S}} f_i q_{\mathrm{DS}, i}=0 $ | (12) |
| $ \varepsilon_{\mathrm{D}} E_{\mathrm{Dn}}-\varepsilon_{\mathrm{X}} E_{\mathrm{Xn}}=\sum\limits_{i=1}^{n_{\mathrm{XD}}} \varepsilon_{\mathrm{D}} f_i q_{\mathrm{XD}, i}-\sum\limits_{i=1}^{n_{\mathrm{DX}}} \varepsilon_{\mathrm{X}} f_i q_{\mathrm{DX}, i}=0 $ | (13) |
式中:
而对于导电缺陷,如金属碎屑和金属外破,满足电位边界条件即可:
| $ \sum\limits_{i=1}^{n_{\mathrm{D}}} p_i q_{\mathrm{D}, i}=\varphi_{\mathrm{D}} $ | (14) |
式中:nD为缺陷内部点电荷的个数;qD, i为缺陷的第i个电荷;φD为导电缺陷的电位。缺陷匹配点和内部模拟电荷坐标均存在于三维笛卡尔坐标系中,引入缺陷时部分模型失去轴对称性。由于环形电荷只有单一电荷密度,电场计算存在一定误差,与所有电荷均为点电荷的精确模型相比,整体电场计算误差小于4.2%,系数矩阵维数降低了61.5%,计算效率提高了73%。
1.3 电树枝生长模型绝缘材料中电树枝生长模型基于随机漫步理论[17]。随机漫步由一系列随机步组成,按照当前状态计算下一步在各方向的概率,漫步的路径具有随机性,漫步长度则由电树能量决定。
电缆接头内电树枝的生长使用一系列模拟点电荷及连接线段表示,如图 5所示。图 5中,P(·)为向各发展方向生长的概率,共有ndir个发展方向。

|
图 5 电树枝生长模型示意 Fig. 5 Schematic diagram of electrical tree propagation model |
电树发展是随时间变化的过程,XLPE区域和硅橡胶区域内电位的计算如下:
| $ \begin{gathered} \varphi_{\mathrm{XLPE}, N}=\sum\limits_{i=1}^{n_{\text {tree }}} p_i q_{\text {tree }, i}+\sum\limits_{i=1}^{n_{\mathrm{C}}} p_i q_{\mathrm{C}, i}+ \\ \sum\limits_{i=1}^{n_{\mathrm{D}}} p_i q_{\mathrm{D}, i}+\sum\limits_{i=1}^{n_{\mathrm{SD}}} p_i q_{\mathrm{SD}, i} \end{gathered} $ | (15) |
| $ \varphi_{\mathrm{S}, N}=\sum\limits_{i=1}^{n_{\text {tree }}} p_i q_{\text {tree }, i}+\sum\limits_{i=1}^{n_{\mathrm{A}}} p_i q_{\mathrm{A}, i}+\sum\limits_{i=1}^{n_{\mathrm{D}}} p_i q_{\mathrm{D}, i}+\sum\limits_{i=1}^{n_{\mathrm{XD}}} p_i q_{\mathrm{XD}, i} $ | (16) |
| $ t_N=t_0+N \Delta t $ | (17) |
式中:
电树枝末端在tn时刻有ndir个发展方向,对于第j个发展方向,其概率为:
| $ P\left(j, t_N\right)=\frac{E_{j, N}^2 \tau\left(E_{j, N}-E_{\text {dielectr }}\right)}{\sum\limits_{j=1}^{n_{\text {dir }}} E_{j, N}^2} \tau\left(\sum\limits_{i=1}^{n_{\text {tree }}} p_i q_{\text {tree }, i}^2-\alpha L_{\text {tree }, N}\right) $ | (18) |
式中:Ej, N为电树枝末端位置tN时刻电场强度沿第j个发展方向的分量;τ(·)为阶跃函数;Edielectr为绝缘材料的电绝缘强度,求和时考虑的是电场强度大于电绝缘强度的方向;α为单位距离导热系数;
在电树生长的过程中,以概率P向可能的方向生长。当新的电树枝生成时,系统中加入新的模拟点电荷,根据当前电荷分布和边界条件重新计算电场分布和电树枝在各方向的生长概率。由于在电树发展的每一步须计算实时电场分布,计算量较大,因此仿真次数为120次。
2 典型缺陷电场分布分析和测量结果 2.1 典型缺陷电场分析结果图 6为正常情况下的电缆接头轴向截面和沿测量线表面的电场分布。

|
图 6 电缆接头截面和表面的电场分布 Fig. 6 Electric field distribution of the axial section and the measuring line of the cable joint |
根据1.1节电缆接头模拟电荷法,沿图 3(a)标注的测量线方向的4种典型缺陷周围的电场分布计算结果如图 7所示。从图 7(a)、(b)中可以看出,由于空气的介电常数较小,气隙缺陷周围的电场强度有所减小;而水的介电常数较大,因此水膜缺陷周围的电场有所增强。从图 7(c)、(d)中可以看出,金属碎屑和金属外破具有导电性,因此这2种导电缺陷附近的电场强度出现了显著增强。

|
图 7 4种典型缺陷周围的电场分布 Fig. 7 Electric field distribution in the vicinity of four types of typical defects |
表 2列出了4种典型缺陷对周围电场分布的影响特征。
|
|
表 2 4种缺陷电场分布对比 Table 2 Comparison of electric field distributions of four types of defects |
其中电场畸变程度的计算如下:
| $ r_{\text {efd }}=\frac{\left|E_{\mathrm{d}}-E\right|}{E} $ | (19) |
式中:refd为电场畸变程度;E为缺陷中心点位置的正常电场强度;Ed为缺陷中心点位置存在缺陷时的电场强度。
可见,导电缺陷(金属碎屑和金属外破)所引起的电场畸变程度要明显高于不导电的缺陷(气隙和水膜);而对于气隙和水膜而言,两者对其周围电场分布的影响效果恰好相反,前者会减弱周围电场,后者会增强。因此,可对比缺陷附近测量电场和无缺陷的电场分布,以根据缺陷部位电场的增强或减弱,以及畸变程度来定位接头中缺陷的位置和类型。
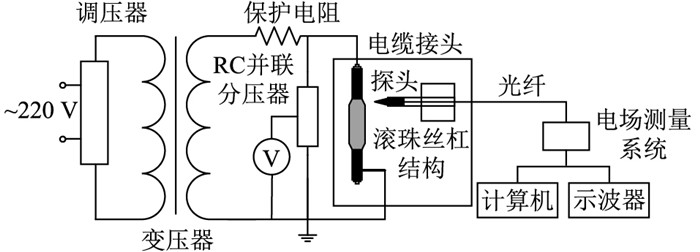
2.3 典型缺陷电场测量结果测量装置示意见图 8,采用基于泡克尔斯效应的探头(型号为Kapteos eoProbe P1TR05-BS5-air-101)进行电场测量,以减少电磁干扰带来的影响。测量探头安装在滚珠丝杠结构上,该装置有x-y-z等3个方向的自由度,可在1 200 mm×1 200 mm×1 700 mm的空间内定点循迹测量,定位精度为0.1 mm。
|
图 8 测量装置示意 Fig. 8 Schematic diagram of measurement device |
测量过程中探头与电缆接头实验样本的距离保持为10 mm。滚珠丝杠结构将测量探头稳定地沿图 3中的测量线移动,得到测量线路径间隔10 mm的离散点的电场数据。通过插值,得到连续的电场测量数据。测量时,电缆芯对地电压为7 kV的交变电压。施加在电缆芯的交变电压决定电缆芯和XLPE内模拟电荷须满足的第一类边界条件的取值。
4种电缆接头缺陷见图 9,在对电缆接头人为制造缺陷时,实验样本的缺陷位置与仿真模型中缺陷位置相一致,以便比较测量结果与仿真计算结果。

|
图 9 缺陷实验样本 Fig. 9 Samples of experimental defects |
4种典型缺陷的电场分布测量结果如图 10所示,测量结果和仿真计算结果的误差如表 3所示。

|
图 10 4种典型缺陷电场分布测量结果 Fig. 10 Measurement results of electric field distribution of four types of typical defects |
|
|
表 3 分析与测量结果之间的误差 Table 3 Errors between analysis and measurement results |
表 3中累积误差的计算如下:
| $ e_{\mathrm{acc}}=\sum\limits_{k=1}^K\left|E_k^{\mathrm{m}}-E_k^{\mathrm{s}}\right| / \sum\limits_{k=1}^K E_k^{\mathrm{s}} $ | (20) |
式中:eacc为累积误差;Eks为第k个测量点的电场计算值;Ekm为第k个测量点的电场测量值;K为测量点的个数。
结合图 10、表 2和表 3可以看出,电缆接头周围的电磁干扰和装置测量误差会影响测量和判断结果。如气隙和水膜,其本身的电场畸变程度略小于或接近测量误差,此时难以通过测量数据检测到此类型的电场畸变。气隙或水膜的体积小于5 mm3时,其引起的电场畸变将被周围的干扰和噪声所掩盖。与此同时,导电缺陷会造成较为显著的电场畸变,畸变程度明显大于测量误差,因此在实际实验中,体积大于2 mm3的导电缺陷可被检测到。
2.4 电树枝生长模拟结果在电树发展过程中,电场会加速带电微粒撞击缺陷壁,导致缺陷沿电场梯度方向发展[22],因此文中在电树发展过程中采用电缆接头内部电场和电树能量作为电树发展的依据。电缆接头缺陷周围电树枝的模拟采用与电场计算相同的模型,电树枝在电场强度最大的位置开始生成,生长时间为9.2 min。图 11展示了4种典型缺陷周围电树枝发展的模拟结果,表 4展示了仿真电树枝的分形维数,从左到右依次为缺陷左上、右上、左下、右下方电树的分形维数。

|
图 11 4种典型缺陷引发的电树枝分布分析结果 Fig. 11 Analysis results of electrical tree distributionof four types of typical defects |
|
|
表 4 电树的分形维数 Table 4 Fractal dimension of electrical tree |
如图 11所示,对4种不同缺陷所产生的电树长度和发展方向进行统计,气隙缺陷周围电树枝轨迹的平均长度为1.3 mm,水膜缺陷的电树枝轨迹的平均长度为2.7 mm,金属碎屑和金属外破的电树枝轨迹的平均长度分别为4.5 mm和5.9 mm。缺陷引起的电树枝轨迹长度与表 2中缺陷周围的电场畸变程度呈正相关,同时图 11(c)、(d)与(a)、(b)相比电树枝向电缆芯方向发展概率更高,这是因为在导电缺陷作用下,电缆芯周围电场的法向分量显著大于其他方向的分量。文献[23]结合分形特征判断电树类型,分形维数≤1.45为枝状树,处于1.45~1.65之间为稠密枝状或混合型树,分形维数≥1.65为丛林状树。表 4中80%的电树分形维数大于1.45,证明仿真的缺陷附近电树大部分为稠密枝状和丛林状树。此外,水汽渗入缺陷可能导致水树产生,进而引发电树和水树的交替发展。文献[24]描述了电树向水树转化过程中的生长特性,通过对比可发现电树尖端电场增强是水树产生的主要因素,并成为电树进一步发展的主要方向,与文中提出的随机漫步模型相符。
3 结论由于制造及安装过程中造成的缺陷,使得电缆接头故障频发。文中提出一种针对配网XLPE电缆接头的缺陷检测手段和电树发展预测方法。采用模拟电荷法计算电缆接头周围的电场分布,并通过实际测量结果进行验证。同时,采用模拟电荷和随机漫步理论相结合的方法对电树枝的生长进行模拟,并分析了电缆接头中典型缺陷所引发电树枝的构型特征。
(1) 4种典型缺陷造成的电场分布具有不同特征,据此可以分辨缺陷的种类。通过泡克尔斯效应可以测量电场分布,且受周围环境干扰的影响较小。同时,可以建立不同缺陷电场分布的特征库以供参考。
(2) 气隙、水膜、金属碎屑和金属外破造成的电场畸变程度分别为8.4%、10.2%、25.8%和28.4%。其中气隙和水膜属于不导电缺陷,体积大于5 mm3时,其引起的电场畸变才不会被周围的干扰和噪声所掩盖,而导电缺陷体积大于2 mm3即可被检测到。
(3) 电树枝的生长过程可用随机漫步理论结合电树能量来描述。模拟电荷法用于计算电树枝周围的电场分布和电树枝内部电荷量,随机漫步理论用于描述电树枝生长的随机性。
(4) 对于不导电缺陷而言,水膜引发的电树枝长度大于气隙引发的电树枝长度,因为两者引发电场畸变的分布特征不同。相较于不导电缺陷,导电缺陷引发的电树枝更容易向电缆芯方向发展,造成绝缘材料击穿。
| [1] |
陈新, 李文鹏, 李震宇, 等. 高压直流XLPE绝缘材料及电缆关键技术展望[J]. 高电压技术, 2020, 46(5): 1571-1579. CHEN Xin, LI Wenpeng, LI Zhenyu, et al. Prospect on key technology of the XLPE insulation materials and HVDC cables[J]. High Voltage Engineering, 2020, 46(5): 1571-1579. (  0) 0) |
| [2] |
周文博, 高冰, 王正平. 绝缘材料用交联聚乙烯的研发进展[J]. 合成树脂及塑料, 2022, 39(1): 79-81, 86. ZHOU Wenbo, GAO Bing, WANG Zhengping. Development of XLPE for insulating materials[J]. China Synthetic Resin and Plastics, 2022, 39(1): 79-81, 86. (  0) 0) |
| [3] |
刘英, 张博剑, 高鑫. 高压XLPE电缆线路状态评估综合体系的建立及应用[J]. 高电压技术, 2022, 48(11): 4437-4444. LIU Ying, ZHANG Bojian, GAO Xin. Establishment and application of a comprehensive system for condition assessment of HV XLPE cable lines[J]. High Voltage Engineering, 2022, 48(11): 4437-4444. (  0) 0) |
| [4] |
李欢, 翟双, 陈杰, 等. 交联聚乙烯电缆绝缘中不同尺度缺陷结构综述[J]. 绝缘材料, 2019, 52(12): 1-9. LI Huan, ZHAI Shuang, CHEN Jie, et al. Review in different size of defect structures in XLPE cable insulation[J]. Insulating Materials, 2019, 52(12): 1-9. (  0) 0) |
| [5] |
邓红雷, 杨浩, 谢月, 等. 基于高温介电谱测量的XLPE老化状态评估[J]. 电力工程技术, 2022, 41(4): 156-161, 219. DENG Honglei, YANG Hao, XIE Yue, et al. Aging assessment of XLPE based on high temperature dielectric spectra[J]. Electric Power Engineering Technology, 2022, 41(4): 156-161, 219. (  0) 0) |
| [6] |
王天, 白银浩, 吕中宾, 等. 交联聚乙烯电缆绝缘老化试验及其检测技术[J]. 绝缘材料, 2022, 55(6): 6-15. WANG Tian, BAI Yinhao, LYU Zhongbin, et al. Progress in insulation ageing test and detecting technology of XLPE cable[J]. Insulating Materials, 2022, 55(6): 6-15. (  0) 0) |
| [7] |
曹俊平, 蒋愉宽, 王少华, 等. XLPE电力电缆接头缺陷检测关键技术分析与展望[J]. 高压电器, 2018, 54(7): 87-97. CAO Junping, JIANG Yukuan, WANG Shaohua, et al. Analysis and prospect of defect detection key technology for XLPE power cable joints[J]. High Voltage Apparatus, 2018, 54(7): 87-97. (  0) 0) |
| [8] |
李继胜, 曹维丽, 刘蓉, 等. 基于超声波的XLPE电力电缆局部放电测量与分析[J]. 陕西师范大学学报(自然科学版), 2017, 45(6): 29-37. LI Jisheng, CAO Weili, LIU Rong, et al. Measurement and analysis of partial discharge in XLPE power cable based on ultrasonic[J]. Journal of Shaanxi Normal University (Natural Science Edition), 2017, 45(6): 29-37. (  0) 0) |
| [9] |
黄金朋, 张哲, 汪伟, 等. 基于分布式光纤测温技术的超导电缆局部失超检测和保护方法[J]. 电力系统保护与控制, 2020, 48(14): 76-84. HUANG Jinpeng, ZHANG Zhe, WANG Wei, et al. A local quench detection and protection method for a superconducting cable based on distributed optical fiber temperature measurement technology[J]. Power System Protection and Control, 2020, 48(14): 76-84. (  0) 0) |
| [10] |
李国倡, 梁箫剑, 魏艳慧, 等. 配电电缆附件复合绝缘界面缺陷类型和位置对电场分布的影响研究[J]. 电工技术学报, 2022, 37(11): 2707-2715. LI Guochang, LIANG Xiaojian, WEI Yanhui, et al. Influence of composite insulation interface defect types and position on electric field distribution of distribution cable accessories[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2707-2715. (  0) 0) |
| [11] |
陶玉宁, 陈皇熹, 赵国伟, 等. 10 kV电缆中间接头典型施工缺陷的电场及局放特性研究[J]. 电力工程技术, 2021, 40(5): 114-120. TAO Yuning, CHEN Huangxi, ZHAO Guowei, et al. Electric field and local discharge characteristics of typical construction defects of 10 kV cable intermediate joint[J]. Electric Power Engineering Technology, 2021, 40(5): 114-120. (  0) 0) |
| [12] |
徐虹, 黄丽秋, 娄建勇. 35 kV XLPE电缆中间接头典型缺陷三维电场仿真分析[J]. 浙江电力, 2020, 39(10): 9-13. XU Hong, HUANG Liqiu, LOU Jianyong. Three-dimensional electric field simulation analysis on typical defects of 35 kV XLPE cable joint[J]. Zhejiang Electric Power, 2020, 39(10): 9-13. (  0) 0) |
| [13] |
方春华, 杨司齐, 叶小源, 等. XLPE表面缺陷对电场及击穿电压的影响[J]. 水电能源科学, 2021, 39(3): 171-175. FANG Chunhua, YANG Siqi, YE Xiaoyuan, et al. Influence of typical cable defects on electric field and breakdown voltage of XLPE[J]. Water Resources and Power, 2021, 39(3): 171-175. (  0) 0) |
| [14] |
周远翔, 胡德雄, 张云霄, 等. 二维微米片复合材料取向调控电树枝生长特性的仿真研究[J]. 绝缘材料, 2022, 55(1): 24-31. ZHOU Yuanxiang, HU Dexiong, ZHANG Yunxiao, et al. Simulation study on growth characteristics of electrical tree in two-dimensional microsheet composite by orientation regulating[J]. Insulating Materials, 2022, 55(1): 24-31. (  0) 0) |
| [15] |
ZHU X, LUO Y, LIU W, et al. Numerical electric breakdown model of heterogeneous granite for electro-pulse-boring[J]. International Journal of Rock Mechanics and Mining Sciences, 2022, 154: 105128. (  0) 0) |
| [16] |
ZHANG Y X, ZHOU Y X, ZHANG T F, et al. Electrical tree evolution of two-dimensional BN sheet composite epoxy resin with different particle size[J]. Energy Reports, 2022, 8: 565-572. (  0) 0) |
| [17] |
MADSHAVEN I, HESTAD O L, STRAND P O. Cerman: software for simulating streamer propagation in dielectric liquids based on the Townsend-Meek criterion[J]. Computer Physics Communications, 2021, 265: 107987. (  0) 0) |
| [18] |
BORDEORI M M, GUPTA N. Electrochemical changes in epoxy resin due to thermal aging and their effect on electrical tree growth[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(5): 1940-1947. (  0) 0) |
| [19] |
李长云, 王伟, 王翰林. 基于微逾渗理论的电树枝引发和生长特性[J]. 中国电机工程学报, 2021, 41(13): 4720-4731. LI Changyun, WANG Wei, WANG Hanlin. Initiation and growth characteristics of electric tree based on micro-percolation theory[J]. Proceedings of the CSEE, 2021, 41(13): 4720-4731. (  0) 0) |
| [20] |
SINGER H, STEINBIGLER H, WEISS P. A charge simulation method for the calculation of high voltage fields[J]. IEEE Transactions on Power Apparatus and Systems, 1974, 93(5): 1660-1668. (  0) 0) |
| [21] |
ALLAL A, BOUBAKEUR A, MUJEZINOVICC A. Improved optimization of the charge simulation method for the calculation of the electric field around overhead transmission lines using statistical methods[J]. Engineering, Technology & Applied Science Research, 2022, 12(4): 8910-8915. (  0) 0) |
| [22] |
TALAAT M, TAYSEER M, EL-ZEIN A. Efficiency of different optimisation approaches for optimal parameters of the CSM for investigating the onset field due to corona point[J]. IET Generation, Transmission & Distribution, 2020, 14(9): 1751-1761. (  0) 0) |
| [23] |
李伟, 任志刚, 刘弘景, 等. 电缆中间接头硅橡胶电树枝生长与形貌特性研究[J]. 电力系统及其自动化学报, 2017, 29(6): 78-82. LI Wei, REN Zhigang, LIU Hongjing, et al. Growth and morphological characteristics of electrical tree in silicone rubber at cable joint[J]. Proceedings of the CSU-EPSA, 2017, 29(6): 78-82. (  0) 0) |
| [24] |
李天华, 周凯, 黄明, 等. 电树向水树转化过程中的生长特性[J]. 绝缘材料, 2018, 51(6): 42-46, 53. LI Tianhua, ZHOU Kai, HUANG Ming, et al. Propagation char-acteristics in conversion of electrical trees to water trees in XLPE cables[J]. Insulating Materials, 2018, 51(6): 42-46, 53. (  0) 0) |

 何嘉弘(1988), 男, 博士, 副教授, 研究方向为高电压与绝缘技术(E-mail:
何嘉弘(1988), 男, 博士, 副教授, 研究方向为高电压与绝缘技术(E-mail: