文章编号: 2096-3203(2022)05-0186-07 中图分类号: TM624
随着可再生能源发电容量及清洁能源占能源消费总量比重的不断增长,模块化多电平换流器(modular multilevel converter, MMC)凭借其模块化设计、扩展性好、转换效率高等优点,被广泛应用于高压直流输电,风电、光伏并网,孤岛供电等方面[1—3]。此外,相比传统电平数不高的电压源换流器,MMC能增加输出电平数,降低输出侧谐波含量以及换流器的整体损耗,因此少子模块MMC也被广泛运用于中低压配电网[4—5]。
调制方式对少子模块MMC的运行性能具有重要影响[6],常见的调制方式有最近电平逼近调制(nearest level modulation, NLM)和载波移相脉宽调制(carrier phase shifted pulse width modulation, CPS-PWM)。采用NLM策略时输出电压的低次谐波含量较高,而采用CPS-PWM策略虽能减少低次谐波含量,但开关频率高,整个系统需要附加复杂的环流抑制和电容均压控制,运行损耗较高。因此,需要针对少子模块MMC调制策略开展研究,以期充分开发和利用新能源,打破新能源在城市中低压配电网大规模发展的限制[7]。
目前,在NLM、CPS-PWM等传统策略的基础上,已有多种新型调制策略被相继提出。文献[8—10]将PWM与NLM结合成一种混合调制方式,虽改善了输出电压质量,扩展了有限的电容电压,但实际开关频率较高,开关损耗大。文献[11—12]在NLM的基础上改进输出电压阶梯波,使输出电平数达到2N+1,从而提高波形质量,但未提及环流问题。文献[13]针对级联H桥型多电平逆变器,采用基于载波形状自由度对载波移相中的三角形载波进行改进,但仅改善了低调制度下的谐波性能。
现有新型调制策略虽可提高输出波形质量,但仍存在开关损耗较高、未提及环流等弊端。为改善少子模块MMC的输出质量与输出能力,文中将NLM下电平数发生变化时波峰处的阶跃点作为调制方式切换点,进行NLM与CPS-PWM模式间的实时切换;再结合环流控制和子模块电压均衡控制进一步保证少子模块MMC的正常运行。该混合调制策略在提高少子模块MMC系统输出质量的同时也提高了其输出能力。
1 MMC拓扑典型的三相MMC拓扑如图 1所示,每相由上下对称的2个桥臂组成,各相桥臂均由多个相同子模块与桥臂电感串联而成。其中,SM为子模块,采用半桥子模块。Uc为子模块电容电压;upj(j=a, b, c)为上桥臂电压;unj为下桥臂电压;uvj为交流侧输出电压;Ipj,Inj分别为上、下桥臂电流;Ljp,Ljn分别为三相的上、下桥臂的串联电感;uSM,iSM分别为每个子模块接口的电压与流过该接口的电流。

|
图 1 三相MMC拓扑 Fig. 1 Topology of three-phase MMC |
该拓扑在直流侧电压Udc一定的情况下,通过控制子模块的开关工作状态可以实现逆变,在交流侧电压一定的情况下,通过类似的子模块控制也可以实现整流。一般MMC主电路每一相单元上、下桥臂子模块数目相等,记为N, 若上桥臂投入的子模块数目为Npj, 下桥臂投入的子模块数目为Nnj, 则上、下桥臂投入的子模块数目满足式(1)。
| $ N_{\mathrm{p} j}+N_{\mathrm{n} j}=N $ | (1) |
根据基尔霍夫定律,忽略桥臂电感压降,可得上、下桥臂电压与直流电压和交流侧输出电压的关系满足式(2)。
| $ \left\{\begin{array}{l} u_{\mathrm{p} j}=U_{\mathrm{dc}} / 2-u_{\mathrm{v} j} \\ u_{\mathrm{n} j}=U_{\mathrm{dc}} / 2+u_{\mathrm{v} j} \end{array}\right. $ | (2) |
NLM的基本原理是根据正弦调制波,采用最接近的电平对其进行瞬时逼近[14—15]。MMC的输出电压由一系列不同幅值的方波构成,该方波取决于上、下桥臂投入子模块数目。NLM使得任意时刻输出的方波幅值都能逼近调制波的幅值,子模块数量越多,输出电压阶梯波越逼近正弦参考波,谐波含量就越低;子模块数量较少,则可实现电平数较少,导致输出电压的低次谐波含量较高。
根据文献[16],在N+1电平MMC系统中采用NLM时,输出电平阶跃点αk为:
| $ \alpha_k=\arcsin \frac{2(k-0.5)}{N m} $ | (3) |
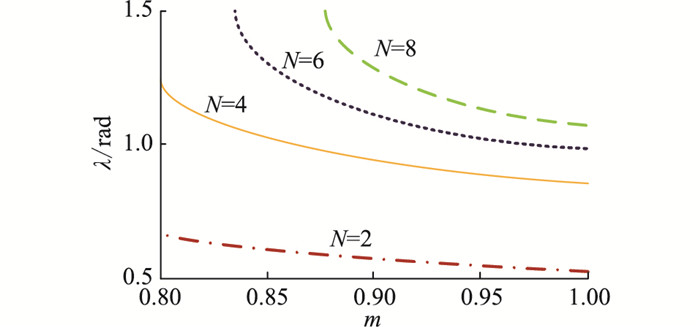
式中: k=1, …, N/2,且k取正整数;m为调制比。一个周期内其余输出电平阶跃点由波形的对称性得知。不同子模块数目下,切换点角度λ和调制比m的关系曲线如图 2所示。
|
图 2 不同子模块数目下m与λ的关系 Fig. 2 Relationship between m and λ with different numbers of sub-modules |
由图 2可知,当子模块数目N确定时,切换点角度随着调制比的减少而增加。当λ≥π/2时,转化为CPS-PWM模式。
以N=4的MMC下桥臂为例,NLM的调制原理如图 3所示。

|
图 3 NLM调制原理 Fig. 3 Modulation principle of NLM |
其中j相调制波可表示为:
| $ u_{\mathrm{s} j}(\omega t)=m U_{\mathrm{dc}} \sin \left(\omega t+\varphi_j\right) $ | (4) |
式中:ωt+φj为j相相位。
该调制方法下,在任意时刻上桥臂与下桥臂需要投入的子模块数目可表示为:
| $ \left\{\begin{array}{l} N_{\mathrm{n} j}=N / 2+\operatorname{round}\left(u_{\mathrm{sj}} / U_c\right) \\ N_{\mathrm{p} j}=N / 2-\operatorname{round}\left(u_{\mathrm{s} j} / U_c\right) \end{array}\right. $ | (5) |
式中:round(·)为四舍五入取整函数。
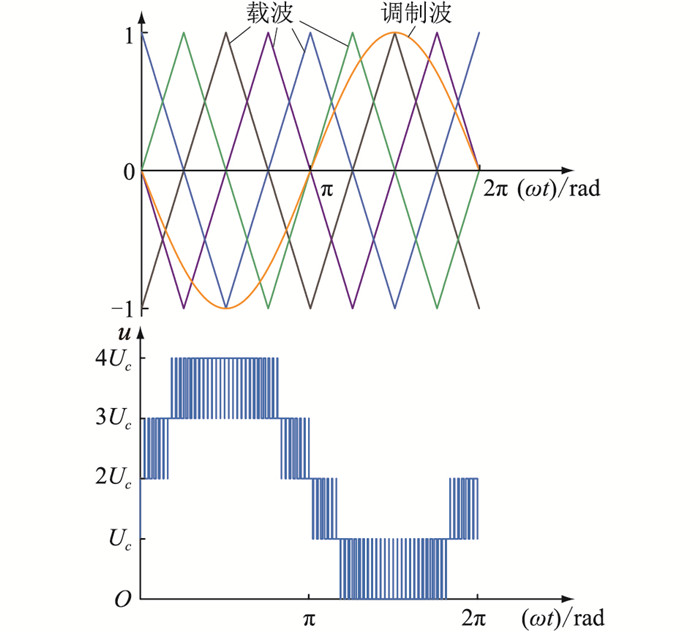
2.2 载波移相调制(CPS-PWM)以其中一相为例,CPS-PWM的调制原理如图 4所示。具体的实现方法为:将同一个正弦调制波与相位互差2π/N的多个三角载波进行比较,当调制波大于载波时,子模块开关导通,输出高电平;当调制波小于载波时,子模块开关闭合,输出低电平,由此生成多组PWM脉冲,以驱动各子模块内的开关[17]。
|
图 4 CPS-PWM调制原理 Fig. 4 Modulation principle of CPS-PWM |
由图 4可知,对比NLM,当子模块数量较少时,CPS-PWM通过提高输出电压的等效开关频率有效降低MMC输出交流电压的低次谐波含量,而此时CPS-PWM的载波频率须维持在较高水平,导致整个系统的开关损耗增加。
3 混合调制策略为满足中低压配电网下少子模块MMC的电压质量与经济性要求,改善2种传统调制策略应用于少子模块MMC的弊端,文中在NLM的基础上结合CPS-PWM,提出了一种在输出电平阶跃点处进行模式转换的混合调制策略。
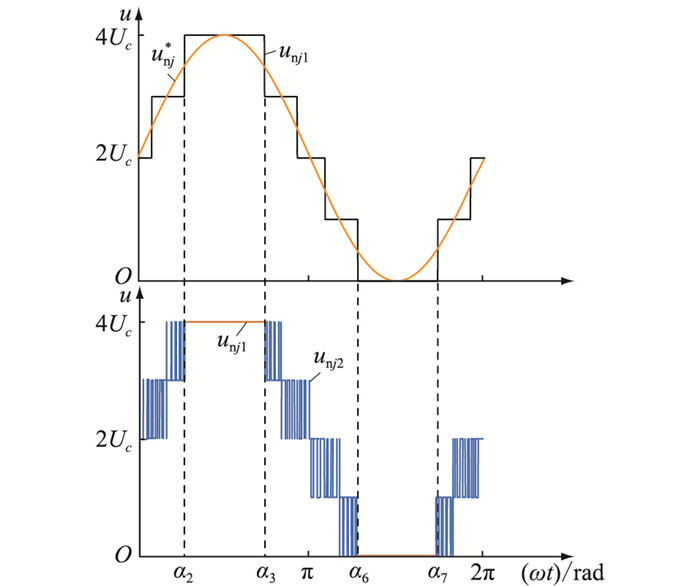
3.1 调制原理以N=4的五电平MMC的j相下桥臂为例,混合调制原理如图 5所示,其中unj*为j相下桥臂参考电压;unj1为在NLM模式下j相下桥臂的输出电压;unj2为在CPS-PWM模式下j相下桥臂的输出电压。
|
图 5 混合调制原理 Fig. 5 Hybrid modulation principle |
根据式(3),得到在0~π/2内五电平MMC输出电平阶跃点α2,再根据对称原理可得:
| $ \alpha_3=\pi-\alpha_2 $ | (6) |
| $ \alpha_6=\pi+\alpha_2 $ | (7) |
| $ \alpha_7=2 \pi-\alpha_2 $ | (8) |
在一个周期内任取角度θt,当0 < θt≤α2时,投入CPS-PWM模式;当α2 < θt≤α3时,投入NLM模式;当α3 < θt≤α6时,再次投入CPS-PWM模式;直至α6 < θt≤α7时,投入NLM模式;最后当θt>α7时,切换为CPS-PWM模式。该混合调制策略的下桥臂输出电压unj满足式(9)。
| $ {u_{{\rm{n}}j}} = {u_{{\rm{n}}j1}} + {u_{{\rm{n}}j2}} $ | (9) |
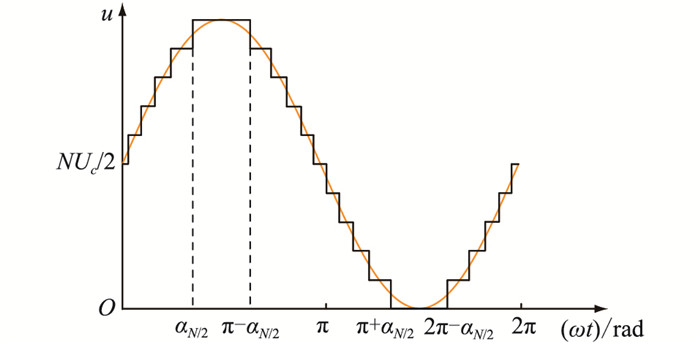
为能够准确平滑地切换2种调制模式,以N+1电平MMC中j相下桥臂为例,在NLM的基础上,由式(3)可得角αN/2,再根据对称原理得到其余电平阶跃点,其转换原理如图 6所示。
|
图 6 混合调制模式下桥臂转换原理 Fig. 6 Bridge arm conversion principle in hybrid modulation mode |
在一个周期0~2π内混合调制模式转换的控制方式表现为:
| $ \begin{array}{*{20}{c}} {{u_{{\rm{ret}}}}(\omega t) = }\\ {\left\{ {\begin{array}{*{20}{l}} {{u_{{\rm{CPS}}}}(\omega t)}&{0 < \, \bmod \, (\omega t, 2\pi ) \le {\alpha _{N/2}}}\\ {{u_{{\rm{NLM}}}}(\omega t)}&{{\alpha _{N/2}} < \, \bmod \, (\omega t, 2\pi ) \le \pi - {\alpha _{N/2}}}\\ {{u_{{\rm{CPS}}}}(\omega t)}&{\pi - {\alpha _{N/2}} < \, \bmod \, (\omega t, 2\pi ) \le \pi + {\alpha _{N/2}}}\\ {{u_{{\rm{NLM}}}}(\omega t)}&{\pi + {\alpha _{N/2}} < \, \bmod \, (\omega t, 2\pi ) \le 2\pi - {\alpha _{N/2}}}\\ {{u_{{\rm{CPS}}}}(\omega t)}&{2\pi - {\alpha _{N/2}} < \, \bmod \, (\omega t, 2\pi ) \le 2\pi }\\ {{u_{{\rm{CPS}}}}(\omega t)}&{\rm{其他}} \end{array}} \right.} \end{array} $ | (10) |
式中:uref(ωt)为调制电压参考波;uCPS(ωt)为CPS-PWM模式下电压参考波;uNLM(ωt)为NLM模式下电压参考波;mod(·)为取模函数。
该混合调制策略在一周期内的转换过程具体为:(1) 在0~π/2内,当0 < θt≤αN/2时投入CPS-PWM模式,当αN/2 < θt≤π/2时切换至NLM模式。(2) 在π/2~π内,当π/2 < θt≤π-αN/2时延续步骤(1)的NLM模式,当π-αN/2 < θt≤π时由NLM模式切换为CPS-PWM模式。(3) 在π~3π/2内,当π < θt≤π+αN/2时延续步骤(2)的CPS-PWM模式,直至π+αN/2 < θt≤3π/2切换为NLM模式。(4) 在3π/2~2π内,当3π/2 < θt≤2π-αN/2时延续步骤(3)的NLM模式,当2π-αN/2 < θt≤2π时切换成CPS-PWM模式。至此一个周期结束,后续周期重复上述步骤(1)—步骤(4)。
3.3 子模块均压控制子模块电容电压的均衡性对于整个系统稳定运行来说不可或缺[18—20]。为维持子模块电容电压动态稳定,将子模块的电压排序算法结合在各调制模式转换过程中,任取αN/2 < θt≤π-αN/2内的切换点为例,具体子模块的工作模式流程见图 7。
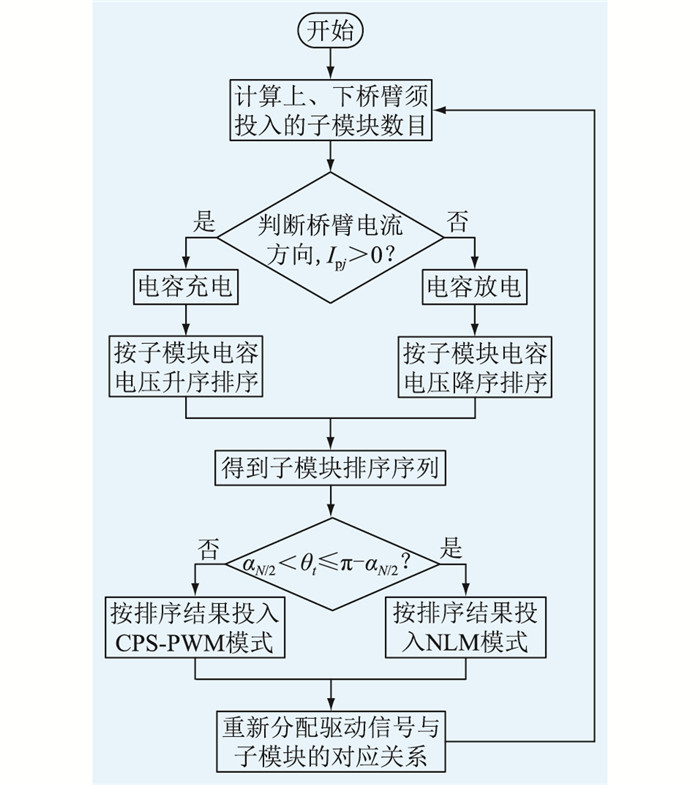
|
图 7 混合调制中子模块工作模式流程 Fig. 7 Process of sub-modules′ operating modes in hybrid modulation mode |
在子模块投入任意工作模式前,判断桥臂电流。令桥臂电流为Ipj,每时刻投入的子模块数目为M。当Ipj>0时,电容充电,所有投入的子模块按电容电压升序排序,在判断完θt后按升序优先选择接入电压最小的M个子模块;当Ipj < 0时,电容放电,所有投入的子模块按电容电压降序排序,在判断完θt后按降序优先选择接入电压最高的M个子模块。
3.4 环流抑制方法在三相MMC中环流与子模块电容电压相互影响。具体表现在二次谐波环流导致子模块三倍频电容电压波动;反之,四倍频谐波环流又源自上述三倍频电容电压的波动。以此类推,环流主要包括直流分量和交流分量里的偶数次谐波,且环流只在内部流动并不会对外电路造成影响。然而,环流会增大电容电压波动程度,导致桥臂电流发生畸变,增加子模块损耗,使得MMC的使用寿命大大减少。为解决上述环流对MMC系统的影响,文中采用准比例谐振控制方法来有效抑制二次环流谐波。由于文章篇幅限制,具体环流的准比例谐振控制设计方法参见文献[21—24]。
4 仿真验证与分析为验证所提调制策略应用于中低压配电网的有效性,文中基于Matlab/Simulink搭建仿真模型,模型参数如表 1所示。
|
|
表 1 模型参数 Table 1 Model parameters |
3种调制策略在稳态运行下a相交流侧输出电压和输出电流波形及各谐波快速傅里叶变换(fast fourier transform, FFT)分析见图 8。表 2为3种调制策略在3个周期内的电压和电流总谐波畸变率(total harmonic distortion, THD), 其中fTHD, U为此3个周期内的电压总谐波畸变率,fTHD, UL为此3个周期内的电压低次谐波畸变率,fTHD, I为此3个周期内的电流总谐波畸变率。
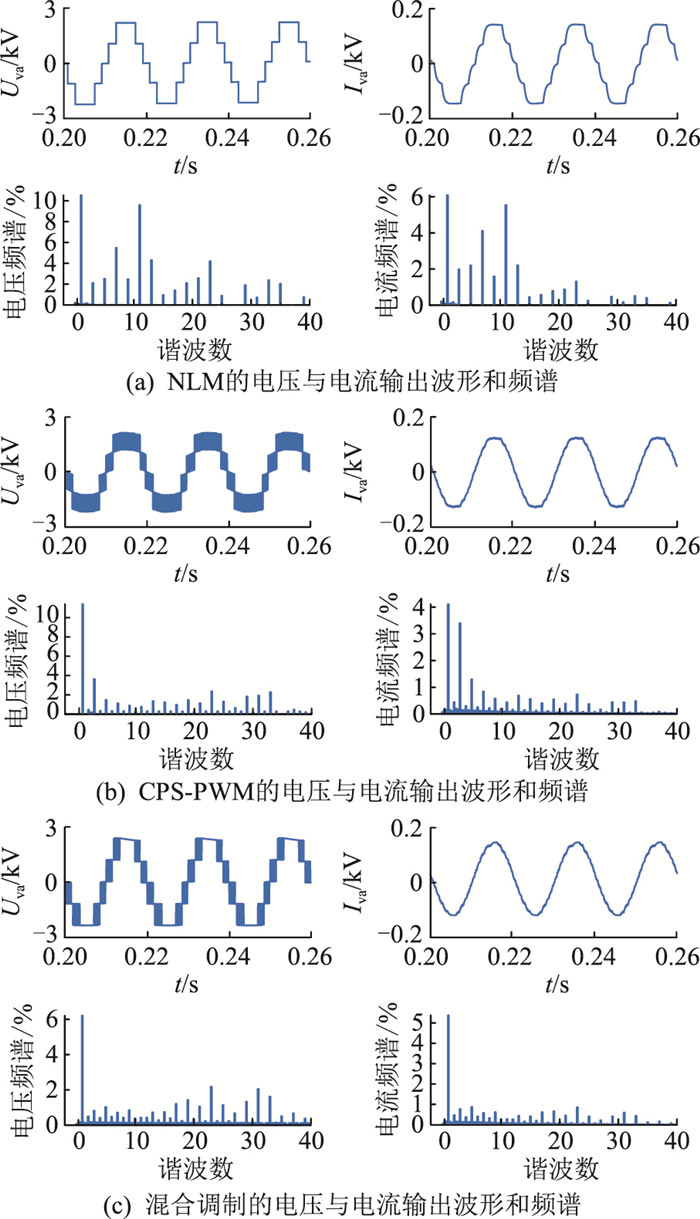
|
图 8 3种调制策略的仿真结果 Fig. 8 Simulation results of three modulation strategies |
|
|
表 2 3种调制策略的电压、电流THD Table 2 THD of voltage and current for three modulation strategies |
对比3种调制策略的电压波形与频谱,当子模块数量较少时,CPS-PWM下所有投入子模块均处于PWM模式,即开关管状态会频繁切换,导致电压高次谐波含量较高且开关的损耗大;NLM下开关不会频繁切换,当子模块数量减少时,其等效输出电平数量随之减少,导致输出电压低次谐波含量较高;文中所提策略结合这2种传统调制策略应用于少子模块MMC时的优点,其开关管切换频率明显低于CPS-PWM,不仅输出电压的高次谐波含量小于CPS-PWM,还克服了NLM下输出电压低次谐波含量较高的缺馅,即输出电压低次谐波较小。对比3种策略的电压波形与频谱,混合调制以及CPS-PWM的电流波形质量较高,而NLM的电压波形由于较高含量的电压低次谐波,而产生较高的谐波畸变率。
4.2 不同子模块数、调制比开关次数差的对比不同子模块数目N下,混合调制与CPS-PWM的开关次数之差Δk与调制比m的关系如图 9所示,其中Δk为:
| $ \Delta k=\frac{n_{\mathrm{CPS}}-n_{\mathrm{H}}}{n_{\mathrm{CPS}}} $ | (11) |
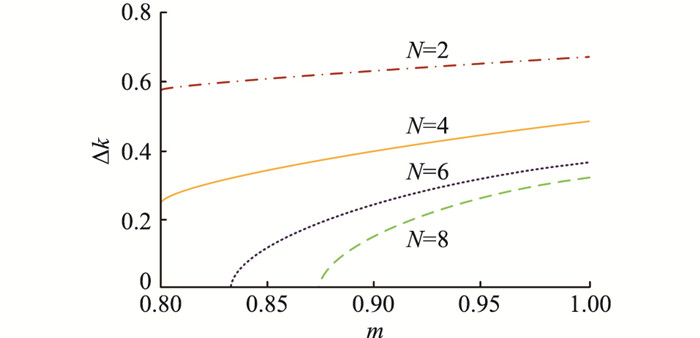
|
图 9 不同子模块数目下Δk与m的关系 Fig. 9 The relationship between Δk and m with different numbers of sub-modules |
式中:nCPS,nH分别为采用CPS-PWM、混合调制时下桥臂子模块开关次数。
由图 9可知,当子模块数目一定时,随着调制比的增大,2种调制方式的子模块开关次数之差增大。以N=4为例,当m=1时,一个周期内CPS-PWM的开关次数为160次,混合调制的开关次数为94次,降低了41.25%,符合图 9中的N=4的轨迹,有效证明了该混合调制比CPS-PWM的开关频率低,从而减少了开关损耗。
4.3 子模块电容电压均压效果对比将子模块的电压排序算法和各调制模式转换程序相结合,并将混合调制的均衡电压效果与常规NLM与CPS-PWM下的均压效果进行对比,如图 10所示,其中虚线表示电容电压标准值1.25 kV。
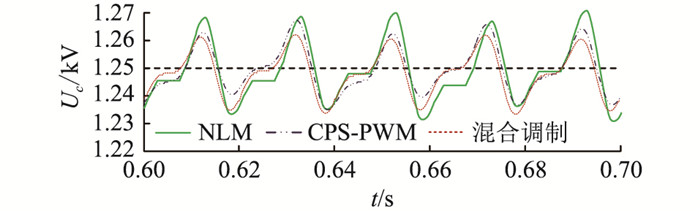
|
图 10 3种调制策略均压仿真结果 Fig. 10 Voltage equalization simulation results of three modulation strategies |
由图 10可知,在波峰处,混合调制比NLM波动值平均减小0.63%;在波谷处,比NLM波动幅度小,比CPS-PWM平均增加0.40%。由此可见,文中所提混合调制下的子模块均衡算法对子模块电容电压具有较好的控制效果,整体波动幅度较小。
4.4 环流抑制对比3种调制策略下的j相环流抑制波形见图 11,Icirj为j相环流。
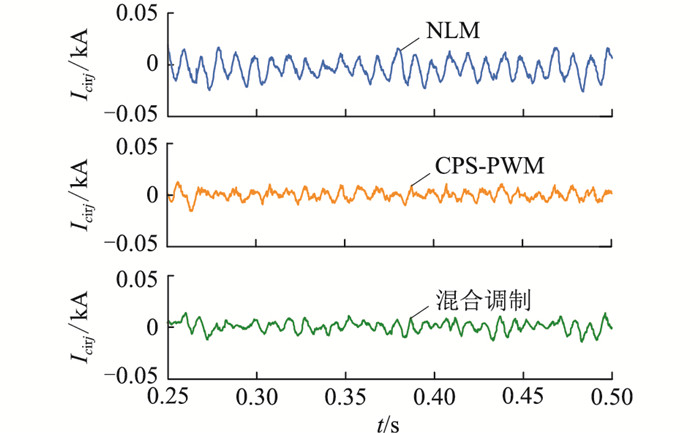
|
图 11 3种调制策略均流仿真结果 Fig. 11 Current equalization simulation results of three modulation strategies |
由图 11可知,文中所提策略适用于已有的环流抑制方法,能有效抑制环流,保证少子模块MMC在该混合调制下的正常运行。
5 结语文中提出了一种适用于少子模块MMC的混合调制策略,利用输出电平阶跃点进行NLM与CPS-PWM模式间的实时切换,同时结合子模块电容电压均衡控制与环流控制进一步保证少子模块MMC系统在该混合调制下的正常运行。结果表明,该混合调制策略在少子模块MMC系统中兼顾低输出谐波和低开关损耗的特点,提高了系统整体的输出质量;且使MMC系统处于高调制度下工作,保证了高直流电压利用率,提高了MMC的输出能力。文中策略主要针对子模块数目较少、中低压配电网下的MMC系统,而对于子模块数较多、电压等级更高的MMC系统的适用性还待进一步研究。
本文得到江苏省研究生科研与实践创新项目(SJCX21_0943)资助,谨此致谢!
| [1] |
陈国平, 李明节, 许涛, 等. 我国电网支撑可再生能源发展的实践与挑战[J]. 电网技术, 2017, 41(10): 3095-3103. CHEN Guoping, LI Mingjie, XU Tao, et al. Practice and challenge of renewable energy development based on interconnected power grids[J]. Power System Technology, 2017, 41(10): 3095-3103. (  0) 0) |
| [2] |
LI C Y, XU J Z, ZHAO C Y. A coherency-based equivalence method for MMC inverters using virtual synchronous generator control[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 1369-1378. DOI:10.1109/TPWRD.2015.2499262 (  0) 0) |
| [3] |
查晓明. 模块化多电平功率变换技术在新型电力系统中的深化应用[J]. 电力工程技术, 2021, 40(4): 1. ZHA Xiaoming. Deepening application of modular multilevel power conversion technology in new power system[J]. Electric Power Engineering Technology, 2021, 40(4): 1. (  0) 0) |
| [4] |
冯俊杰, 周诗嘉, 陈付强, 等. 中压应用场景下模块化多电平换流器直流侧谐波等值电路建模研究[J]. 电力电容器与无功补偿, 2021, 42(5): 136-142. FENG Junjie, ZHOU Shijia, CHEN Fuqiang, et al. Study on modeling of DC side harmonic equivalent circuit of MMC for medium voltage application scenario[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(5): 136-142. (  0) 0) |
| [5] |
陈志业. 面向中低压配电网的柔性多状态开关拓扑选型研究[D]. 杭州: 浙江大学, 2020. CHEN Zhiye. Research on topology selection analysis of flexible multi-state switch for medium and low voltage distribution network[D]. Hangzhou: Zhejiang University, 2020. (  0) 0) |
| [6] |
王琛, 许同, 王毅, 等. 一种适用于少子模块MMC的等效电平调制策略[J]. 中国电机工程学报, 2021, 41(14): 4954-4964. WANG Chen, XU Tong, WANG Yi, et al. An equivalent level modulation strategy for MMC with small quantities of submodules[J]. Proceedings of the CSEE, 2021, 41(14): 4954-4964. (  0) 0) |
| [7] |
季一润. 中压柔性直流配电网关键控制技术研究[D]. 南京: 东南大学, 2019. JI Yirun. Research on the key control techniques of medium voltage flexible DC distribution network[D]. Nanjing: Southeast University, 2019. (  0) 0) |
| [8] |
杨喆明, 付超, 王彦旭, 等. 一种应用于中压领域的MMC混合调制策略[J]. 电力电子技术, 2016, 50(7): 10-11, 56. YANG Zheming, FU Chao, WANG Yanxu, et al. A hybrid modulation strategy applied to medium voltage of MMC[J]. Power Electronics, 2016, 50(7): 10-11, 56. DOI:10.3969/j.issn.1000-100X.2016.07.004 (  0) 0) |
| [9] |
徐云飞, 肖湘宁, 龙云波, 等. 模块化多电平变换器混合调制策略[J]. 电力电子技术, 2015, 49(12): 59-61. XU Yunfei, XIAO Xiangning, LONG Yunbo, et al. A hybrid modulation and control of modular multilevel converter[J]. Power Electronics, 2015, 49(12): 59-61. DOI:10.3969/j.issn.1000-100X.2015.12.019 (  0) 0) |
| [10] |
姚钢, 杨晨, 黎灿兵, 等. 一种改进的中压MMC混合调制策略[J]. 电力电子技术, 2021, 55(4): 120-123, 136. YAO Gang, YANG Chen, LI Canbing, et al. An improved hybrid modulation strategy for medium voltage MMC[J]. Power Electronics, 2021, 55(4): 120-123, 136. (  0) 0) |
| [11] |
LIN L, LIN Y Z, HE Z, et al. Improved nearest-level modulation for a modular multilevel converter with a lower submodule number[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5369-5377. DOI:10.1109/TPEL.2016.2521059 (  0) 0) |
| [12] |
CHEN X X, LIU J J, SONG S G, et al. Circulating harmonic currents suppression of level-increased NLM based modular multilevel converter with deadbeat control[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 11418-11429. DOI:10.1109/TPEL.2020.2982781 (  0) 0) |
| [13] |
叶满园, 童子威, 陈子豪, 等. 改进的新型Ⅱ型不对称CHB逆变器调制策略[J]. 高电压技术, 2021, 47(6): 2186-2194. YE Manyuan, TONG Ziwei, CHEN Zihao, et al. Modified new modulation strategy of type Ⅱ asymmetric hybrid CHB inverter[J]. High Voltage Engineering, 2021, 47(6): 2186-2194. (  0) 0) |
| [14] |
刘追, 刘振兴, 李翠. 一种基于最近电平调制方式的MMC电压均衡改进方法[J]. 电测与仪表, 2017, 54(24): 87-93. LIU Zhui, LIU Zhenxing, LI Cui. An improved voltage balancing method based on MMC nearest level modulation[J]. Electrical Measurement & Instrumentation, 2017, 54(24): 87-93. (  0) 0) |
| [15] |
王昆. 最近电平调制下模块化多电平变换器工频排序平衡方法与故障诊断技术研究[D]. 杭州: 浙江大学, 2020. WANG Kun. Research on capacitor voltage balancing and failure diagnosis methods of MMC based on fundamental frequency sorting strategy with nearest level modulation[D]. Hangzhou: Zhejiang University, 2020. (  0) 0) |
| [16] |
李鹏鹏, 郭家虎, 梁克靖. 基于MMC的最近电平逼近调制谐波特性分析[J]. 电源技术, 2014, 38(4): 759-763. LI Pengpeng, GUO Jiahu, LIANG Kejing. Analysis of harmonic characteristics for nearest level modulation based on MMC[J]. Chinese Journal of Power Sources, 2014, 38(4): 759-763. (  0) 0) |
| [17] |
魏新伟, 何志兴, 徐千鸣, 等. 载波移相调制模块化多电平换流器双均压系数电压平衡方法[J]. 中国电机工程学报, 2018, 38(24): 7314-7325, 7458. WEI Xinwei, HE Zhixing, XU Qianming, et al. Dual voltage-sharing coefficients voltage balance method for modular multilevel converter with carrier phase shifted modulation[J]. Proceedings of the CSEE, 2018, 38(24): 7314-7325, 7458. (  0) 0) |
| [18] |
钟伟, 王晓刚. 阈值区间双向逼近的MMC电容电压均衡策略研究[J]. 自动化仪表, 2020, 41(9): 10-14. ZHONG Wei, WANG Xiaogang. Research on capacitor voltage balancing method for MMC with bi-directional approaching in threshold interval[J]. Process Automation Instrumentation, 2020, 41(9): 10-14. (  0) 0) |
| [19] |
粟咏梅, 粟时平, 李琳, 等. 模块化多电平换流器电容电压优化均衡法研究[J]. 电力科学与技术学报, 2019, 34(2): 76-83. SU Yongmei, SU Shiping, LI Lin, et al. An improved capacitor voltage balancing strategy of modular multilevel converter[J]. Journal of Electric Power Science and Technology, 2019, 34(2): 76-83. (  0) 0) |
| [20] |
张婕, 曾国辉, 赵晋斌, 等. 基于改进冒泡排序的模块化多电平换流器电容电压均衡策略[J]. 电力系统保护与控制, 2020, 48(6): 92-99. ZHANG Jie, ZENG Guohui, ZHAO Jinbin, et al. Modular multilevel converter capacitor voltage balancing strategy based on improved bubble sorting[J]. Power System Protection and Control, 2020, 48(6): 92-99. (  0) 0) |
| [21] |
邵文权, 王立宝, 程远, 等. MMC子模块均压及相间环流抑制方案研究[J]. 电气传动, 2019, 49(5): 67-72. SHAO Wenquan, WANG Libao, CHENG Yuan, et al. Research on voltage balance of MMC sub-module and phase-to-phase loop suppression scheme[J]. Electric Drive, 2019, 49(5): 67-72. (  0) 0) |
| [22] |
吴凡. 模块化多电平变换器环流控制策略研究[D]. 徐州: 中国矿业大学, 2019. WU Fan. Circulating current control strategy for modular multilevel converter[D]. Xuzhou: China University of Mining and Technology, 2019. (  0) 0) |
| [23] |
李慧, 张鹏, 刘思嘉. MMC环流抑制策略的暂态分析[J]. 电力系统保护与控制, 2021, 49(2): 30-38. LI Hui, ZHANG Peng, LIU Sijia. Transient analysis of MMC circulating current suppression strategy[J]. Power System Protection and Control, 2021, 49(2): 30-38. (  0) 0) |
| [24] |
马秀娟, 滕佳怡, 姚统. 基于环流抑制策略的MMC电容电压平衡控制[J]. 控制工程, 2019, 26(9): 1745-1750. MA Xiujuan, TENG Jiayi, YAO Tong. Capacitor voltage balancing control of modular multilevel converter based on circulation current suppression strategy[J]. Control Engineering of China, 2019, 26(9): 1745-1750. (  0) 0) |

 陈静(1998),女,硕士在读,研究方向为模块化多电平变换器保护与控制(E-mail:
陈静(1998),女,硕士在读,研究方向为模块化多电平变换器保护与控制(E-mail: