文章编号: 2096-3203(2022)05-0094-09 中图分类号: TM713
2. 国网智能电网研究院有限公司, 北京 102209
多端柔性直流(柔直)(modular multilevel converter based multi-termnal direct current,MMC-MTDC) 技术已被广泛应用于直流输电领域[1—2]。随着换流站端数的增多及直流电网的扩大,现有状态空间法计算故障电流的繁杂程度变高,计算速度下降。因此,寻求影响故障电流的主要拓扑范围及换流站数目,对简化故障电流的计算具有重要意义。
柔直电网接线方式分为对称双极接线(真双极系统)与对称单极接线(伪双极系统),针对2种接线的柔直电网故障机理研究及故障电流计算已取得了一定成果,但鲜有关于柔直电网拓扑对故障电流的影响研究。关于故障机理研究,文献[3]给出基于模块化多电平换流器的高压直流(modular multilevel converter based high voltage direct current,MMC- HVDC)输电系统中单极接地故障计算的近似分析模型;文献[4—5]提出MMC-HVDC输电系统中单极接地故障的保护策略;文献[6]深入分析MMC-HVDC输电系统单极接地故障、极间短路故障后电流演变规律及过电压产生机理。但研究均未涉及柔直电网拓扑对故障电流的影响机理。文献[7—9]依据张北柔直工程,仅对故障演变机理、检测原理及影响因素进行定性分析。
关于故障电流的定量研究主要有微分方程法和状态空间方程法。文献[10—11]提出基于原始微分方程的极间短路故障电流计算方法,讨论了影响故障电流的关键器件。然而,计算故障电流的高阶微分方程较为繁琐,在大型柔直电网故障电流分析中应用有限。为了解决计算问题,文献[12—14]提出采用状态空间模型计算MMC-MTDC电网的极间短路故障电流。该方法虽不能直接得到故障电流的解析表达式,但可以高精度、高效率地求解其数值解,且基于MMC状态空间模型,可在一定程度上分析故障电流特性。
真双极和伪双极系统适用的容量与电压等级不同,因此在配置、拓扑和接地方案方面差异较大。文献[15—18]已对容量、电压等级等参数的配置给出了一定的设计标准,故应进一步分析发生不同故障时不同柔直电网接线方式对故障电流的影响。
文中主要研究柔直电网拓扑对不同接线方式柔直电网故障电流的影响机理。基于高频分析理论,建立多端系统故障后的RLC等效模型,提出简化的故障电流频域表达式。分析并对比计及不同拓扑范围时频域阻抗差的表达式,提出简化指标k,快速评估真双极、伪双极系统分别发生单极接地故障、极间短路故障时影响故障电流的主要拓扑范围。最后,基于PSCAD仿真平台搭建五端系统,验证所提高频分析方法及简化指标的正确性和有效性。
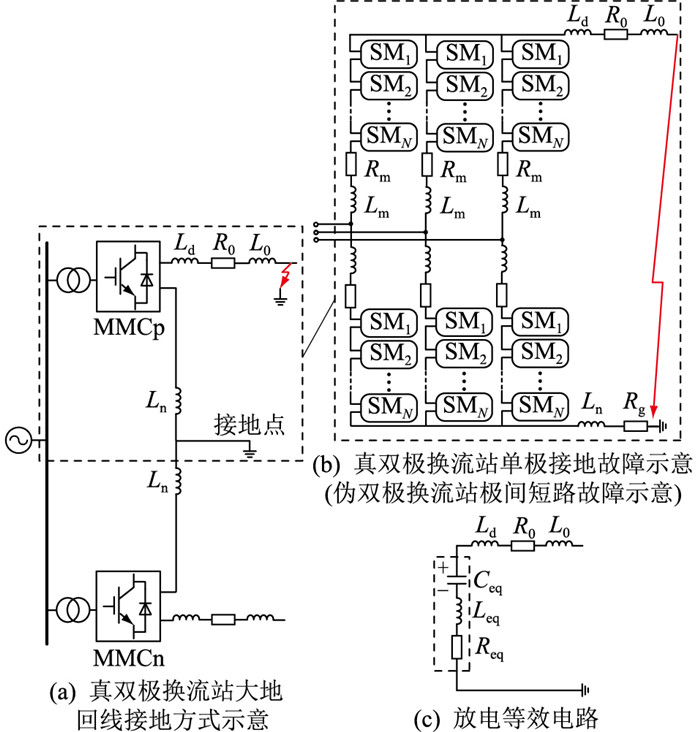
1 换流站等效电路及接地方式分类 1.1 换流站通用等效模型真双极与伪双极换流站均为MMC子模块(sub-module, SM)级联后再串联桥臂电感的结构,二者在内部结构上相同。二者的差异主要体现在两方面:一是真双极换流站在中性点具有真实的接地回路,如金属回线、大地回线等,而伪双极换流站无真实接地回线,具体接地方式详见1.2节;二是真双极换流站具有正负极对称的SM级联结构,如图 1(a)所示,可实现正负极完全分离并单独运行,伪双极换流站可参见图 2,正负极不可分离,且2个伪双极换流站级联后构成真双极换流站[1],因此伪双极换流站也叫对称单极换流站,真双极换流站也叫对称双极换流站。
|
图 1 换流站通用模型 Fig. 1 General model of converter station |
|
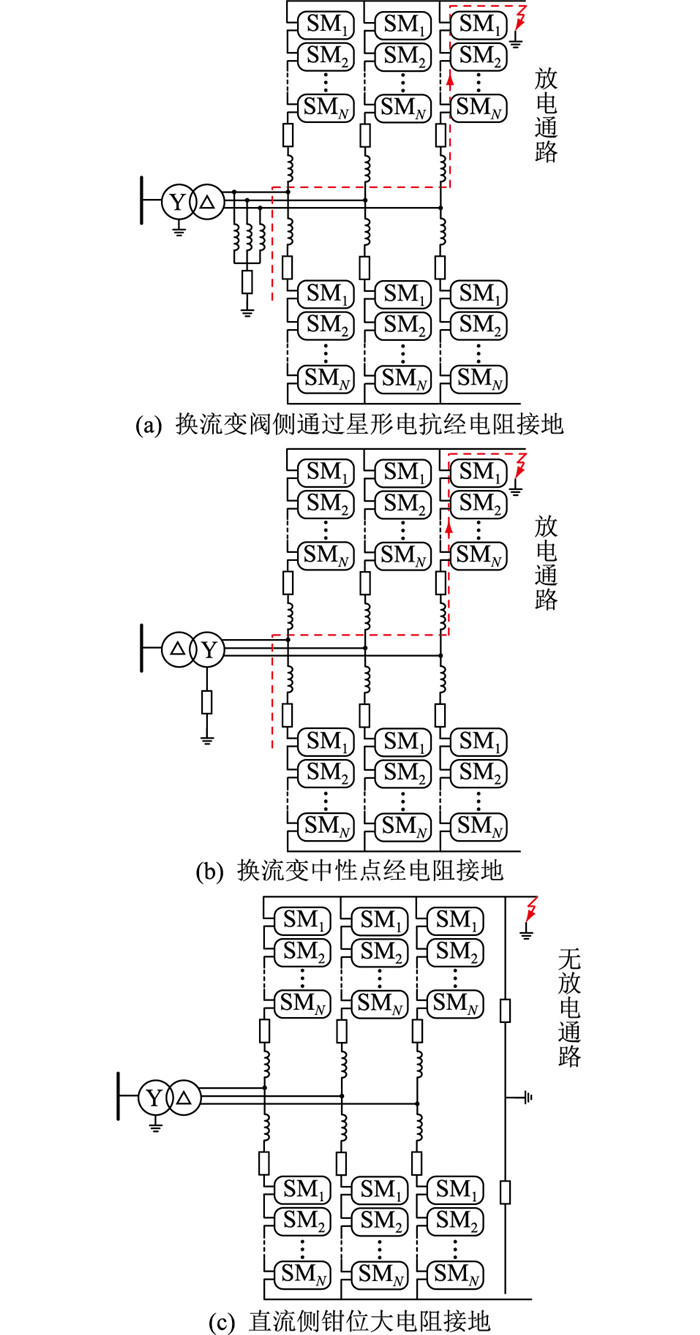
图 2 伪双极系统3种接地方式示意 Fig. 2 Schematic diagram of three grounding methods of pseudo-bipolar system |
由于真双极与伪双极换流站内部结构相同,可建立换流站通用模型如图 1所示。图 1以真双极换流站大地回线接地方式为例,Ld为平波电抗器的电感;Ln为极间电抗器的电感;R0,L0分别为直流线路等效电阻和等效电感;Rg为故障层接地点的接地等效电阻;N为每个桥臂SM的数目;Lm,Rm分别为单相桥臂电感和等效电阻。图 1(b)既是真双极换流站单极接地故障示意,也是伪双极换流站极间短路故障示意[1]。
故障发生后10 ms内的故障电流主要为SM电容放电形成的浪涌电流,剧烈增大的电流使桥臂电感的反电动势增大,抑制了交流系统的馈入[19]。另外,该阶段换流站控制方式对故障电流几乎无影响[20]。文献[13]表明,故障发生10 ms内换流站的放电电路可近似等效成RLC电路,如图 1(c)所示。
放电等效电路参数为:
| $ R_{\text {eq }}=\frac{2 R_{\mathrm{m}}}{3}+R_{\mathrm{g}} $ | (1) |
| $ L_{\mathrm{eq}}=\frac{2 L_{\mathrm{m}}}{3}+L_{\mathrm{n}} $ | (2) |
| $ C_{\mathrm{eq}}=\frac{3 C_0}{2 N} $ | (3) |
式中:Req,Leq,Ceq分别为放电等效电路的等效电阻、电感和电容;C0为SM电容。
伪双极换流站故障极换流器与真双极换流站结构相同,均可用式(1)—式(3)表示,但由于伪双极换流站不安装接地回线,故不存在与接地回线相连的Ln。针对伪双极换流站建模时,式(2)中Ln取0。
目前实际工程中换流站SM结构均采用半桥结构,而针对未来采用混合型SM的换流站,Ceq可表示为:
| $ C_{\mathrm{eq}}=\frac{3}{2}\left(\frac{C_{\mathrm{H}}}{N_{\mathrm{H}}}+\frac{C_{\mathrm{F}}}{N_{\mathrm{F}}}\right) $ | (4) |
式中:NH,NF分别为每个桥臂半桥型、全桥型SM的数目;CH,CF分别为半桥型、全桥型SM电容。
1.2 接地方式与对应故障电流路径分析故障类型主要分为单极接地故障、极间短路故障。其中,单极接地故障由故障点与接地点之间构成通路,与接地方式密切相关;极间短路故障由换流站、输电线路以及极间短路点构成放电通路,与接地方式无关,放电通路较为固定。首先分析不同柔直电网接地方式下发生单极接地故障时的故障电流路径。
伪双极系统接地方式主要有3种,即换流变阀侧通过星型电抗经电阻接地、换流变中性点经电阻接地、直流侧钳位大电阻接地,具体接线原理如图 2所示。当伪双极系统采用图 2(a)、(b)接地方式时,存在单极接地故障电流,且正负极各个线路均存在故障电流;当采用图 2(c)接地方式时,钳位电阻极大,故不存在单极接地故障电流。
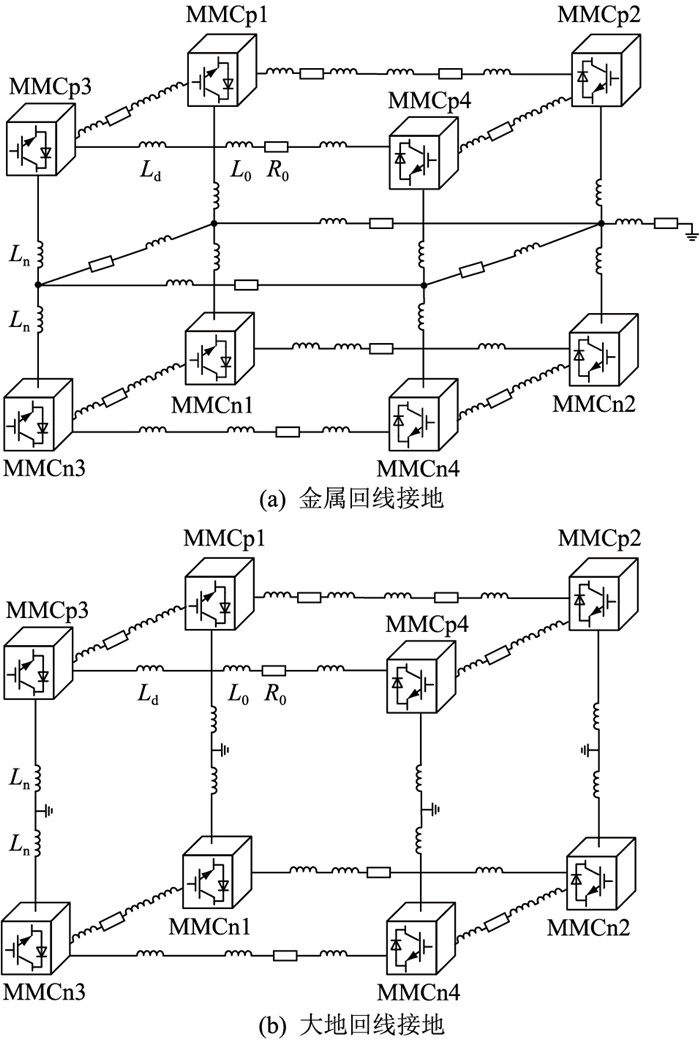
真双极系统接地方式主要分为金属回线接地和大地回线接地。金属回线接地方式是目前换流站端数较少的真双极系统(如张北柔直工程)较为常用的一种接地方式,金属回线与输电线路具有相同的拓扑,连接各换流站中性点,且在金属回线网络有且仅有一个接地点。大地回线接地方式是在各个换流站均专门设置接地极。真双极系统可实现正负极的彻底分离且正负极可单独运行。真双极系统2种接地方式示意如图 3所示。
|
图 3 真双极系统接地方式示意 Fig. 3 Schematic diagram of true bipolar system grounding methods |
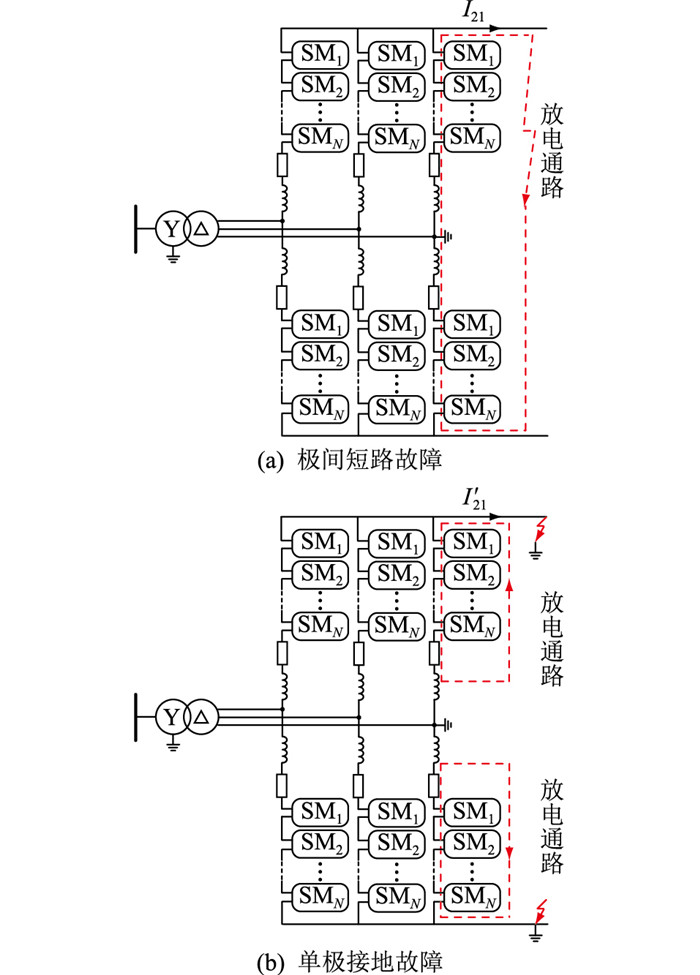
另外,当真双极系统采用大地回线接地方式时,系统发生极间短路故障可看作正负极线路在同位置同时发生单极接地故障,如图 4所示。针对某一层故障线路流过的电流而言,由于正负极完全对称,系统极间短路与单极接地故障时流过线路的故障电流I21和I′21完全相同。
|
图 4 真双极系统大地回线接地方式时极间短路故障电流路径示意 Fig. 4 Schematic diagram of fault current path of inter-pole short-circuit when the earth return line of the true bipolar system is grounded |
故障电流由稳态分量和故障分量组成,分别对应图 5中的I0,If,可以通过稳态和故障电路分别进行计算[21]。故障电流的稳态分量由潮流计算获得,而故障分量由电感、电容的暂态电流、电压变化决定。由文献[22—24]可知,故障初始时刻即故障发生后的0~10 ms,大于100 Hz的阻抗区域对故障电流的影响明显,处于此频段的直流输电线路频变参数模型中,电感值变化量较小且远小于与线路直接串联的2个平波电抗器电感总和,故采用线路集中参数模型进行近似简化分析。另外,故障分量由故障电路通过频域变化进行单独计算,如图 5所示。在故障时刻于故障点加入-Udc0/s瞬时阶跃信号模拟故障瞬间故障点的电压变化,其中Udc0为稳态时直流电压,包含的电感、电容进行拉氏变换,s=j2πf,f为频率[24]。由图 5可知,If(s)为:
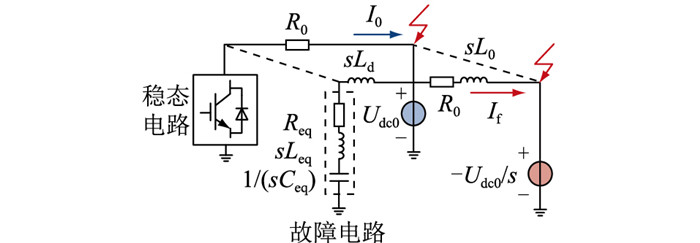
|
图 5 通用高频等效模型 Fig. 5 General high frequency equivalent model |
| $ I_{\mathrm{f}}(s)=\frac{U_{\mathrm{dc} 0} / s}{R_{\mathrm{eq}}+R_0+s\left(L_{\mathrm{eq}}+L_{\mathrm{d}}+L_0\right)+1 /\left(s C_{\mathrm{eq}}\right)} $ | (5) |
在故障发生时刻,系统阻抗处于高频段,电阻与频率无关,容抗随频率的增加而减小,感抗随频率的增加而增大。在故障发生0~10 ms内,频率大于100 Hz部分,感抗远远大于电阻和容抗[24],故可近似忽略式(5)中的电阻和容抗,即式(5)可近似表示为:
| $ I_{\mathrm{f}}(s)=\frac{U_{\mathrm{dc} 0} / s}{s\left(L_{\mathrm{eq}}+L_{\mathrm{d}}+L_0\right)} $ | (6) |
基于张北柔直工程实际参数[8],在PSCAD仿真平台搭建五端链网,当发生单极接地故障时换流站出口电压如图 6所示。U1,U2为故障线路两端换流站出口电压;U3为次近端换流站出口电压;U4,U5为远端换流站出口电压。8 s时发生故障, 故障线路电压快速变化,而非故障线路电压变化很小,故可忽略非故障线路电容的对地放电电流。
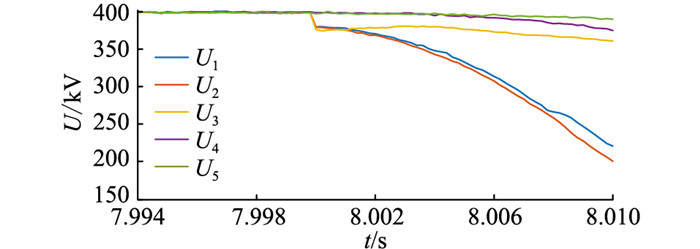
|
图 6 五端链网换流站出口电压 Fig. 6 The output voltage of the five-terminal chain network converter station |
为了研究柔直电网拓扑对故障电流的影响,使用高频等效模型进行分析。高频等效模型表明故障发生后10 ms内故障电流主要由故障电路等效阻抗的高频特性决定。
根据文献[24],MMC-MTDC电网拓扑等效电路可通过解耦计算解耦成链式网络,进而得到直流电网的通用高频等效模型,见图 7。Zeqx(x=1, 2,…,n)为第x个换流站的等效阻抗;Zfx(x=1, 2,…,n)为计及x个链式连接换流站的等效阻抗;2个换流站之间的等值阻抗主要取决于输电导线材料、长度及平波电抗器感抗等。定义与故障点直接相连的换流站为近端换流站,即故障站(如图 7中第1个换流站);与近端换流站直接相连的换流站称为次近端换流站(如图 7中第2个换流站);其余站称为远端换流站。
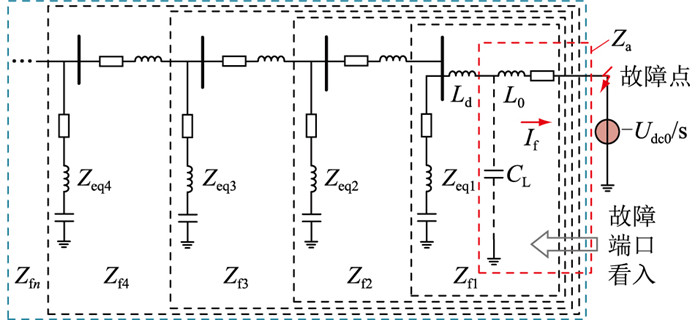
|
图 7 MMC-MTDC通用高频等效模型 Fig. 7 General high frequency equivalent model of MMC-MTDC |
MMC-MTDC电网拓扑主要通过电气距离影响故障电流,即从故障端口看入的总等效阻抗Zfn。因此,可通过分析计及不同拓扑范围的等效阻抗差,分析拓扑对线路故障电流的影响。由于感抗远远大于电阻和容抗,则:
| $ I_{\mathrm{f}}(s)=\frac{U_{\mathrm{dc} 0} / s}{s L_{\mathrm{f} n}} $ | (7) |
式中:Lfn为从故障端口看入的总等效电感。
令平波电抗器出口到故障点间的等效阻抗Za为:
| $ Z_{\mathrm{a}}=\frac{L_0 / C_{\mathrm{L}}}{s L_0+1 /\left(s C_{\mathrm{L}}\right)} $ | (8) |
式中:CL为故障线路π型等效电路的等效电容。
令简化指标k为:
| $ k=\frac{L_{\mathrm{eq}}}{L_{\text {line }}}=\frac{L_{\mathrm{n}}+2 L_{\mathrm{m}} / 3}{2 L_{\mathrm{d}}+L_0} $ | (9) |
式中:Lline为线路等效电感。
则:
| $ Z_{\mathrm{fl}}=s L_{\mathrm{d}}+Z_{\mathrm{a}}+s L_{\mathrm{eq}} $ | (10) |
| $ Z_{\mathrm{f} 2}=s L_{\mathrm{d}}+Z_{\mathrm{a}}+\left(\frac{k+1}{2 k+1}\right) s L_{\mathrm{eq}} $ | (11) |
| $ Z_{\mathrm{f} 3}=s L_{\mathrm{d}}+Z_{\mathrm{a}}+\left(\frac{k^2+3 k+1}{3 k^2+4 k+1}\right) s L_{\mathrm{eq}} $ | (12) |
| $ Z_{\mathrm{f} 4}=s L_{\mathrm{d}}+Z_{\mathrm{a}}+\left(\frac{k^3+6 k^2+5 k+1}{4 k^3+10 k^2+6 k+1}\right) s L_{\mathrm{eq}} $ | (13) |
当Zf(x-1)与Zfx差距很小时,x号换流站对故障电流的贡献可忽略。同理,若Zf2与Zf4接近,则拓扑中远端换流站对故障电流的影响可忽略。可见,拓扑对故障电流的影响取决于指标k,而与Za无关。以下分3种情况对式(10)—式(13)进行分析。
(1) 当0<k<0.5时,由式(10)—式(13)可知,Lf1≈Lf2≈Lf3≈…≈Lfn,即从故障端口看入的等效阻抗与仅考虑近端换流站对故障点放电的等效阻抗几乎相同。由于在伪双极系统接地方式中不存在Ln,故该种情况通常出现在伪双极系统中。
(2) 当0.5≤k≤1时,令:
| $ Z_{\mathrm{f} 2}-Z_{\mathrm{f} 4}=M s L_{\mathrm{eq}} $ | (14) |
即:
| $ M=\frac{k+1}{2 k+1}-\frac{k^3+6 k^2+5 k+1}{4 k^3+10 k^2+6 k+1} $ | (15) |
则M与k的关系如图 8所示。当0.5≤k≤1时,Lf2与Lf4很接近,可仅考虑近端与次近端换流站及相邻拓扑部分进行简化快速计算。
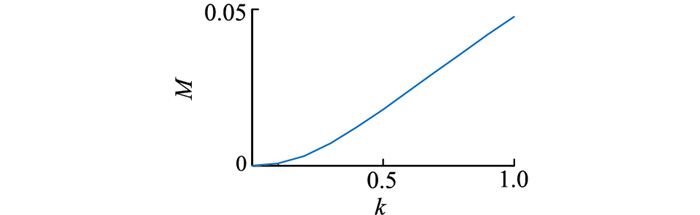
|
图 8 M与k的关系 Fig. 8 The relationship between M and k |
(3) 当k>1时,不能忽略远端换流站的放电,只能考虑全拓扑内换流站放电。当k很大时,Lf1→1,Lf2→1/2,Lf3→1/3,…,Lfn→1/n,即各阻抗间差距较大。但当k很大时,通常是由于平波电抗器极小且线路较短,同时极间电抗器却很大,可等效为几个换流站并联于同一母线上放电,从而简化计算过程。但该种情况在实际工程中几乎不可能出现。
另外,从物理意义上看,在频域等效模型分析中,虽然拓扑中任意位置的电感都对故障电流有抑制作用,但位于拓扑中不同位置的电感对换流站放电程度的影响却不同。以单端换流站的频域等效电路为例,如图 9所示,位于换流站内部的等效电感Leq两端电压为换流站出口电压的下降量ΔU(s)。Leq/Lline越大时,ΔU(s)越大,换流站放电程度越高,因此k可作为表征换流站放电程度的指标。将结论推广到多端换流站系统同样适用,k越大,Zf2与Zf4差距越大,表示远端换流站放电程度也随k的增大而增大。
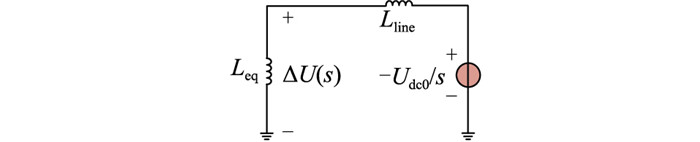
|
图 9 单端换流站频域等效电路 Fig. 9 Frequency domain equivalent circuit of a single-ended converter station |
伪双极系统与真双极系统最根本的区别在于伪双极系统不存在真实的接地回路[25—27],因此也不存在Ln。这使真双极系统的k值比伪双极系统的k值大。文献[15—18]给出桥臂电感、平波电抗及换流变电抗的参数设计方法。文献[28—30]中的现有实际工程参数表明,经计算后,伪双极系统中通常k小于0.5,而真双极系统中通常k略小于等于1。
伪双极系统中,发生极间短路故障时,仅近端换流站放电,与拓扑无关。伪双极系统中,发生单极接地故障时,当采用如图 2(a)所示换流变阀侧通过星形电抗经电阻接地、如图 2(b)所示换流变中性点经电阻接地方式时,式(6)中Leq为桥臂电感与星型电抗器的等效总电感,此时k较大,全拓扑换流站均存在较大程度的放电;当采用如图 2(c)所示直流侧钳位大电阻接地方式时,单极接地故障无法形成通路,不存在单极接地故障电流。
真双极系统中,发生极间短路故障时,仅近端、次近端换流站放电,与远端换流站的拓扑结构无关。真双极系统中,发生单极接地故障时,当采用大地回线接地时,仅近端、次近端换流站放电,与远端换流站的拓扑无关;当采用金属回线接地时,由于金属回线层可通过解耦计算等效为各个换流站等效电感的增加[31],故Leq增加,使k增大,从而使全拓扑换流站均存在较大程度的放电。
拓扑中换流站放电程度主要取决于k,若某些工程中,如伪双极系统经计算后k>1,则远端换流站也会存在不可忽略的放电现象。
3 仿真验证 3.1 拓扑对伪双极电网故障电流的影响验证为验证拓扑对伪双极电网故障电流的影响,在PSCAD平台搭建如图 10所示的五端伪双极系统,采用换流变阀侧通过星形电抗经电阻接地。各换流站位置、线路长度、定功率值已在图中标示,换流站MMC3为定电压站,系统电压等级为±400 kV,其余站为定功率站。其余系统参数如下:Lm为50 mH;Rm为0.27 Ω;C0为15 000 μF;星形电感为1 H;Ld为150 mH;线路电阻为0.009 9 Ω/km;线路电感为0.82 mH/km。
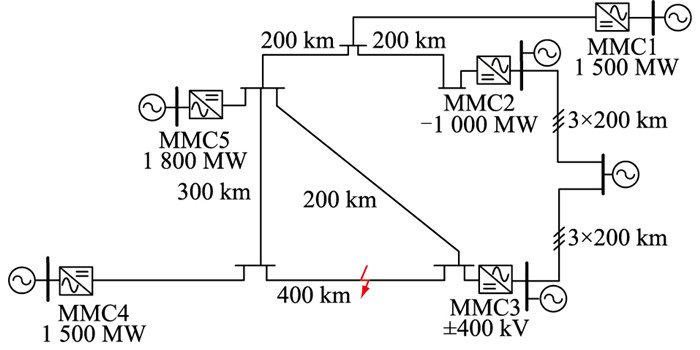
|
图 10 五端伪双极系统拓扑 Fig. 10 Five-terminal pseudo-bipolar system topology |
根据计算可知,图 10拓扑发生极间短路故障时,k=0.07,此时仅近端换流站(故障站、MMC3与MMC4)放电,其余换流站几乎不放电;发生单极接地故障时,k=1.50,此时所有换流站放电。系统故障线路电流如图 11所示。其中,i30,i′30分别为近端换流站MMC3侧非故障线路开路前(全拓扑)和开路后(仅考虑近端换流站)的故障电流;i40,i′40分别为近端换流站MMC4侧非故障线路开路前(全拓扑)和开路后(仅考虑近端换流站)的故障电流。由图 11(a)可知,系统发生极间短路故障时,除近端换流站以外的其他换流站对故障电流的贡献小于1%,可认为仅近端换流站放电,拓扑对故障电流无影响;由图 11(b)可知,系统发生单极接地故障时,除近端换流站以外的其他换流站对故障电流的贡献大于10%,不可忽略,应计及全拓扑计算故障电流。
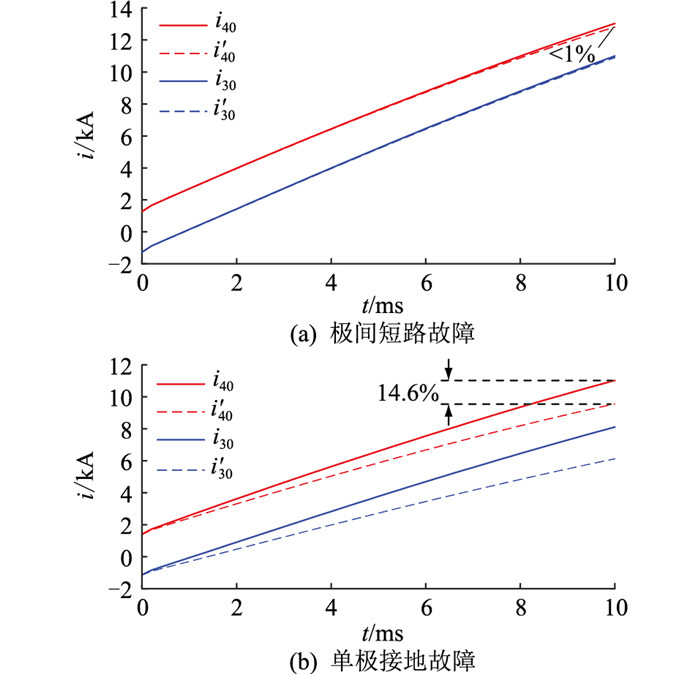
|
图 11 五端伪双极系统故障电流对比 Fig. 11 Comparison of fault currents of five-terminal pseudo-bipolar system |
为验证拓扑对真双极电网故障电流的影响,在PSCAD平台搭建如图 12所示的五端真双极链式系统。参数与3.1节一致,Ln为0.3 H,故障点在MMC1与MMC2之间线路L21的中点,在金属回线接地与大地回线接地方式下分别发生单极接地故障。
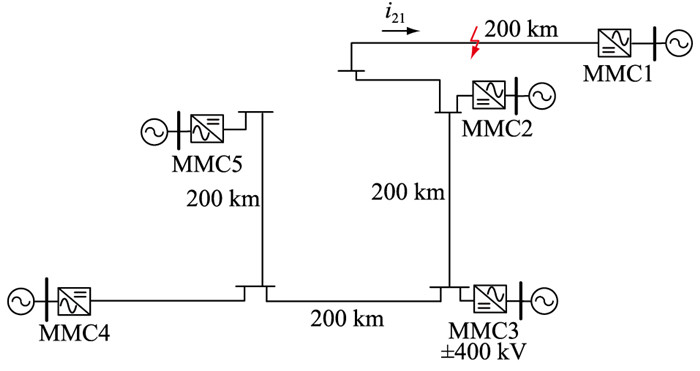
|
图 12 五端真双极系统拓扑 Fig. 12 Five-terminal true bipolar system topology |
图 12发生单极接地故障时,根据计算可知,当采用大地回线接地方式时k=0.72,此时仅近端换流站、次近端换流站(图中MM1、MM2与MM3)放电,其余换流站几乎不放电;当采用金属回线接地方式时k=2.61,此时所有换流站均存在较大程度放电。
以下定义4个案例。首先,仅连接MMC1和MMC2换流站,测量由MMC2到MMC1方向的线路电流i21,称为案例1。将换流站MMC3连接到MMC2,测量i21,此时近端与次近端换流站同时向线路L21放电,称为案例2。再将换流站MMC4连接到MMC3,测量i21,此时近端、次近端、远端换流站同时向线路L21放电,称为案例3。最后,将MMC5连接到MMC4,4个换流站同时向线路L21放电,称为案例4。五端真双极系统故障电流对比如图 13所示。
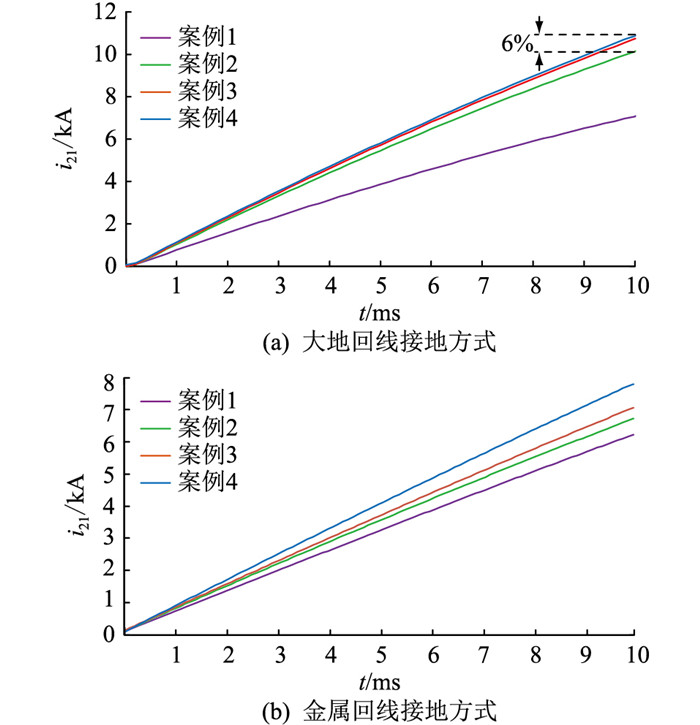
|
图 13 五端真双极系统故障电流对比 Fig. 13 Comparison of fault currents of five-terminal true bipolar system |
由图 13(a)可知,故障电流主要由近端、次近端换流站决定,再增加换流站对故障电流增量无明显影响。由图 13(b)可知,随着接入换流站的增多,故障电流增量不断增大,表明所有换流站均影响故障电流。仿真结果与理论分析吻合。
另外,真双极系统发生极间短路故障时与真双极系统在大地回线接地方式下发生单极接地故障时的线路故障电流完全相同。故真双极系统在发生极间短路故障时主要受近端、次近端换流站影响,可忽略其他换流站的影响。
4 结论文中分别对真、伪双极系统中不同接地方式下发生故障时的电流情况进行分析,明确了拓扑对不同接线方式柔直电网故障电流的影响机理。结论如下:
(1) 由高频等效模型可知,系统中电感参数对故障电流具有显著影响,而电阻、电容参数对故障电流影响极小。
(2) 伪双极系统中,发生极间短路故障时,仅近端换流站放电,与拓扑无关;发生单极接地故障时,全拓扑换流站均存在较大程度的放电。
(3) 真双极系统中发生极间短路故障与大地回线接地方式下发生单极接地故障的线路故障电流几乎完全相同。
(4) 真双极系统发生单极接地故障时,当采用大地回线接地方式时,仅近端、次近端换流站放电,与远端换流站的拓扑无关;当采用金属回线接地方式时,全拓扑换流站均存在较大程度的放电。
(5) 文中提出的电网拓扑对故障电流的影响机理可用于故障电流的简化计算,同时可为柔直电网拓扑优化、故障电流限制等工作提供参考。
| [1] |
徐政, 屠卿瑞, 管敏渊. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2013. XU Zheng, TU Qingrui, GUAN Minyuan. Flexible DC transmission system[M]. Beijing: China Machine Press, 2013. (  0) 0) |
| [2] |
史先强, 蔡旭, 姚为正, 等. 计及直流侧大电感的MMC建模与控制[J]. 中国电机工程学报, 2021, 41(12): 4261-4275. SHI Xianqiang, CAI Xu, YAO Weizheng, et al. Modeling and control of the MMC with consideration of large reactors on its DC side[J]. Proceedings of the CSEE, 2021, 41(12): 4261-4275. (  0) 0) |
| [3] |
LACERDA V A, MONARO R M, CAMPOS-GAONA D, et al. An approximated analytical model for pole-to-ground faults in symmetrical monopole MMC-HVDC systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 7009-7017. DOI:10.1109/JESTPE.2020.3028937 (  0) 0) |
| [4] |
张浩, 王先为, 马焕, 等. 基于MMC的直流电网短路电流分析及保护策略[J]. 智慧电力, 2019, 47(2): 93-100. ZHANG Hao, WANG Xianwei, MA Huan, et al. Short circuit current analysis in DC grid and its protection strategy based on modular multilevel converter[J]. Smart Power, 2019, 47(2): 93-100. (  0) 0) |
| [5] |
宋国兵, 侯俊杰, 郭冰, 等. 计及主动故障限流策略的柔性直流电网纵联保护[J]. 电力自动化设备, 2021, 41(4): 123-131, 138. SONG Guobing, HOU Junjie, GUO Bing, et al. Pilot protection of flexible DC grid considering active fault current limiting strategy[J]. Electric Power Automation Equipment, 2021, 41(4): 123-131, 138. (  0) 0) |
| [6] |
李岩, 黄豫, 龚雁峰, 等. 柔性直流电网直流线路故障的过电压机理分析[J]. 电力系统自动化, 2020, 44(5): 146-153. LI Yan, HUANG Yu, GONG Yanfeng, et al. Analysis on overvoltage mechanism of DC line fault in flexible DC grid[J]. Automation of Electric Power Systems, 2020, 44(5): 146-153. (  0) 0) |
| [7] |
赵翠宇, 齐磊, 陈宁, 等. ±500 kV张北柔性直流电网单极接地故障健全极母线过电压产生机理[J]. 电网技术, 2019, 43(2): 530-536. ZHAO Cuiyu, QI Lei, CHEN Ning, et al. Research on producing mechanism of healthy pole bus overvoltage for monopolar grounding fault in ±500 kV Zhangbei flexible DC power grid[J]. Power System Technology, 2019, 43(2): 530-536. (  0) 0) |
| [8] |
刘麒麟, 张英敏, 陈若尘, 等. 张北柔直电网单极接地故障机理分析[J]. 电网技术, 2020, 44(8): 3172-3179. LIU Qilin, ZHANG Yingmin, CHEN Ruochen, et al. Pole-to-ground fault mechanism in Zhangbei flexible DC power grid[J]. Power System Technology, 2020, 44(8): 3172-3179. (  0) 0) |
| [9] |
陈玉林, 张建锋, 虞晓阳, 等. 张北柔直电网金属回线故障监测研究[J]. 电力工程技术, 2019, 38(4): 56-61. CHEN Yulin, ZHANG Jianfeng, YU Xiaoyang, et al. Fault monitoring research of the metallic return line in Zhangbei VSC-HVDC grid[J]. Electric Power Engineering Technology, 2019, 38(4): 56-61. (  0) 0) |
| [10] |
王姗姗, 周孝信, 汤广福, 等. 模块化多电平换流器HVDC直流双极短路子模块过电流分析[J]. 中国电机工程学报, 2011, 31(1): 1-7. WANG Shanshan, ZHOU Xiaoxin, TANG Guangfu, et al. Analysis of submodule overcurrent caused by DC pole-to-pole fault in modular multilevel converter HVDC system[J]. Proceedings of the CSEE, 2011, 31(1): 1-7. (  0) 0) |
| [11] |
段国朝, 王跃, 尹太元, 等. 模块化多电平变流器直流短路故障电流计算[J]. 电网技术, 2018, 42(7): 2145-2152. DUAN Guozhao, WANG Yue, YIN Taiyuan, et al. DC short circuit current calculation for modular multilevel converter[J]. Power System Technology, 2018, 42(7): 2145-2152. (  0) 0) |
| [12] |
LI C Y, ZHAO C Y, XU J Z, et al. A pole-to-pole short-circuit fault current calculation method for DC grids[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4943-4953. DOI:10.1109/TPWRS.2017.2682110 (  0) 0) |
| [13] |
李俊松, 张英敏, 曾琦, 等. MMC-MTDC系统单极接地故障电流计算方法[J]. 电网技术, 2019, 43(2): 546-555. LI Junsong, ZHANG Yingmin, ZENG Qi, et al. Pole-to-ground fault current calculation method for MMC-MTDC systems[J]. Power System Technology, 2019, 43(2): 546-555. (  0) 0) |
| [14] |
汤兰西, 董新洲. MMC直流输电网线路短路故障电流的近似计算方法[J]. 中国电机工程学报, 2019, 39(2): 490-498, 646. TANG Lanxi, DONG Xinzhou. Anapproximate method for the calculation of transmission line fault current in MMC-HVDC grid[J]. Proceedings of the CSEE, 2019, 39(2): 490-498, 646. (  0) 0) |
| [15] |
李卫国, 秦敬明, 陈璟毅, 等. MMC-HVDC系统子模块电容与桥臂电感的选取和计算[J]. 东北电力大学学报, 2019, 39(2): 47-53. LI Weiguo, QIN Jingming, CHEN Jingyi, et al. Selection and calculation for sub-module capacitance and inductance of bridge arm in MMC-HVDC system[J]. Journal of Northeast Electric Power University, 2019, 39(2): 47-53. (  0) 0) |
| [16] |
陈继开, 孙川, 李国庆, 等. 双极MMC-HVDC系统直流故障特性研究[J]. 电工技术学报, 2017, 32(10): 53-60, 68. CHEN Jikai, SUN Chuan, LI Guoqing, et al. Study on characteristics of DC fault in bipolar MMC-HVDC system[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 53-60, 68. (  0) 0) |
| [17] |
李弸智, 周万迪, 王新颖, 等. 直流电网用混合式直流断路器开断参数影响因素研究[J]. 电网技术, 2021, 45(4): 1377-1387. LI Pengzhi, ZHOU Wandi, WANG Xinying, et al. Breaking parameter influencing factors of hybrid DC circuit breaker applied to DC power grids[J]. Power System Technology, 2021, 45(4): 1377-1387. (  0) 0) |
| [18] |
胡凯凡, 茆美琴, 何壮, 等. 直流短路故障下基于暂态能量抑制的MMC-HVDC电网主电路电感参数优化[J]. 中国电机工程学报, 2022, 42(5): 1680-1690. HU Kaifan, MAO Meiqin, HE Zhuang, et al. Optimization of inductance parameters of main circuit for MMC-HVDC grid based on transient energy suppression under DC short-circuit faults[J]. Proceedings of the CSEE, 2022, 42(5): 1680-1690. (  0) 0) |
| [19] |
张野, 洪潮, 李俊杰, 等. MMC-HVDC双极短路故障机理及暂态特性研究[J]. 南方电网技术, 2018, 12(4): 7-15. ZHANG Ye, HONG Chao, LI Junjie, et al. Research on short circuit fault mechanism and transient characteristics of MMC-HVDC bipolar system[J]. Southern Power System Technology, 2018, 12(4): 7-15. (  0) 0) |
| [20] |
张明奇, 刘麒麟, 张英敏. MMC型换流器双极故障电流影响因素分析及其优化[J]. 电力建设, 2020, 41(5): 124-132. ZHANG Mingqi, LIU Qilin, ZHANG Yingmin. Analysis and optimization of factors influencing current during MMC bipolar fault[J]. Electric Power Construction, 2020, 41(5): 124-132. (  0) 0) |
| [21] |
LI C Y, GOLE A M, ZHAO C Y. A fast DC fault detection method using DC reactor voltages in HVDC grids[J]. IEEE Transactions on Power Delivery, 2018, 33(5): 2254-2264. DOI:10.1109/TPWRD.2018.2825779 (  0) 0) |
| [22] |
BEERTEN J, D'ARCO S, SUUL J A. Frequency-dependent cable modelling for small-signal stability analysis of VSC-HVDC systems[J]. IET Generation, Transmission & Distribution, 2016, 10(6): 1370-1381. (  0) 0) |
| [23] |
LI Y J, LI J P, XIONG L S, et al. DC fault detection in meshed MTDC systems based on transient average value of current[J]. IEEE Transactions on Industrial Electronics, 2020, 67(3): 1932-1943. DOI:10.1109/TIE.2019.2907499 (  0) 0) |
| [24] |
TAO Y, LI B H, LIU T Q, et al. Practical fault current level evaluation and limiting method of bipolar HVDC grid based on topology optimization[J]. IEEE Systems Journal, 2021, 99: 1-11. (  0) 0) |
| [25] |
李继红, 陆翌, 王朝亮, 等. 一种柔性直流输电前馈解耦无功补偿控制系统设计[J]. 电力电容器与无功补偿, 2021, 42(5): 28-33. LI Jihong, LU Yi, WANG Chaoliang, et al. Design of flexible HVDC feedforward decoupling reactive power compensation control system[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(5): 28-33. (  0) 0) |
| [26] |
纪斌, 王立永. 基于模块化多电平换流器的无功补偿控制策略研究[J]. 电力电容器与无功补偿, 2020, 41(5): 46-53. JI Bin, WANG Liyong. Research on reactive power compensation control strategy based on modular multilevel converter[J]. Power Capacitor & Reactive Power Compensation, 2020, 41(5): 46-53. (  0) 0) |
| [27] |
何英静, 李继红, 但扬清, 等. 柔性直流输电系统对多直流馈入系统运行性能的改善作用研究[J]. 电力电容器与无功补偿, 2020, 41(3): 106-111. HE Yingjing, LI Jihong, DAN Yangqing, et al. Study on performance improvement of multiple DC infeed systems by MMC-HVDC system[J]. Power Capacitor & Reactive Power Compensation, 2020, 41(3): 106-111. (  0) 0) |
| [28] |
樊云龙, 任建文, 叶小晖, 等. 基于MMC的渝鄂直流背靠背联网工程控制策略研究[J]. 中国电力, 2019, 52(4): 96-103. FAN Yunlong, REN Jianwen, YE Xiaohui, et al. Study on control strategy of back to back MMC-HVDC connecting Chongqing and Hubei power grid[J]. Electric Power, 2019, 52(4): 96-103. (  0) 0) |
| [29] |
刘黎, 蔡旭, 俞恩科, 等. 舟山多端柔性直流输电示范工程及其评估[J]. 南方电网技术, 2019, 13(3): 79-88. LIU Li, CAI Xu, YU Enke, et al. Zhoushan multi-terminal VSC-HVDC transmission demonstration project and its evaluation[J]. Southern Power System Technology, 2019, 13(3): 79-88. (  0) 0) |
| [30] |
罗琴, 李丹, 潘广泽, 等. 中国柔性直流输电系统可靠性标准需求研究[J]. 南方电网技术, 2022, 16(2): 121-129. LUO Qin, LI Dan, PAN Guangze, et al. Requirements analysis on reliability standards for flexible DC transmission system in China[J]. Southern Power System Technology, 2022, 16(2): 121-129. (  0) 0) |
| [31] |
刘麒麟, 张英敏, 张明奇, 等. 直流电网输电线路短路故障的单端化近似解析计算方法[J/OL]. 电测与仪表, 2020: 1-7[2022-03-05]. http://kns.cnki.net/kcms/detail/23.1202.TH.20201217.1743.005.html. LIU Qilin, ZHANG Yingmin, ZHANG Mingqi, et al. A single terminal approximate analytical method for short circuit fault of transmission lines in DC power grid[J/OL]. Electrical Measurement and Instrumentation, 2020: 1-7[2022-03-05]. http://kns.cnki.net/kcms/detail/23.1202.TH.20201217.1743.005.html. (  0) 0) |
2. State Grid Smart Grid Research Institute Co., Ltd., Beijing 102209, China

 张英敏(1974),女,博士,教授,研究方向为柔性直流输电技术、高压直流输电保护与控制(E-mail:
张英敏(1974),女,博士,教授,研究方向为柔性直流输电技术、高压直流输电保护与控制(E-mail: