文章编号: 2096-3203(2022)05-0193-09 中图分类号: TM726
2. 湖南大学电气与信息工程学院,湖南 长沙 410082
在国家“双碳”目标激励下,基于可再生能源规模化接入的新型电力系统将成为发展趋势,配电网结构形态也将随之变化[1—2]。配电网网络结构复杂、遍布范围广,设备种类和数量众多、位置分散,且易遭受自然灾害。当突发灾害后,利用分布式电源(distributed generation,DG)和拓扑变换可迅速恢复重要负荷,降低故障损失,但配电网故障恢复能力有限,仍可能存在负荷停电。因此,为适应电力系统的发展趋势,主动配电网(active distribution network,ADN)的故障风险预警须计及拓扑变换和DG并网。有效预警配电网运行过程中存在的故障风险,是提高配电网供电可靠性的关键途径[3]。
配电网多源异构数据中蕴含了丰富的信息,利用特征筛选和相关性分析方法,从多源异构数据和各类型特征中挖掘与配电网故障强相关的特征十分必要[4]。目前,有关配电网故障预警方面的研究方法主要为神经网络[5—6]、支持向量机[7—8]、Apriori[9]等。文献[10]采用极限梯度提升(extreme gradient boosting,XGBoost)算法建立考虑天气因素的区域线路停电数量预测模型。文献[11]采用因子分析法提取了4类气象主要因素,并利用Logistic回归建立气象因素对电力事故的影响模型。文献[12]通过分析灾害天气的特征,采用N-m故障分析评估得出电网风险控制决策。文献[13]提出一种考虑天气因素的组合型神经网络组合预测配电网故障数量。文献[14]提出一种基于Adaboost+算法的配电网故障停电评估模型,其主要针对风和雷电造成的故障。然而,上述文献仅考虑天气因素对故障的影响,忽略多种相关因素的共同影响,对信息挖掘不够全面。文献[15]采用多元回归和时间序列分析手段,分季节构建因气象条件造成的故障量预测和非气象因素造成的故障数量预测,但其应用仅限于短期预测。文献[16]采用情景分析方法进行配电网风险预警,考虑的因素涉及外部环境和时间,但数据分析方法较为简单。文献[17]基于Apriori算法将典型故障与环境场景关联识别,实现了配电网运行风险等级预警。文献[18]提出改进G-ReliefF算法进行特征筛选,采用集成学习算法实现配电网故障风险等级预测。文献[19]提出改进的Relief-Wappaer算法和基于径向基函数-支持向量机(radial basis function-support vector machine, RBF-SVM)的方法进行配电网故障关联分析与风险等级预警。传统配电网故障风险预警研究忽视配电网故障自愈能力,未考虑配电网拓扑变换和DG故障支撑对线路停电的积极作用。
针对上述问题,文中综合考虑内外部多重因素相互作用对配电网故障的影响,提出多维度的基于数据驱动的故障等级预警方法。首先,通过对配电网运维、故障数据和天气数据进行数据预处理,并采用基于卡方检验和Pearson相关系数特征选择方法筛选出最优故障特征集;其次,以故障后损失电量最小化为目标,提出计及DG并网的配电网故障重构优化模型,从而构建基于网络重构与DG故障支撑策略下各线路对应的预想负荷停电集;再次,选取损失电量、停电用户小时数、停电用户级别加权3个指标表征线路重要程度,综合评估各线路重要程度进而确定故障风险等级;最后采用XGBoost算法进行配电网线路故障风险等级智能预警,挖掘故障风险和故障特征的关联。在算例仿真分析中,文中所提方法与随机森林(random forest,RF)和反向传播(back propagation,BP)神经网络算法进行对比,所提方法的预警召回率、精准率及准确率都显著高于其他2种方法,有助于提高配电网的安全运行水平。
1 配电网故障特征选取获取影响配电网运行安全的因素是风险预警的关键,从众多因素中筛选出与配电网故障强相关联的特征可提高风险预警的高效性,因此提出一种改进的χ2-Pearson特征选择方法。
1.1 初始特征提取通过对配电网信息管理系统进行调研,获取从2019年1月—2019年12月的10 kV线路故障相关数据,此外从气象信息系统中获取温度、湿度、风速等天气数据。分析数据类型,并进行数据预处理[13]。将配电网故障特征最终分成气象条件、时间维度、设备因素3类,其分类方式如表 1所示。
|
|
表 1 配电网故障特征 Table 1 Fault features of distribution network |
(1) 数据转换:收集到的数据中天气情况、季节、风向等为文字描述,故将数据转换为便于分析和应用的数值类型,即数据分类、数据量化。例如,将所有天气情况分为4种类型,用特征数值表示。数值1表示扬沙,浮尘;数值2表示晴,雾;数值3表示阵雨,阴,多云;数值4表示小雨,小雪,雨夹雪,冻雨。天气预警分蓝、黄、橙、红4种颜色等级,可用数值1—4来表示气象预警程度。
(2) 数据集成:由于现有各类数据来源不同,处于分散的状态,因此应进行合并。根据时间和地区,将运维情况、时间维度、气象条件一一关联映射,形成一组特征数组,每个特征数组都有相对应的配电网状态标签,可构成一组特征和标签的对应关系,从而确定故障初始特征集合。
1.2 特征选取为了提高配电网故障风险预警的准确性,要从海量数据和各类型特征中筛选出与配电网故障强关联的特征,剔除相关性不强和冗余的特征。因此,文中提出一种改进的χ2-Pearson特征选择方法,改进了卡方检验不能有效剔除冗余的特点,其由两部分组成:基于卡方检验的特征选择和基于Pearson相关系数的冗余特征剔除。
(1) 卡方检验。卡方检验可用于判断2个分类变量间的相关性[20]。假设2个变量是相互独立的,通过计算变量列联表的理论值和实际值,进而得到卡方值,通过查卡方分布表获取卡方值对应的概率p。选定显著性水平α,α一般取0.05。当p≤α时,应否定原假设,否则接受原假设。卡方检验的基本公式为:
| $ \chi^2=\sum \frac{(T-E)^2}{E} $ | (1) |
式中:χ2为卡方值;T为实际值;E为理论值。χ2表示实际值和理论值的差异程度,χ2越大,说明变量关联度越强。
(2) 关联度。卡方检验未能剔除冗余特征,故利用Pearson相关系数寻得相似特征,其用于衡量向量间相似度关系。相关系数ρ(X, Y)的取值范围为[-1, 1],计算公式为:
| $ \rho(X, Y)=\frac{\operatorname{cov}(X, Y)}{\sigma_X \sigma_Y} $ | (2) |
式中:cov(X, Y)为数据集X和Y的协方差;σX,σY分别为X和Y的标准差。根据2个数据集(X, Y)的Pearson相关系数得出特征之间的关联性ρ(X, Y)。ρ(X, Y)接近于0说明数据集间无相关性,ρ(X, Y)越接近于1或者-1说明数据集间相关性越强。
2 计及DG并网的配电网故障重构优化模型当出现极端天气或者设备老化引发停电事故后,配电网可通过联络支路转供或DG实现负荷恢复。拓扑重构后潮流随之变化,在保障重要负荷持续供电的同时仍存在部分负荷停电。当发生多线路故障时,仅靠转供负荷与DG支撑无法完全降低故障损失,应尽快对线路故障进行恢复。根据线路等级进行依次抢修可进一步降低故障造成的损失,加快重要线路的恢复速度。
配电网故障风险为故障发生的概率乘以故障停电影响程度[21]。故障停电影响程度与故障后果相关,应构建不同线路对应的预想负荷停电集S。文中构建的预想负荷停电集是考虑配电网拓扑变换和DG支撑后的各线路停电影响程度,故应建立配电网故障重构优化模型。
2.1 目标函数文中的故障重构模型主要考虑计及天气因素的配电网故障场景,以故障后损失电量最小为目标,并优先保障重要负荷持续供电。根据负荷分级赋予相应的权重,在安全稳定运行的前提下尽可能恢复更多的负荷。目标函数为:
| $ \min \sum\limits_{i \in N} {{\delta _i}} {P_{i, {\rm{L}}}}\left( {1 - {x_{i, {\rm{L}}}}} \right) $ | (3) |
式中:δi为节点i负荷的权重;Pi, L为节点i处负荷有功功率;xi, L为节点i的负荷供电状态,xi, L=1表示供电;N为节点集合。
2.2 约束条件(1) 配电网潮流约束。文中使用的是辐射性网络的DistFlow潮流约束,由于考虑拓扑变换,加入了线路的开关状态变量。配电网拓扑结构变换后仍应满足节点电压和功率约束。式(4)和式(5)为相邻节点电压间的关系。
| $ \begin{gathered} U_i-U_j \leqslant 2\left(r_{i j} P_{i j}+x_{i j} Q_{i j}\right)+M\left(1-s_{i j}\right) \\ (i, j) \in B \end{gathered} $ | (4) |
| $ \begin{gathered} U_i-U_j \geqslant 2\left(r_{i j} P_{i j}+x_{i j} Q_{i j}\right)-M\left(1-s_{i j}\right) \\ (i, j) \in B \end{gathered} $ | (5) |
式中:Pij,Qij分别为线路ij流通的有功和无功功率;rij,xij分别为线路ij的电阻和电抗;B为线路合集;M为取值很大的常系数;sij为线路ij开端系数,当线路ij连通时sij=1,此时线路两端电压应满足电压降落的关系,当线路断开时sij=0,此时约束式(4)和式(5)不起作用。
式(6)和式(7)为节点i的功率平衡约束。
| $ \sum\limits_{h:(h, i) \in B} {{P_{hi}}} + {p_{i, {\rm{pv}}}} + {p_{i, {\rm{g}}}} = \sum\limits_{j:(i, j) \in B} {{P_{ij}}} + {p_{i, {\rm{L}}}}\;\;\;{\kern 1pt} i \in N $ | (6) |
| $ \sum\limits_{h:(h, i) \in B} {{Q_{hi}}} + {q_{i, {\rm{pv}}}} + {q_{i, {\rm{g}}}} = \sum\limits_{j:(i, j) \in B} {{Q_{ij}}} + {q_{i, {\rm{L}}}}\;\;\;{\kern 1pt} i \in N $ | (7) |
式中:
式(8)和式(9)为节点i处光伏有功和无功出力约束,式(10)和式(11)为节点i处柴油发电机有功和无功出力约束,式(12)为负荷的功率约束。
| $ 0 \leqslant p_{i, \mathrm{pv}} \leqslant x_{i, \mathrm{pv}} \bar{P}_{i, \mathrm{pv}} \quad i \in N_{\mathrm{pv}} $ | (8) |
| $ x_{i, \mathrm{pv}} \underline{Q}_{i, \mathrm{pv}} \leqslant q_{i, \mathrm{pv}} \leqslant x_{i, \mathrm{pv}} \bar{Q}_{i, \mathrm{pv}} \quad i \in N_{\mathrm{pv}} $ | (9) |
| $ x_{i, \mathrm{~g}} \underline{P}_{i, \mathrm{~g}} \leqslant p_{i, \mathrm{~g}} \leqslant x_{i, \mathrm{~g}} \bar{P}_{i, \mathrm{~g}} \quad i \in N_{\mathrm{g}} $ | (10) |
| $ x_{i, \mathrm{~g}} \underline{Q}_{i, \mathrm{~g}} \leqslant q_{i, \mathrm{~g}} \leqslant x_{i, \mathrm{~g}} \bar{Q}_{i, \mathrm{~g}} \quad i \in N_{\mathrm{g}} $ | (11) |
| $ \left\{\begin{array}{l} p_{i, \mathrm{~L}}=x_{i, \mathrm{~L}} P_{i, \mathrm{~L}} \\ q_{i, \mathrm{~L}}=x_{i, \mathrm{~L}} Q_{i, \mathrm{~L}} \end{array} \quad i \in N\right. $ | (12) |
式中:Pi, pv,Qi, pv分别为节点i处光伏最大有功和无功出力;Qi, pv为节点i处最小无功出力;Npv为接入光伏的节点集合;Pi, g,Qi, g分别为节点i处柴油发电机最大有功和无功出力;Pi, g,Qi, g分别为节点i处最小有功和无功出力;Ng为接入柴油发电机的节点集合;Qi, L为节点i处负荷无功功率;xi, pv,xi, g分别为节点i处光伏、柴油发电机的并网状态,若并网则为1,若节点i位于故障区域则为0。
式(13)和式(14)分别为线路流通有功和无功功率的最大约束,式(15)为配电网节点电压约束。
| $ -P_{i j, \max } s_{i j} \leqslant P_{i j} \leqslant P_{i j, \max } s_{i j} \quad(i, j) \in B $ | (13) |
| $ -Q_{i j, \max } s_{i j} \leqslant Q_{i j} \leqslant Q_{i j, \max } s_{i j} \quad(i, j) \in B $ | (14) |
| $ U_{\min } \leqslant U_i \leqslant U_{\max } \quad i \in N $ | (15) |
式中:Pij, max,Qij,max分别为线路ij流通的最大有功功率和无功功率;Umin,Umax分别为节点电压平方项的下界和上界。
(2) 拓扑变换约束。式(16)为不包含隔离开关的非故障支路处于连通状态,式(17)为故障支路为断开状态,式(18)表示对于包含联络开关的支路,其开关闭合时应是线路两端有一端供电,式(19)表示在重构过程中不可形成环网。
| $ s_{i j}=1 \quad(i, j) \in B_{\mathrm{sw}} \backslash B_{\mathrm{F}} $ | (16) |
| $ s_{i j}=0 \quad(i, j) \in B_{\mathrm{F}} $ | (17) |
| $ s_{h k} \leqslant s_{i j}\;\;\;\;\;(i, j) \in B_{\mathrm{F}} ;(h, k) \in H_{i j, \mathrm{U}} \cup H_{i j, \mathrm{D}} $ | (18) |
| $ \sum\limits_{(i, j) \in {B_l}} {{s_{ij}}} \le g - 1\;\;\;{\kern 1pt} l \in O $ | (19) |
式中:Bsw为不含隔离开关的支路集;BF为故障支路集;h, k为支路ij上、下游支路集包含的支路;Hij, U为支路ij上游含隔离开关的支路集;Hij, D支路ij下游含隔离开关的支路集;O为配电网可形成的环网集;Bl为环网l所包含的所有支路集; g为所有支路集个数。
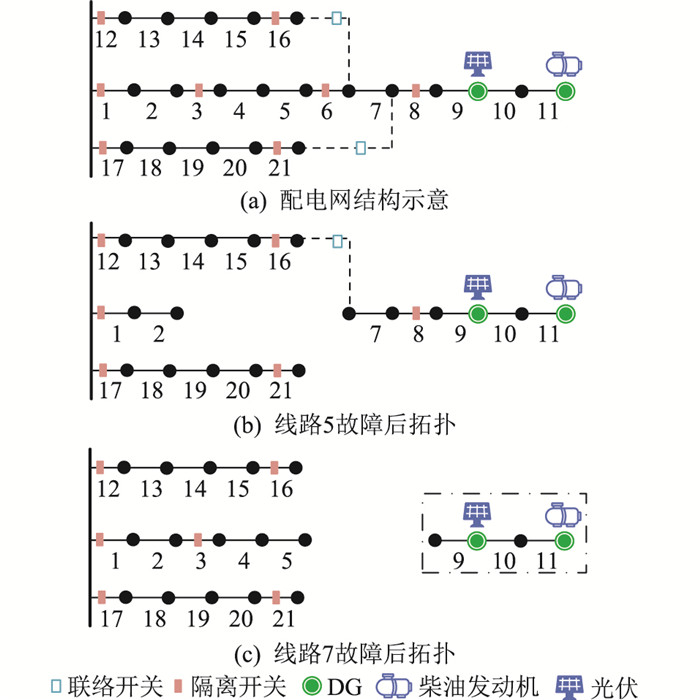
当线路故障时,隔离开关将故障支路隔离,故障线路下游负荷失电。此时,利用配电网网络重构和DG进行故障恢复,尽可能地恢复更多负荷。图 1(a)为配电网结构示意,当线路5发生故障后,线路6—11失电,支路3与支路6的隔离开关断开,隔离故障后拓扑变换为图 1(b)所示,联络开关闭合为线路7—11恢复供电。当线路7发生故障后,线路8—11失电,线路6与支路8的隔离开关断开,隔离故障后拓扑变换为图 1(c)所示,线路9—11形成孤岛,线路11处的发电机黑启动,线路9末端分布式光伏并网发电,恢复线路9—11的供电。
|
图 1 配电网故障重构示意 Fig. 1 Schematic diagram of distribution network fault reconstruction |
当线路发生故障,经配电网重构与DG故障支撑后,部分负荷仍未恢复供电,应进一步评估配电网故障恢复后的停电风险。通过遍历线路故障构建对应的预想负荷停电集S,评估各线路对应的负荷停电集S的停电影响程度,进而划分风险等级。
损失电量、停电用户重要级别、停电时长是评估故障停电影响程度的主要指标[22]。因此,选取损失电量E、停电用户小时数T、停电用户级别加权D来表征线路重要程度。
若某一线路发生故障,对应预想负荷停电集S的损失电量为:
| $ E=\sum\limits_{i \in \mathcal{S}} e_i $ | (20) |
式中:ei为S内负荷i对应的电量。
该线路停电用户小时数为:
| $ T = {T_{{\rm{avr}}}}\sum\limits_{i \in S} {{K_i}} $ | (21) |
式中:Tavr为该线路的年平均停电时长;Ki为S内负荷i对应的用户数量。
各级负荷其停电影响程度不同,应分级考虑。停电用户级别加权计算公式为:
| $ D = \sum\limits_{i \in S} {\sum\limits_{n = 1}^{{K_i}} {{\delta _{i, n}}} } $ | (22) |
式中:δi, n为S内负荷i中第n个用户的级别值。
各指标可从不同方面反映线路故障的停电影响程度,应综合各指标进行线路故障风险等级的评估。文中采用层次分析法(analytic hierarchy process, AHP)确定各指标的贡献值,利用K-means算法确定各线路故障风险等级,并作为分类标签。
3 基于XGBoost的配电网故障风险智能预警XGBoost算法属于集成学习算法,可分为两部分:决策树算法和梯度提升算法[23]。其以决策树为基学习器,每迭代一次增加一棵树,每棵新树都是在前一棵树上损失的负梯度形成的,保证了最终决策的可靠性[24—25]。决策树要确定最佳分割点,确定的方式是采用贪心策略遍历每个特征并计算其增益,将最大增益的特征作为最佳分割点进行分裂。当训练完K个决策树或多次迭代后目标函数为变化则停止迭代。
XGBoost模型目标函数为:
| $ L = \sum\limits_{m = 1}^M l \left( {{z_m}, {{\hat z}_m}} \right) + \sum\limits_{k = 1}^K \mathit{\Omega } \left( {{f_k}} \right) $ | (23) |
式中:第一项为预测值和实际值的差,第二项则是正则化项Ω,即树的复杂度,可防止过拟合。Ω定义为:
| $ \mathit{\Omega }\left( {{f_k}} \right) = \gamma T + \frac{1}{2}\lambda {\left\| \mathit{\boldsymbol{w}} \right\|^2} $ | (24) |
式中:T为叶子节点个数;w为叶子节点的得分值;γ,λ为树模型参数。
训练目标函数,第t次迭代中,第m个样本的预测值
| $ {L_t} = \sum\limits_{m = 1}^M l \left( {{z_m}, {{\hat z}_{m, t - 1}} + {f_t}\left( {{\mathit{\boldsymbol{X}}_m}} \right)} \right) + \sum\limits_{k = 1}^{t - 1} \mathit{\Omega } \left( {{f_k}} \right) + \mathit{\Omega }\left( {{f_t}} \right) $ | (25) |
文中采用预警召回率和精准率作为故障风险预警模型评估指标。召回率R指在真实为正类的样本中被预测为正类的比例。精准率P是指预测为正类的样本中真实为正类样本的比例。计算公式分别为:
| $ R=F_1 /\left(F_1+F_0\right) $ | (26) |
| $ P=F_1 /\left(F_1+F_2\right) $ | (27) |
式中:F1为实际为正类且预测正确的个数;F0为实际为正类但预测错误的个数;F2为实际为负类但预测为正类的个数。
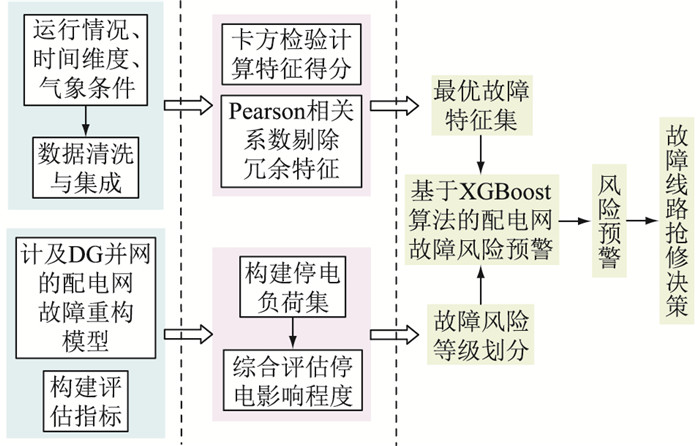
文中风险预警框架如图 2所示。
|
图 2 ADN故障风险预警方案架构示意 Fig. 2 Structure diagram of ADN fault risk forecast scheme |
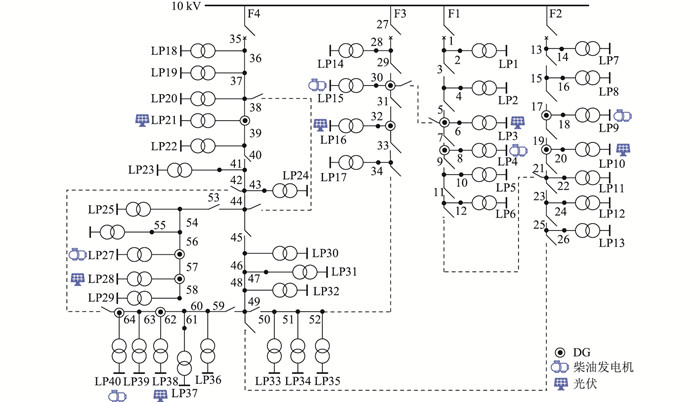
文中采用IEEE RBTS Bus6配电网系统为算例,在网络中加入DG。IEEE RBTS Bus6配电网系统结构如图 3所示。LP代表负荷,虚线为联络线,即常开线路。系统的负荷参数[26]为:每个光伏的额定发电功率为0.3 MW,柴油发动机用于黑启动,单组额定发电功率为0.5 MW。
|
图 3 含DG的IEEE RBTS Bus6配电网系统 Fig. 3 IEEE RBTS Bus6 distribution network system with DGs |
抽取湖南省4个市公司配网10 kV部分线路,每条馈线对应于某个市的某条馈线,所选取馈线的分支数量可覆盖算例中馈线的分支数量,并将抽取线路对应的故障停电数据、运维数据和该线路所属地区的天气数据映射到算例中的馈线上,剔除外力因素导致的故障,以此作样本进行仿真分析。
编程环境为Matlab 2015,采用YALMIP工具箱进行建模,并用Cplex求解器求解配电网重构优化模型。
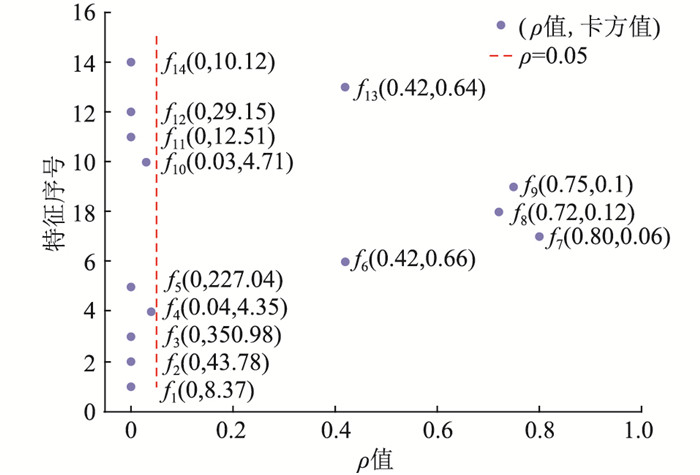
4.1 特征选取与分析采用改进χ2-Pearson的特征选择方法对初步特征集进行筛选。选定显著性水平α=0.05。当ρ≤0.05时,说明该特征相关性强,即拒绝原假设。图 4中按照特征序号标注了ρ值与卡方值,即(ρ值,卡方值),红色线条表示ρ=0.05。通过比较ρ值的大小,最终被筛选剔除的特征为f6—f9和f13。从选取结果来看,保留了与故障强相关的特征,形成最优特征集I1为{f1,f2,f3,f4,f5,f10,f11,f12,f14}。
|
图 4 各特征ρ值与卡方值分布 Fig. 4 The distribution of ρ and chi-square value distribution of each feature |
最优特征集I1中未剔除冗余特征,故将各特征间进行关联度分析。分别设9个特征作为参考序列,对应余下8个特征作为比较序列,解得Pearson相关系数,其中仅ρ(10, 11)和ρ(11, 10)的值大于0.5,且均为0.913,即f10和f11的关联度为0.913。f10代表风力等级,f11代表风速。因风速的卡方值大于风力等级,故剔除f10,选择f11。最终确定配电网最优故障特征集I2为{f1,f2,f3,f4,f5,f11,f12,f14}。
4.2 基于AHP和K-means的故障风险等级划分利用配电网拓扑变换特性或配电侧的DG实现负荷恢复,通过遍历线路故障并使用文中制定的故障恢复方案进行求解得到各线路预想负荷停电集S,然后计算3个指标用于评估线路停电影响程度。为了界定各线路的重要程度,利用AHP和K-means法综合评估。根据配电网运行经验,给出指标重要程度判断矩阵,即:
| $ \left[\begin{array}{ccc} 1 & 3 & 1 \\ 1 / 3 & 1 & 1 / 3 \\ 1 & 3 & 1 \end{array}\right]。$ |
在此利用AHP法可得到各指标权重向量,可表示为A=[0.428 6 0.142 9 0.428 6],判断矩阵的一致性指标2.220 4×10-16 < 0.1,因此AHP法得出的权重是合理的。进而综合3个指标值计算得到线路停电影响程度。采用K-means法将各线路的停电影响程度分类,获取风险等级标签。表 2为各线路的故障风险等级。
|
|
表 2 各线路的故障风险等级 Table 2 Fault risk level of each line |
文中在非故障与故障2个情景下进行验证,即情景0和情景1。情景0为非故障情况,故风险等级为0。情景1根据故障停电影响程度进行风险分级,即风险等级1,2,3。为验证文中XGBoost算法进行故障风险预警的优越性,分别与基于RF、BP神经网络的预警方法进行对比,总体准确率对比如表 3所示,各风险等级预警召回率和精准率对比如表 4所示,混淆矩阵对比如图 5所示。
|
|
表 3 配电网风险预警总体准确率对比 Table 3 Comparison of overall accuracy of distribution network risk early warning |
|
|
表 4 配电网风险预警召回率和精准率对比 Table 4 Comparison of recall and precision of distribution network risk early warning |
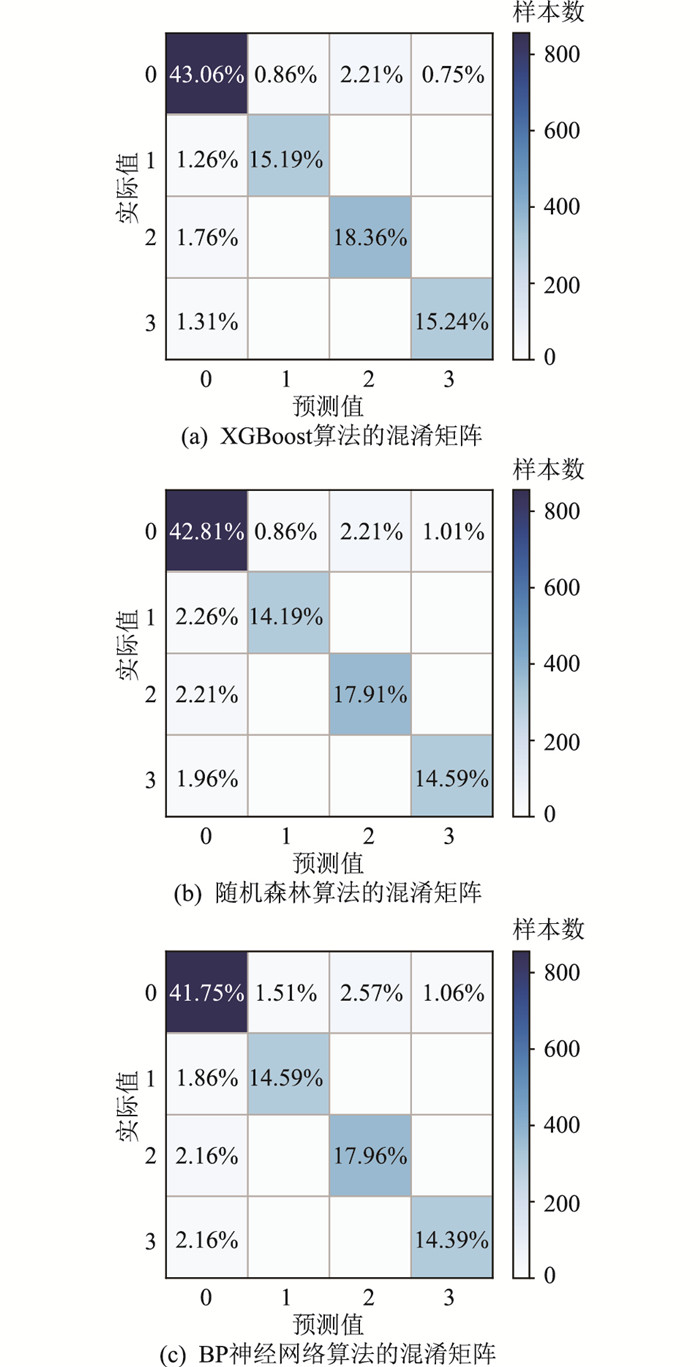
|
图 5 混淆矩阵对比 Fig. 5 Confusion matrix comparison |
从表 3和表 4可以得出,基于XGBoost算法的召回率在情景0和情景1下都达90%以上,说明基于XGBoost算法对不同预测样本具有较好的适应性。虽然基于RF算法在情景0的召回率达90%,基于BP神经网络算法在情景0时的召回率低于90%,但情景1下各风险等级的召回率均低于90%,2个场景下的召回率均低于XGBoost算法,说明对情景1样本的适应性不高。基于XGBoost算法的总体准确率为91.85%,高于随机森林算法和BP神经网络算法。
图 5中,混淆矩阵的行表示模型预警风险等级结果,列表示真实风险等级。矩阵内数字表示各风险等级中预测结果占总样本的比例。如基于XGBoost算法在情景0时,真实风险等级为0,预测等级也为0的样本个数有856,总体样本个数为1 988,故样本比例为43.06%。格子颜色深度反映样本个数,与比例相关,颜色越深说明预测风险等级所占百分比越大。对角线框格代表实际情况和预测结果完全相符,其所占比例较大故颜色较深。风险等级0时,基于XGBoost算法预测准确的样本比例为43.06%,基于随机森林算法和BP神经网络算法的准确样本比例分别为42.81%,41.75%,低于XGBoost算法。此外,风险等级1,2,3时基于XGBoost算法的预测准确样本比例也均高于其他2种方法,说明所提方法在不同风险等级预警效果表现较好。
由图 5可知,文中的风险预警在预测故障发生可能性的同时判定出该线路的风险等级。因每条线路风险等级已根据故障停电影响程度确定,故只有非故障与该线路故障后的风险等级2种预测结果。
4.4 基于风险预警的故障线路抢修策略当发生多线路故障时,根据线路风险等级进行顺序抢修可尽可能的减少停电损失。为了分析文中风险等级预警对配电网运行维护决策的作用,文中设置多种故障场景分别使用2种抢修策略,对停电影响程度进行对比分析。
策略1:各线路抢修不存在顺序规则。
策略2:根据线路风险等级顺序抢修,风险等级越高,次序最优,同一风险等级时比较线路的停电影响程度。
设置3种多线路故障场景,并设定同一时间最多抢修2条线路。场景1为线路7,13,19同时故障,其线路风险等级分别为1,2,1,且线路7和线路19停电影响程度相同;场景2为线路36,40,42同时故障,其线路风险等级分别为3,1,3,且线路42停电影响程度大于线路36;场景3为线路45,49,53同时故障,其线路风险等级分别为1,2,3。
图 6为3种场景下2种抢修策略结果对比。

|
图 6 3种场景下2种抢修策略对比 Fig. 6 Comparison of two repair strategies in three scenarios |
策略1的各场景抢修顺序均为6种,且每种顺序的概率均为1/6,带“#”字符的为策略2的抢修顺序,带“*”字符的表示与策略2相同的停电影响程度,括号前的数字为线路编号,括号中的数字代表抢修2条线路后的风险。
由图 6可知,按照策略1进行线路抢修,场景1有2/3的概率与策略2的停电影响程度相同,1/3的概率处于风险等级2;场景2有2/3的概率处于风险等级3,1/3的概率与策略2的停电影响程度相同。场景3有1/3的概率处于风险等级2,1/3的概率处于风险等级3,1/3的概率与策略2的停电影响程度相同。
在策略2下,场景1中线路7和线路19停电影响程度相同,故抢修顺序为线路13—7或者13—19;场景2中线路42停电影响程度大于线路36,故抢修顺序为线路42—36;场景3按照风险等级排序,其抢修顺序为线路53—49;各场景均能在最短时间内尽可能降低故障损失程度。可见,基于风险预警的故障线路抢修策略能够加快重要负荷恢复供电的速度,降低故障损失,提高配电网故障恢复的可靠性。
5 结论(1) 提出了基于卡方检验和Pearson相关系数法的特征选取方法,从运维情况、时间维度、气象条件3个层面分析了故障特征之间的强耦合关系,提取了8个与故障强相关的特征构成最优故障特征集,提高了配电网故障风险预警的效率。
(2) 提出了计及线路重要度和拓扑变换的故障风险等级划分依据。采用XGBoost算法和最优故障特征集实现配电网线路故障风险等级智能预警,风险预警兼顾了兼顾故障发生可能性和故障风险等级;此外,其预测精度和泛化能力均优于随机森林和BP神经网络算法,验证了所提故障风险预警方法的有效性和优越性,能够为配电网风险防控的运行维护决策提供理论依据,提高配电网供电可靠性。
(3) 在配电网发生多线故障时,基于风险预警的故障线路抢修策略可加快故障恢复速度,优先保障重要线路恢复供电,降低故障损失。
配电网故障关联因素繁多,未来在配电网故障预警研究中可考虑地形地貌因素,如供电区域、植被情况、海拔。未来在配电网故障恢复策略中可考虑DG的不确定性及多种DG的互补特性。
本文得到国网湖南省电力有限公司科技项目(5216A5200007)资助,谨此致谢!
| [1] |
郝丽丽, 王辉, 王国栋, 等. 含分布式电源配电网运行风险的影响因素溯源[J]. 电力自动化设备, 2021, 41(1): 27-37. HAO Lili, WANG Hui, WANG Guodong, et al. Influence factor tracing of operation risk for distribution network with distributed generations[J]. Electric Power Automation Equipment, 2021, 41(1): 27-37. (  0) 0) |
| [2] |
PRAKASH SINGH P, PALU I. State coordinated voltage control in an active distribution network with on-load tap changers and photovoltaic systems[J]. Global Energy Interconnection, 2021, 4(2): 117-125. DOI:10.1016/j.gloei.2021.05.005 (  0) 0) |
| [3] |
LEI J Z, GONG Q W. Comprehensive prediction method for failure rate of transmission line based on multi-dimensional cloud model[J]. IET Generation, Transmission & Distribution, 2019, 13(9): 1672-1678. (  0) 0) |
| [4] |
LEITE J B, MANTOVANI J R S, DOKIC T, et al. Resiliency assessment in distribution networks using GIS-based predictive risk analytics[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4249-4257. DOI:10.1109/TPWRS.2019.2913090 (  0) 0) |
| [5] |
陈哲. 基于BP神经网络的配网设备故障预测[D]. 广州: 广东工业大学, 2017. CHEN Zhe. Fault prediction of distribution equipment based on BP neural network[D]. Guangzhou: Guangdong University of Technology, 2017. (  0) 0) |
| [6] |
LIAOZ, HE G J, XU H, et al. Study on forecasting method of transmission line galloping via BP neural network[C]//2018 International Conference on Power System Technology (POWERCON). Guangzhou, China. IEEE, 2018: 4305-4312.
(  0) 0) |
| [7] |
高小芹, 王梓玮, 卢晨, 等. 基于最小二乘支持向量机的配电网故障量预测模型[J]. 武汉理工大学学报(信息与管理工程版), 2020, 42(1): 23-29. GAO Xiaoqin, WANG Ziwei, LU Chen, et al. Prediction model of distribution network fault based on least squares support vector machine[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2020, 42(1): 23-29. DOI:10.3963/j.issn.2095-3852.2020.01.005 (  0) 0) |
| [8] |
刘科研, 董伟杰, 肖仕武, 等. 基于电压数据SVM分类的有源配电网故障判别及定位[J]. 电网技术, 2021, 45(6): 2369-2379. LIU Keyan, DONG Weijie, XIAO Shiwu, et al. Fault identification and location of active distribution network based on SVM classification of voltage data[J]. Power System Technology, 2021, 45(6): 2369-2379. (  0) 0) |
| [9] |
林卫铭, 吴泽君, 周恒旭, 等. 基于Apriori算法的气象与电网缺陷关联研究[J]. 电气技术, 2019, 20(6): 44-49. LIN Weiming, WU Zejun, ZHOU Hengxu, et al. Research on mining association between weather and power grid based on Apriori algorithm[J]. Electrical Engineering, 2019, 20(6): 44-49. (  0) 0) |
| [10] |
严道波, 杨勇, 邱丹, 等. 基于天气因素和XGBoost算法的配电线路故障停电预测[J]. 电力与能源, 2019, 40(2): 168-171. YAN Daobo, YANG Yong, QIU Dan, et al. Failure prediction of distribution line based on weather factors and XGBoost algorithm[J]. Power & Energy, 2019, 40(2): 168-171. (  0) 0) |
| [11] |
李彦斌, 韩颖, 张嵘, 等. 气象因素对电力安全事故影响的模型[J]. 电网技术, 2013, 37(6): 1683-1687. LI Yanbin, HAN Ying, ZHANG Rong, et al. Research on impact model of meteorological factors on the power accidents[J]. Power System Technology, 2013, 37(6): 1683-1687. (  0) 0) |
| [12] |
方丽华, 熊小伏, 方嵩, 等. 基于电网故障与气象因果关联分析的系统风险控制决策[J]. 电力系统保护与控制, 2014, 42(17): 113-119. FANG Lihua, XIONG Xiaofu, FANG Song, et al. Power system risk control decision based on cause and effect correlation analysis of fault and meteorology[J]. Power System Protection and Control, 2014, 42(17): 113-119. DOI:10.7667/j.issn.1674-3415.2014.17.019 (  0) 0) |
| [13] |
贺电, 谭渡渡, 何海零, 等. 基于气象大数据的配网故障数量预测[J]. 吉首大学学报(自然科学版), 2019, 40(1): 53-56. HE Dian, TAN Dudu, HE Hailing, et al. Quantity prediction of distribution network faults based on big meteorological data[J]. Journal of Jishou University (Natural Sciences Edition), 2019, 40(1): 53-56. (  0) 0) |
| [14] |
KANKANALA P, DAS S, PAHWA A. AdaBoost+: an ensemble learning approach for estimating weather-related outages in distribution systems[J]. IEEE Transactions on Power Systems, 2014, 29(1): 359-367. DOI:10.1109/TPWRS.2013.2281137 (  0) 0) |
| [15] |
张鹏飞, 瞿海妮, 肖其师, 等. 基于气象因素和时间序列分析的配电网故障数量预测[J]. 陕西电力, 2016, 44(1): 68-72. ZHANG Pengfei, QU Haini, XIAO Qishi, et al. Distribution network faults prediction based on meteorological factors and time series analysis[J]. Shaanxi Electric Power, 2016, 44(1): 68-72. (  0) 0) |
| [16] |
侯慧, 耿浩, 肖祥, 等. 台风灾害下用户停电区域预测及评估[J]. 电网技术, 2019, 43(6): 1948-1954. HOU Hui, GENG Hao, XIAO Xiang, et al. Research on prediction and evaluation of user power outage area under typhoon disaster[J]. Power System Technology, 2019, 43(6): 1948-1954. (  0) 0) |
| [17] |
徐特威, 鲁宗相, 乔颖, 等. 基于典型故障与环境场景关联识别的城市配电网运行风险预警方法[J]. 电网技术, 2017, 41(8): 2577-2584. XU Tewei, LU Zongxiang, QIAO Ying, et al. A risk warning method for urban distribution network based on associated recognition of typical fault and environment scenario[J]. Power System Technology, 2017, 41(8): 2577-2584. (  0) 0) |
| [18] |
张稳, 盛万兴, 刘科研, 等. 计及天气因素相关性的配电网故障风险等级预测方法[J]. 电网技术, 2018, 42(8): 2391-2398. ZHANG Wen, SHENG Wanxing, LIU Keyan, et al. A prediction method of fault risk level for distribution network considering correlation of weather factors[J]. Power System Technology, 2018, 42(8): 2391-2398. (  0) 0) |
| [19] |
刘科研, 吴心忠, 石琛, 等. 基于数据挖掘的配电网故障风险预警[J]. 电力自动化设备, 2018, 38(5): 148-153. LIU Keyan, WU Xinzhong, SHI Chen, et al. Fault risk early warning of distribution network based on data mining[J]. Electric Power Automation Equipment, 2018, 38(5): 148-153. (  0) 0) |
| [20] |
陈谌, 梁雪春. 基于基尼指标和卡方检验的特征选择方法[J]. 计算机工程与设计, 2019, 40(8): 2342-2345, 2360. CHEN Chen, LIANG Xuechun. Feature selection method based on Gini index and Chi-square test[J]. Computer Engineering and Design, 2019, 40(8): 2342-2345, 2360. (  0) 0) |
| [21] |
周天, 郝丽丽, 王昊昊, 等. 兼顾风险与收益的主动配电网非正常停运恢复策略[J]. 电力系统自动化, 2018, 42(13): 136-144. ZHOU Tian, HAO Lili, WANG Haohao, et al. Unscheduled outage restoration strategy of active distribution network considering risk and gain[J]. Automation of Electric Power Systems, 2018, 42(13): 136-144. DOI:10.7500/AEPS20170823004 (  0) 0) |
| [22] |
赵会茹, 李娜娜, 郭森, 等. 配电网设备故障停电风险实时评估[J]. 电力自动化设备, 2014, 34(11): 89-94. ZHAO Huiru, LI Nana, GUO Sen, et al. Real-time risk assessment on equipment failure outage of distribution network[J]. Electric Power Automation Equipment, 2014, 34(11): 89-94. DOI:10.3969/j.issn.1006-6047.2014.11.014 (  0) 0) |
| [23] |
RENJ H. Dynamic security assessment method of power system based on improved XGBoost[J]. Journal of Physics: Conference Series, 2021, 1750(1): 012004. DOI:10.1088/1742-6596/1750/1/012004 (  0) 0) |
| [24] |
HUW P, LIANG J F, JIN Y T, et al. Online evaluation method for low frequency oscillation stability in a power system based on improved XGboost[J]. Energies, 2018, 11(11): 3238. DOI:10.3390/en11113238 (  0) 0) |
| [25] |
吴琼, 余文铖, 洪海生, 等. 基于XGBoost算法的配网台区低压跳闸概率预测[J]. 中国电力, 2020, 53(4): 105-113. WU Qiong, YU Wencheng, HONG Haisheng, et al. Probability prediction of low-voltage tripping failures in distribution transformer station areas based on XGBoost algorithm[J]. Electric Power, 2020, 53(4): 105-113. (  0) 0) |
| [26] |
RASTEGAR M. Impacts of residential energy management on reliability of distribution systems considering a customer satisfaction model[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6062-6073. DOI:10.1109/TPWRS.2018.2825356 (  0) 0) |
2. College of Electrical and Information Engineering, Hunan University, Changshang 410082, China

 唐海国(1985),男,硕士,高级工程师,从事配电智能运检、配电自动化、配电网数字化等相关工作(E-mail:
唐海国(1985),男,硕士,高级工程师,从事配电智能运检、配电自动化、配电网数字化等相关工作(E-mail: