文章编号: 2096-3203(2021)06-0062-10 中图分类号: TM73;U469.72
电动汽车充电站(electric vehicle charging station,EVCS)是支撑电动汽车(electric vehicle,EV)发展的重要基础设施[1-5],随着EV的日益普及,亟需进行充电网络优化规划,减少EVCS大规模接入对配电网的不利影响。在EVCS大规模接入配电网的同时,分布式光伏电站(distributed photovoltaic generation,DPVG)在配电网中的渗透率日益提升,对配电网运行的影响日益显著[6-9]。作为配电网源、荷两侧同时出现的新型元件,DPVG与EVCS将共同影响配电网运行,因此,进行DPVG-EVCS联合规划研究具有重要意义。
现有研究中,文献[10]提出基于电压稳定指标的充电网络规划模型,并采用自适应粒子群算法进行求解。文献[11]根据潮流越限和电压偏移指标衡量配电网运行风险,并提出基于该指标的充电网络规划方法。文献[12-13]分别建立以总建设成本、年费用最小为优化目标的充电网络规划模型,并利用遗传算法(genetic algorithm,GA)进行求解。文献[14]提出考虑交通网、电网耦合特性的DPVG-EVCS联合规划模型。文献[15]建立用于DPVG-EVCS联合规划的二阶锥模型,并采用通用代数建模系统(general algebraic modeling system,GAMS)进行求解。文献[16]提出考虑投资成本、网损成本与环境成本的DPVG-EVCS多目标联合规划模型,并采用非支配排序GA进行求解。文献[17]提出综合考虑交通满意度、系统网损与投资的DPVG-EVCS联合规划模型,并采用蝙蝠算法进行求解。
上述文献均未充分考虑EVCS充电负荷与DPVG出力的随机特性,具有一定的局限性。针对该问题,文中提出同时考虑DPVG出力与EVCS充电负荷随机特性的DPVG-EVCS联合规划模型,其中,节点电压偏移约束与支路潮流约束均建模为机会约束。为提高求解效率,采用基于GA的协同进化算法(co-evolutionary algorithm,CA)[18-19]求解DPVG-EVCS联合规划模型。基于IEEE 33节点配电系统的仿真分析表明,采用CA求解文中所提模型时效率更高,可显著提高规划人员工作效率。
1 基于机会约束的DPVG-EVCS联合规划模型DPVG和EVCS共同接入后,配电系统运行工况具有随机特性。为合理规划,文中建立基于机会约束的DPVG-EVCS联合规划模型,将节点电压偏移约束与支路潮流约束建模为机会约束[20-21]。
1.1 优化目标DPVG-EVCS联合规划模型的优化目标为配电系统规划典型日内的网损电量期望Fs最小,即:
| $ \min F_{\mathrm{s}}=\frac{24}{T_{\mathrm{d}}} \sum\limits_{t=1}^{T_{\mathrm{d}}} \sum\limits_{k \in \varOmega_{\mathrm{c}}} E\left(\Delta P_{k, t}\right) $ | (1) |
式中:ΔPk, t为配电线路k在潮流分析时段t的损耗功率,ΔPk, t为随机变量,其概率分布特性与DPVG、EVCS的规划方案相关,可由概率潮流分析得出;E(·)为期望函数;Td为典型日内的潮流分析时段数;Ωc为配电线路集合。
1.2 模型约束(1) EVCS建设数目约束。
| $ \sum\limits_{i=1}^{N_{\mathrm{ev}}} x_{i}=N_{1} $ | (2) |
式中:N1为待建EVCS数量,由规划人员根据规划区域内的EV总数与市政规划等因素综合考虑确定;xi为是否在候选地址i建设EVCS的0-1变量,1表示是,0表示否;Nev为EVCS候选地址总数,为规划区域内可接入EVCS的配电节点数。
(2) DPVG建设数目约束。
| $ \sum\limits_{j=1}^{N_{\mathrm{pv}}} y_{j}=N_{2} $ | (3) |
式中:N2为待建DPVG数量;yj为是否在候选地址j建设DPVG的0-1变量,1表示是,0表示否;Npv为DPVG候选地址总数,为规划区域内可接入DPVG的配电节点数。
(3) EVCS建设容量约束。
| $ \sum\limits_{i=1}^{N_{\mathrm{ev}}}\left(x_{i} z_{i}\right)=C_{\mathrm{ev}} $ | (4) |
式中:zi为建于候选地址i的EVCS容量,规划中按容量不同将待建EVCS分为Qev类,此时,zi有Qev种不同取值,即zi为DPVG-EVCS联合规划模型中的离散优化变量;Cev为规划中所有EVCS的总建设容量,由待规划区域内EVCS建设成本、EV数目、EVCS建设投资总额等因素共同确定。
(4) DPVG建设容量约束。
| $ \sum\limits_{j=1}^{N_{\mathrm{pv}}}\left(y_{j} w_{j}\right)=C_{\mathrm{pv}} $ | (5) |
式中:wj为建于候选地址j的DPVG容量,与EVCS类似,文中按容量不同将待建DPVG分为Qpv类,此时,wj有Qpv种不同取值,即wj为DPVG-EVCS联合规划模型中的离散优化变量;Cpv为规划中所有DPVG的总建设容量,由待规划区域内DPVG建设成本和DPVG建设拟投资总额等因素共同确定。
(5) 节点电压偏移机会约束。
| $ P_{\mathrm{r}}\left(\frac{U_{l}-U_{\mathrm{N}}}{U_{\mathrm{N}}} \times 100 \%>\alpha\right) \leqslant \beta_{1} \quad l \in \varOmega_{\mathrm{b}} $ | (6) |
式中:Pr(·)为事件发生概率;UN为配电系统额定电压;Ul为节点l电压,Ul为随机变量,其概率分布特性由概率潮流分析得出;Ωb为配电节点索引集合;α为节点电压幅值允许偏移百分数的上限;β1为节点电压幅值越限的置信度。
(6) 线路潮流越限机会约束。
| $ P_{\mathrm{r}}\left(I_{k}>I_{k, \max }\right) \leqslant \beta_{2} \quad k \in \varOmega_{\mathrm{c}} $ | (7) |
式中:Ik为配电线路k的负荷电流,Ik为随机变量,其概率分布特性由概率潮流分析得出;Ik, max为配电线路k的最大允许电流;β2为潮流越限置信度。
2 配电系统概率潮流分析EVCS和DPVG接入后,配电系统运行工况呈现明显的随机性。因此,DPVG-EVCS联合规划中,需要对配电系统进行概率潮流分析,并以此为依据进行规划方案比选。文中采用场景概率法进行配电系统概率潮流分析。
2.1 EVCS充电负荷概率场景集构建目前,EVCS充电负荷实测数据不足,无法以此为基础构建EVCS充电负荷概率场景集。因此,文中采用蒙特卡洛模拟(Monte Carlo simulation,MCS)技术对EVCS日充电负荷进行模拟,生成日充电负荷曲线集。模拟中考虑电动汽车起始充电时的荷电状态、充电起始时间、充电持续时间、充电功率等多个随机因素,具体流程参见文献[22]。而后,采用K-means聚类法对模拟后的充电负荷曲线集进行聚类,形成EVCS充电负荷概率场景集。
2.2 DPVG出力概率场景集构建目前,已有大量DPVG并网发电,且大多配有数据采集与监视控制(supervisory control and data acquisition,SCADA)系统。因此,可采用K-means聚类法对SCADA系统提供的DPVG历史出力数据进行聚类,构建DPVG出力概率场景集。
2.3 配电系统概率场景潮流计算EVCS充电负荷和DPVG出力的随机性是配电系统概率潮流计算需要考虑的2个随机因素。因此,可基于EVCS充电负荷概率场景集和DPVG出力概率场景集生成潮流分析概率场景集。在此过程中,假定EVCS充电负荷的随机变化和DPVG出力的随机波动互相独立。潮流分析概率场景集构建方法可参见文献[22],此处不再赘述。
基于潮流分析概率场景集,采用近似前推回代法实现全部场景下的潮流计算。而后,以场景概率为权重汇总所有场景下的潮流计算结果,最终得出配电系统典型日内的概率潮流。
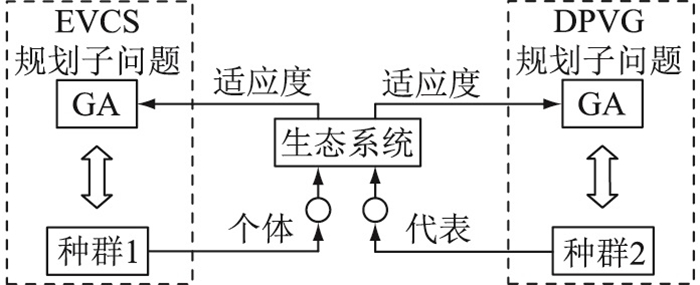
3 模型求解 3.1 协同进化算法(CA)作为模拟生态系统进化机制的优化算法,CA将待求复杂优化问题建模为多种群构成的生态系统,通过多种群协同进化获得待求优化问题的最优解。文中利用CA求解DPVG-EVCS联合规划模型时,将其解耦为2个相对独立的子优化问题,即EVCS规划子问题和DPVG规划子问题,2个子优化问题均采用GA独立进化,并由2个GA种群代表组成的生态系统协作实现模型求解,求解框架见图 1。
|
图 1 基于CA的DPVG-EVCS联合规划模型求解框架 Fig. 1 Solution framework of CA-based DPVG-EVCS joint programming model |
图 1中,种群1、2分别为利用GA求解EVCS和DPVG规划子问题时的算法种群。对图 1中的任一种群进行进化时,从另一种群中挑选优秀染色体作为代表放入生态系统,并将待进化种群中所有染色体放入生态系统进行评价,获取适应度。而后,基于适应度,对进化种群进行遗传操作,更新种群,并将当前种群中的最优染色体放入生态系统,供另一个种群进化使用。
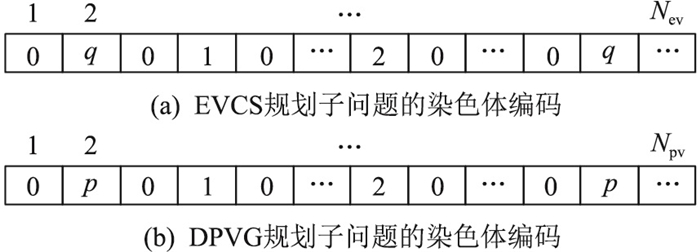
3.2 染色体编码种群1中的每条染色体对应EVCS规划子问题的1个可行解,包含Nev个码位,如图 2(a)所示。图 2(a)中,第i个码位取值为0表示不在候选地址i建设EVCS(i=1, 2, …, Nev);取值为q表示在候选地址i建设第q类EVCS(q=1, 2, …, Qev),对应的建设容量为Cev, q。
|
图 2 染色体编码示意 Fig. 2 Schematic diagram of chromosome coding |
与种群1类似,种群2中的每条染色体对应DPVG规划子问题的一个可行解,包含Npv个码位,如图 2(b)所示。图 2(b)中,第j个码位取值为0表示不在候选地址j建设DPVG(j=1, 2, …, Npv); 取值为p表示在候选地址j建设第p类DPVG(p=1, 2, …, Qpv),对应的建设容量为Cpv, p。
3.3 适应度求解以种群1为例,阐述染色体适应度求取方法。首先,对种群1中的待评价染色体和生态系统中表示DPVG建设方案的染色体进行解码,确定N1个EVCS与N2个DPVG的建设位置和建设容量,EVCS总建设容量为Ct-ev,DPVG总建设容量为Ct-pv。而后,进行概率潮流分析,确定配电系统规划典型日内的网损电量期望Fs、各节点电压幅值与各线路潮流的概率分布特性。采用罚函数法分别处理式(4)-式(7)的约束,计算种群中各染色体的适应度Vfit。
| $ V_{\mathrm{fit}}=\frac{F_{\max }}{F_{\mathrm{s}}}-\eta_{1} V_{\mathrm{p} 1}-\eta_{2} V_{\mathrm{p} 2}-\eta_{3} V_{\mathrm{p} 3}-\eta_{4} V_{\mathrm{p} 4} $ | (8) |
式中:Fmax,Fs同量纲;Vfit非负;η1,η2,η3,η4为罚系数;Vp1,Vp2,Vp3,Vp4分别为式(4)-式(7)约束的违背程度。
| $ V_{\mathrm{p} 1}=\left|C_{\mathrm{ev}}-C_{\mathrm{t}-\mathrm{ev}}\right| $ | (9) |
| $ V_{\mathrm{p} 2}=\left|C_{\mathrm{pv}}-C_{\mathrm{t}-\mathrm{pv}}\right| $ | (10) |
| $ V_{\mathrm{p} 3}=\sum\limits_{l \in \varOmega_{\mathrm{b}}} \max \left(P_{\mathrm{r}}\left(\frac{\left|U_{l}-U_{\mathrm{N}}\right|}{U_{\mathrm{N}}} \times 100 \%>\alpha\right)-\beta_{1}, 0\right) $ | (11) |
| $ V_{\mathrm{p} 4}=\sum\limits_{k \in \varOmega_{\mathrm{c}}} \max \left(P_{\mathrm{r}}\left(I_{k}>I_{k, \max }\right)-\beta_{2}, 0\right) $ | (12) |
基于适应度评价结果,对生态系统进行更新,并借助遗传操作对种群1、2进行进化。以种群1为例,详细阐述生态系统更新方法和用于该种群进化的遗传操作。
3.4.1 生态系统更新根据适应度计算结果,从种群1中挑选最优染色体作为种群代表放入生态系统,更新生态系统。
3.4.2 选择操作对GA来说,常用的选择操作方法有“锦标赛”法和“轮盘赌”法,文中采用“轮盘赌”法进行选择操作,以适应度为依据,择优选择个体。
3.4.3 交叉操作为确保交叉后的染色体满足式(2)的EVCS建设数目约束,文中对传统交叉操作算子进行改进。
步骤1:在种群1中选取2条染色体作为待交叉染色体。
步骤2:随机生成待选交叉位,直至找到可行交叉位Ncross。若2条待交叉染色体待选交叉位后取值非0的码位数目相等,则该待选交叉位为Ncross。
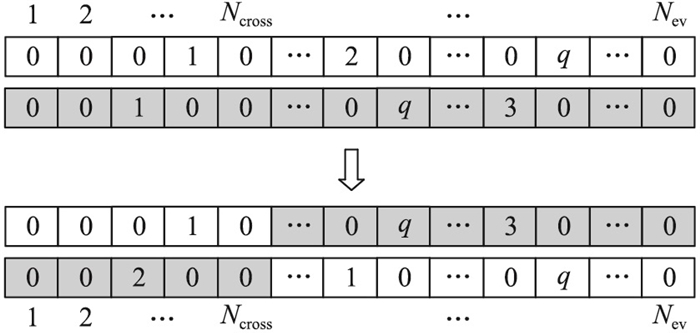
步骤3:针对2条待交叉染色体,以交叉概率Pc交换Ncross后的码串,如图 3所示。
|
图 3 种群1交叉操作示意 Fig. 3 Schematic diagram of cross operator for population 1 |
为确保变异后的染色体满足式(2)的EVCS建设数目约束,文中同样对变异操作算子进行改进。
步骤1:在种群1中选取1条染色体作为待变异染色体。
步骤2:随机生成2个待变异码位Nmu1,Nmu2,并确保2个待变异码位不能同时取0且不能同时取非0整数。
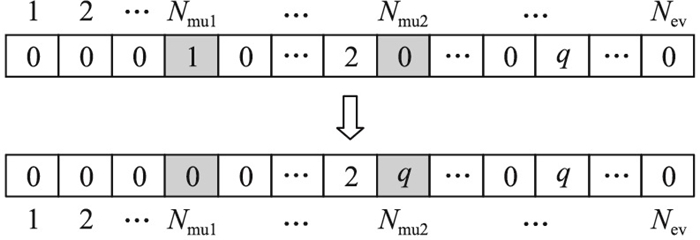
步骤3:以变异概率Pm同时对Nmu1,Nmu2进行变异操作。变异时,取值非0的码位变异为0,取值为0的码位变异为不大于Qev的随机整数,见图 4。
|
图 4 种群1变异操作示意 Fig. 4 Schematic diagram of mutation operator for population 1 |
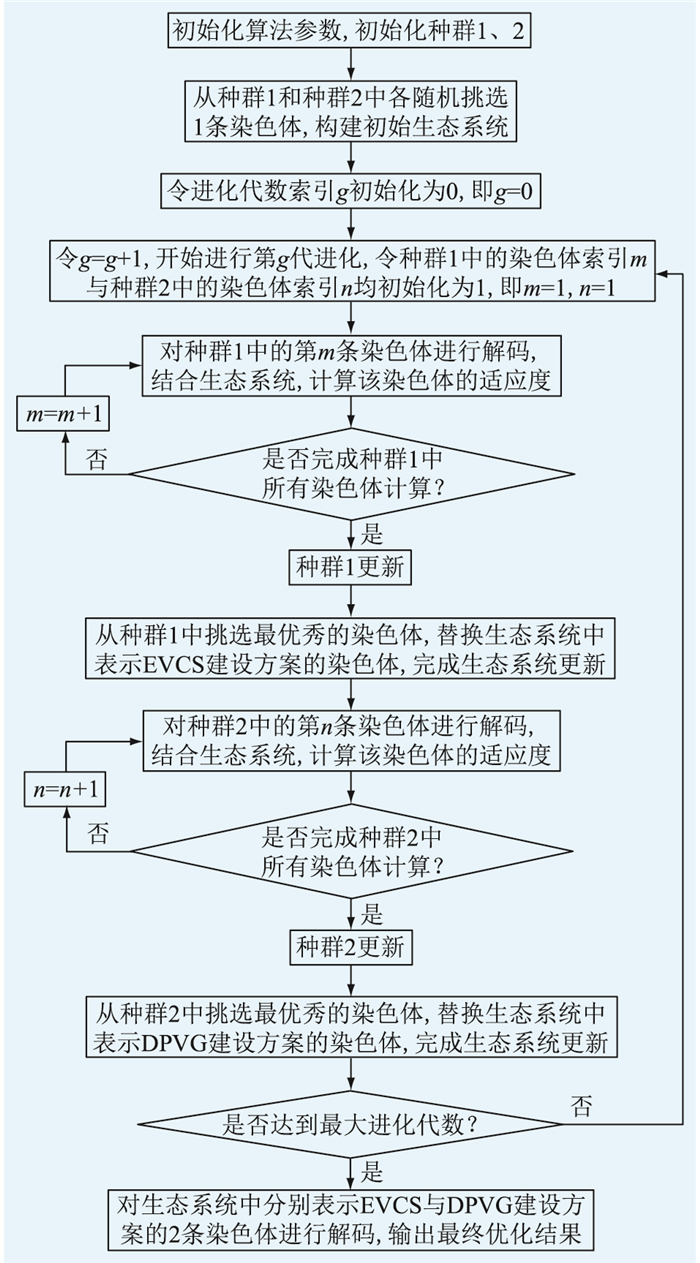
基于CA的DPVG-EVCS联合规划模型求解流程如图 5所示。
|
图 5 基于CA的DPVG-EVCS联合规划模型求解流程 Fig. 5 Solution flow of CA-based DPVG-EVCS joint programming model |
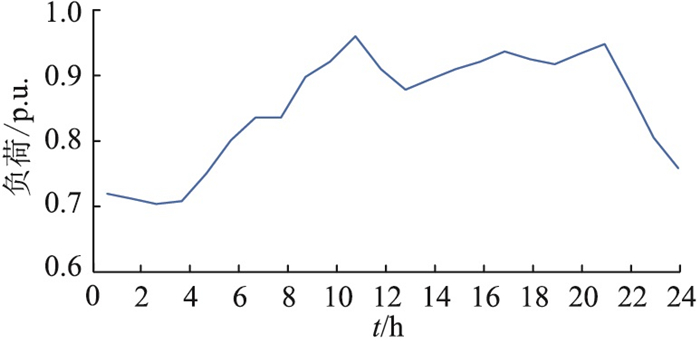
文中基于IEEE 33节点配电系统进行DPVG-EVCS联合规划仿真实验。配电线路阻抗参数和配电节点基准有功、无功负荷参见文献[23]。为便于分析,算例假定规划典型日内各配电节点标幺化后的有功负荷曲线一致,见图 6。工程实际中,各配电节点标幺化后的有功负荷曲线并不一致,计算时需替换成典型日内的实际负荷数据。此外,算例假定规划典型日内各节点负荷的功率因数恒定不变。各配电线路最大允许电流为算例系统基准负荷下的负荷电流上浮10%,具体参见文献[24],此处不再赘述。
|
图 6 典型日有功负荷曲线 Fig. 6 Typical daily active power curve |
算例中,按容量不同,将待建EVCS分为6类,即Qev=6,容量分别为0.4 MW,0.8 MW,1.2 MW,1.6 MW,2 MW,2.4 MW。规划区域内,为满足EV充电需求,EVCS建设的N1为4,Cev为8 MW。按容量不同,同样将待建DPVG分为6类,即Qpv=6,容量分别为0.5 MW,1 MW,1.5 MW,2 MW,2.5 MW,3 MW。规划区域内,DPVG建设的N2为4,Cpv为5 MW。α为10%;β1,β2均为0.05。
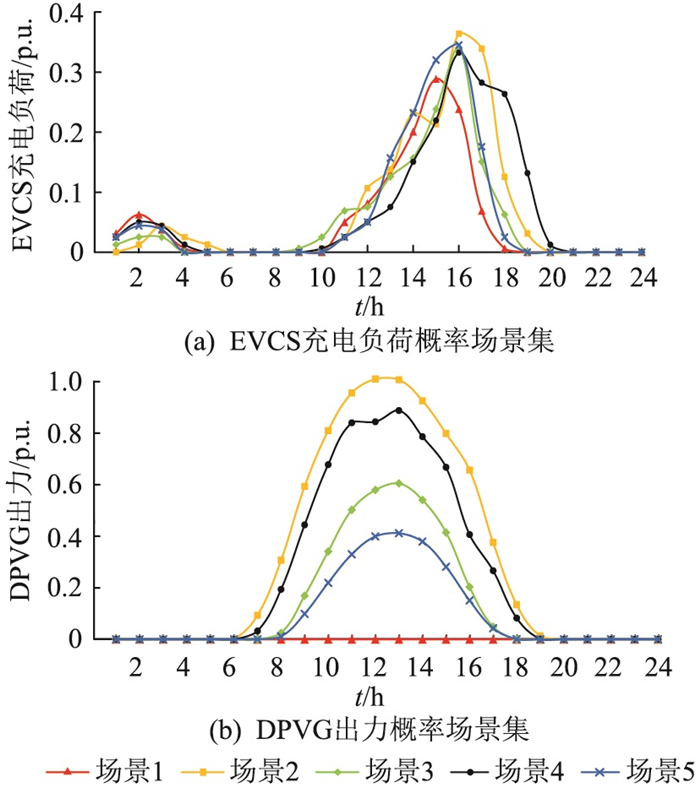
4.2 充电负荷与光伏出力概率场景集概率潮流计算中,分别利用EVCS充电负荷概率场景集和DPVG出力概率场景集描述EVCS充电负荷和DPVG出力的随机特性[22],并形成潮流分析概率场景集。EVCS充电负荷概率场景集和DPVG出力概率场景集如图 7所示。
|
图 7 EVCS充电负荷和DPVG出力概率场景集 Fig. 7 Probability scenario set of EVCS charging load and DPVG output |
5个EVCS充电负荷场景对应的概率分别为22.8%,19.5%,20.4%,16.4%, 20.9%。采用K-means方法对MCS所得EVCS充电负荷场景集进行聚类,聚类数设为5,得到5个EVCS充电负荷场景,见图 7(a)。K-means方法能按设置的聚类参数识别复杂数据间的相关性,并对待分类数据进行分类,因此,图 7(a)中的5个场景可覆盖EVCS常见的负荷曲线。DPVG出力概率场景集同样由5个场景构成,对应的概率分别为25.7%,15.1%,20.3%,18.9%,20%。5个DPVG出力场景由K-means方法聚类获得,可覆盖DPVG常见的出力曲线,见图 7(b)。
4.3 算法性能分析利用CA求解DPVG-EVCS联合规划模型时,种群1、2的染色体规模均设为20。遗传操作中Pc为0.2,Pm为0.08,最大进化代数gmax为200。式(8)中,Fmax为4 000;η1,η2,η3,η4分别为0.5,0.4,0.04,0.7。
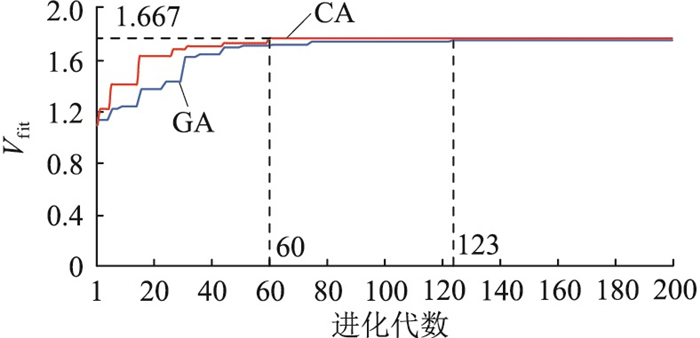
利用CA求解DPVG-EVCS联合规划模型时,Vfit如图 8中红色曲线所示。为体现CA的优越性,文中同时利用GA求解DPVG-EVCS联合规划模型,染色体包含Nev+Npv个码位,对应EVCS和DPVG的整体规划方案,前Nev个码位表示EVCS的规划方案,后Npv个码位表示DPVG的规划方案,分别如图 2(a)、图 2(b)所示,此处不再赘述。利用GA求解DPVG-EVCS联合规划模型时,Vfit如图 8中蓝色曲线所示。
|
图 8 Vfit与进化代数的关系 Fig. 8 Relationship between Vfit and evolutionary generation |
由图 8可知,DPVG-EVCS协同规划模型分解为2个相对独立的子优化问题并行求解时,CA求解性能显著优于GA。由图 8中红色曲线可知,仅进化60代,CA即可收敛于DPVG-EVCS联合规划模型的最优解,对应的Vfit为1.667。由图 8中蓝色曲线可知,GA需进化123代才可收敛于同样的解。从收敛过程看,CA能快速收敛于最优解。而GA虽在第76代已逼近最优解,却在第123代才收敛于最优解,收敛性能欠佳。由以上分析可知,CA与GA用于求解DPVG-EVCS联合规划模型时,虽可获得同样质量的解,但CA的收敛速度更快,求解性能更好。
利用GA与CA分别对算例进行求解,计算时间分别为210 s,100 s,即利用CA求解该算例,可节约52.38%的计算时间。因此,在进行大规模实际系统规划时,CA收敛速度快的优势尤为明显,可显著节约规划人员时间,提高工作效率。
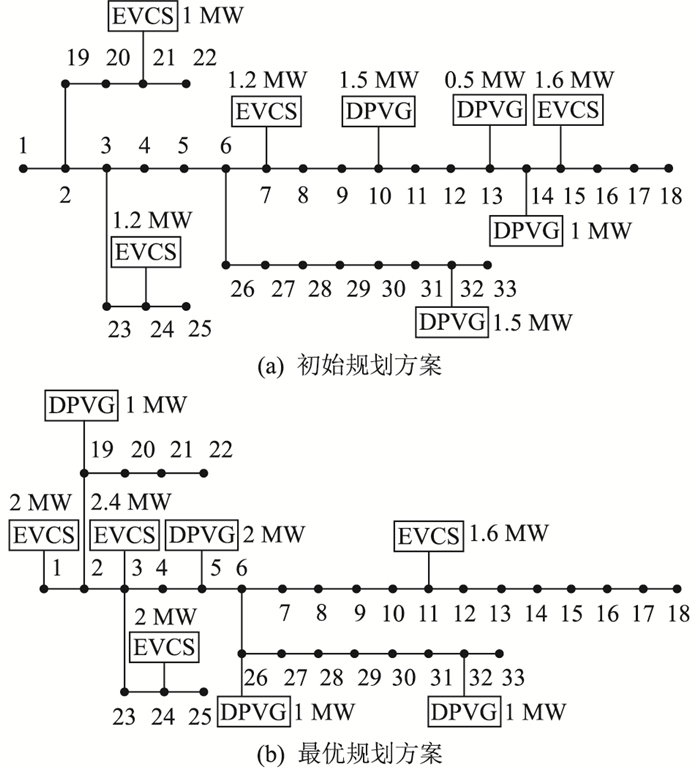
4.4 规划结果分析CA初始生态系统对应的DPVG-EVCS联合规划方案和CA优化后的最优规划方案如图 9所示。由图 9可知,与初始生态系统对应的DPVG-EVCS联合规划方案相比,最优DPVG-EVCS联合规划方案中,EVCS与DPVG的建设位置和容量均发生了显著变化。4座EVCS分别建在配电节点1,3,11,24处,建设容量分别为2 MW,2.4 MW,1.6 MW,2 MW。4座DPVG分别建在配电节点5,19,26,32处,建设容量分别为2 MW,1 MW,1 MW,1 MW。与此同时,典型日网损期望由初始生态系统对应规划方案的3 034 kW ·h下降为最优规划方案对应的2 400 kW ·h,降幅为20.9%。
|
图 9 DPVG-EVCS规划方案 Fig. 9 Planning scheme of DPVG-EVCS |
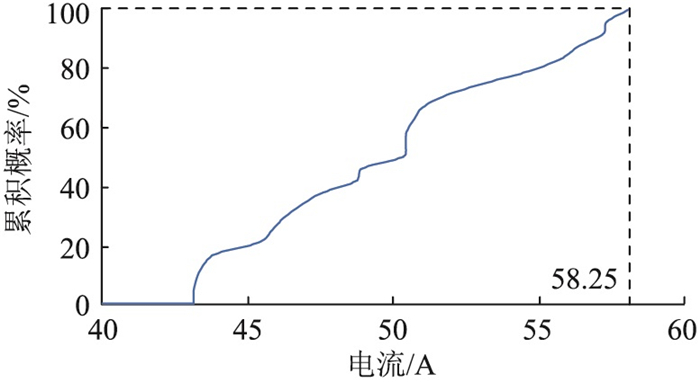
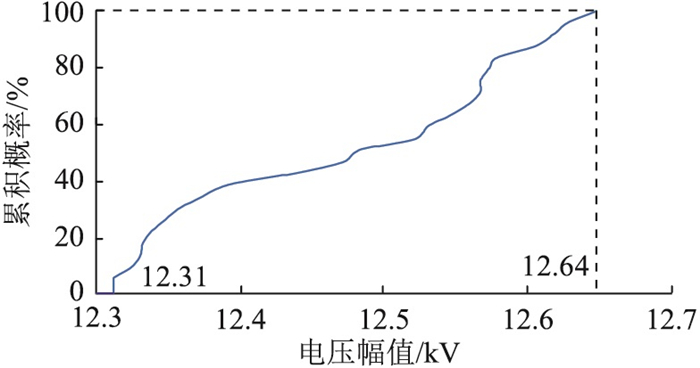
EVCS与DPVG大规模接入会显著增加配电系统运行工况的随机特性,即各配电线路电流和节点电压幅值均为随机变量。文中以靠近光伏接入点的节点6与配电线路5-6为例,分析最优DPVG-EVCS规划方案对应的配电系统潮流分布。配电线路5-6的负荷电流在典型日内的累积概率分布见图 10。配电节点6的电压幅值在典型日内的累积概率分布见图 11。
|
图 10 线路5-6负荷电流的累积概率分布 Fig. 10 Cumulative probability distribution of the load current in line 5-6 |
|
图 11 节点6电压幅值的累积概率分布 Fig. 11 Cumulative probability distribution of voltage amplitude at bus 6 |
由图 10可知,该线路最大负荷电流为58.25 A,未超过其最大允许电流60.82 A。与配电线路5-6一样,其他线路在典型日内均未出现潮流越限。由图 11可知,该节点电压幅值的最大、最小值分别为12.64 kV,12.31 kV,均在允许范围内。与节点6一样,其他节点在典型日内均未出现电压幅值越限。
综上,文中所提DPVG-EVCS联合规划模型可确保配电系统运行工况合理以及配电系统运行成本最小化。
5 结论在同时考虑DPVG出力与EVCS充电负荷随机特性的基础上,文中提出了基于机会约束的DPVG-EVCS联合规划模型,并采用CA进行求解,具体结论如下:(1) 基于IEEE 33节点配电系统的仿真实验表明,文中所提DPVG-EVCS联合规划模型可给出满足配电系统运行工况的最优规划结果,为配电网中的EVCS和DPVG建设提供理论参考。(2) 文中所提DPVG-EVCS联合规划模型是大规模优化问题,优化变量多,约束强。文中将其解耦为2个相对独立的子优化问题,并采用CA进行求解,显著提高了求解效率。
| [1] |
王建明, 潘志新, 李春, 等. 配电网电动汽车接纳能力分析[J]. 供用电, 2019, 36(5): 42-47. WANG Jianming, PAN Zhixin, LI Chun, et al. Distribution network electric vehicle hosting capability assessment[J]. Distribution & Utilization, 2019, 36(5): 42-47. (  0) 0) |
| [2] |
ZHANG J, LIU C, YUAN R M, et al. Design scheme for fast charging station for electric vehicles with distributed photovoltaic power generation[J]. Global Energy Interconnection, 2019, 2(2): 150-159. DOI:10.1016/j.gloei.2019.07.003 (  0) 0) |
| [3] |
FANG C, ZHAO X J, XU Q, et al. Aggregator-based demand response mechanism for electric vehicles participating in peak regulation in valley time of receiving-end power grid[J]. Global Energy Interconnection, 2020, 3(5): 453-463. DOI:10.1016/j.gloei.2020.11.005 (  0) 0) |
| [4] |
倪凯旋. 基于分布式博弈的电动汽车充电站最优调度方法[J]. 供用电, 2020, 37(2): 79-84. NI Kaixuan. Optimal scheduling of electric vehicle charging station based on distributed game[J]. Distribution & Utilization, 2020, 37(2): 79-84. (  0) 0) |
| [5] |
HUANG Q L. Insights for global energy interconnection from China renewable energy development[J]. Global Energy Interconnection, 2020, 3(1): 1-11. DOI:10.1016/j.gloei.2020.03.006 (  0) 0) |
| [6] |
TAN Q K, WU P, TANG W, et al. Benefit allocation model of distributed photovoltaic power generation vehicle shed and energy storage charging pile based on integrated weighting-Shapley method[J]. Global Energy Interconnection, 2020, 3(4): 375-384. DOI:10.1016/j.gloei.2020.10.009 (  0) 0) |
| [7] |
孙安国, 吴俊勇, 戴玮, 等. 基于配电物联网的跨台区光伏消纳研究[J]. 供用电, 2020, 37(4): 33-38. SUN Anguo, WU Junyong, DAI Wei, et al. Research on photovoltaic consumption across multiple stations based on distribution Internet of Things[J]. Distribution & Utilization, 2020, 37(4): 33-38. (  0) 0) |
| [8] |
BELAY KEBEDE A, BIRU WORKU G. Comprehensive review and performance evaluation of maximum power point tracking algorithms for photovoltaic system[J]. Global Energy Interconnection, 2020, 3(4): 398-412. DOI:10.1016/j.gloei.2020.10.008 (  0) 0) |
| [9] |
WANG S Y, ZHANG Y P, ZHANG C, et al. Improved artificial neural network method for predicting photovoltaic output performance[J]. Global Energy Interconnection, 2020, 3(6): 553-561. DOI:10.1016/j.gloei.2021.01.005 (  0) 0) |
| [10] |
程杉, 许林峰, 孙伟斌, 等. 基于电压稳定性的电动汽车充电站最优规划[J]. 电力科学与技术学报, 2020, 35(4): 3-12. CHENG Shan, XU Linfeng, SUN Weibin, et al. Optimal planning of charging stations for electric vehicles based on voltage stability of distribution system[J]. Journal of Electric Power Science and Technology, 2020, 35(4): 3-12. (  0) 0) |
| [11] |
张永明, 姚志力, 李菁, 等. 基于配电网概率潮流计算的电动汽车充电站规划策略[J]. 电力系统保护与控制, 2019, 47(22): 9-16. ZHANG Yongming, YAO Zhili, LI Jing, et al. Electric vehicle charging station planning strategy based on probabilistic power flow calculation of distribution network[J]. Power System Protection and Control, 2019, 47(22): 9-16. (  0) 0) |
| [12] |
孙元, 丁茂生, 柳劲松, 等. 电动汽车充电设施分层递进式定址定容最优规划[J]. 电测与仪表, 2014, 51(11): 114-119. SUN Yuan, DING Maosheng, LIU Jinsong, et al. Optimal planning of the capacity and site of EV charging facilities by the analytical hierarchy process[J]. Electrical Measurement & Instrumentation, 2014, 51(11): 114-119. DOI:10.3969/j.issn.1001-1390.2014.11.024 (  0) 0) |
| [13] |
李菱, 李燕青, 姚玉海, 等. 基于遗传算法的电动汽车充电站的布局规划[J]. 华东电力, 2011, 39(6): 1004-1006. LI Ling, LI Yanqing, YAO Yuhai, et al. Layout planning of electric vehicle charging stations based on genetic algorithm[J]. East China Electric Power, 2011, 39(6): 1004-1006. (  0) 0) |
| [14] |
ZHANG H C, MOURA S J, HU Z C, et al. Joint PEV charging network and distributed PV generation planning based on accelerated generalized benders decomposition[J]. IEEE Transactions on Transportation Electrification, 2018, 4(3): 789-803. DOI:10.1109/TTE.2018.2847244 (  0) 0) |
| [15] |
ERDINC O, TASICKARAOGLU A, PATERAKIS N G, et al. Comprehensive optimization model for sizing and siting of DG units, EV charging stations, and energy storage systems[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3871-3882. DOI:10.1109/TSG.2017.2777738 (  0) 0) |
| [16] |
耿晓娜, 刘伟东, 范振亚. 光伏电源与电动汽车充电站在配电网中的选址定容[J]. 陕西电力, 2015, 43(10): 24-29. GENG Xiaona, LIU Weidong, FAN Zhenya. Locating and sizing of photovoltaic power and electric vehicle charging stations in distribution network[J]. Shaanxi Electric Power, 2015, 43(10): 24-29. (  0) 0) |
| [17] |
裴文杰, 汪沨, 谭阳红, 等. 含光伏分布式电源配电网的电动汽车充电站机会约束规划[J]. 电力系统及其自动化学报, 2017, 29(6): 45-52. PEI Wenjie, WANG Feng, TAN Yanghong, et al. Chance-constrained programming for electric vehicle charging stations in distribution network containing photovoltaic distributed generations[J]. Proceedings of the CSU-EPSA, 2017, 29(6): 45-52. DOI:10.3969/j.issn.1003-8930.2017.06.007 (  0) 0) |
| [18] |
王凌, 沈婧楠, 王圣尧, 等. 协同进化算法研究进展[J]. 控制与决策, 2015, 30(2): 193-202. WANG Ling, SHEN Jingnan, WANG Shengyao, et al. Advances in co-evolutionary algorithms[J]. Control and Decision, 2015, 30(2): 193-202. (  0) 0) |
| [19] |
魏士伟, 邓维. 基于多精英协同进化遗传算法的云资源调度[J]. 计算机应用与软件, 2021, 38(5): 274-280. WEI Shiwei, DENG Wei. Cloud resource scheduling based on multi-elite coevolutionary genetic algorithm[J]. Computer Applications and Software, 2021, 38(5): 274-280. DOI:10.3969/j.issn.1000-386x.2021.05.045 (  0) 0) |
| [20] |
管永丽. 基于概率潮流的机会约束规划方法及求解[J]. 电工电气, 2016(1): 17-20. GUAN Yongli. Chance-constrained programming methods based on probabilistic load flow[J]. Electrotechnics Electric, 2016(1): 17-20. DOI:10.3969/j.issn.1007-3175.2016.01.005 (  0) 0) |
| [21] |
孙玲玲, 赵美超, 王宁, 等. 基于电压偏差机会约束的分布式光伏发电准入容量研究[J]. 电工技术学报, 2018, 33(7): 1560-1569. SUN Lingling, ZHAO Meichao, WANG Ning, et al. Research of permitted capacity of distributed photovoltaic generation based on voltage deviation chance constrained[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1560-1569. (  0) 0) |
| [22] |
钱科军, 刘乙, 张新松, 等. 考虑电动汽车充电负荷的配电系统场景概率潮流分析[J]. 电力系统保护与控制, 2020, 48(24): 62-70. QIAN Kejun, LIU Yi, ZHANG Xinsong, et al. Scenario-based probabilistic power flow calculation of distribution systems with electric vehicle charging loads[J]. Power System Protection and Control, 2020, 48(24): 62-70. (  0) 0) |
| [23] |
BARAN M E, WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407. DOI:10.1109/61.25627 (  0) 0) |
| [24] |
徐杨杨, 张新松, 陆胜男, 等. 多重随机特性下的电动汽车充电网络机会约束规划[J]. 电力系统保护与控制, 2021, 49(6): 30-39. XU Yangyang, ZHANG Xinsong, LU Shengnan, et al. Chance constrained optimization of an electric vehicle charging network with multiple stochastic characteristics[J]. Power System Protection and Control, 2021, 49(6): 30-39. (  0) 0) |

 姜柯柯(1996), 男, 硕士在读, 研究方向为电动汽车充电网络规划(E-mail:
姜柯柯(1996), 男, 硕士在读, 研究方向为电动汽车充电网络规划(E-mail: