文章编号: 2096-3203(2023)01-0243-08 中图分类号: TM73
2. 南京工程学院电力工程学院, 江苏 南京 211167
截至2021年年底,中国并网风电3.3亿kW,并网光伏3.1亿kW[1]。新能源装机容量增加导致系统调峰需求越来越大,目前电网调峰电源仍以火电为主[2]。提高新能源消纳,火电机组须进行深度调峰改造[3-4]。深度调峰火电机组运行成本增加,但也提高了新能源的消纳,给电网带来了收益[5]。因此,如何平衡深度调峰运行成本与电网收益,研究新能源及火电机组深度调峰下的优化调度策略显得尤为必要[6]。
目前关于新能源并网与深度调峰经济性分析的研究较少。文献[7]以风电场计划出力实现的概率为约束,建立含风电场的电力系统动态经济调度模型。文献[8]使用弃风分段惩罚因子,提出考虑电网安全的风火协调优化调度策略。文献[9]建立考虑随机因素的风光荷联合概率分布函数,得到了风光荷联合作用下的经济调度模型。文献[10]以综合成本最优为目标,考虑火电机组成本、风光热设备维护成本、调峰容量购买成本、系统备用成本、环境效益和电网安全运行约束,提出风电、光伏及光热联合出力调度策略。文献[11]考虑各参与方的效益和约束条件,提出基于卡尔多改进的风火复合系统深度调峰新机制。
火电机组深度调峰优化既要考虑发电成本变化,还要考虑新能源并网所带来的收益。文献[5]建立不同调峰阶段的能耗成本模型及基于煤耗和产出的能效模型,提出火电机组深度调峰的多角度经济性方案。文献[12]使用核密度估计方法分析光伏出力的随机特性,考虑系统的调峰裕度和能耗成本,建立火电机组深度调峰经济性和灵活性的多目标优化调度模型。文献[13]计及机组损耗成本,分段表示深度调峰成本函数,建立全额消纳风电的分级深度调峰经济模型。文献[14]对东北地区深度调峰市场规则、运行实践及存在的问题进行了详细介绍。
目前,对于新能源和火电机组深度调峰下多能源互补联合调度研究较少,且大多忽略了提高新能源消纳所带来的收益。文中对大规模新能源并网下火电机组深度调峰优化调度模型进行研究,以综合成本最低为目标,引入备用容量来应对风光荷的预测误差及突发事件;考虑油耗、机组寿命、环境等因素对深度调峰经济性的影响,分别从调峰深度、新能源消纳量、火电企业收益等方面对大规模新能源并网下火电机组深度调峰优化调度进行分析。
1 深度调峰成本数学模型火电机组深度调峰分为不投油深度调峰(deep peak regulation without oil, DPR)和投油深度调峰(deep peak regulation with oil, DPRO)2个阶段[15-17]。根据《华东区域并网发电厂辅助服务管理实施细则》规定,华东某地区调度管辖的发电机组基本调峰范围为41%,规定调峰机组出力低于额定功率的60%即为深度调峰阶段[18-20]。大规模新能源并网,火电机组深度调峰将成为常态。目前,火电机组通过灵活性改造,充分挖掘火电机组调峰能力,纯凝机组出力下限能达到机组额定功率的25%~30%,一些具备先进改造技术条件的电厂的机组出力下限能达到额定功率的15%~20%[21-23]。我国电源以火电为主,随着新能源并网容量持续增长,火电机组进行深度调峰势在必行。
1.1 深度调峰运行能耗成本计算不同于常规调峰,深度调峰不仅包含燃料等显性成本,还包括锅炉稳燃的投油成本、磨损寿命损失、燃烧不充分而产生的环境污染等隐性成本,导致火电厂经济效益大幅降低。
(1) 火电机组煤耗成本。通常采用耗量特性计算煤耗成本,表达式[24]为:
| $ C_{\mathrm{c}}\left(P_{i, t}\right)=\left(a P_{i, t}^2+b P_{i, t}+c\right) S_{\text {coal }} $ | (1) |
式中:Cc(Pi, t)为机组煤耗成本;Pi, t为t时段机组i发电量;a、b、c为煤耗特性系数;Scoal为煤炭价格。
(2) 机组寿命损耗成本。用转子低周疲劳特性计算机组寿命损耗成本,参考Manson-Coffin公式,寿命损耗成本[13]为:
| $ A\left(P_{i, t}\right)=\frac{1}{2 N_{\mathrm{f}}\left(P_{i, t}\right)} \delta S_{\mathrm{u}} $ | (2) |
式中:A(Pi, t)为机组寿命损耗成本;Nf(Pi, t)为转子致裂循环周次;δ为实际运行损耗系数,投油比不投油深度调峰的损耗系数大;Su为购机成本。
参考文献[2]的计算方法,当负荷率为30%、40%、45%、50%、60%时,所计算的机组损耗率分别为0.001 9%、0.001 6%、0.001 3%、0.001 0%、0.000 6%。实际优化时,使用寿命损耗率等效计算机组寿命损耗成本。对机组损耗率数据进行线性拟合,得到不同负荷率下机组寿命损耗的计算公式为:
| $ A\left(P_{i, t}\right)=\left(-0.000\;045 P_{i, t} / P_{\mathrm{N}}+0.000\;033\right) S_{\mathrm{u}} $ | (3) |
式中:PN为机组额定容量。
(3) 投油成本。在DPRO阶段,锅炉的燃烧稳定性下降,须投油助燃以保障机组的正常运行。投油成本为:
| $ B\left(P_{i, t}\right)=O_{\operatorname{cost}} S_\mathrm{o} $ | (4) |
式中:B(Pi, t)为投油成本;Ocost为耗油量;So为油价。
(4) 环境附加成本。在DPRO阶段,投油燃烧后会产生烟尘、氮氧化物等污染物,导致火电厂废弃排污增加,而过量污染物排放将带来政府罚款。故DPRO阶段的环境附加成本为:
| $ E_{\mathrm{v}}=O_{\text {cost }} W_{\mathrm{p}}+S_{\mathrm{p}}\left(P_{i, t}, O_{\text {cost }}\right) $ | (5) |
式中:Ev为环境附加成本;Wp为单位燃油排污成本;Sp为排污惩罚函数,代表排污超标时的罚款。
基于上述成本,火电机组正常运行及深度调峰阶段的运行成本函数为:
| $ \begin{gathered} C_{\mathrm{cost}}= \\ \left\{\begin{array}{l} C_{\mathrm{c}}\left(P_{i, t}\right) \quad P_{\mathrm{a}} \leqslant P_{i, t} \leqslant P_{\max } \\ C_{\mathrm{c}}\left(P_{i, t}\right)+A\left(P_{i, t}\right) \quad P_{\mathrm{b}}<P_{i, t}<P_{\mathrm{a}} \\ C_{\mathrm{c}}\left(P_{i, t}\right)+A\left(P_{i, t}\right)+B\left(P_{i, t}\right)+E_{\mathrm{v}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_{\min } \leqslant P_{i, t} \leqslant P_{\mathrm{b}} \end{array}\right. \end{gathered} $ | (6) |
式中:Ccost为t时段机组运行成本;Pmax、Pmin分别为机组最大、最小出力;Pa为机组DPR阶段最大出力;Pb为机组DPRO阶段最大出力。
一段时间内机组启停成本为:
| $ \begin{gathered} C_{\mathrm{s}}=\sum\limits_{t=1}^T \sum\limits_{i=1}^N U_{i, t}\left[U_{i, t}\left(1-U_{i, t-1}\right) S_{i, \text { up }}+\right. \\ \left.U_{i, t-1}\left(1-U_{i, t}\right) S_{i, \text { down }}\right] \end{gathered} $ | (7) |
式中:Cs为机组启停成本;T为调度时段数;N为机组台数;Ui, t、Ui, t-1分别为t、t-1时段机组i启停状态,运行时为1,停机时为0;Si, up为机组i启动成本;Si, down为机组i停机成本。
考虑机组启停成本的深度调峰成本fcost为:
| $ \begin{gathered} f_{\text {cost }}= \\ \left\{\begin{array}{l} C_{\mathrm{c}}\left(P_{i, t}\right)+C_{\mathrm{s}} \quad P_{\mathrm{a}} \leqslant P_{i, t} \leqslant P_{\max } \\ C_{\mathrm{c}}\left(P_{i, t}\right)+A\left(P_{i, t}\right)+C_{\mathrm{s}} \quad P_{\mathrm{b}}<P_{i, t}<P_{\mathrm{a}} \\ C_{\mathrm{c}}\left(P_{i, t}\right)+A\left(P_{i, t}\right)+B\left(P_{i, t}\right)+E_{\mathrm{v}}+C_{\mathrm{s}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_{\min } \leqslant P_{i, t} \leqslant P_{\mathrm{b}} \end{array}\right. \end{gathered} $ | (8) |
以华东区域有偿调峰服务补偿标准为例,有偿调峰基准为机组负荷率的60%,常规燃煤机组按低于基本调峰下限少发电量给予补偿。补偿标准分为4档,如表 1所示。
|
|
表 1 华东区域深度调峰补偿标准 Table 1 Compensation standard of deep peak shaving in East China |
以每小时为1个单位统计周期计算火电机组深度调峰的补偿收益[14],其补偿收益为:
| $ C_{\mathrm{Rev}}=\sum\limits_{j=1}^4 t_j c_{\mathrm{p} j} P_{\mathrm{de}j} $ | (9) |
式中:CRev为补偿收益;tj为第j档有偿调峰小时数;cpj为第j档调峰补偿价格;Pdej为第j档深度调峰容量,大小为总调峰容量减去常规调峰容量。
1.3 备用容量成本计算新能源并网须要增加额外备用容量来应对预测误差与突发事件[10]。文中在深度调峰运行下引入旋转备用成本:
| $ C_{\mathrm{by}}=\sum\limits_{t=1}^T k_{\mathrm{b}}\left(L P_{\mathrm{l} t}+F P_{\mathrm{f}t}+G P_{\mathrm{g}t}\right) $ | (10) |
式中:Cby为旋转备用成本;kb为备用成本系数;L、F、G分别为负荷、风电及光伏的预测误差率;Plt、Pft、Pgt分别为t时段负荷、风电和光伏的功率。
2 火电机组深度调峰调度模型 2.1 目标函数根据火电机组深度调峰成本分析,以综合运行成本最小为目标函数,即:
| $ \min C=f_{\text {cost }}+C_{\mathrm{by}}-C_{\mathrm{Rev}} $ | (11) |
参与深度调峰,火电机组运行约束主要包括机组出力约束、系统功率平衡约束、机组爬坡约束、机组启停时间约束、新能源出力约束以及旋转备用约束[25-30],各约束条件如下。
(1) 火电机组出力约束。
| $ P_{\min } \leqslant P_{i, t} \leqslant P_{\max } $ | (12) |
(2) 系统功率平衡约束(忽略网络损耗)。
| $ \sum\limits_{i=1}^N U_{i, t} P_{i, t}+P_{\mathrm{f}t}+P_{\mathrm{g} t}=P_{\mathrm{l} t} $ | (13) |
(3) 机组爬坡约束。
| $ U_{i, t-1} P_{i, t-1}-\alpha_{\mathrm{d} i} \leqslant P_{i, t} \leqslant \alpha_{\mathrm{u} i}+U_{i, t-1} P_{i, t-1} $ | (14) |
式中:αdi、αui分别为机组i向下、向上爬坡率限制值。
(4) 机组启停时间约束。
| $ \left\{\begin{array}{l} \left(U_{i, t-1}-U_{i, t}\right)\left(T_{i, t-1}^{\mathrm{on}}-T_{\text{on}i}\right) \geqslant 0 \\ \left(U_{i, t}-U_{i, t-1}\right)\left(T_{i, t-1}^{\mathrm{off}}-T_{\text{off}i}\right) \geqslant 0 \end{array}\right. $ | (15) |
式中:Ti, t-1on、Ti, t-1off分别为机组i在t-1时段内持续运行、持续停机时间;Toni、Toffi分别为机组i的最小连续运行时间和最小停机时间。
(5) 新能源出力约束。
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{f}t} \leqslant P_{\mathrm{f}t}^{\mathrm{pre}} \\ 0 \leqslant P_{\mathrm{g} t} \leqslant P_{\mathrm{g} t}^{\text {pre }} \end{array}\right. $ | (16) |
式中:Pftpre、Pgtpre分别为风电、光伏t时段出力预测值。
(6) 系统旋转备用约束。
| $ \left\{\begin{array}{l} \sum\limits_{i=1}^N U_{i, t}\left(P_{\mathrm{M} i, t}-P_{i, t}\right) \geqslant P_{\mathrm{p} t} \\ \sum\limits_{i=1}^N U_{i, t}\left(P_{i, t}-P_{\mathrm{m} i, t}\right) \geqslant P_{\mathrm{p} t} \end{array}\right. $ | (17) |
式中:PMi, t、Pmi, t分别为机组i在t时段内的最大和最小出力;Ppt为系统t时段出力预测误差。
| $ P_{\mathrm{p} t}=L P_{\mathrm{l} t}+F P_{\mathrm{f}t}+G P_{\mathrm{g} t} $ | (18) |
机组优化调度是一个混合整数非线性规划问题,文中采用分支定界法寻求全局最优解,这种方法具有很好的收敛度,其本质是以“松弛”、“分支”、“定界”、“剪枝”为基础,通过反复迭代寻找最优解[31-32],算法流程如下。
步骤1:设定最优解的值f=+∞,求解相应的松弛问题;判断原松弛问题是否可行,若找到满足要求的最优解,则为原问题最优解;否则对原问题进行分支寻求最优解。
步骤2:分支。最优解中选择一个不符合整数约束条件的解,其值设为Bj,分别以Bj和Bj+1为上界构造2个约束条件形成2个子问题。
步骤3:定界。判断子问题是否存在整数解,若存在,找出原松弛问题的目标值并将其设为分支问题的下界。
步骤4:从待分支队列中依次选取松弛子问题进行分支求解,并且修正原问题的上、下界。
步骤5:根据剪枝原则,剪去部分无效子问题。
步骤6:检查所有分支的解及目标。
3 算例分析 3.1 算例参数以8台火电机组、1个风电场、1个光伏电站构造算例系统进行仿真分析,火电机组参数参见表 2。其中火电机组装机容量为5 200 MW(1 000 MW、800 MW、500 MW、300 MW机组各2台);新能源装机容量为2 000 MW,其中风电装机1 200 MW,光伏装机800 MW。
|
|
表 2 火电机组参数 Table 2 Parameters of thermal power unit |
参照华东地区火电机组调峰标准,机组负荷率低于60%时即表示已经进行深度调峰,机组负荷率低于45%则表示已经进行DPRO。假设所有机组的最小技术出力为30%机组额定容量,煤炭价格为545元/t,油耗成本为6 092元/t,环境附加成本为408元/t,负荷预测误差率L为12%,风电预测误差率F和光伏预测误差率G均为5%,系统备用成本系数为110元/MW。
3.2 不同调峰深度下的计算分析参照华东地区火电机组调峰标准,文中设置了5种调峰深度场景,调峰深度分别为50%、55%、60%、65%和70%,以某地24个时段内总的弃风率和弃光率来表征新能源消纳能力,采用分支定界算法求解5种不同调峰深度下的优化调度模型,计算结果如表 3所示。某地某天的日负荷预测曲线及不同调峰深度下火电机组实际出力如图 1所示。
|
|
表 3 不同调峰深度下经济调度指标 Table 3 Optimal dispatch index under different peak load regulation depths |
|
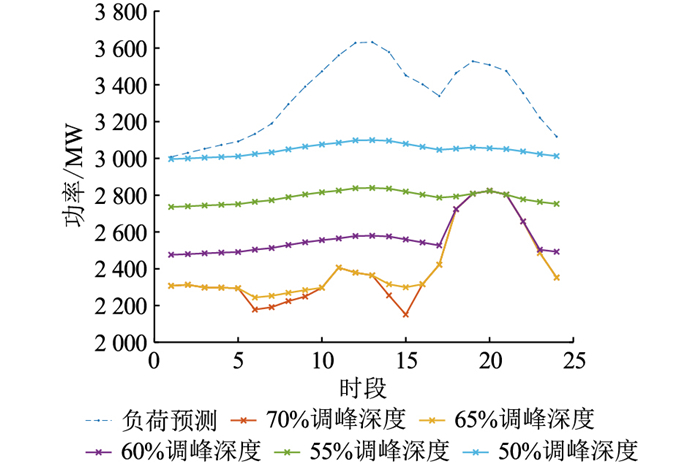
图 1 负荷预测功率及火电机组出力 Fig. 1 Load forecast power and thermal power unit output |
由图 1可知,当火电机组调峰深度为50%、55%、60%时,系统负荷的峰谷差明显降低。结合表 3得出的经济调度指标可以看出,大规模风电、光伏并网能够显著降低火电机组的上网电量,从而降低系统的运行成本。但在深度调峰运行期间,火电机组会产生额外的寿命损耗和投油成本,以及环境附加成本,在调峰深度达到60%时,机组的经济性明显下降;在上网电量减少的情况下,尽管有政府的调峰辅助服务补偿收益,但并不能降低火电厂的单位发电成本。
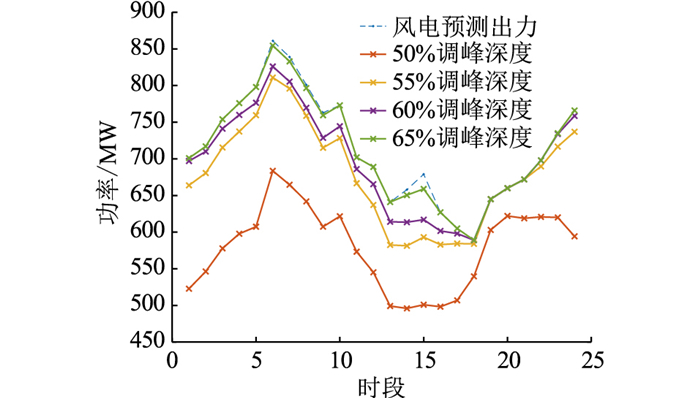
风电、光伏出力预测曲线及不同调峰深度下风电、光伏的并网消纳功率分别如图 2、图 3所示。在计及电网约束条件下,调峰深度和新能源消纳量成正相关。结合表 3可知:调峰深度为50%时,单位发电成本最低,弃风、弃光率分别为16.9%和30.3%;当调峰深度增加至60%时,弃风、弃光现象明显减少。可见,当调峰深度大于55%时,新能源消纳率将超过90%,新能源的消纳得到明显改善。
|
图 2 风电预测功率及并网消纳功率 Fig. 2 Prediction wind power and grid connected power consumption |
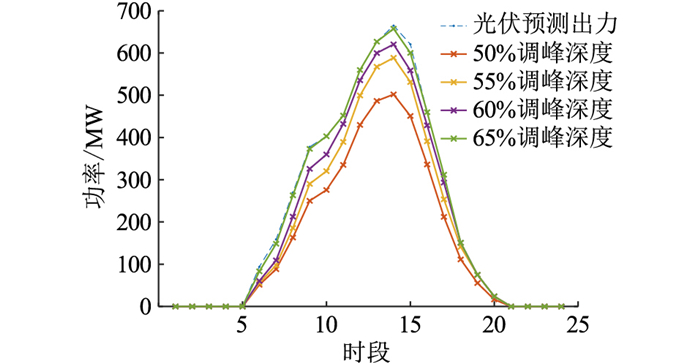
|
图 3 光伏预测功率及并网消纳功率 Fig. 3 Photovoltaic prediction power and grid connected power consumption |
调峰深度为55%时各火电机组出力见图 4。此时,机组4出力变化最为明显,其承担着新能源并网下系统主要的调峰压力。结合图 1可知,调峰深度为55%时火电机组出力平稳,减少了机组频繁动作而带来的机械损耗和运行损耗。同时,新能源消纳量也保持在较高的水平。
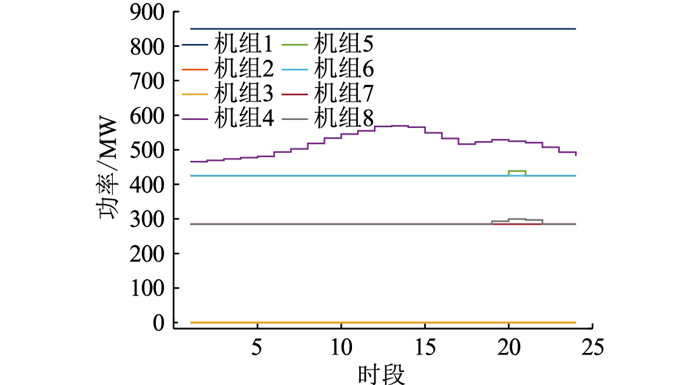
|
图 4 55%调峰深度下火电机组出力 Fig. 4 Output of thermal power unit under 55% peak load regulation depth |
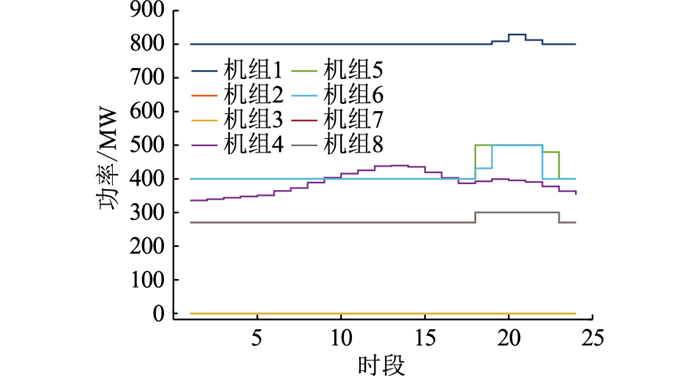
调峰深度为60%时各火电机组出力见图 5。在18—24时段各火电机组出力都出现较小波动,因为调峰深度的增加使风电、光伏的上网电量增加,对比负荷预测值和风电、光伏出力预测,在20时段光伏出力降为0,而风电出力预测值逐渐增加,所以此时段火电机组须要增加出力来平衡功率,与图 1中18—24时段火电机组出力出现波峰情况一致。
|
图 5 60%调峰深度下火电机组出力 Fig. 5 Output of thermal power unit under 60% peak load regulation depth |
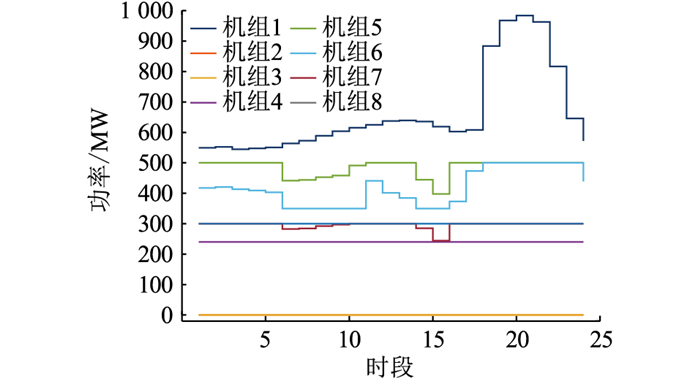
调峰深度为65%时各火电机组出力见图 6。此时,新能源基本被全部消纳,各机组出力出现剧烈波动,机组上下爬坡更频繁,在夜晚用电高峰尤其显著。虽然进一步提高了新能源消纳能力,但此时系统机组运行的安全性却有所下降。
|
图 6 65%调峰深度下火电机组出力 Fig. 6 Output of thermal power unit under 65% peak load regulation depth |
综上,如果允许弃风弃光,当火电机组调峰深度控制在55%~60%时,既能获得比较理想的新能源消纳水平,又能够避免机组出力的大幅度波动,提升调峰时系统机组的安全性。
3.3 火电企业收益分析假定以上8台机组隶属于同一个火电企业,在不考虑其他成本的前提下,火电企业上网电价为0.3元/(kW ·h)。以当前调度日为例,计算火电企业日收益SR:
| $ S_{\mathrm{R}}=\left(S_{\mathrm{p}}-S_{\mathrm{pl}}\right) P_{\mathrm{w}} $ | (19) |
式中:Sp为单位上网电价;Sp1为单位发电成本;Pw为当天上网电量。
计算不同调峰深度下火电企业整体日收益,结果如表 4所示。
|
|
表 4 火电企业日收益 Table 4 Daily income of thermal power enterprises |
由表 4可以看出,电网经济调度以系统运行成本最小为目标,忽略火电机组深度调峰所增加的其他成本。随着调峰深度的增加,火电企业的收益逐渐下降。调峰深度从50%增加至70%时,火电企业收益减少了212.1万元,不到50%调峰深度收益的一半,难以调动火电企业参与深度调峰的积极性。考虑新能源消纳量及带来的环境效益,深度调峰期间火电企业将牺牲自身利益。
4 结论基于深度调峰下火电机组运行状态和特性,文中建立了火电机组不同调峰阶段的成本模型,引入备用容量成本来应对新能源出力预测的波动性和一些突发事件所带来的额外成本,研究风电、光伏并网下火电机组深度调峰优化调度问题。通过算例分析得到以下结论:
(1) 从算例仿真看,火电机组深度调峰运行能显著提升新能源消纳量,随着调峰深度的增加,火电企业的单位发电成本增加,其增加的主要原因是深度调峰期间获得的调峰收益不能弥补机组磨损、投油成本和环境附加成本。在进行深度调峰优化调度时,仅以火电机组煤耗特性来表征火电成本的经济优化调度具有一定局限性。这对规模化新能源接入的调峰控制具有一定借鉴意义。
(2) 火电机组深度调峰能够有效促进新能源消纳,减少系统负荷峰谷差。但随着调峰深度的增加,机组出力会出现剧烈波动,导致系统运行安全性下降。在制定深度调峰调度计划时,应对系统安全性给予考虑。
(3) 在文中设定的深度调峰补偿标准下,对于算例系统,即使考虑深调收益,火电机组的整体效益仍然很低;同时,火电企业还要承担深度调峰过程中所产生的事故风险。在进行调峰调度时,应制定一个合理双赢的补偿制度,如提高有偿调峰服务的补偿标准、对进行灵活性改造的机组进行补偿、建立电力用户分担调峰辅助服务费用等,提升火电企业参与深度调峰的积极性,推动更多火电企业参与深度调峰,促进新能源消纳。
致谢
本文得到江苏方天电力技术有限公司科技项目(KJ201926)资助,谨此致谢!
| [1] |
国家统计局. 中华人民共和国2021年国民经济和社会发展统计公报[EB/OL]. [2022-06-28]. http://www.stats.gov.cn/xxgk/sjfb/zxfb2020/202202/t20220228_1827971.html. National Bureau of Statistics. Statistical bulletin of the People's Republic of China on national economic and social development in 2021[EB/OL]. [2022-06-28]. http://www.stats.gov.cn/xxgk/sjfb/zxfb2020/202202/t20220228_1827971.html. (  0) 0) |
| [2] |
邹兰青. 规模风电并网条件下火电机组深度调峰多角度经济性分析[D]. 北京: 华北电力大学, 2017. ZOU Lanqing. Multi-angle economic analysis for deep peak regulation of thermal units with large scale wind power connected power system[D]. Beijing: North China Electric Power University, 2017. (  0) 0) |
| [3] |
杨寅平, 曾沅, 秦超, 等. 面向深度调峰的火电机组灵活性改造规划模型[J]. 电力系统自动化, 2021, 45(17): 79-88. YANG Yinping, ZENG Yuan, QIN Chao, et al. Planning model for flexibility reformation of thermal power units for deep peak regulation[J]. Automation of Electric Power Systems, 2021, 45(17): 79-88. (  0) 0) |
| [4] |
王淑云, 娄素华, 吴耀武, 等. 计及火电机组深度调峰成本的大规模风电并网鲁棒优化调度[J]. 电力系统自动化, 2020, 44(1): 118-125. WANG Shuyun, LOU Suhua, WU Yaowu, et al. Robust optimal dispatch of large-scale wind power integration considering deep peak regulation cost of thermal power units[J]. Automation of Electric Power Systems, 2020, 44(1): 118-125. (  0) 0) |
| [5] |
林俐, 邹兰青, 周鹏, 等. 规模风电并网条件下火电机组深度调峰的多角度经济性分析[J]. 电力系统自动化, 2017, 41(7): 21-27. LIN Li, ZOU Lanqing, ZHOU Peng, et al. Multi-angle economic analysis on deep peak regulation of thermal power units with large-scale wind power integration[J]. Automation of Electric Power Systems, 2017, 41(7): 21-27. (  0) 0) |
| [6] |
赵书强, 吴杨, 李志伟, 等. 考虑风光出力不确定性的电力系统调峰能力及经济性分析[J]. 电网技术, 2022, 46(5): 1752-1761. ZHAO Shuqiang, WU Yang, LI Zhiwei, et al. Analysis of power system peaking capacity and economy considering uncertainty of wind and solar output[J]. Power System Technology, 2022, 46(5): 1752-1761. (  0) 0) |
| [7] |
张海峰, 高峰, 吴江, 等. 含风电的电力系统动态经济调度模型[J]. 电网技术, 2013, 37(5): 1298-1303. ZHANG Haifeng, GAO Feng, WU Jiang, et al. A dynamic economic dispatching model for power grid containing wind power generation system[J]. Power System Technology, 2013, 37(5): 1298-1303. (  0) 0) |
| [8] |
徐帆, 王颖, 杨建平, 等. 考虑电网安全的风电火电协调优化调度模型及其求解[J]. 电力系统自动化, 2014, 38(21): 114-120. XU Fan, WANG Ying, YANG Jianping, et al. Generation scheduling model and application for wind-thermal power system considering security constraints[J]. Automation of Electric Power Systems, 2014, 38(21): 114-120. (  0) 0) |
| [9] |
冉晓洪, 苗世洪, 刘阳升, 等. 考虑风光荷联合作用下的电力系统经济调度建模[J]. 中国电机工程学报, 2014, 34(16): 2552-2560. RAN Xiaohong, MIAO Shihong, LIU Yangsheng, et al. Modeling of economic dispatch of power system considering joint effect of wind power, solar energy and load[J]. Proceedings of the CSEE, 2014, 34(16): 2552-2560. (  0) 0) |
| [10] |
崔杨, 杨志文, 张节潭, 等. 计及综合成本的风电-光伏-光热联合出力调度策略[J]. 高电压技术, 2019, 45(1): 269-275. CUI Yang, YANG Zhiwen, ZHANG Jietan, et al. Scheduling strategy of wind power-photovoltaic power-concentrating solar power considering comprehensive costs[J]. High Voltage Engineering, 2019, 45(1): 269-275. (  0) 0) |
| [11] |
菅学辉, 张利, 杨立滨, 等. 高比例风电并网下基于卡尔多改进的深度调峰机制[J]. 电力系统自动化, 2018, 42(8): 110-118. JIAN Xuehui, ZHANG Li, YANG Libin, et al. Deep-peak regulation mechanism based on kaldor improvement under high-penetration wind power[J]. Automation of Electric Power Systems, 2018, 42(8): 110-118. (  0) 0) |
| [12] |
应益强, 王正风, 吴旭, 等. 计及新能源随机特性的电网深度调峰多目标策略[J]. 电力系统保护与控制, 2020, 48(6): 34-42. YING Yiqiang, WANG Zhengfeng, WU Xu, et al. Multi-objective strategy for deep peak shaving of power grid considering uncertainty of new energy[J]. Power System Protection and Control, 2020, 48(6): 34-42. (  0) 0) |
| [13] |
林俐, 田欣雨. 基于火电机组分级深度调峰的电力系统经济调度及效益分析[J]. 电网技术, 2017, 41(7): 2255-2263. LIN Li, TIAN Xinyu. Analysis of deep peak regulation and its benefit of thermal units in power system with large scale wind power integrated[J]. Power System Technology, 2017, 41(7): 2255-2263. (  0) 0) |
| [14] |
刘永奇, 张弘鹏, 李群, 等. 东北电网电力调峰辅助服务市场设计与实践[J]. 电力系统自动化, 2017, 41(10): 148-154. LIU Yongqi, ZHANG Hongpeng, LI Qun, et al. Design and practice of peak regulation ancillary service market for northeast China power grid[J]. Automation of Electric Power Systems, 2017, 41(10): 148-154. (  0) 0) |
| [15] |
李铁, 李正文, 杨俊友, 等. 计及调峰主动性的风光水火储多能系统互补协调优化调度[J]. 电网技术, 2020, 44(10): 3622-3630. LI Tie, LI Zhengwen, YANG Junyou, et al. Coordination and optimal scheduling of multi-energy complementary system considering peak regulation initiative[J]. Power System Technology, 2020, 44(10): 3622-3630. (  0) 0) |
| [16] |
邓婷婷, 娄素华, 田旭, 等. 计及需求响应与火电深度调峰的含风电系统优化调度[J]. 电力系统自动化, 2019, 43(15): 34-41. DENG Tingting, LOU Suhua, TIAN Xu, et al. Optimal dispatch of power system integrated with wind power considering demand response and deep peak regulation of thermal power units[J]. Automation of Electric Power Systems, 2019, 43(15): 34-41. (  0) 0) |
| [17] |
杨力俊, 潘伟, 田闻旭. 计及需求响应和风光不确定性的微电网多目标优化模型[J]. 电力需求侧管理, 2022, 24(3): 1-8. YANG Lijun, PAN Wei, TIAN Wenxu. Multi-objective optimization model of microgrid considering demand response and uncertainty of wind power and photovoltaic[J]. Power Demand Side Management, 2022, 24(3): 1-8. (  0) 0) |
| [18] |
国家能源局华东监管局. 关于修订印发《华东电力调峰辅助服务市场运营规则》的通知[Z]. 上海: 国家能源局华东监管局, 2022. East China Energy Regulation Bureau of National Energy Administration of the People's Republic of China. Modification and notice on issuing the operation rules of east China electric power peak shaving auxiliary service market[Z]. Shanghai: East China Energy Regulation Bureau of NEA, 2022. (  0) 0) |
| [19] |
杨萌, 张粒子, 杨巍巍. 考虑可再生能源参与的调峰交易机制设计[J]. 电力系统自动化, 2018, 42(20): 45-52, 79. YANG Meng, ZHANG Lizi, YANG Weiwei. Design of trading mechanism for peak shaving service considering participation of renewable energy[J]. Automation of Electric Power Systems, 2018, 42(20): 45-52, 79. (  0) 0) |
| [20] |
LIANG J, ZHAO X, YANG S. Collaborative optimization model of renewable energy development considering peak shaving costs of various flexibility resources[J]. Global Energy Interconnection, 2021, 4(4): 394-404. (  0) 0) |
| [21] |
向红吉. 考虑风电接入和负调峰能力的机组组合优化研究[D]. 成都: 西南交通大学, 2017. XIANG Hongji. Research on unit commitment optimization considering wind and negative peak load regulation ability[D]. Chengdu: Southwest Jiaotong University, 2017. (  0) 0) |
| [22] |
付蔷. 促进风电消纳的火电灵活性改造深度及经济效益研究[D]. 北京: 北京交通大学, 2018. FU Qiang. Study on depth and economic benefits of thermal power flexibility transformation to promote wind power consumption[D]. Beijing: Beijing Jiaotong University, 20 18. (  0) 0) |
| [23] |
魏文, 姜飞, 戴双凤, 等. 计及需求侧储能事故备用风险与火电机组深度调峰的经济优化研究[J]. 电力系统保护与控制, 2022, 50(10): 154-163. WEI Wen, JIANG Fei, DAI Shuangfeng, et al. Economic optimization of deep peak regulation of thermal power units taking intoaccount the risk of emergency storage on the demand side[J]. Power System Protection and Control, 2022, 50(10): 154-163. (  0) 0) |
| [24] |
LIANGH J, LIU Y G, LI F Z, et al. Dynamic economic/emission dispatch including PEVs for peak shaving and valley filling[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2880-2890. (  0) 0) |
| [25] |
张敏, 王建学, 王秀丽, 等. 面向新能源消纳的调峰辅助服务市场双边交易机制与模型[J]. 电力自动化设备, 2021, 41(1): 84-91. ZHANG Min, WANG Jianxue, WANG Xiuli, et al. Bilateral trading mechanism and model of peak regulation auxiliary service market for renewable energy accommodation[J]. Electric Power Automation Equipment, 2021, 41(1): 84-91. (  0) 0) |
| [26] |
郝艺博, 杜锡力, 李笑竹, 等. 考虑储能性能差异的新能源场站群共享储能交易模式[J]. 发电技术, 2022, 43(5): 687-697. HAO Yibo, DU Xili, LI Xiaozhu, et al. Shared energy storage trading mode of new energy station group considering energy storage performance difference[J]. Power Generation Technology, 2022, 43(5): 687-697. (  0) 0) |
| [27] |
高春辉, 肖冰, 尹宏学, 等. 新能源背景下储能参与火电调峰及配置方式综述[J]. 热力发电, 2019, 48(10): 38-43. GAO Chunhui, XIAO Bing, YIN Hongxue, et al. Energy storage participating in thermal power peaking and configuration in background of new energy: a review[J]. Thermal Power Generation, 2019, 48(10): 38-43. (  0) 0) |
| [28] |
陈晓光, 杨秀媛, 卜思齐, 等. 考虑经济功能性的风电场储能系统容量配置[J]. 发电技术, 2022, 43(2): 341-352. CHEN Xiaoguang, YANG Xiuyuan, BU Siqi, et al. Capacity allocation of wind farm energy storage system considering economic function[J]. Power Generation Technology, 2022, 43(2): 341-352. (  0) 0) |
| [29] |
陈长青, 李欣然, 张冰玉, 等. 基于多时间尺度的储能调峰调频协同控制策略[J]. 电力系统保护与控制, 2022, 50(5): 94-105. CHEN Changqing, LI Xinran, ZHANG Bingyu, et al. Energy storage peak and frequency modulation cooperative control strategy based on multi-time-scale[J]. Power System Protection and Control, 2022, 50(5): 94-105. (  0) 0) |
| [30] |
程基峰, 贠靖洋, 严正, 等. 富余风电参与调峰权交易的电力市场均衡分析[J]. 电网技术, 2019, 43(8): 2702-2710. CHENG Jifeng, YUN Jingyang, YAN Zheng, et al. Equilibrium analysis of peak regulation right trading market between wind farms and thermal power plants considering deep peak regulation[J]. Power System Technology, 2019, 43(8): 2702-2710. (  0) 0) |
| [31] |
丁涛, 郭庆来, 柏瑞, 等. 考虑风电不确定性的区间经济调度模型及空间分支定界法[J]. 中国电机工程学报, 2014, 34(22): 3707-3714. DING Tao, GUO Qinglai, BO Rui, et al. Interval economic dispatch model with uncertain wind power injection and spatial branch and bound method[J]. Proceedings of the CSEE, 2014, 34(22): 3707-3714. (  0) 0) |
| [32] |
DING T, BO R, LI F X, et al. A bi-level branch and bound method for economic dispatch with disjoint prohibited zones considering network losses[J]. IEEE Transactions on Power Systems, 2015, 30(6): 2841-2855. (  0) 0) |
2. School of Electric Power Engineering, Nanjing Institute of Technology, Nanjing 211167, China

 于国强(1979), 男, 硕士, 高级工程师, 从事电厂热工自动化控制与应用工作(E-mail:
于国强(1979), 男, 硕士, 高级工程师, 从事电厂热工自动化控制与应用工作(E-mail: