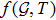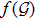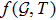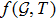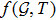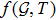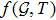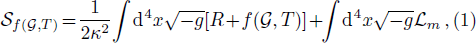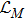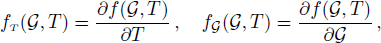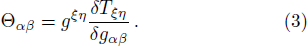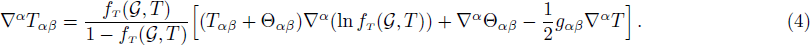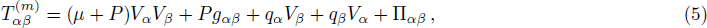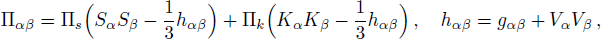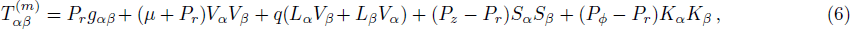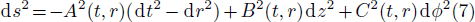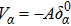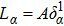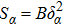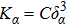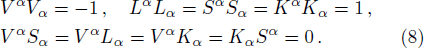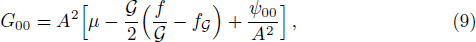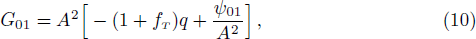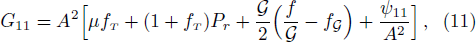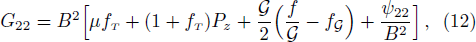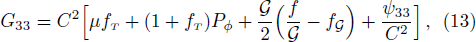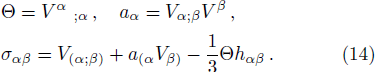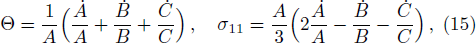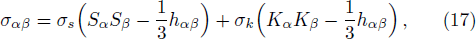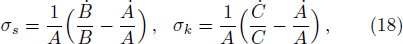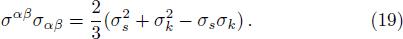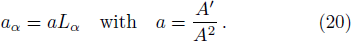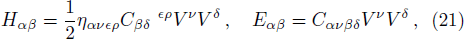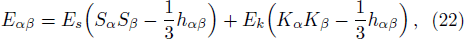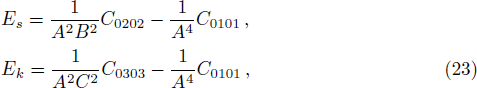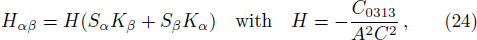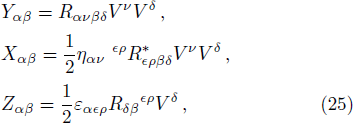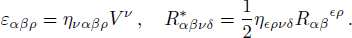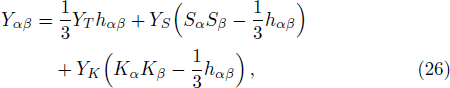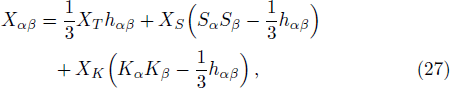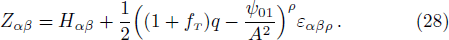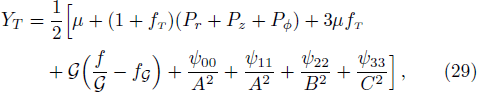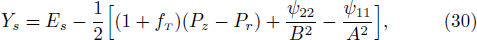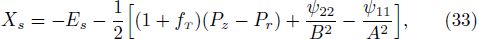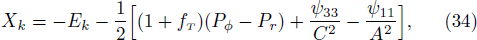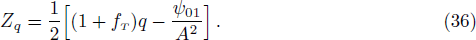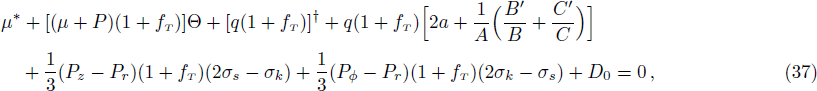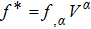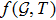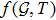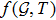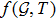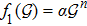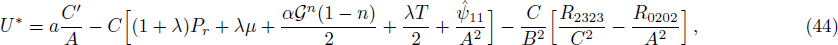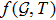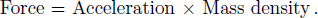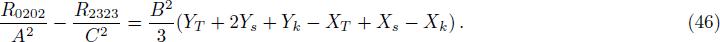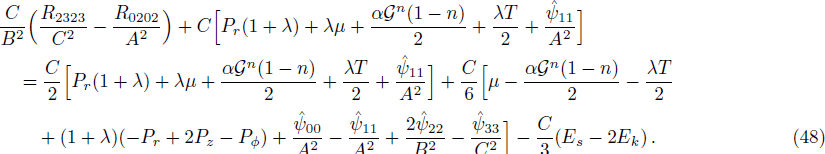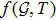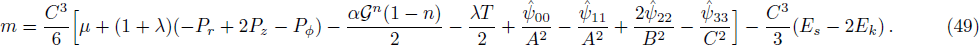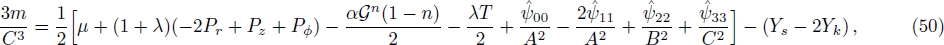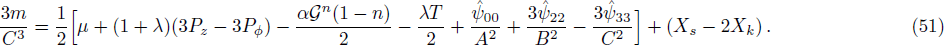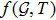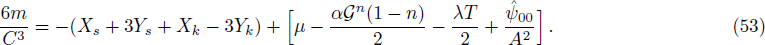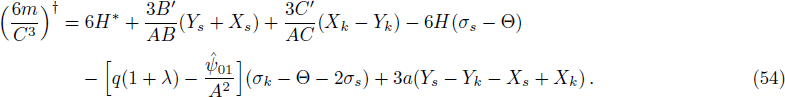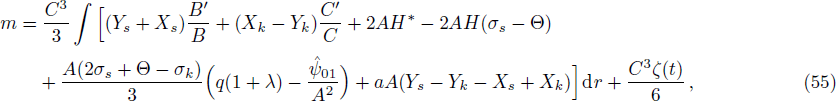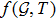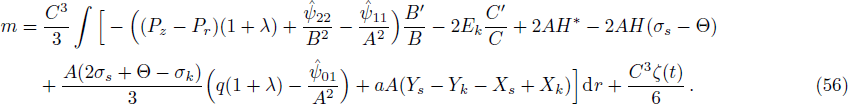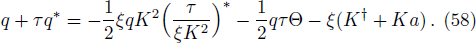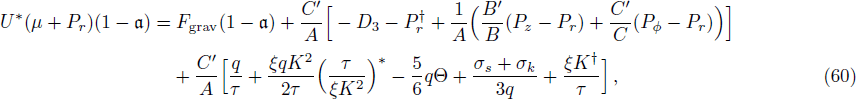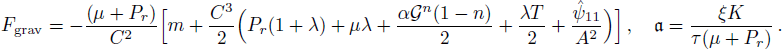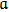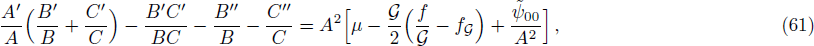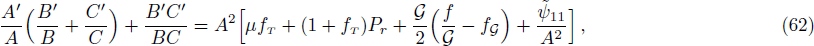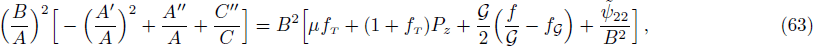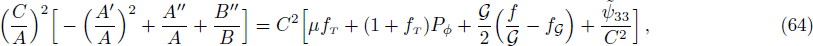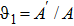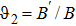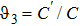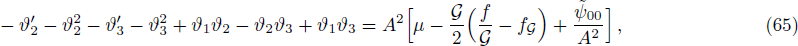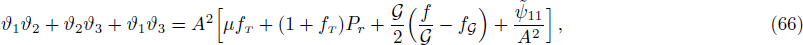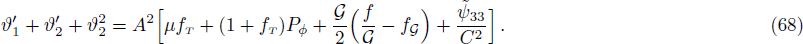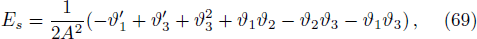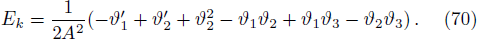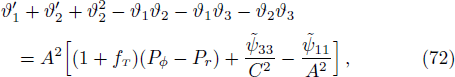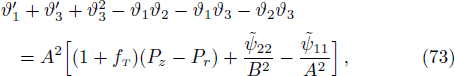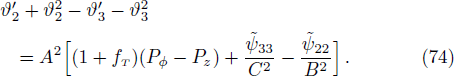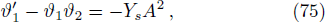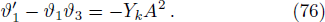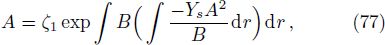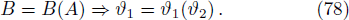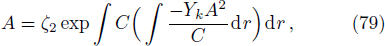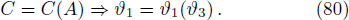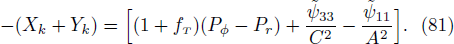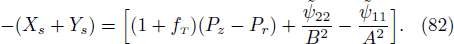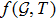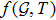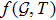As indicated by late perceptions, the expansion of universe is amongst the most stunning disclosure in this new age of astronomy. In order to examine the gravitational stellar framework, relativistic consequences must be taken into consideration. Neutron stars, hybrid stars, white dwarfs, black holes are lucid examples of relativistic stellar structures in which these effects have essential outcomes. So it is important to consider observationally applicable gravitational theories in order to study these systems. Further, numerous intriguing outcomes originating from observational elements of cosmic microwave background radiations and type Ia Supernova^[1–3] have made an incredible revolution in the recent past, therefore opening a new platform for research. These observations exhibit that the universe is expanding at an accelerating rate. Recent results generating from the BICEP2 experiment,^[4–6] the Planck satellite,^[7–9] sloan digital sky surveys^[10] and the wilkinson microwave anisotropy probe^[11–12] reveal that 68% of the universe comprises dark energy, while the dark and ordinary matter is 27% and 5% respectively. The dark energy contains a large amount of negative pressure and it is believed that this mysterious energy causes the expansion of our cosmos. It has also been proved that the dark energy causes accretion onto blackholes as well as wormholes.^[13] Chattopadhyay et al.^[14] studied the accretion of three holographic dark energies onto wormholes in modified gravity and concluded that when dark energies accrete on wormhole, it causes an increase in the mass of wormhole in the phantom phase of the universe. Some important modified gravitational theories are introduced in the recent two decades. These modified theories can well explain the dark energy issue. The modified gravity theories are introduced after generalizing the Einstein-Hilbert action to discuss the accelerating expansion of our universe. Nojiri and Odintsov^[15] explained that how these theories of gravity are significant in investigating the evolutionary stages of our universe. The simplest gravity theory is f(R), which can be obtained by replacing f(R) with Ricci scalar in Einstein Hilbert action. Some important research related to modified gravitational theories can be seen in Refs. [16–27].

Modified Guass-Bonnet gravity is another attractive gravitational theory which has grabbed importance over the recent couple of years and it is trusted that the astronomical expansion might be noticed in 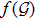gravity due to the existence of de-Sitter point.^[28–32] The Guass-Bonnet four dimensional topological invariant provides information about the topology of the space-time manifold on which the theory is formulated.^[33] Gauss-Bonnet invariant is strictly connected with the trace anomaly and may play an important role in the early time expansion of the universe. The remarkable quality of this theory is that the Gauss-Bonnet term plays an essential part as it may ignore ghost contributions and regularize the gravitational action.^[34] Nojiri and Odintsov^[35] clarified that the cosmological order of matter dominance deceleration-acceleration transformation and accelerating stage could appear in modified gravity. A further generalized theory that has gained prominence over recent couple of years is 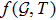theory of gravity where f is generic function of Gauss-Bonnet topological invariant and T the trace of stress energy tensor.^[27] Shamir and Ahmad^[36] explored some exact solutions through Noether symmetry approach and used anisotropic distributions to explore cosmological models in 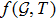gravity. Some interesting work has been done recently in this theory in different contexts.^[37–39]

The orthogonal decomposition of curvature tensor was first introduced by Bel.^[40] Gomez-Lobo^[41] carried out the orthogonal splitting of Bel and Bel-Robinson tensor and also obtained the particular canonical forms valid for some Petrov types by expressing the orthogonal decomposition in terms of electric and magnetic parts of Weyl tensor. Herrera et al.^[42] used this idea to build up a connection between structure scalars and fundamental properties of fluid. Herrera and his collaborators^[43] analyzed the physical meaning of the scalars functions for charged spherical fluids. Herrera et al.^[43] found the structure scalars for cylindrically symmetric relativistic fluids and also obtained the solutions to Einstein equations with static anisotropic cylindrical symmetry. Sharif and Yousaf^[44] discussed structure scalars for cylindrically self gravitating system in f(R) gravity. Yousaf et al.^[45] studied the influence of f(R, T) gravity on the dynamics of radiating spherical fluids and concluded that the evolutionary stages of relativistic stellar systems could be explored with the help of modified structure scalars. Recently, we^[46] investigated the structure scalars in the context of theory of gravity to analyze the evolutionary phases of compact objects. The cylindrical symmetry is the next closest approach to nature after spherical symmetry. In fact cylindrical solutions are related to cosmic strings and the family of solutions with constant Ricci scalar in f(R) gravity are associated with a cosmic string.^[47] Moreover, in Horava-Lifshitz gravity static cylindrically symmetric solutions describe cosmic string as a special case.^[48] Houndjo et al.^[49] explored the cylindrically symmetric solutions in f(T) gravity, it was found that the solution metric is similar to Levi-Civita spacetime with mass parameter having both positive and negative values and for a special case the spacetime is conical with a deficit angle corresponding to an exterior metric of a cosmic string. Thus it looks an interesting task to further explore the cylindrical symmetry and role of structure scalars in the context of modified gravity.

The main purpose of this work is to investigate the impacts of fluid variables and 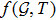corrections on the structure and evolution of radiating cylindrical compact object. The motivation to attempt this work is to understand the physical significance of scalar quantities and how these scalar functions play an important role in exploring the evolutionary behaviors of compact objects in the presence of modified gravity. The plan of paper is as follows: In Sec. 2, we develop the modified field equations for non-radiating cylindrically symmetric spacetime with anisotropic fluid distribution. Modified scalar functions as well as conservation equations are constructed in Sec. 3. Section 4 contains the formulations of mass function and transport equation. Static anisotropic cylinders and their solutions are demonstrated in Sec. 5. The conclusion of the work is presented in the last section.

Modified Gauss-Bonnet theories of gravity have a wide space to explore new results and making better approaches to deal with different issues. It has been demonstrated that modified Gauss-Bonnet gravity has numerous favorable advantages when contrasted with other gravitational theories.^[32] In addition, the modified Gauss-Bonnet gravity is very intriguing to explain the astronomical acceleration of universe with more freedom and instabilities do not exist in this theory. Specifically, the recently presented 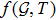gravity has picked up prominence because of the addition of matter content alongside Gauss-Bonnet invariant in the shape of a bivariate function. The general action for 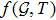gravity is defined as^{[27, 46]}
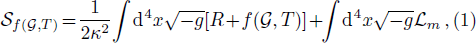
where R is the Ricci scalar, 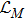indicates the Lagrangian coupled with matter, g is the determinant of metric tensor, and κ represents the coupling constant. Variation of action (1) with respect to metric tensor gives the following field equations^[27,46]
where
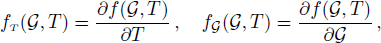
and Θ_αβ can be found as follows
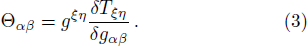
The covariant divergence of Eq. (2) is given as
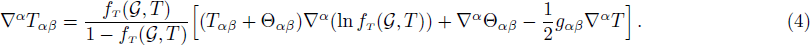
We consider a non-static collapsing cylinder coupled with dissipative and anisotropic fluid distribution. Moreover, we assume that the fluid configuration is bounded by a timelike cylindrical surface Σ. Thus, the mathematical expression of energy momentum tensor is given by
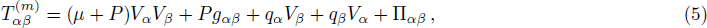
where μ indicates the energy density, P signifies the principle pressure,
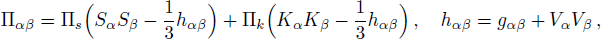
and q_α = qL_α is the heat flux. The energy momentum tensor can be written in an alternative form as
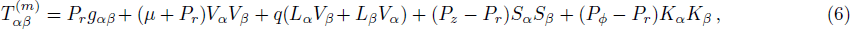
where P_z − P_r ≡ Π_s, P_φ − P_r ≡ Π_k, and P ≡ (P_r + P_z + P_φ)/3. We further consider a non-static cylindrically symmetric spacetime
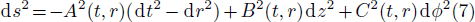
composed of radiating anisotropic fluid configuration. To indicate cylindrical symmetry, we implement the following constraints on the coordinates
where we consider C = 0 at r = 0, which signifies non singular axis. The four vectors 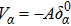, , 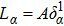, 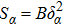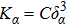satisfy
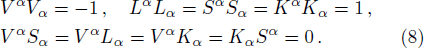
The non zero components of field equations using spacetime (7) are given as




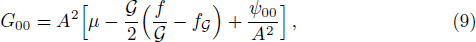
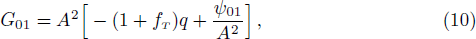
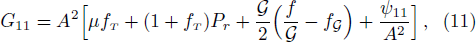
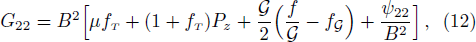
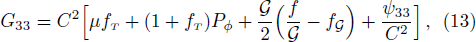
where ψ₀₀, ψ₀₁, ψ₁₁, ψ₂₂, and ψ₃₃ are mentioned in Appendix A. The shear σ_{α β}, expansion Θ, and four acceleration a^α of the fluid are given by^[50]
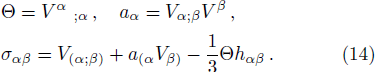
Using line element (7) and Eq. (14), we obtain

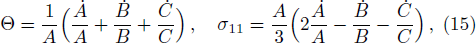
where primes and dots represent partial derivatives with respect to r and t respectively. We can also signify the shear tensor in another form as
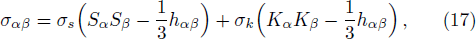
where

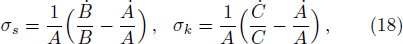
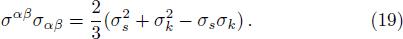
The four acceleration of the fluid is given as
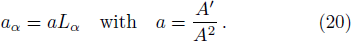
The usual components of Weyl tensor can be decomposed in magnetic and electric parts. In contrast to the spherically symmetric case, the magnetic component of Weyl tensor does not vanish. The magnetic and electric parts of Weyl tensor are defined as
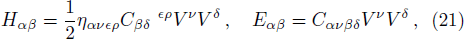
where η_ανϵρ is the Levi-Civita tensor. The electric and magnetic parts of Weyl tensor can be rewritten as
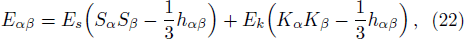
where

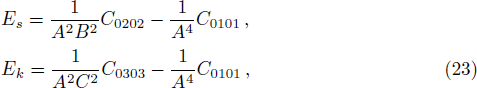
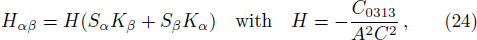
where C0101, C0202, C0303, and C0313 are given in Appendix B.

We orthogonally split the Riemann curvature tensor in order to develop the formalism for structure scalars. We get three tensors X_αβ, Y_αβ, and Z_αβ by the decomposition of curvature tensor which further divide into their trace and trace-free components i.e., X_T, X_s, X_k, Y_T, Y_s, Y_k, Z_H, and Z_q also known as structure scalars. The tensors are defined as^[42]
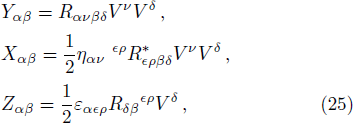
where
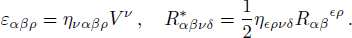
Now writing these tensors by means of matter variables and the magnetic and electric components of Weyl tensor,^[51] we get


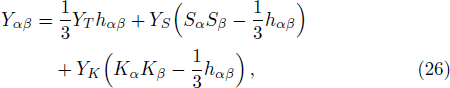
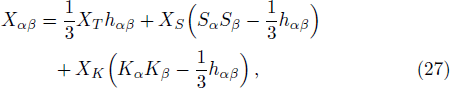
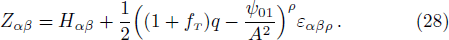
The above tensors can be written as their trace and traceless parts. Using Eqs. (9)–(13), (23), and (24), we obtain







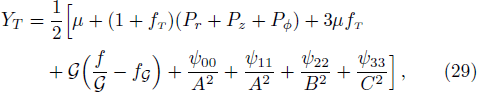
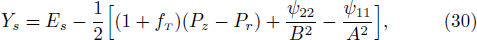
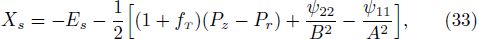
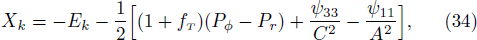
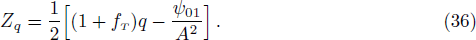
This shows that these scalars functions, which are eight in number are related to modelling of collapsing celestial body in gravity. The expression of covariant derivative of effective stress energy tensor for gravity is defined as Eq. (4), which would give two equations of motion in theory. Making use of G^αβ_;β = 0 and Eqs. (9)–(13) with α = 0, 1, Eq. (4) gives

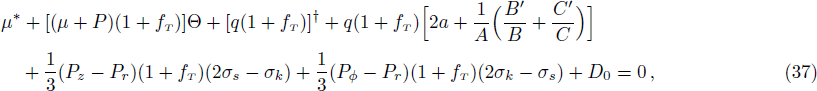
where D₀, D₁ are the dark source variables, given in Appendix B and the operators are defined as 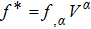and . Some important equations which are necessary to discuss the dynamics of relativistic cylindrical geometry can be acquired by using Eqs. (9)–(13) and Eqs. (37)–(46). Herrera et al.^[51] determined these equations in general relativity and these equations were also computed by Sharif and Yousaf^[44] in f(R) gravity. The corresponding relations in 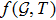gravity are

The above two equations relates structure scalars Y_s, Y_k, X_s, X_k with energy density inhomogeneity and consequently present a definition of inhomogeneity factor in terms of some scalar functions. These equations give a relationship between 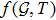extra curvature terms, fluid parameters and structure scalars.

4 Dynamical and Transport Equations, Mass Function and 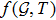Gravity

The selection of model holds great importance to investigate a number of obscure features of gravitational physics. One can choose different 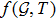models for further exploration. However, we have chosen the following model for the sake of simplicity^[46]
with 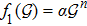and f₂(T) = λ T, α and λ being arbitrary real numbers. The four-velocity U of collapsing cylindrical system can be acquired by varying the areal radius with respect to proper time.
Using Eqs. (11) and (41), we get
This equation can be organized in form of Rieman curvature tensor as
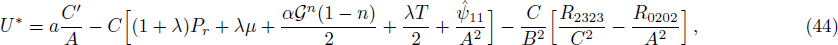
where R₀₂₀₂ and R₂₃₂₃ are given in Appendix B. Substituting the value of a from the above equation in Eq. (38), we have
where D₃ represents the dark source variables merged with 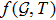corrections. The above equation contains four types of terms. The terms on the left side are the product of inertial mass (density) and proper time derivative of fluid velocity U. There are three different terms on the right side. The first term exemplifies impacts of gravitational force. The second one incorporates hydrodynamics force because it includes pressure gradient with anisotropic distributions, while the third term represents the dissipative process. Thus, the above equation has the Newtonian form
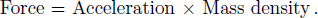
Now we continue to analyze mass function with cylindrically symmetric distributions in gravity. For this motive, we write R₀₂₀₂/A² − R₂₃₂₃/C² in terms of scalar functions.
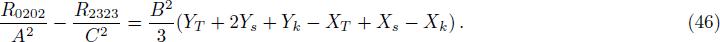
Using Eqs. (29)–(34), we have
Making use of the above equation, we obtain
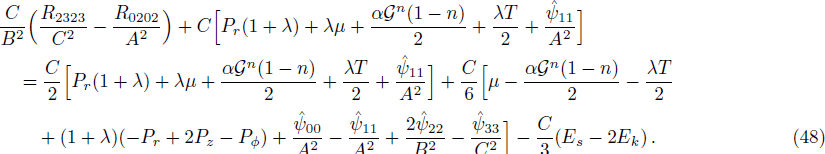
In order to characterize the mass function, we apply the general relativity procedure given in Ref. [52]. We further suppose that pressure impact remains the same as in spherically symmetric case, which gives the conceivable generalization of Misner-Sharp mass function for cylindrically symmetric system with 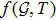configurations and is given as
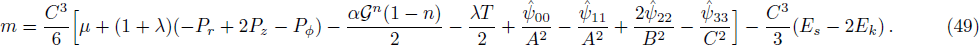
Using Eqs. (30), (31), (33), and (34), the above expression can be written as

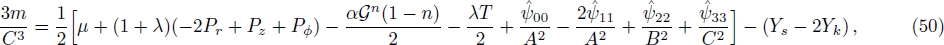
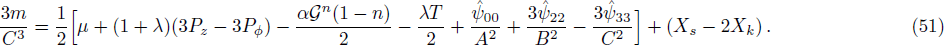
The alternate form of mass function with reference to 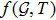structure scalars can be found by using Eqs. (30), (31), (33), (34), (38), and (40) as follows
Using Eqs. (50) and (51), is follows that
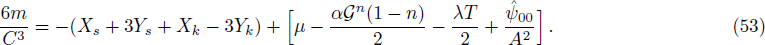
Now applying the operator † on the above equation and using Eq. (52), we get
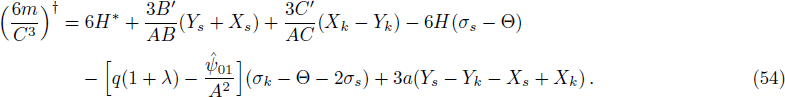
Taking integral on both sides of above equation, it leads to
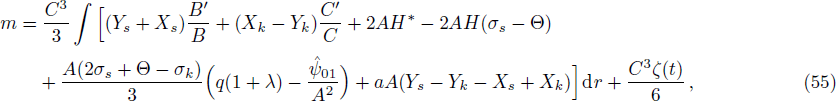
where ζ is an arbitrary integration function. Equation (55) shows that the mass function is influenced by 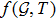dark source variables, scalar functions and other physical factors. Substituting the values of Y_s, Y_k, X_s, and X_k in Eq. (55), we have
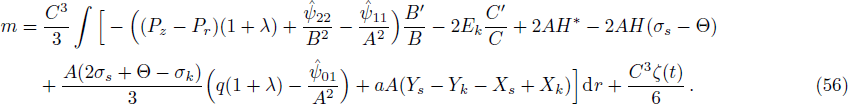
This shows that the Weyl tensor, shear, expansion, anisotropic pressure, dissipative fluid and modified scalar functions influence the presence of mass of relativistic cylindrical body with configurations. The above equation portrays the role of modified structure scalars in refining the dissipative cylindrical relativistic framework.

The investigation of radiating factors in fluid configurations possesses tempting interest in the analysis of collapsing event of astronomical objects. Herrera et al.^[53] analyzed the impacts of thermal conductivity in spherically symmetric configurations of collapsing fluid with anisotropic background. In another context, Herrera et al.^[54] discussed the thermo-inertial bouncing of self gravitating collapsing sphere through numerical procedure and showed that these bouncing effects are due to decreasing inertial mass density of the transport equation. Next we consider the transport equation which is given by^[55]
where τ, ξ, and K represent relaxation time, thermal conductivity and temperature respectively. The only non zero component is
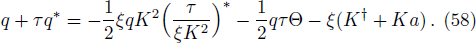
Using Eqs. (49) and (58) in Eq. (45), we get
The above equation can be rewritten as
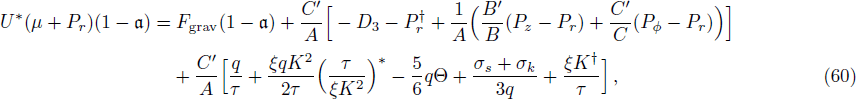
where

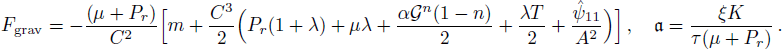
The product of F_grav and 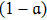in Eq. (60) indicates that the gravitational attraction on dissipative relativistic fluid decreases by the same factor as effective mass density. It can be observed from Eq. (60) when 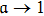, the inertial mass (density) approaches to zero. This demonstrates that the inertial force and matter would not encounter a gravitational attraction, which is the source of collapse. The inertial mass density decreases when 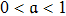while signifies the increase of inertial mass density. There should be increase or decrease of mass by the equivalence principle. In this way, it is easy to differentiate between expanding and collapsing system all along the dynamics of dissipative procedure.

If we assume that the collapsing cylinder alter in such a way that the value of 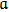increases and approaches to 1 for some region of cylinder, then during this process the gravitational force decreases and this would cause the change of sign of the right hand side of Eq. (60). Since this would occur for small values of effective inertial mass density and this implies a strong bouncing of that region of cylinder, even for a small value of right hand side of Eq. (60). This event causes dissipation of energy from the framework and henceforth the collapsing cylinder with non adiabatic source causes the discharge of gravitational radiations.

In this section, we will discuss the possible static solutions of field equations. The field equations (9)–(13) in static case are



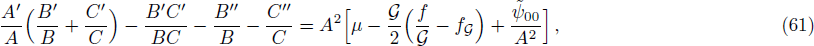
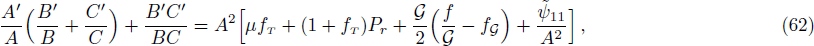
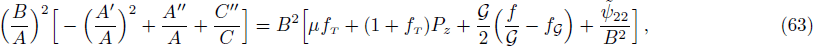
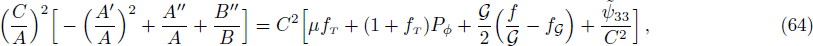
where tilde represents that ψ₀₀, ψ₁₁, ψ₂₂, and ψ₃₃ are evaluated for static cylindrical case. Let us introduce some auxiliary variables, 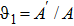, 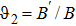and 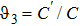. The above equations in terms of auxiliary entities can be written as



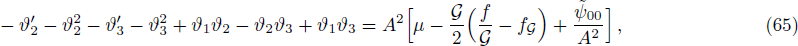
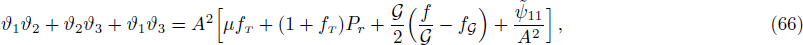
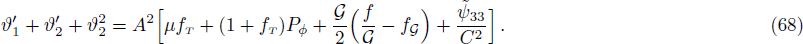
The scalars E_s and E_k in terms of auxiliary variables are

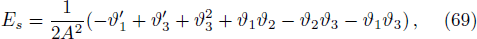
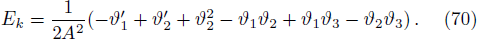
If we add Eqs. (65)–(68), we get one of the structure scalars which is
From Eqs. (66)–(68), it follows that


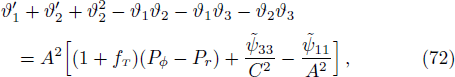
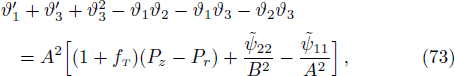
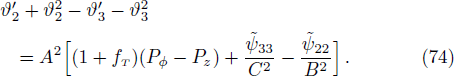
Making use of Eqs. (30), (31), (69), (70), (72), and (73), we get

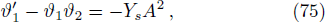
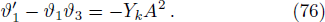
Integration of Eq. (75) yields
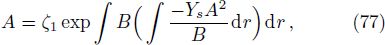
where ζ₁ is a constant. Equation (77) implies that for any Y_s, we get a link between A and B,
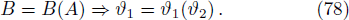
Next, Integrating Eq. (76)
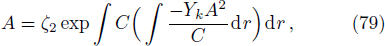
where ζ₂ is another constant. Equation (79) gives the relationship between A and C for any Y_k,
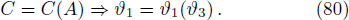
Thus, from Eqs. (78) and (80) we can express any of the auxiliary variable in terms of the others. Subsequently in Eq. (74), we can indicate ϑ₂ and ϑ₃ in terms of ϑ₁. It can be solved for P_φ − P_z and once we get ϑ₁, we can obtain ϑ₂ and ϑ₃ from Eqs. (78) and (80). Equations (31) and (34) provide
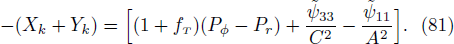
Equations (30) and (33) give
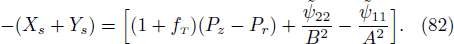
This shows that any static anisotropic solution can be found via triplet of structure scalars (Y_s, Y_k, X_s) or (Y_s, Y_k, X_k).

In this paper, the structure and evolution of radiating cylindrical compact objects have been investigated by taking gravity into account. For this purpose, non-static cylindrically symmetric spacetime coupled with radiating anisotropic fluid distribution is considered. We have constructed modified structure scalars by orthogonally splitting the Riemann curvature tensor from the generic formula of scalar functions. We have also linked Weyl scalar with matter variables for usual and effective matter distributions. We have formulated dynamical and transport equations to analyze the impacts of relaxation time for the cylindrical collapsing system. Further, we have explored the role of structure scalars for anisotropic cylindrical solutions.

(i) We have defined the set of eight structure scalars (Y_T, Y_s, Y_k, X_T, X_s, X_k, Z_H, Z_q) together with scalars (σ_s, σ_k) interpreting the shear tensor and Weyl scalars (E_s, E_k, H) which are necessary for dynamical analysis of cylindrically symmetric gravitating object. We have also determined a set of equations administering the structure and evolution of the framework and yielded the role of scalar functions in those equations.

(ii) The scalar functions Z_q, Z_H, X_T describe heat radiation, energy density and magnetic part curvature impacts emerging from Weyl tensor alongside dark source terms of dissipative anisotropic cylindrical distribution.

(iii) The structure scalars Y_s, Y_k, and Y_T control the evolution of shear and expansion in the dynamical stages of compact objects. We have computed these scalar functions with corrections and found that the dark source variables interrupt the role played by these scalars in evolution of celestial system.

(iv) In Eq. (56), the role of Weyl tensor and fluid parameters in affecting the existence of mass of cylindrical self gravitating body is shown. The mass function explains the contribution of modified scalar functions in developing the cylindrical dissipative self gravitating system. Additionally 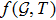higher curvature terms attempts to make mass function more complex due to its non attractive nature.

(v) In the case of static cylinders, we have determined that all possible solutions of static field equations can be represented in terms of a triplet of scalar functions (Y_s, Y_k, X_s) or (Y_s, Y_k, X_k).

The above investigation provides dynamical behaviour of self gravitating cylindrical system with model. The acquired results may correspond to cosmological inflation where extra curvature variables emerge into dynamics.