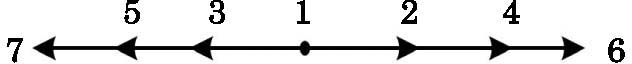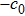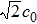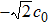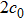† Corresponding author. E-mail:
A one-dimensional discrete Boltzmann model for detonation simulation is presented. Instead of numerical solving Navier-Stokes equations, this model obtains the information of flow field through numerical solving specially discretized Boltzmann equation. Several classical benchmarks including Sod shock wave tube, Colella explosion problem, and one-dimensional self-sustainable stable detonation are simulated to validate the new model. Based on the new model, the influence of negative temperature coefficient of reaction rate on detonation is further investigated. It is found that an abnormal detonation with two wave heads periodically appears under negative temperature coefficient condition. The causes of the abnormal detonation are analyzed. One typical cycle of the periodic abnormal detonation and its development process are discussed.
Detonation is one kind violent combustion mode accompanied with a large amount of heat release within a short time.[1] It can be treated as a shock wave driven by chemical reaction and propagates with a supersonic speed.[2] Detonation is closely related to the energy use and production safety.
In some cases, it is necessary to generate detonation waves to improve the utilization efficiency of fuels. Because detonation possesses an approximate isovolumetric characteristic during chemical reaction, it has a higher mechanical efficiency than the general combustion mode.[3] Based on the detonation mechanism, several kinds of aero-engines conception including pulse detonation engine,[4] rotating detonation engine,[5] oblique detonation ramjet-in-tube,[6] etc. have been presented and well investigated recently. While in other cases, the formation of detonation should be avoided as far as possible such as in coal mines.[7] Detonation is closely related to both the industrial production and our daily life. However, there still exists much unknown for its deep formation and propagation mechanisms.[3,8]
It has been well known that combustion and detonation are complex chemical reaction processes with various non-equilibrium behaviors including Hydrodynamic Non-Equilibrium (HNE), Thermodynamic Non-Equilibrium (TNE) and chemical reaction non-equilibrium.[9–10] For detonation research, traditional methods are mainly by using Navier-Stokes (NS) equations to describe the flow behaviour and using phenomenological reaction rate formula to describe the reaction process.[11] In addition, high resolution difference schemes are often needed to track the detonation interface and improve the numerical accuracy.[12–13] Of course, great progress has been made on the studies of detonation by the traditional method, especially in recent years.[3,9] However, NS equations themselves are not sufficient in describing the non-equilibrium effects in the reactive flow. The coefficients of viscosity and heat conduction in NS equations are generally calculated by empirical formula, such as Sutherland equation, or measured by experiments.[14–15] This method is not accurate enough when simulating the flow phenomena with strong non-equilibrium characteristics. Compared with NS equations, Boltzmann equation is more fundamental to describe the flow process. Rooted from the non-equilibrium statistic mechanics, Boltzmann equation is a mesoscale model and contains more kinetic information. By means of the Chapman-Enskog analysis,[16] a well-known multi-scale asymptotic expansion, the Euler equations can be obtained from the Boltzmann equation when the system is exactly in its local thermodynamic equilibrium state, and the NS equations can be obtained when the system linearly, in the Knudsen number, deviates from its local thermodynamic equilibrium state. However, when the system deviates much farther from its local thermodynamic equilibrium state, NS equations will not be accurate enough and fail to capture many important flow behaviors, whereas the Boltzmann equation naturally adapts to all of the above situations.
Unfortunately, the original Boltzmann equation is too complex to be solved directly, and some attempts have been made to simplify this model, among which the Lattice Boltzmann Model (LBM)[17–20] is a typical one. The first LBM for combustion simulation was presented by Succi in 1997.[21] Subsequently, Filippova,[22] Yamamoto,[23] Chiavazzo,[24] Chen[25] and other researchers further developed the application of LBM to combustion simulation. However, all of those previous works aim only at simulating incompressible combustion and cannot satisfy the requirements of detonation simulation which shows pronounced compressible behaviors. Recently, Xuʼs group made some attempts in simulating high speed compressible flows using LBM and developed it into a kinetic modeling method to investigate non-equilibrium characteristics.[26–30] To distinguish from the LBM aiming at numerical solving partial differential equations, the kinetic modeling LBM is referred to simply as discrete Boltzmann method/model (DBM). Discrete Boltzmann method now has been well developed and widely used in various complex flow simulations including compressible flows,[31] multiphase flows,[32] Rayleigh-Taylor instability,[33–34] combustion and detonation.[35–38] The new observations brought by DBM are helpful to understand the mechanisms for formation and effects of shock wave, phase transition, energy transformation, and entropy increase in various complex flows. Besides by theory, results of DBM have been confirmed and supplemented by results of molecular dynamics,[39–41] direct simulation Monte Carlo[42–43] and experiment.[44] In the system containing both material interface and mechanical interface (such as shock wave and rarefaction wave), non-equilibrium characteristics have been used to recover the main feature of real distribution function, and to provide physical criteria for discriminating various interfaces. The latter has been used to design appropriate tracking schemes for various interfaces.[28,33,45–46] In recent studies,[34,47] the correlations between the various macroscopical nonuniformity and the relevant non-equilibrium strengths in systems with Rayleigh-Taylor instability and/or Richtmyer-Meshkov instability are used to probe the material mixing processes. In 2013, the first DBM for detonation was presented[35] then a series of extensions have been made. For example, the Multiple-relaxation-time DBM[38,48] and double-distribution-function DBM[36] have been developed. However, those works are all two-dimensional model and at least 16 discrete velocities are needed.[37] The calculation efficiency is much low for some cases where the main behaviors can be described by one-dimensional model. In those cases, a one-dimensional DBM model for detonation is in demand.
Generally speaking, during a combustion process, many species of reactants and a large number of reactions are involved. For example, the combustion of CH4 in air involves 53 species and 325 reactions.[49] The reaction rate varies with the special reaction paths. A detonation process may guide the reactions into different reaction chains because of the type of fuel, shock strength, premixing homogeneity, etc. Consequently, the global reaction rates show different behaviors for different conditions and may possess a non-monotonic dependence on the temperature. Although most of the reaction rates have an exponential temperature dependence and the Arrhenius model is commonly be adopted to describe the reaction rate, the phenomenon of Negative Temperature Coefficient (NTC) in reaction rate has been observed in combustion process and has drawn great attention in recent years.[9,50–51] The existence of NTC may also cause significantly special phenomena during the detonation process. However, to the authors’ knowledge, possible effects of NTC on detonation have not been well studied. In 2016, we conducted a preliminary study on the effects of NTC during detonation.[37] In that work, we found that the effect of NTC during detonation is to lower the reaction rate and delay the formation of detonation wave. In this paper, we further study the characteristics of detonation under NTC based on the one-dimensional DBM. An abnormal detonation phenomenon with two wave heads is observed and carefully studied.
For the one-dimensional discrete Boltzamnn model, the evolution of the distribution function fi for the discrete velocity vi is governed by Eq. (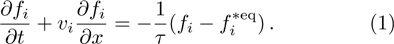
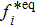
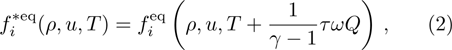
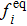


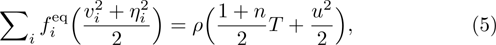

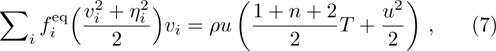
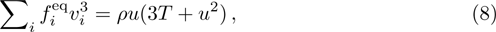
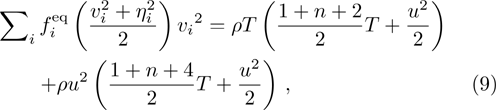
From multi-scale asymptotic expansion, we know that NS equations with chemical reactions, Eqs. (
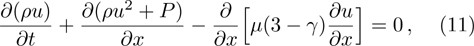
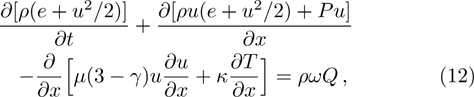
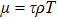
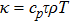
In order to solve the above seven equations, at least seven velocities are needed. The discrete velocities model adopted in this paper is shown schematically in Fig.
| Table 1.
Values of discrete velocities. . |
The chemical reaction rate ω is described by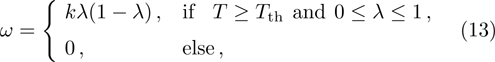
In addition to being able to recover to NS equations with chemical reactions, DBM provides a set of non-equilibrium measurements, which is also its advantage over the traditional hydrodynamic model. The non-equilibrium quantities are represented by the difference between the moments of distribution function and its corresponding local equilibrium distribution function at a certain time. Those non-equilibrium quantities are defined as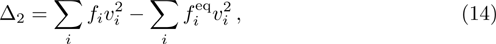
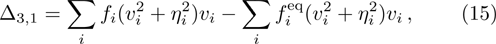
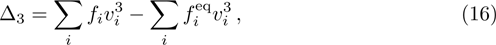
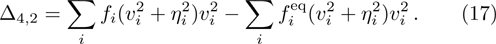
In order to validate the new model, several typical benchmarks are carried out. Firstly, two shock wave problems, including the Sod shock tube and Colella explosion wave problem, are simulated and compared with the Riemann solutions. Then a one-dimensional self-sustainable stable detonation is simulated and compared with CJ theoretical solutions.
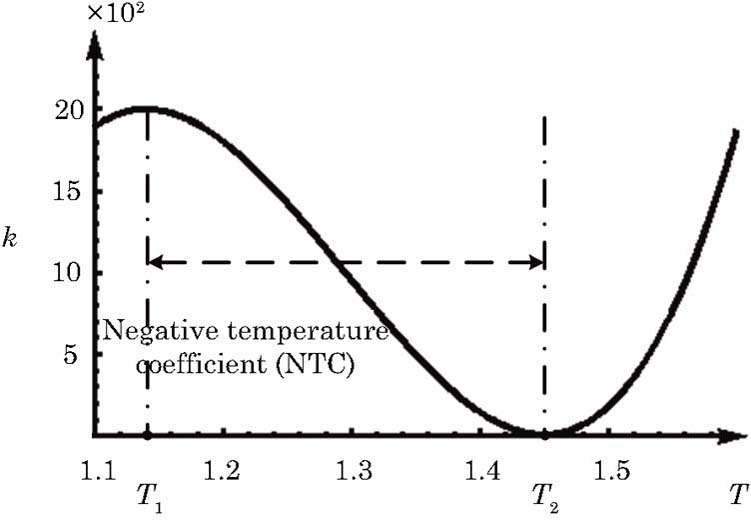
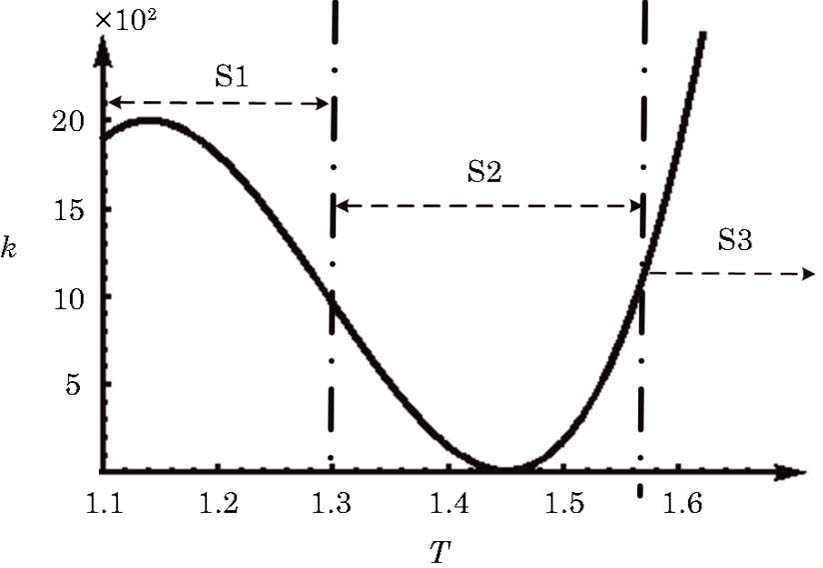
In order to investigate the NTC of chemical reaction rate, we adopt the following formula to describe the temperature dependence of rate constant k in Eq. (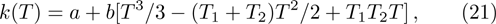
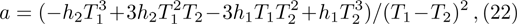
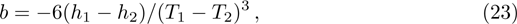
Except the chemical reaction rate and Nx = 50000, other simulation conditions are all the same with those in Fig.
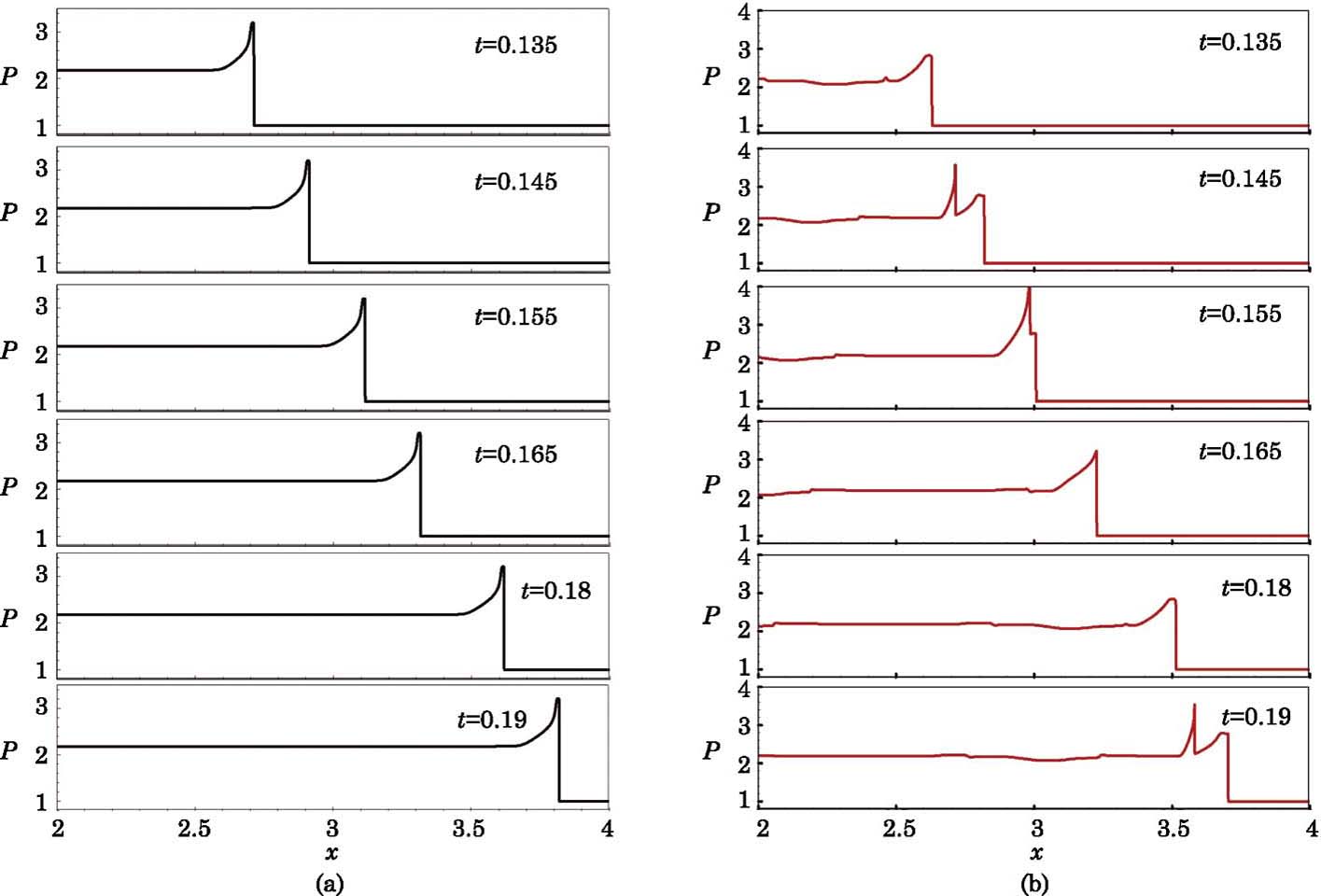
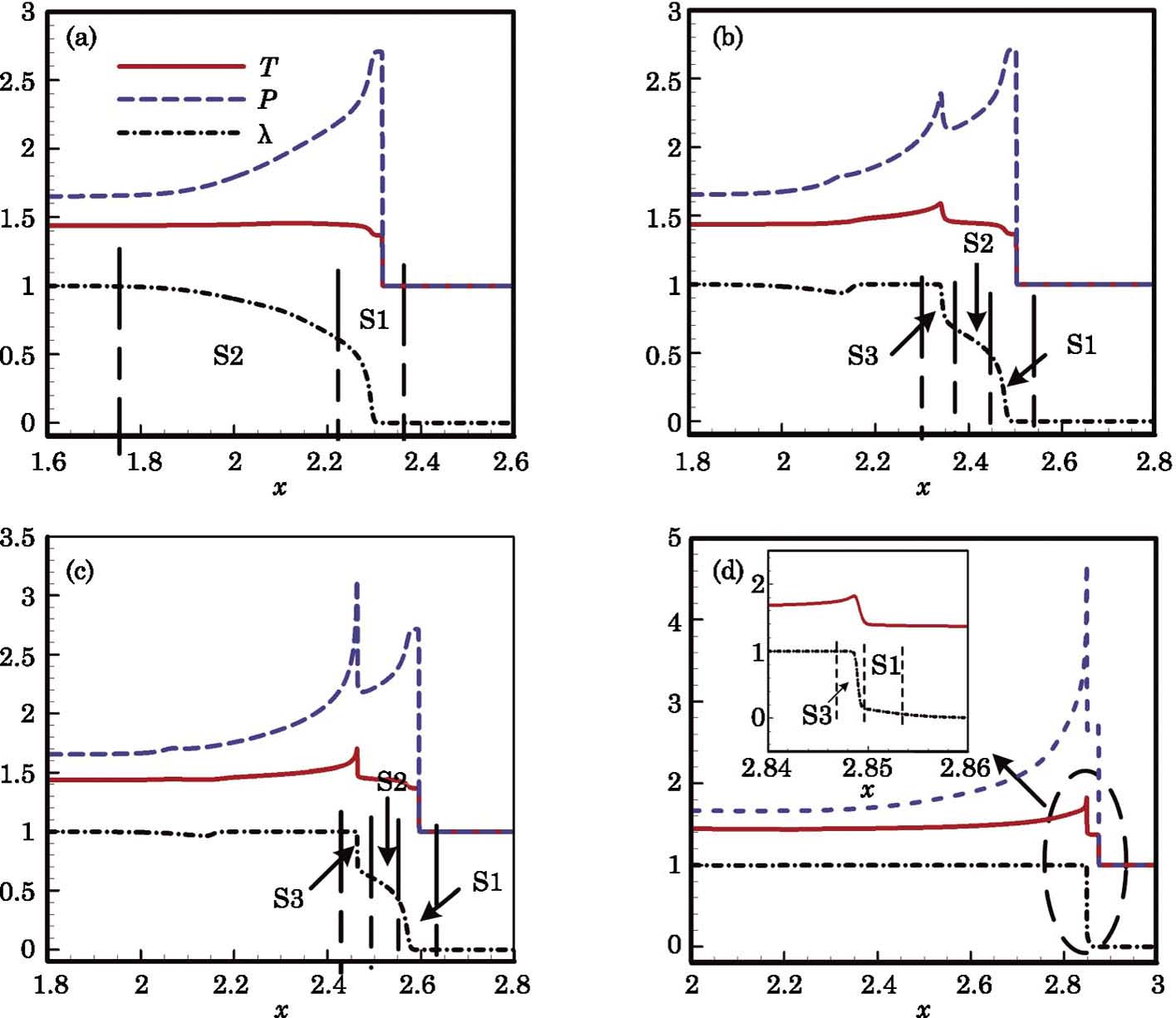
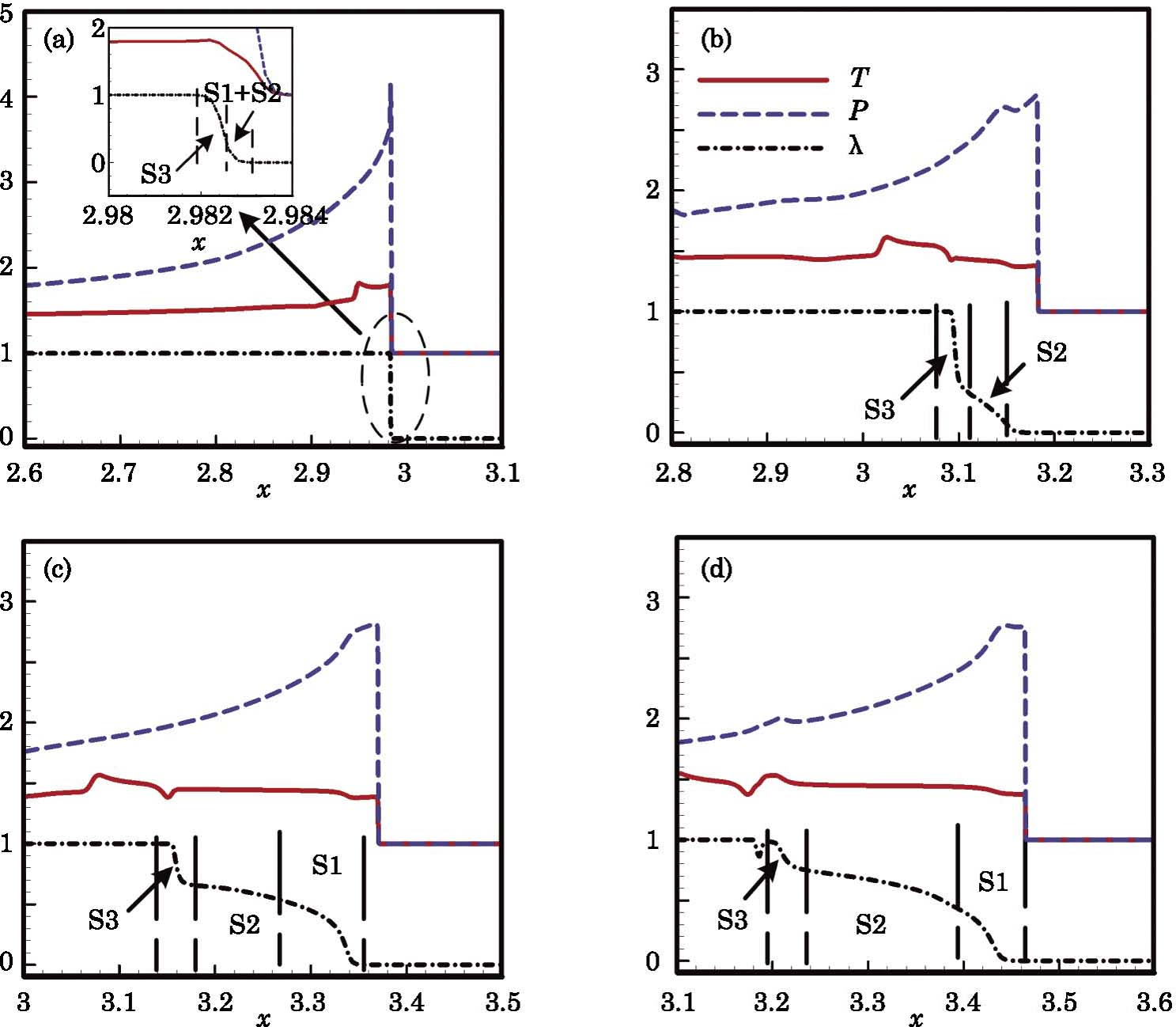
Figure
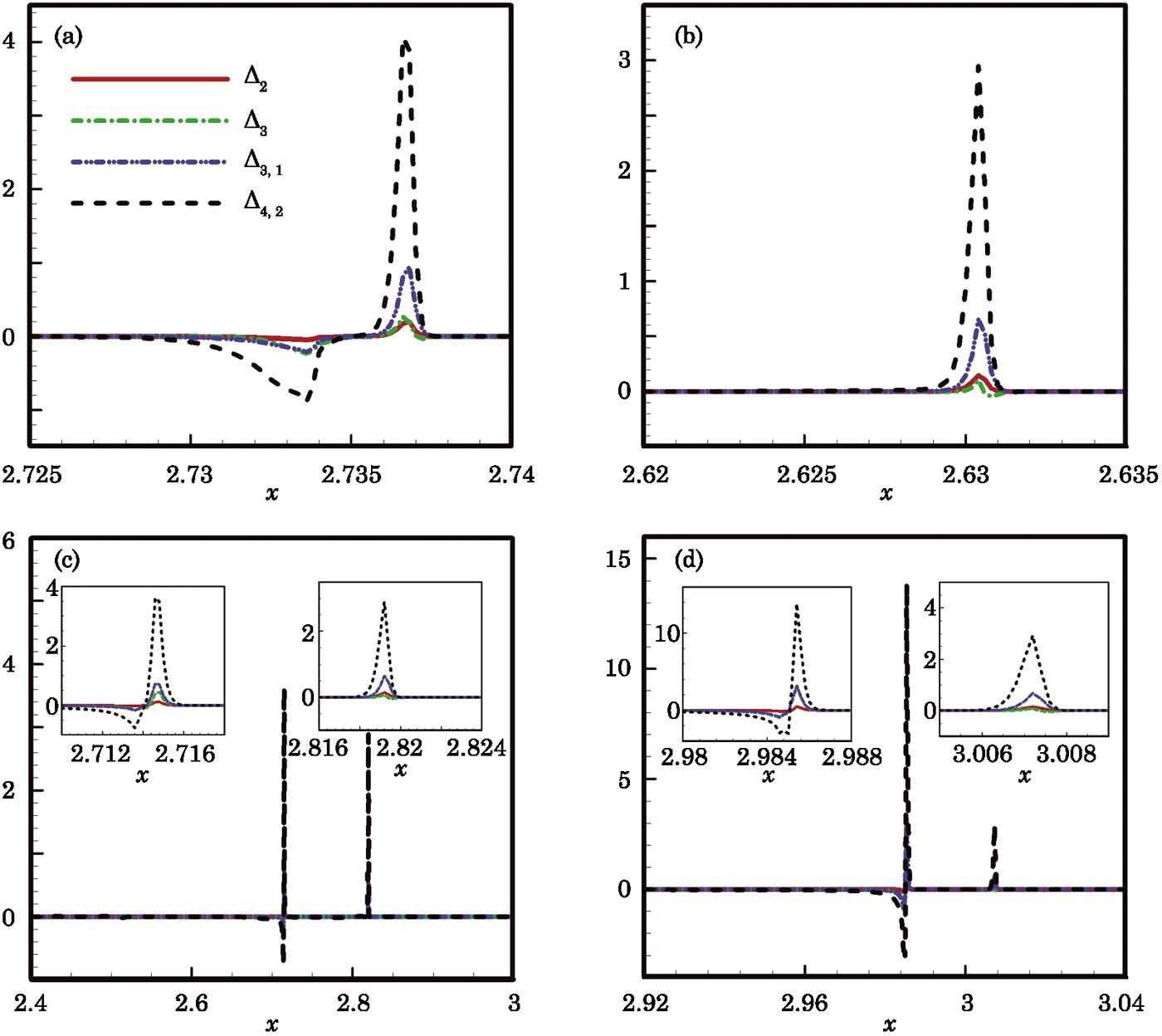
The corresponding non-equilibrium quantities Δ2, Δ3, Δ3,1, and Δ4,2 defined in Eqs. (
In this section, we will discuss the causes of the abnormal detonation wave. For convenience, we roughly divide the reaction into three stages according to the temperature. Those three stages are denoted as S1, S2, and S3, respectively, as shown in Fig.
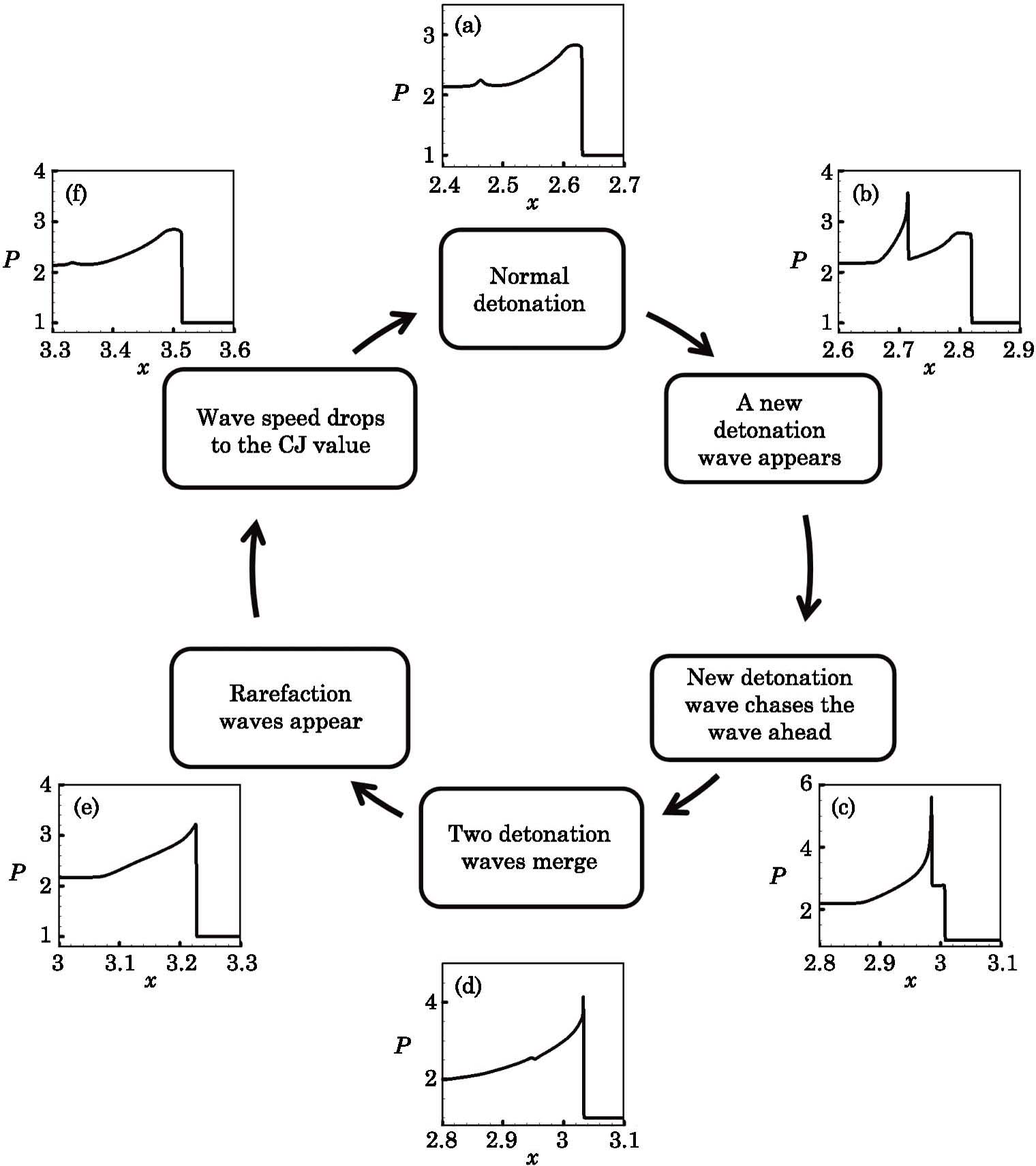
The development of the abnormal detonation is shown in Fig.
The evolution of the process from overdriven detonation to the normal detonation is shown in Fig.
After that, a local hotspot reappears and a new local detonation wave is developed again, which means the above process is repeated. The whole process of the development of the abnormal detonation within a period can be summarized by Fig.
In this work, we present a one-dimensional discrete Boltzmann model for detonation. The validity of the new model is verified by three tests. The new detonation model possesses both high computational efficiency and numerical accuracy. Based on the new model, the effects of negative temperature coefficient of reaction rate in a detonation are further investigated. An abnormal detonation phenomenon is presented and its development process is analyzed. It is found that the main reason for the abnormal detonation is that the chemical reaction has three stages, namely S1, S2, and S3. The first stage, S1, is in the low temperature region but has a fast reaction rate, the second stage, S2, has a slower reaction rate at a specific temperature range, and the third stage, S3, has a fast reaction rate at high temperature and the reaction rate increases dramatically with the increase of temperature. For a normal detonation, the chemical reactions occur mainly in S1 and S2. For the abnormal detonation, however, at a certain time a local hotspot is formed as a consequence of the S3. Then a new detonation with a more violent chemical reaction appears behind the old detonation wave front. The new detonation wave has a faster speed than the wave ahead, it catches up with the front wave and finally two waves merge. Then the speed of the detonation wave begins to slow down until it reaches a CJ detonation value. After that, the local hotspot appears again and the previous process reappears.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] |