† Corresponding author. E-mail:
The potential of nonharmonic systems has several applications in the field of quantum physics. The photon-added coherent states for annharmonic oscillators in a nonlinear Kerr medium can be used to describe some quantum systems. In this paper, the phase properties of these states including number-phase Wigner distribution function, Pegg-Barnett phase distribution function, number-phase squeezing and number-phase entropic uncertainty relations are investigated. It is found that these states can be considered as the nonclassical states.
The standard coherent state is a particular kind of the quantum states, which its dynamics is similar to oscillatory behavior of a classical harmonic oscillator.[1] These states are defined by the annihilation and creation operators of the harmonic oscillator. Some quantum mechanical systems can be described by the nonharmonic potentials.[2–3] The Gazeau-Klauder coherent state of the anharmonic oscillator has been introduced by Roy.[4] Also, the coherent states for nonharmonic oscillators using generalized Heisenberg algebra have been constructed.[5]
Construction and generation of the nonclassical states is one of the most exciting subjects in quantum optics because their applications in the fields of quantum information processing and quantum computation. Therefore, with the aim of finding nonclassical states many generalizations on the standard coherent states have been nominated. One of the most important generalizations is the photon-added coherent states.[6] The photon-added coherent states can be considered as the nonlinear coherent states with certain nonlinearity function.[7] Also, the photon-subtracted and photon-added coherent states corresponding to the inverse bosonic operators have been introduced in 2004.[8] Furthermore, Zavatta et al. produced the single photon-added coherent state |α, 1⟩ experimentally in 2005.[9] A method for generating the two photon-added coherent state |α,2⟩ has been suggested by Kalamidas et al.[10] The photon-added coherent states and their generalizations have received considerable attention in recent years.[11–14] Roman-Ancheyta et al. constructed deformed Photon-added nonlinear coherent states for a one-mode field in a Kerr medium.[15]
Recently, the photon-added coherent states for nonharmonic oscillators in a nonlinear Kerr medium have been introduced by Al-Rajhi using generalized Heisenberg algebra.[16] In the present paper, the phase properties as well as the number-phase entropic uncertainty relation of these states are investigated. For these purpose, the photon-added coherent states for nonharmonic oscillators are reviewed in Sec.
The Hamiltonian for anharmonic oscillators can be expressed by[4]
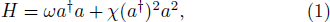
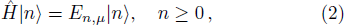
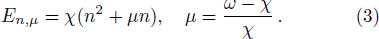
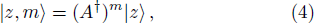
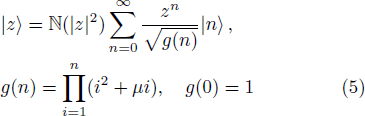
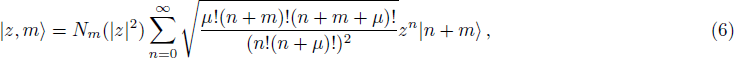
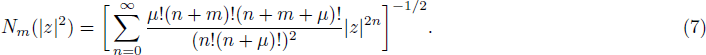
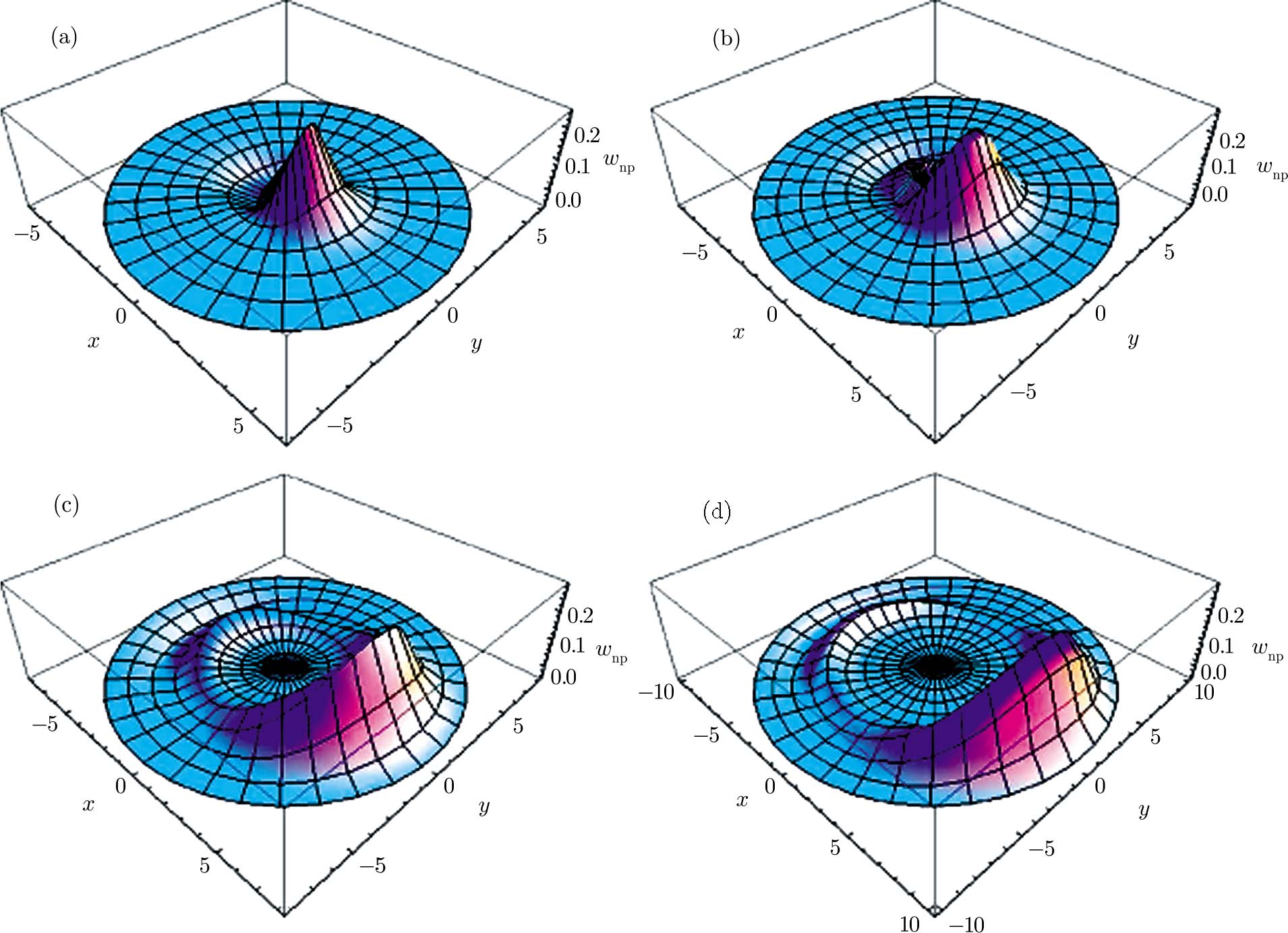
The number-phase Wigner function characterizes the quantum statistics of the photons and phase observable of a quantum state. This distribution function may be negative in some regions of number-phase space for specific quantum states that represents the nonclassical signature of these states. The number-phase Wigner operator can be expressed as follows:[17–18]
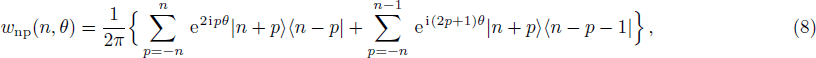

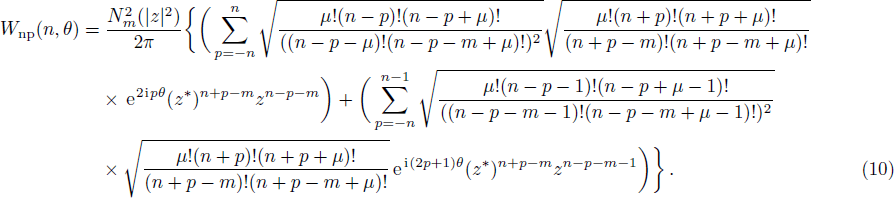
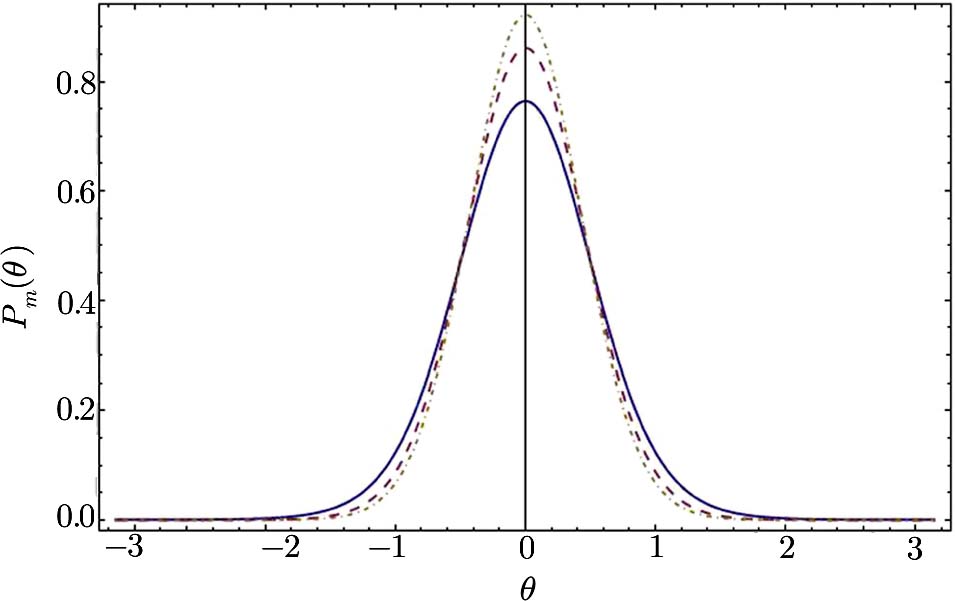
Based on Pegg-Barnett method, a complete set of s + 1 dimension phase state are well-defined by[19]
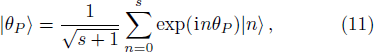
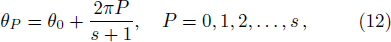
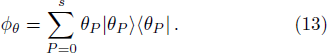
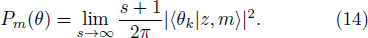
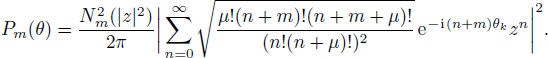
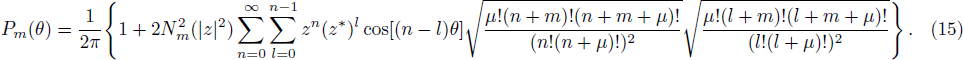
Figure
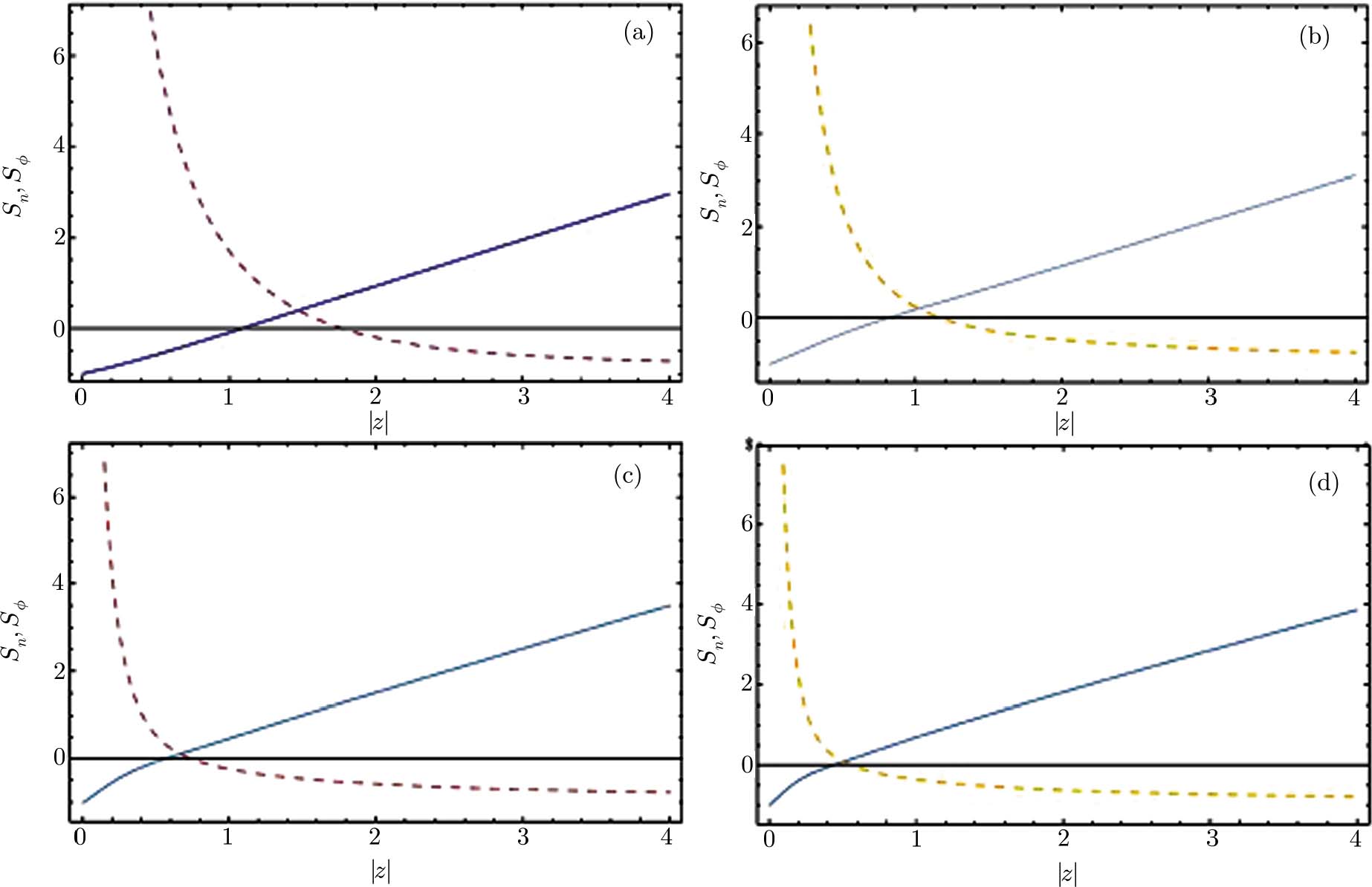
The phase and number operators are conjugate to each other and consequently, satisfy the following uncertainty relation

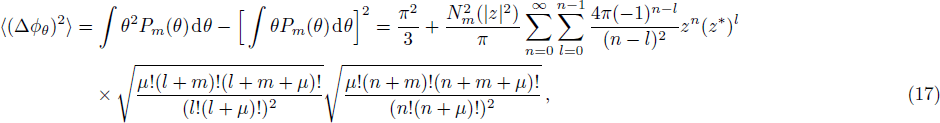
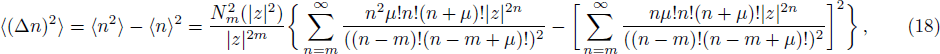


The number and phase squeezing parameters associated with these states are shown in Fig.
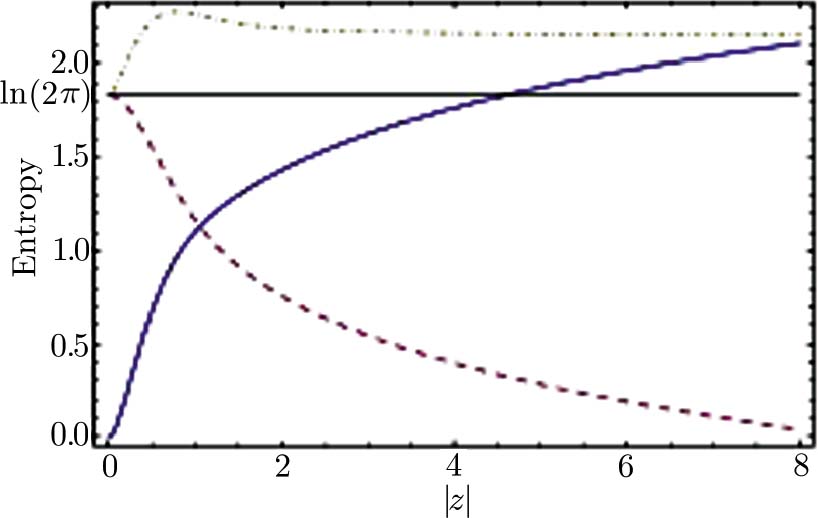
The Shannon entropies (SA and SB) of two conjugate operators A and B, with eigenvalue equations A|an⟩ = an|an⟩ and B|bn⟩ = bn|an⟩, are limited by the entropy uncertainty relation SA + SB ≥ ln(s + 1). Here A and B are defined on the (s + 1)-dimensional space. This uncertainty relation which has been suggested by Kraus[20] and then proven by Massen and Uffink,[21] depends on dimension of the state space. Vaccaro et al. defined new quantities RA and RB as follows


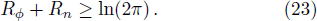
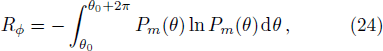
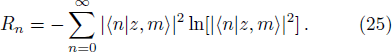
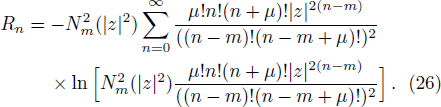
The phase and number properties of physical systems are very important. In this work, the number-phase Wigner function, phase distribution function, number-phase squeezing and number-phase entropic uncertainty relation of the photon-added coherent states for anharmonic oscillators are studied using Pegg-Barnett formalism. The number-phase Wigner function corresponding to these generalized coherent states is negative in some regions. The results show also that these states represent number or phase squeezing for different ranges of |z|. Therefore, these states are nonclassical states. The photon-added coherent state for anharmonic oscillators can be considered as an intermediate state between the coherent states for anharmonic oscillators and the Fock states. Construction of a photon-added coherent state for anharmonic oscillators by adding photon to the coherent state for anharmonic oscillators is a proper way to have a quantum state with more nonclassicality. The curves of Pegg-Barnett phase distribution function show that this distribution function has only a single peak in θ = 0 and as m increases, the peak is more localized with respect to θ. Finally, it is found that the number-phase entropic uncertainty relation associated with the photon-added coherent states for anharmonic oscillators has a lower bound ln(2π) for all values of photon added number m.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] |