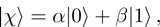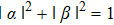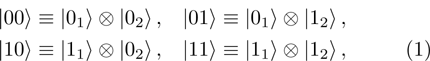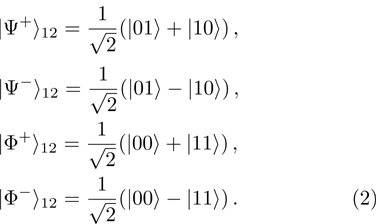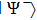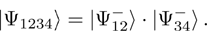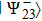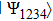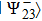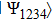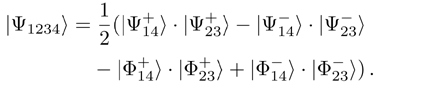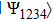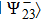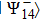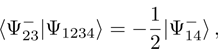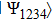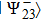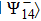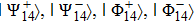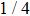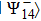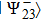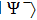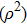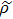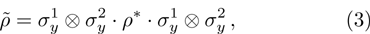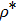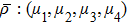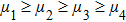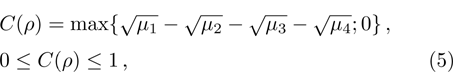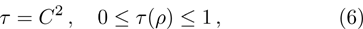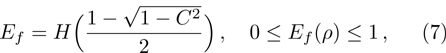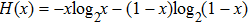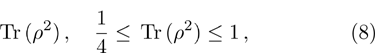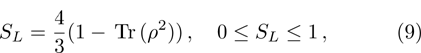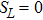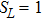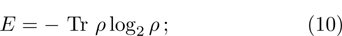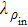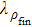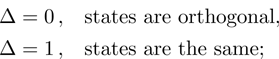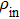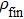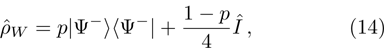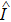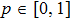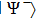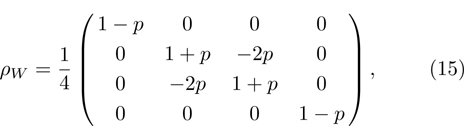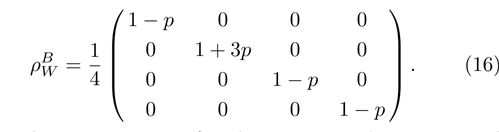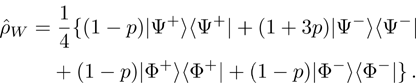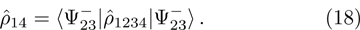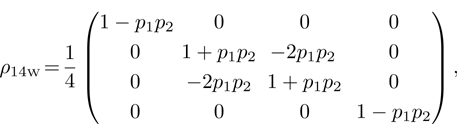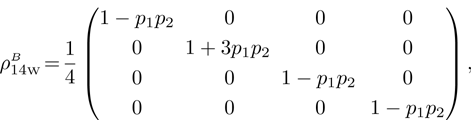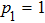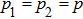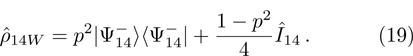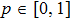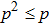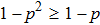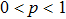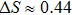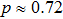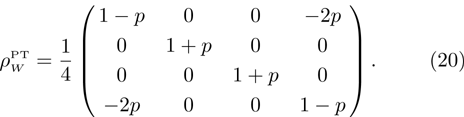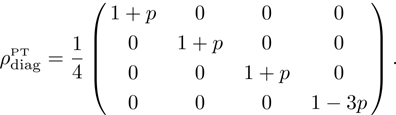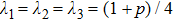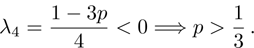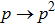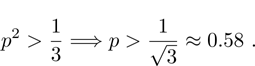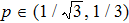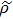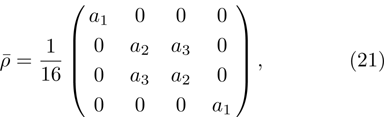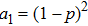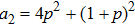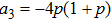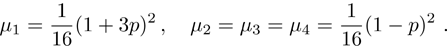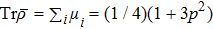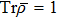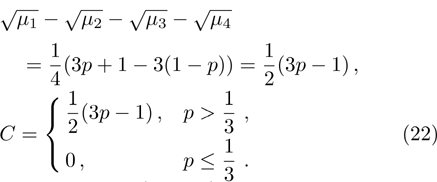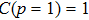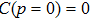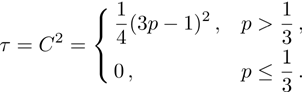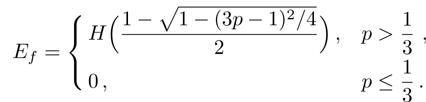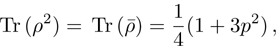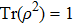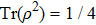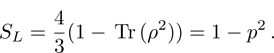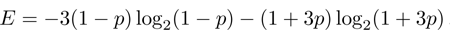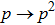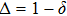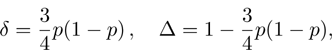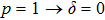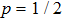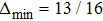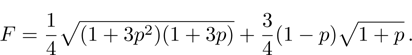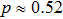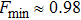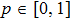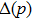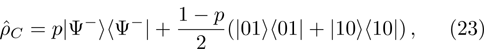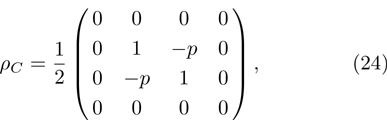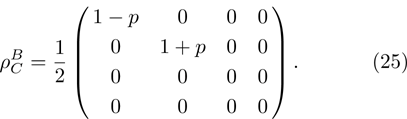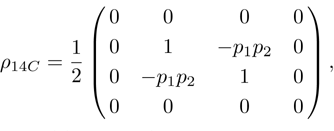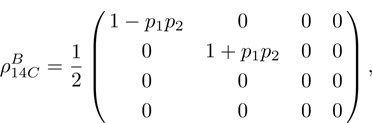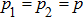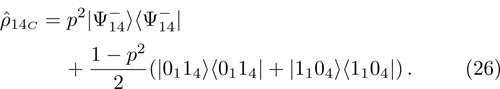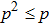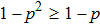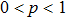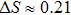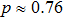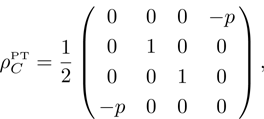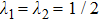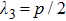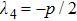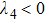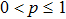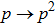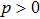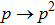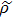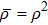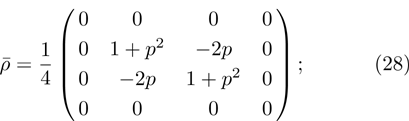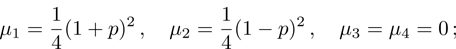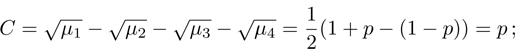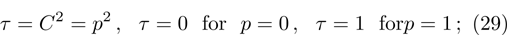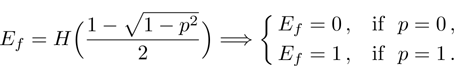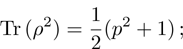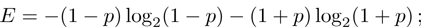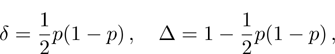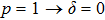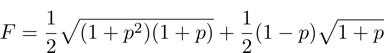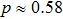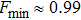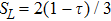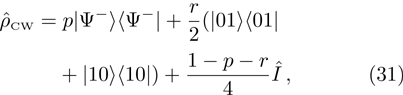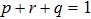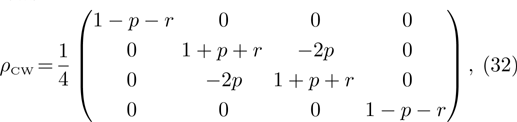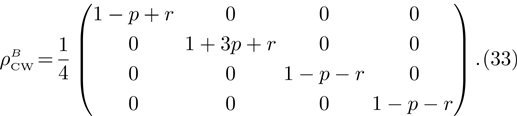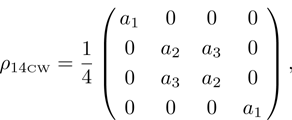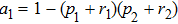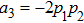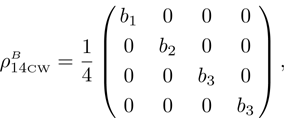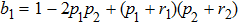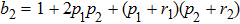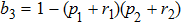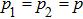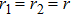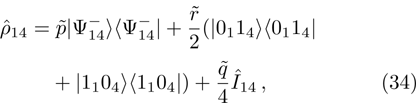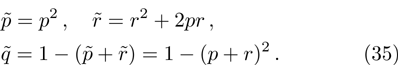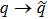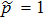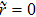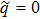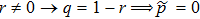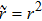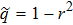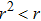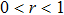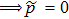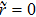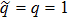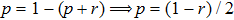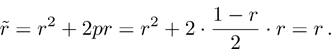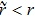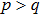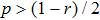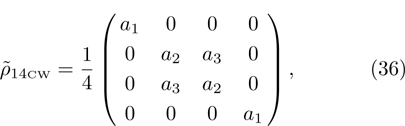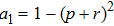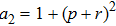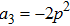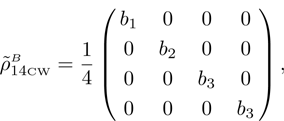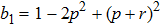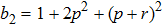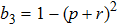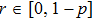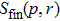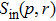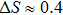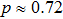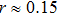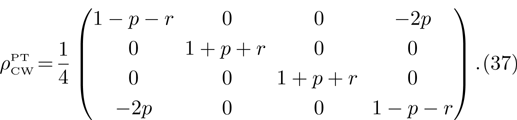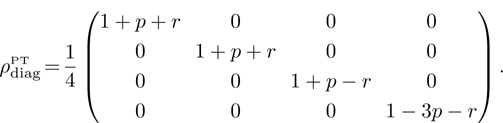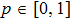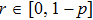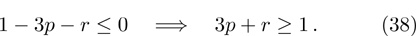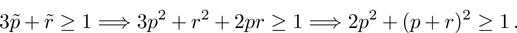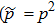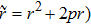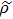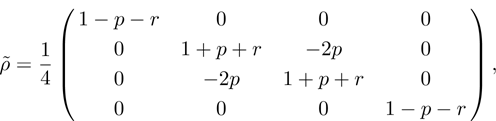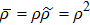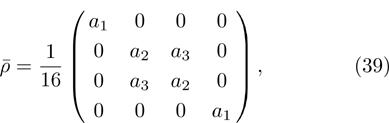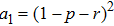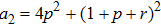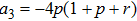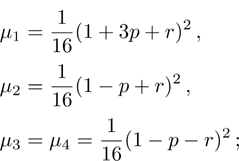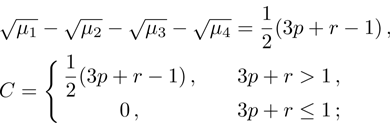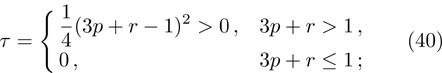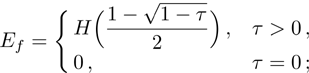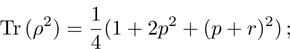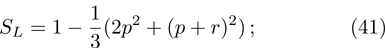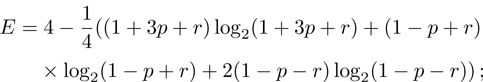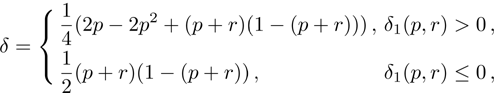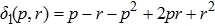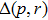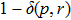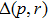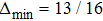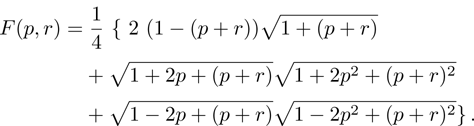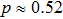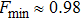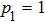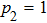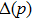Cite this Article
Dotsenko Ivan S., Korobka R.. Entanglement Swapping in the Presence of White and Color Noise. Communications in Theoretical Physics, 2018, 69(2): 143  
Permissions
Entanglement Swapping in the Presence of White and Color Noise
Dotsenko Ivan S. *, Korobka R. †
Taras Shevchenko National University of Kyiv, Kyiv, Ukraine

 

† Corresponding author. E-mail: ivando@ukr.net roman.korobka@gmail.com

Abstract
Abstract

The influence of white and color noise on the outcome of the entanglement swapping process is investigated in a four-qubit system. Critical degree of noise in initial state, that could destroy entanglement in a result state is presented. The entanglement characteristics, such as concurrence, tangle, etc. are compared. Results could be helpful for experiments regarding entanglement swapping as conditions for initial quantum entangled states, to obtain entangled result state.

PACS: ;03.67.Bg;
Keyword:entanglement;entanglement swapping;white noise;entanglement
1 Introduction

The entanglement phenomenon gradually became an object of intensive research after Aspect’s group[1] had convincingly (through experiments) proven the violation of Bell’s inequalities by the entangled states.

It became clear with time that entanglement is a new resource of nature, which can be created, preserved, distributed, concentrated and transmitted over a distance. Nowadays, entanglement is actually being created and processed in many physics laboratories. Entangled states carriers are quite versatile, it could be photons, ions, atoms, molecules, crystals and more. Discovering the role of entangled states stimulated emergence of new areas in modern physics, such as quantum computing, quantum cryptography and quantum communication.

As it is well known, an arbitrary state of any single qubit can always be represented as a vector in two-dimensional Hilbert space:

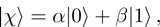
with normalization .

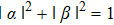
The principal difference between qubits and classical bits is a possibility of existence of states in a form of superposition of basis vectors.

The state of two-qubit system is described by a vector in a 4-dimensional Hilbert space, which is the tensor product of Hilbert spaces of individual qubits. The most common bases in this space are computational (standard) basis in the form of a tensor product of relevant basis states of individual qubits:

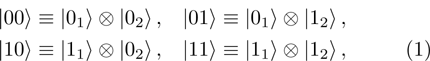
and Bell basis:

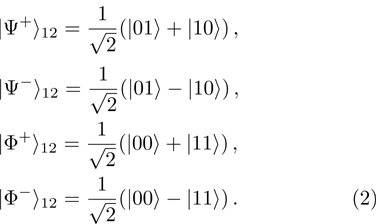
It is customary to call Bell states the EPR pairs, because that type of states is discussed in the Einstein, Podolsky, Rosen work.[2] All Bell (2) states are entangled, because they cannot be represented in a form of a product of individual qubits vector states.

The most interesting and unusual phenomenon, based on entanglement, is a quantum teleportation and entanglement swapping (ES). First, the scheme (protocol) of unknown qubit state teleportation was proposed in Ref. [3] (Bennett et al.). Detailed reference to the original work on quantum teleportation can be found, for example in Refs. [4] and [5].

For some time it was believed that entangled system state, consisting of two or more quantum subsystems (particles, photons), is created only during their simultaneous birth in a single event from a common source, or as a result of subsystems interaction. However, in 1993[6] (Zukowski et al.) a protocol was proposed, as a result of which the quantum correlations (entanglement) could be created between the particles that may be located at great distance from each other, and which did not share a common history. This process is called the entanglement swapping (ES).

A paper by Zukowski et al. for a short time was widely appraised among scholars. Dur et al.[7] developed a quantum communication protocol for long distances using quantum repeaters with ES as their element. Xue et al.[8] proposed ES scheme, which is based on three-particle GHZ state for the needs of quantum cryptography. The entanglement swapping process is sometimes called the entanglement teleportation or teleportation of entangled states. Tsai et al.[9] used GHZ-like state for teleportation of pure EPR state. At the same time in addition to theoretical developments of teleportation protocols and ES, the real experiments[10–13] are gradually improved in physics laboratories. For a correct assessment of real possibilities to transfer quantum state over long distances, all factors that affect the signal quality at all stages of its formation and passage through channels of communication should be taken into consideration. A detailed discussion of this topic can be found at Ref. [14]. To study the overall influence of all these factors, it is necessary, in our point of view, to display full understanding of physical processes in each single element of the communication channel.

Entanglement swapping is used in real elements of quantum communication channels, such as quantum repeaters. Quantum states at the input of these elements always have some level of noise. Motivation of this research is to get to know how type and level of noise at the input of such elements will affect on the quality of output state. The aim of this work is a theoretical study of the effect made by the presence of noises in initially created entangled states on the final state obtained as a result of entanglement swapping operation.

For better explanation of the gist of this paper we remind the essence of the entanglement swapping phenomenon that can be illustrated by a specific example.

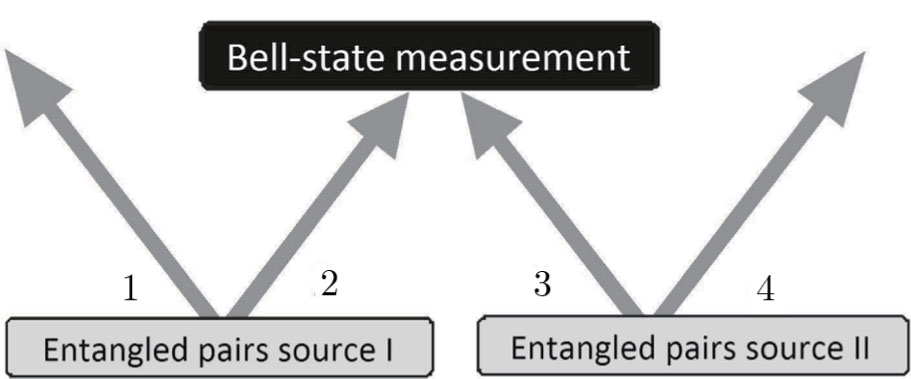
Let two sources independently form one pair of qubits each in one of the entangled EPR states of Eq. (2). For example, in the experiment[10] short UV pulses were flown through nonlinear BBO-crystal (β-BaB2O4). As a result of parametric down-conversion type II, pairs of photons were formed in polarizingly entangled Bell state 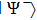. Due to independent formation of two such entangled pairs, four-qubit system state is represented as a tensor product of individual qubit-pair states (number of qubits marked by symbols):

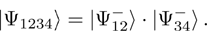
A pair of qubits (photons) 2 and 3 further undergoes a projective measurement in Bell basis (2). A measuring device is adjusted in such a way, so in compliance with the scheme of signal coincidences, an event emerges from detectors, when a pair of photons 2 and 3 is in state .

This operation is called an incomplete projective measurement. Mathematically, the operation is considered as a projection of the state 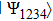on the state .

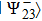By regrouping summands, the state vector 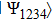can be written as:

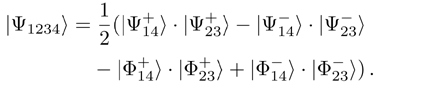
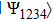
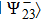
Thus, as a result of projecting on , state of qubits 1 and 4 “collapses” into Bell’s state :

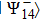
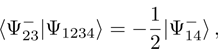
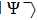
that is, a pair of qubits which numbered 1 and 4 is in the same state , as previously prepared two-pair states of qubits 1 and 2 or qubits 3 and 4.

Since the operation of projection on a particular state is incomplete von Neumann measurement, so as a result of projection we obtain state vector, which is non-normalized. In this very case, multiple repeating of the operation preparing 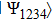state and subsequent projection on 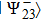theoretically, on average, only one event out of 4 attempts to provide the desired effect 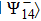. But after the event was recorded, the state vector is considered normalized to one. Basically one can also consider complete measurement of von Neumann in the Bell basis. Then, as a result of each act ES, particles 1 and 4 are in one of four possible states: 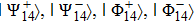with probability 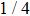for each state. Further use of LOCC can convert these states, so with a probability w = 1 the final state will be 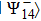. Note that preliminary prepared qubit couples were created independently from each other and particles 1 and 4 by no means interacted with each other.

ES process can be represented as a simple scheme (Fig. 1).[10]

Fig. 1 Scheme of entanglement swapping process implementation.

Note that the entanglement of 1 and 4 qubits occurs just at the moment of projecting on the state 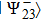. Theoretically, qubits 1 and 4 in this connection can be at any distance from each other.

It is considered in the analyzed example, that both qubit pairs are prepared in a pure Bell’s state 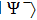and as a result of ES, we obtain the same pure entangled state of qubits 1 and 4, which can be located at a distance from the initially prepared pairs of qubits. In quantum information science the pure states are sometimes called coherent states because unlike the mixed states, they can be represented as a coherent superposition of basis states.

In this paper the process of entanglement swapping is considered under condition of presence of different types of noise in initially prepared entangled states.

For a comparative analysis of states of initially prepared and final pairs of qubits, below we use known characteristics of entanglement: concurrence (C), tangle (τ), entanglement of formation (Ef); characteristics of degree of mixture: von Neumann entropy of two-qubit state condition (E), purity (Tr 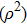), linear entropy SL; degree of coincidence (or differences) of initial and final states: trace metric δ and fidelity F.

For the initial state of two-qubit system and for states, produced by ES we will calculate next sequence of characteristics (points (i)–(ix) will be calculated in next chapters for initial state, and (x)–(xi) as comparative characteristics between initial and final states):

(i) Matrix 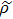(spin flipped state) by converting:

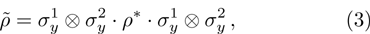
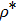
where, σ 1y and σ 2y-Pauli matrices σy, acting respectively to the state spaces of the first and second qubits, and -matrix is complex conjugated of matrix ρ;

(ii) Product

(iii) Eigenvalues of the matrix 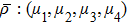. We order the eigenvalues according to the rule ;

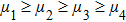(iv) Concurrence:

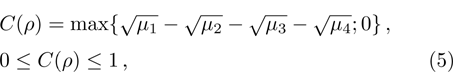
in this paper the value C = 1 corresponds to the most entangled pure state, and C = 0 – to white noise;

(v) Tangle:

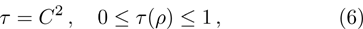
τ = 1 for the most entangled (pure) state and τ = 0 for non-entangled state;

(vi) Entanglement of formation:

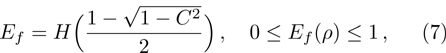
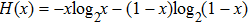
where, binary Shannon entropy;

(vii) Purity:

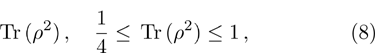
purity = 1 for the pure state, and 1/4 for most mixed state (white noise);

(viii) Linear entropy:

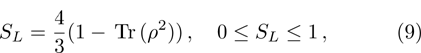
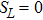
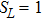
for the pure state, and for most mixed state;

(ix) Von Neumann entropy:

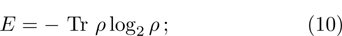
(x) Trace metric δ, which is a measure of the distance between two states:

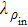
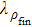
where are eigenvalues of matrix density of each of the initially prepared qubit pairs, are eigenvalues of matrix density obtained by the operation ES. If δ is a measure of the distance between two states, so the parameter

characterizes the degree of their coincidence:

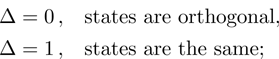
(xi) Fidelity

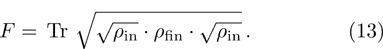
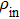
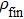
As in our case and commute, then

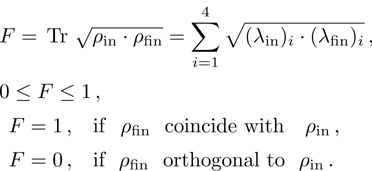
Let us consider the phenomenon of entanglement swapping in a case where each of the two qubit pairs is formed in a mixed state.

2 Entanglement Swapping in the Case of Presence of White Noise in the Initial State

Let us add all the basic states with the same weight coefficients to the pure state 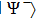in a mixture. Density operator of such a state is called the Werner state[15] and represented as:

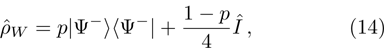
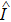
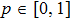
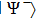
where is unit operator in four-dimensional space, p is a variable parameter, . As p = 1, Eq. (14) is a pure state , and for p = 0, Eq. (14) is white noise. The corresponding density matrix in the computational basis is:

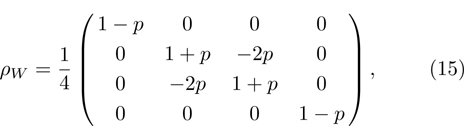
but in Bell basis (2) it is represented by a diagonal matrix:

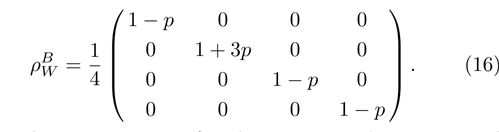
The density operator of such a state can be represented as a mixture of Bell states:

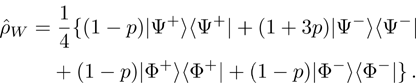
Supposing that qubit pairs with numbers (1, 2) and (3, 4) are prepared independently, the density operator of two pairs of qubits system is represented as tensor product of states (14):

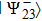
As a result of the projection (17) on Bells state we obtain density matrix of a pair of qubits 1 and 4:

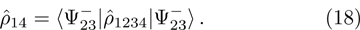
Normalized matrix representation has the form

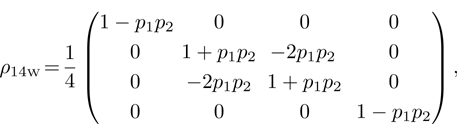
in computational basis, and

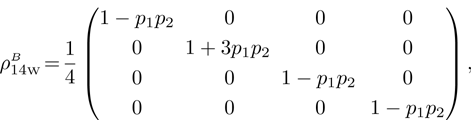
in Bell’s basis, where p1 and p2 are pure state weight coefficients with respect to the first and the second initial qubit pairs (pairs of particles 1, 2 and 3, 4). Hence,

(i) If one of the qubit pairs is prepared in a pure state (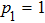 or ), so the density matrix ρ14 duplicates a density matrix of the second pair of qubits prepared in the mixed initial state.

(ii) If both qubit pairs are prepared in the mixed state, then the resulting state of qubits pair 1 and 4 will be noisier than the state of each of the initially prepared pairs.

Let us consider the case 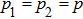in detail. Then the density operator of the final state of qubits for ES operation will be similar to Eq. (14):

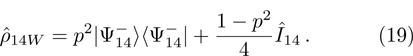
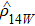
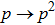
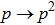
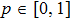
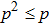
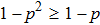
Thus, is obtained from Eq. (14) by replacement of (), the density matrix of this state in the computational and in Bell’s basis looks like Eqs. (15) and (16) after replacing in them. That means that the states of initial and final qubits pairs are similar with accuracy up to the replacement mentioned above. Since , then and, thus, , which indicates an increase in admixture of white noise as a result of transition from the initial to the final state.

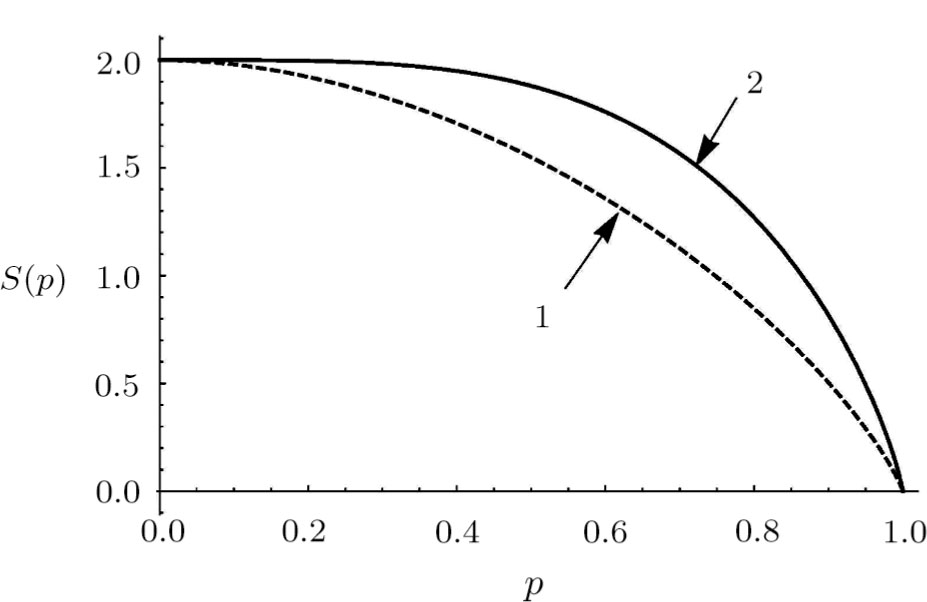
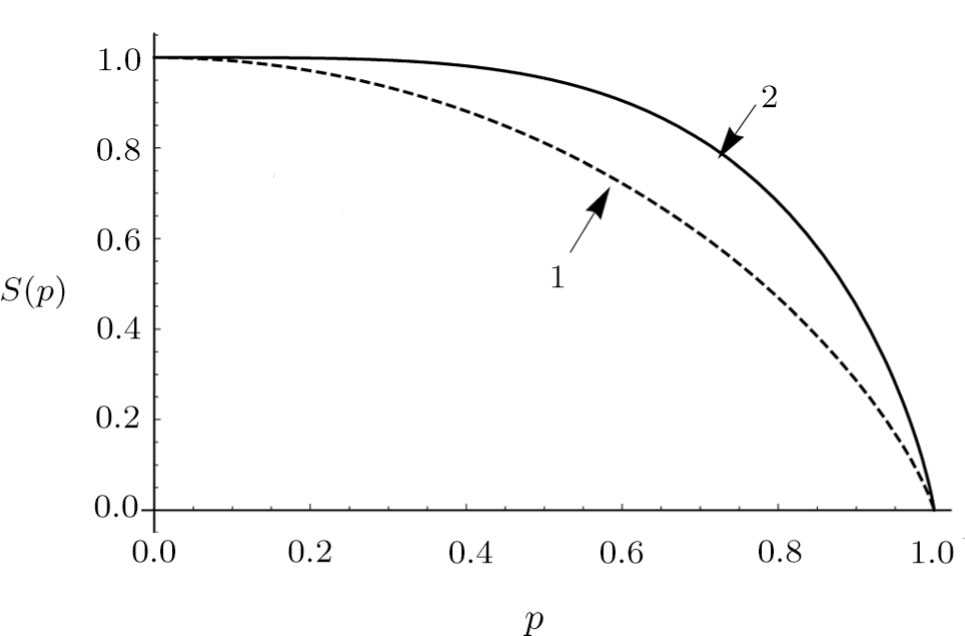
Comparison of the von Neumann entropy values for each of the initial and final pairs of qubits gives a clear demonstration of an increase in admixture of white noise. Figure 2 reproduces the entropy dependence on the parameter p for both systems. The solid-line curve corresponds to the entropy of pair of 1 and 4 qubits, a dashed-line curve corresponds to the entropy of each of the initial qubit pairs.

Fig. 2 Dependence of the von Neumann entropy on parameter p. Curve 1 for each initial qubit pairs (Werner state), curve 2 for qubit pair, obtained by ES procedure.

The figure shows that the entropy of the final pair of qubits for 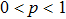exceeds the entropy of each pair of qubits in the initial state, that just shows the increase of noise. The biggest difference of entropies 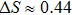is observed at 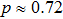. For p = 1 and p = 0 values S(p) for both curves are the same, since under ES the pure state in the initial state gives pure in the final, and white noise can transform only into white noise.

According to the Perez-Gorodetsky criterion[16–17] the positive partially transposed (PPT) density matrix is necessary and sufficient condition for the absence of entanglement in the two-qubit systems. Violation of this condition indicates the presence of entanglement.

Partially transposed density matrix of initial state (15) in the standard basis is presented as:

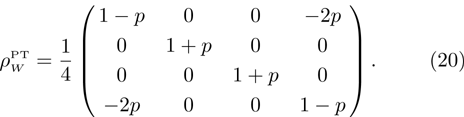
Let us find the range of parameter p, which provides the entanglement of initial qubits pair. After diagonalization of Eq. (20) we obtained:

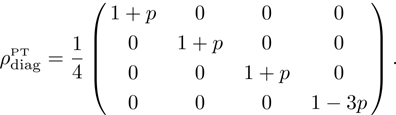
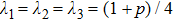
The eigenvalues of the matrix (20) for are nonnegative. The only eigenvalue that can take negative values is λ4:

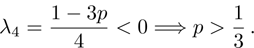
For Werner state this result is well known and was first presented in Ref. [3].

The range of p, for which final state is entangled, is defined by similarity of 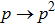between initial and final pairs:

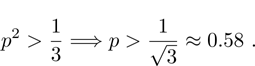
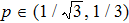
Thus, the initial entangled states of two qubit pairs with form non-entangled state after entanglement swapping operation, i.e. the entanglement property is lost.

Now let us consistently follow point-by-point the steps (i)–(xi) mentioned above in Sec. 1. Analytical expressions for points (i)–(ix) are presented only for the characteristics of initial qubits states (Werner states). The corresponding values for the final states could be obtained by simple replacing 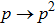. Other characteristics ((x) and (xi)) are obtained using initial and final states. Comparison of corresponding characteristics of the initial and final states was conducted by means of graphs. In accordance with points (i)–(xi) we consistently find:

(i) Matrix (3):

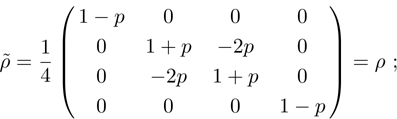
(ii) Product (4). Since , then :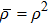

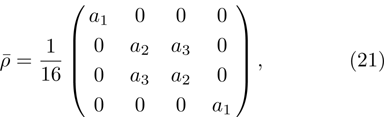
where , , ;

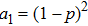
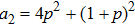
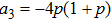
(iii) Eigenvalues of matrix (21):

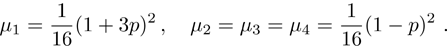
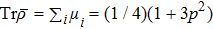
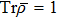
Let us indicate that and for p = 1, , as it should be for a pure state;

(iv) “Concurrence” (5):

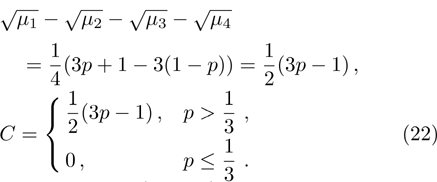
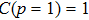
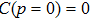
Let us indicate that for a pure state, for a white noise;

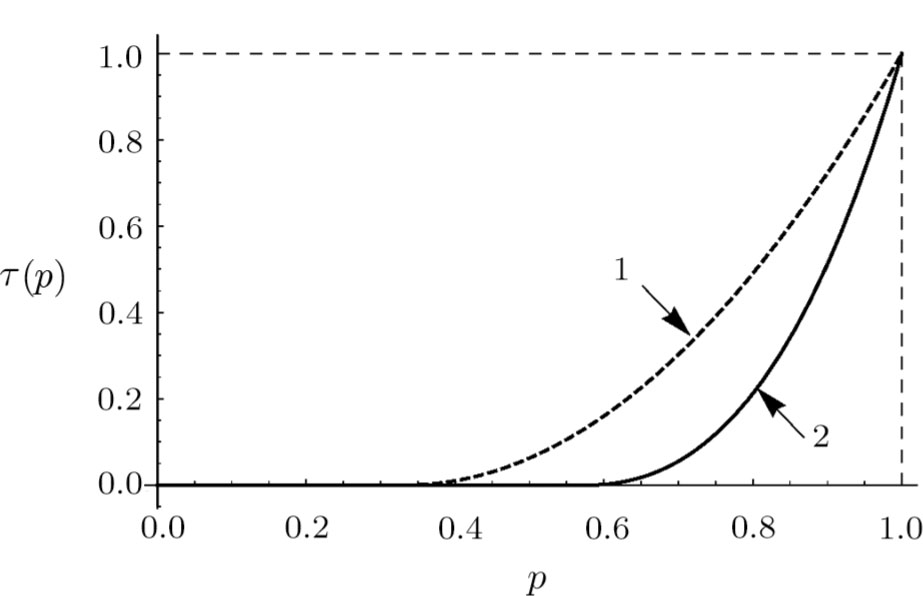
(v) “Tangle” (6):

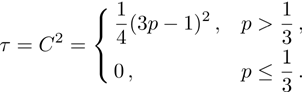
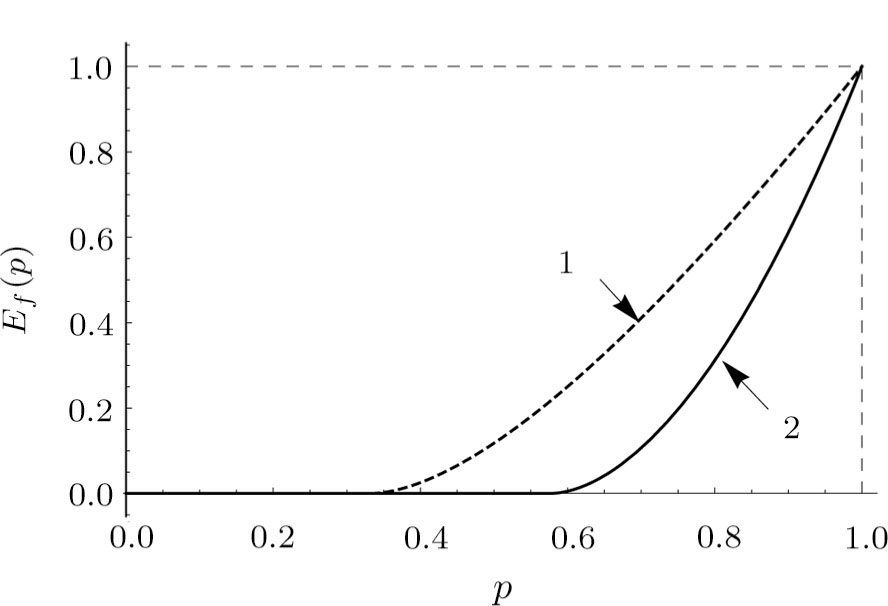
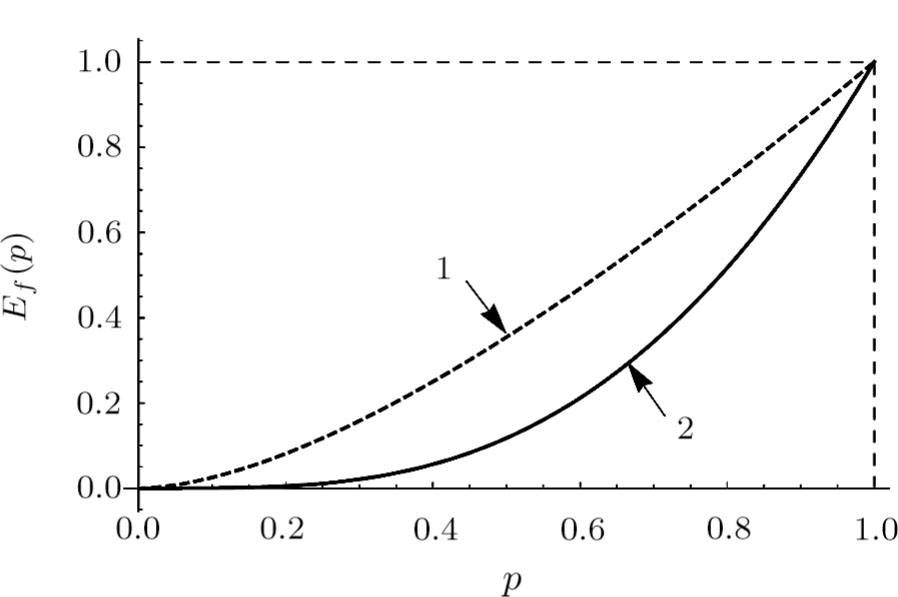
(vi) “Entanglement of formation” (7):

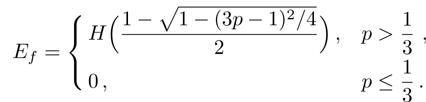
(vii) Purity (8):

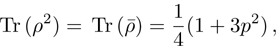
for a pure state, for a white noise;

(viii) Linear entropy (9):

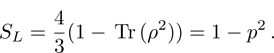
(ix) Von Neumann entropy (10), which can be obtained by taking the eigenvalues of the matrix ρ (16):

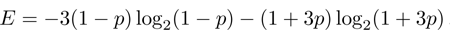
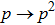
We remind that similar characteristics of the final state are obtained by replacing of in points (i)–(ix). Let us indicate the value of similarity (or difference) of characteristics of initial and final qubits states.

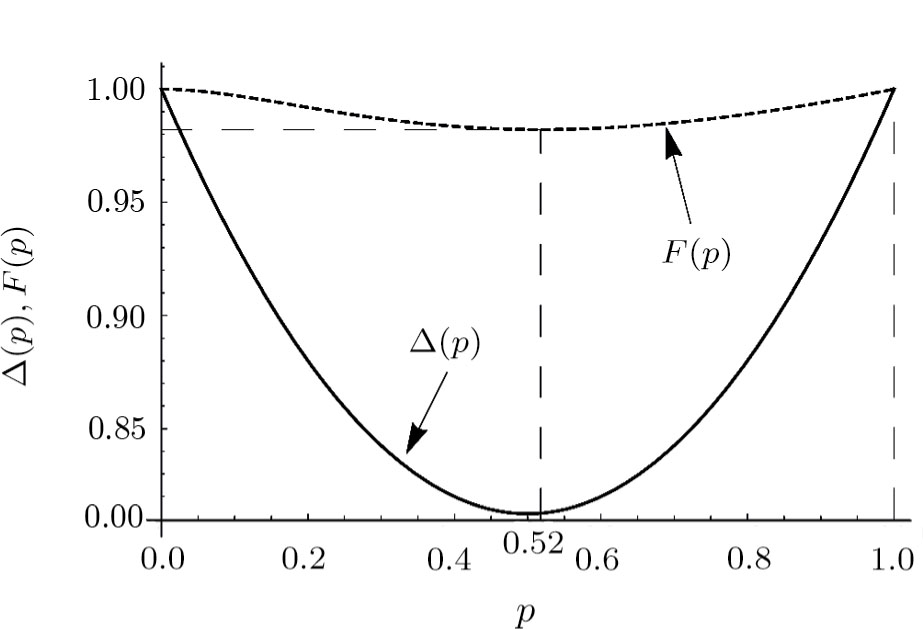
(x) Trace metric δ (11) and parameter :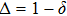

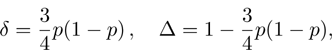
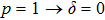
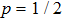
for p = 0 and : white noise becomes white noise and pure state becomes pure state. The final state is the least similar to the original if and .

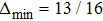
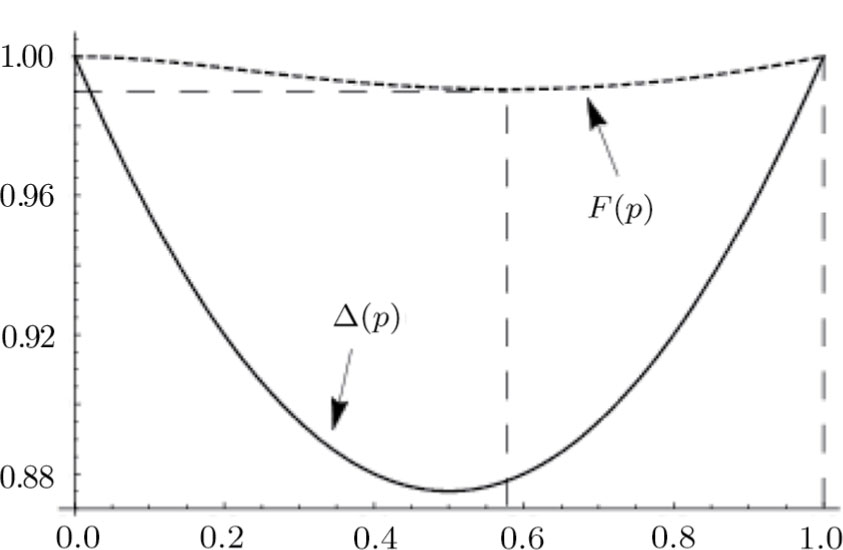
(xi) Fidelity (13)

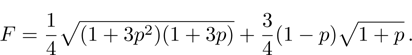
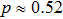
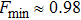
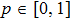
This similarity measure has its minimum for , . It follows thence that for all fidelity value differs little from F = 1.0, thus indicating a weak sensitivity of the given characteristics to a state change as a result of ES. The parameter Δ turns out to be more sensitive measure.

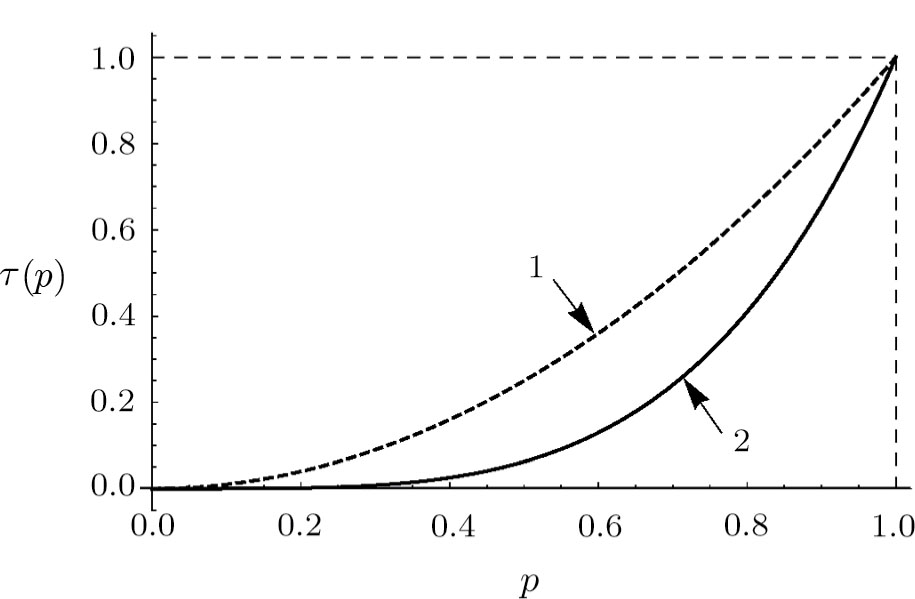
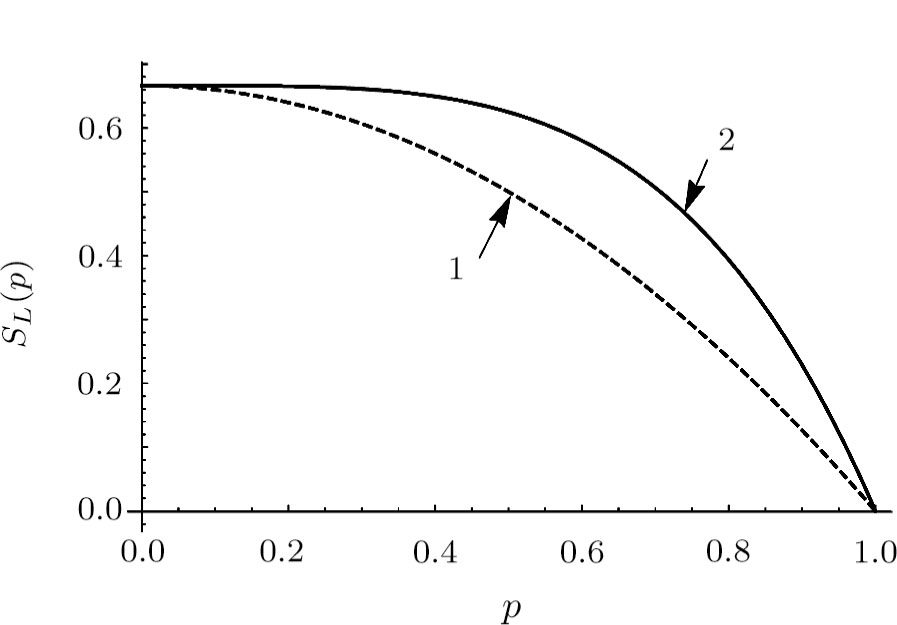
Figures 3–5 show corresponding dependencies “tangle”, “entanglement of formation”, linear entropy on the parameter p for the state of initially prepared qubits pairs (dashed-line curve) and a pair of qubits state produced by ES (solid-line curve). Figure 6 depicts dependencies graphs 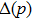and F(p), which characterize the similarity between the initial and final states.

Fig. 3 “Tangle” dependence of state qubits pairs on parameter p. Curve 1 is for initially prepared state of qubits pair (Werner state), curve 2 for qubits pair state obtained as a result of the ES operation.
Fig. 4 Dependence “entanglement of formation” of qubits pair state on parameter p. Curve 1 is for initially prepared state of qubits pair (Werner state), curve 2 for qubits pair state obtained as a result of the operation ES.
Fig. 5 Dependence of linear entropy of qubit pair on parameter p. Curve 1 is for initially prepared state of qubits pair (Werner state), curve 2 for qubits pair state obtained as a result of the operation ES.
Fig. 6 Dependences of similarity characteristics between initial and final states and fidelity F(p) for Eqs. (14) and (18) states, if the white noise is presented in the initial states.
3 Entanglement Swapping in the Case of Presence of Color Noise in the Initial States

Let us now analyze the final state of qubits pair after ES operation in the case of presence of color noise in the initial states.

The initial state of each qubits pair (ρ12 and ρ34) now looks as follows:[18]

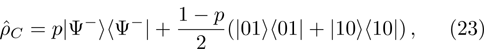
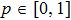
where . Density matrix of the state looks as follows in the standard basis:

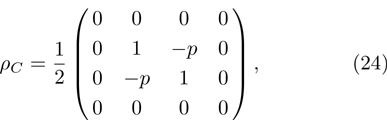
and in Bell’s basis (2):

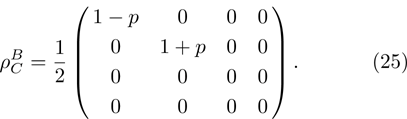
Substituting the initial density operator of qubit pairs (23) with different parameters p1 and p2 in expression (17) and (18) we obtain the following matrix representation ρ14:

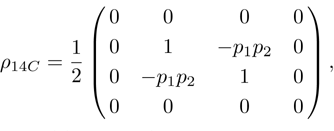
n computational basis, and

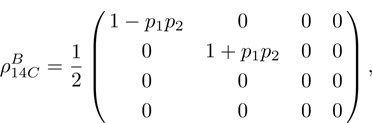
in Bell basis.

Hence, it follows that if one of the qubit pairs (e.g. a pair from first and second qubits) is prepared in the pure state (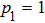), then final state density matrix ρ14 duplicates density matrix ρ34 of second qubits pair in the initial state.

For 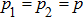density operator of qubits final state can be represented in a similar way to Eq. (23), namely:

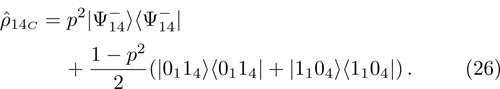
Since, as it was in previous case, the states of initial and final qubit pairs are similar, then corresponding final state density matrices in the computational and Bell basis can be obtained from Eqs. (24) and (25), following the replacement .

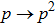
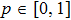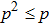As a result of the operation ES, the share of color noise increases. So far , and then 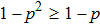. If p = 0 or p = 1 the final state fully duplicates initial state.

Figure 7 represents comparative graphs of the von Neumann entropy two-qubit system dependence on the parameter p for the state of each initially prepared qubit pairs (dashed-line curve) and qubits pair state obtained by means of operation ES (solid-line curve).

Fig. 7 Dependence of von Neumann entropy on p in the presence of color noise. Curve 1 is for initially prepared states of qubits pairs, curve 2 for qubits pair state obtained as a result of the ES operation.

The figure shows that the entropy of the final qubits pair for 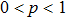exceeds entropy of qubits pairs in the initial state, that is a result of increasing of noise. The biggest difference of entropies 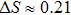is observed if .

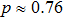Let us also indicate that the maximum entropy value (for p = 0) equals 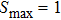, while in the previous case (white noise) 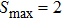. This difference is quite standable since white noise is the most chaotic state.

Reduced density matrix corresponding to the matrices (24) and (25), is proportional to the identity matrix, as well as in the previous case, and therefore von Neumann entropy for the reduced matrix of each qubit from pair does not depend on p and equals 1 — the highest possible value for a single qubit.

Partially transposed density matrix of the initial state of qubits pair in the standard basis looks as follows:

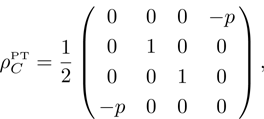
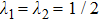
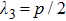
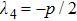
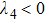
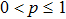
and the eigenvalues of the matrix have the values , , . Thus for indicates that each initially prepared states is the entangled state.

Using the similarity of initial and final states (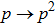), we come to conclusion that pair of qubits 1 and 4 after performing the operation entanglement swapping will also be entangled for any value of the parameter 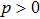. In this case it is impossible situation when entangled state becomes non-entangled after ES.

Below we present the values of characteristics (i)–(ix) only for initially prepared pairs of qubits. The same values for the qubit state pairs obtained by ES operation, are defined by similarity 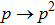. Other characteristics ((x) and (xi)) are obtained using initial and final states. Thus we find:

(i) Matrix 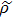(3):

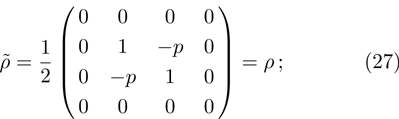
(ii) Product 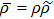(4). Since 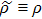, then :

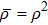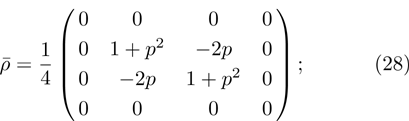
(iii) Eigenvalues of the matrix (28):

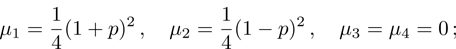
(iv) “Concurrence” (5):

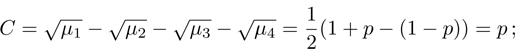
(v) “Tangle” (6):

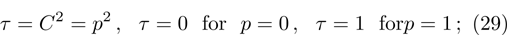
(vi) “Entanglement of formation” (7):

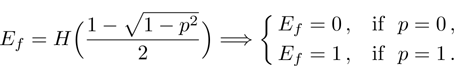
(vii) Purity (8):

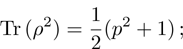
(viii) Linear entropy (9):

(ix) von Neumann entropy (10), which can be obtained by taking the eigenvalues of the matrix ρ from Eq. (25):

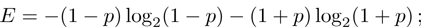
(x) Parameters δ (11) and Δ (12)

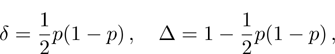
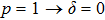
for p = 0 and , Δ = 1. The initial and final state are the most different from each other while p = 1/2, Δ = 7/8;

(xi) Fidelity (13)

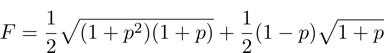
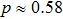
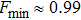
has minimum for , . So, in this case fidelity is not sensitive to operation ES.

Figures 8–10 show corresponding dependencies of “tangle”, “entanglement of formation” and linear entropy on the parameter p for initial and final states.

Fig. 8 Dependence of “tangle” on p parameter. Curve 1 is for initially prepared states of qubits pairs (color noise), curve 2 for qubits pair state obtained as a result of the ES operation.
Fig. 9 Dependence of “entanglement of formation” on p parameter. Curve 1 is for initially prepared states of qubits pairs (color noise), curve 2 for qubits pair state obtained as a result of the ES operation.
Fig. 10 Dependence of linear entropy on p parameter. Curve 1 is for initially prepared states of qubits pairs (color noise), curve 2 for qubits pair state obtained as a result of the ES operation.

Figure 11 depicts dependencies of Δ and F on p. From Eqs. (29) and (30) it immediately follows that between SL and τ there is a simple dependence 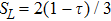, which is the same for both the initial and final states.

Fig. 11 Dependence of and F(p) for Eqs. (23) and (26) states.
4 Entanglement Swapping in the Case of Presence of White and Color Noise in the Initial States

Let us assume now that there is simultaneous presence of white and color noise in the initial states of two pairs of qubits.

State of initially prepared pairs in this case is defined by density operator:[19]

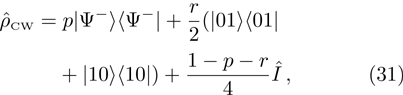
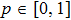
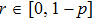
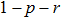
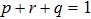
where, , r is share of color noise (weight coefficient), . Weight coefficient of white noise, which equals to , we denote below as q. is condition of density normalization.

Density matrix (31) in the standard basis looks as follows:

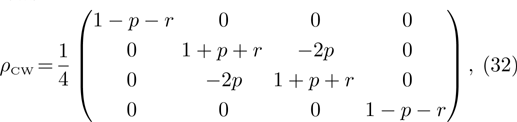
and in Bell basis:

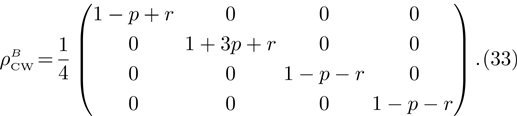
Substituting the initial density operator of qubits pairs (31) with different parameters p1, p2, r1 and r2 into expression (17) and (18) the matrix representation of qubits pair state 1 and 4 as a result of operation ES will look as follows:

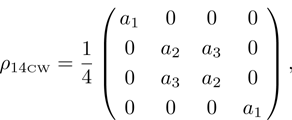
where , , n computational basis, and

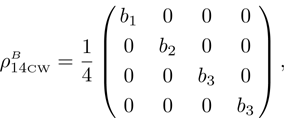
in Bell basis, where , , .

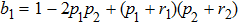
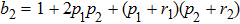
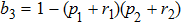
While 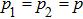, , 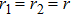density operator of final state of qubits can be represented in a way similar to Eq. (31), namely:

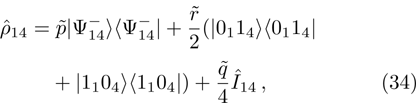
where:

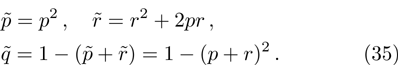
Let us analyze now the redistribution 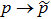, , 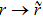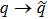as a result of the ES process.

For p = 1 (then r = 0 and q = 0) we obtain: 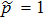, , 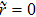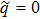. Thus, as mentioned above, the initial pure state becomes a pure state.

For p = 0 and 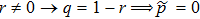, , 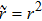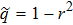. Since, 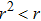(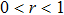) and , then a share of white noise is increased only by reducing the color noise.

For p = 0, r = 0 (then q = 1) 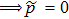, , 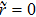, 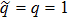i.e. the state does not change.

If in the initial state (31) share of pure state equals to the share of white noise: 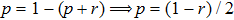, then, as a result of ES the share of color noise does not change, the increase of white noise occurs only by reducing the share of pure state. Actually:

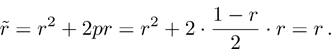
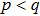
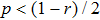
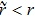
Then it is clear that for () we obtain — share of color noise reduces, i.e. an increase of white noise occurs as the result of decreasing pure state and color noise shares.

For 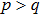(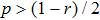) the color and white noises increase by reducing the share of pure state.

Density matrix of state (34) in the standard basis has the form

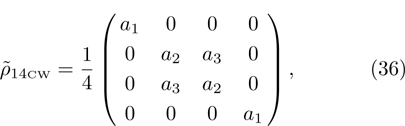
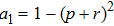
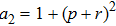
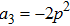
where, , , , and in Bell basis

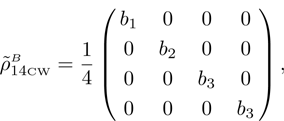
where , , .

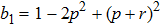
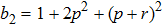
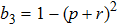
For any 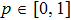and 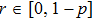von Neumann entropy values 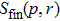of final state will exceed the entropy value 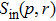of each initial states. The biggest difference of entropies 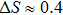is observed if , .

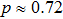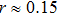Reduced density matrices corresponding to the matrices (32) and (36), will be proportional to the identity matrix, as in the previous case, and therefore von Neumann entropy for state of each qubit equals 1 and does not depend on p and r.

Let us find a range of p and r when a state of each initially prepared pairs is entangled. Partially transposed density matrix for the state of each initially prepared pairs in standard basis looks as follows:

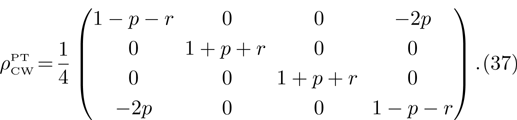
After diagonalization of Eq. (37) we have:

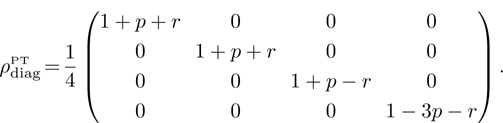
Due to conditions (, ) only one eigenvalue of partially transposed matrix may be less than zero, namely:

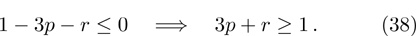
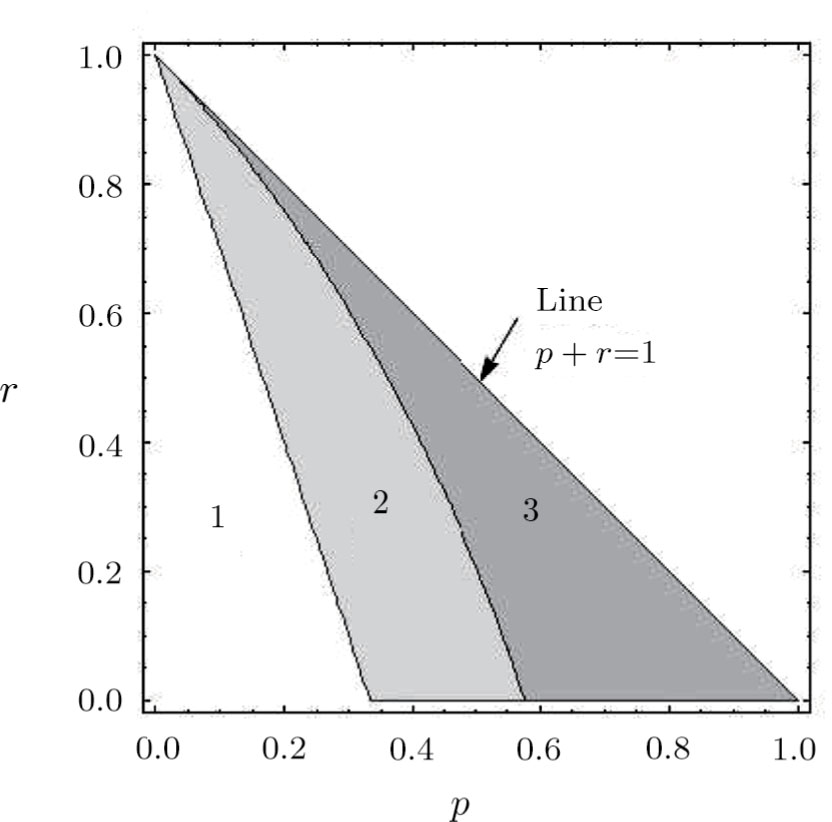
This result was obtained earlier in the paper.[19]

Let us now find the range of values p and r, for which the final states are entangled. Such a range one can express by means of inequality, which results from Eqs. (35) and (38):

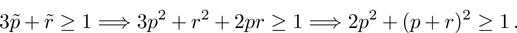
Figure 12 shows ranges of parameter values p and r, in which the initial and final system are or not entangled.

Fig. 12 Ranges of parameters p and r: 1 is for initial and final states are nentangled (separable), 2 for initial state is entangled, final is unentangled, 3 for initial and final states are entangled.

The graph shows that there is a range of parameter values (in Fig. 12 denoted as 2), in which the state of each initially prepared pair is entangled, but a pair state obtained as a result of operation ES, is unentangled. Thus, the ES process makes possible a situation when the final state of qubits 1 and 4, as a result of noises influence, will not be entangled, while the initial qubit pairs are entangled.

Let us now give initial state characteristics according to points (i)–(ix). Corresponding characteristics for final state could be found from below values for initial state, by applying designations from Eq. (35) 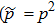, 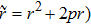. Two last points (x)–(xi) are calculated using initial and final states. Thus we find:

(i) Matrix 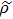(3):

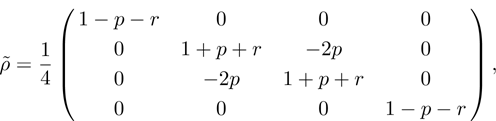
which exactly equals to ρ;

(ii) Product (4):

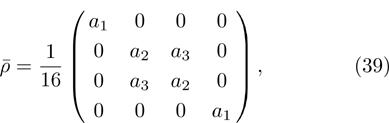
where , , ;

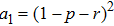
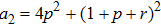
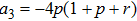
(iii) Eigenvalues of the matrix (39):

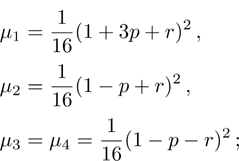
(iv) “Concurrence” (5):

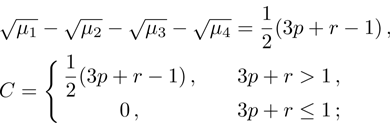
(v) “Tangle” (6):

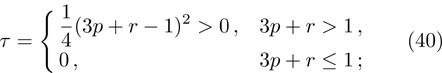
(vi) “Entanglement of formation” (7):

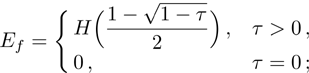
(vii) Purity (8):

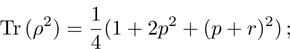
(viii) Linear entropy (9):

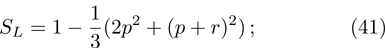
(ix) von Neumann entropy (10), which can be obtained by the eigenvalues of the matrix ρ from Eq. (33):

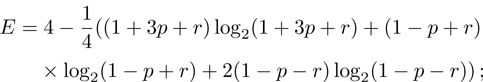
(x) Parameter δ (11):

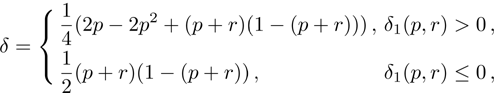
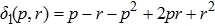
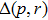
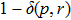
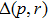
where . Different values of δ for different δ1 are caused by absolute values of differences between eigenvalues of initial and final state matrices. Parameter may be obtained by Eq. (12) as . The minimum value obtained for p = 0.5, r = 0, ;

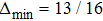
(xi) Parameter F (13):

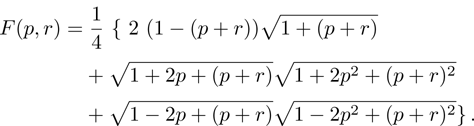
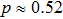
This measure of similarity has minimum for , r = 0, .

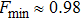
5 Conclusions

(i) If one of the qubits pair is prepared in a pure state (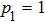, or 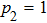), then density matrix of qubits pair ρ14, that is obtained by the ES process, duplicates density matrix of the second pair of qubits, prepared in a mixed state. If both pairs of qubits are prepared in a mixed state, then the final state of qubits pair 1 and 4 will be noisier than a state of each initially prepared pair that leads to an increase in von Neumann entropy of qubits pair.

(ii) Entanglement swapping produces various schemes of white and color noise redistribution. It depends on ratio between white and color noise in the initial states. (Detailed description of different schemes of redistribution see above in the text).

(iii) In the entanglement swapping process for some range of parameters values p and r occur total decoherentization of state –entangled state becomes an unentangled one.

(iv) Results could be helpful for experiments regarding entanglement swapping as conditions for prepared quantum entangled states, to obtain result state as also entangled. It could be used for configuration of quantum communication channels devices such as quantum repeaters.

Reference
[1] Aspect A. Dalibard J. Roger G. Phys. Rev. Lett. 49 1982 1804
[2] Einstein A. Podolsky B. Rosen N. Phys. Rev. 47 1935 777
[3] Bennett C. H. Brassard G. Crepeau C. et al. Phys. Rev. Lett. 70 1993 1895
[4] Horodecki R. Horodecki P. Horodecki M. Horodecki K. Rev. Mod. Phys. 81 2009 865
[5] Hu C. Y. Rarity J. G. Phys. Rev. B 83 2011 115303
[6] Zukowski M. Zeilinger A. Horne M. A. Ekert A. K. Phys. Rev. Lett. 71 1993 4287
[7] Dur W. Briegel H. J. Cirac J. I. Zoller P. Phys. Rev. A 59 1999 169
[8] Xue Z. Y. Yi Y. M. Cao Z. L. Chin. Phys. 15 2006 1421
[9] Tsai C. W. Hwang T. Phys. Scr. 84 2011 045006
[10] Pan J. W. Bouwmeester D. Weinfurter H. Zeilinger A. Phys. Rev. Lett. 80 1998 3891
[11] Jennewein T. Weihs G. Pan J. W. Zeilinger A. Phys. Rev. Lett. 88 2001 017903
[12] de Riedmatten H. Marcikic I. van Houwelingen J. A. W. et al. Phys. Rev. A 71 2005 050302(R)
[13] Lu C. Y. Yang T. Pan J. W. Phys. Rev. Lett. 103 2009 020501
[14] Scherer A. Howard R. B. Sanders B. C. Tittel W. Phys. Rev. A 80 2009 062310
[15] Werner R. F. Phys. Rev. A 40 1989b 4277
[16] Peres A. Phys. Rev. Lett. 77 1996b 1413
[17] Horodecki M. Horodecki P. Horodecki R. Phys. Lett. A 223 1996 1
[18] Cabello A. Feito A. Lamas-Linares A. Phys. Rev. A 72 2005 052112
[19] Dotsenko I. S. Voronov V. G. Opt. Commun. 282 2009 2889