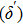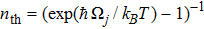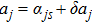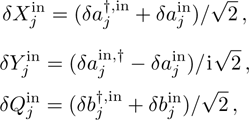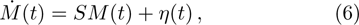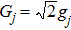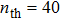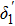Cite this Article
Gebremariam Tesfay, Zeng Ye-Xiong, Chen Xin-Yu, Li Chong. Observation and Measures of Robust Correlations for Continuous Variable System. Communications in Theoretical Physics, 2017, 68(5): 661  
Permissions
Observation and Measures of Robust Correlations for Continuous Variable System
Gebremariam Tesfay, Zeng Ye-Xiong, Chen Xin-Yu, Li Chong †
School of Physics, Dalian University of Technology, Dalian 116024, China

 

† Corresponding author. E-mail: lichong@dlut.edu.cn

Abstract
Abstract

In this work, we examine the robust continuous variable quantum correlation by analyzing two coupled optomechanical systems. Under the linearization approximation, the steady state correlation is quantified through correlation function of two non-Hermitian operators and we find that quantum correlation is always existence between two optical fields, two-oscillators and optical field-oscillator. Unlike the discrete variable system, we show quantum correlation in our model seems to be independent without any close transfer relationship. We further emphasize the influence of cavity-cavity coupling parameter on the amount of quantum correlations.

PACS: 42.50.Dv
Keyword:steady state correlations;quantum measurement;continuous variable systems
1 Introduction

Quantum correlations are fundamental resource in quantum information process (QIP), and it plays a key role in many QIP,[1] such as quantum cryptography,[2] quantum teleportation,[3–4] and quantum dense coding.[5–6] In particular, recent researches have proven that the continuous variable (CV) correlations are more appropriate and perfect candidates for many-body QIP in quantum network.[7–9]

Recently, different theoretical researchers have been proposed to dynamics and improvement of quantum correlations, and correlation criteria.[10] Among the quantum correlation criteria; Simon criterion,[11] Duan criterion,[12] which has been demonstrated for separability of bipartite CV states, and Henderson and Vedral,[13] and Olivier and Zurek[14] introduced a new measure, called Quantum Discord (QD), and concluded that quantum entanglement did not properly span all non-classical correlations. In addition a measure of quantum correlation for arbitrary dimension bipartite states using nonlocal coherence is proposed, and it can be easily generalized to the multipartite case.[15] Recently, the dynamics of quantum correlation of four qubits system using quantum consonance and concurrence has been demonstrated.[16] Thus, criteria as well as some other measures are useful measurements in describing quantum correlations for the bipartite systems.[17] However, as the dimensions of the subsystems increasing, the computation of quantum correlations becomes formidably complicated. A few exact formulae for multipartite quantum correlations have been given only in some special cases.[18–19] Therefore, how to quantify and understand quantum correlations is still the subject of active research.

Recently, it has been widely recognized that optomechanical systems have become a cornerstone for many research activities.[20–22] Several interesting optomechanical devices can be used in two-mode squeezed states,[23] performing high-precision measurements,[24] studying the transitions from Micro-to-Macro entanglement,[25] and processing quantum information.[26] Quantum correlation criteria is prerequisite to judge whether or not quantum correlation exists in the systems, however most of the criteria they can not tell us how much quantum correlations exists in the system. Recently, Yang et al.[27] propose a correlation measurement (by using photon correlations function for quantum correlation of CV systems, and they showed that it is fit for most CV systems and it is a convenient measurement for quantum correlation dynamic of two mode CV systems. Recently, there are considerable interest in studying quantum correlation in mesoscopic optomechanical system.[28] All these novel phenomena become an interesting research topics and potential platforms to study quantum correlation at macroscopic and mesoscopic scales.

In this work, we study quantum correlation measurement (QC) in two coupled optomechanical systems. In order to judge and observe whether correlation is presented in the coupled system, we employed a measure of QC [27] in two coupled optomechanical systems. By this measurement, we study quantum correlation between two CV system such as: two-optical fields (, two-oscillators ( and optical field-oscillator (), and showing the influence of cavity-cavity coupling strength on quantum correlation of coupled system. We observed that the minimum value of quantum correlation is non zero, this approves the possibility quantum correlations are exist in proposed model.

The paper is organized as follows. In Sec. 2, we introduce the model and details of the formalism that describes the system. In Sec. 3, we introduce and present correlation measures, in particular quantum correlation measurement . In Sec. 4, we present and discuss the results of the quantum correlations between measurement 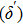between two optical fields, two-oscillators and optical field-oscillator. The conclusions are drawn in Sec. 5.

2 Model and Hamiltonian

We consider a model of two coupled optomechanical systems,[29–31] shown schematically in Fig. 1, focusing on the characterize the two different measures, which quantify the level of correlations of coupled CV systems[32–33] as a specific example. Each of optomechanical system j = 1, 2 is represented by an optical cavity modes. The Hamiltonian of this system is

Here, the first term describes the sum of energy corresponding to the optical cavity modes, with photon operators , with frequency ωcj and the mechanical modes, with phonon operators and frequency Ωj, the second term is the usual optomechanical interaction term with optomechanical interaction strength gj, the third term corresponds to driving field, and the last term describes the coupling between the two cavity modes a1 and a2, with the optical fiber term of intensity J.

Fig. 1 Schematic diagram of two coupled optomechanical system corresponding to our model. The coupling between the two optomechanical system is via. an optical fiber with J being the coupling parameter, and the other symbols are defined in the main text.

The Hamiltonian of the whole system is written as follows after a frame rotating;

where, is the optical detuning and is the driving amplitude, related to driving power P and optical decay κj by , and (L, cavity length; m, effective mass).

In addition, the system dynamics also includes fluctuation-dissipation processes affecting both the two optical fields and two mechanical oscillators. Starting from Hamiltonian Eq. (2), the time evolution of the optomechanical system is given by the following nonlinear quantum Langevin equations;[34–36]

Here, κj and γj are, respectively, the optical and mechanical damping rates while and are the input bath operators, which satisfies .[37] Correspondingly, is the Brownian noise operator, which describes the dissipative friction force acting on the mirror and its autocorrelation function is

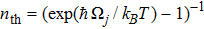
under the Markovian approximation,[38] where is the mean occupation number of the mechanical baths, which gauges the temperature T of the system.[38–39] (since we are only interested in the situation in which , the parameter can be safely taken to be equal for both mechanical modes).

Under intense laser driving, we now expand each field operators as a sum of its coherent amplitudes (semi-classical) steady-state value plus an additional small fuctuation operator with zero-mean value as 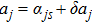and . The steady-state values are given by the following nonlinear equations;

where, is the effective optical detuning. As for the fuctuations, their dynamics is given by the linearized quantum Langevin equations[40–41]

Next, we introduce the dimensionless quadrature operators, respectively, for the optical and mechanical modes:

and similarly for the corresponding Hermitian input noise operators:

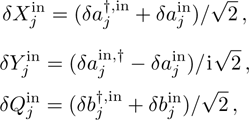
.[45] With the above definitions, we express Eq. (5) in a more compact form

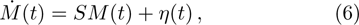
with setting M(t) is the column vector of the quantum fluctuations and being the column vector of the noise sources. Their transposes elements are given by;

and the corresponding S is 8× 8 time-dependent coefficient matrix

Here, 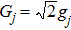is the effective optomechanical coupling strength, and S matrix contains an information of the mean values of the system. Moreover, the system is stable only if all the eigenvalues of the matrix S have negative real parts. The stability conditions can be given explicitly by using the Routh–Hurwitz criterion.[41] However, they are too cumbersome to be given here.

Since the dynamics is linearized and the initial state of the system is Gaussian in nature and the steady state for the quantum fluctuation is simply a zero-mean Gaussian bipartite state, which is fully characterized by the following correlation matrix[42]

Moreover, the stability criteria[41] are satisfied to our system, and the steady-state correlation matrix of the quantum fluctuation can be derived directly by Refs. [43–44] meets the following Lyapunov equation;

where is the diagonal noise correlation matrix with diagonal entries. Note that Eq. (10) is a linear equation in V, which can be straightforwardly solved. However, an exact analytical expression is too cumbersome and will not be reported here.

3 Quantum Correlation Measurement

In order to explain our idea more clearly and measure quantum correlation between the subsystems, we utilize quantum correlation measurement , which is defined as the correlation function of two non-Hermitian operators

this kind of measurement were used to demonstrating entanglement in two-mode states, and it is a covenant and simple to measure the correlation between the subsystems,[27,46] For some specific kinds of state of CV system (e.g. two mode squeezed vacuum state, two mode entangled coherent state, and two mode thermal state) is consistent evolution with the corresponding to quantum correlation measurement of four qubits system and quantum entanglement.[16,47] Therefore, let us utilize this quantum correlation measurement for two coupled optomechanical systems in the following.

Using Eq. (11), we obtained quantum correlation measurement between two-optical fields

Similarly, the quantum correlation measurement between two-oscillators;

and the quantum correlation measurement between optical fields-oscillator can be written as

4 Results and Discussion

To explicitly observe and study the robust continuous variable quantum correlation, we start our discussion by considering the quantum correlation measurement between two optical fields, two-oscillators, and optical fields-oscillator for two coupled optomechanical system. For simplicity, we choose all the following experimental parameter setting of the cavities and the mechanical oscillators to be the same, for example, , , , , and .[48–50] In the computation, we normalize the above parameters by Ωm and for calculation of the quantum correlation measure to be described below, we set 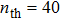(see also the caption of Fig. 2). Moreover, the accuracy of the approximation is also related to the quantum parameter , which is defined in Ref. [51]. In our model we set . With our assumptions about the cavity and mechanical oscillator parameters we show that the expected values and the quantum correlation measurement of the system can be described accurately.

Fig. 2 Quantum correlation measurement versus the normalized detuning , and the physical parameters that have been used in the simulation are g = 0.005, κ = 0.35, γ = 0.008, E = 14, and cavity-cavity coupling strength .

A simulation of optomechanical quantum correlation measurement between two optical fields is plotted in Fig. 2, using realistic values for the parameters[20,22] for which a significant amount of quantum correlation is achievable. Moreover, we observe that the optomechanical quantum correlation measurement between two optical fields is generated in the steady-state. We can see that, when the detuning frequencies between the external laser and cavity field is bigger, the quantum correlation measurement will be small and decay. More important, in our model one can observe that the minimum value is non zero, this shows that there is quantum correlation between two optical fields.

In Fig. 3, we plot the optomechanical quantum correlation measurement , versus the normalized detuning and the parameters that have been used in the simulation are the same as Fig. 2. From this figure, we can see that the quantum correlations measure between two-oscillators decreases with increasing detuning and it becomes quickly decay. Hence, is a very sensitive to the cavity-cavity coupling strength since, in our model there is no direct interaction between two mechanical oscillators, so the correlation is entirely transferred due to the cavity-cavity coupling strength J. This result reveals that by fixing the value of , one can measure the effective optomechanical quantum correlation between two-oscillators. Moreover, the minimum value of the quantum correlations 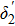is non zero, and it coincisdes with Fig. 2.

Fig. 3 Quantum correlation measurement versus the normalized detuning and the physical parameters that have been used in the simulation are same as Fig. 2.

Figure 4 illustrate the optomechanical quantum correlation measurement between , versus the normalized detuning for , and the other parameters are same as Fig. 2. Here, we find bigger amount of quantum correlation between optical field-oscillator, and we observe that, the minimum value of quantum correlation is non zero, this allows the possibility of quantum correlation can be conveniently observed in the systems. Comparing this quantum correlation measurement with early works of a Fabry–Perot cavity with an oscillating micro mirror and driven by coherent light,[45] this shows will take on the consistent evolution with the corresponding quantum entanglement.

Fig. 4 Quantum correlation measurement versus the normalized detuning and parameters are the same as Fig. 2.

Finally, we discuss how the quantum correlation is influenced by the parameter of cavity-cavity coupling strength, to this purpose we plot in Figs. 5 and 6. For simplicity, taking , and different choices of cavity-cavity coupling strength and , and the other parameters are the same as Fig. 2. The main reason for the choices of the cavity-cavity coupling strength parameter J is to see an evident difference in the quantum correlation measurement in the coupled system. From both figures we note that for different choices of cavity-cavity coupling strength, we obtain different quantum correlation measurement. This implies that, when cavity-cavity coupling strength increases the quantum correlation between two-fields (two-oscillators) decreases, because, the relative ordering of quantum correlation measurement depends on cavity-cavity coupling strength parameter. Furthermore, the amount of correlations between two optical fields have bigger correlations than the two-oscillators, since the two-oscillators do not directly interact with the each others. Moreover, we have observed that the minimum value of quantum correlation measurement is non zero.

Fig. 5 Quantum correlation measurement versus the normalized detuning with different choices of cavity-cavity coupling strengths J.
Fig. 6 Quantum correlation measurement versus the normalized detuning with different choices of cavity-cavity coupling strengths J.
5 Conclusions

We have described measurement of quantum correlation in two coupled optomechanical systems through quantum correlation measurement . We mainly obtained quantum correlation measurement between two-optical fields, two-oscillators and optical field-oscillator. Moreover, we have shown that the minimum value of quantum correlation is non zero, this shows that there exist correlations between the subsystem at a reasonable temperature, which is experimentally relevant. We have further shown that the amount of quantum correlation between two CV systems increases with the decreases of the parameter of cavity-cavity coupling strength. Compare with the discrete variable system, we show that quantum correlation in our model seems to be independent without any close transfer relationship. Our results provide a realistic route toward quantum non-destructive detection and a framework for future optomechanical information processing applications.

Reference
[1] Nielsen M. A. Chuang I. L. Quantum Computation and Quantum Information Cambridge University Press Cambridge 2000
[2] Li C. Song H. S. Zhou L. Wu C. F. J. Opt. B: Quantum and Semi-Classical Optics 5 2003 155
[3] Bennett C. H. Brassard G. Crepeau C. Jozsa R. Peres A. Wootters W. K. Phys. Rev. Lett. 70 1993 1895
[4] Bouwmeester D. Pan J. W. Mattle K. Eibl M. We-infurter H. Zeilinger A. Nature (London) 390 1997 575
[5] Bennett C. H. Wiesner S. J. Phys. Rev. Lett. 69 1992 2881
[6] Braunstein S. L. Kimble H. J. Phys. Rev. A 61 2000 042302
[7] Qin W. Wang C. Cao Y. Lu G. Phys. Rev. A 89 2014 062314
[8] Clader B. D. Phys. Rev. A 90 2014 012324
[9] Braunstein S. L. Pati A. K. Quantum Information with Continuous Variables Kluwer Academic Publishers Netherlands 2001
[10] Feng L. J. Zhang Y. J. Xia Y. J. Optics Commun 366 2016 328
[11] Simon R. Phys. Rev. Lett. 84 2000 2726
[12] Duan L. M. Giedke G. Cirac J. I. Zoller P. Phys. Rev. Lett. 84 2000 2722
[13] Henderson L. Vedral V. J. Phys. A 34 2001 6899
[14] Ollivier H. Zurek W. H. Phys. Rev. Lett. 88 2001 017901
[15] Pei P. Wang W. Li C. Song H. S. Int. J. Theor. Phys. 51 2012 3350
[16] Gebremariam T. Li W. Li C. Physica A 457 2016 437
[17] Xie C. Liu Y. Chen J. et al. Quantum Inf. Process 16 2017 71
[18] Guo J. L. Mi Y. J. Eur. Phys. J. D 68 2014 39
[19] Man Z. X. Zhang Y. J. Su F. Xia Y. J. Eur. Phys. J. D 58 2010 147
[20] Marquardt F. Girvin S. M. Physics 2 2009 40
[21] Meystre P. Ann. Phys. (Berlin) 525 2013 3
[22] Aspelmeyer M. Kippenberg T. J. Marquardt F. Rev. Mod. Phys. 86 2014 1391
[23] Woolley M. J. Clerk A. A. Phys. Rev. A 89 2014 063805
[24] Barzanjeh S. Guha S. Weedbrook C. Vitali D. Shapiro J. H. Pirandola S. Phys. Rev. Lett. 114 2015 080503
[25] Ghobadi R. Kumar S. Pepper B. Bouwmeester D. Lvovsky A. I. Simon C. Phys. Rev. Lett. 112 2014 080503
[26] Zhang W. Z. Cheng J. Liu J. Y. Zhou L. Phys. Rev. A 91 2015 063836
[27] Hua Yang Z. Li C. Shi Y. Yu X. Int. J. Theor. Phys. 55 2016 1036
[28] Li W. Zhang F. Li C. Song H. Int. J. Theor. Phys. 55 2016 2097
[29] Stannigel K. Komar P. Habraken S J M Bennett S. D. Lukin M. D. Zoller P. Rabl P. Phys. Rev. Lett. 109 2012 013603
[30] Chan J. Mayer Alegre T. P. Safavi-Naeini A. H. Hill J. T. Krause A. Groblacher S. Aspelmeyer M. Painter O. Nature (London) 478 2011 89
[31] Ying L. Lai Y. C. Grebogi C. Phys. Rev. A 90 2014 053810
[32] Mari A. Farace A. Didier N. Giovannetti V. Fazio R. Phys. Rev. Lett. 111 2013 103605
[33] Chang D. E. Safavi-Naeini A. H. Hafezi M. Painter O. New J. Phys. 13 2011 023003
[34] Farace A. Giovannetti V. Phys. Rev. A 86 2012 013820
[35] Genes C. Mari A. Vitali D. Tombesi S. Adv. At. Mol. Opt. Phys. 57 2009 33
[36] Wang Y. D. Clerk A. A. Phys. Rev. Lett. 110 2013 253601
[37] Gardiner C. W. Zoller P. Quantum Noise Springer Berlin 2000
[38] Giovannetti V. Vitali D. Phys. Rev. A 63 2001 023812
[39] Liu Y. C. Shen Y. F. Gong Q. Xiao Y. F. Phys. Rev. A 89 2014 053821
[40] Scully M. O. Zubairy M. S. Quantum Optics Cambridge University Press Cambridge 1997
[41] Leng H. Y. Wang J. F. Yu Y. B. et al. Phys. Rev. A 79 2009 032337
[42] Walls D. F. Milburn G. J. Quantum Optics Springer Berlin 1994
[43] Li W. et al. Sci. Rep. 6 2016 31095
[44] Wang G. L. Huang L. Lai Y. C. Grebogi C. Phys. Rev. Lett. 112 2014 110406
[45] Vitali D. et al. Phys. Rev. Lett. 98 2007 030405
[46] Hillery M. Zubairy M. S. Phys. Rev. Lett. 96 2006 050503
[47] Maleki Y. Int. J. Theor. Phys. 56 2017 757
[48] Kippenberg T. J. Vahala K. J. Science 321 2008 1172
[49] Mari A. Eisert J. Phys. Rev. Lett. 103 2009 213603
[50] Eichenfield M. Camacho R. Chan J. Vahala K. J. Painter O. Nature (London) 459 2009 550
[51] Ludwig M. Kubala B. Marquardt F. New J. Phys. 10 2008 095013