Proper Teleparallel Homothetic Vector Fields in General Cylindrically Symmetric Space-Times in Teleparallel Theory of Gravitation Using Diagonal Tetrads

Cite this Article

Shabbir Ghulam, Ali Shahani Masoom, Amer Qureshi M., Mahomed F. M.. Proper Teleparallel Homothetic Vector Fields in General Cylindrically Symmetric Space-Times in Teleparallel Theory of Gravitation Using Diagonal Tetrads. Communications in Theoretical Physics, 2017, 68(5): 611 Copy to clipboard

Permissions

Proper Teleparallel Homothetic Vector Fields in General Cylindrically Symmetric Space-Times in Teleparallel Theory of Gravitation Using Diagonal Tetrads

Shabbir Ghulam^{1, 2, *}, Ali Shahani Masoom¹, Amer Qureshi M.¹, Mahomed F. M.²

1Faculty of Engineering Sciences, GIK Institute of Engineering Sciences and Technology, Topi, Swabi, KPK, Pakistan

2School of Mathematics, University of the Witwatersrand, Johannesburg, Wits 2050, South Africa

† Corresponding author. E-mail: shabbir@giki.edu.pk

Abstract

In this paper we consider the most general form of non-static cylindrically symmetric space-times in order to study proper teleparallel homothetic vector fields using the direct integration technique and diagonal tetrads. This study also covers static cylindrically symmetric, Bianchi type I, non-static and static plane symmetric space-times as well. Here, we will only discuss the cases which do not fall in the category of static cylindrically symmetric, Bianchi type I, non-static and static plane symmetric space-times. From the above study we show that very special classes of the above space-times yield 6, 7 and 8 teleparallel homothetic vector fields with non-zero torsion.

PACS: 04.20.-q;04.20.Jb

Keyword:proper teleparallel homothetic vector field;Weitzenbck geometry;Torsion

Show Figures

1. Introduction

The idea of symmetries of space-time is nearly as old as the origination of the theory of general relativity itself. Symmetries have a vital role in general relativity, which enables one to understand the physical and geometrical aspects of space-times (the details can be found in Refs. [1–2]). Symmetries provide the laws of conservation^[3] and physical information about the underlying space-time. For example, self-similarity solutions are extensively used for cosmological perturbations, star formation, gravitational collapse, primordial black holes, cosmological voids, and cosmic censorship.^[4] Furthermore, symmetries have been studied in the theory of general relativity based on Riemannian geometry and in the theory of teleparallel gravity based on the Weitzenbck geometry.^[5] In general relativity, Einstein’s field equations are invoked to illustrate the interaction of matter. These gravitational field equations being non-linear require some symmetry restrictions on the space-time metric. Symmetries are useful in the study of laws of conservation of matter in a space-time.^[3] In general relativity many exact solutions of Einstein’s field equations are obtained, the details of which can be found in Ref. [6]. Solutions of these equations are then classified according to its Killing, homothetic and conformal vector fields.^[7–11] The theory of general relativity uses Einstein’s field equations to unify mass and energy with the geometric structure of the space-time. Geometric description of the theory has been verified through experiments at the classical level and seems to be true in nature while at the quantum level interactions among the particles do not follow such a description. The quest to obtain consistency and a unified field theory started at this point and Einstein made an attempt at the unification of the laws of the general theory of relativity and quantum gravity. He introduced the notion called absolute parallelism. Although Einstein did not succeed in his attempt, modern researchers have taken up the challenge to unify other known interactions with quantum gravitation. Various endeavors make it possible to give a structure to gravitation other than the metric tensor. In these investigations the metric tensor can be written as a by-product of these structures. One of these structures, known as a tetrad field, is now an elementary entity in teleparallel theory.^[12] In this theory the gravitational interaction of particles are defined only by torsion in the space-time and the curvature is zero due to mass in the space-time. Much interest has been expended to explore the teleparallel versions of exact solutions in general relativity. Pereira et al.^[13] obtained stationary axisymmetric Kerr and Schwarzschild solutions of teleparallel versions in general relativity. An investigation on the energy contents as well as the energy and momentum distribution in both general relativity and teleparallel theory of gravitation was carried out by Sharif and his collaborators.^[14–15] The localization of energy and momentum in general relativity remains a focal problem. Different investigators like Einstein,^[16] Landau–Lifshitz,^[17] Papapetrou,^[18] Tolman,^[19] and Bergmann^[20] defined their own energy momentum complexes to tackle this problem. These definitions to localize energy and momentum complexes have limitations and do not provide a meaningful physical local energy momentum density. Moller^[21] was the first to introduce and define an energy momentum complex which is consistent in all coordinate systems. Many workers^[22–23] have dealt with the energy localization problem in the teleparallel theory of gravitation. The crux of this theory is that energy can be localized and the results of teleparallel theory of gravitation and general relativity are consistent. Keeping in mind the interest of symmetries in the teleparallel theory of gravitation, the authors in Ref. [24] introduced the teleparallel version of the Lie derivative for Killing vector fields and utilized these equations to find the teleparallel Killing vector fields in the Einstein universe. In Refs. [25–32] the researchers have made further progress to classify different space-times according to their teleparallel Killing vector fields. From the above study they showed that some time teleparallel theory gives more conservation laws as compared with the theory of general relativity. In Refs. [33–36] the authors extended this work to proper teleparallel homothetic vector fields and they classified different space-times according to their proper teleparallel homothetic vector fields. In this paper, we classify non-static cylindrically symmetric space-times according to their proper teleparallel homothetic vector fields. The teleparallel homothetic equation is defined as^[33–34]

where

and

. The

denotes the teleparallel Lie derivative with respect to the vector field X and

denotes the torsion tensor which is anti-symmetric with respect to its lower two indices. In Eq. (1) the vector field X is called teleparallel homothetic (proper teleparallel homothetic when

whereas if α = 0 it becomes teleparallel Killing). It is important to mention at the outset that we assume the torsion is non-zero in the sequel.

2. Main Results

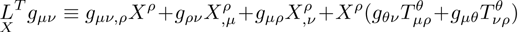
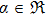
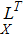
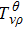
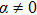
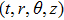
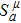
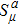
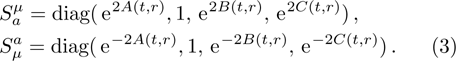
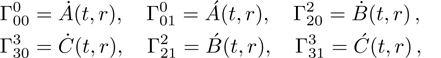
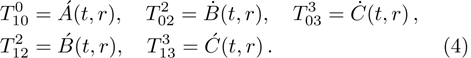
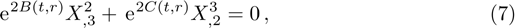
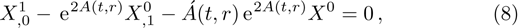
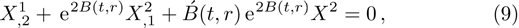
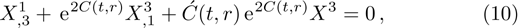
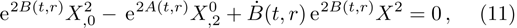
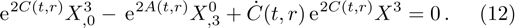
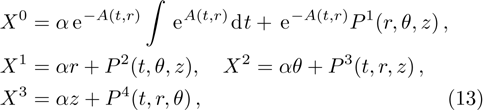
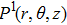
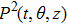
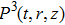
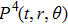
Consider the non-static cylindrically symmetric space-times in usual coordinates (given by respectively) with the line elements^[6]

where A(t,r), B(t,r), and C(t,r) are functions of t and r only. For the space-time (2), the non-trivial tetrad components denoted by

and also its inverse non-trivial components

can be obtained as

The non-vanishing Weitzenbck connections for the above mentioned tetrads (3) are^[37]

where dash represents the partial derivative with respect to t and dot the partial derivative with respect to t only. The non-zero torsion components are given in Ref. [37] as

A vector field X is said to be a teleparallel homothetic vector field if it satisfies Eq. (1). Expanding Eq. (1) and using Eqs. (2) and (4), one arrives at

After solving Eqs. (5) and (6), one determines

where

, and

are functions of integration. In order to find solutions for Eqs. (5) to (12) we need to determine the above functions. If one proceeds further after some tedious calculations, there exist the following cases which are:

It is significant to note that when A = constant, B = constant, and C = constant then all the torsion components are zero and the space-time becomes the Minkowski space-time, which gives contradicts our assumption. We do not consider this case further. It is also important to mention here in Cases 1, 2, 3, 4, and 5 the space-times become non-static plane symmetric and its proper homothetic vector files were discussed in Ref. [35]. In Cases 6, 7, 8, 9, and 10 the space-times become Bianchi type I and its proper homothetic vector files were discussed in Ref. [33]. Case 11 the space-time becomes static cylindrically symmetric and its proper homothetic vector files were discussed in Ref. [34]. Hence we only discuss each of the remaining cases from 12 to 21 in turn.

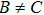
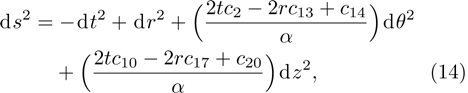
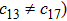
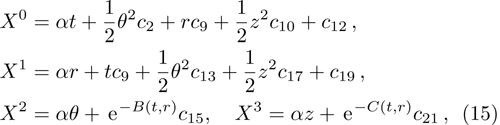
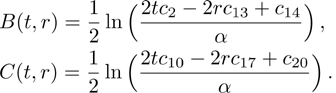
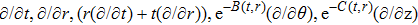
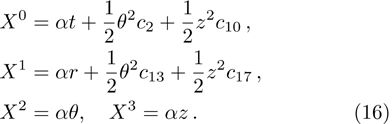
In Case 12 we have A = constant, B = B(t, r), C = C(t, r), and . After an appropriate rescaling of t the space-time (2) becomes

where c₂, c₁₀, c₁₃, c₁₄, c₁₇,

and

. The teleparallel homothetic vector fields are

where c₉, c₁₂, c₁₅, c₁₉,

. Here

The space-time (14) admits six linearly independent teleparallel homothetic vector fields, in which five are teleparallel Killing vector fields which are given as the following:

and one is a proper teleparallel homothetic vector field. After eliminating the teleparallel Killing vector fields from Eq. (15) the proper teleparallel homothetic vector fields are

In Case 13 we have C = C(t, r), and A = B = constant. After rescalings of t and θ the space-time (2) becomes

where c₁₀, c₁₃,

and

. Solving Eq. (5) to (12) we deduce

where c₂, c₄, c₆, c₉, c₁₀, c₁₂, c₁₅,

. Here

The space-time (17) admits eight linearly independent teleparallel homothetic vector fields in which seven are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields, after subtracting the teleparallel Killing vector fields from Eq. (18), are as follows

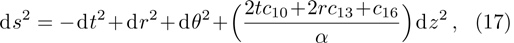
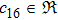
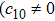
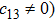
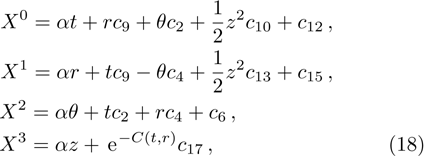
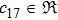
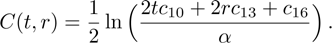
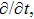
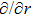
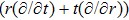
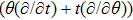
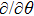
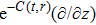
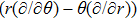
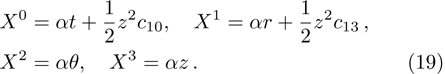
In Case 14 we have B = B(t, r), and A = C = constant. After appropriate rescalings of t and z the space-time (2) becomes

where c₁₂, c₁₅,

and

. Solving Eqs. (5) to (12) we find the teleparallel homothetic vector fields

where c₄, c₇, c₈, c₁₁, c₁₄, c₁₇,

. Here

The space-time (20) admits eight linearly independent teleparallel homothetic vector fields in which seven are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields after subtracting the teleparallel Killing vector fields from Eq. (21) are given by

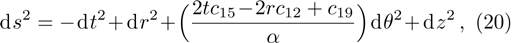
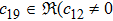
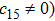
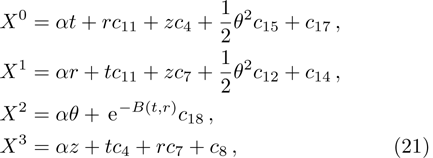
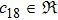
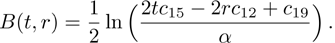
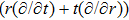
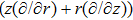
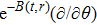
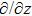
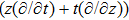
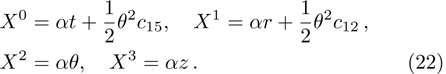
In Case 15 we have A = A(t), B = B(t), C = C(t), and A = C. In this case the space-time (2) becomes

where c₉, c₁₀, c₁₅,

and

. Solving Eqs. (5) to (12) we deduce the teleparallel homothetic vector fields

where c₆, c₈, c₁₂, c₁₄, c₁₆, c₁₇,

Here

and

. The above space-time (23) admits eight linearly independent teleparallel homothetic vector fields in which seven are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields after eliminating the teleparallel Killing vector fields from Eq. (24) are given as follows

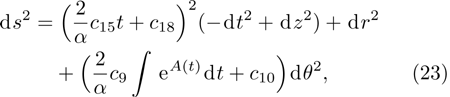
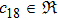
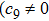
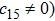
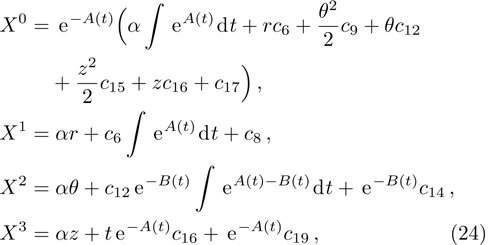
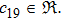
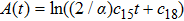
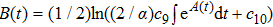
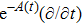
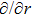
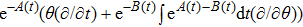
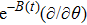
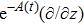
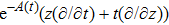
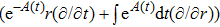
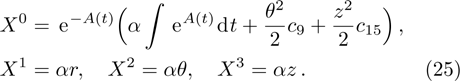
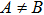
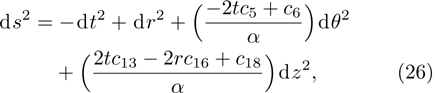
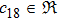
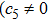
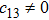
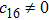
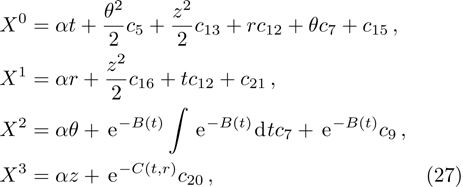
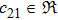
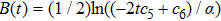
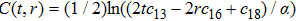
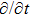
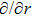
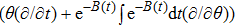
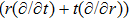
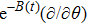
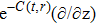
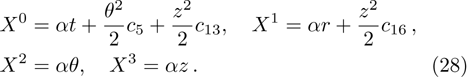
In Case 16 we have A = A(t), B = B(t), C = C(t, r), and . After a rescaling of t the space-time (2) becomes

where c₅, c₆, c₁₃, c₁₆,

, and

). Solving Eqs. (5) to (12) we find the teleparallel homothetic vector fields

where c₇, c₉, c₁₂, c₁₅, c₁₉,

. Here

and

. The space-time (26) admits seven linearly independent teleparallel homothetic vector fields in which six are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields after subtracting the teleparallel Killing vector fields from Eq. (27) are given as follows

In the present Case 17 we have A = A(t), B = B(t), C = C(t, r), and A = B. The space-time (2) becomes

where c₅, c₆, c₁₅, c₁₈,

, and

. Solving Eqs. (5) to (12) we find the teleparallel homothetic vector fields

where c₈, c₁₀, c₁₄, c₁₇, c₂₀,

Here

and

. The above space-time (29) admits seven linearly independent teleparallel homothetic vector fields in which six are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields after subtracting the teleparallel Killing vector fields from Eq. (30) are as

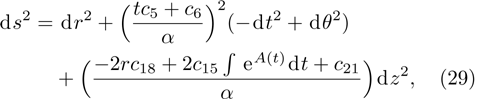
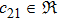
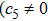
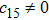
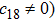
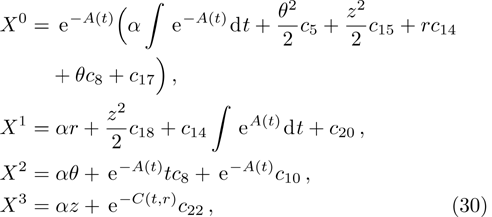
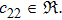
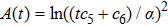
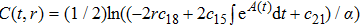
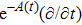
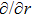
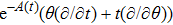
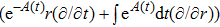
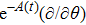
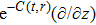
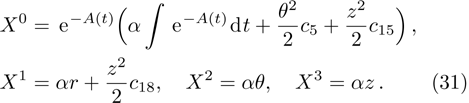
In Case 18 we have A = constant, B = B(t, r), and C = C(t). After a rescaling of t the space-time (2) becomes

where c₅, c₆, c₁₄, c₁₇,

, and

. Solving Eqs. (5) to (12) we arrive at the teleparallel homothetic vector fields

where c₈, c₁₀, c₁₃, c₁₆, c₁₉,

Here

and

The space-time (32) admits seven linearly independent teleparallel homothetic vector fields in which six are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields after subtracting the teleparallel Killing vector fields from Eq. (33) are

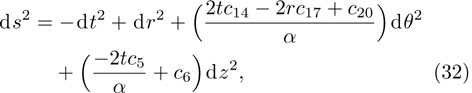
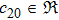
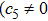
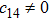
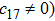
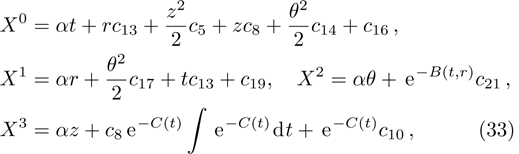
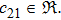
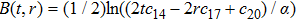
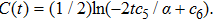
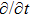
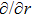
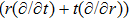
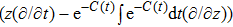
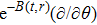
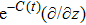
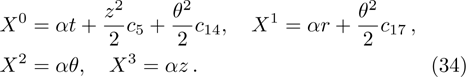
In Case 19 we have , , and After an appropriate rescaling of t the space-time (2) becomes

where c₅, c₆, c₁₄, c₁₈,

, and

. Solving Eqs. (5) to (12) we find the teleparallel homothetic vector fields

where c₈, c₁₀, c₁₃, c₁₆, c₂₀,

. Here

and

The above space-time (35) admits seven linearly independent teleparallel homothetic vector fields in which six are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields after subtracting the teleparallel Killing vector fields from Eq. (36) are given as follows

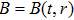
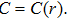
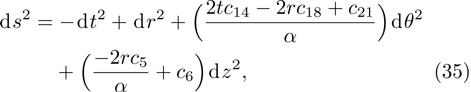
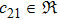
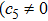
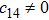
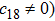
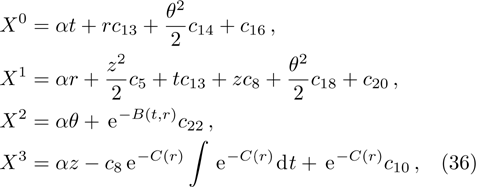
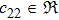
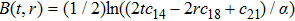
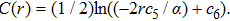
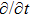
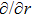
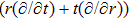
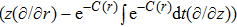
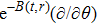
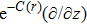
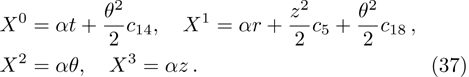
In Case 20 we have A = A(t), B = B(r), C = C(t), and A = C. The space-time (2) in this case becomes

where c₁₁, c₁₄, c₁₆,

, and

. Solving Eqs. (5) to (12) we find the teleparallel homothetic vector fields

where c₆, c₁₂, c₁₃, c₁₅, c₁₇, c₁₈,

. Here

and

. The above space-time (38) admits eight linearly independent teleparallel homothetic vector fields in which seven are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields after subtracting the teleparallel Killing vector fields from Eq. (39) are as below

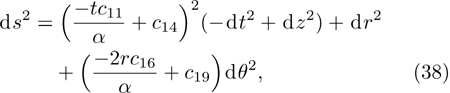
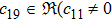
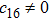
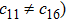
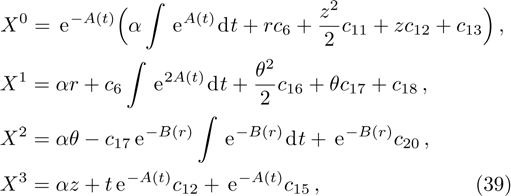
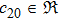
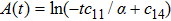
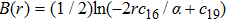
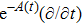
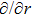
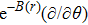
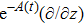
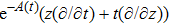
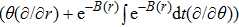
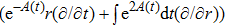
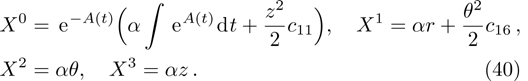
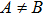
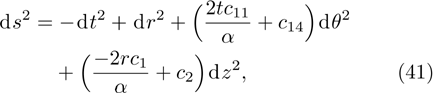
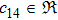
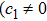
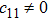
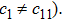
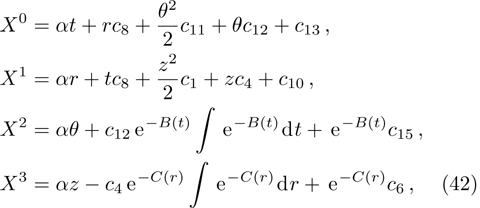
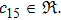
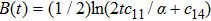
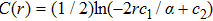
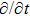
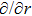
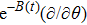
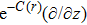
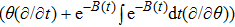
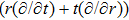
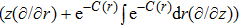
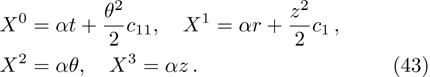
In the present Case 21 we have A = A(t), B = B(t), C = C(r) and . After a rescaling of t the space-time (2) becomes

where c₁, c₂, c₁₁,

, and

Solving Eqs. (5) to (12) we deduce the teleparallel homothetic vector fields

where c₄, c₆, c₈, c₁₀, c₁₂, c₁₃,

Here

and

. The above space-time (41) admits eight linearly independent teleparallel homothetic vector fields in which seven are teleparallel Killing vector fields given as

and one is a proper teleparallel homothetic vector field. Proper teleparallel homothetic vector fields after subtracting the teleparallel Killing vector fields from Eq. (42) are as given below

3. Summary

In this paper, a study of most general form of the cylindrically symmetric non-static space-times for proper teleparallel homothetic vector fields in teleparallel theory of gravitation is given by using a direct integration technique. This study also covers static cylindrically symmetric, Bianchi type I, non-static and static plane symmetric space-times which we do not include because it is given in Refs. [33–35]. From this study, we find that the space-time (2) admits six, seven or eight teleparallel homothetic vector fields. In all the cases we obtain only one proper teleparallel homothetic vector field which is same as in general relativity. The results are as follows:

(a) The case for which the space-time (2) admits six teleparallel homothetic vector fields are presented in Eq. (15).

(b) The cases when the space-time (2) admit seven teleparallel homothetic vector fields are given in Eqs. (27), (30), (33), and (36).

(c) The cases when the space-time (2) admit eight teleparallel homothetic vector fields are provided in Eqs. (18), (21), (24), (39), and (42).

It is significant to note that in this work we have discussed only those cases in which proper teleparallel homothetic vector fields exist. Otherwise the space-time (2) becomes Minkowski or no proper teleparallel homothetic vector fields exist.

Acknowledgement

One of the authors FMM is grateful to the National Research Foundation, NRF, of South Africa for research funding through two grants.

Reference

[1]	Harvey A. Schucking E. Surowitz E. J. Am. J. Phys. 74 2006 1017
[2]	Krisch J. P. Glass E. N. Phys. Rev. D 80 2009 044001
[3]	Petrov A. Z. Physics Einstein Spaces Oxford University Press Pergamon 1969
[4]	Harada T. Maeda H. Class. Quant. Grav. 21 2004 371
[5]	Weitzenbck R. Invarianten Theorie Gronningen Noordhoft 1923
[6]	Stephani H. Kramer D. Maccallum M. Hoenselaers C. Herlt E. Exact Solutions of Einstein’s Field Equations 2 Cambridge University Press Cambrige 2003
[7]	Bokhari A. H. Qadir A. J. Math. Phys. 28 1987 1019
[8]	Feroz T. Qadir A. Ziad M. J. Math. Phys. 42 2001 4947
[9]	Shabbir G. Ramzan M. Appl. Sci. 9 2007 148
[10]	Shabbir G. Amur K. B. Appl. Sci. 8 2006 153
[11]	Maartens R. Maharaj S. D. Tupper B. O. J. Class. Quant. Grav. 12 1995 2577
[12]	De Andrade V. C. Pereira J. G. Gen. Rel. Grav. 30 1998 263
[13]	Pereira J. G. Vargas T. Zhang C. M. Class. Quant. Grav. 18 2001 833
[14]	Sharif M. Amir M. J. Mod. Phys. Lett. A 23 2008 3167
[15]	Sharif M. Taj S. Mod. Phys. Lett. A 25 2010 221
[16]	Trautman A. Gravitation: An Introduction to Current Research Witten L. Wiley New York 1962
[17]	Landau L. D. Lifshitz E. M. The Classical Theory of Fields Addison–Wesley Press New York 1962
[18]	Papapetrou A. Proc. R. Irish Acad. A 52 1948 11
[19]	Tolman R. C. Relativity, Thermodynamics and Cosmology Oxford University Press Oxford 1934
[20]	Bergmann P. G. Thomson R. Phys. Rev. 89 1958 400
[21]	Moller C. Ann. Phys. (NY) 4 1958 347
[22]	Nashed G. G. L. Phys. Rev. D 66 2002 060415
[23]	Vergas T. Gen. Rel. Grav. 30 2004 1255
[24]	Sharif M. Amir M. J. Mod. Phys. Lett. A 23 2008 963
[25]	Shabbir G. Khan S. Mod. Phys. Lett. A 25 2010 55
[26]	Shabbir G. Khan S. Mod. Phys. Lett. A 25 2010 525
[27]	Shabbir G. Khan S. Mod. Phys. Lett. A 25 2010 1733
[28]	Shabbir G. Khan S. Commun. Theor. Phys. 54 2010 469
[29]	Shabbir G. Ali A. Khan S. Chin. Phys. B 20 2011 070401
[30]	Shabbir G. Khan S. Jamil Amir M. Braz. J. Phys. 41 2011 184
[31]	Sharif M. Majeed B. Commun. Theor. Phys. 52 2009 435
[32]	Shabbir G. Khan S. Ali A. Commun. Theor. Phys. 55 2011 268
[33]	Shabbir G. Khan S. Mod. Phys. Lett. A 25 2010 2145
[34]	Shabbir G. Khan S. Commun. Theor. Phys. 54 2010 675
[35]	Shabbir G. Khan S. Rom. J. Phys. 57 2012 571
[36]	Shabbir G. Shahani M. A. Int. J. Theor. Phys. 54 2015 3027
[37]	Shahani Masoom Ali MS Thesis GIK Institute Pakistan 2013