† Corresponding author. E-mail:
In this work, a second order smoothed particle hydrodynamics is derived for the study of relativistic heavy ion collisions. The hydrodynamical equation of motion is formulated in terms of the variational principle. In order to describe the uid of high energy density but of low baryon density, the entropy is taken as the base quantity for the interpolation. The smoothed particle hydrodynamics algorithm employed in this study is of the second order, which guarantees better particle consistency. Furthermore, it is shown that the variational principle preserves the translational invariance of the system, and therefore improves the accuracy of the method. A brief discussion on the potential implications of the model in heavy ion physics as well as in general relativity are also presented.
Hydrodynamics is one of the most venerable theoretical tools which has been playing an important role in our understanding of nature. Its applications are widely spread as well as deeply rooted in many distinct areas of physics. For instance, the hydrodynamic description of heavy-ion nuclear collisions plays an essential part in the study of the properties of the hot and dense matter created at RHIC and LHC,[1–3] and it is further reinforced by the onging investigations of fluid/gravity duality.[4–7] Although the validity and the origin of the hydrodynamic model have been long under extensive discussions,[8–10] simulation results[11–15] on azimuthal correlations for various systems have firmly demonstrated the success of the approach. The smoothed particle hydrodynamics (SPH)[16–17] is one of the oldest meshfree methods for the partial different equation which describes the dynamics of continuum media. Distinct from any grid-based method such as the finite element method or the finite difference method, the SPH makes use of a set of arbitrarily distributed fluid elements, referred to as particles, to represent the system. Each particle has a smoothing length, h, over which their properties are smoothed by a kernel function. In terms of the kernel function, the contribution of each particle is weighted according to their distance from the position in question. Therefore, a physical quantity at a given spatial point is obtained by summing the relevant contribution from all the particles lying within the range of the kernel. The SPH was firstly introduced to study astrophysical problems.[16–18] Nowadays, it is widely used to model fluid motion, as well as solid mechanics.[19]
Despite its wide applications, the original SPH suffers some inherent problems which lead to low numerical accuracy under certain circumstances. Among others, particle consistency is one of the notable issues which reflects the discrepancy between the spatially discretized particles and the corresponding continuous form of the kernel function. Particle inconsistency demonstrates itself as the discretized SPH particles to be incapable of properly reproducing a constant function. It usually results from the particle approximation process, which is closely associated with the boundary particles, non-uniformed particle distribution as well as the smoothing length. The finite particle method (FPM)[20–21] was proposed by Liu et al. to improve the particle consistency. The key idea of the approach is to perform the Taylor series expansion of the function to be approximated before multiplying both sides of the equality by the kernel function and integrating over relevant volume. It was shown that the particle consistency is related to the order of the above Taylor series, and it is guaranteed independent of the specific form of the kernel function, neither to the particle distribution.
In implementing the SPH to the partial different equation, some rules are proposed to symmetrize or asymmetric the terms involving the gradient operator.[22] In the case of pressure gradient, the term is symmetrized in order to respect Newton’s third law: the pair of forces acting on the two particles are equal in size but opposite in direction. Alternatively, it is shown that the above result can be obtained naturally, if one derives the hydrodynamic equation by using the variational principle,[23–25] which is a consequence that the system conserves linear and angular momentum. For event by event fluctuating initial conditions, even though SPH particles are distributed uniformly at the initial instant, the distribution is likely to be disturbed as the system evolves in time. Therefore, FPM formalism is particularly suitable to handle such physical system. Since the momentum conservation is important for small systems created in the relativistic heavy ion collisions, one needs to develop a model which explicitly preserves the conservation law. Owing to the complicated form of the FPM, it is not straightforward to guarantee the momentum conservation by symmetrizing certain physical quantities. In order to apply the FPM to relativistic heavy ion collisions, one shall employ the variational principle to obtain the corresponding equation of motion. In addition, the system created in the collision is of significantly high energy density with mostly vanishing baryon density, therefore the entropy should be chosen as the base of SPH algorithm. This is the main goal of the present study. In the following section, we briefly review the main feature of FPM and discuss its advantage. The entropy based hydrodynamical equation is derived Sec.
For a physical quantity f(x), the Taylor series expansion gives
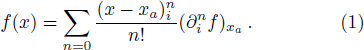
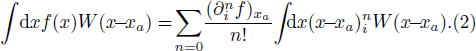
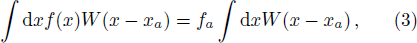
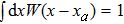
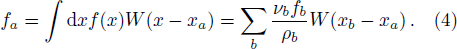
However, if one applies the following particle approximation directly to Eq. (
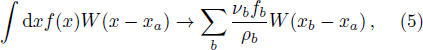
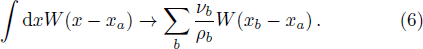
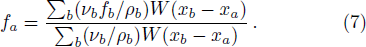
It is intuitive to generalize the above procedure to higher order. By retaining the right hand side of Eq. (
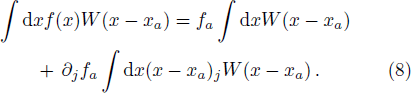
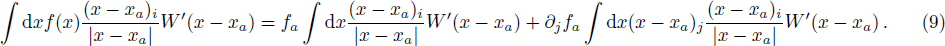
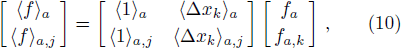
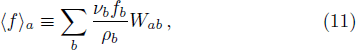
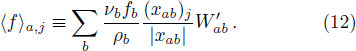
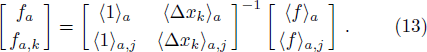

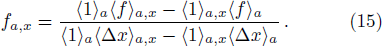
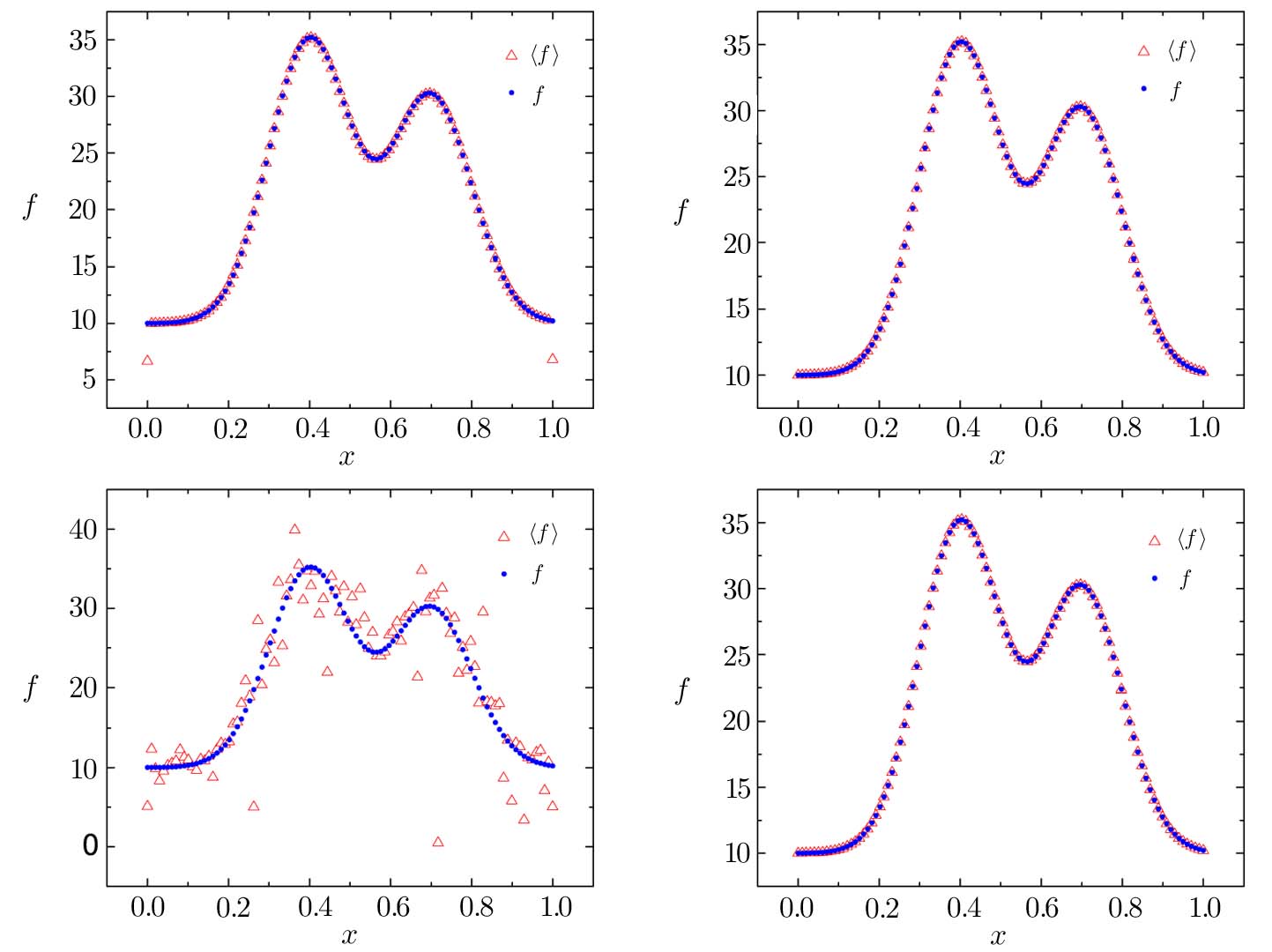
In Fig.
The relativistic hydrodynamic equation for ideal fluid can be obtained by the conservation of energy-momentum flux,[2]
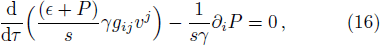
It is noted that the conservation of the entropy flow is valid once there is no viscosity, and it is consistent with the standard form of entropy based SPH formula,[2] namely,
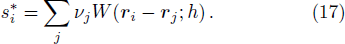
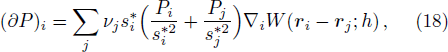
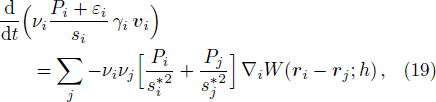
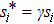
Similarly, in the case of FPM, the pressure gradient on the right hand side of Eq. (
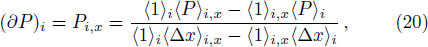
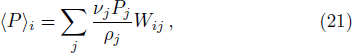
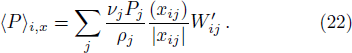
However, the above hydrodynamic equation does not take into consideration the momentum conservation. Unlike the case of standard SPH, it is not obvious how to straightforwardly write down a symmetrized form as in Eq. (

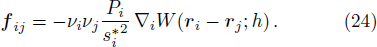

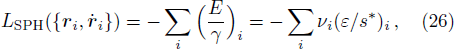
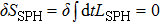
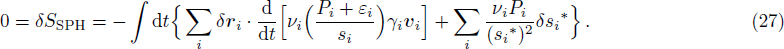
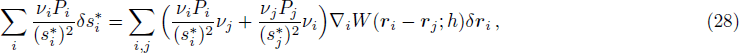
Now, to calculate the hydrodynamic equation for the FPM case in a one-dimensional system, we make use of Eq. (
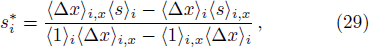
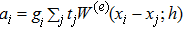
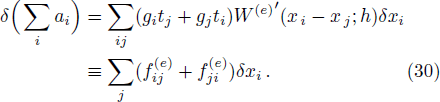
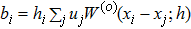
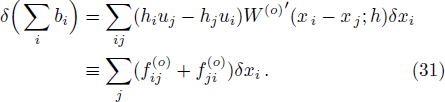
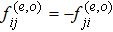
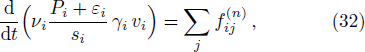

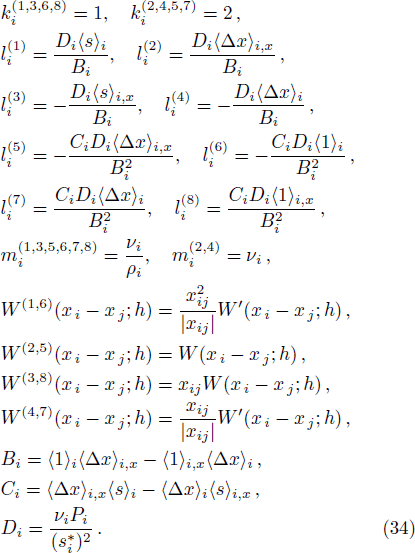
It is instructive to see how the resulting hydrodynamic equation reduces to the standard SPH formulae in its limit. By comparing Eq. (
To summarize, in this work, we make a preliminary attempt to study the implementation of FPM into the entropy-based SPH hydrodynamic model. It is argued that the equation of motion obtained by using variational principle, though more complicated in its form, is more suitable to small and/or fluctuating systems where the conservation law plays a more stringent role in the dynamics. We discussed possible implementations and in particular, derived the hydrodynamic equation of motion by using variational principle, where the momentum conservation of the system is assured. It is shown how the obtained equation of motion reduces to the standard SPH form as a limit, which might be instructive to study the contributions of individual terms when one needs to introduce approximation for practical reasons.
Owing to the observation of the “ridge” effect in two-particle correlation in relativistic heavy ion collision, the fluctuating initial conditions play an increasingly important role in the hydrodynamical description of nuclear collisions. The AdS/CFT correspondence states the duality that two apparently distinct physical theories are closely connected. It provides another insightful viewpoint of hydrodynamics as a gradient expansion in the long wavelength limit. The applications of the SPH algorithm, from both aspects, strengthen the ongoing studies on heavy-ion physics as well as on gravitation theory. The improvement of particle consistency brought by the FPM, therefore, can be significant in the context of precision and efficiency of the numerical approach. It is interesting to implement the obtained equation of motion for realistic collision simulations, which will be carried out in our subsequent study.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |