Cite this Article
Aadel Y., Belhaj A., Bensed M., Benslimane Z., Sedra M. B., Segui A.. Qubit Systems from Colored Toric Geometry and Hypercube Graph Theory. Communications in Theoretical Physics, 2017, 68(3): 285  
Permissions
Qubit Systems from Colored Toric Geometry and Hypercube Graph Theory
Aadel Y.1, Belhaj A.2, Bensed M.1, Benslimane Z.1, Sedra M. B.1, Segui A.3
1LabSIMO, Département de Physique, Faculté des Sciences,Université Ibn Tofail Kénitra, Morocco
2LIRST, Département de Physique, Faculté Polydisciplinaire, Université Sultan Moulay Slimane Béni Mellal, Morocco
3Departamento de Física Teórica, Universidad de Zaragoza, E-50009-Zaragoza, Spain

 

† Corresponding author. E-mail:

Supported by FPA2012-35453

Abstract
Abstract

We develop a new geometric approach to deal with qubit information systems using colored graph theory. More precisely, we present a one to one correspondence between graph theory, and qubit systems, which may be explored to attack qubit information problems using toric geometry considered as a powerful tool to understand modern physics including string theory. Concretely, we examine in some details the cases of one, two, and three qubits, and we find that they are associated with CP1, CP1 × CP1 and CP1 × CP1 × CP1 toric varieties respectively. Using a geometric procedure referred to as a colored toric geometry, we show that the qubit physics can be converted into a scenario handling toric data of such manifolds by help of hypercube graph theory. Operations on toric information can produce universal quantum gates.

PACS: 02.10.Ox;02.40.-k;02.40.Ky;02.40.Tt
Keyword:toric geometry;information theory and graph theory
1 Introduction

Toric geometry is considered as a nice tool to study complex varieties used in physics including string theory and related models.[1–2] The key point of this method is that the geometric properties of such manifolds are encoded in toric data placed on a polytope consisting of vertices linked by edges. The vertices satisfy toric constraint equations which have been explored to solve many string theory problems such as the absence of non abelian gauge symmetries in ten dimensional type II superstring spectrums.[3]

Moreover, toric geometry has been also used to build mirror manifolds providing an excellent way to understand the extension of T-duality in the presence of D-branes moving near toric Calabi–Yau singularities using combinatorial calculations.[4] In particular, these manifolds have been used in the context of N = 2 four-dimensional quantum field theories in order to obtain exact results using local mirror symmetry.[3] Besides such applications, toric geometry has been also explored to understand a class of black hole solutions obtained from type II superstrings on local Calabi–Yau manifolds.[5–6]

Recently, the black hole physics has found a place in quantum information theory using qubit building blocks. More precisely, many connections have been established in the context of STU black holes as proposed in Refs. [7–9].

More recently, an extension to extremal black branes derived from the Tn toroidal compactification of type IIA superstring have been proposed in Ref. [10]. Concretely, it has been shown that the corresponding physics can be related to n qubit systems via the real Hodge diagram of such compact manifolds. The analysis has been adopted to Tn|n supermanifolds by supplementing fermionic coordinates associated with the superqubit formalism and its relation to supersymmetric models.

The aim of this paper is to contribute to this program by introducing colored toric geometry and its relation to graph theory to approach qubit information systems. The main objective to deal with qubit systems using geometry considered as a powerful tool to understand modern physics such as string theory and related models. As an illustration, we examine lower dimensional qubit systems. We consider in some details the cases of one, two and three qubits. In particular we find that they are linked with CP1, CP1 × CP1 and CP1 × CP1 × CP1 toric varieties respectively. Using a geometric procedure referred to as colored toric geometry, we show that the qubit physics can be converted into a scenario working with toric data of such manifolds by help of graph theory.

The present paper is organized as follows. Section 2 provides materials on colored toric geometry which is used to discuss qubit information systems. The connection with graph theory is investigated in Sec. 3 where focus is on a one to one correspondence between colored toric geometry and qubit systems. Operations on toric graphs are employed in Sec. 4 when studying universal quantum gates. Section 5 is devoted to some concluding remarks.

2 Colored Toric Graph Geometry

Before giving a colored toric realization of qubit systems, we present an overview on ordinary toric geometry. It has been realized that such a geometry is considered as a powerful tool to deal with complex Calabi-Yau manifolds used in the string theory compactification and related subjects.[2] Many examples have been elaborated in recent years producing non trivial geometries.

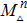
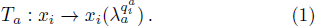
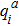
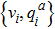
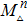
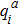
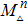
Roughly speaking, n-complex dimensional toric manifold, which we denote as , is obtained by considering the (n + r)-dimensional complex spaces Cn+r parameterized by homogeneous coordinates {x = (x1, x2, x3, …, xn+r)}, and r toric transformations acting on the xi’s as follows

Here, λa’s are r non vanishing complex parameters. For each a, are integers which called Mori vectors encoding many geometrical information on the manifold and its applications to string theory physics. In fact, these toric manifolds can be identified with the coset space Cn+r/C*r. In this way, the nice feature is the toric graphic realization. Concretely, this realization is generally represented by an integral polytope Δ, namely a toric diagram, spanned by (n + r) vertices vi of the standard lattice Zn. The toric data should satisfy the following r relations

Thus, these equations encode geometric data of . In connection with lower dimensional field theory, it is worth noting that the integers are interpreted, in the gauged linear sigma model language, as the U(1)r gauge charges of chiral multiples. Moreover, they have also a nice geometric interpretation in terms of the intersections of complex curves Ca and divisors Di of .[3–4,11] This remarkable link has been explored in many places in physics. In particular, it has been used to build type IIA local geometry.

The simplest example in toric geometry, playing a primordial role in the building block of higher dimensional toric varieties, is CP1. It is defined by r = 1 and the Mori vector charge takes the values qi = (1, 1). This geometry has a U(1) toric action CP1 acting as follows

where z = x1/x2, with two fixed points v0 and v1 placed on the real line. The latters describing the North and south poles respectively of such a geometry, considered as the (real) two-sphere S2 ∼ CP1, satisfy the following constraint toric equation

In toric geometry language, CP1 is represented by a toric graph identified with an interval [v0, v1] with a circle on top. The latter vanishes at the end points v0 and v1. This toric representation can be easily extended to the n-dimensional case using different ways. The natural one is the projective space CPn. In this way, the S1 circle fibration, of CP1, will be replaced by Tn fibration over an n-dimensional simplex (regular polytope). In fact, the Tn collapses to a Tn−1 on each of the n faces of the simplex, and to a Tn−2 on each of the (n − 2)-dimensional intersections of these faces, etc.

The second way is to consider a class of toric varieties that we are interested in here given by a trivial product of one-dimensional projective spaces CP1’s admitting a similar description. We will show later on that this class can be used to elaborate a graphic representation of quantum information systems using ideas inspired by graph theory and related issues. For simplicity reason, we deal with the case of CP1 × CP1. 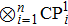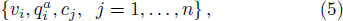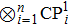For higher dimensional geometries and their blow ups, the toric descriptions can be obtained using a similar way. In fact, they are n-dimensional toric manifolds exhibiting U(1)n toric actions. A close inspection shows that there is a similarity between toric graphs of such manifolds and qubit systems using a link with graph theory. To make contact with quantum systems, we reconsider the study of toric geometry by implementing a new toric data associated with the color, producing a colored toric geometry. In this scenario, the toric data will be replaced by

where c indicates the color of the edges linking the vertices, which be associated with qubit states. Roughly speaking, the connection that we are after requires that the toric graph should consist of n + r vertices and n colors, where n will indicate the number of qubits. In fact, consider a special class of toric manifolds associated with with U(1)n toric actions exhibiting 2n fixed points vi. In toric geometry langauge, the manifolds are represented by 2n vertices vi belonging to the Zn lattice satisfying n toric equations. It is observed that these graphs share a strong resemblance with hypercube graph formed by 2n nodes connected with 2n. n edges where each vertex has n colored edges incident to it.[9] This number of colors which is called the chromatic index of the graph is associated with the number of qubits. These types of graphs which are called n regular can be used to present graphically the physics of n-qubit quantum systems.

3 Graph Theory and Colored Toric Geometry of Qubits

Inspired by combinatorial computations in quantum physics, we explore colored toric geometry to deal with qubit information systems.[7–20] Concretely, we elaborate a toric description in terms of a trivial fibration of one-dimensional projective space CP1’s. To start, it is recalled that the qubit is a two state system which can be realized, for instance, by a 1/2 spin atom. A superposition of a single qubit is generally given by the following Dirac notation

where ai are complex numbers satisfying the normalization condition

It is remarked that this constraint can be interpreted geometrically in terms of the so called Bloch sphere, identified with SU(2)/U(1) quotient Lie group.[1–4] The analysis can be extended to more than one qubit which has been used to discuss entangled states. In fact, the two qubits are four quantum level systems. Using the usual notation ∣i1i2〉 = ∣i1〉∣i2〉, the corresponding state superposition can be expressed as follows

where aij are complex numbers verifying the normalization condition

describing the CP3 projective space. For n qubits, the general state has the following form

where aij satisfy the normalization condition

This condition defines the CP2n−1 projective space generalizing the Bloch sphere associated with n = 1.

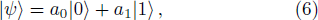
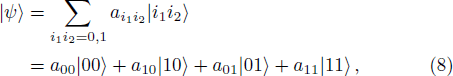
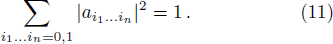
Roughly, the qubit systems can be represented by colored toric diagrams having a strong resemblance with hypercube graphs. A close inspection in hypercube graph theory and toric varieties shows that we can propose the following correspondence connecting three different subjects.

Table 1

This table presents a one to one correspondence between colored toric geometry, hypercube graphs, and qubit systems.

.

To see how this works in practice, we first change the usual toric geometry notation. Inspired by combinatorial formalism used in quantum information theory, the previous toric data can be rewritten as follows

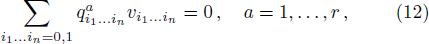
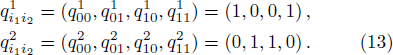
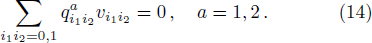
where the vertex subscripts indicate the corresponding quantum states. To illustrate this notation, we present the model associated with CP1 × CP1 toric variety. This model is related with n = 2 classification of hypercube graphs. In this case, the combinatorial Mori vectors can take the following form

The manifold corresponds to the toric equations

In colored toric geometry langauge, it is represented by 4 vertices vi1i2, belonging to Z2, linked by four edges with two different colors c1 and c2. The toric data require the following vertices

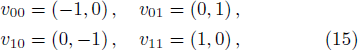
with two colors. These data can be encoded in a toric graph describing two qubits and it is illustrated in Fig. 1.

Fig. 1 Colored Toric graph representation of n = 2 qubits.

Due to this representation, we can relate the basis of n-qubit with the toric geometry. The mapping is given by

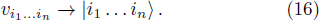
This link can be explored to study many related applications including quantum gates.

4 Quantum Gates from Colored Hypercube Graphs

Having examined the qubit object, we move now to build the quantum gates using colored toric geometry and graph theory. The general study is beyond of the scope of this paper. We consider, however, lower dimensional cases. To do so, it is recalled that the classical gates can be obtained by combining Boolean operations as AND, OR, XOR, NOT, and NAND. In fact, these operations act on input classical bits, taking two values 0 and 1, to produce new bits as output results. In quantum computation, gates are unitary operators in a 2n-dimensional Hilbert space. In connection with representation theory, they can be represented by 2n × 2n matrix, belonging to SU(2n) Lie group, satisfying the following properties

As in the classical case, there is a universal notation for the gates depending on the input qubit number. The latters are considered as building blocks for constructing circuits and transistors. For 1-qubit computation, the usual one is called NOT acting on the basis state as follows

In this toric geometry language, this operation corresponds to permuting the two toric vertices of CP1

This operation can be represented by the following matrix

which can be identified with UNOT defining the NOT quantum gate. In this case, it is worth noting that the corresponding color operation is trivial since we have only one.

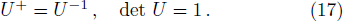
For 2-qubits, there are many universal gates. As mentioned previously, this system is associated with the toric geometry of CP1 × CP1. Unlike the 1-qubit case corresponding to CP1 × CP1, the quantum systems involve two different data namely the vertices and colors. Based on this observation, such data will produce two kinds of operations:

Color actions.

Vertex actions.

In fact, these operations can produce CNOT and SWAP gates. To get such gates, we fix the color action according to particular orders used in the corresponding notation. Following the colored toric realization of the 2-qubits, the color actions can be formulated as follows

In this color language, the CNOT gate

can be obtained by using the following actions

A close inspection shows that the SWAP gate

can be derived from the following permutation action

We expect that this analysis can be adopted to higher dimensional toric manifolds. For simplicity reason, we consider the geometry associated with TOFFOLI gate being a universal gate acting on a 3-qubit. It is remarked that geometry can be identified with the blow up of CP1 × CP1 × CP1 toric manifold. In colored toric geometry language, this manifold is described by the following equations

where 23 vertices vi1i2i3 belong to Z3. They are connected by three different colors c1, c2 and c3. These combinatorial equations can be solved by the following Mori vectors

Thus, the corresponding vertices vi1i2i3 are given by

and they are connected with three colors. This representation can be illustrated in Fig. 2.

Fig. 2 Colored toric geometry of n = 3.

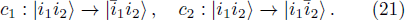
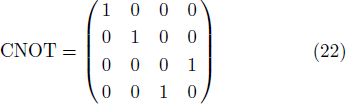
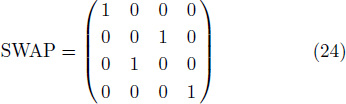
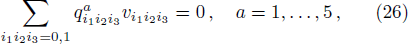
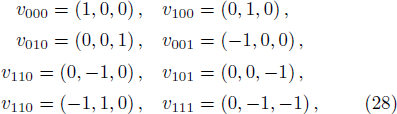
The TOFFOLI gate represented by 23 × 23 matrix

can be obtained by the following color transformation

We expect that this analysis can be pushed further to deal with other toric varieties having non trivial Betti numbers.

5 Conclusion

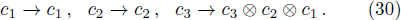
Using toric geometry/hypercube graph correspondence, we have discussed qubit information systems. More precisely, we have presented a one to one correspondence between three different subjects namely toric geometry, Hypercube graph and quantum information theory. We believe that this work may be explored to attack qubit system problems using geometry considered as a powerful tool to understand modern physics. In particular, we have considered in some details the cases of one, two and three qubits, and we find that they are associated with CP1, CP1 × CP1 and CP1 × CP1 × CP1 toric varieties respectively. Developing a geometric procedure referred to as colored toric geometry, we have revealed that the qubit physics can be converted into a scenario turning toric data of such manifolds by help of graph theory. We have shown that operations on such data can produce universal quantum gates.

This work comes up with many open questions. A natural one is to examine super-projective spaces. We expect that this issue can be related to superqubit systems. Another question is to investigate the entanglement states in the context of toric geometry and its application including mirror symmetry. Instead of giving a speculation, we prefer to comeback to these open questions in future.

Reference
[1] Fulton W. Introduction to Toric varieties Annals of Math. Studies 131 Princeton University Press Princeton 1993
[2] Leung N. C. Vafa C. Adv. Theor. Math. Phys. 2 1998 91 hep-th/9711013
[3] Katz S. Mayr P. Vafa C. Adv. Theor. Math. Phys. 1 1998 53 hep-th/9706110
[4] Aganagic M. Karch A. Lust D. Miemiec A. Nucl. Phys. B 569 2000 277 hep-th/9903093
[5] Aganagic M. Jafferis D. Saulina N. J. High Energy Phys. 0612 2006 018 hep-th/0512245
[6] Belhaj A. et al. Nucl. Phys. B 776 2007 287 hep-th/0611289
[7] Duff M. J. Ferrara S. Lect. Notes Phys. 755 2008 93 arXiv:hep-th/0612036
[8] Borsten L. Duff M. J. Lévay P. Class. Quant. Grav. 29 2012 224008 arXiv:hep-th/1206.3166
[9] Borsten L. Duff M. J. Marrani A. Rubens W. Eur. Phys. J. Plus 126 2011 37 arXiv:1101.3559
[10] Belhaj A. Sedra M. B. Segui A. J. Phys. A: Math. Theor. 48 2015 045401 arXiv:1406.2578
[11] Belhaj A. Diaz P. Garcia del Moral M. P. Segui A. Int. J. Geom. Meth. Mod. Phys. 09 2012 1250050 arXiv:1106.5335
[12] Lévay P. Phys. Rev. D 84 2001 125020
[13] Borsten L. Dahanayake D. Duff M. J. Rubens W. Ebrahim H. Phys. Rev. A 80 2009 032326 arXiv:0812.3322[quant-ph]
[14] Borsten L. Dahanayake D. Duff M. J. Marrani A. Rubens W. Phys. Rev. Lett. 105 2010 100507 arXiv:1005.4915[hep-th]
[15] Borsten L. Bradler K. Duff M. J. Proc. Roy. Soc. Lond. A 470 2014 20140235 arXiv:quant-ph/1206.6934
[16] Castellani L. Grassi P. A. Sommovigo L. Quantum Computing with Superqubits arXiv:1001.3753
[17] Lévay P. Sárosi G. Phys. Rev. D 86 2012 105038
[18] Nielsen M. A. Chuang I. L. Quantum Computation and Quantum Information Cambridge University Press New York 2000
[19] Terno D. R. Introduction to Relativistic Quantum Information arXiv:quant-ph/0508049
[20] Kargarian M. Phys. Rev. A 78 2008 062312 arXiv:0809.4276