† Corresponding author. E-mail:
Quantum watermarking is a technique to embed specific information, usually the owner’s identification, into quantum cover data such for copyright protection purposes. In this paper, a new scheme for quantum watermarking based on quantum wavelet transforms is proposed which includes scrambling, embedding and extracting procedures. The invisibility and robustness performances of the proposed watermarking method is confirmed by simulation technique. The invisibility of the scheme is examined by the peak-signal-to-noise ratio (PSNR) and the histogram calculation. Furthermore the robustness of the scheme is analyzed by the Bit Error Rate (BER) and the Correlation Two-Dimensional (Corr 2-D) calculation. The simulation results indicate that the proposed watermarking scheme indicate not only acceptable visual quality but also a good resistance against different types of attack.
Since the introduction of the first quantum key distribution protocol,[1] many researchers have contributed to treat the representation and processing of classical media quantum mechanically.[2–23]
Quantum information hiding including digital watermarking and steganography are efficient tools in secure digital information transmission and processing.
In 2010, Qu et al.[24] proposed a quantum steganography protocol using the entanglement swapping of Bell states, in which the secret messages are transmitted in a hidden channel. Later, Shaw et al. proposed two types of quantum steganography protocols with noisy quantum channels.[25] In the first protocol the secure quantum information was locally stored in the codeword. In the later protocols the hidden information was embedded in the space of error syndromes. In 2012, using entanglement swapping a secure quantum watermarking scheme was proposed by Fatahi, and Naseri.[26] Afterwards, a quantum method for images watermarking based on the flexible representation for quantum images (FRQI) was proposed in in 2013.[27] Very recently we proposed a novel LSB-based quantum watermarking protocol, where the NEQR method of quantum images representation is employed to represent the quantum images.[28]
In 2013, using the flexible representation of quantum image,[29] a quantum watermarking scheme based on quantum wavelet transform (QWT) was proposed by Song et al.,[30] where, to control the embedding strength a dynamic vector was used. In this scheme, the wavelet coefficients are extracted by executing QWT on quantum image. However, Yang et al. in 2014 analyzed the protocol and showed that the protocol proposed by Song et al. is not as applicable as the authors claimed.[31] Then they presented a simple improvement on the original protocol of dynamic watermarking scheme based on quantum wavelet transform.
Needles to say that there are two key properties that are required of a quantum data hiding scheme for an application, the invisibility and the robustness. However, to watermark, where the main purpose is copyright protection, the resistance against attacks, robustness is more important than the invisibility characteristics of the scheme. Unfortunately, in most of the proposed quantum watermarking schemes the authors only analyze the invisibility of their protocol.
In this contribution, a new quantum wavelet transforms based watermarking is proposed. By simulation analysis not only the invisibility but also the robustness of the proposed scheme is confirmed. The paper is organized as follows:
The next section presents a general preliminaries, which are used in the scheme. The quantum wavelet transform watermarking protocol is presented in Sec.
A novel enhanced quantum representation of digital images (NEQR) was introduced by Zhang et al. in 2013.[32] Based on NEQR scheme, a 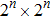

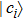
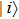
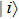
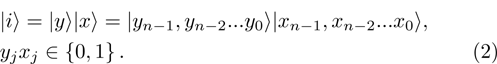
The first n-qubit 
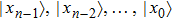
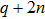
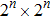
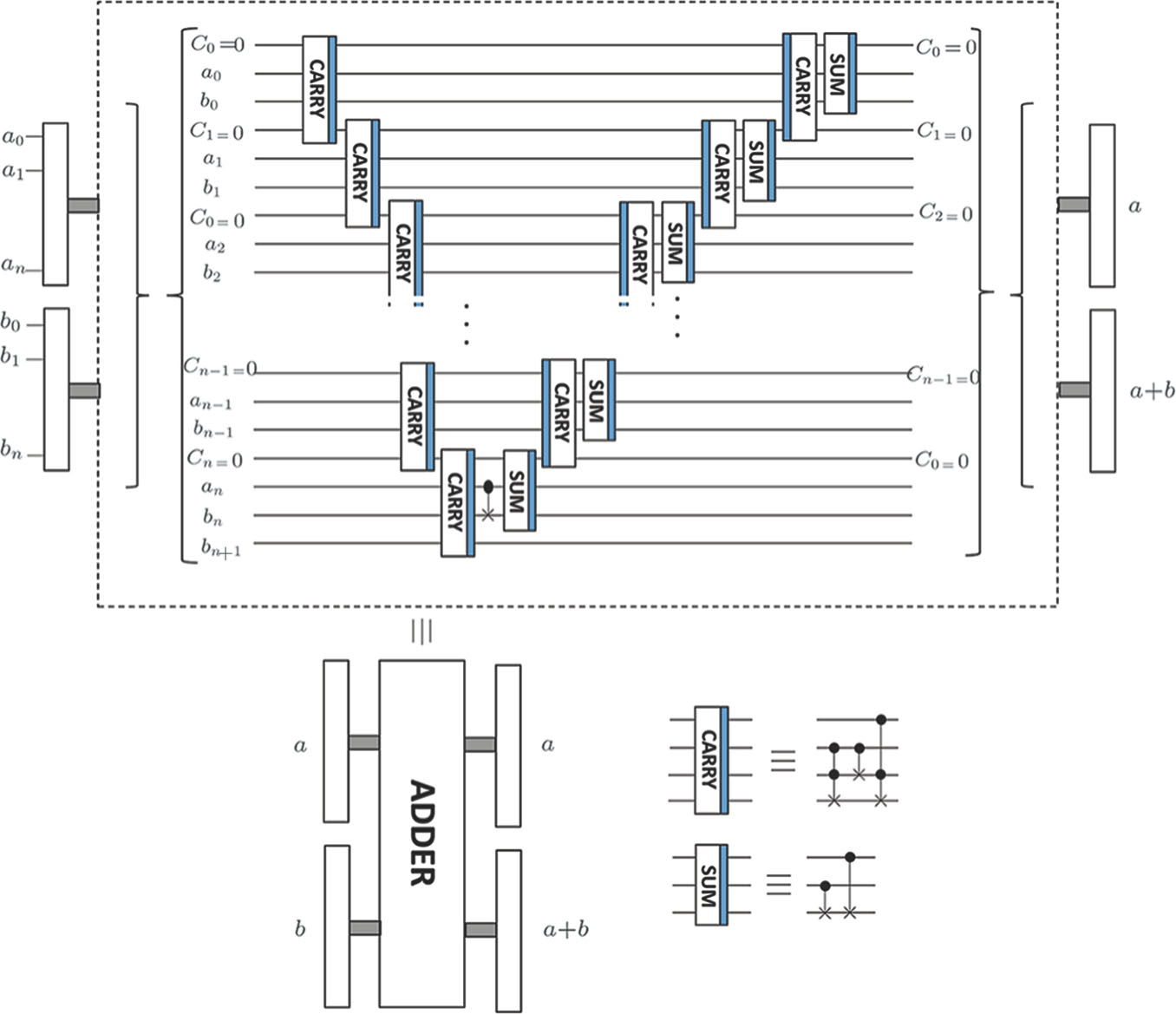
Figure
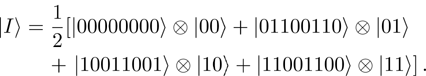
A quantum circuit for plain adding includes of quantum logic gates with time synchronized computational steps,[33] where the digital binaries are encoded in the quantum basis which are often called quantum registers. The addition of two quantum registers 
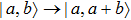
By reversing the quantum plain adder circuit, the quantum circuit for subtracting is resulted. The output of quantum subtracter with the input 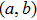
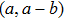
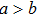

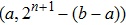
A circuit for quantum Xoring of two qubits is illustrated in Fig. 

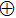
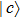
 | Fig. 3. Two qubit Xoring circuit, the symbols “   |
| Table 1.
Procedure for the Xing. . |
Fourier transform is a useful and powerful tool in many area of science. However, there is another kind of unitary transforms, the wavelet transforms, which are as useful as the Fourier transform and can be used to expose the multi-scale structure of a signal and very useful for image processing and data compression.
To analyze continuous waves, a mathematical representation is used. Therefore it is needed to transform continuous waves into a digital signal and analyze it. There are three kind of transformation, Fourier transform, short time Fourier transform, and wavelets transform.
In definition, a wavelet is a small wave that start and stop. The energy of a wavelet which is concentrated in time is used to analyze transient, non-stationary, or time-varying phenomena.
Two class of useful wavelets in signal processing are Haar and Daubechies wavelets. Quantum Haar and Daubechies wavelets circuits are proposed in Ref. [34], The whole quantum circuit of Daubechies fourth-order wavelet kernel is illustrated in Fig. 
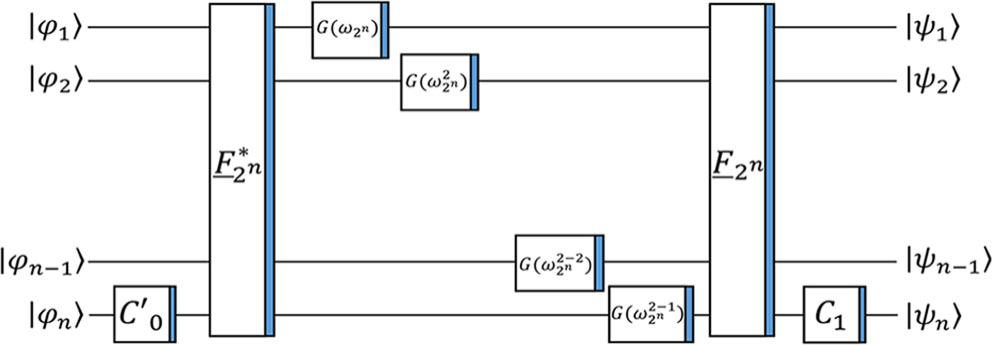 | Fig. 4. Quantum circuit of Daubechies fourth-order wavelet kernel.[35] |
In this section, our method for quantum watermarking based on QWT is presented, in which a 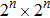
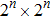
The scrambling methods are considered as preprocessing tasks in most of the image processing algorithms, where an image is transformed into another disordered one. In the proposed watermarking scheme, to increase the security of the proposed methods, a simple scrambling method is employed.[28]
Consider a binary 
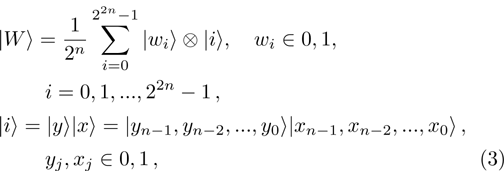
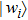
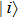
For the aim of scrambling, two 2n-bit keys 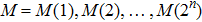
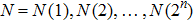
The scrambling task is accomplished as follows:

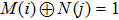
The I operation is applied to the color value at position 

The X operation is applied to the color value at position 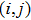
where,
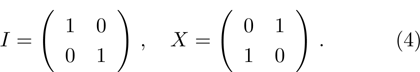
To sum up, prior to embedding process watermark image 
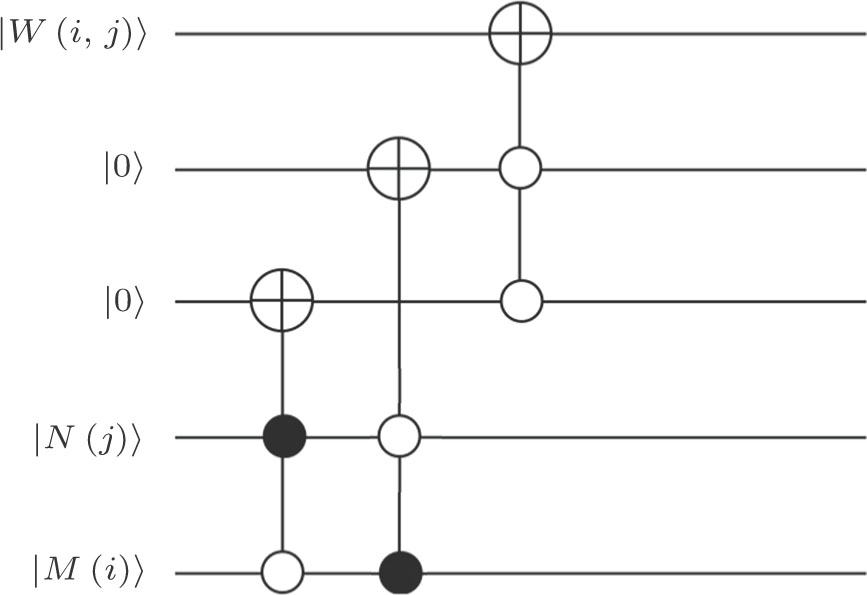 | Fig. 5. Quantum circuit for scrambling.[28] |
Consider a 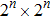

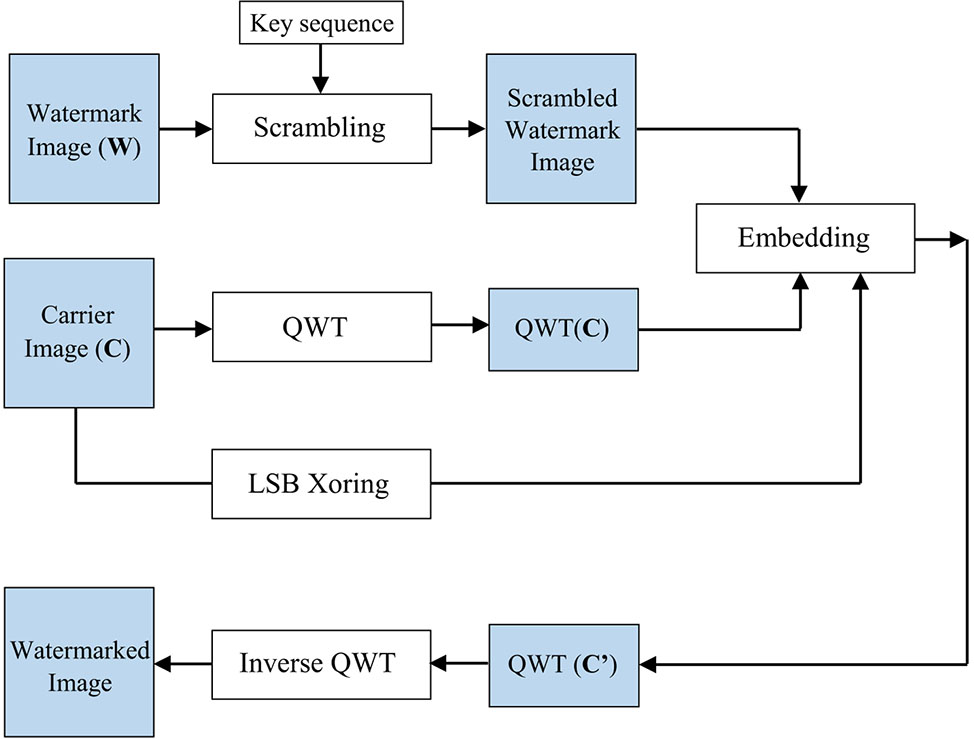
For embedding purpose, the LSB XORing technique[36] and Quantum Wavelet Transform on carrier image are employed. The outline of the proposed embedding method is given in Fig.
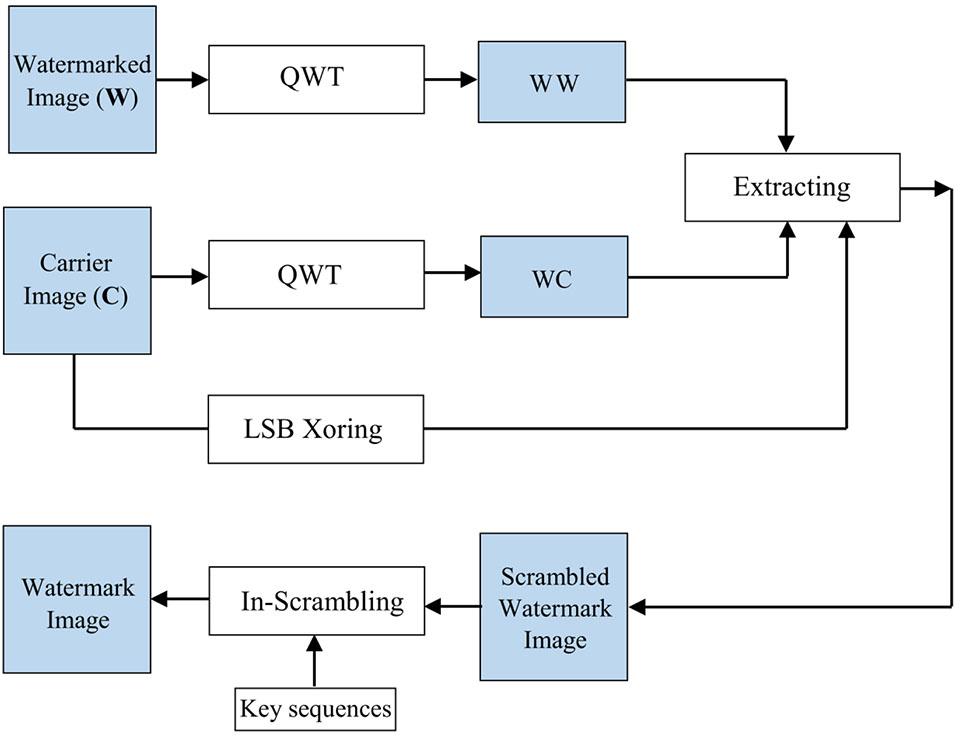
To extract the watermark image from embedded image, the original carrier image, its quantum wavelet transform, the proportion φ and the scrambling key sequences for In-scrambling procedure are needed. The procedure is as follows:
The details of the extracting procedure are shown in Table
| Table 3.
Procedure for extracting. . |
There are two key properties to be analyzed here, invisibility and robustness. Since the present state-of-the-art quantum hardware currently cannot go beyond proof-of-principle outcomes, to analyze these two properties, using a computer with Intel(R) Core(TM) i7-4500u CPU 2.40 GHz, 8.00 GB Ram equipped with the MATLAB R2015a environment, the proposed scheme is simulated. The carrier images and the watermark images employed in the simulations are given in Fig.
Invisibility represents the similarity between the original covers and the watermarked image. To analyze the invisibility of the proposed scheme two analyze methods are: taken into account the peak-signal-to-noise ratio (PSNR) analysis and the histogram analysis.
(i) The peak-signal-to-noise ratio (PSNR)
To compare the fidelity of a watermarked image with its original version, the peak-signal-to-noise ratio (PSNR) is often used. The PSNR is defined as follows:
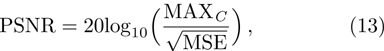
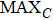


The results of the PSNR calculation in our simulation are given in Table
| Table 4.
The calculated PSNR for different images in our simulations. . |
The visual effects of the proposed watermarking procedure are illustrated in Fig.
 | Fig. 10. The original carrier images are given in the first row, and the watermarked images are presented in the second row. Watermark image in all of second image is the watermark 1. |
(ii) Histogram
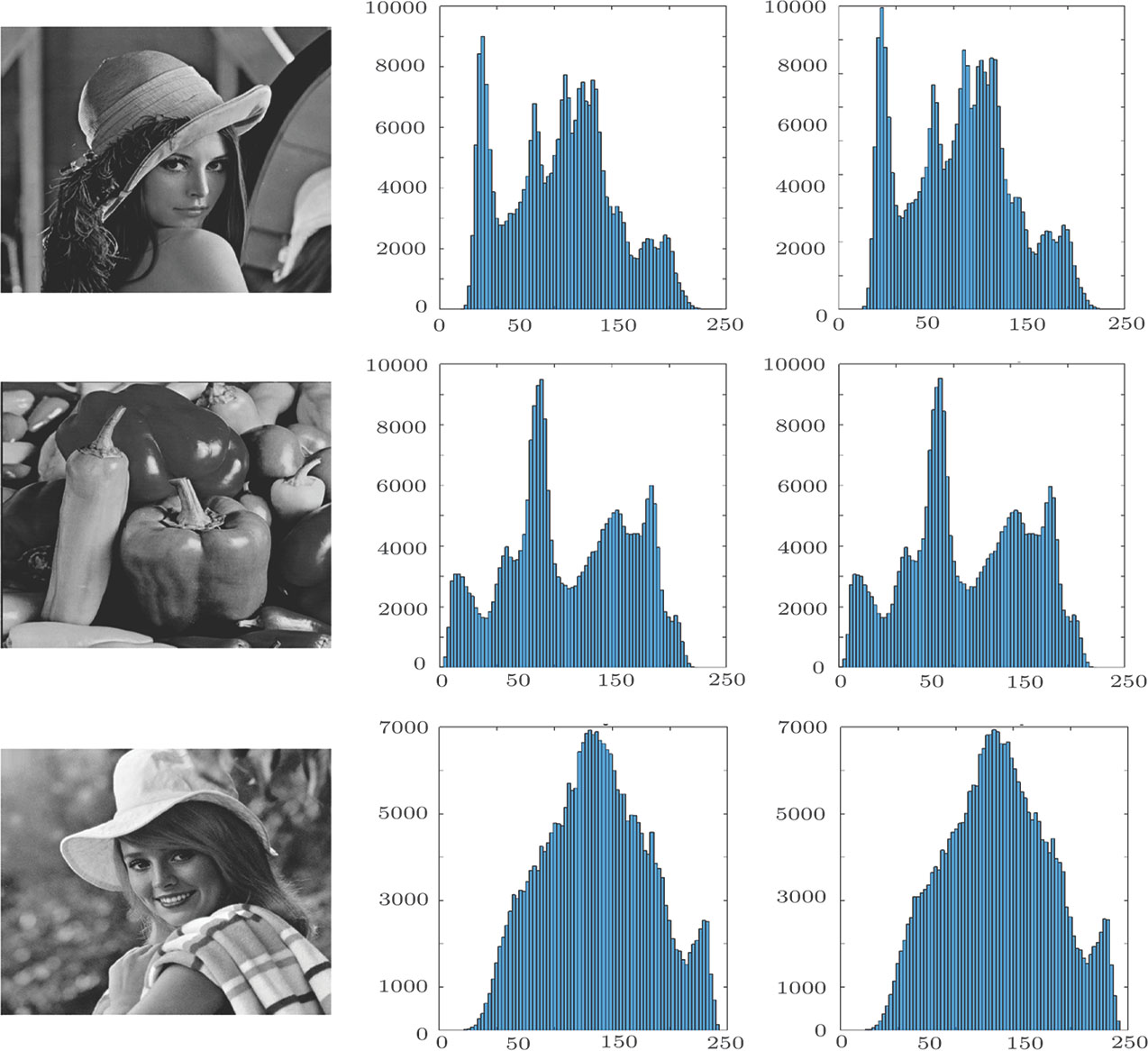
The images histogram analysis is an important method to evaluate the fidelity of a watermarked image with the carrier image. The histogram graph, indicates the frequency of pixels intensity values, where, the x axis refers to the gray level intensities and the y axis refers to the frequency of these intensities. Using the histogram analyzing one can judge if the images are match or not.
The histogram graphs of the three carrier images and the histogram graphs of their corresponded watermarked images where the watermark 1. is considered as a watermark image are given in Fig.
Robustness refers to the ability of message to survive in attacks.[37] The Bit Error Rate (BER) and the Correlation Two-Dimensional (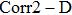
(i) The Bit Error Rate (BER)
This Bit Error Rate (BER) is defined as the inverse of PSNR:

The BER determines the portion of the original image’s bits, which are changed during the watermarking procedure. For example, if the PSNR is 50 db, the BER would be 0.02, i.e., %2 of bits have been changed during the watermarking. The result of the BER values calculated in our simulation are given in Table
| Table 5.
All the images’ BER in our simulations. . |
(ii) Correlation Two-Dimensional (Corr 2–D)
The Correlation Two-Dimensional, i.e., Corr 2–D, determines the correlation rate between two images, say A and B, which is calculated as follow:

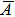
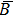
The Corr 2–D is a real number in the range of [−1, 1]. The positive or negative sign means the two input images have positive or negative correlation respectively. Notice that the output 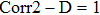
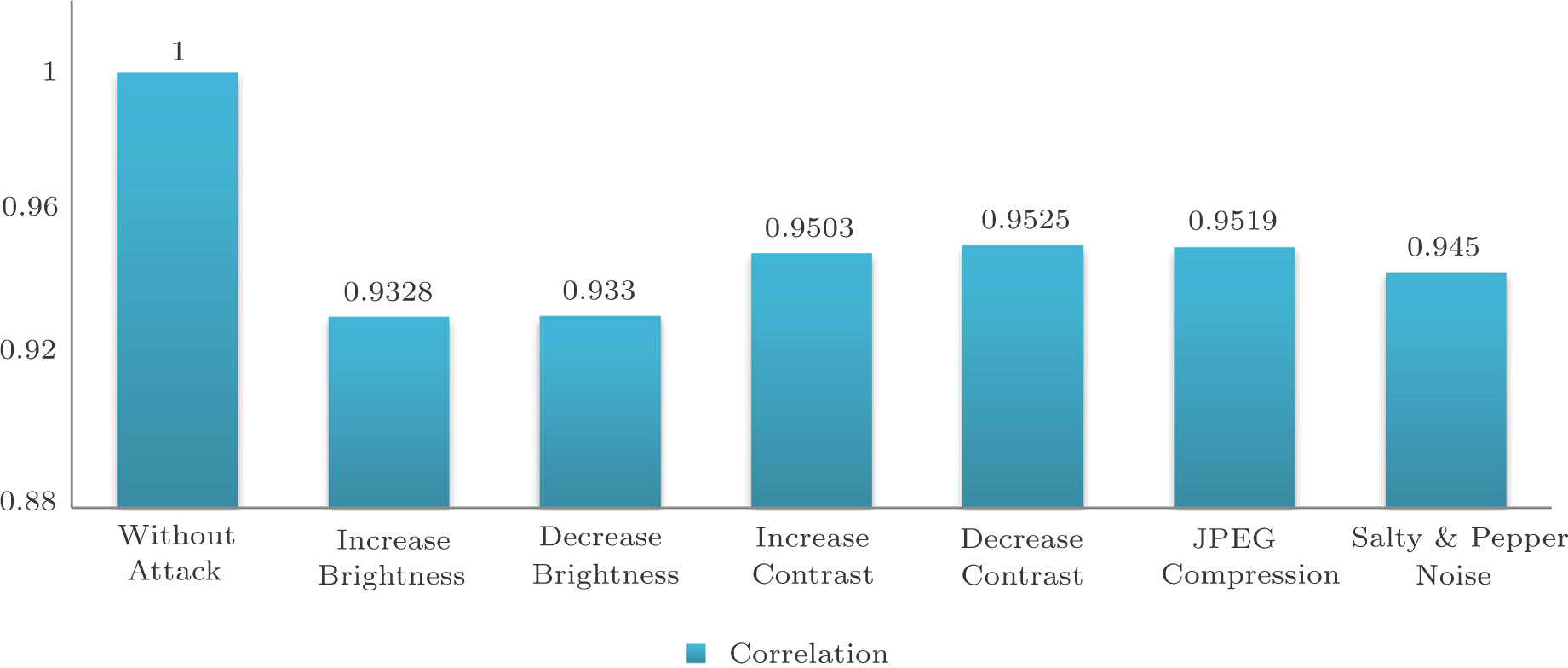
In our simulation, to analyze the algorithm’s resistance against attacks, we consider 6 different types of attacks which are exerted on the watermarked image. The watermarked image, after attack, is extracted and corresponded Corr 2–D is calculated. i.e., the correlation between original and extracted watermark image is achieved. The results are given in Table
| Table 6.
The correlation rate of extracted watermarks after attacks. . |
Considering the results, which are presented in Table
Any applicable protocol of watermarking has to satisfy two key properties, invisibility and robustness. Invisibility means that there is an acceptable similarity between the original covers image and the watermarked image. Robustness refers to the resistance of the scheme against attacks. Here we have introduced a novel robust quantum watermarking protocol exhibits acceptable invisibility performance. In the proposed scheme, employing quantum wavelet transformation, a binary 
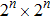
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] |