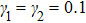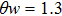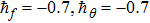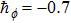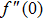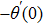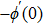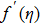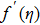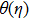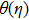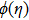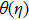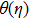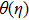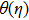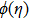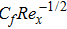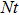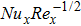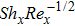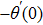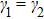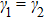† Corresponding author. E-mail:
Present analysis discusses the boundary layer flow of Eyring Powell nanofluid past a constantly moving surface under the influence of nonlinear thermal radiation. Heat and mass transfer mechanisms are examined under the physically suitable convective boundary condition. Effects of variable thermal conductivity and chemical reaction are also considered. Series solutions of all involved distributions using Homotopy Analysis method (HAM) are obtained. Impacts of dominating embedded flow parameters are discussed through graphical illustrations. It is observed that thermal radiation parameter shows increasing tendency in relation to temperature profile. However, chemical reaction parameter exhibits decreasing behavior versus concentration distribution.
It is generally an accepted fact that non-Newtonian fluids are more industry oriented as compared to Newtonian fluids. Glue, coal water, custard, ketchup, inks, cosmetics, toothpaste and jellies are some examples of non-Newtonian fluids. Unlike Newtonian fluids, no single relation can be predicted for non-Newtonian fluids as each non-Newtonian fluid possesses varying properties of viscosity and elasticity, which makes the mathematical modeling of these fluids more complicated as compared to Newtonian fluids. Many researchers are involved in exploring the new dimensions in this area.[1–5] Each non-Newtonian fluid model holds different features to exhibit a physical phenomenon. Eyring Powell fluid model[6–8] is one such model that can be extracted from kinetic theory of gases instead of Power law model. However, at low and high sheer rates, it exhibits the Newtonian behavior rather than pseudo-plastic systems’ behavior. At different polymer concentrations, Eyring Powell model is considered to be more precise and reliable in estimating the fluid time scale.[9]
In the present era of industrial revolution, Choi’s pioneering work[10] in nanofluids characterized by their ability to upsurge the thermal conductivity of base liquid, has opened the gates for followers to work in new dimensions. Choi found that heat transfer rate can be doubled by adding a small amount of nano particles. The novel characteristics of thermophoresis and Brownian motion of such fluids also make them potentially practical. Applications of nanofluids include cooling of micro chips, nano-drug delivery, and cancer therapy. Many researchers are exploring new dimensions and adding valuable contributions toward nanofluids. Some of these include exploration by Sohail and Saleem[11] that explores a time dependent flow on a rotating cone of Eyring Powell nanofluid under the impact of mixed convection. Waqar et al.[12] studied three-dimensional heat generation/absorption flow of an Oldroyd-B nanofluid. Khan et al.[13] focused 3D nanofluid flow in lateral directions over a nonlinearly stretched sheet. Jalilpour et al.[14] focused MHD stagnation point nanofluid flow in the presence of prescribed heat flux and heat generation/absorption past a porous stretching sheet. In recent literature, various dimensions have been explored in the presence of nanofluids.[15–20]
In general, four heating processes are available in the literature namely (i) prescribed surface heat flux, (ii) prescribed wall temperature, (iii) Newtonian heating, and (iv) conjugate/convective boundary conditions. In today’s modern world, demand for compact and light weight devices for technological and engineering machinery urge researchers to explore more avenues in heat transfer equipment with enhanced efficiency. Due to this increasing demand of small and light weight units, researchers have been focusing on effects on interface between axial wall conduction and thermal boundary layers in fluids that directly influence the heat exchange performances. Convective boundary condition is the generalized concept of prescribed surface temperature and prescribed heat flux conditions. Convective boundary condition is derived from the amalgamation of Newton’s law of cooling and Fourier’s law of heat conduction. It can be reduced to both prescribed surface temperature and heat flux conditions by making Biot number tends to infinity and zero respectively. Many researchers are exploring new mathematical models involving convective heat condition. To mention few amongst these, the study by Ibrahim[21] who examined the magnetohydrodynamic flow of nanofluid near the stagnation point under the influence of convective boundary condition. Ibanez[22] studied MHD flow past a channel with permeable walls in attendance of convective and hydrodynamic slip boundary conditions. Mustafa et al.[23] addressed the radiative Maxwell fluid flow with impact of convective condition. Recently, a variety of alluring problems highlighting effects of convective boundary condition are discussed, see Refs. [24–27].
In above referred studies, none of these have disused combined effects of non-linear thermal radiation and variable thermal conductivity with amalgamation of chemical reaction. This has motivated us to study the problem of Eyring Powell nanofluid flow in presence of heat and mass convective boundary conditions past a continuously moving surface. No such study has been carried out till now in the literature as far as our knowledge is concerned. Series solutions have been obtained using famed Homotopy Analysis method (HAM).[28–31] Partial differential equations with high nonlinearity are changed into nonlinear ordinary differential equations using appropriate transformation. Graphs of Skin friction coefficient, local Nusselt and Sherwood numbers with mandatory conversation versus various parameters are also added.
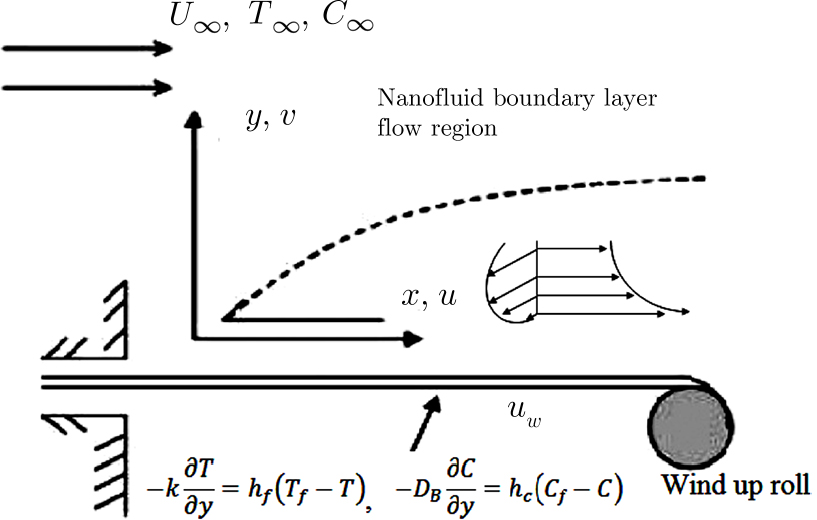
We assume 2D steady flow of an incompressible Eyring Powell nanofluid past a surface moving with constant velocity uw. Both constant velocity uw and uniform free stream velocity 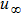

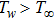
The Cauchy stress tensor in an Eyring–Powell model[6] is governed by the relation:
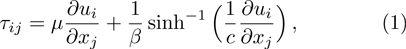
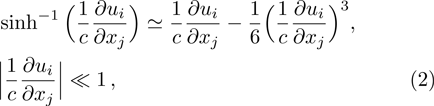

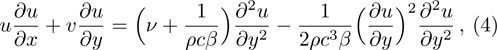
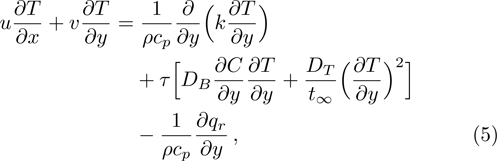
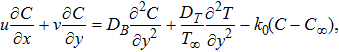
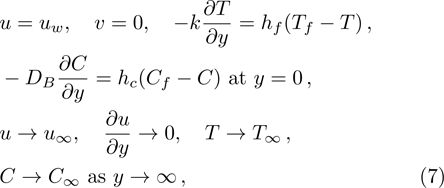
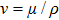
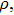
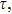
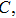
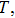
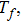
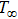

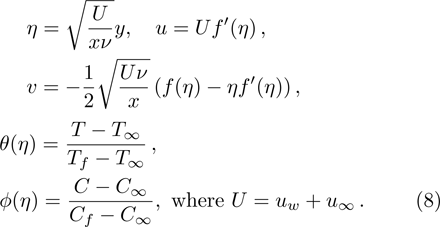
Considering variable thermal conductivity 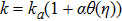
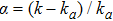
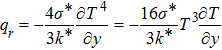
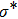

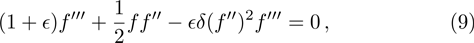
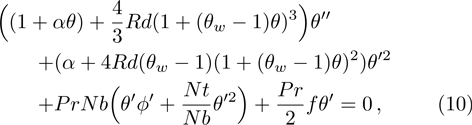

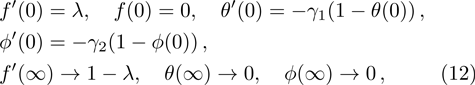

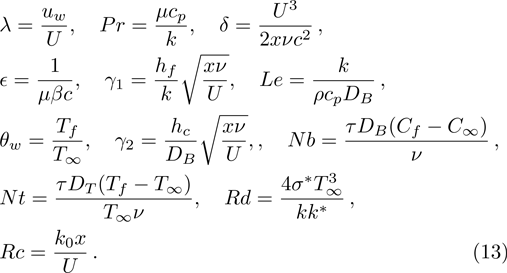
The case λ = 0 relates to the flow over an immobile surface because of free stream velocity. However, λ = 1 points out the moving plate in the fluid. The flow of fluid and plate moving in the same direction is represented by the case 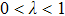
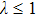
The skin friction coefficient 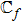
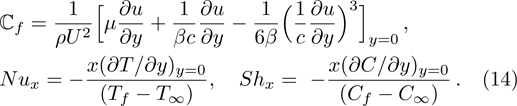
In non-dimensional forms Skin friction, local Nusselt and Sherwood numbers are


Liao[36] suggested Homotopy Analysis method in 1992 for the construction of series solutions of differential equations with high nonlinearity. This method has advantages over the contemporary methods because of the following reasons:
(i) This method is independent of selection of large or small parameters.
(ii) Convergence of series solution in this method is guaranteed.
(iii) Ample choice for the selection of base functions and linear operatos is available in this method.
Initial guess estimates 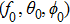
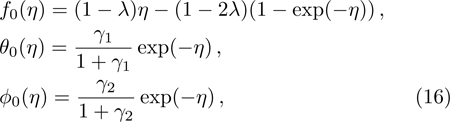
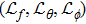
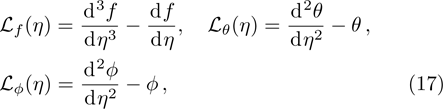
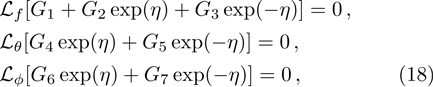
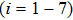
The problem at zeroth order is assembled as
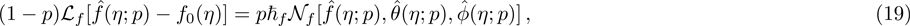
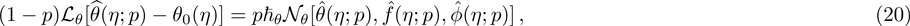
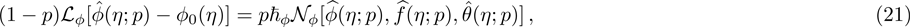


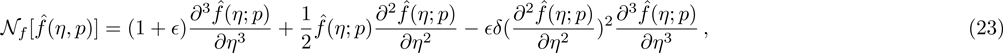
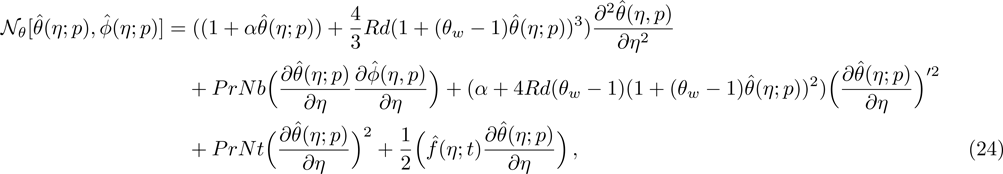

Here, non-zero auxiliary parameters are 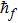




If we change p from 0 to 1, the values of the functions 

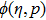



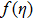


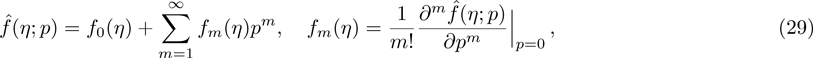
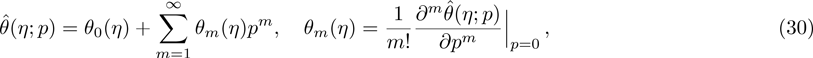
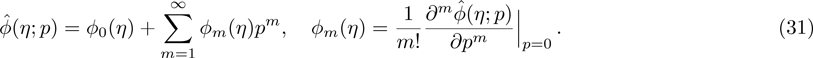
The value of auxiliary parameters 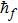
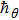
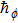



The m-th order deformation problem is obtained by taking successive derivatives m times of Eqs. (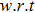



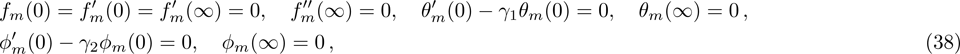
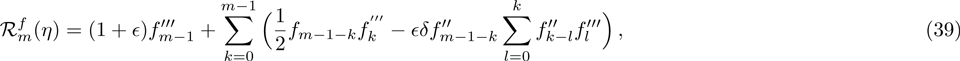
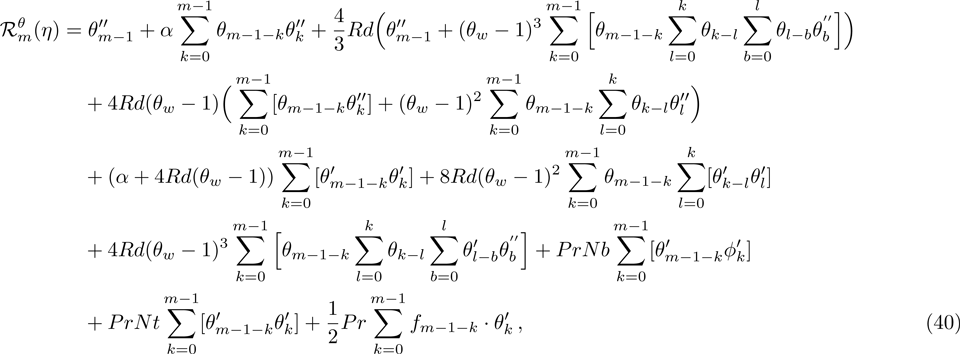
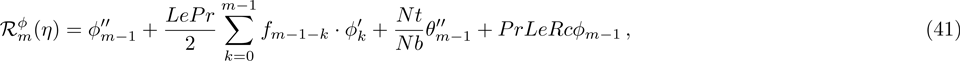

The general solutions in the form of special solutions 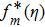
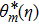
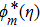
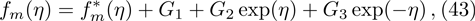
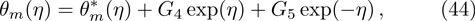

Here, constants Gi (i=1–7) through boundary conditions (38) are appended as

The problems comprise of Eqs. (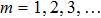
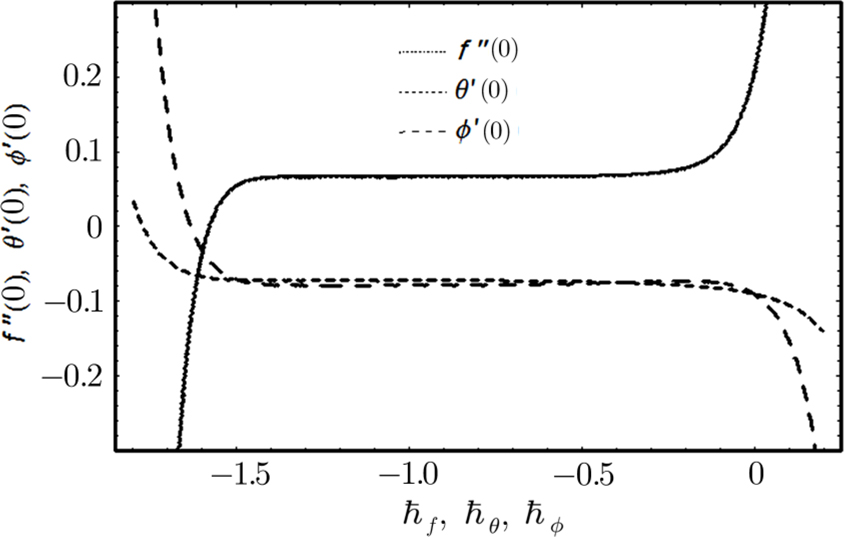
Series solution requires convergence region. Auxiliary parameters 
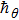
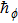
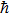


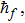
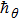
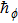
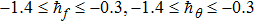
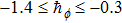
| Table 1
Series solutions’ convergence for varied order of approximations when ϵ = 0.4, δ = 0.4, λ = 0.4, Nb= 0.2, Le = 1.0, |
This segment emphasis on the discussion of graphical illustrations of different emerging parameters on all dimensionless distributions.
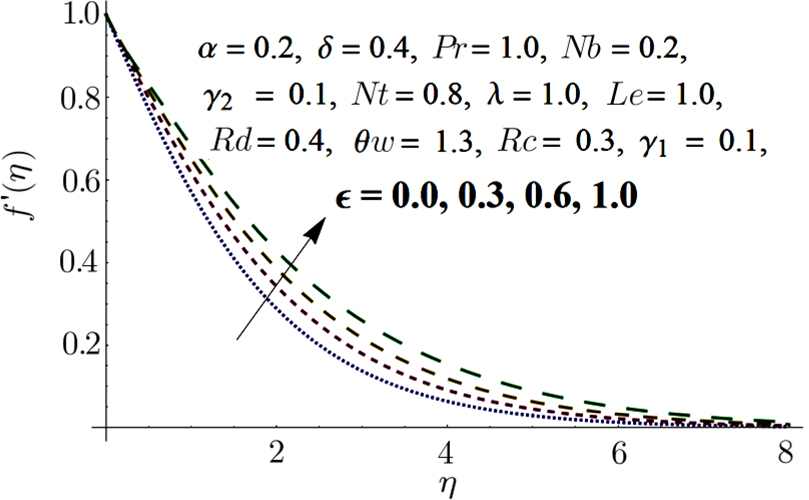
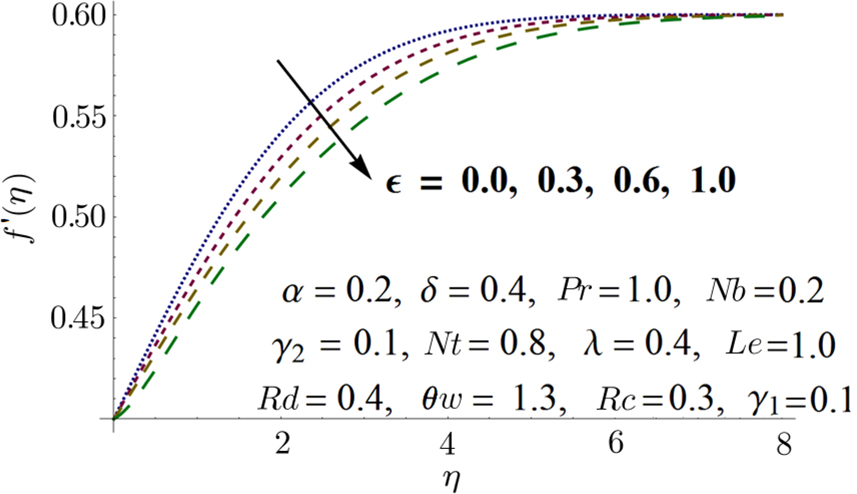
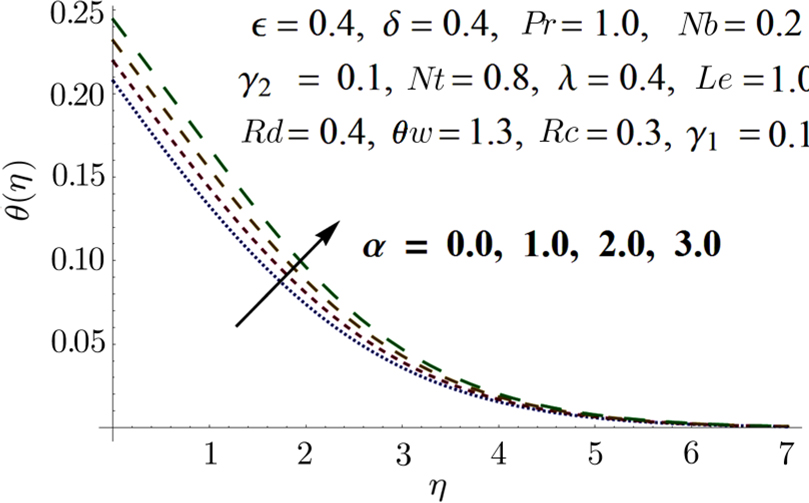
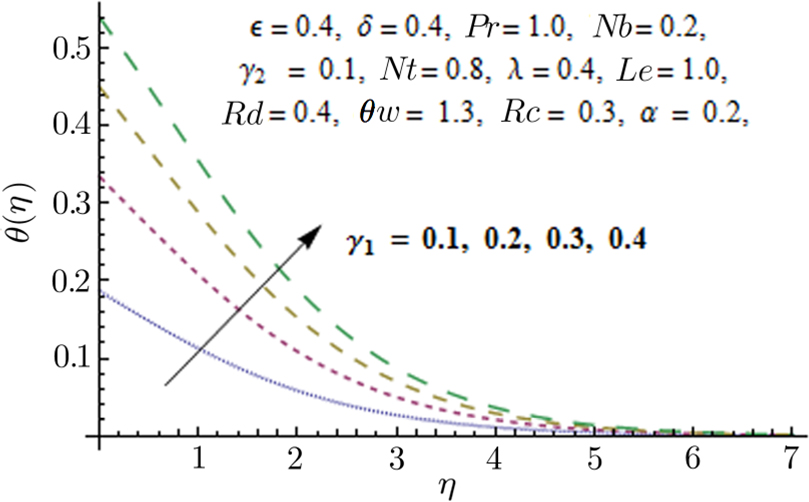
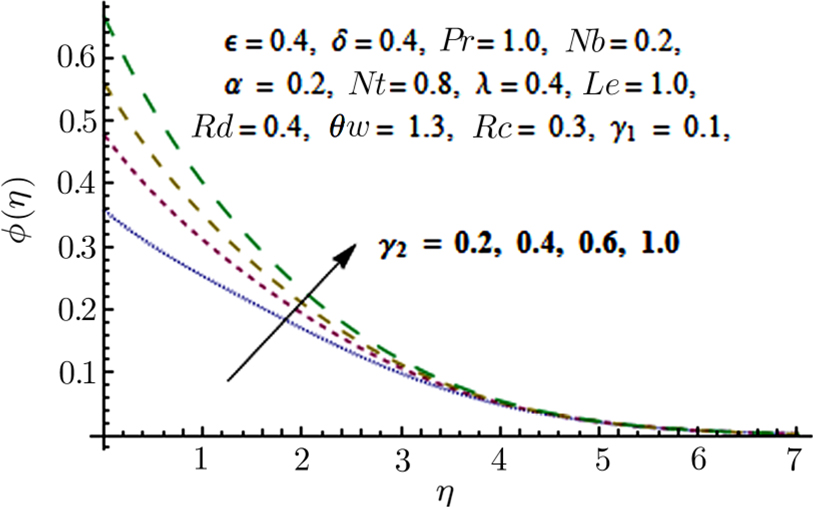
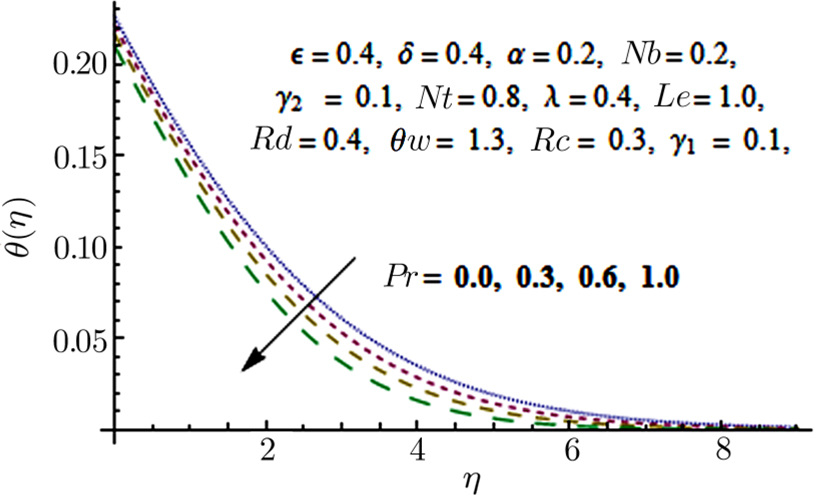
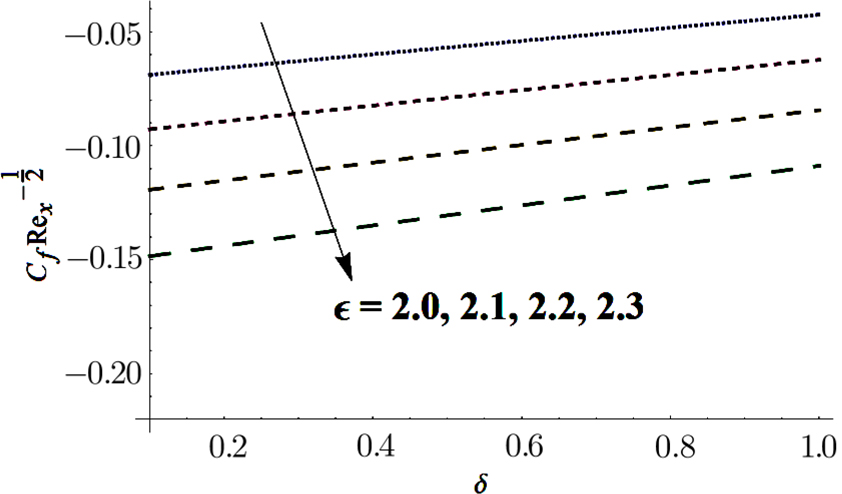
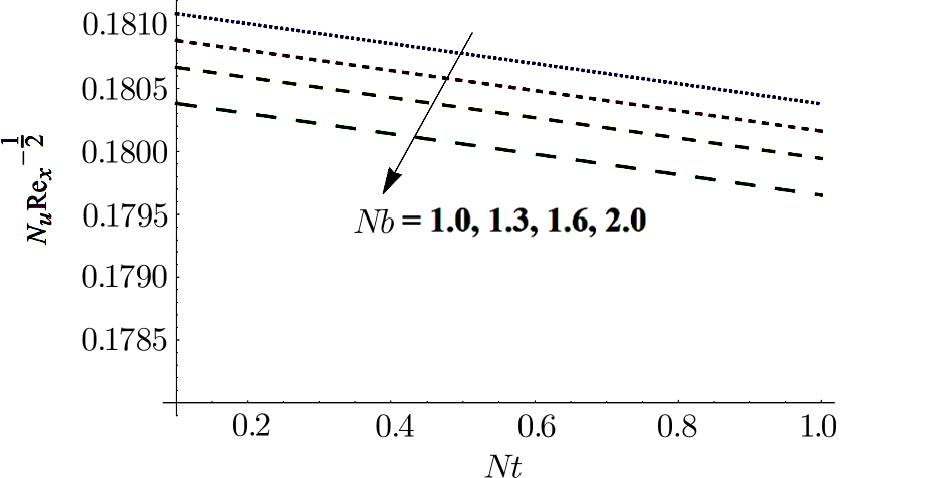
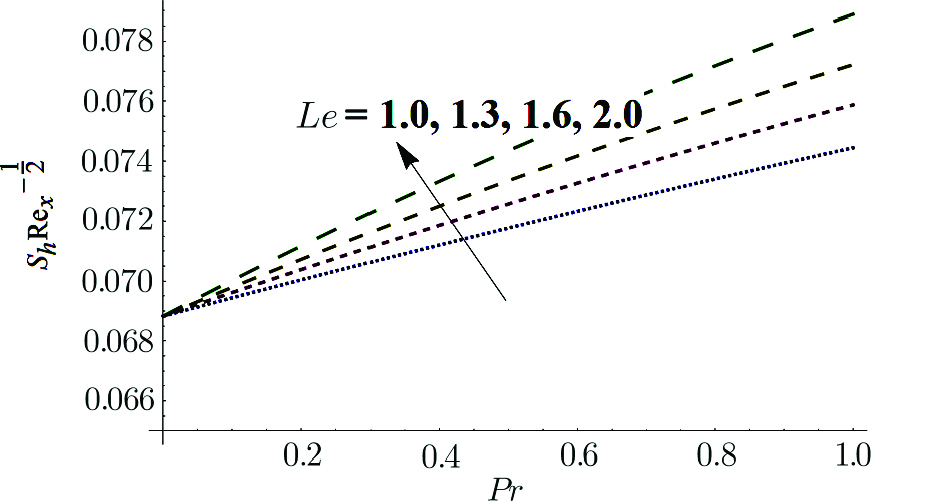
Figures 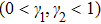
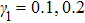
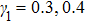
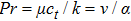
From Fig. 

Figure
Table
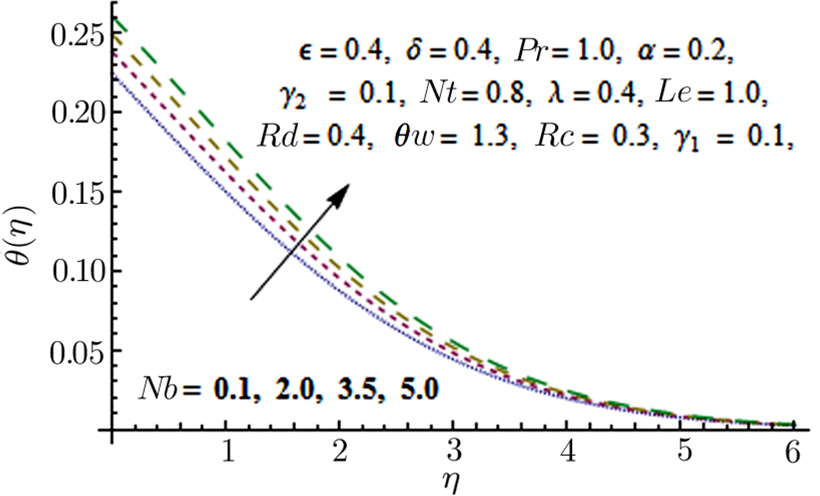
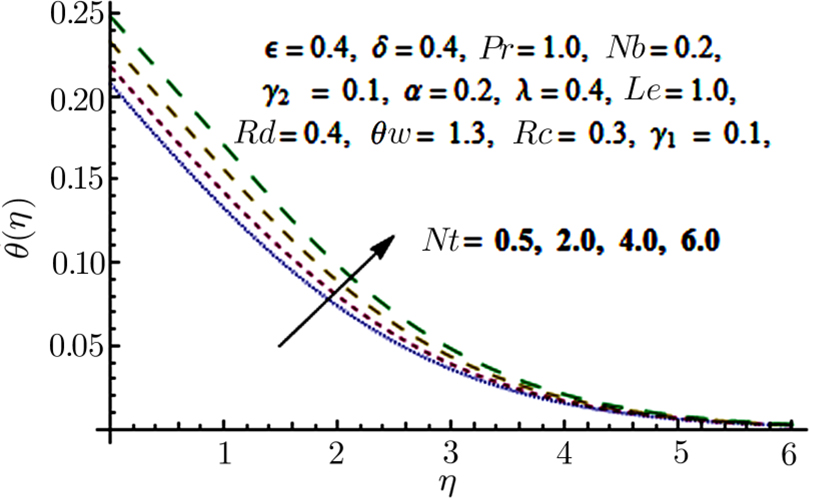
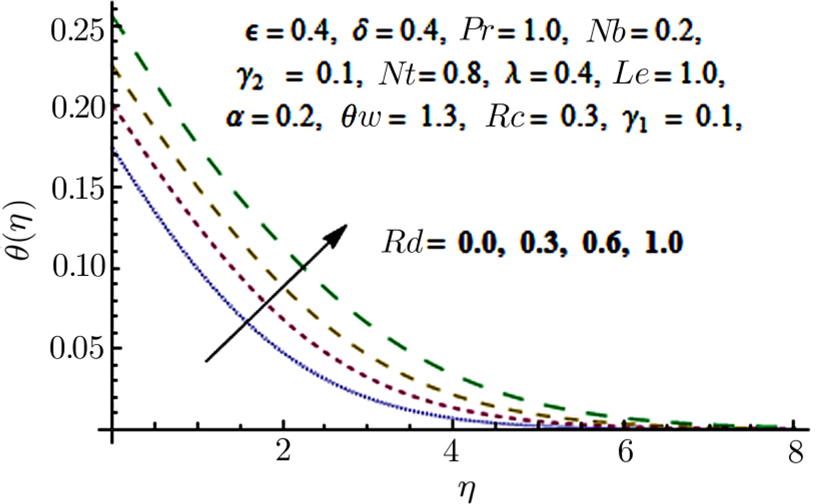
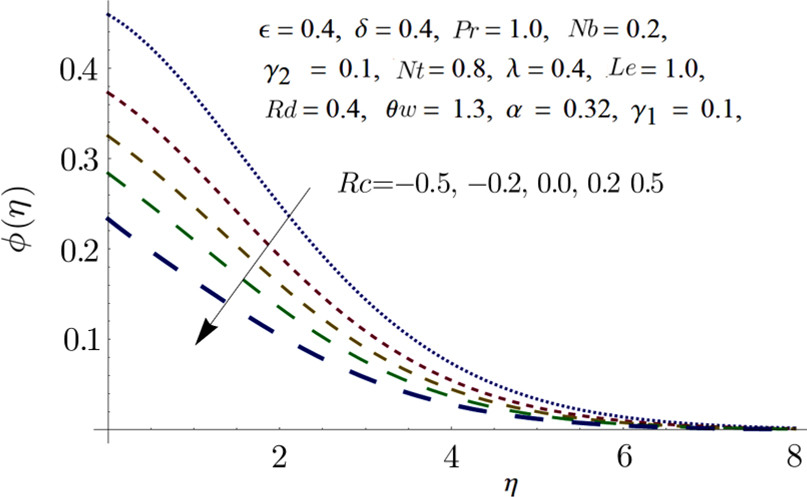
Effects of convective boundary conditions on time independent boundary layer Eyring Powell nanofluid flow past a constantly moving surface in attendance of free stream velocity is discussed. Effects of non linear thermal radiation, chemical reaction, and variable thermal conductivity are also taken into account. Series solution for the said problem is obtained using Homotopy Analysis method (HAM). The prominent outcomes of this problem are: Temperature field is declining function of Pr. Temperature distribution is growing function of Nb and Nt. Chemical reaction parameter Rc is a dwindling function of concentration profile. Temperature distribution shows increasing tendency when values of thermal conductivity parameter α is increased. Temperature distribution is growing function of Rd. Values of Sherwood number are increased when the values of Le and Pr are larger.
The authors declare no competing interests.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |