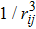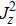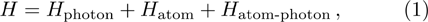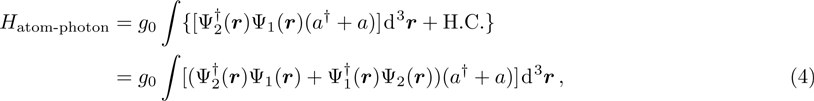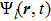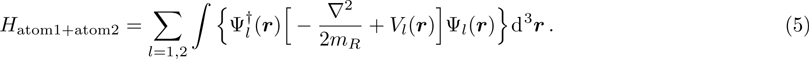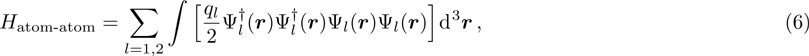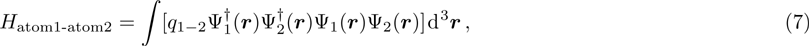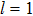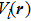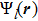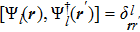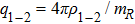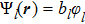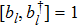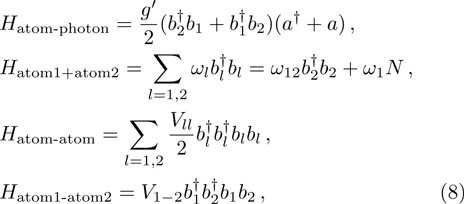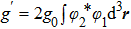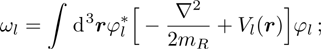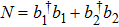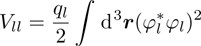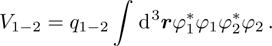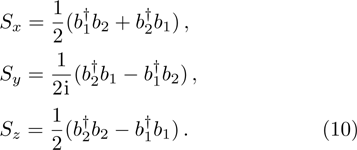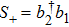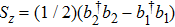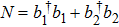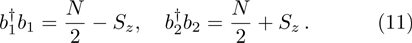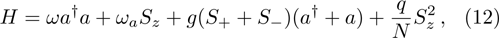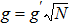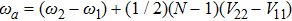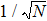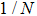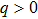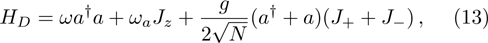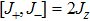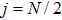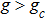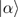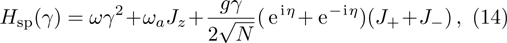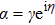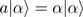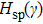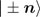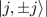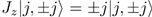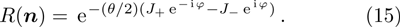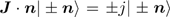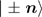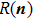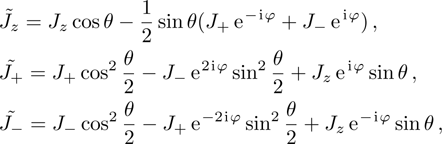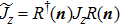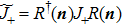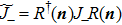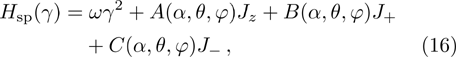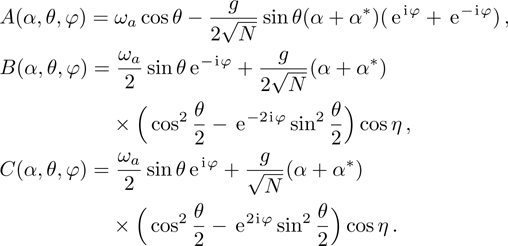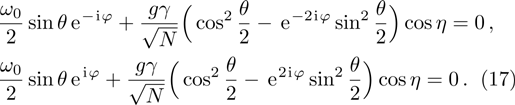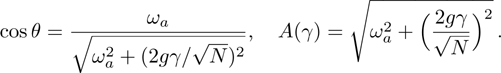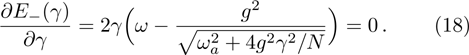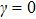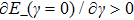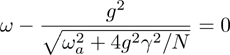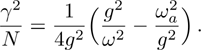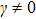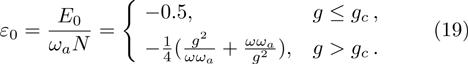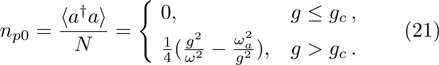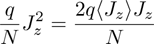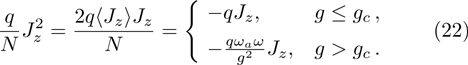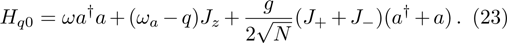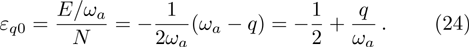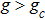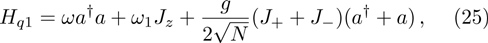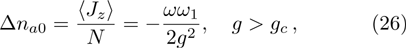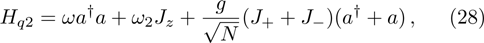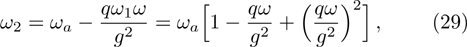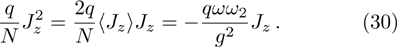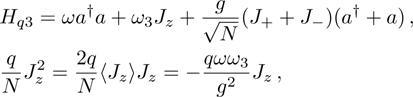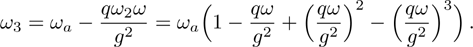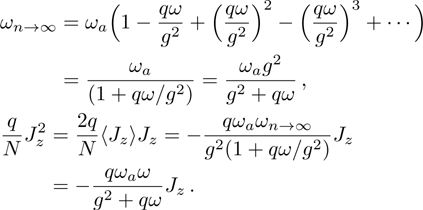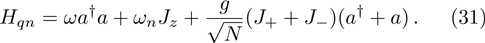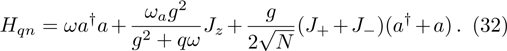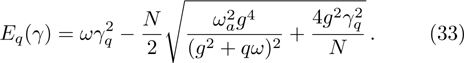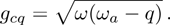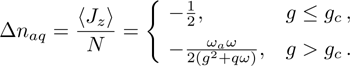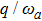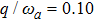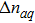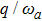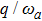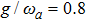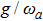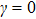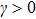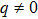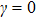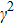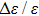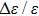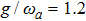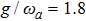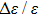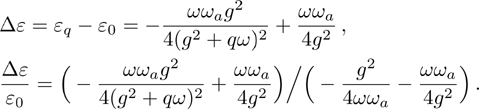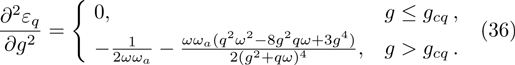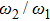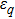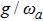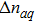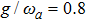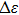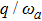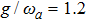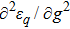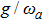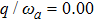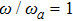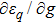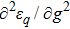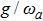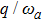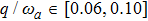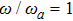First-Order Quantum Phase Transition for Dicke Model Induced by Atom-Atom Interaction
1 IntroductionIn contrast to classical phase transition, quantum phase transition (QPT),[1] which occurs at absolute zero temperature, can only be accessed by changing the physical parameters, for instance, the magnetic field strength. QPT takes place in many-body system and such QPT is a second-order phase transition.
Dicke model (DM)[2] is mainly used to describe the interaction between an ensemble of N identical two-level atoms and a quantized single-mode bosonic field. Although the form of DM is simple, it contains a rich physical meaning. Moreover, the Dicke Hamiltonian, which contains a phase transition from the normal phase to the super-radiant phase,[3–6] is extensively used in theoretical research. In the atomic physics and solid state physics, the Dicke model has a wide range of research. In the processing of quantum information and quantum computing, QPT has a certain relationship between quantum entanglement and quantum chaos.[3–4,7–9]
The Dicke-type QPT,[10–11] which is useful to understand quantum many body systems, has been observed in recent experimental setup in 2010.[12] At the same time, a series of theoretical analysis are presented,[10,13–20] especially controlling the atom-atom interactions by the Feshbach resonances.[21] It is highlighted that the effective atomic interaction strength can be manipulated by Feshbach resonance, and in Feshbach resonance point, that is near its size and even up to the magnitude of MHz. Noting that the effective dipole-dipole interactions between the atoms are ignored in the above mentioned DM. In fact, the dipole-dipole interactions, which are spatially dependent on the leading term varying as 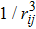 for small samples, where rij is the distance between i-th and j-th atoms, have a significant contribution to dephasing.[22] Meanwhile, the fluorescent spectrum and the second-order intensity correlation function are strongly dependent on the inter-atom interactions.[22–24] The hamiltonian of DM shows the great importance of the spin-spin interactions.[24]
for small samples, where rij is the distance between i-th and j-th atoms, have a significant contribution to dephasing.[22] Meanwhile, the fluorescent spectrum and the second-order intensity correlation function are strongly dependent on the inter-atom interactions.[22–24] The hamiltonian of DM shows the great importance of the spin-spin interactions.[24]
In this paper, we discuss the extended Dicke model including the atom-atom interaction. Based on the spin coherent-state (SCS) variational method,[25–26] we reveal the exact solutions of the ground state about the extended Dicke Hamiltonian. According to the analytic solutions, the mean photon numbers, the scaled atomic population and the average energy have been plotted. We also plot the critical curves and ground state phase figure. For the 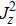 item, the SCS variational method can not deal with the square item of the atom-atom interaction. In order to solve the
item, the SCS variational method can not deal with the square item of the atom-atom interaction. In order to solve the  item, the self-consistent-field method[27–36] are introduced. Finally, a first-order phase transition[37] for the extended DM, which is different from the previous conclusion,[24] are revealed. It is demonstrated that the critical phase transition point from the normal phase to the superradiant phase is shifted by the dipole-dipole interaction and the self-consistent method applies to the case of small change.
item, the self-consistent-field method[27–36] are introduced. Finally, a first-order phase transition[37] for the extended DM, which is different from the previous conclusion,[24] are revealed. It is demonstrated that the critical phase transition point from the normal phase to the superradiant phase is shifted by the dipole-dipole interaction and the self-consistent method applies to the case of small change.
2 The Extended HamiltonianThe proposed DM Hamiltonian describing the interaction of an ensemble of N identical two-level atoms coupled to a single mode high-finesse optical cavity is given. For the atom-atom interaction, we only consider a simple two-body interactional potential and obtain the following Hamiltonian, which is expressed as the following three parts
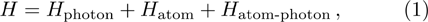
where the Hamiltonian of the photon is

and the Hamiltonian of the atomic part and the part of the atom-photon interaction are respectively

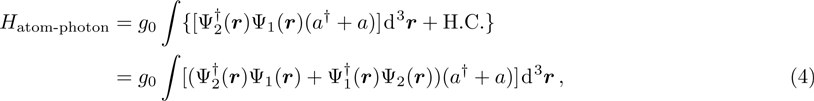
where
g0 is the coefficient of the atom-photon coupling strength.
In order to properly represent the elastic collision between the atoms, we only consider the two-body interaction with the δ potential and introduce the wave functions of the macroscopic condensate states 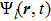 . According to the second quantization of Gross–Pitaevskii equation, the Hamiltonian of the atomic part in Eq. (3) could be obtained that
. According to the second quantization of Gross–Pitaevskii equation, the Hamiltonian of the atomic part in Eq. (3) could be obtained that
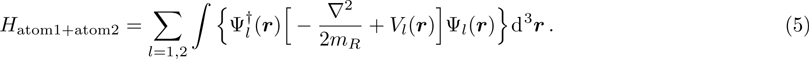
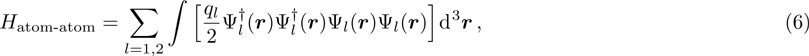
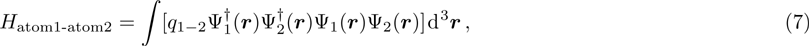
where
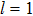
, 2 refer to the different atomic components;
mR is the atomic mass,
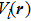
is the coulomb potential of the atoms;
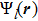
satisfy the commutation relation of the boson field operator
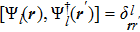
;

and
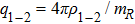
describe the interaction between the intraspecies and interspecies
s-wave scattering lengths of the atoms, and the
s-wave scattering lengths could be tuned via the Feshbach resonance technique in the experiments.
Based on the two-mode approximation and 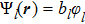 , where two boson annihilation operators b1 and b2 respectively represent two atomic modes and they satisfy the commutation
, where two boson annihilation operators b1 and b2 respectively represent two atomic modes and they satisfy the commutation 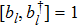 , Eqs. (4)–(7) of the atom-photon interaction and the atomic part reduce to the following
, Eqs. (4)–(7) of the atom-photon interaction and the atomic part reduce to the following
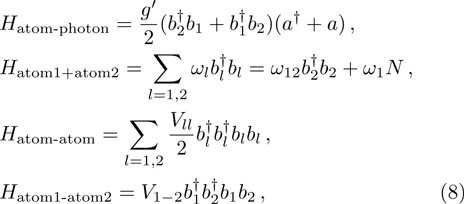
where
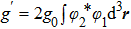
; The atomic frequency
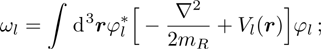
ω12 being the atomic transition frequency between the frequency of the ground state
ω1 and the frequency of the excited state
ω2;
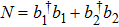
being the total atom number; the intraspecies and interspecies potential energies are respectively
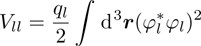
and
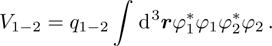
Substituting Eqs. (2)–(8) into the total Hamiltonian (1), finally the system’s Hamiltonian takes the form

For simplicity, we introduce the Schwinger angular momentum operators
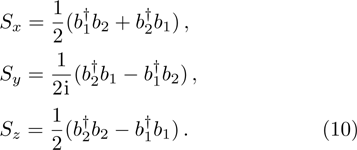
From Eq. (10), we can obtain that 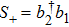 ,
,  . On the basis of
. On the basis of 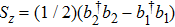 and
and 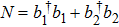 , we get
, we get
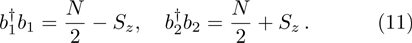
Substituting Eq. (11) into Eq. (9) and using the boson commutation relation, the Hamiltonian (9) is rewritten as
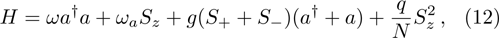
where defining the atom-photon interaction strength
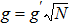
,

being the atomic average interaction strength,
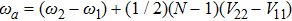
being the effective atomic frequency. The prefactor
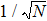
and
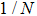
give a finite free energy per atom in the thermodynamical limit (

). Meanwhile, the constant terms related to the particle numbers have been ignored in Hamiltonian (
12). For the atomic interaction strength
q is very weak, it was often overlooked. In the absence of the atomic interaction, the system Hamiltonian (
12) reduces to the standard single-mode Dicke Hamiltonian. Hamiltonian (
12) is to be used to describe the atom-photon collective nonlinear interaction and the atom-atom interaction. In the present paper, we mainly discuss the influence of the atom-atom interaction on the ground state properties of the generalized DM. In whole paper, we give the examples of the atom-atom repulsive interaction, i.e.,
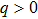
.
3 Spin Coherent-State Variational Method and Ground State EnergyThe Dicke Hamiltonian for N identical two-level atoms interacting with a single mode of the electromagnetic field is written by[12,38]
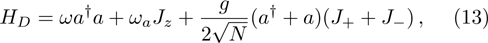
with
, where
ωa is the frequency of the two-level atoms,
ω is the frequency of the cavity-field mode, and
g is the atom-field coupling strength. The boson operators
a,
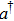
are the annihilation and creation operators for the cavity field, and the pseudospin
Ji (

, ±) is the collective atomic operators, which satisfy the angular momentum commutation relations (
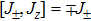
,
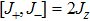
) with the spin length
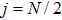
. As a classic problem in quantum optics, DM continually provides a fascinating avenue of research in a variety of contexts and is seen as a striking example for the macroscopic many-particle quantum state, which can be solved rigorously. The QPT from the normal phase to the superradiant phase occurs at the critical coupling strength

and the system enters the superradiant phase
[12] for
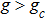
.
Under the optical coherent state 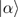 , we make the average of the DM’s Hamiltonian (13)
, we make the average of the DM’s Hamiltonian (13)
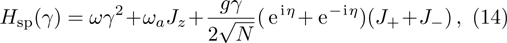
where
α is the complex eigenvalue of photon annihilation operator
a, i.e.,
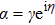
and satisfies
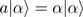
.
The average Hamiltonian 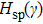 possesses two macroscopic eigenstate, i.e., the SCS
possesses two macroscopic eigenstate, i.e., the SCS 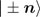 of south and north pole gauge. The SCS, which correspond to the normal and inverted pseudospin states in the dynamics of the DM, can be generated from the extreme Dicke states
of south and north pole gauge. The SCS, which correspond to the normal and inverted pseudospin states in the dynamics of the DM, can be generated from the extreme Dicke states 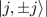 (
(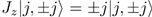 ) with the SCS transformation
) with the SCS transformation  .[25–26] And the unitary operator is explicitly given by
.[25–26] And the unitary operator is explicitly given by
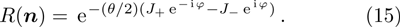
In fact, the SCS of the north and south pole gauges are the eigenstates of the spin projection operator 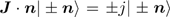 , where
, where  is the unit vector with the directional angles θ and φ. And the spin operators satisfy the minimum uncertainty relation (
is the unit vector with the directional angles θ and φ. And the spin operators satisfy the minimum uncertainty relation ( ) and therefore the SCSs
) and therefore the SCSs 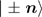 are called the macroscopic quantum states, which are orthogonal. Using the unitary transformations
are called the macroscopic quantum states, which are orthogonal. Using the unitary transformations 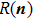 for the spin operators Jz,
for the spin operators Jz, 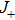 ,
, 
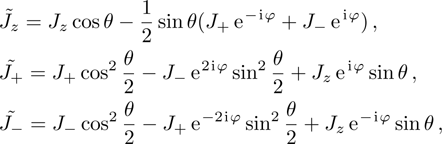
where
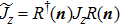
,
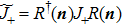
,
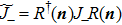
.
Through a series of complicated and tedious calculation, we finally get the following spin Hamiltonian
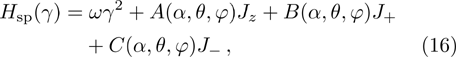
where
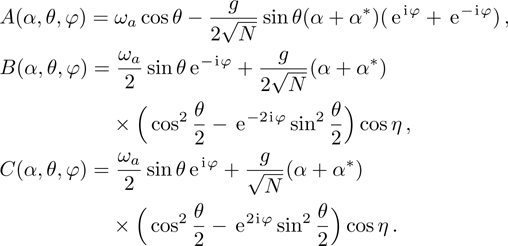
In order to obtain the diagonalized spin Hamiltonian, it needs to satisfy the conditions  , i.e.,
, i.e.,
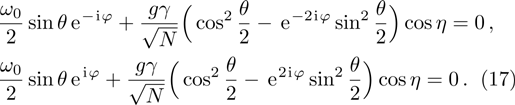
In principle, the angle parameters θ, φ can be determined based on the above conditions Eq. (17). Meanwhile, we get the following relations of the parameters θ and A
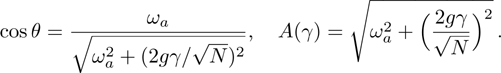
Finally, the ground state energy functional of one variable is obtained:

By the usual extremum condition of the energy function for the first-order derivative equal to zero, the macroscopic many-particle quantum state solutions are found:
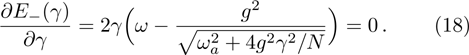
From Eq. (18), we find it possesses two solutions. One solution is the parameter  , corresponding to a zero-photon-number solution and giving rise to the normal phase (NP) only if the second-order derivative is positive, namely,
, corresponding to a zero-photon-number solution and giving rise to the normal phase (NP) only if the second-order derivative is positive, namely, 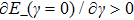 . The other solution satisfies the condition
. The other solution satisfies the condition
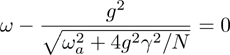
and we obtain the average photon number
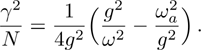
If the second-order derivative in the solution 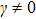 is positive, we define the system into the superradiant phase (SP). In the critical phase transition point
is positive, we define the system into the superradiant phase (SP). In the critical phase transition point  , the Dicke system undergoes a QPT from the NP to the SP, which has a wide range of research.[2–4,6,11–14,18–19,24]
, the Dicke system undergoes a QPT from the NP to the SP, which has a wide range of research.[2–4,6,11–14,18–19,24]
The ground-state energy of the DM system is
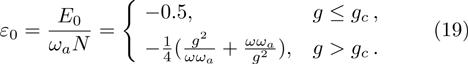
The atomic population difference is proportional to the atom-field interaction strength in the SP region and satisfies the following relation

The mean photon number distribution meets the following nonlinear relationship when 
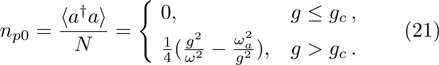
It is worth while to emphasize that the SCS method is completely consistent to the Holstein–Primakoff transformation[3] in deal with the ground state properties of the standard DM and is valid for arbitrary atom number N, which is superior to the Holstein–Primakoff transformation under the condition of the thermodynamic limit.
4 Self-Consistent Field Theory for Extended DM with Atomic InteractionIn some physical theories, mean field theory also can be seen as the self-consistent field theory,[27] which can be used to research the behavior of the large and complex stochastic models in a simple manner. Both the strong-interaction[34] and the weak-interaction[29] are compatible with the self-consistent field theory. The self-consistent field theory has been applied in the atoms,[30] the condensed matter,[31] the Lorentz gas[32] and so on. A series of literature have studied the exact-energy self-consistent field,[28] the self-consistent-field perturbation theory for the Schrödinger equation,[39] the self-consistent mean-field theory,[35] the self-consistent mean-field theory of asymmetric first-order structural phase transition,[33] the quantum quench in interacting field theory,[40] polariton condensation with nonlinear photons described by the generalized Dicke Hamiltonian on the mean-field level.[41]
In this article, we begin the following discussion based on the mean field approximation and the self-consistent field theory to solve the extended DM containing the atom-atom interaction.
For the atom-atom interaction  , by the means of the self-consistent mean field theory,[27] we obtain
, by the means of the self-consistent mean field theory,[27] we obtain
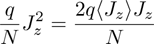
and substitute Eq. (
20) into this item
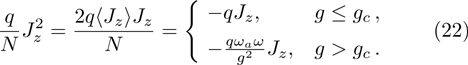
Substituting Eq. (22) for  into Hamiltonian (12), it turns into
into Hamiltonian (12), it turns into
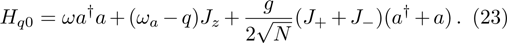
It is to be highlighted that Hamiltonian (23) only satisfies the case of the normal phase. And the corresponding scaled ground state energy
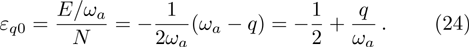
Substituting Eq. (22) for  again into Hamiltonian (12), it turns into
again into Hamiltonian (12), it turns into
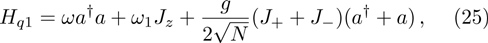
where

which contained the atomic interaction part.
For Hamiltonian (25), the atomic population difference has such form
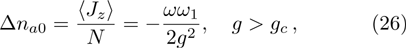
and the coresponding atom-atom interaction is

Once again, we substitute Eq. (27) into Hamiltonian (12), it turns into
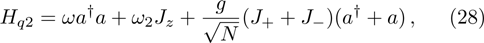
where the effective atom frequency
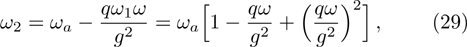
and at this time the coresponding atom-atom interaction is
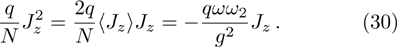
Hamiltonian (12) repeats the above steps (26), (27), and (29), (30) we obtain the third order case
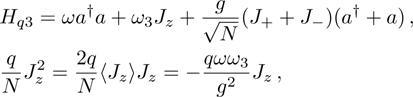
where
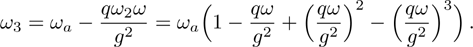
Repeating the above iteration until the k-th grade and  -th grade approximation have almost no influence on to the system’s total energy and meet the permissible error of the self-consistent field theory. Finally we obtain the n-th atomic effective frequency and the coresponding atom-atom interaction are respectively
-th grade approximation have almost no influence on to the system’s total energy and meet the permissible error of the self-consistent field theory. Finally we obtain the n-th atomic effective frequency and the coresponding atom-atom interaction are respectively
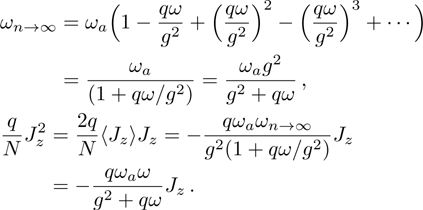
And the coresponding total Hamiltonian
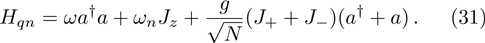
When  , Hamiltonian (31) returns to
, Hamiltonian (31) returns to
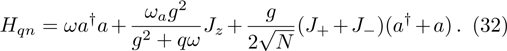
When the atom-atom interaction is not considered, i.e., q = 0, Hamiltonian (32) returns to the standard Dicke hamiltonian (13). If n changes into infinity, the self-consistent method has quite high accuracy and there is almost no error. In fact, there is so little difference between ω2 and ω1 or between ω3 and ω2. From Fig. 1, we may more clearly see this small differences. In the whole paper, the unite vector is ωa and we choose 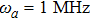 .
.
5 Ground State Properties for Extended DMBased on the above SCS method and Hamiltonian (32), the ground state energy functional
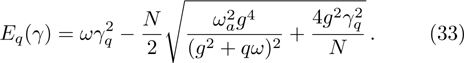
We also obtain that the extended DM goes through a quantum phase transition with the phase transition point
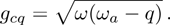
We also calculate the three corresponding physical quantity: the mean photon number, the atomic population imbalance, and the quasi-ground-state energy.
The mean photon number

The atomic population imbalance
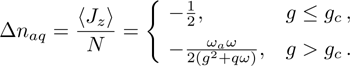
The quasi-ground-state energy

Figure 2 shows the influence of the atom-atom interaction parameter 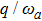 on the mean photon number (a), the atomic population imbalance (b), and the average ground-state energy (c). The average ground-state energy are continuous and slippy at the critical phase transition point gcq, which shifts toward the lower g direction with the increasing of the atom-atom interaction. In NP, the mean photon number and the atomic population imbalance have not been excited and the average energy is stable. On the opposite of NP, in the SP area, the excited photon or atom number are non-zero and increases as the collective coupling strength increases. At the same time, the average energy become low, but is continuous with the case of the NP zero. The three physical quantities are more and more close to the each other with the increasing of the collective coupling strength in the case of the atom-atom interaction
on the mean photon number (a), the atomic population imbalance (b), and the average ground-state energy (c). The average ground-state energy are continuous and slippy at the critical phase transition point gcq, which shifts toward the lower g direction with the increasing of the atom-atom interaction. In NP, the mean photon number and the atomic population imbalance have not been excited and the average energy is stable. On the opposite of NP, in the SP area, the excited photon or atom number are non-zero and increases as the collective coupling strength increases. At the same time, the average energy become low, but is continuous with the case of the NP zero. The three physical quantities are more and more close to the each other with the increasing of the collective coupling strength in the case of the atom-atom interaction  , 0.05, 0.10. The existence of the atom-atom interaction makes the phase transition point move left. Especially when
, 0.05, 0.10. The existence of the atom-atom interaction makes the phase transition point move left. Especially when 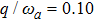 , there is a big movement.
, there is a big movement.
Figure 3 displays variations of the average photon number npq (a), the atomic population imbalance 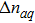 (b), and the average energy εq (c) with respect to
(b), and the average energy εq (c) with respect to 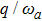 for the given
for the given  , 1.2, 1.5. The average photon number and the atomic population imbalance have not been excited, which are respectively a horizontal line, meanwhile the average energy increases obviously as the increase of the atom-atom interaction
, 1.2, 1.5. The average photon number and the atomic population imbalance have not been excited, which are respectively a horizontal line, meanwhile the average energy increases obviously as the increase of the atom-atom interaction 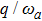 in the case of
in the case of 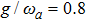 . With the increase of
. With the increase of 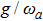 , there exists the excited photon or atom number and the average energy decreases. But the excited particle number almost has no change and the average energy is the lowest and almost keeps a straight line when
, there exists the excited photon or atom number and the average energy decreases. But the excited particle number almost has no change and the average energy is the lowest and almost keeps a straight line when  .
.
In Fig. 4 we plot the mean photon number γ
2 as a function of the collective atom-photon coupling strength g and the atom-atom interaction strength q. The green region (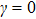 ) belongs to the NP and the color region (
) belongs to the NP and the color region (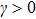 ) is the SP. The critical line of the two regions are gcq, which shifts toward the lower g direction when
) is the SP. The critical line of the two regions are gcq, which shifts toward the lower g direction when 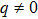 and the more moving to the left is seen when the q increases from 0 to 0.10.
and the more moving to the left is seen when the q increases from 0 to 0.10.
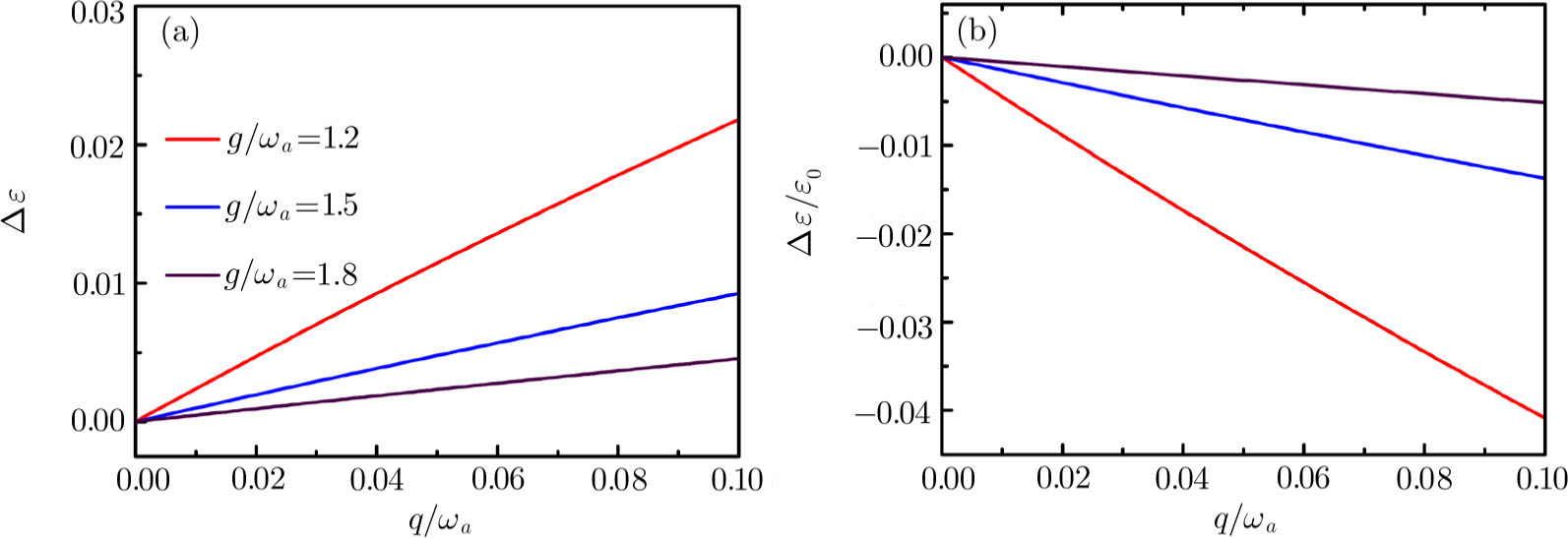
In order to compared to the effect of the atom-atom interaction strength q and the collective atom-photon coupling strength g on the average ground state energy, in the following we introduce the difference in the SP between the average ground state energy and the case of q = 0, i.e.,  . At the same time, the relative difference
. At the same time, the relative difference 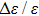 has been introduced. The conclusion has been plotted in Fig. 5. For the given collective atom-photon coupling strength g, the difference of
has been introduced. The conclusion has been plotted in Fig. 5. For the given collective atom-photon coupling strength g, the difference of  or
or 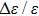 increases or decreases with the increased atom-atom interaction. While the difference is more obvious when
increases or decreases with the increased atom-atom interaction. While the difference is more obvious when 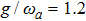 than the case of
than the case of  or
or 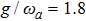 .
.
We give the results of  and
and 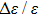 .
.
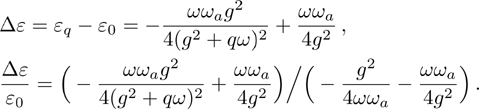
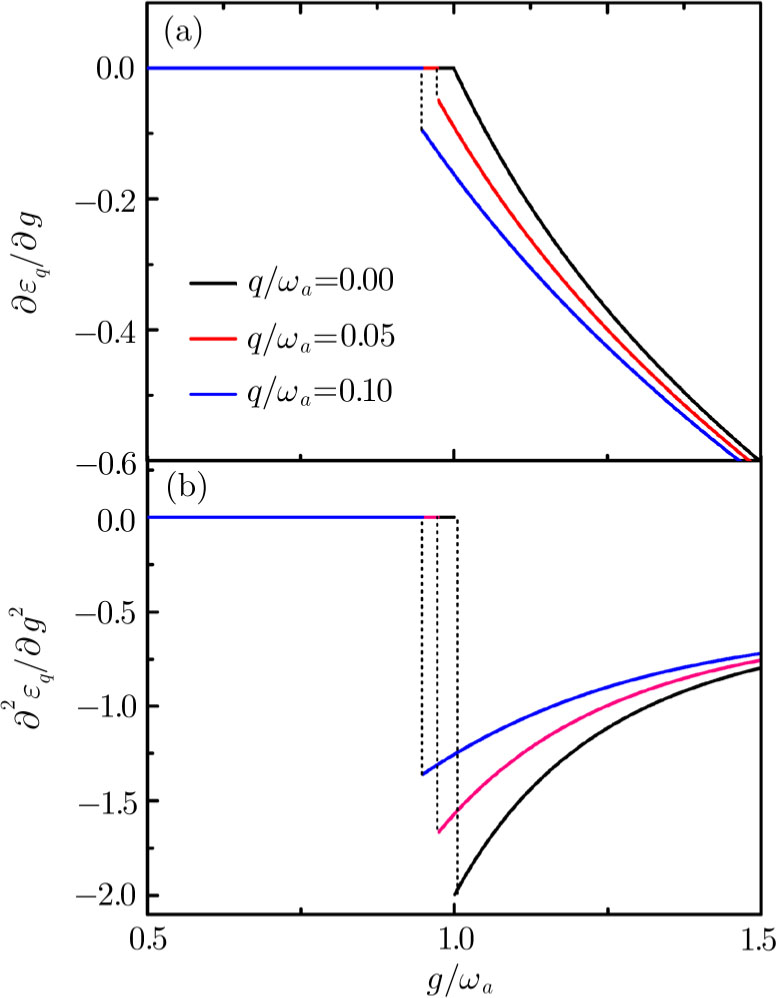
6 The First-Order Superradiant Phase TransitionsBased on the average ground-state energy Eq. (34), which is the function of the atom-field coupling constant g and the atom-atom interaction strength q, the first-order and second-order partial derivatives of the average ground-state energy are given

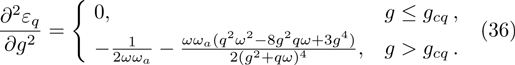
Based on Eqs. (35), (36) Fig. 6 and Fig. 7 give the first-order and second-order derivatives in different system’s parameters. In the absence of the atom-atom interaction, i.e., q = 0, the first-order derivative is continuous in the phase boundary of the NP and the SP, but the second-order derivative is discontinuous. So we come to the conclusion that the standard DM exists a second-order QPT from the NP to the SP in the critical phase transition point  . While the atom-atom interaction is existent, the extented DM belongs to the first-order quantum phase transition, for the first-order and second-order derivative are both discontinuous in the critical phase transition point gcq, which shifts to the left.
. While the atom-atom interaction is existent, the extented DM belongs to the first-order quantum phase transition, for the first-order and second-order derivative are both discontinuous in the critical phase transition point gcq, which shifts to the left.
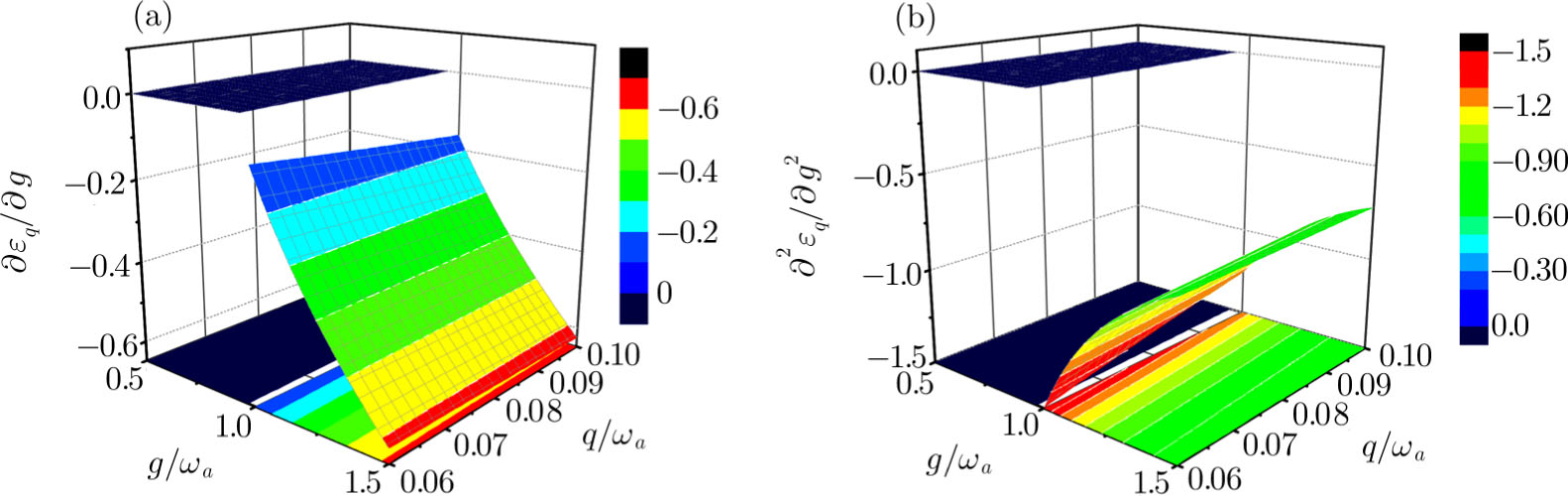
Figure 7 displays the three-dimensional curves about the first-order derivative  and the second-order derivative
and the second-order derivative  for the parameters
for the parameters 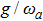 and
and  . They are discontinuous at the every critical phase transition point, which shifts to the left with the increasing q. They imply that the system undergoes a first-order QPT from the NP to the SP and the exclusive atom-atom interaction makes the phase transition point shift toward the lower atom-photon collective coupling strength.
. They are discontinuous at the every critical phase transition point, which shifts to the left with the increasing q. They imply that the system undergoes a first-order QPT from the NP to the SP and the exclusive atom-atom interaction makes the phase transition point shift toward the lower atom-photon collective coupling strength.
7 ConclusionIn summary, an interesting prediction of the extended DM is that it undergoes a first-order QPT between the NP and the SP. In order to detect this first-order transition, we plotted the mean photon number, the scaled mean atom population and the average ground-state energy for different atom-atom interaction and discovered the QPT point shifts to left for the increasing atom-atom interaction. By the discontinuous first-order and second-order derivative, we come to the conclusion that the atom-atom interaction induces a first-order phase transition, which is different from the second-order QPT of the standard DM. We believe the atom-atom interaction can also have a deep influence on the physical properties such as the entanglement and the geometric phase in quantum information process.