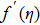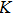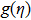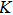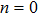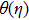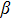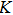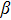† Corresponding author. E-mail:
This theoretical study investigates the microrotation effects on mixed convection flow induced by a stretching sheet. Casson fluid model along with microrotation is considered to model the governing flow problem. The system is assumed to undergo internal heating phenomenon. The governing physical problem is transformed into system of nonlinear ordinary differential equations using scaling group of transformations. These equations are solved numerically using Runge Kutta Fehlberg scheme coupled with shooting technique. Influence of sundry parameters for the case of strong and weak concentration of microelements on velocity, temperature, skin friction and local heat flux at the surface are computed and discussed. Lower skin friction and heat flux is observed for the case of weak concentration (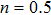

Fluids with microstructures are termed as micropolar fluids. These fluids comprise of rigid, randomly oriented particles submerged in a glutinous medium. Micropolar fluids find tremendous applications in blood, foodstuffs, polymers, liquid metal and alloys, plasma and drilling of oil and gas wells etc. Such type of fluid model contains non-symmetric stress tensors. Eringen[1–2] introduced the theoretical explanations of micropolar fluids and discovered the effects of micro motion of fluid elements. He proposed a logical and significant overview of the classical Navier–Stokes model, covering, both in theory and applications, many more phenomena than the classical one. Moreover his generalization was well-designed and not too complex. Airman et al.[3,4] presented a detailed review on application of fluids experiencing micro rotation at particle level. Khonsari and Brewe[5] examined the effects of viscous dissipation on lubrication characteristics of micropolar fluids. They reported that existence of microstructure, according to the micropolar theory, tends to enhance the load-carrying capacity and friction coefficient. Rotating micropolar fluid between parallel plates with heat transfer under the influence of transverse magnetic field has been investigated by Rashid et al.[6] They concluded that the micro rotation is an increasing function of coupling parameter, magnetic field and Reynolds number for strong concentration and it is a decreasing function of viscosity parameter. Nazar et al.[7] analyzed the stagnation point flow of a micropolar fluid over a stretching sheet. They carried out numerical investigation by employing Keller Box method. Non-Newtonian fluids have been an intense topic of research for the past few decades. Much focus had been given to the modeling and analysis of non-Newtonian fluids with rheological characteristics because of usage of various non-Newtonian fluids such as lubricants in industry. The non-linearity can manifest itself in a variety of ways in many fields, such as in food processing, drilling operations and bio-engineering. In this regard Ellahi et al.[8] presented numerical analysis of MHD steady non-Newtonian flows in presence of heat transfer and nonlinear slip effects. Similarly, Makinde et al.[9] analyzed unsteady flow of a reactive variable viscosity non-Newtonian fluid through a porous saturated medium with asymmetric convective boundary conditions and observe that there is a transient increase in both fluid velocity and temperature with an increase in the reaction strength, viscous heating and fluid viscosity parameter. Among the class of several other non-Newtonian fluid models, Casson fluid is one such model with yield stress characteristics. Casson fluid falls in the category of dilatant fluids. It is assumed that Casson fluid has an infinite viscosity at zero shear rates. If the applied shear stress is less than the yield stress then fluid behave like a solid and when shear stress applied is greater than yield stress fluid starts to move. Casson fluid model best fit to rheological data for numerous materials such as jelly, sauce, honey, soup and concentrated fruit juices, etc.[10] The presence of protein, fibrinogen and globulin in aqueous base plasma, red blood cells makes human blood an ideal example of Casson fluid. Number of researchers used Casson fluid to mathematically model and examine the blood flow under a low shear rate in narrow arteries. Shahzad et al.[11] studied effects of mass transfer on generalized non-Newtonian fluid. They analyzed the influence of chemical reaction and suction on Casson fluid in presence of magnetic field. Nadeem et al.[12] observed analytically flow of Casson nanofluid. Mustafa et al.[13] discussed unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Similarly Bhattacharya et al.[14] presented analytic solution for magneto hydrodynamic boundary layer flow of Casson fluid over a stretching/shrinking sheet with wall mass transfer. Heat transfer of viscous non-Newtonian fluids past a stretching sheet is a considerable problem in fluid dynamics. The problems arise in the field of engineering and metallurgy depends on hydrodynamic flow and heat transfer rate. In polymer technology, stretching plastic sheets are used in manufacturing products. In electrically conducting fluids, strips are used to control the cooling process. Chen[15] worked out laminar mixed convection of stretching sheet adjacent to vertical wall. Ali et al.[16] examined laminar mixed convection boundary layers induced by a linearly stretching permeable surface. Ishak et al.[17] inspected mixed convection boundary layers in the stagnation-point flow toward a stretching vertical sheet. The thermal effects in fluid flows may cause heat transfer effects in manufacturing processes. In these processes, thermal buoyancy force arises due to heating of a surface that may be in rest or moving continuously under some circumstances. Shateyi et al.[18] analyzed the effects of thermal radiation, hall currents, soret and dufour on MHD flow and heat and mass transfer in a micro polar fluid by mixed convection over stretching surfaces in porous media. Vajravelu et al.[19] studied the heat transfer in a viscous fluid over a stretching sheet with viscous dissipation and internal heat generation. Some more studies related to the current topic can be found in Refs. [20–31].
Most of researches have been carried out in micro polar fluids for characterizing the impact of magnetic field, heat transfer, mixed convection and viscous dissipation etc. To the best of our knowledge, micro polar fluids with rheological characteristics have not been discussed in past. Novelty of present study is to examine micro polar Casson fluid towards a stretching sheet influenced by internal heat generation. Recent research is a fresh contribution in this regard. Effects of sundry parameters on flow and heat transfer characteristics are examined and discussed in a physical manner.
Consider steady 2D flow of an incompressible micropolar Casson fluid towards a linear stretching convective sheet. Heat and mass transfer flow due to stretching of a heated or cooled surface of variable temperature 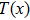
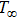
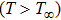

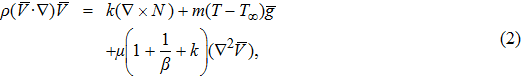
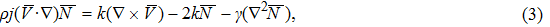
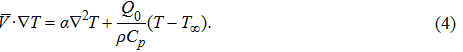

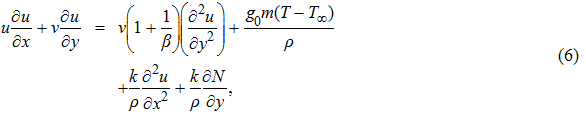

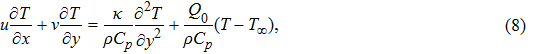
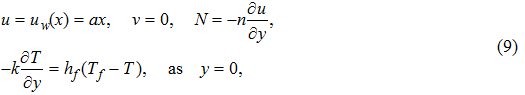
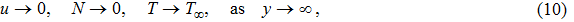
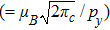
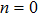
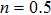
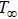
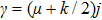
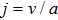
To convert above system of partial differential equations, we introduce following similarity transformations[32]

Equation (

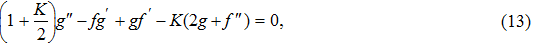




The physical quantities of interest are skin friction coefficient Cf and local Nusselt number Nux which are defined as
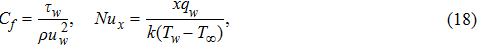
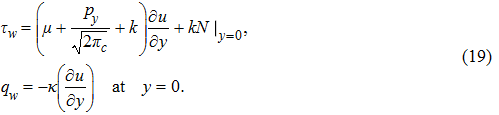

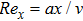
Shooting method along with Runge Kutta fifth order technique was incorporated to tackle the system of nonlinear differential equations. Thus, solution of coupled nonlinear governing boundary layer Eqs. (
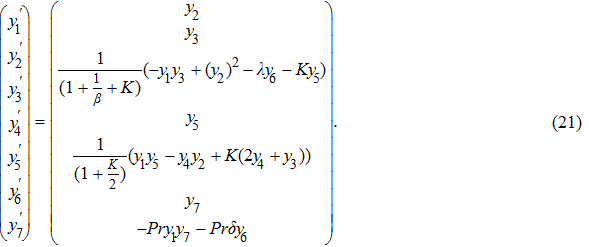
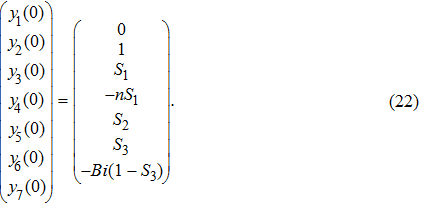
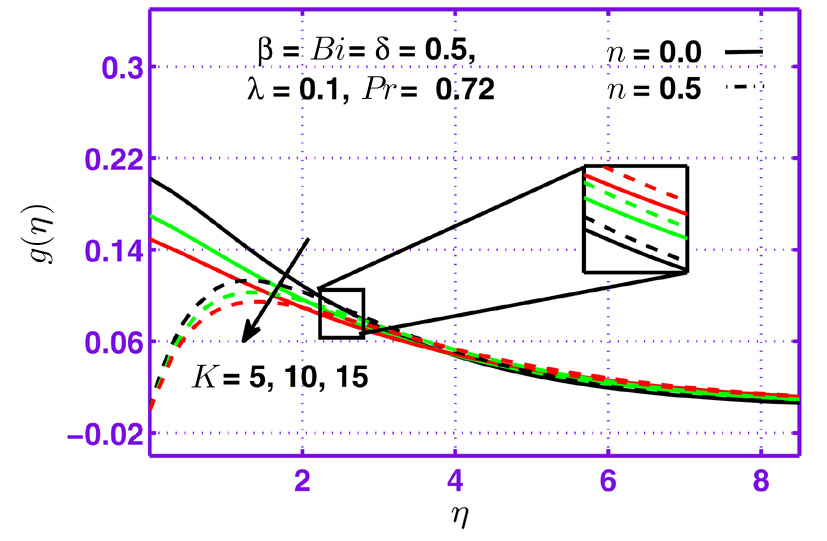
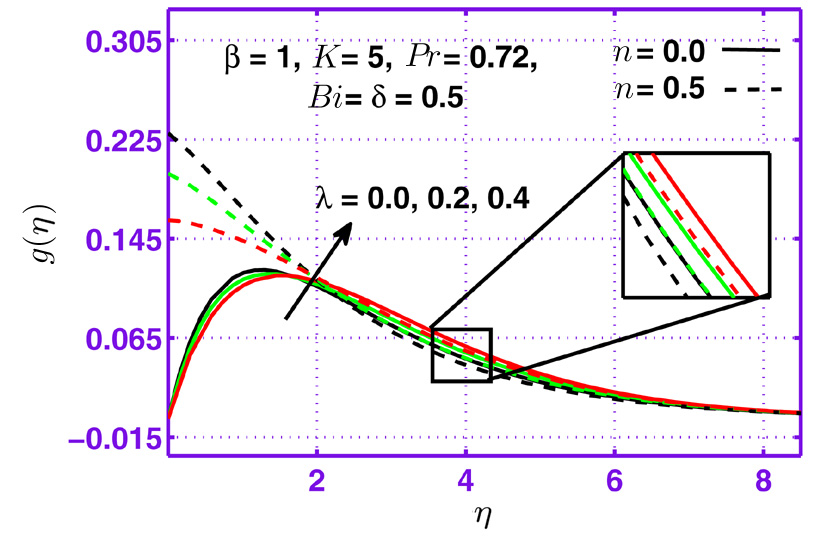
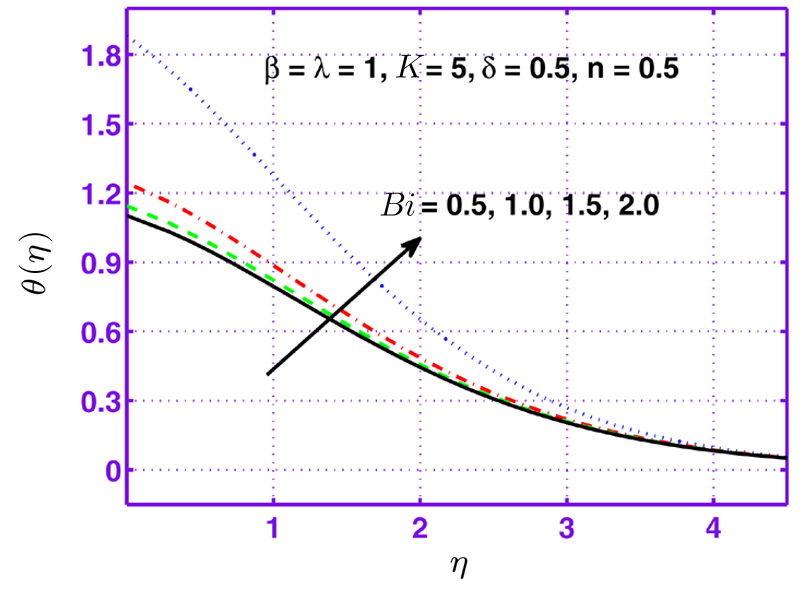
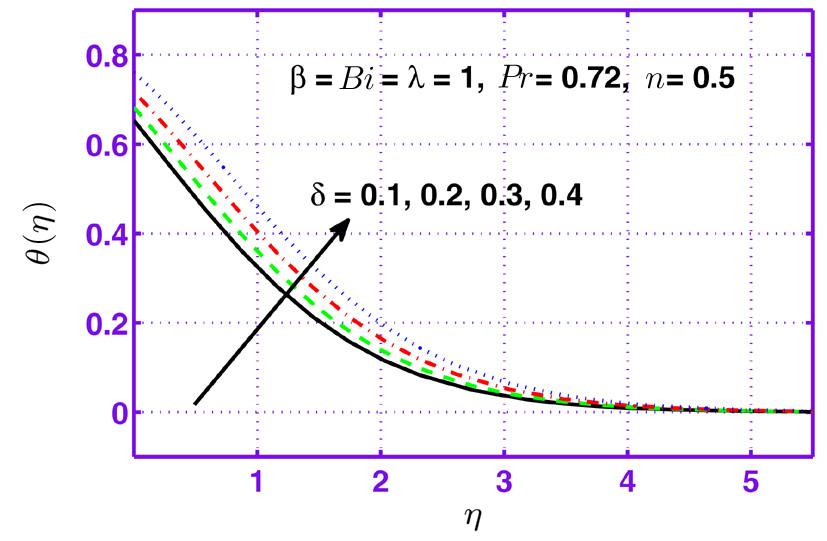
This section is dedicated to examine the influence of sundry parameters on velocity 

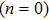
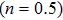

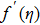

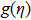
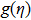


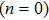
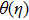
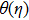

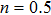
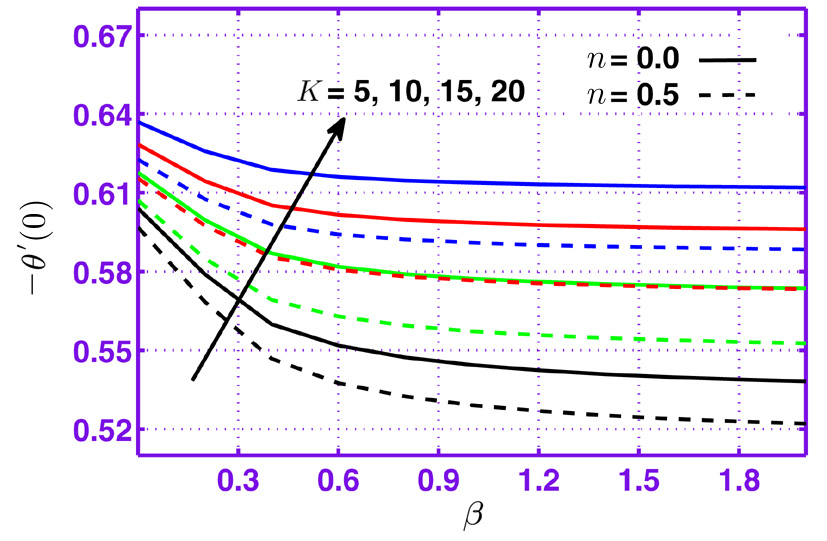
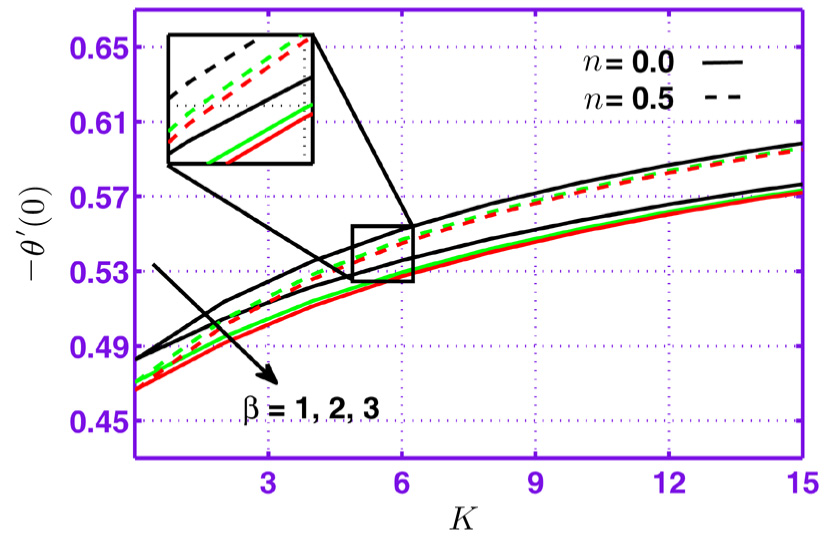
To investigate effects of parameters on skin friction coefficient 

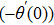
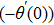
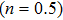
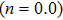
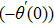
The aim of this study is to investigate microrotation effects on mixed convective flow of a Casson fluid induced by a stretching sheet. The governing physical problem is tackled numerically using Runge Kutta Fehlberg scheme coupled with shooting. The core outcomes of this study are: The velocity profile Microrotation profile Skin friction coefficient Higher skin friction coefficient


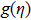


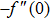
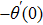
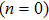
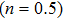
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |