† Corresponding author. E-mail:
Supported by the Algerian Ministry of Higher Education and Scientific Research under the CNEPRU project No. D01720140001
We determine explicitly the exact transcendental bound states energies equation for a one-dimensional harmonic oscillator perturbed by a single and a double point interactions via Green’s function techniques using both momentum and position space representations. The even and odd solutions of the problem are discussed. The corresponding limiting cases are recovered. For the harmonic oscillator with a point interaction in more than one dimension, divergent series appear. We use to remove this divergence an exponential regulator and we obtain a transcendental equation for the energy bound states. The results obtained here are consistent with other investigations using different methods.
In the past few decades, much attention has been paid to understanding and realization of one-dimensional quantum systems. The tremendous progress in nanotechnology has made it possible to obtain realizations of isolated one-dimensional systems such as quantum wires,[1] Josephson junction arrays,[2] edge states in quantum Hall systems,[3] and nanotubes[4] see also the book.[5] From a theoretical point of view, the one-dimensional character makes the problem simple enough so that some complete solutions of particular quantum mechanical models could be obtained using specific methods. In addition, one of the important motivating factors for the study of these simple models was the extraction of physical insight that would be useful for the study of their higher-dimensional counterparts.
Spectral properties of the Schrödinger equation for the one-dimensional harmonic oscillator with one Dirac delta function have been studied by several authors.[6–9] This simple model has been used to describe the quark physics at small distances, in particular, the toponium physics.[10] In the present paper, we will consider the bound state energy problem of the one-dimensional harmonic oscillator plus two attractive point interactions of equal strength, by considering both momentum space and position space representations. This model could be regarded as a possible one-dimensional counterpart of the three-dimensional hydrogen molecule ion subjected to a static magnetic field in which the coulomb interactions are replaced by the corresponding one of simple point interactions.[11–12] The content of this work might be useful since the molecules, even the simplest diatomic molecules and their ionization are much more difficult to treat theoretically.
As we know, the bound state problem for one-dimensional Hamiltonian that involves delta function potentials has an exact implicit solution whenever the eigenvalue problem without the delta function potentials can be solved exactly. In this context, we determine the exact transcendental energy bound state equation for the aforementioned one-dimensional harmonic oscillator perturbed by two attractive Dirac delta potentials, using Green’s function techniques which are widely recognized as a powerful mathematical tools suitable for obtaining solutions of complex interacting systems.[13]
Recently, the multidimensional quantum harmonic oscillator with point interactions problem has attracted great interest in connection to few body systems, especially in view of recent experiences in the field of ultra-cold atoms.[14–16] In these experiments neutral atoms are first cooled to extremely low temperatures (of the order nano-Kelvin) and then confined in an optical lattice formed by standing wave laser beams. Typically, the lattice sites that confine these atoms can be considered as harmonic oscillator potentials. The physical interaction between two ultra-cold atoms is replaced by a point interaction potentials to avoid the complications of a realistic atom-atom interaction. However, if we try to solve the problem of quantum harmonic oscillator with point interactions for more than one dimension, divergent sums appear and one needs a regularization scheme to extract a meaningful result for the energy bound states.[17] In this paper, we will use an exponential regulator to deal with this divergence, the idea of this technique is inspired from that used to remove divergence appeared when considering the Casimir effect.[18–19] The result obtained here is consistent with that obtained by Ref. [17] in which the authors have replaced the Dirac delta potential by another regularized form to avoid the divergence problem.
The further content of this paper will be as follows. In Sec.
Let us consider a particle of a mass m subjected to a harmonic oscillator potential of frequency ω and perturbed by a single point interaction represented by delta function potential. The system is described by the following Schrödinger equation
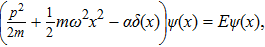
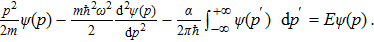
To transform Eq. (
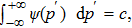
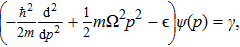
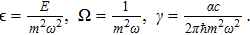
Let us recall that the eigenstates 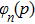
We consider now the Fourier transform between the position and momentum representations as
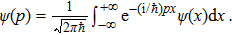
First, it is well known that the eigenstates of a nondegenerate even operator have definite parity; they are either even or odd. Then, since the Fourier transform preserves the parity of the wave function, ψ(p) should have a definite parity.[20] In addition, the delta function has no effect on odd states because in this case c = 0. Hence the solution to the previous equation can be found by expanding ψ(p) as
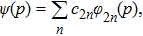
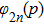
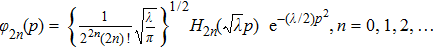
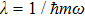
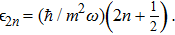
As the second member of the inhomogeneous equation (
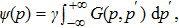
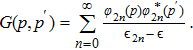
Inserting Eq. (
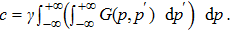
The Green’s function (
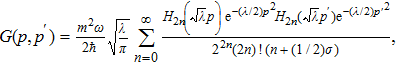
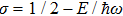
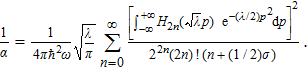
Then, by using the following formula[22]
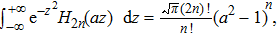
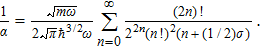
Noting that
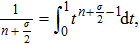
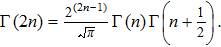
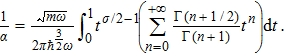
Then, with the help of the binomial formula
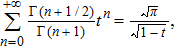
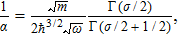
To end this section, let us recall some special cases. First, for α = 0, the right hand side of Eq. (
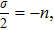
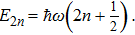
For ω = 0, one can use the asymptotic behavior of the gamma function described by the famous Stirling formula[22]
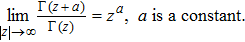
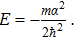
Let us now consider a system described by two attractive delta functions of strength −α < 0, separated by a distance 2a and subjected to a harmonic oscillator potential. The Hamiltonian is then expressed as
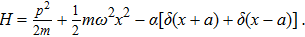
In the momentum representation, the Schrödinger equation corresponding to the Hamiltonian (
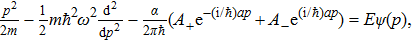
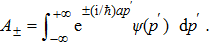
Thus Eq. (
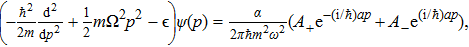
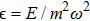
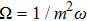
If ψ(p) is an even function, therefore, it can be written only in terms of even eigenstates
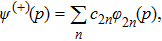
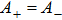
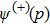
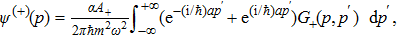
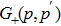
To obtain the energy eigenvalues, we insert Eq. (
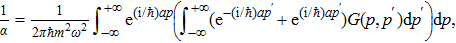
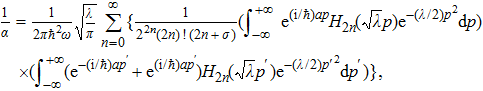
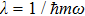
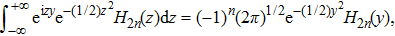
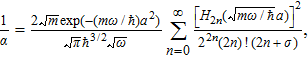
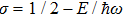
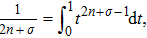
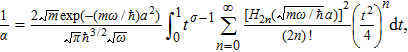
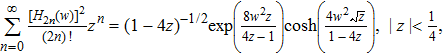
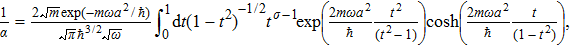
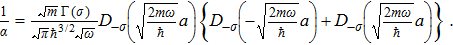
If ψ(p) is an odd function, then it can be expressed in terms of odd eigenstates
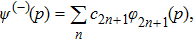
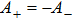
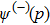
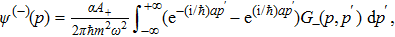
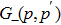
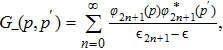
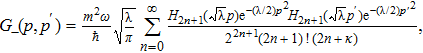
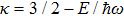
Now, inserting Eq. (
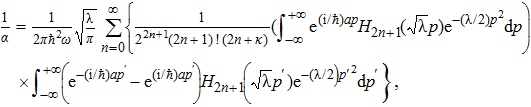
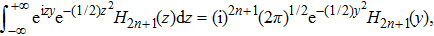
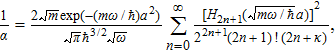
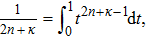
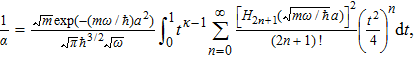
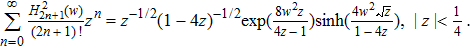
Equation (
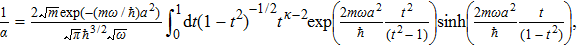
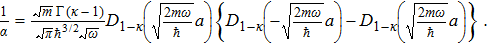
Equation (
As a check of the above results, let us consider some special cases.
First, we consider the 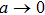
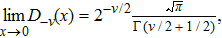
Thus, Eq. (
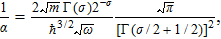
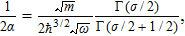
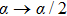
Now we consider the 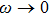
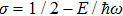
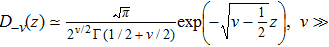
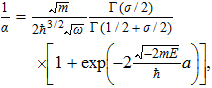
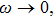
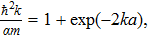
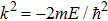
In addition, the 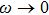
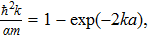
To enrich further the content of the current study, we consider in this section the system described by the Hamiltonian (
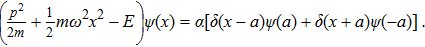
The Green’s function reads
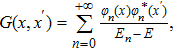
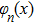
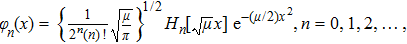
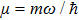
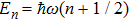
We can write the solution 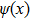
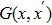
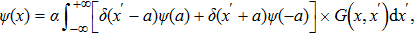
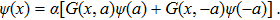
First, it is straightforward to see that the Green’s function satisfies the following two properties Since
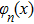
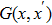
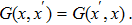
The Green function 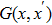
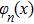
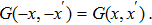
As mentioned above, the even solution is written as
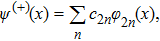
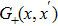
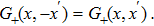
Therefore, for even solution, Eq. (
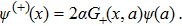
Now, taking the limit x = a, the energy eigenvalues are determined from the following equation
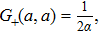
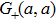
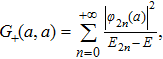
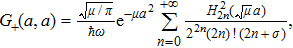
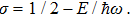
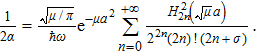
As one can see, the last expression is the same as Eq. (
The odd solution reads
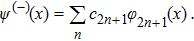
In addition to properties (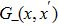
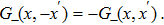
From Eq. (
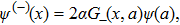
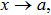
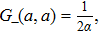
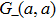
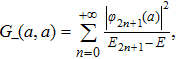
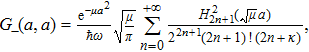
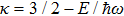
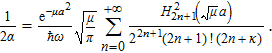
Again, the expression (
To end this section, let us mention that a solution to the transcendental equations (
As discussed in the introduction, a system formed by two confined ultra-cold atoms of mass μ in interaction is described by the following Hamiltonian
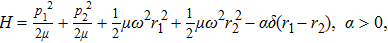
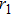
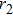
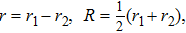
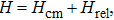
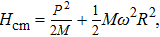
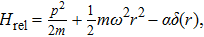
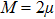
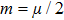
As the solution of the center of mass part is well known, we will focus our attention on the relative part which represents a harmonic oscillator perturbed by a point interaction. The Schrödinger equation corresponds to the Hamiltonian (
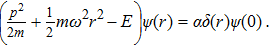
Following similar steps as the previous section, one arrives to the following condition for the bound states energies
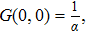
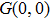
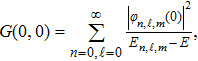
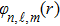
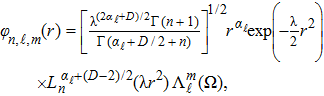
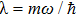
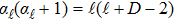
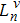
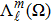
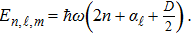
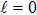
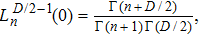
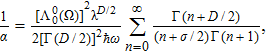
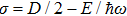
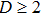
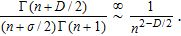
To remove this pathology, we need a regularization scheme. To this aim, we will introduce an exponential regulator where the general idea of this technique is inspired from that used for dealing with divergences appeared when considering the Casimir effect.[18–19] Thus, we rewrite the expression (
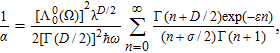
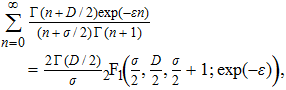
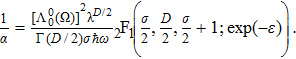
First, we note that for D = 1 and 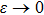
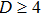
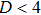
First, we consider the case D = 3. One can use the following relation[22] to leading order in ε
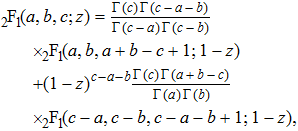
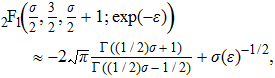
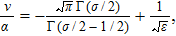
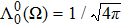
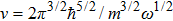
As the energy is a physical observable it should be independent of the extra parameter ε. The dependence on this parameter can be absorbed in a redefinition of the parameters of the theory
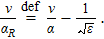
The constant 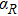
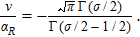
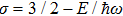
The expression (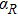
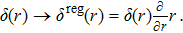
For the case D = 2, the expression (
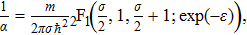
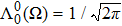
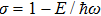
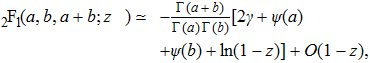
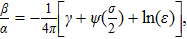
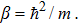
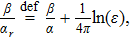
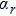
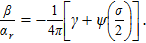
Finally, let us mention that when 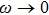
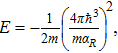
For D = 2, we use the fact that 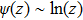
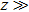
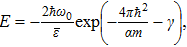
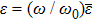
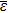
Equations (
In summary, we have used the momentum space representation to derive an exact transcendental bound state energy equation for one-dimensional harmonic oscillator perturbed by a single and double attractive delta functions via Green’s function techniques. We have considered the even and odd solutions of the system and their corresponding limiting cases. We have also considered the problem in the position space and we have shown that we obtain the same transcendental equations as expected.
For a system described by a harmonic oscillator plus delta function potential in two or more dimensions, divergent series appear. We have introduced an exponential regulator to deal with this divergence and we have succeeded to give the transcendental equation for the energies bound states for the problem. The result of this paper essentially agrees with Ref. [17] for D = 3 in which the authors have replaced the Dirac delta potential by a regularized form.
In closing let us also mention that the problem of the two- and three-dimensional harmonic oscillator potential plus δ-function systems is considered in [34] by incorporating a different renormalization scheme and the self-adjoint extension method.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |

